Следы прямой
Следами прямой называют точки её пересечения с плоскостями проекций. В зависимости от того, какую плоскость проекций пересекает прямая в данной точке, различают горизонтальный, фронтальный и профильный след.
Прямые, занимающие общее положение, пересекают три плоскости проекций, линии уровня – две, а проецирующие прямые – одну.
Алгоритм построения следов на эпюре
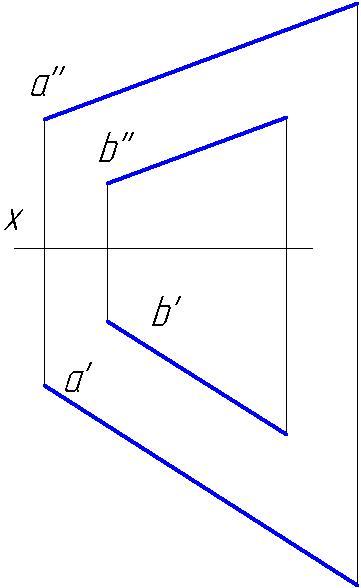
Найдем следы прямой a, заданной отрезком AB. Как видно на рисунке ниже, AB занимает общее положение, поэтому для решения задачи необходимо построить проекции трех точек.
- Горизонтальный след Ha. Продлим фронтальную проекцию прямой a до пересечения с осью X в точке Ha». Полученная точка – фронтальная проекция горизонтального следа. По линии связи на a’ найдем точку Ha‘. Она является горизонтальной проекцией горизонтального следа и совпадает с т. Ha.
- Фронтальный след Fa. Продлим горизонтальную проекцию a’ до пересечения с осью X в точке Fa‘. Полученная точка – горизонтальная проекция фронтального следа*. По линии связи на прямой a» найдем точку Fa«. Она является фронтальной проекцией фронтального следа и совпадает с т. Fa.
- Профильный след Wa строится аналогично. Для нахождения двух его проекций, Wa» и Wa‘, необходимо продлить a» и a’ до пересечения с осью Z.
На следующем рисунке показано построение следов горизонтали b, заданной отрезком CD. Как и другие линии уровня, горизонталь пересекает только две плоскости проекций.
Несмотря на то, что рассмотренный нами алгоритм универсален, лучше понять смысл геометрических построений позволяет наглядное изображение прямой в пространстве.
Примечание
* Фронтальный след прямой по определению является точкой, которая лежит во фронтальной плоскости. Её координата Y равна нулю. Из этого следует, что горизонтальная проекция F’ фронтального следа находится на оси X.
Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
1.1. Условие задания
Построить следы плоскости, заданной ∆BCD, и определить расстояние от точки А до заданной плоскости методом прямоугольного треугольника (координаты точек А, В, С и D см. в Таблице 1 раздела Задания);
1.2. Пример выполнения задания № 1
Первое задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам трех точек B, C, D построить горизонтальную и фронтальную проекции плоскости, заданной ∆BCD;
2. Следы прямой, следы плоскости, свойства принадлежности прямой плоскости: построить следы плоскости, заданной ∆BCD;
3. Плоскости общего и частного положения, пересечение прямой и плоскости, перпендикулярность прямой и плоскости, пересечение плоскостей, метод прямоугольного треугольника: определить расстояние от точки А до плоскости ∆BCD.
1.2.1. По известным координатам трех точек B, C, D построим горизонтальную и фронтальную проекции плоскости, заданной ∆BCD (Рисунок 1.1), для чего необходимо построить горизонтальные и фронтальные проекции вершин ∆BCD, а затем одноименные проекции вершин соединить.
Известно, что следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с плоскостью проекций.
У плоскости общего положения 3 следа: горизонтальный, фронтальный и профильный.
Для того чтобы построить следы плоскости, достаточно построить следы (горизонтальный и фронтальный) любых двух прямых, лежащих в этой плоскости, и соединить их между собой. Таким образом, след плоскости (горизонтальный или фронтальный) будет однозначно определен, поскольку через две точки на плоскости (в данном случае этими точками будут следы прямых) можно провести прямую, и при том, только одну.
Основанием для такого построения служит свойство принадлежности прямой плоскости: если прямая принадлежит заданной плоскости, то ее следы лежат на одноименных следах этой плоскости.
Следом прямой называется точка пересечения этой прямой с плоскостью проекций.
Горизонтальный след прямой лежит в горизонтальной плоскости проекций, фронтальный – во фронтальной плоскости проекций.
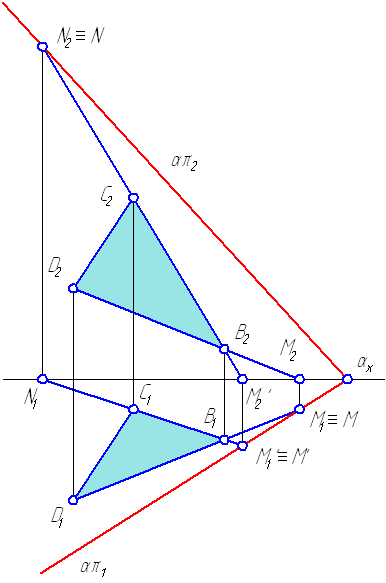
Рассмотрим построение горизонтального следа прямой DB, для чего необходимо:
1. Продолжить фронтальную проекцию прямой DB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
2. Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой DB или ее продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа (Рисунок 1.1), которая совпадает с самим следом М.
Аналогично выполняется построение горизонтального следа отрезка СВ прямой: точка М’.
Чтобы построить фронтальный след отрезка CB прямой, необходимо:
1. Продолжить горизонтальную проекцию прямой CB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
2. Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой CB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Соединив точки M′1 и M1 отрезком прямой, получим горизонтальный след плоскости απ1. Точка αx пересечения απ1 с осью X называется точкой схода следов. Для построения фронтального следа плоскости απ2 необходимо соединить фронтальный след N2 с точкой схода следов αx
Рисунок 1.1 — Построение следов плоскости
Алгоритм решения этой задачи может быть представлен следующим образом:
- (D2B2 ∩ OX) = M2;
- (MM1 ∩ D1B1) = M1 = M;
- (C2B2 ∩ OX) = M′2;
- (M′2M′1 ∩ C1B1) = M′1 = M′;
- (CВ ∩ π2) = N2= N;
- (MM′) ≡ απ1;
- (αxN) ≡ απ2.
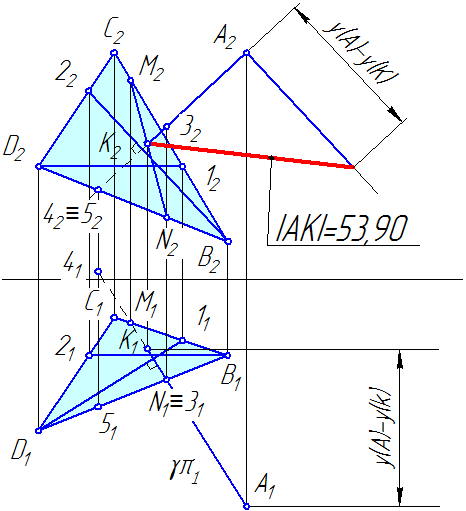
1.2.2. Для решения второй части первого задания необходимо знать, что:
- расстояние от точки А до плоскости ∆BCD определяется длиной перпендикуляра, восстановленного из этой точки на плоскость;
- любая прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- на эпюре проекции прямой, перпендикулярной плоскости, перпендикулярны наклонным проекциям горизонтали и фронтали этой плоскости или одноименным следам плоскости (рис. 1.2) (см. в лекциях Теорему о перпендикуляре к плоскости).
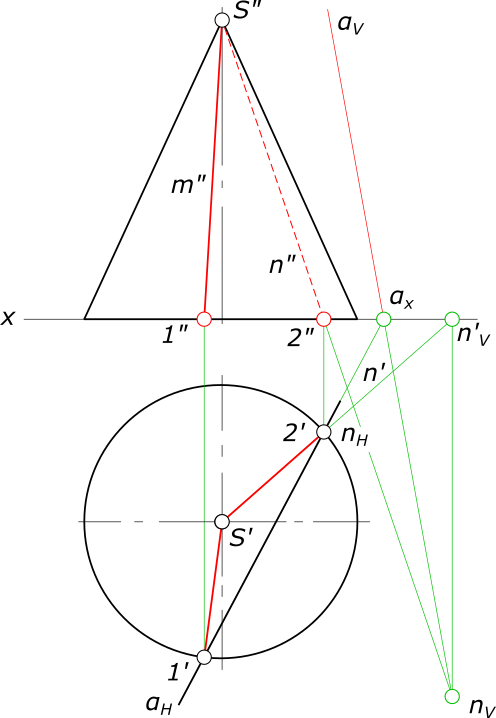
Чтобы найти основание перпендикуляра, необходимо решить задачу на пересечение прямой (в данной задаче такой прямой является перпендикуляр к плоскости) с плоскостью:
1. Заключить перпендикуляр во вспомогательную плоскость, в качестве которой следует взять плоскость частного положения (горизонтально-проецирующую или фронтально-проецирующую, в примере в качестве вспомогательной плоскости взята горизонтально-проецирующая γ, то есть перпендикулярная к π1, ее горизонтальный след γ1 совпадает с горизонтальной проекцией перпендикуляра);
2. Найти линию пересечения заданной плоскости ∆BCD со вспомогательной γ (MN на рис. 1.2);
3. Найти точку пересечения линии пересечения плоскостей MN с перпендикуляром (точка К на рис. 1.2).
4. Для определения истинной величины расстояния от точки А до заданной плоскости ∆BCD следует воспользоваться методом прямоугольного треугольника: истинная величина отрезка есть гипотенуза прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность расстояний от его концов до плоскости проекций, в которой ведётся построение.
5. Определите видимость участков перпендикуляра методом конкурирующих точек. На примере — точки N и 3 для определения видимости на π1, точки 4, 5 — для определения видимости на π2.
Рисунок 1.2 — Построение перпендикуляра к плоскости
Рисунок 1.3 — Пример оформления контрольного задания №1
Видеопример выполнения задания №1
1.3. Варианты задания 1
| Вариант | Координаты (x, y, z) точек | |||
|---|---|---|---|---|
| А | В | С | D | |
| 1 | 15; 55; 50 | 10; 35; 5 | 20; 10; 30 | 70; 50; 40 |
| 2 | 80; 65; 50 | 50; 10; 55 | 10; 50; 25 | 75; 25; 0 |
| 3 | 95; 45; 60 | 130; 40; 50 | 40; 5; 25 | 80; 30; 5 |
| 4 | 115; 10; 0 | 130; 40; 40 | 40; 5; 25 | 80; 30; 5 |
| 5 | 55; 5; 60 | 85; 45; 60 | 100; 5; 30 | 50; 25; 10 |
| 6 | 55; 5; 60 | 70; 40; 20 | 30; 30; 35 | 30; 10; 10 |
| 7 | 60; 10; 45 | 80; 45; 5 | 35; 0; 15 | 10; 0; 45 |
| 8 | 5; 0; 0 | 35; 0; 25 | 20; 0; 55 | 40; 40; 0 |
| 9 | 50; 5; 45 | 65; 30; 10 | 30; 25; 55 | 20; 0; 20 |
| 10 | 60; 50; 35 | 40; 30; 0 | 30; 15; 30 | 80; 5; 20 |
| 11 | 65; 35; 15 | 50; 0; 30 | 20; 25; 25 | 5; 0; 10 |
| 12 | 75; 65; 50 | 45; 10; 35 | 60; 20; 10 | 10; 65; 0 |
| 13 | 95; 0; 15 | 85; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 14 | 45; 40; 40 | 80; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 15 | 80; 20; 30 | 55; 30; 60 | 15; 10; 20 | 70; 65; 30 |
| 16 | 75; 35; 35 | 55; 30; 60 | 25; 10; 20 | 70; 65; 30 |
| 17 | 75; 65; 50 | 45; 5; 55 | 5; 45; 10 | 70; 20; 0 |
| 18 | 65; 15; 20 | 40; 5; 60 | 0; 5; 25 | 60; 60; 20 |
| 19 | 70; 20; 10 | 45; 15; 60 | 5; 10; 20 | 60; 65; 10 |
| 20 | 20; 50; 45 | 10; 20; 10 | 55; 50; 10 | 80; 0; 60 |
| 21 | 0; 5; 50 | 50; 50; 40 | 5; 55; 10 | 45; 5; 0 |
| 22 | 55; 50; 65 | 45; 55; 5 | 0; 10; 45 | 70; 0; 40 |
| 23 | 65; 5; 15 | 40; 60; 10 | 0; 20; 5 | 60; 20; 60 |
| 24 | 50; 20; 45 | 45; 60; 30 | 5; 20; 10 | 60; 30; 5 |
| 25 | 55; 15; 40 | 40; 50; 25 | 5; 15; 10 | 50; 40; 10 |
| 26 | 15; 45; 40 | 10; 25; 5 | 20; 10; 30 | 65; 40; 35 |
| 27 | 70; 30; 30 | 55; 30; 60 | 20; 5; 15 | 65; 60; 25 |
| 28 | 90; 0; 15 | 80; 45; 10 | 10; 10; 10 | 50; 10; 45 |
| 29 | 110; 10; 0 | 120; 35; 30 | 35; 5; 20 | 70; 20; 5 |
| 30 | 45; 40; 40 | 80; 45; 10 | 10; 10; 10 | 55; 10; 40 |
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
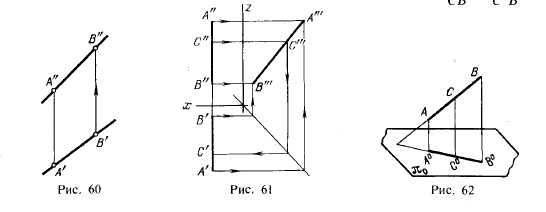
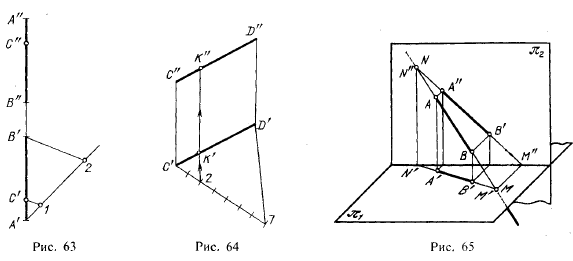
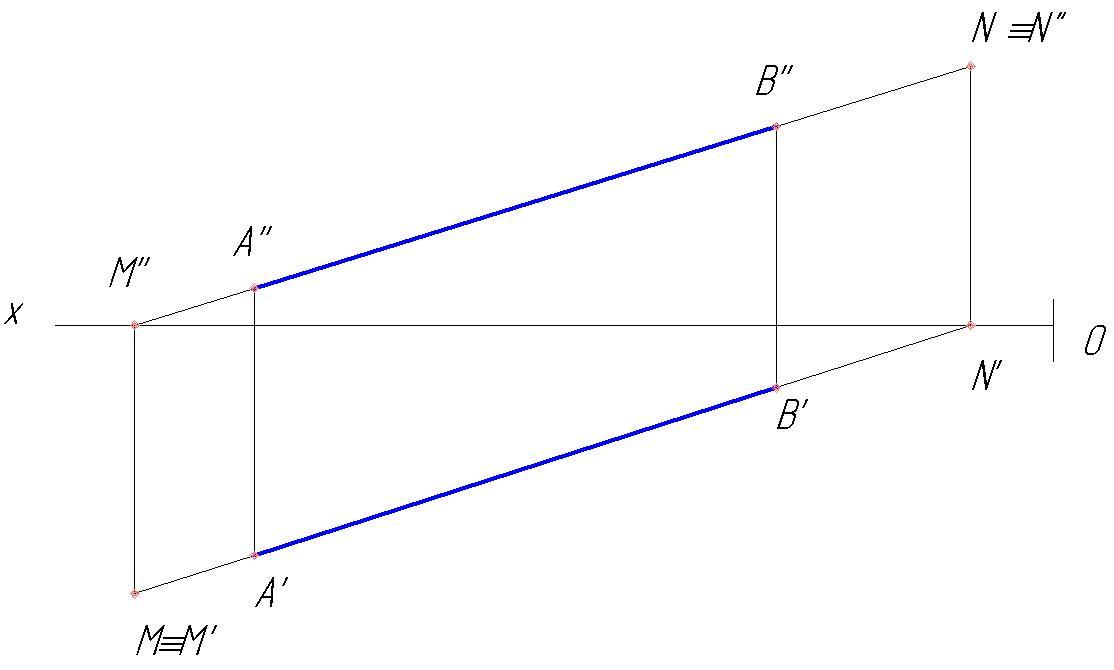
На рис. 60 дан чертеж некоторой прямой общего положения, проходящей через точку А. Если известно, что точка В принадлежит этой прямой и что горизонтальная проекция точки В находится в точке В’, то фронтальная проекция В» определяется так, как показано на рис. 60.
На рис. 61 показано построение точки на профильной прямой. Положим, что задана проекция С» этой точки; надо найти ее горизонтальную проекцию. Построение выполнено при помощи профильной проекции А’”В’” отрезка АВ, взятого на профильной прямой. Ход построения показан стрелками. Сначала определена проекция С'», а по ней — искомая проекция С’.
Одним из свойств параллельного проецирования является то, что отношение
отрезков прямой линии равно отношению их проекций (рис. 62): AC/CB= A°C°/C°B°, так
как прямые АА°, СС° и ВВ° параллельны между собой. Аналогично, отношение отрезков на проекции прямой линии равно отношению отрезков на этой прямой. Если бы точка делила пополам отрезок прямой, то проекция этой точки также делила бы проекцию отрезка пополам, и наоборот.
Из сказанного следует, что на рис. 61 деление проекций А»В» и А’В’ точками С» и С’ соответствует делению в пространстве отрезка АВ точкой С в том же отношении. Этим можно воспользоваться для более простого построения точки на профильной прямой. Если (как и на рис. 61) на проекции А»В» (рис. 63) задана проекция С», то, очевидно, надо разделить А’В’ в том же отношении, в каком точка С» делит проекцию А»В». Проведя из точки А’ некоторую вспомогательную прямую, откладываем на ней А’1 = А»С» и 1—2 = ѻ». Проводим прямую В’2 и параллельно ей через точку 1 прямую до пересечения с А’В’ в точке С’. Эта точка представляет собой искомую горизонтальную проекцию точки С, принадлежащей отрезку АВ.
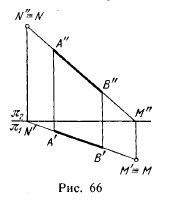
На рис. 64 дан пример деления отрезка прямой линии в некотором заданном отношении.
Отрезок CD разделен в отношении 2:5. Из точки С’ проведена вспомогательная прямая, на которой отложено семь (2 + 5) отрезков произвольной длины, но равных между собой. Проведя отрезок D’7 и параллельно ему через точку 2 прямую, получаем точку К’, причем С’К’: K’D’ = 2: 5; затем находим К». Точка К делит отрезок CD в отношении 2:5.
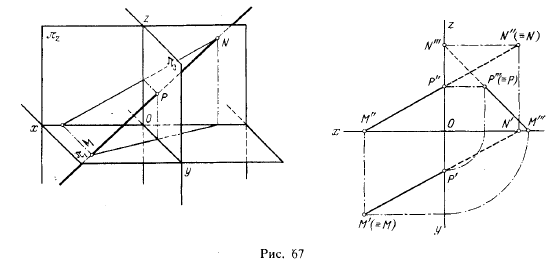
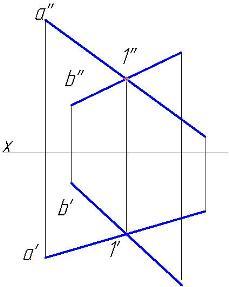
На рис. 65 показаны точки М и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Эти точки называются следами: точка М — горизонтальный след прямой, точка N — ее фронтальный след.
Горизонтальная проекция горизонтального следа (точка М’) совпадает с самим следом, а фронтальная проекция этого следа М» лежит на оси проекций. Фронтальная проекция фронтального следа N» совпадает с точкой N, а горизонтальная проекция N’ лежит на той же оси проекций.
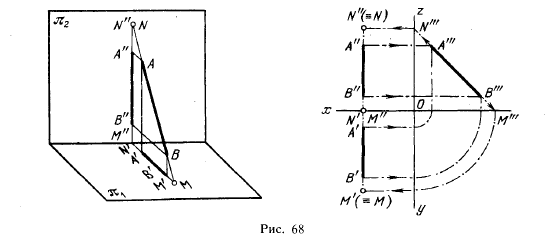
Следовательно, чтобы найти горизонтальный след, надо (рис. 66) продолжить фронтальную проекцию А»В» до пересечения с осью π2/π1 и через точку М» (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси π2/π1 до пересечения с продолжением горизонтальной проекции А’В’. Точка М’ — горизонтальная проекция горизонтального следа; она совпадает с самим следом (≡ знак совпадения).
Для нахождения фронтального следа продолжаем горизонтальную проекцию А’В’ до пересечения с π2/π1 через точку N’ (горизонтальную проекцию фронтального следа) проводим перпендикуляр до пересечения с продолжением фронтальной проекции А»В». Точка N» — фронтальная проекция фронтального следа; она совпадает с самим следом.
По положению точек М и N можно судить, к каким четвертям пространства отнесена данная прямая. На рис. 65 прямая АВ проходит через IV, I и II четверти.
Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.
На рис. 67 прямая пересекает не только пл.π1 и π2, но и пл. π3. Точка Р — профильный след прямой, т. е. след на профильной плоскости проекций. Этот след совпадает с его собственной проекцией на пл. π3, а фронтальная и горизонтальная проекции его лежат соотвегственно на осях z и у.
В данном случае прямая проходит за точкой Р через пятый октант и, встречая далее пл. π2, уходит в шестой октант; прямая из первого октанта выходит в четвертый октант 1).
Соответствующий чертеж дан на рис. 67 справа. Прямая показана в первом октанте — проекции М’Р’. М»Р» п М»‘Р»‘ и в пятом октанте — проекции P’N’, P»N» и P»‘N»‘.
Если плоскости проекций принять за плоскости координат, то у горизонтального следа прямой координата z = 0, у фронтального следа у = 0, у профильного следа х = 0.
Построение следов профильной прямой (рис. 68) может быть выполнено следующим способом (рис. 68, справа).
1) Условимся показывать на чертежах сплошными линиями те проекции, которые соответствуют положению ^отрезка в первой четверти или в первом октанте.
Строим профильную проекцию (А»‘В»‘), определяем положение профильных проекций горизонтального следа (М'») и фронтального следа (N'») и затем находим положение остальных проекций этих следов (последовательность построения на чертеже показана стрелками).
ВОПРОСЫ К §§ 10-12
- При каком положении относительно плоскостей проекций прямая называется прямой общего положения?
- Как доказывается, что чертеж, содержащий две связанные между собой проекции в виде отрезков прямой линии, выражает именно отрезок прямой линии?
- Как выражается соотношение между проекцией отрезка прямой и самим отрезком?
- Как расположена прямая в системе π1,π2, π3, если все три проекции отрезка этой прямой равны между собой?
- Как построить профильную проекцию отрезка прямой общего положения по данным фронтальной и горизонтальной проекциям?
- Как выполнить построение по вопросу 5 на чертеже без осей проекций?
- Какие положения прямой линии в системе π1,π2, π3 считаются «особыми» (иначе — «частными»)?
- Как располагается фронтальная проекция отрезка прямой линии, если его горизонтальная проекция равна самому отрезку?
- Как располагается горизонтальная проекция отрезка прямой линии, если его фронтальная проекция равна самому отрезку?
- Какое свойство параллельного проецирования касается отношения отрезков прямой линии?
- Как разделить на чертеже отрезок прямой линии в заданном отношении?
- Что называется следом прямой линии на плоскости проекций?
- Какая координата равна нулю: а) для фронтального следа прямой, б) для горизонтального следа прямой?
- Где располагается горизонтальная проекция фронтального следа прямой линии?
- Где располагается фронтальная проекция горизонтального следа прямой линии?
- Может ли быть случай, когда прямая линия в системе π1,π2, π3 имеет следы на каждой к: этих плоскостей, сливающиеся в одну точку?
Следы прямой
Следом
прямой называют точку пересечения
прямой с плоскостью проекций. Прямая
общего положения пересекается со всеми
тремя плоскостями проекций и имеет три
следа. Прямая, параллельная одной
плоскости проекций, имеет два следа.
Прямая, параллельная двум плоскостям
проекций (проецирующая), имеет один
след. М
— горизонтальный след, N
–фронтальный след. Там, где отрезок АВ
пересекается с горизонтальной плоскостью
проекций, получаем горизонтальный след
М.
Фронтальный след N
получаем
при пересечении отрезка АВ
с фронтальной плоскостью проекции.
Профильный след рассматривать в задачах
не будем (рис. 29).
Рис.29
След
прямой
— это точка, лежащая на плоскости проекций
и самой прямой одновременно. Если точка
лежит на плоскости, то одна ее проекция
совпадает с самой точкой, а вторая
обязательно лежит на оси х.
Для
построения следов прямой АВ
на эпюре поступают следующим образом:
продолжают А»В»
до пересечения с осью х
и отмечают фронтальную проекцию М»,
из М»
восстанавливают перпендикуляр до
пересечения с А’В’
или ее продолжением. Получаем горизонтальный
след М’
и сам след М.
При
продолжении А’В’
до пересечения с осью х
получаем горизонтальную проекцию N’
фронтального следа. Из N’
восстанавливаем ┴
до пересечения с А»В»
или ее продолжением для получения
фронтального следа N».
N»
совпадает с фронтальным следом N
(рис.30). В наших примерах мы рассматриваем
только горизонтальные и фронтальные
следы прямых.
Два
следа прямой вполне определяют положение
прямой в пространстве. По следам прямой
можно определить через какие четверти
пространства она проходит, если отрезок
прямой продолжить в обе стороны. До
следа N
прямая проходит через I четверть, между
следами М
и N
— II четверть, за следом М
— III четверть. Можно записать: прямая,
заданная отрезком АВ,
проходит через I-II-III
четверти (рис.31)
Рис.31
Взаимное положение прямых
Две
прямые могут быть: пересекающимися,
параллельными, скрещивающимися.
Две
пересекающиеся прямые
имеют общую точку. На эпюре, при пересечении
одноименных проекций, есть общая точка
(рис.32).
У
параллельных
прямых
а
и b
одноименные проекции параллельны между
собой (рис.33).
Рис.32
Скрещивающиеся
прямые
не имеют общей точки. На эпюре точки
пересечения их одноименных проекций
не лежат на одной линии проекционной
связи (рис.34).

Две
точки скрещивающихся прямых, лежащие
на одном перпендикуляре к плоскостям
проекций, называются конкурирующими.
Конкурирующими точками в нашем примере
являются 1, 2, 3, 4. Точки 1 и 3 принадлежат
прямой а,
а 2, 4 — прямой b.
Точка 2 находится дальше от плоскости
π2.
На фронтальной проекции l» не увидим —
она закрыта проекцией 2″. На горизонтальной
проекции не будет видна проекция 3′, она
ближе к плоскости π1
и закрывается проекцией 4″. Определение
взаимного положения конкурирующих
точек необходимо для установления
видимости элементов изображаемого
объекта.
Плоскость Способы задания плоскости
Плоскость
на эпюре можно задавать:
1. тремя
точками, не лежащими на одной прямой;
2. прямой
и точкой, не лежащей не прямой;
3. плоской
фигурой;
4. двумя
параллельными прямыми;
5. двумя
пересекающимися прямыми;
6. следами
(рис. 35).
Следы
плоскости
Соседние файлы в папке Kompyuternaya_grafika
- #
- #
15.03.20153.99 Mб12Геометрическое черчение учебно-методическое пособие.wbk
- #
Построение следов плоскости
Построение следов плоскости бывает необходимо, когда плоскость задана прямыми, точкой и прямой и тремя точками.
Построение следов плоскости производят из условия: если прямая общего положения лежит в плоскости, то ее следы лежат на одноименных следах этой плоскости.
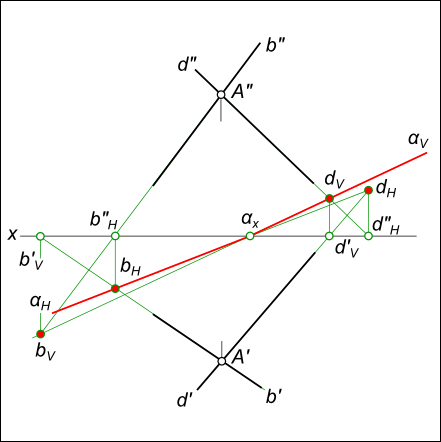
Построение следов плоскости α, заданной двумя пересекающимися прямыми
Построение следов плоскости
выполняют исходя из того что следы плоскости — это пересекающиеся прямые. Для проведения каждого следа на эпюре необходимы две точки:
— для горизонтального следа αH найдены bH и dH, горизонтальные следы прямых b и d соответственно;
— для фронтального следа αV найдены dV и αx, фронтальный след прямой d и точка схода следов соответственно.
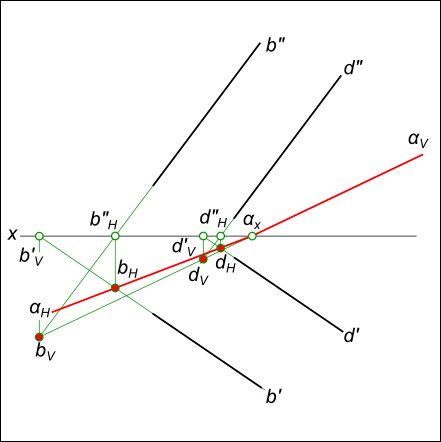
Построение следов плоскости α, заданной двумя параллельными прямыми
Построение следов плоскости
Для проведения каждого следа на эпюре необходимы две точки:
— для горизонтального следа αH найдены bH и dH, горизонтальные следы прямых b и d соответственно;
— для фронтального следа αV найдены bV и αx, фронтальный след прямой d и точка схода следов соответственно.
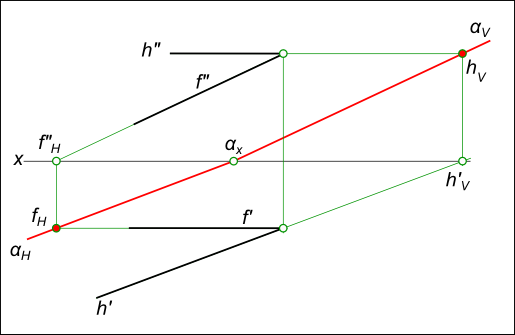
Построение следов плоскости α, заданной пересекающимися горизонталью и фронталью
Построение следов плоскости
Для проведения каждого следа на эпюре необходима одна точка:
— для горизонтального следа αH найдены fH ;
— для фронтального следа αV могут быть использованы hV или αx, фронтальный след прямой h или точка схода следов соответственно.
Если требуется выполнить построение следов плоскости, заданной тремя точками, тогда следует соединить одноименные проекции точек прямыми линиями, которые или пересекаются или параллельны между собой . Дальнейший ход решения показан в выше изложенных примерах.
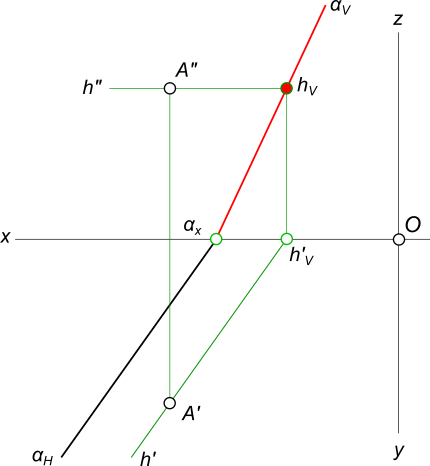
Построение следов плоскости заданной одним из следов и точкой
Построение следов плоскости
Через точку A проводим горизонталь h плоскости и находим ее след hV.
Проводим фронтальный след плоскости α через след прямой hV и точку схода следов αx.
или
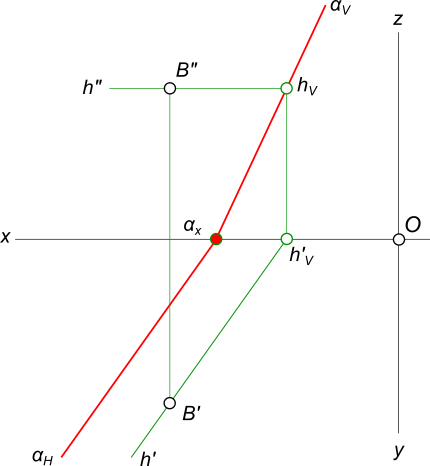
Построение следов плоскости
Построение следов плоскости бывает необходимо, из условия принадлежности точки или прямой плоскости.
Построение следов плоскости
Через точку B проводим произвольную прямую h — горизонталь плоскости и находим ее след hV.
Проводим фронтальный след αV через след hV произвольного направления. Проводим горизонтальный след αH через точку схода следов αx.
+