Это относится к метрикам ПО
Метрики размера программы — оценки по номинальной шкале (согласно ГОСТ Р ИСО/МЭК 27004-2011 «Информационная технология. Методы и средства обеспечения безопасности. Менеджмент информационной безопасности. Измерения» шкала, которая классифицирует программы на типы по признаку наличия или отсутствия некоторой характеристики без учета градаций), на основе которой определяются только категории программ без уточнения оценки для каждой категории.
К группе оценок размера программ можно отнести метрику М. Холстеда.
Основу метрики составляют шесть измеряемых характеристик программы:
n1 — число уникальных операторов программы, включая символы-разделители, имена процедур и знаки операций (словарь операторов);
n2 — число уникальных операндов программы (словарь операндов);
N1 — общее число операторов в программе;
N2 — общее число операндов в программе;
n1′ — теоретическое число уникальных операторов;
n2′ — теоретическое число уникальных операндов.
Опираясь на эти характеристики, получаемые непосредственно при анализе исходных текстов программ, М. Холстед вводит следующие оценки:
словарь программы:
n = n1 + n2;
длина программы:
N = N1 + N2; (3.1)
измеряемый в битах объем программы:
V = N log2n. (3. 2)
Под битом подразумевается логическая единица информации — символ, оператор, операнд (аргумент операции).
0
Подборка по базе: Законодательсво ВКЛ. Статуты и литовская метрика.docx, Лабораторная № 6. Метрики Холстеда.pdf, Метрики Холстеда_2_2.pdf, 25. Работа с метриками на JavaScript (2).pdf, контрольная работа Метрика. (1).docx, [SW.BAND] Глоссарий по метрикам контекстной рекламы.docx, Ахмед метрика.pptx
ЛАБОРАТОРНАЯ РАБОТА №1
по дисциплине: Метрология и квалиметрия программного обеспечения
тема: «Метрика Холстеда»
ОГЛАВЛЕНИ
ЦЕЛЬ РАБОТЫ И ЗАДАНИЕ 2
1МЕТРИКА ХОЛСТЕДА ДЛЯ ОЦЕНКИ СЛОЖНОСТИ ПРОГРАММ 3
2ПРОЦЕСС РАСЧЁТА МЕТРИКИ 4
3АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ 8
ЗАКЛЮЧЕНИЕ 10
ЦЕЛЬ РАБОТЫ И ЗАДАНИЕ 3
1 МЕТРИКА ХОЛСТЕДА ДЛЯ ОЦЕНКИ СЛОЖНОСТИ ПРОГРАММ 4
2 ПРОЦЕСС РАСЧЁТА МЕТРИКИ 5
3 АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ 9
ЗАКЛЮЧЕНИЕ 11
СПИСОК ЛИТЕРАТУРЫ 12
ЦЕЛЬ РАБОТЫ И ЗАДАНИЕ
Целью работы является изучение метрики Холстеда для оценки сложности размера кодов трех компьютерных программ. Результатом лабораторной работы № 1 является отчёт, в котором должны быть приведена метрика Холстеда в табличном виде для трех видов программ.
Для выполнения лабораторной работы № 1 студент должен изучить приведённый ниже теоретический материал на тему «Метрика Холстеда». Для вычисления параметров метрики Холстеда необходимо подсчитать число используемых в программе операторов и операндов (общее число и число различных). Далее в соответствии с формулами из теоретического материала рассчитать все метрические параметры. Отчёт сдаётся в электронном (файл Word) виде.
-
МЕТРИКА ХОЛСТЕДА ДЛЯ ОЦЕНКИ СЛОЖНОСТИ ПРОГРАММ
При оценке сложности программ, как правило, выделяют три основные группы метрик: метрики размера программ, метрики сложности потока управления программ и метрики сложности потока данных программ. Оценки первой группы наиболее просты и поэтому получили широкое распространение.
Основу метрики Холстеда составляют четыре измеряемые характеристики программы: 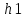
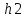
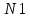
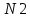
Опираясь на эти характеристики, получаемые непосредственно при анализе исходных текстов программ, Холстед вводит следующие оценки:
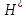
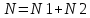
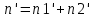
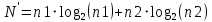
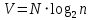
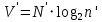
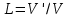
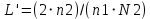
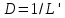
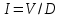
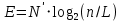
При применении метрик Холстеда частично компенсируются недостатки, связанные с возможностью записи одной и той же функциональности разным количеством строк и операторов.
-
ПРОЦЕСС РАСЧЁТА МЕТРИКИ
Программа 1. Найти наименьшее число, большее заданного N, такое, что сумма квадратов его десятичных цифр есть полный квадрат (например, таким является число 442: 42+42+22=36=62).
Листинг 1
| int check_number(unsigned long value) {
unsigned long checkSum = 0; int numeral; while (value) { numeral = value % 10; checkSum += pow(numeral, 2); value = (value — numeral) / 10; } long double trueQuad; trueQuad = sqrt(checkSum); if (trueQuad * trueQuad == checkSum) return 1; else return 0; } |
Проведём подсчёт операторов и операндов программы 1.
Таблица 1 – Операторы и операнды программы 1
| Операторы | Число вхождений | Операнды | Число вхождений |
| int | 2 | check_number | 1 |
| () | 6 | value | 5 |
| while | 1 | checkSum | 4 |
| unsigned long | 2 | 0 | 2 |
| {} | 2 | numeral | 4 |
| = | 4 | 10 | 2 |
| ; | 9 | trueQuad | 4 |
| % | 1 | 1 | 1 |
| += | 1 | ||
| pow | 1 | ||
| , | 1 | ||
| — | 1 | ||
| / | 1 | ||
| long double | 1 | ||
| sqrt | 1 | ||
| if | 1 | ||
| * | 1 | ||
| == | 1 | ||
| return | 2 | ||
| else | 1 |
Программа 2. Найти в заданном диапазоне от N1 до N2 (N2>N1) два простых числа, имеющие минимальное и максимальное значения произведений начала и конца своего десятичного представления.
Листинг 2
| std::pair<int, int> find(int N1, int N2) {
int globalMax = 1; int globalMin = N2; int globalPrimeWithMinProduct = 0; int globalPrimeWithMaxProduct = 0; int i = 0; for (i = N1; i <= N2; i++) { if (isPrime(i)) { std::pair<int, int> p = MaxMin(i); if (p.first < globalMin) { globalMin = p.first; globalPrimeWithMinProduct = i; } if (p.second > globalMax) { globalMax = p.second; globalPrimeWithMaxProduct = i; } } } return std::make_pair(globalPrimeWithMinProduct, globalPrimeWithMaxProduct); } |
Проведём подсчёт операторов и операндов программы 2.
Таблица 2 – Операторы и операнды программы 2
| Операторы | Число вхождений | Операнды | Число вхождений |
| int | 11 | i | 8 |
| () | 8 | p | 5 |
| {} | 5 | 0 | 3 |
| std | 3 | N2 | 3 |
| if | 3 | globalMax | 3 |
| pair | 2 | globalMin | 3 |
| for | 1 | globalPrimeWithMinProduct | 3 |
| ++ | 1 | globalPrimeWithMaxProduct | 3 |
| return | 1 | N1 | 2 |
| :: | 3 | first | 2 |
| ; | 13 | second | 2 |
| . | 4 | 1 | 1 |
| > | 1 | find | 1 |
| <= | 1 | isPrime | 1 |
| = | 11 | MaxMin | 1 |
| < | 1 | make_pair | 1 |
| , | 4 |
Программа 3. Найти первые N последовательно возрастающих на величину k чисел, меньших заданного числа, все нетривиальные делители которых различны (два таких числа, возрастающих на 1 – это 14=2*7 и 15=3*5).
Листинг 3
| void calcOnCPU(unsigned long long* answer, unsigned long long N, unsigned long long k, unsigned long long M)
{ unsigned long long allocationSize = sizeof(bool) * M; bool *data = (bool*) malloc(allocationSize); for(unsigned long long i = 0; i < M; i++) { unsigned long long number = i + 1; data[number-1] = true; for (unsigned long long j = 2; j <= sqrt(number); j++) { unsigned long long numberClone = number; while (numberClone % j == 0 && numberClone != 0) numberClone /= j; if(numberClone == 1) { data[number-1] = false; break; } } } findSlove(answer, data, N, k, M); free(data); } |
Проведём подсчёт операторов и операндов программы 3.
Таблица 3 – Операторы и операнды программы 3
| Операторы | Число вхождений | Операнды | Число вхождений |
| void | 1 | data | 5 |
| () | 11 | number | 5 |
| unsigned long long | 9 | j | 5 |
| * | 4 | numberClone | 5 |
| {} | 4 | 1 | 4 |
| bool | 3 | M | 4 |
| for | 2 | i | 4 |
| ++ | 2 | 0 | 3 |
| [] | 2 | answer | 2 |
| — | 2 | N | 2 |
| , | 7 | k | 2 |
| ; | 14 | allocationSize | 2 |
| false | 1 | 2 | 1 |
Окончание таблицы 3
| Операторы | Число вхождений | Операнды | Число вхождений |
| break | 1 | calcOnCPU | 1 |
| while | 1 | findSlove | 1 |
| sqrt | 1 | ||
| true | 1 | ||
| free | 1 | ||
| sizeof | 1 | ||
| malloc | 1 | ||
| + | 1 | ||
| % | 1 | ||
| && | 1 | ||
| == | 2 | ||
| /= | 8 | ||
| != | 1 | ||
| < | 1 | ||
| <= | 1 | ||
| / | 1 | ||
| if | 1 |
-
АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Проанализируем полученные результаты в таблицах 1-3 и проведём расчёт характеристик метрики Холстеда для всех программ. Результаты отобразим в таблице 4.
Таблица 4 – Сводная таблица характеристик метрики Холстеда
| Характеристика | Обозначение | Программа 1 | Программа 2 | Программа 3 |
| H1 | Число уникальных операторов программы | 20 | 17 | 30 |
| H2 | Число уникальных операндов программы | 8 | 16 | 15 |
| N1 | Общее число операторов в программе | 40 | 73 | 87 |
| N2 | Общее число операндов в программе | 23 | 42 | 46 |
| H* | Теоретический словарь программы | 2 | 3 | 5 |
| V* | Потенциальный объем программы | 110,44 | 211,57 | 477,88 |
| H | Словарь программы | 28 | 33 | 45 |
| N | Длина программы | 63 | 115 | 133 |
| V | Объем программы | 302,86 | 580,11 | 730,42 |
| N‘ | Теоретическая длина программы | 110,44 | 133,49 | 205,81 |
| L | Уровень качества программирования | 0,36 | 0,36 | 0,65 |
| L‘ | Фактический уровень программы | 0,03 | 0,04 | 0,02 |
| I | Интеллектуальное содержание алгоритма | 10,53 | 26,00 | 15,88 |
| D | Средний коэффициент сложности | 28,75 | 22,31 | 46,00 |
| E | Количество элементарных решений | 691 | 867 | 1256 |
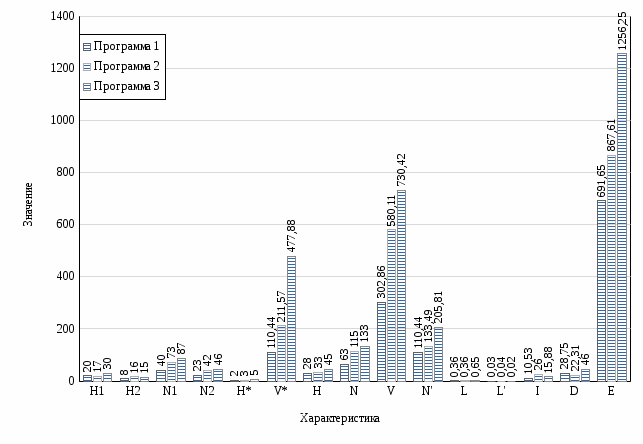
Рисунок 1 – Сравнение характеристик метрики Холстеда между 3 программами
Программы имеют приблизительно одинаковое количество уникальных операндов и операторов, однако при этом имеют различную сложность. Уровень качества программирования всех программ меньше единицы, содержательная нагрузка на каждый компонент программы небольшая, так как все три функции полностью реализуют уникальную логику. Интеллектуально содержание алгоритмов также примерно одинаково, только у программы 2 оно выше почти в 2 раза. Если сравнивать количество мысленных элементарных решений, принимаемых в процессе написания программ, то заметен рост этого показателя с усложнением исходной задачи алгоритма.
ЗАКЛЮЧЕНИЕ
В результате выполненной работы были получены навыки использования метрики Холстеда с целью оценки сложности размера кода программ. В ходе работы была произведена оценка (было подсчитано число используемых в программе операторов и операндов для последующего расчёта по приведённым формулам) трёх компьютерных программ, результаты которой были приведены в табличном виде и в виде графика.
Метод Холстеда хоть и позволяет выделить определённые закономерности и оценить эффективность программы, однако, на практике необходимо более комплексное исследование, которое не ограничивается лишь одним методом.
Одной из тем в программировании, к которым интерес периодически то появляется, то пропадает, является вопрос метрик кода программного обеспечения. В крупных программных средах время от времени появляются механизмы подсчета различных метрик. Волнообразный интерес к теме так выглядит потому, что до сих пор в метриках не придумано главного — что с ними делать. То есть даже если какой-то инструмент позволяет хорошо подсчитать некоторые метрики, то что с этим делать дальше зачастую непонятно. Конечно, метрики — это и контроль качества кода (не пишем большие и сложные функции), и «производительность» (в кавычках) программистов, и скорость развития проекта. Эта статья — обзор наиболее известных метрик кода программного обеспечения.
Введение
В статье приведен обзор 7 классов метрик и более 50 их представителей.
Будет представлен широкий спектр метрик программного обеспечения. Естественно, все существующие метрики приводить не целесообразно, большинство из них никогда не применяется на практике либо из-за невозможности дальнейшего использования результатов, либо из-за невозможности автоматизации измерений, либо из-за узкой специализации данных метрик, однако существуют метрики, которые применяются достаточно часто, и их обзор как раз будет приведен ниже.
В общем случае применение метрик позволяет руководителям проектов и предприятий изучить сложность разработанного или даже разрабатываемого проекта, оценить объем работ, стилистику разрабатываемой программы и усилия, потраченные каждым разработчиком для реализации того или иного решения. Однако метрики могут служить лишь рекомендательными характеристиками, ими нельзя полностью руководствоваться, так как при разработке ПО программисты, стремясь минимизировать или максимизировать ту или иную меру для своей программы, могут прибегать к хитростям вплоть до снижения эффективности работы программы. Кроме того, если, к примеру, программист написал малое количество строк кода или внес небольшое число структурных изменений, это вовсе не значит, что он ничего не делал, а может означать, что дефект программы было очень сложно отыскать. Последняя проблема, однако, частично может быть решена при использовании метрик сложности, т.к. в более сложной программе ошибку найти сложнее.
1. Количественные метрики
Прежде всего, следует рассмотреть количественные характеристики исходного кода программ (в виду их простоты). Самой элементарной метрикой является количество строк кода (SLOC). Данная метрика была изначально разработана для оценки трудозатрат по проекту. Однако из-за того, что одна и та же функциональность может быть разбита на несколько строк или записана в одну строку, метрика стала практически неприменимой с появлением языков, в которых в одну строку может быть записано больше одной команды. Поэтому различают логические и физические строки кода. Логические строки кода — это количество команд программы. Данный вариант описания так же имеет свои недостатки, так как сильно зависит от используемого языка программирования и стиля программирования [2].
Кроме SLOC к количественным характеристикам относят также:
- количество пустых строк,
- количество комментариев,
- процент комментариев (отношение числа строк, содержащих комментарии к общему количеству строк, выраженное в процентах),
- среднее число строк для функций (классов, файлов),
- среднее число строк, содержащих исходный код для функций (классов, файлов),
- среднее число строк для модулей.
Иногда дополнительно различают оценку стилистики программы (F). Она заключается в разбиении программы на n равных фрагментов и вычислении оценки для каждого фрагмента по формуле Fi = SIGN (Nкомм.i / Ni — 0,1), где Nкомм.i — количество комментариев в i-м фрагменте, Ni — общее количество строк кода в i-м фрагменте. Тогда общая оценка для всей программы будет определяться следующим образом: F = СУММА Fi. [2]
Также к группе метрик, основанных на подсчете некоторых единиц в коде программы, относят метрики Холстеда [3]. Данные метрики основаны на следующих показателях:
n1 — число уникальных операторов программы, включая символы-
разделители, имена процедур и знаки операций (словарь операторов),
n2 — число уникальных операндов программы (словарь операндов),
N1 — общее число операторов в программе,
N2 — общее число операндов в программе,
n1′ — теоретическое число уникальных операторов,
n2′ — теоретическое число уникальных операндов.
Учитывая введенные обозначения, можно определить:
n=n1+n2 — словарь программы,
N=N1+N2 — длина программы,
n’=n1’+n2′ — теоретический словарь программы,
N’= n1*log2(n1) + n2*log2(n2) — теоретическая длина программы (для стилистически корректных программ отклонение N от N’ не превышает 10%)
V=N*log2n — объем программы,
V’=N’*log2n’ — теоретический объем программы, где n* — теоретический словарь программы.
L=V’/V — уровень качества программирования, для идеальной программы L=1
L’= (2 n2)/ (n1*N2) — уровень качества программирования, основанный лишь на параметрах реальной программы без учета теоретических параметров,
EC=V/(L’)2 — сложность понимания программы,
D=1/ L’ — трудоемкость кодирования программы,
y’ = V/ D2 — уровень языка выражения
I=V/D — информационное содержание программы, данная характеристика позволяет определить умственные затраты на создание программы
E=N’ * log2(n/L) — оценка необходимых интеллектуальных усилий при разработке программы, характеризующая число требуемых элементарных решений при написании программы
При применении метрик Холстеда частично компенсируются недостатки, связанные с возможностью записи одной и той же функциональности разным количеством строк и операторов.
Еще одним типом метрик ПО, относящихся к количественным, являются метрики Джилба. Они показывают сложность программного обеспечения на основе насыщенности программы условными операторами или операторами цикла. Данная метрика, не смотря на свою простоту, довольно хорошо отражает сложность написания и понимания программы, а при добавлении такого показателя, как максимальный уровень вложенности условных и циклических операторов, эффективность данной метрики значительно возрастает.
2. Метрики сложности потока управления программы
Следующий большой класс метрик, основанный уже не на количественных показателях, а на анализе управляющего графа программы, называется метрики сложности потока управления программ.
Перед тем как непосредственно описывать сами метрики, для лучшего понимания будет описан управляющий граф программы и способ его построения.
Пусть представлена некоторая программа. Для данной программы строится ориентированный граф, содержащий лишь один вход и один выход, при этом вершины графа соотносят с теми участками кода программы, в которых имеются лишь последовательные вычисления, и отсутствуют операторы ветвления и цикла, а дуги соотносят с переходами от блока к блоку и ветвями выполнения программы. Условие при построении данного графа: каждая вершина достижима из начальной, и конечная вершина достижима из любой другой вершины [4].
Самой распространенной оценкой, основанной на анализе получившегося графа, является цикломатическая сложность программы (цикломатическое число Мак-Кейба) [4]. Она определяется как V(G)=e — n + 2p, где e — количество дуг, n — количество вершин, p — число компонент связности. Число компонентов связности графа можно рассматривать как количество дуг, которые необходимо добавить для преобразования графа в сильно связный. Сильно связным называется граф, любые две вершины которого взаимно достижимы. Для графов корректных программ, т. е. графов, не имеющих недостижимых от точки входа участков и «висячих» точек входа и выхода, сильно связный граф, как правило, получается путем замыкания дугой вершины, обозначающей конец программы, на вершину, обозначающую точку входа в эту программу. По сути V(G) определяет число линейно независимых контуров в сильно связном графе. Так что в корректно написанных программах p=1, и поэтому формула для расчета цикломатической сложности приобретает вид:
V(G)=e — n + 2.
К сожалению, данная оценка не способна различать циклические и условные конструкции. Еще одним существенным недостатком подобного подхода является то, что программы, представленные одними и теми же графами, могут иметь совершенно разные по сложности предикаты (предикат — логическое выражение, содержащее хотя бы одну переменную).
Для исправления данного недостатка Г. Майерсом была разработана новая методика. В качестве оценки он предложил взять интервал (эта оценка еще называется интервальной) [V(G),V(G)+h], где h для простых предикатов равно нулю, а для n-местных h=n-1. Данный метод позволяет различать разные по сложности предикаты, однако на практике он почти не применяется.
Еще одна модификация метода Мак-Кейба — метод Хансена. Мера сложности программы в данном случае представляется в виде пары (цикломатическая сложность, число операторов). Преимуществом данной меры является ее чувствительность к структурированности ПО.
Топологическая мера Чена выражает сложность программы через число пересечений границ между областями, образуемыми графом программы. Этот подход применим только к структурированным программам, допускающим лишь последовательное соединение управляющих конструкций. Для неструктурированных программ мера Чена существенно зависит от условных и безусловных переходов. В этом случае можно указать верхнюю и нижнюю границы меры. Верхняя — есть m+1, где m — число логических операторов при их взаимной вложенности. Нижняя — равна 2. Когда управляющий граф программы имеет только одну компоненту связности, мера Чена совпадает с цикломатической мерой Мак-Кейба.
Продолжая тему анализа управляющего графа программы, можно выделить еще одну подгруппу метрик — метрики Харрисона, Мейджела.
Данные меры учитывает уровень вложенности и протяженность программы.
Каждой вершине присваивается своя сложность в соответствии с оператором, который она изображает. Эта начальная сложность вершины может вычисляться любым способом, включая использование мер Холстеда. Выделим для каждой предикатной вершины подграф, порожденный вершинами, которые являются концами исходящих из нее дуг, а также вершинами, достижимыми из каждой такой вершины (нижняя граница подграфа), и вершинами, лежащими на путях из предикатной вершины в какую-нибудь нижнюю границу. Этот подграф называется сферой влияния предикатной вершины.
Приведенной сложностью предикатной вершины называется сумма начальных или приведенных сложностей вершин, входящих в ее сферу влияния, плюс первичная сложность самой предикатной вершины.
Функциональная мера (SCOPE) программы — это сумма приведенных сложностей всех вершин управляющего графа.
Функциональным отношением (SCORT) называется отношение числа вершин в управляющем графе к его функциональной сложности, причем из числа вершин исключаются терминальные.
SCORT может принимать разные значения для графов с одинаковым цикломатическим числом.
Метрика Пивоварского — очередная модификация меры цикломатической сложности. Она позволяет отслеживать различия не только между последовательными и вложенными управляющими конструкциями, но и между структурированными и неструктурированными программами. Она выражается отношением N(G) = v *(G) + СУММАPi, где v *(G) — модифицированная цикломатическая сложность, вычисленная так же, как и V(G), но с одним отличием: оператор CASE с n выходами рассматривается как один логический оператор, а не как n — 1 операторов.
Рi — глубина вложенности i-й предикатной вершины. Для подсчета глубины вложенности предикатных вершин используется число «сфер влияния». Под глубиной вложенности понимается число всех «сфер влияния» предикатов, которые либо полностью содержатся в сфере рассматриваемой вершины, либо пересекаются с ней. Глубина вложенности увеличивается за счет вложенности не самих предикатов, а «сфер влияния». Мера Пивоварского возрастает при переходе от последовательных программ к вложенным и далее к неструктурированным, что является ее огромным преимуществом перед многими другими мерами данной группы.
Мера Вудворда — количество пересечений дуг управляющего графа. Так как в хорошо структурированной программе таких ситуаций возникать не должно, то данная метрика применяется в основном в слабо структурированных языках (Ассемблер, Фортран). Точка пересечения возникает при выходе управления за пределы двух вершин, являющихся последовательными операторами.
Метод граничных значений так же основан на анализе управляющего графа программы. Для определения данного метода необходимо ввести несколько дополнительных понятий.
Пусть G — управляющий граф программы с единственной начальной и единственной конечной вершинами.
В этом графе число входящих вершин у дуг называется отрицательной степенью вершины, а число исходящих из вершины дуг — положительной степенью вершины. Тогда набор вершин графа можно разбить на две группы: вершины, у которых положительная степень <=1; вершины, у которых положительная степень >=2.
Вершины первой группы назовем принимающими вершинами, а вершины второй группы — вершинами отбора.
Каждая принимающая вершина имеет приведенную сложность, равную 1, кроме конечной вершины, приведенная сложность которой равна 0. Приведенные сложности всех вершин графа G суммируются, образуя абсолютную граничную сложность программы. После этого определяется относительная граничная сложность программы:
S0=1-(v-1)/Sa,
где S0 — относительная граничная сложность программы, Sa — абсолютная граничная сложность программы, v — общее число вершин графа программы.
Существует метрика Шнейдевинда, выражающаяся через число возможных путей в управляющем графе.
3. Метрики сложности потока управления данными
Следующий класс метрик — метрики сложности потока управления данных.
Метрика Чепина: суть метода состоит в оценке информационной прочности отдельно взятого программного модуля с помощью анализа характера использования переменных из списка ввода-вывода.
Все множество переменных, составляющих список ввода-вывода, разбивается на 4 функциональные группы :
1. P — вводимые переменные для расчетов и для обеспечения вывода,
2. M — модифицируемые, или создаваемые внутри программы переменные,
3. C — переменные, участвующие в управлении работой программного модуля (управляющие переменные),
4. T — не используемые в программе («паразитные») переменные.
Поскольку каждая переменная может выполнять одновременно несколько функций, необходимо учитывать ее в каждой соответствующей функциональной группе.
Метрика Чепина :
Q = a1*P + a2*M + a3*C + a4*T,
где a1, a2, a3, a4 — весовые коэффициенты.
Весовые коэффициенты использованы для отражения различного влияния на сложность программы каждой функциональной группы. По мнению автора метрики, наибольший вес, равный 3, имеет функциональная группа C, так как она влияет на поток управления программы. Весовые коэффициенты остальных групп распределяются следующим образом: a1=1, a2=2, a4=0.5. Весовой коэффициент группы T не равен 0, поскольку «паразитные» переменные не увеличивают сложность потока данных программы, но иногда затрудняют ее понимание. С учетом весовых коэффициентов:
Q = P + 2M + 3C + 0.5T
Метрика спена основывается на локализации обращений к данным внутри каждой программной секции. Спен — это число утверждений, содержащих данный идентификатор, между его первым и последним появлением в тексте программы. Следовательно, идентификатор, появившийся n раз, имеет спен, равный n-1. При большом спене усложняется тестирование и отладка.
Еще одна метрика, учитывающая сложность потока данных — это метрика, связывающая сложность программ с обращениями к глобальным переменным.
Пара «модуль-глобальная переменная» обозначается как (p,r), где p — модуль, имеющий доступ к глобальной переменной r. В зависимости от наличия в программе реального обращения к переменной r формируются два типа пар «модуль — глобальная переменная»: фактические и возможные. Возможное обращение к r с помощью p показывает, что область существования r включает в себя p.
Данная характеристика обозначается Aup и говорит о том, сколько раз модули Up действительно получали доступ к глобальным переменным, а число Pup — сколько раз они могли бы получить доступ.
Отношение числа фактических обращений к возможным определяется
Rup = Aup/Pup.
Эта формула показывает приближенную вероятность ссылки произвольного модуля на произвольную глобальную переменную. Очевидно, что чем выше эта вероятность, тем выше вероятность «несанкционированного» изменения какой-либо переменной, что может существенно осложнить работы, связанные с модификацией программы.
На основе концепции информационных потоков создана мера Кафура. Для использования данной меры вводятся понятия локального и глобального потока: локальный поток информации из A в B существует, если:
1. Модуль А вызывает модуль В (прямой локальный поток)
2. Модуль В вызывает модуль А и А возвращает В значение, которое используется в В (непрямой локальный поток)
3. Модуль С вызывает модули А, В и передаёт результат выполнения модуля А в В.
Далее следует дать понятие глобального потока информации: глобальный поток информации из А в В через глобальную структуру данных D существует, если модуль А помещает информацию в D, а модуль В использует информацию из D.
На основе этих понятий вводится величина I — информационная сложность процедуры:
I = length * (fan_in * fan_out)2
Здесь:
length — сложность текста процедуры (меряется через какую-нибудь из метрик объёма, типа метрик Холстеда, Маккейба, LOC и т.п.)
fan_in — число локальных потоков входящих внутрь процедуры плюс число структур данных, из которых процедура берёт информацию
fan_out — число локальных потоков исходящих из процедуры плюс число структур данных, которые обновляются процедурой
Можно определить информационную сложность модуля как сумму информационных сложностей входящих в него процедур.
Следующий шаг — рассмотреть информационную сложность модуля относительно некоторой структуры данных. Информационная мера сложности модуля относительно структуры данных:
J = W * R + W * RW + RW *R + RW * (RW — 1)
W — число процедур, которые только обновляют структуру данных;
R — только читают информацию из структуры данных;
RW — и читают, и обновляют информацию в структуре данных.
Еще одна мера данной группы — мера Овиедо. Суть ее состоит в том, что программа разбивается на линейные непересекающиеся участки — лучи операторов, которые образуют управляющий граф программы.
Автор метрики исходит из следующих предположений: программист может найти отношение между определяющими и использующими вхождениями переменной внутри луча более легко, чем между лучами; число различных определяющих вхождений в каждом луче более важно, чем общее число использующих вхождений переменных в каждом луче.
Обозначим через R(i) множество определяющих вхождений переменных, которые расположены в радиусе действия луча i (определяющее вхождение переменной находится в радиусе действия луча, если переменная либо локальна в нём и имеет определяющее вхождение, либо для неё есть определяющее вхождение в некотором предшествующем луче, и нет локального определения по пути). Обозначим через V(i) множество переменных, использующие вхождения которых уже есть в луче i. Тогда мера сложности i-го луча задаётся как:
DF(i)=СУММА(DEF(vj)), j=i…||V(i)||
где DEF(vj) — число определяющих вхождений переменной vj из множества R(i), а ||V(i)|| — мощность множества V(i).
4. Метрики сложности потока управления и данных программы
Четвертым классом метрик являются метрики, близкие как к классу количественных метрик, классу метрик сложности потока управления программы, так и к классу метрик сложности потока управления данными (строго говоря, данный класс метрик и класс метрик сложности потока управления программы являются одним и тем же классом — топологическими метриками, но имеет смысл разделить их в данном контексте для большей ясности). Данный класс метрик устанавливает сложность структуры программы как на основе количественных подсчетов, так и на основе анализа управляющих структур.
Первой из таких метрик является тестирующая М-Мера [5]. Тестирующей мерой М называется мера сложности, удовлетворяющая следующим условиям:
Мера возрастает с глубиной вложенности и учитывает протяженность программы. К тестирующей мере близко примыкает мера на основе регулярных вложений. Идея этой меры сложности программ состоит в подсчете суммарного числа символов (операндов, операторов, скобок) в регулярном выражении с минимально необходимым числом скобок, описывающим управляющий граф программы. Все меры этой группы чувствительны к вложенности управляющих конструкций и к протяженности программы. Однако возрастает уровень трудоемкости вычислений.
Также мерой качества программного обеспечения служит связанность модулей программы [6]. Если модули сильно связанны, то программа становится трудномодифицируемой и тяжелой в понимании. Данная мера не выражается численно. Виды связанности модулей:
Связанность по данным — если модули взаимодействуют через передачу параметров и при этом каждый параметр является элементарным информационным объектом. Это наиболее предпочтительный тип связанности (сцепления).
Связанность по структуре данных — если один модуль посылает другому составной информационный объект (структуру) для обмена данными.
Связанность по управлению — если один посылает другому информационный объект — флаг, предназначенный для управления его внутренней логикой.
Модули связаны по общей области в том случае, если они ссылаются на одну и туже область глобальных данных. Связанность (сцепление) по общей области является нежелательным, так как, во-первых, ошибка в модуле, использующем глобальную область, может неожиданно проявиться в любом другом модуле; во-вторых, такие программы трудны для понимания, так как программисту трудно определить какие именно данные используются конкретным модулем.
Связанность по содержимому — если один из модулей ссылается внутрь другого. Это недопустимый тип сцепления, так как полностью противоречит принципу модульности, т.е. представления модуля в виде черного ящика.
Внешняя связанность — два модуля используют внешние данные, например коммуникационный протокол.
Связанность при помощи сообщений — наиболее свободный вид связанности, модули напрямую не связаны друг с другом, о сообщаются через сообщения, не имеющие параметров.
Отсутствие связанности — модули не взаимодействуют между собой.
Подклассовая связанность — отношение между классом-родителем и классом-потомком, причем потомок связан с родителем, а родитель с потомком — нет.
Связанность по времени — два действия сгруппированы в одном модуле лишь потому, что ввиду обстоятельств они происходят в одно время.
Еще одна мера, касающаяся стабильности модуля — мера Колофелло [7], она может быть определена как количество изменений, которые требуется произвести в модулях, отличных от модуля, стабильность которого проверяется, при этом эти изменения должны касаться проверяемого модуля.
Следующая метрика из данного класса — Метрика Мак-Клура. Выделяются три этапа вычисления данной метрики:
1. Для каждой управляющей переменной i вычисляется значениt её сложностной функции C(i) по формуле: C(i) = (D(i) * J(i))/n.
Где D(i) — величина, измеряющая сферу действия переменной i. J(i) — мера сложности взаимодействия модулей через переменную i, n — число отдельных модулей в схеме разбиения.
2. Для всех модулей, входящих в сферу разбиения, определяется значение их сложностных функций M(P) по формуле M(P) = fp * X(P) + gp * Y(P)
где fp и gp — соответственно, число модулей, непосредственно предшествующих и непосредственно следующих за модулем P, X(P) — сложность обращения к модулю P,
Y(P) — сложность управления вызовом из модуля P других модулей.
3. Общая сложность MP иерархической схемы разбиения программы на модули задаётся формулой:
MP = СУММА(M(P)) по всем возможным значениям P — модулям программы.
Данная метрика ориентирована на программы, хорошо структурированные, составленные из иерархических модулей, задающих функциональную спецификацию и структуру управления. Также подразумевается, что в каждом модуле одна точка входа и одна точка выхода, модуль выполняет ровно одну функцию, а вызов модулей осуществляется в соответствии с иерархической системой управления, которая задаёт отношение вызова на множестве модулей программы.
Также существует метрика, основанная на информационной концепции — мера Берлингера [8]. Мера сложности вычисляется как M=СУММАfi*log2pi, где fi — частота появления i-го символа, pi — вероятность его появления.
Недостатком данной метрики является то, что программа, содержащая много уникальных символов, но в малом количестве, будет иметь такую же сложность как программа, содержащая малое количество уникальных символов, но в большом количестве.
5. Объектно-ориентированные метрики
В связи с развитием объектно-ориентированных языков программирования появился новый класс метрик, также называемый объектно-ориентированными метриками. В данной группе наиболее часто используемыми являются наборы метрик Мартина и набор метрик Чидамбера и Кемерера. Для начала рассмотрим первую подгруппу.
Прежде чем начать рассмотрение метрик Мартина необходимо ввести понятие категории классов [9]. В реальности класс может достаточно редко быть повторно использован изолированно от других классов. Практически каждый класс имеет группу классов, с которыми он работает в кооперации, и от которых он не может быть легко отделен. Для повторного использования таких классов необходимо повторно использовать всю группу классов. Такая группа классов сильно связна и называется категорией классов. Для существования категории классов существуют следующие условия:
Классы в пределах категории класса закрыты от любых попыток изменения все вместе. Это означает, что, если один класс должен измениться, все классы в этой категории с большой вероятностью изменятся. Если любой из классов открыт для некоторой разновидности изменений, они все открыты для такой разновидности изменений.
Классы в категории повторно используются только вместе. Они настолько взаимозависимы и не могут быть отделены друг от друга. Таким образом, если делается любая попытка повторного использования одного класса в категории, все другие классы должны повторно использоваться с ним.
Классы в категории разделяют некоторую общую функцию или достигают некоторой общей цели.
Ответственность, независимость и стабильность категории могут быть измерены путем подсчета зависимостей, которые взаимодействуют с этой категорией. Могут быть определены три метрики :
1. Ca: Центростремительное сцепление. Количество классов вне этой категории, которые зависят от классов внутри этой категории.
2. Ce: Центробежное сцепление. Количество классов внутри этой категории, которые зависят от классов вне этой категории.
3. I: Нестабильность: I = Ce / (Ca+Ce). Эта метрика имеет диапазон значений [0,1].
I = 0 указывает максимально стабильную категорию.
I = 1 указывает максимально не стабильную категорию.
Можно определять метрику, которая измеряет абстрактность (если категория абстрактна, то она достаточно гибкая и может быть легко расширена) категории следующим образом:
A: Абстрактность: A = nA / nAll.
nA — количество_абстрактных_классов_в_категории.
nAll — oбщее_количество_классов_в_категории.
Значения этой метрики меняются в диапазоне [0,1].
0 = категория полностью конкретна,
1 = категория полностью абстрактна.
Теперь на основе приведенных метрик Мартина можно построить график, на котором отражена зависимость между абстрактностью и нестабильностью. Если на нем построить прямую, задаваемую формулой I+A=1, то на этой прямой будут лежать категории, имеющие наилучшую сбалансированность между абстрактностью и нестабильностью. Эта прямая называется главной последовательностью.
Далее можно ввести еще 2 метрики:
Расстояние до главной последовательности: D=|(A+I-1)/sqrt(2)|
Нормализированной расстояние до главной последовательности: Dn=|A+I-2|
Практически для любых категорий верно то, что чем ближе они находятся к главной последовательности, тем лучше.
Следующая подгруппа метрик — метрики Чидамбера и Кемерера [10]. Эти метрики основаны на анализе методов класса, дерева наследования и т.д.
WMC (Weighted methods per class), суммарная сложность всех методов класса: WMC=СУММАci, i=1…n, где ci — сложность i-го метода, вычисленная по какой либо из метрик (Холстеда и т.д. в зависимости от интересующего критерия), если у всех методов сложность одинаковая, то WMC=n.
DIT (Depth of Inheritance tree) — глубина дерева наследования (наибольший путь по иерархии классов к данному классу от класса-предка), чем больше, тем лучше, так как при большей глубине увеличивается абстракция данных, уменьшается насыщенность класса методами, однако при достаточно большой глубине сильно возрастает сложность понимания и написания программы.
NOC (Number of children) — количество потомков (непосредственных), чем больше, тем выше абстракция данных.
CBO (Coupling between object classes) — сцепление между классами, показывает количество классов, с которыми связан исходный класс. Для данной метрики справедливы все утверждения, введенные ранее для связанности модулей, то есть при высоком CBO уменьшается абстракция данных и затрудняется повторное использование класса.
RFC (Response for a class) — RFC=|RS|, где RS — ответное множество класса, то есть множество методов, которые могут быть потенциально вызваны методом класса в ответ на данные, полученные объектом класса. То есть RS=(({M}({Ri}), i=1…n, где M — все возможные методы класса, Ri — все возможные методы, которые могут быть вызваны i-м классом. Тогда RFC будет являться мощностью данного множества. Чем больше RFC, тем сложнее тестирование и отладка.
LCOM (Lack of cohesion in Methods) — недостаток сцепления методов. Для определения этого параметра рассмотрим класс C с n методами M1, M2,… ,Mn, тогда {I1},{I2},…,{In} — множества переменных, используемых в данных методах. Теперь определим P — множество пар методов, не имеющих общих переменных; Q — множество пар методов, имеющих общие переменные. Тогда LCOM=|P|-|Q|. Недостаток сцепления может быть сигналом того, что класс можно разбить на несколько других классов или подклассов, так что для повышения инкапсуляции данных и уменьшения сложности классов и методов лучше повышать сцепление.
6. Метрики надежности
Следующий тип метрик — метрики, близкие к количественным, но основанные на количестве ошибок и дефектов в программе. Нет смысла рассматривать особенности каждой из этих метрик, достаточно будет их просто перечислить: количество структурных изменений, произведенных с момента прошлой проверки, количество ошибок, выявленных в ходе просмотра кода, количество ошибок, выявленных при тестировании программы и количество необходимых структурных изменений, необходимых для корректной работы программы. Для больших проектов обычно рассматривают данные показатели в отношении тысячи строк кода, т.е. среднее количество дефектов на тысячу строк кода.
7. Гибридные метрики
В завершении необходимо упомянуть еще один класс метрик, называемых гибридными. Метрики данного класса основываются на более простых метриках и представляют собой их взвешенную сумму. Первым представителем данного класса является метрика Кокола. Она определяется следующим образом:
H_M = (M + R1 * M(M1) +… + Rn * M(Mn)/(1 + R1 +… + Rn)
Где M — базовая метрика, Mi — другие интересные меры, Ri — корректно подобранные коэффициенты, M(Mi) — функции.
Функции M(Mi) и коэффициенты Ri вычисляются с помощью регрессионного анализа или анализа задачи для конкретной программы.
В результате исследований, автор метрики выделил три модели для мер: Маккейба, Холстеда и SLOC, где в качестве базовой используется мера Холстеда. Эти модели получили название «наилучшая», «случайная» и «линейная».
Метрика Зольновского, Симмонса, Тейера также представляет собой взвешенную сумму различных индикаторов. Существуют два варианта данной метрики:
(структура, взаимодействие, объем, данные) СУММА(a, b, c, d).
(сложность интерфейса, вычислительная сложность, сложность ввода/вывода, читабельность) СУММА(x, y, z, p).
Используемые метрики в каждом варианте выбираются в зависимости от конкретной задачи, коэффициенты — в зависимости от значения метрики для принятия решения в данном случае.
Заключение
Подводя итог, хотелось бы отметить, что ни одной универсальной метрики не существует. Любые контролируемые метрические характеристики программы должны контролироваться либо в зависимости друг от друга, либо в зависимости от конкретной задачи, кроме того, можно применять гибридные меры, однако они так же зависят от более простых метрик и также не могут быть универсальными. Строго говоря, любая метрика — это лишь показатель, который сильно зависит от языка и стиля программирования, поэтому ни одну меру нельзя возводить в абсолют и принимать какие-либо решения, основываясь только на ней.
Метрическая
теория программ (метрика Холстеда).
-
Вероятностная
модель текста программы.
На основании
исследований количественных характеристик
текстов в лингвистике уже относительно
давно установлен ряд эмпирических
закономерностей. Одна из них, так
называемый закон Ципфа [2],
является зависимостью между частотой
появления тех или иных слов в тексте
(выбранных из словаря текста) и его
длиной. В конце 70-х годов аналогичные
результаты были получены М.Холстедом
[3]
при изучении текстов программ, написанных
на различных алгоритмических языках.
Также чисто эмпирически им было найдено
соотношение, связывающее общее количество
слов в программах с величиной их словарей.
Как оказалось впоследствии, эти
закономерности могут быть получены и
осмыслены теоретически на основе
представлений алгоритмической теории
сложности, основные результаты которой
приведены выше.
Если считать,
что словарь любой программы (соответствующий
алфавиту последовательности) состоит
только из имен операторов и операндов,
то тексты программ всегда удовлетворяют
следующим условиям:
-
маловероятно
появление какого-либо имени оператора
или операнда много раз подряд. Как
правило, языки программирования
позволяют построить такую конструкцию,
в которой подобные фрагменты программы
имели бы минимальную длину; -
циклическая
организация программ исключает
многократное повторение какой-либо
группы операторов и операндов; -
блоки программ,
требующие периодического повторения
при ее исполнении, обычно оформляются
как процедуры или функции, так что в
тексте программы присутствуют лишь их
имена; -
имя каждого
операнда должно появляться в тексте
программы хотя бы один раз.
Таким образом,
каждая программа может рассматриваться
как результат сжатия ее развертки (с
раскрытыми циклами, подстановкой в
нужных местах функций, процедур,
макрокоманд и т.п.) Поэтому, используя
терминологию алгоритмической теории
сложности можно утверждать, что длина
программы есть мера сложности развертки
и ее текст не может быть существенно
сокращен, так как все закономерности
(периодичность) развертки уже использованы
для этой цели.
-
Математическое
ожидание длины текста программы
(соотношение
Холстеда).
Рассуждения
предыдущего параграфа позволяет
заключить, что текст программы, независимо
от его семантики, представляет собой
внешне случайную последовательность
слов (операторов и операндов), составляющих
словарь программы. Поэтому представляется
естественной идея поставить в соответствие
процессу написания программы некоторый
генератор случайных последовательностей
[5].
Наиболее подходящей для этой цели
является выборка с возвратом из некоторой
генеральной совокупности элементов.
Технически дело можно представить
следующим образом. Имена всех операторов
и операндов, составляющих словарь
программы, записываются на отдельных
карточках, помещаются в урну и
перемешиваются. Затем наудачу вынимают
одну карточку, фиксируют имя и снова
опускают в урну тщательно, перемешивая
ее содержимое. Опять вынимают карточку,
фиксируют имя и т.д., повторяя все сначала.
Этот процесс продолжается до тех пор,
пока каждая карточка не будет выбрана
хотя бы один раз. Задача заключается в
том, чтобы найти математическое ожидание
длины серий таких испытаний. Пусть
— число карточек (для удобства сохраним
обозначения, принятые в [3]
и [4]).
Зафиксируем имя, выпавшее при первом
извлечении. Для того, чтобы в выборку
вошла следующая карточка, отличная от
первой, потребуется некоторое число
извлечений, в общем случае больше одного.
Это число является случайной величиной.
Вообще, пусть
будет числом извлечений, следующих за
выборомr-ой
карточки до выборки новой (r+1)-ой
включительно. Тогда
Q1
= 1 + L1
+ L2
+ ….+ Lr-1
+
Lr
+ …+ L-1
будет полным
объемом выборки, исчерпывающим всю
генеральную совокупность (словарь
программы). Аналогичным образом проводятся
повторные серии испытаний, в результате
которых получаются объемы выборок Q2,
Q3
и т.д.
Такой способ регистрации событий
позволяет полиномиальное распределение
их вероятностей свести к биномиальному.
Ясно, что распределение случайной
величины Lr
совпадает с распределением номера
первого успеха в последовательности
испытаний Бернулли с вероятностью
.
Следовательно,
математическое ожидание
(подобный вывод
этого утверждения приведен в Приложении
1) и по теореме сложения математических
ожиданий
.
Так как
(сумма гармонического
ряда), то
или, при переходе
к двоичным логарифмам
(более точное
выражение M(Q),
подтвержденное
статистикой, приводится в Приложении
3). Это и есть теоретически полученное
соотношение Холстеда, представляющее
собой математическое ожидание количества
слов в программе (проще, ее длину N),
если ее словарь состоит из
слов (операторов и операндов). Ввиду
практической и теоретической важности
этого соотношения оно было подвергнуто
тщательному статистическому анализу.
Специально разработанные программные
средства позволили в автоматическом
режиме для многих тысяч программ
проверить зависимость между
и N.
Оказалось, что более точным является
выражение [4]
причем отклонение
расчетной длины от фактически наблюдаемой
не превосходило
Словарь операндов, то есть множество
имен входных и выходных переменных,
которое должно обрабатывать проектируемое
программное средство, становится точно
известным уже на стадии постановок
задач. Как будет показано дальше, словарь
операторов также поддается достаточно
точной оценке. Таким образом, на основе
постановок задач рассчитывается длина
(количество слов) будущего программного
обеспечения, которая, в свою очередь,
позволяет с удовлетворительной для
практики точностью оценить трудоемкость
проекта и другие его характеристики.
-
Дисперсия длины
программы. Точность соотношения
Холстеда.
Учитывая
независимость случайных величин
согласно
теореме сложения дисперсий, будем иметь
Так как
распределена
биномиальному закону, то
Следовательно,
(Полный вывод этих
выражений дан в Приложении 2).
При выводе
выраженийи
предполагалось,
что все программы «монолитны».
Поэтому найдем эти соотношения для
модульных программ, для чего воспользуемся
известным неравенством Иенсена: если
некоторая функциявыпуклая,
то имеет место
Очевидно, что для
условие выпуклости выполняется. Поэтому
можно записать
или в окончательном
виде
где
Таким образом,
разбиение программы на модули не только
удобно с точки зрения обозримости, но
выгодно также с точки зрения сокращения
длины. В этом смысле эффект модульности,
как будет показано в последующих
разделах, имеет принципиально важное
значение.
Предположим
далее, что все модули равны (к чему всегда
стремятся на практике). Тогда количество
слов в словаре одного модуля будет
а его длина и дисперсия соответственно
Поэтому значения
N
и D(Q)
для всей программы согласно теоремам
сложения будут
Для оценки точности
соотношения Холстеда воспользуемся
величиной соотношения абсолютного
разброса длины
N
к ее математическому ожиданию:
Таким образом,
соотношение Холстеда выполняется тем
точнее, чем больше длина программы.
Чтобы оценить порядок величины ,
положим
(что также, как правило, имеет место на
практике) иk=50.
Тогда для относительной точности
получим значение, равное
6%.
-
Метрические
характеристики программ.
-
Один из наиболее
важных количественных показателей —
длина программы, нами уже получен. Он
представляет собой математическое
ожидание количества слов в тексте
программы при фиксированном словаре.
Ясно, что программы, реализующие один
и тот же алгоритм, написанные разными
программистами, будут несколько
различаться длиной. Фундаментальное
значение формулы Холстеда заключается
в том, что это различие с ростом словаря
программы весьма быстро уменьшается.
Длина
программы — исходная величина для расчета
остальных ее
характеристик.
-
Другая важная
характеристика программы — ее объем
V. В отличие
от N
он измеряется не количеством слов, а
числом двоичных разрядов. Если в словаре
имеетсяслов, то для задания номера любого из
них требуется минимумбит. Объем программы определяется как
Теперь, когда
получены две расчетные метрические
характеристики программ, имеет смысл
вернуться к пункту 1.2.4. Если алфавиту
поставить в соответствие словарь, а
произвольной последовательности
символов — последовательность слов в
программе, трактуемой как результат
выборки из генеральной совокупности,
то с точностью до обозначений полученные
соотношения
совершенно
идентичны, хотя смысл их различен. В
первом случае при фиксированной
(заданной) длине N
была определена величина словаря; во
втором — решена обратная задача: по
заданному словарю найдена длина
программы. Идентичность этих выражений
говорит о том, что соотношение между
величиной словаря и длиной текста
единственно и взаимнооднозначно.
Во-вторых, вероятностная модель текста
программы, основанная на наглядном
представлении выборки из генеральной
совокупности с возвратом, равносильна
формальному подходу алгоритмической
теории сложности.
Выше было
отмечено, что словарь программы состоит
только из операторов и операндов. Если
количество первых обозначить за
,
а вторых —,
тои соотношение Холстеда примет вид
При статистическом
исследовании текстов программ[3]
к словарю
операторов отнесены: имена арифметических
и логических операций, присваивания,
условных и безусловных переходов,
разделители, скобки, имена процедур и
функций и т.п. Выражения типа BEGIN…END,
IF…THEN…ELSE, DO…WHILE и
др. Рассматриваются как единые операторы
( то же относится и к парам скобок).
Ясно, что
величиныи
независимы и могут принимать произвольные
значения. Однако этого нельзя сказать
относительноN1
и
N2,
то есть
числа всех операторов
и
всех операндовв тексте программы: между ними можно
установить приблизительное
взаимно-однозначное соответствие.
Действительно, каждый операнд входит
в текст, по крайней мере, хотя бы с одним
оператором — например, с разделителем
(запятой), отделяющим его от других
операторов. В то же время применение
нескольких операторов к одному операнду
маловероятно. Поэтому, можно утверждать,
чтоN1N2,
хотя
величины словарей 1
и 2
могут сильно отличаться друг от друга.
Это позволяет прийти к весьма важному
практическому выводу:
N
2N2
=
22log2.
Размер словаря
операндов 2,
как будет показано в п.2.4.3. легко
определяется из постановок задач.
-
Основной исходный
параметр, на котором базируются все
расчеты метрических характеристик
будущего ПС — это количество имен входных
и выходных переменных 2,
представленных в предельно краткой
(сжатой, с точки зрения алгоритмической
сложности) записи. Например, для задания
одномерного массива (строки), каково
бы ни было число его элементов, требуется
всего два имени: а) указатель адреса
начала массива, б) количество элементов
в нем. Аналогично, для задания двумерного
массива достаточно иметь три имени: а)
указатель адреса первого элемента, б)
число столбцов, в) число строк. Такой
подход к представлению входной и
выходной информации обеспечивает
инвариантность программ относительно
размерности решаемых задач.
Если таким
образом определенный параметр 2
рассматривать как численность
генеральной совокупности имен входных
и выходных переменных, то величина
словаря программы 2
в соответствии с соотношением Холстеда
не будет превосходитьТаким образом, принимаем, что
Последнее равенство
также хорошо подтверждается статистикой.
-
Предположим, что
существует некоторый язык программирования,
называемый потенциальным, в котором
все программы (по крайней мере для
некоторой предметной области) уже
написаны и представлены в виде процедур
или функций. Тогда для реализации любого
алгоритма на этом языке потребуется
всего два оператора (функция и
присваивание) и
имен входных и выходных переменных.
Поскольку в такой записи никакие слова
не повторяются, то длина программы
совпадает с ее объемом и равна
Эта величина
называется потенциальным (минимально
возможным) объемом, а отношение
-уровнем реализации
программы. Данный метрический показатель
характеризует степень компактности
программы, экономичность использования
изобразительных средств алгоритмического
языка. Чем ближе значение L
к единице, тем совершеннее программа.
-
Оптимизация
количества модулей в программе и их
длины.
Соотношение
Холстеда позволяет контролировать, то
есть выходить на заданную длину модулей
проектируемых ПС. Действительно, длина
модулей, в пределах точности этого
соотношения, определяется только их
словарями. В свою очередь, величина
последних зависит исключительно от
числа групп, на которые разбивается
входных и выходных переменных
программируемой задачи. Таким образом,
величина словаря модуля — контролируемый
параметр, а вместе с ней и его длина.
Итак, пусть k
— число модулей. Тогда словарь операндов
одного модуля будет
(в соответствии с
выражением, полученным в п.2.4.3.), а всей
программы
Ясно, что каждой
группе присваивается имя, которое ее
замещает в тексте программы. С учетом
этого обстоятельства окончательно
имеем
Варьирование
числом групп разбиения входных и выходных
переменных будет приводить к изменению
словаря программы. Дифференцируя
поk
и приравнивая производную нулю, получим
после преобразований
или
Решив последнее
уравнение методом последовательных
приближений, находим наилучшее (с точки
зрения минимизации длины программы)
количество модулей
kопт
При этом число
входных имен каждого модуля будет
опт
Рассмотрим один
численный пример. Пусть
= 256, что соответствует довольно большой
программе. Из полученных формул сразу
находим: число модулейkопт28,
число входных переменных одного модуля
Вычислим длину такого модуля, используя
полученные ранее соотношения:
Итак, длина модуля
составляет 280 слов, соответственно его
объем
бит.
Исследование надежности ПС показало[3],
что наименьшее количество ошибок
обнаруживается в модулях, число входных
переменных, которых не превосходит
восьми —
(при этом длина модуля составляет200
слов).
Программные
средства реальных информационных систем
имеют сложную иерархическую структуру.
Как правило, самый нижний уровень —
«исполнительные модули» — наиболее
многочисленный, в то время как вершина
управляющей «пирамиды» оканчивается
одним модулем. Исследования структур
больших программных систем обнаружили
[6],
что наиболее жизнеспособными являются
те из них, число уровней которых не
превосходит 78.
Покажем это,
используя полученные в данном пункте
результаты. Пустьчисло входных переменных проектируемого
программного обеспечения ИС. Тогда
число исполнительных модулей, следуя
приведенной выше практической
рекомендации, примем равнымЕсли их количество велико (k8),
то полученный словарь имен модулей
снова придется таким же образом разбивать
на группы и т.д. Этот процесс продолжается
до тех пор, пока не будет выполнено,
очевидно, следующее условие
где i
— число
уровней.
Логарифмируя обе
части этого выражения и разрешая его
относительно i,
получим
где скобки означают
целую часть заключенного в них числа.
Для рассмотренного примера
,
как следует из формулы,i=3.
Таким образом,
число иерархических уровней действительно
медленно (логарифмически) растет с
изменением
.
Проблема
структуризации проектируемых ПС,
разумеется, имеет сугубо содержательный
характер и принципиально не может быть
формализована. Однако, каким бы образом
она ни решалась, расчетные метрические
характеристики (длина модулей, их число,
количество иерархических уровней)
задают оптимальные параметры структуры
ПС, наиболее рациональные с точки зрения
качества реализации проекта.
-
Количественная
оценка работы программирования.
Квалификационное
и фактическое
время программирования.
Из теории
сортировки известно, что наименьшее
количество сравнений для поиска одного
элемента массива имеет место при так
называемой дихотомической выборке и
равно logm,
если m
— общее количество элементов. Аналогичный
результат установлен в инженерной
психологии (закон Хика): длительность
мысленной выборки какого-либо символа
из некоторого множества также
пропорциональна численности последнего.
Следовательно, число сравнений выборок
может служить объективной мерой работы
программирования в принятой нами модели
этого процесса (см. разделы 2.1. и 2.2.).
Если N
— длина программы, а
— словарь, то общее количество выборок
— работа программирования — будет, в
соответствии с законом Хика,
Nlog,
то есть, объем программы. Однако необходимо
еще учесть уровень ее реализации L:
количество выборок при этом возрастет
враз. Обозначив работу программирования
буквой Е, окончательно получим
так как
В инженерной
психологии также установлено, что число
мысленных сравнений, производимых
человеком в единицу времени (секунду),
лежит в пределах s
S
20. Это так
называемое число Страуда. Среднее его
значение принято считать равным 18.
(Косвенным подтверждением этого факта
является кино: при частоте кадров 25
1/сек,
то есть выше верхнего значения S,
движения на экране воспринимаются как
непрерывные; ниже — как прерывистые).
Отсюда следует, что время программирования
будет
по очевидным
причинам эта формула для оценки
календарного времени разработки ПС не
годится. Обычно она применяется для
тестирования обучающихся программированию
на степень усвоения того или иного
алгоритмического языка, причем на
небольших программах. Поэтому величину
Т называют квалификационным временем.
Оценка реального
календарного времени разработки нового
оригинального ПС основана на статистике
производительности труда программистов.
Установлено, что при пересчете на команды
ассемблера эта производительность
составляет от 5 до 30 отлаженных (!) команд
за рабочий день, принимаемый обычно за
семь часов. В каждом программистском
коллективе эта величина устанавливается,
исходя реальных экономических условий,
директивным образом[10].
Предполагается также, что за основу
организации труда принята «бригада
главного программиста».
Если на основе
постановок задач найдено, что ПС содержит
N
слов, то количество команд ассемблера
определяется как
где
коэффициент
пересчета Кнута.
Пусть, далее, n
— количество программистов и v
— заданная производительность их труда
(в указанном выше смысле). Тогда календарное
время Тк программирования ПС будет
Тк
=
(дней).
-
Количественная
оценка уровня языков программирования.
Одним из
следствий субъективного представления
об «уровне» алгоритмического языка
явилась разработка в предыдущие
десятилетия невероятно большого
количества языков программирования,
их версий и т.п. В программистском
сообществе сформировалось стойкое
убеждение, что возможно создание такого
языка «высокого» или «сверхвысокого»
уровня, который позволит осуществить
прорыв в технологии производства ПС.
В начале 80-х
годов Холстед [3]
ввел формальное определение уровня
языка программирования, определив
последний как
=
L2V,
где L
— уровень реализации программы, а V
— ее объем. Статистические исследования,
проведенные на огромном фактическом
материале, показали, что величина
действительно зависит только от
конкретного языка программирования и
практически не зависит от объема
программы, так как
Иными словами,
=const
в пределах
одного и того же языка.
Вследствие
содержательной неясности введенного
таким образом параметра уровня языка
последний остался неоцененным должным
образом программистами.
Используя
понятие работы программирования,
введенное в предыдущем пункте, покажем,
что
имеет достаточно простой смысл [6].
При этом необходимо условиться об
эталонном языке, «уровень» которого
воспринимался бы как предельно высокий.
Ясно, что эту роль может выполнить
определенный нами в п.2.4.4. потенциальный
язык. Он предполагает, что все программы,
по крайней мере, в некоторой предметной
области, уже написаны, так что теоретически
мы будем иметь дело с огромной библиотекой
функций или подпрограмм. Найдем работу
программирования в этом языке. Как уже
было отмечено в п.2.4.3., в записи на
потенциальном языке программа имеет
минимально возможную длину, и так как
слова (операнды и операторы) в ней не
повторяются, то она совпадает с объемом
Но при этом надо
иметь ввиду, что работа программирования
здесь сводится к выбору из конечного,
но колоссального по величине числа имен
функций:
21
+ 22
+23 +
…+ 2V-1
+
2V
2V+1.
где V
— объем программы. Тогда в соответствии
с законом Хика работа выбора из библиотеки
функций составит log2V+1
V, и полная
работа программирования на потенциальном
языке будет
En
= VV.
Для характеристики
уровня конкретного языка программирования
представляется естественным сопоставить
работу программирования Е в этом языке,
найденную в предыдущем пункте, с En.,
а именно: отношение
считать количественной
мерой уровня любого алгоритмического
языка.
Ниже приведена
таблица уровней некоторых известных
языков программирования.
-
Язык
Примечание
Естественный
язык2,16
Для
небольших научных текстовPL/1
1,53
Паскаль
1,25
Бейсик
1,22
Фортран
1,14
Ассемблер
0,88
Как видно, значения
заключены в довольно узком диапазоне.
Это обстоятельство во многом объясняет
тот факт, что длительные поиски «самого
эффективного» языка ни к чему не
привели. Оценим максимально возможный
выигрыш производительности программирования
только за счет повышения уровня языка.
Так как
и
то исключив V,
получим
Тогда время
программирования (квалификационное)
будет
где S
— число Страуда.
Допустим теперь,
что один и тот же алгоритм реализован
двумя разными программами, одна из
которых написана на языке с уровнем 1,
а другая — 2.
В этом случае
и
Очевидно, что
Положив 2
= 2,16 (предельный уровень — естественный
язык), 1
= 0,88 (ассемблер), находим
Для Паскаля этот
выигрыш по сравнению с Ассемблером
будет только
По всей видимости,
резервы повышения производительности
программирования за счет повышения
уровня алгоритмических языков к
настоящему времени исчерпаны (имеются
ввиду универсальные языки).
-
Оценка надежности
ПС в начальный период эксплуатации.
Одна из главных
составляющих качества ПС — его надежность.
Последняя оценивается средним временем
проявления ошибок tн
— так называемой «наработкой на отказ».
Ясно, что в первое время после сдачи в
эксплуатацию интенсивность проявления
ошибок будет наибольшей и, следовательно,
надежность минимальной. Этот период в
жизненном цикле ПС является наиболее
критичным. Поэтому весьма важно оценить
величину tн
одновременно с другими метрическими
параметрами, рассмотренными выше. В
конечном итоге это позволит варьировать
временем написания и длительностью
отладки
(от которой в первую очередь зависитtн)
в пределах общей календарной длительности
Тк
разработки ПС.
К настоящему
времени разработано [6]
довольно
много методов оценки tн,
однако наиболее просто и эффективно
эта задача решена в рамках экспоненциальной
модели надежности.
Предположим,
что в начале отладки ПС (=0)
в нем содержалось В0
первичных ошибок; после отладки в течение
времени
устраненоb
ошибок и b0
осталось не выявленными (В0
= b
+ b0).
При постоянных
усилиях на отладку интенсивность
обнаружения ошибок следует считать
пропорциональной оставшемуся их
количеству. Это предположение проверено
анализом реальных характеристик
процессов обнаружения ошибок. Таким
образом, интенсивность — скорость —
обнаружения ошибок и число устраненных
ошибок могут быть связаны дифференциальным
уравнением
где А — некоторый
коэффициент пропорциональности.
Решением этого
уравнения (при начальных условиях
является функция
Из этой зависимости
следует, что интенсивность обнаружения
ошибок будет
Поскольку наработка
на отказ tн
есть величина, обратная интенсивности
проявления ошибок, то
н
=
Непосредственное
теоретическое и практическое определение
коэффициента А весьма затруднительно,
поэтому желательно его выразить через
другие параметры, более доступные
прямому измерению на практике. Так как
то
Логарифмируя обе
части этого равенства, получим
Считая, что В0>>b0
(количество
оставшихся ошибок много меньше начального
их числа), получим
или
Подставив это
значение А в выражение для tн,
окончательно будем иметь
н
Итак, надежность
ПС (в смысле наработки на отказ)
пропорциональна длительности отладки
и обратно пропорциональна логарифму
начального количества ошибок.
Если принять,
что основная масса ошибок выявляется
во время отладки, т.е. приблизительно
равна В0,
то оценка tн
по завершении отладки не составляет
труда: согласно формуле достаточно
зафиксировать
и количество обнаруженных ошибок на
это время. На практике надежность больших
программных систем[6]
в начале опытной эксплуатации обычно
составляет 200300
часов на отказ. (Заметим, что сказанное
выше не относится к ПС, предназначенным
для работы в реальном масштабе времени).
Однако величина В0
на основе изложенной в данной главе
теории с привлечением некоторых
результатов инженерной психологии
может быть рассчитана на основе
метрических характеристик ПС.
Действительно, опытно установлено, что
количество ошибок в текстах программ
пропорционально работе программирования,
которая, как показано, может быть
вычислена. Во-вторых, «генерация»
текста программы человеком происходит
некоторыми фрагментами фиксированного
объема. Известно, что объем кратковременной
памяти человека, измеряемой числом
каких-либо символов (слов, цифр, фигур
и других объектов), которые он может
запомнить и воспроизвести сразу же
после предъявления, составляет в среднем
8. Это — так называемый закон Миллера
«72».
Тогда работа программирования каждого
фрагмента может быть оценена в соответствии
с выше изложенным как
Предположив, что
с каждым из них связана, по крайней мере,
одна ошибка (это доказано на основе
многочисленных статистических
исследований), получим
где V
— расчетный объем ПС. Здесь следует
обратить внимание на факт отсутствия
в последнем выражении параметра L
— уровня реализации программы. Он
характеризует больше концептуальный
подход к постановке задач и связан с
выбранным алгоритмом, а не с «операторским»
режимом непосредственного кодирования.
Операнды
При расчете метрики Холстеда используются следующие операнды:
Идентификаторы – все идентификаторы, которые не являются
зарезервированными словами.
Идентификаторы типов — зарезервированные слова, обозначающие
тип данных: bool, char, double, float, int, long, short, signed, unsigned, void.
Константы — числовые, символьные, строковые.
Операторы
Ключевые слова следующих категорий, которые интерпретируются
как операторы:
Идентификаторы класса памяти: inline, register, static,
typedef, virtual, mutable.
Квалификаторы типа: const,
friend, volatile.
Зарезервированные слова: asm, break, case, class, continue, default, delete, do, else, enum,
for, goto, if, new, operator, private, protected, public, return, sizeof,
struct, switch, this, union, while, namespace, using, try, catch, throw,
const_cast, static_cast, dynamic_cast, reinterpret_cast, typeid, template,
explicit, true, false, typename.
Операторы языка программирования: ! != % %= &&& || &= ( ) *
*= + ++ += и т.д.
Следующие управляющие структуры: for(…), if (…), switch (…), while for (…) and catch (...) интерпретируются как один оператор.
Поэтому for (var col = 0; col < 4; col++) это один оператор.
Из приведенного кода cell и i операнды.
Все остальное операторы.