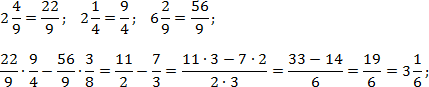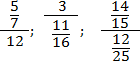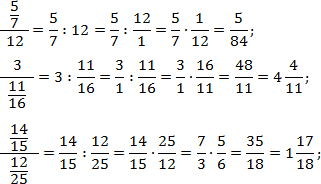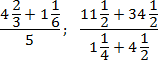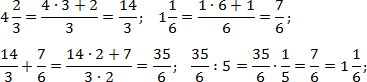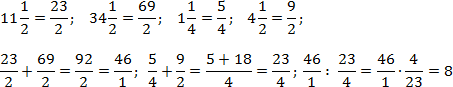Урок
математики в 3 классе «Порядок действий в сложных
выражениях»
Тема урока: «Порядок действий в сложных выражениях»
Тип урока : урок
систематизации знаний
Цели урока:
учебная:
формировать умения решать сложные выражения, определять порядок действия в
числовых выражениях без скобок и со скобками
воспитательная: расширение
и укрепление ценностно-смысловой сферы: сотрудничество, общение, взаимовыручка,
товарищество; побуждение учеников к самоанализу своей деятельности;
развивающая: формирование
умения сравнивать, анализировать, обобщать;
·формирование умения вести диалог,
высказывать свои мысли.
Личностные: способствовать созданию условий
для осознания значимости своей деятельности в учебном процессе; умения
высказывать и отстаивать свою точку зрения.
Метапредметные задачи:
Регулятивные: создавать условия для
формирования умения ставить учебные цели и задачи и добиваться их реализации,
планировать свою деятельность и оценивать результат своих действий.
Познавательные: содействовать развитию
умения исследовать и анализировать полученную информацию по теме, с целью
выделения отличительных признаков и критериев, необходимых для сравнения и
анализа.
Коммуникативные: создавать условия для
развития устной речи учащихся, умения слушать и вступать в диалог,
интегрироваться в группы и строить продуктивное сотрудничество, учиться на
принципах толерантности обсуждать вопросы, учитывать позиции других людей.
Задачи предметные:
Способствовать формированию умения находить значения
сложных выражений, зная алгоритм и правила порядка выполнения действий.
Формы роботы: фронтальная, групповая, индивидуальная
Ход урока:
1. Этап самоопределения
— Здравствуйте, ребята! Я
рада приветствовать вас на уроке математики.
И чтобы у нас все сегодня
получилось, давайте скажем следующие слова:
— Я умный, способный и у
меня все получится
— А теперь улыбнитесь друг
другу и садитесь на свои места.
2. Актуализация опорных знаний
Нам сегодня на уроке
придётся очень много считать.
ЗАДАНИЕ №1
Кто быстро считает, тому легче учиться.
Проведём РАЗМИНКУ (Приложение
1) и определим Лидеров Быстрого и правильного счёта!
524 + 378 814 –
276 329 * 6 428 : 2
(У детей карточка-разминка,
они решают примеры разминки в тетради, проверяют себя по ключу(он на обратной
стороне листа) и если все 4 примера решены верно, ребёнок встаёт. Учитель
озвучивает его место – 1-й. 2-й. 3-й и т.д. Ребёнок фиксирует на полях тетради
какое место он занял. Затем он составляет и решает СВОИ ПРИМЕРЫ, пока другие
дети продолжают решать разминку. Если ребёнок допустил ошибки в вычисления и
узнал о них при проверке по ключу, то он выполняет работу над ошибками, только
потом имеет право встать. Таким образом определяются Лидеры Быстрого и
Правильного Счёта!)
Встаньте 10-ка Лидеров
Быстрого и Правильного Счёта! 5-ка!
И самый лучший результат –
3-е место — Бронзовый, 2-е место-Серебряный, 1-е место-Золотой Уровень Быстрого
и Правильного счёта на сегодняшнем уроке! Поздравим этих ребят с отличным
результатом аплодисментами!
Оцените себя в КАРТЕ
УСПЕХА! (Приложение 2)
В предыдущем домашнем
задании, где нужно было найти значение выражений, у некоторых ребят были
допущены ошибки. Логические, в определении порядка действий, и–
вычислительные. Выполним задания, которые вам помогут решать числовые выражения
без ошибок.
ЗАДАНИЕ №2
Давайте для начала
вспомним правила «Порядок выполнения действий в числовых выражениях».
Учитель показывает
карточку(+/-) (Приложение 3). (У детей на партах такие же мини-карточки).
1. Если числовое выражение содержит только действия
сложения и вычитания, то….
(Правило произносит один
ученик, затем дети его проговаривают друг другу в парах)
Учитель показывает
карточку(*/:)(Приложение 3)
2. Если числовое выражение содержит только действия
умножения и деления, то…
(Правило произносит один
ученик, затем дети его проговаривают друг другу в парах)
Учитель показывает карточки
(+/- и */:) (Приложение 3)
3. Если числовое выражение
содержит не только сложение и вычитание, но и умножение с делением,
то…
(Правило произносит один
ученик, затем дети его проговаривают друг другу в парах)
Учитель показывает
карточку ( ( ) )(Приложение 3)
4.Если запись выражения
содержит одну или несколько пар скобок, то …
(Правило произносит один
ученик, затем дети его проговаривают друг другу в парах)
Оцените себя в КАРТЕ
УСПЕХА! (Приложение 2)
ЗАДАНИЕ №3
Возьмите конверт.
Достаньте из него карточки и составьте из них – Алгоритм нахождения
значения сложного выражения . (Приложение 4)
(Один ребёнок делает такое
же задание и доски с крупными карточками).
Проверяем! Оцените
себя в КАРТЕ УСПЕХА! (Приложение 2)
Проговорите алгоритм в
парах друг другу.
Образец правильного
алгоритма:
|
1.Посмотрите, есть ли в и расставьте действия |
|
|
2. Найдите действия * и |
|
|
3. Расставьте действия + и – слева направо. |
|
ЗАДАНИЕ №4
Расставьте порядок действий в выражениях,
пользуясь знаниями алгоритма (Приложение 5):
Проверьте по ключу ( ключ
на обратной стороне).
Оцените себя в КАРТЕ
УСПЕХА! (Приложение 2)
ЗАДАНИЕ №5
«Составьте программу
вычисления значения выражения и найдите значение этого выражения» (в группах)
(Каждому ряду
предлагается найти значение выражения своего выражения. Группа из 4-х ребят,
каждый ребёнок выполняет одно из действий выражения)
Выполняйте работу по
алгоритму, осуществляя пошаговый контроль:
1. Прочтите задание.
2. Распределите
обязанности в группе.
3. Выполните задание.
4. Выберите на доске из
предложенных результатов — свой!
4. Прикрепите его на доске!
1 ряд: 6 * 5 : 10 *
9 : 27 * 8
2 ряд: 16 * 2 – 35 :
7 + 73
3 ряд: 360 : ( 47
– 19 * 2)+1
(На доске висят
карточки со следующими значениями:
7 8 100 10 41 14)
(В результате
проверки данного задания, карточки со значениями переворачиваются, и получается
высказывание М.Ломоносова)
8 = Кто малого не может, 100 = тому и большее невозможно.
41= Ломоносов.
Кто малого не может, тому и большее невозможно. Ломоносов. (Презентация слайд 1)
Оцените себя в КАРТЕ
УСПЕХА! (Приложение 2) Поставьте себе итоговую оценку за 1 часть урока.
– Что вы о нём знаете? (Родился в Архангельской губернии, в
рыбацкой семье. Пешком отправился учиться в Москву, стал поэтом, химиком,
физиком, астрономом. Ломоносов -гениальный русский учёный во многих отраслях
знаний, поэт, просветитель, один из самых выдающихся светил мировой науки.)
-Его именем назван самое
известное учебное заведение нашей страны – МГУ, чтобы попасть в него учиться,
нужно очень хорошо учиться.
-Кто хочет в будущем
учиться в МГУ? Отличное желание!
3. Постановка учебной проблемы,
формулирование темы урока.
— На доске схематичная запись:
3 * (4 + 3) : 3 + 60 : (6 + 4) * 5 – 12 =
Как вы думаете будет
звучать тема нашего урока? ( Порядок действий в сложных выражениях)
Чему будем сегодня учиться? (Учиться вычислять значения сложных
числовых выражений, опираясь на правила; проверять себя…)
-Что важно знать при решении сложных
выражений, содержащих много действий и скобки?
(Необходимо знать алгоритм и правила нахождения значений выражений. Они помогут определять
порядок действий в сложных выражениях)
ЗАДАНИЕ №6
Составляем программу
действий
3 * (4 + 3) : 3 +
60 : (6 + 4) * 5 – 12 =
Если программа действий составлена
правильно, можно ли утверждать, что каждый ученик верно справится с нахождением
значения данного выражения? Где могут допустить ученики ошибку?
Есть рациональный способ решения сложных
числовых выражений – деление его на блоки! (Презентация слайд 2)
(Фронтальная работа –
нахождение значения данного выражения)
Физкультминутка (проводят ученики класса)
Вновь у нас физкультминутка,
Наклонились, ну-ка, ну-ка!
Распрямились, потянулись,
А теперь назад прогнулись.
Разминаем руки, плечи,
Чтоб сидеть нам было
легче,
Чтоб писать, читать,
считать
И совсем не уставать.
Голова устала тоже.
Так давайте ей поможем!
Вправо-влево, раз и два.
Думай, думай, голова.
Хоть зарядка коротка,
Отдохнули мы слегка.
4. Систематизация знания
ЗАДАНИЕ №7
13 * 10 + (64 – 18 + 24) : 10 – 5 * 0
Посмотрим, как вы
справитесь с решением данного выражения. Есть смелые ребята, желающие его
решить у доски?
Те, кому трудно решайте,
опираясь на образец решения ученика, работающего у доски.
Те, кому легко, вы решаете
данное выражение самостоятельно и можете выполнить ещё дополнительное
выражение
(карточка у детей на
партах)
Дополнительное выражение:
3 * (4 + 3) : 3 – 53 * (4 + 3) : 3 –
5
– Ребята, где нам может пригодиться умение находить
значение сложного выражения? (Решать задачи)
ЗАДАНИЕ №8
Задача:
Купили 3 м шерстяной
ткани, по 100 рублей за метр, и столько же метров льняной ткани, по 50 рублей
за метр. Сколько денег израсходовали на всю покупку?
— О чём говорится в
задаче?
-Как предлагаете
оформить краткую запись?
Цена Кол-во Стоимость
Ш.т. 100 руб
3м ? руб
Л.т. 50 руб 3 м ? руб
-Что нужно найти?
-Восстановим в памяти формулу нахождения
стоимости.
С= Ц * К
-Можно ли решить данную задачу, составив выражение?
1 способ:
100 * 3 + 50 * 3
=300+150=450(руб)
2 способ:
(100 + 50) * 3 =150
* 3=450 (руб)
Ответ: 450 рублей
израсходовали на всю покупку.
– Давайте ещё раз проговорим алгоритм — порядок
выполнения действий в сложных выражениях.
5.Включение новых знаний в систему знаний
ЗАДАНИЕ №9
Самостоятельная работа (Приложение 6)
Проверка умения находить значения выражений в
несколько действий.
Предлагаю выполнить самостоятельную работу. Она состоит из
трёх уровней. От уровня А к С задания усложняются. Уровень С – задания
олимпиадного характера. Каждый из вас может выбрать и решить карточку любого
уровня. Начать предлагаю с того уровня, который вам наиболее интересен. После
выполнения одного уровня нужно проверить себя по ключу, только потом переходить
к выполнению заданий следующего уровня.
(Карточки каждого уровня различаются по цвету).
Уровень А:
( 91 – 83 ) • 3 : 4 + 12 : 6
42 : 6 + ( 19 + 6 ) : 5 – 6 • 2
60 – (13 + 22 ) : 5 – 6 • 4 + 25
Уровень В:
7 • 6 + 9 • 4 – ( 2 • 7 + 54 : 6 • 5 )
( 27 – 19 ) • 4 + 18 : 3 + ( 8 + 27 ) : 5 – 17
( 9 • 7 + 56 : 7) – ( 2 • 6 – 4 ) • 3 + 54 :
9
Уровень С:
Расставь скобки в выражении так, чтобы его
значение было равно числу:
48 : 4 + 8 * 7 – 5 = 63
48 : 4 + 8 * 7 – 5 = 23
48 : 4 + 8 * 7 – 5 = 135
48 : 4 + 8 * 7 – 5 = 8
6. Итог урока. Рефлексия
Рефлексивный
ринг
Учащиеся высказываются
одним предложением, выбирая начало фразы из рефлексивного экрана на экране (Презентация
слайд 3):
Сегодня я узнал…
Я научился …
Было интересно …
У меня получилось…
Я попробую…
Было трудно …
Я теперь могу…
Мне захотелось …
7.Домашнее задание
Проверь правильность выполнения
самостоятельной работы!
Исходя из этого, ты получаешь индивидуальное
д/з (Приложение 7)
Тех ребят, которые справились с самым сложным
заданием – карточкой Уровня С – ждёт задание со ****. (Приложение 
Выражение — это любое сочетание чисел, букв и знаков операций. Сложное выражение, как правило, состоит из нескольких операций, в отличие от простого, который состоит из одной операции.
Допустим, нам даны несколько простых выражений: 525-25; 300+30; 500:5; 330*3; 990-100. Запишем их в ряд и посчитаем результаты:
525-25=500
300+30=330
500:5=100
330*3=990
990-100=890
Можно заметить, что результаты в некоторых примерах идентичны некоторым числам в других примерах, данных в выражении. По этому признаку можно объединить эти все выражения в одно сложное.
(300+30)*3-(525-25):5=890
Урок математики во 2-м классе «Сложные выражения без скобок с действиями разных степеней и порядок выполнения в них действий»
Ход урока
1. Организационный момент
Долгожданный дан звонок.
Начинается урок.
2. Актуализация опорных знаний
Учитель: Сегодня на уроке математики мы:
– проведем математическую разминку;
– получим новые знания;
– продолжим работу с задачами.
– Предлагаю начать урок с математической разминки.
– Ребята, что вы можете сказать о данных числах?
(- натуральные числа;
– 28, 25, 22 – двузначные числа, а 276 – трехзначное число;
– 276 – “лишнее” число;
– в записи каждого числа использована цифра “2”)
– Запишите, пожалуйста, двузначные числа в тетрадь.
– Что вы заметили? (Есть ли в числовом ряду какая-то закономерность?)
(- числа расположены в порядке уменьшения;
– каждое следующее число на 3 меньше, чем предыдущее).
– Можно ли продолжить записанный ряд, сохраняя закономерность? (Да. 28, 25, 22, 19, 16, 13, 10, 7, 4, 1)
– Назовите однозначные числа. (7, 4, 1) Используя эти числа, я составила следующее выражение: 1 + 7 • 4
– Что вы можете о нем сказать? Письменно найдите значение данного выражения.
3. Постановка учебной проблемы
Учащиеся записывают варианты решения примера в тетради, а затем выносят их на доску:
1 + 7 • 4 = 8 • 4 = 32
1 + 7 • 4 = 1 + 28 = 29
– Сравните полученные записи.
– Что вы заметили? (Оба выражения одинаковые, а имеют различные знания)
– Давайте разберемся, кто же прав?
– Почему возникло затруднение? (Вычисления делали по-разному)
– Сравните выражения: в 1-ом выражении – действия одной ступени, во 2-ом выражении – действия двух ступеней.
– Значит, какой вопрос возникает? Чего мы еще не знаем? Какую проблему необходимо решить на уроке?
(Мы не знаем, в каком порядке выполняют действия разных ступеней в выражении без скобок.)
– Сформулируйте тему урока. (Порядок выполнения действий разных ступеней в сложных выражениях без скобок.)
4. Открытие новых знаний
– Как же поступить с данным выражением? Поработайте в группах и попробуйте найти верное решение.
1) Заменить действие “•” на действие “+” и найти правильный ответ.
2) Сравнить полученные результаты с правильным ответом, выбрать правильное решение.
– Так в каком же порядке выполняют действия разных ступеней в выражениях без скобок? Сделайте вывод.
(Чтобы выполнить действия разных ступеней в выражениях без скобок, нужно сначала сделать действие “•”, а затем “+”.)
– Сравните свое правило с тем, что дано в учебнике на странице № 108.
– Чтобы лучше запомнить это правило, давайте построим схему:
« • » и « : » 
– О чем мы не договорили? (Сначала выполняются по порядку все действия…)
5. Первичное закрепление
– Давайте посмотрим, как вы поняли новое правило. Укажите порядок действий в записанных выражениях.
68 – 28 : 4 5 • 2 + 24 : 3 63 + 9 • 3 71 – 7 • 3
– Найдите значение этих выражений. (“Сильные” ребята выполняют самостоятельно, “слабые” – с комментированием у доски).
– Кому было легко справиться с заданием? У кого возникли затруднения? В чем?
– Так в каком же порядке выполняют действия разных ступеней в выражениях без скобок? (Повторение правила)
Физкульминутка
1, 2, 3, 4, 5!
Все умеем мы считать.
Отдыхать умеем тоже.
Руки за спину положим,
Голову поднимем выше
И легко – легко подышим.
Поднимаем руки класс – это раз.
Повернулась голова – это 2.
Руки вниз, вперед смотри – это 3.
Руки в стороны пошире развернули на 4.
Самого себя обнять – это 5.
Всем ребятам дружно сесть – это 6.
6. Самостоятельная работа с проверкой в классе
– А сейчас предлагаю вам выполнить небольшую самостоятельную работу:
I. Выберите выражение, в котором правильно указан порядок действий:
II. Самостоятельно расставьте порядок действий и найдите значения выражений:
45 : 9 + 2 • 4
9 • 2 – 5 • 3 + 27
(36 + 12) : 8 + 7
(Взаимопроверка в паре.)
– Вам удалось найти значения всех выражений? (Возникли трудности при решении третьего примера).
– Почему? (Не знакомы с порядком выполнения действий в выражениях со скобками).
– На следующем уроке математики мы познакомимся с порядком выполнения действий в выражениях со скобками, содержащих действия одной или разных ступеней.
III. Задание для тех, кто быстро справится с 1-м и 2-м заданием:
– Запишите из 1-ого задания выражения, в которых допущены ошибки, правильно расставьте порядок действий и найдите значения данных выражений.
– Так в каком же порядке выполняют действия разных ступеней в выражениях без скобок?
7. Повторение ранее изученного материала
Витрину магазина украшают 27 мягких игрушек, а механических в 3 раза меньше, чем мягких.
– Можно ли назвать этот текст задачей? Почему?
– Дополните текст так, чтобы получилась простая задача.
(Витрину магазина украшают 27 мягких игрушек, а механических в 3 раза меньше, чем мягких. Сколько механических игрушек украшают витрину магазина?)
– Решите задачу. (27 : 3 = 9 (иг.).)
– А теперь дополните этот текст так, чтобы получилась составная задача.
(Витрину магазина украшают 27 мягких игрушек, а механических в 3 раза меньше, чем мягких. Сколько всего игрушек украшают витрину магазина?)
– Пригодилось ли вам умение выполнять действия разных ступеней в выражениях без скобок? (Да.)
8. Итог урока. Рефлексия
– Наш урок подошел к концу.
– Какое же открытие вы сделали на уроке? (Научились выполнять действия разных ступеней в выражениях без скобок?)
– Только ли при решении выражений необходимы эти знания? ( Нет. Они нужны и при решении задач.)
– Что вам кажется самым главным на этом уроке?
– Кто испытал затруднения на уроке и в чем?
– Кто запомнил, какое открытие нас ждет на следующем уроке? (Познакомимся с порядком выполнения действий в выражениях со скобками, содержащих действия одной или разных ступеней.)
– Что больше всего понравилось в уроке?
– А мне понравилось, как вы сегодня работали на уроке. Спасибо!
Источник
Числовые и буквенные выражения
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Источник
Урок математики по теме «Сложные выражения»
Выбранный для просмотра документ Конспект урока.docx
Урок математики в 3 классе «Порядок действий в сложных выражениях»
Тема урока: «Порядок действий в сложных выражениях»
Тип урока : урок систематизации знаний
учебная: формировать умения решать сложные выражения, определять порядок действия в числовых выражениях без скобок и со скобками
воспитательная: расширение и укрепление ценностно-смысловой сферы: сотрудничество, общение, взаимовыручка, товарищество; побуждение учеников к самоанализу своей деятельности;
развивающая: формирование умения сравнивать, анализировать, обобщать;
·формирование умения вести диалог, высказывать свои мысли.
Личностные: способствовать созданию условий для осознания значимости своей деятельности в учебном процессе; умения высказывать и отстаивать свою точку зрения.
Регулятивные: создавать условия для формирования умения ставить учебные цели и задачи и добиваться их реализации, планировать свою деятельность и оценивать результат своих действий.
Познавательные: содействовать развитию умения исследовать и анализировать полученную информацию по теме, с целью выделения отличительных признаков и критериев, необходимых для сравнения и анализа.
Коммуникативные: создавать условия для развития устной речи учащихся, умения слушать и вступать в диалог, интегрироваться в группы и строить продуктивное сотрудничество, учиться на принципах толерантности обсуждать вопросы, учитывать позиции других людей.
Способствовать формированию умения находить значения сложных выражений, зная алгоритм и правила порядка выполнения действий.
Формы роботы: фронтальная, групповая, индивидуальная
— Здравствуйте, ребята! Я рада приветствовать вас на уроке математики.
И чтобы у нас все сегодня получилось, давайте скажем следующие слова:
— Я умный, способный и у меня все получится
— А теперь улыбнитесь друг другу и садитесь на свои места.
2. Актуализация опорных знаний
Нам сегодня на уроке придётся очень много считать.
Проведём РАЗМИНКУ (Приложение 1) и определим Лидеров Быстрого и правильного счёта!
524 + 378 814 – 276 329 * 6 428 : 2
(У детей карточка-разминка, они решают примеры разминки в тетради, проверяют себя по ключу(он на обратной стороне листа) и если все 4 примера решены верно, ребёнок встаёт. Учитель озвучивает его место – 1-й. 2-й. 3-й и т.д. Ребёнок фиксирует на полях тетради какое место он занял. Затем он составляет и решает СВОИ ПРИМЕРЫ, пока другие дети продолжают решать разминку. Если ребёнок допустил ошибки в вычисления и узнал о них при проверке по ключу, то он выполняет работу над ошибками, только потом имеет право встать. Таким образом определяются Лидеры Быстрого и Правильного Счёта!)
Встаньте 10-ка Лидеров Быстрого и Правильного Счёта! 5-ка!
В предыдущем домашнем задании, где нужно было найти значение выражений, у некоторых ребят были допущены ошибки. Логические, в определении порядка действий, и– вычислительные. Выполним задания, которые вам помогут решать числовые выражения без ошибок.
Давайте для начала вспомним правила «Порядок выполнения действий в числовых выражениях».
Учитель показывает карточку(+/-) (Приложение 3). (У детей на партах такие же мини-карточки).
1. Если числовое выражение содержит только действия сложения и вычитания, то….
(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)
Учитель показывает карточку(*/:)(Приложение 3)
2. Если числовое выражение содержит только действия умножения и деления, то…
(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)
Учитель показывает карточки (+/- и */:) (Приложение 3)
3. Если числовое выражение содержит не только сложение и вычитание, но и умножение с делением, то…
(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)
Учитель показывает карточку ( ( ) )(Приложение 3)
4.Если запись выражения содержит одну или несколько пар скобок, то …
(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)
(Один ребёнок делает такое же задание и доски с крупными карточками).
Проговорите алгоритм в парах друг другу.
Образец правильного алгоритма:
и расставьте действия над ними;
2. Найдите действия * и : расставьте действия над ними слева направо;
3. Расставьте действия над знаками
Расставьте порядок действий в выражениях, пользуясь знаниями алгоритма (Приложение 5):
Проверьте по ключу ( ключ на обратной стороне).
«Составьте программу вычисления значения выражения и найдите значение этого выражения» (в группах)
(Каждому ряду предлагается найти значение выражения своего выражения. Группа из 4-х ребят, каждый ребёнок выполняет одно из действий выражения)
Выполняйте работу по алгоритму, осуществляя пошаговый контроль:
1. Прочтите задание.
2. Распределите обязанности в группе.
3. Выполните задание.
4. Прикрепите его на доске!
1 ряд: 6 * 5 : 10 * 9 : 27 * 8
2 ряд: 16 * 2 – 35 : 7 + 73
3 ряд: 360 : ( 47 – 19 * 2)+1
(На доске висят карточки со следующими значениями: 7 8 100 10 41 14)
( В результате проверки данного задания, карточки со значениями переворачиваются, и получается высказывание М.Ломоносова)
8 = Кто малого не может, 100 = тому и большее невозможно. 41= Ломоносов.
Кто малого не может, тому и большее невозможно. Ломоносов. (Презентация слайд 1)
— Его именем назван самое известное учебное заведение нашей страны – МГУ, чтобы попасть в него учиться, нужно очень хорошо учиться.
-Кто хочет в будущем учиться в МГУ? Отличное желание!
3. Постановка учебной проблемы, формулирование темы урока.
— На доске схематичная запись: 3 * (4 + 3) : 3 + 60 : (6 + 4) * 5 – 12 =
Как вы думаете будет звучать тема нашего урока? ( Порядок действий в сложных выражениях)
-Что важно знать при решении сложных выражений, содержащих много действий и скобки?
(Необходимо знать алгоритм и правила нахождения значений выражений. Они помогут определять порядок действий в сложных выражениях )
Составляем программу действий
3 * (4 + 3) : 3 + 60 : (6 + 4) * 5 – 12 =
Если программа действий составлена правильно, можно ли утверждать, что каждый ученик верно справится с нахождением значения данного выражения? Где могут допустить ученики ошибку?
Есть рациональный способ решения сложных числовых выражений – деление его на блоки! (Презентация слайд 2)
(Фронтальная работа – нахождение значения данного выражения)
Физкультминутка (проводят ученики класса)
Наклонились, ну-ка, ну-ка!
А теперь назад прогнулись.
Разминаем руки, плечи,
Чтоб сидеть нам было легче,
Чтоб писать, читать, считать
И совсем не уставать.
Голова устала тоже.
Так давайте ей поможем!
Вправо-влево, раз и два.
Думай, думай, голова.
Хоть зарядка коротка,
Отдохнули мы слегка.
4. Систематизация знания
13 * 10 + (64 – 18 + 24) : 10 – 5 * 0
Посмотрим, как вы справитесь с решением данного выражения. Есть смелые ребята, желающие его решить у доски?
Те, кому трудно решайте, опираясь на образец решения ученика, работающего у доски.
Те, кому легко, вы решаете данное выражение самостоятельно и можете выполнить ещё дополнительное выражение
(карточка у детей на партах)
3 * (4 + 3) : 3 – 53 * (4 + 3) : 3 – 5
– Ребята, где нам может пригодиться умение находить значение сложного выражения? (Решать задачи)
Купили 3 м шерстяной ткани, по 100 рублей за метр, и столько же метров льняной ткани, по 50 рублей за метр. Сколько денег израсходовали на всю покупку?
— О чём говорится в задаче?
-Как предлагаете оформить краткую запись?
Цена Кол-во Стоимость
-Восстановим в памяти формулу нахождения стоимости.
-Можно ли решить данную задачу, составив выражение?
100 * 3 + 50 * 3 =300+150=450(руб)
(100 + 50) * 3 =150 * 3=450 (руб)
Ответ: 450 рублей израсходовали на всю покупку.
5.Включение новых знаний в систему знаний
Самостоятельная работа (Приложение 6)
Проверка умения находить значения выражений в несколько действий.
Предлагаю выполнить самостоятельную работу. Она состоит из трёх уровней. От уровня А к С задания усложняются. Уровень С – задания олимпиадного характера. Каждый из вас может выбрать и решить карточку любого уровня. Начать предлагаю с того уровня, который вам наиболее интересен. После выполнения одного уровня нужно проверить себя по ключу, только потом переходить к выполнению заданий следующего уровня.
(Карточки каждого уровня различаются по цвету).
( 91 – 83 ) • 3 : 4 + 12 : 6
42 : 6 + ( 19 + 6 ) : 5 – 6 • 2
60 – (13 + 22 ) : 5 – 6 • 4 + 25
7 • 6 + 9 • 4 – ( 2 • 7 + 54 : 6 • 5 )
( 27 – 19 ) • 4 + 18 : 3 + ( 8 + 27 ) : 5 – 17
( 9 • 7 + 56 : 7) – ( 2 • 6 – 4 ) • 3 + 54 : 9
Расставь скобки в выражении так, чтобы его значение было равно числу:
48 : 4 + 8 * 7 – 5 = 63
48 : 4 + 8 * 7 – 5 = 23
48 : 4 + 8 * 7 – 5 = 135
6. Итог урока. Рефлексия
Учащиеся высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на экране (Презентация слайд 3):
Проверь правильность выполнения самостоятельной работы!
Исходя из этого, ты получаешь индивидуальное д/з (Приложение 7)
Тех ребят, которые справились с самым сложным заданием – карточкой Уровня С – ждёт задание со ****. (Приложение
Источник
Сложные выражения с дробями. Порядок действий
8 августа 2011
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:
- Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
- Затем — деление и умножение;
- Последним шагом выполняется сложение и вычитание.
Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Задача. Найдите значения выражений:

Переведем все дроби из первого выражения в неправильные, а затем выполним действия:
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2. Тогда:
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3, имеем:
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
Здесь и далее мы будем называть эти дроби многоэтажными. Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:
В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
Это выражение можно прочитать по-разному:
- В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
- В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Смотрите также:
- Умножение и деление дробей
- Тест к уроку «Сложные выражения с дробями» (легкий)
- Тест к уроку «Округление с избытком и недостатком» (1 вариант)
- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
- Формула простого процента: как найти исходное значение
- Сложная задача B14 на смеси и сплавы
Найдем значения заданных выражений:
1) 72 : 8 = 9,
2) 9 + 36 = 45,
3) 5 + 17 = 22,
4) 45 : 9 = 5.
Запишем сложное выражение и решим его, соблюдая порядок арифметических действий:
(72 : 8 + 36) : 9 + 17 = ?
1) 72 : 8 = 9,
2) 9 + 36 = 45.
3) 45 : 9 = 5,
4) 5 + 17 = 22.
Таким образом, получаем, что значение выражения (72 : 8 + 36) : 9 + 17 равно 22.