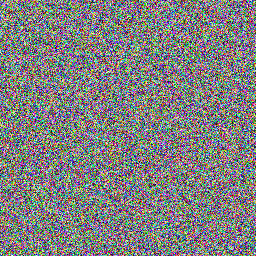
Я работаю программистом в игровой студии IT Territory, а с недавних пор перешел на направление экспериментальных проектов, где мы проверяем на прототипах различные геймплейные гипотезы. И работая над одним из прототипов мы столкнулись с задачей генерации случайных чисел. Я хотел бы поделиться с вами полученным опытом: расскажу о псевдогенераторах случайных чисел, об альтернативе в виде хеш-функции, покажу, как её можно оптимизировать, и опишу комбинированные подходы, которые мы применяли в проекте.
Случайными числами пользовались с самого зарождения математики. Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях.
Есть разные способы получения случайных чисел. Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди.
К первым техническим способам получения случайных чисел можно отнести различные генераторы с использованием энтропии. Это устройства, основанные на физических свойствах, например, емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.
Сегодня мы с вами поговорим о генераторах псевдослучайных чисел — вычисляемых функциях. К ним предъявляются следующие требования:
-
Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.
-
Портируемость алгоритма на различные системы.
-
Скорость получения последовательности. Чем быстрее, тем лучше.
-
Повторяемость результата. Это очень важный показатель. От него зависят все компьютерные игры, которые используют генераторы миров и различные системы с аналогичной функциональностью. Воспроизводимость даёт нам общий контент для всех, то есть мы можем генерировать на отдельных клиентах одинаковое содержимое. Также мы можем генерировать контент на лету в зависимости от входных данных, например, от местоположения игрока в мире. Ещё повторяемость случайных чисел используется для сохранения конкретного контента в виде зерна. То есть мы можем держать у себя только какое-то число или массив чисел, на основе которых будут генерироваться нужные нам параметры для заранее отобранного контента.
Зерно
Зерно — это основа генерирования. Оно представляет собой число или вектор чисел, который мы отправляем при инициализации генератора.
var random = new Random(0);
var rn0 = random.Next();
var rn1 = random.Next();
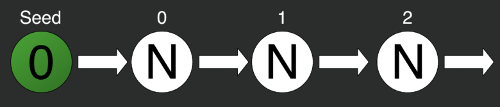
var rn2 = random.Next();На иллюстрации просто инициализирован стандартный генератор случайных чисел из стандартной библиотеки C#. При инициализации отправляем в него некоторое число — seed (зерно), — в данном случае это 0. Затем по очереди берём по одному числу методом Next. Но тут мы столкнёмся с первой проблемой: генерирование всегда будет последовательным. Мы не можем получить сразу i-тый элемент последовательности. Для получения второго элемента последовательности необходимо сначала задать зерно, потом вычислить нулевой элемент, за ним первый и только потом уже второй, третий и i-й.
Решить эту проблему можно будет с помощью разделения одного генератора на несколько отдельных.
var X = 0;
var Y = 1;
var Z = 2;
var rs0 = new Random(X);
var rs1 = new Random(Y);
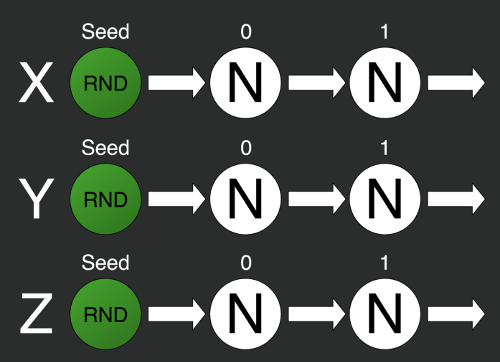
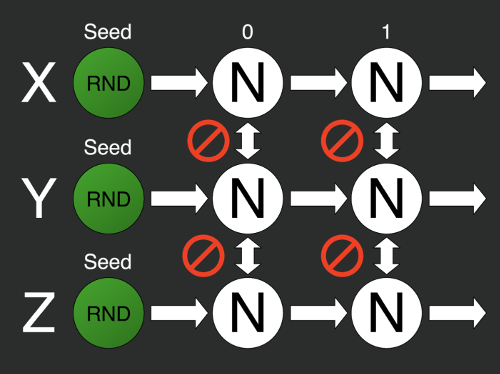
var rs2 = new Random(Z);То есть берём несколько генераторов и задаём им разные зёрна. Но тут мы можем столкнуться со второй проблемой: нельзя гарантировать случайность i-тых элементов разных последовательностей с разными зёрнами.
На иллюстрации изображён результат генерирования нулевого элемента последовательности с помощью стандартной библиотекой C#. Мы постепенно меняли зерно от 0 до N.
Качество генератора
Предлагаю оценивать качество генератора с помощью изображений разного типа. Первый тип — это просто сгенерированная последовательность, который мы визуализируем с помощью первых трёх байтов полученного числа, конвертированных в RGB-представление.
private static uint GetBytePart(uint i, int byteIndex)
{
return ((i >> (8 * byteIndex)) % 256 + 256) % 256;
}
public static Color GetColor(uint i)
{
float r = GetBytePart(i, 0) / 255f;
float g = GetBytePart(i, 1) / 255f;
float b = GetBytePart(i, 2) / 255f;
return new Color(r, g, b);
}Второй тип изображений — это пространственная интерпретация сгенерированной последовательности. Мы берём первые два бита числа (Х и Y), затем считаем количество попаданий в заданные точки и при визуализации вычитаем из 1 отношение количества попаданий в конкретный пиксель к максимальному количеству попаданий в какой-то другой пиксель. Черные пиксели — это точка, куда мы попадаем чаще всего, а белые — куда мы либо почти, либо совсем не попали.
var max = 0;
for (var i = 0; i < ints.Length; i += 2)
{
var x = GetBytePart(ints[i], ByteIndex);
var y = GetBytePart(ints[i + 1], ByteIndex);
var value = coords[x, y];
value++;
max = Mathf.Max(value, max);
coords[x, y] = value;
}Сравнение генераторов
Стандартные средства C#
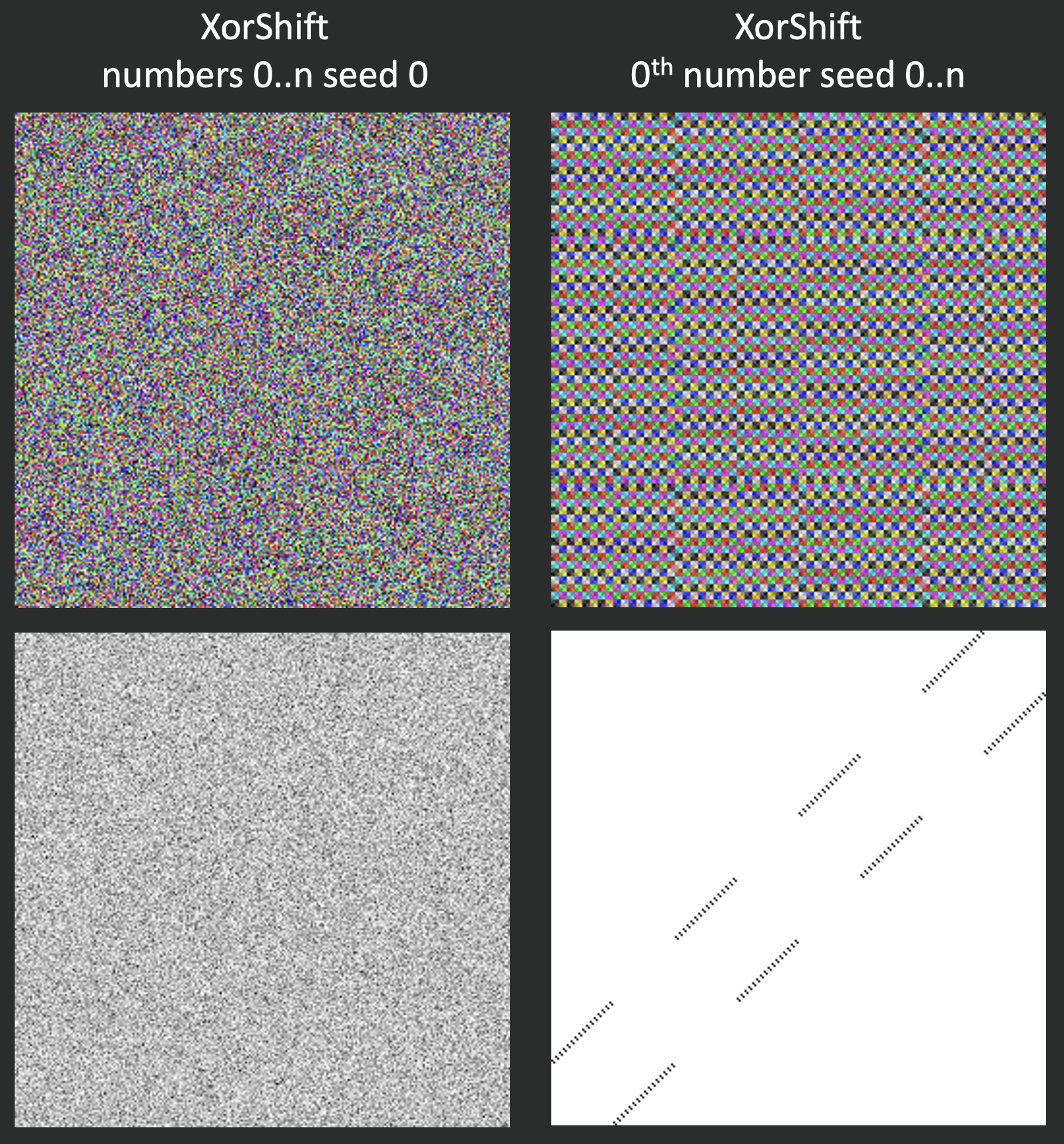
Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом.
В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности.
Линейный конгруэнтный генератор (LCG)
Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом.
const long randMax = 4294967296;
state = 214013 * state + 2531011;
state ^= state >> 15;
return (uint) (state % randMax);При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu.
const long randMax = 2147483648;
state = 65539 * state + 0;
return (uint) (state % randMax);Этот генератор страшен тем, что умножает одно большое число на другое и берёт остаток от деления на 231. В результате формируется вот такая красивая картинка.
XorShift
Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.
state ^= state << 13;
state ^= state >> 17;
state ^= state << 5;
return state;Вихрь Мерсенна
Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.
ulong x;
if (mti >= NN)
{
// generate NN words at one time
for (var i = 0; i < NN - MM; i++)
{
x = (mt[i] & UM) | (mt[i + 1] & LM);
mt[i] = mt[i + MM]
^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
}
for (var i = NN - MM; i < NN - 1; i++)
{
x = (mt[i] & UM) | (mt[i + 1] & LM);
mt[i] = mt[i + (MM - NN)]
^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
}
x = (mt[NN - 1] & UM) | (mt[0] & LM);
mt[NN - 1] = mt[MM - 1]
^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
mti = 0;
}
x = mt[mti++];
x ^= (x >> 29) & 0x5555555555555555L;
x ^= (x << 17) & 0x71d67fffeda60000L;
x ^= (x << 37) & 0xfff7eee000000000L;
x ^= x >> 43;
return x;Unity — Random
Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность.
Перемешанный конгруэнтный генератор (PCG)
Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.
Длительность последовательного генерирования
Это важная характеристика генераторов. В таблице приведена длительность для алгоритмов в миллисекундах. Замеры проводились на моём MacBook Pro 2019 года.
|
0..n |
0 seed 0..n |
100 seed 0..n |
|
|
Вихрь Мерсенна |
11 |
1870 |
2673 |
|
Random (C#) |
30 |
842 |
1364 |
|
LCG |
10 |
28 |
699 |
|
XorShift |
7 |
26 |
420 |
|
Unity Random |
20 |
40 |
1455 |
|
PCG |
18 |
60 |
1448 |
Вихрь Мерсенна работает дольше всего, но даёт качественный результат. Стандартный генератор Random из библиотеки C# подходит для задач, в которых случайность вторична и не имеет какой-то значимой роли, то есть его можно использовать в рамках одного зерна. LCG (линейный конгруэнтный генератор) — это уже более серьёзный алгоритм, но требуется время на подбор нужных коэффициентов, чтобы получить адекватный паттерн. XorShift — самый быстрый алгоритм из всех рассмотренных. Его можно использовать там, где нужно быстро получить случайное значение, но помните про ярко выраженный паттерн с повторяющимся значением. Unity Random и PCG (перемешанный конгруэнтный генератор) сопоставимы по длительности работы, поэтому в разных ситуациях мы можем менять их местами: для длительных последовательностей использовать Unity, а для коротких — PCG.
Альтернатива генераторам — хеш-функции
Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.
Требования к генераторам на основе хеш-функций предъявляются те же самые, что и к простым генераторам, кроме длительности получения последовательности. Дело в том, что такому генератору можно отправить на вход одновременно зерно и требуемое состояние, потому что хеш-функции принимают на вход массивы данных.
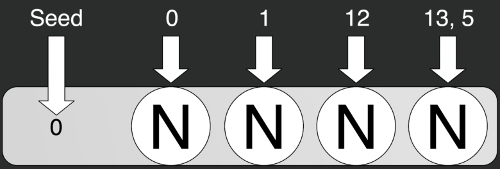
Вот пример использования хеш-функции: можно либо создать конкретный класс, отправить туда зерно и постепенно запрашивать только конкретные состояния, либо написать статичную функцию, и отправить туда сразу и зерно, и конкретное состояние. Слева показан алгоритм работы MD5 из стандартной библиотеки C#.
var hash = new Hash(0);
var rn0 = hash.GetHash(0);
var rn1 = hash.GetHash(1);
var rn2 = hash.GetHash(12);
var rn3 = hash.GetHash(13, 5);
var rn4 = Hash.GetHash(0, 0);
var rn5 = Hash.GetHash(0, 1);
var rn6 = Hash.GetHash(0, 12);
var rn7 = Hash.GetHash(0, 13, 5);Сделать генератор на основе хеш-функции можно так. Непосредственно при инициализации генератора задаём зерно, увеличиваем счётчик на 1 при запросе следующего значения и выводим результат хеша по зерну и счётчику.
class HashRandom
{
private int seed;
private int counter;
public HashRandom(int seed)
{
this.seed = seed;
}
public uint Next()
{
return Hash.GetHash(seed, counter++);
}
}Одни из самых популярных хеш-функций — это MurMur3 и WangHash.
MurMur3 не создаёт паттернов при использованиии i-тых элементов разных последовательностей при разных зёрнах. У WangHash статистические показатели образуют заметный паттерн. Но любую функцию можно прогнать через себя два раза и получить улучшенные показатели, как это показано в правом крайнем столбце WangDoubleHash.
Также сегодня активно развивается и набирает популярность алгоритм xxHash.
Забегая вперёд, скажу, что мы выбрали этот генератор для наших проектов и активно его используем.
Длительность последовательного генерирования у всех хеш-функций примерно одинакова. Однако у MD5 эта характеристика заметно отличается, но не потому, что алгоритм плохой, а потому что в стандартной реализации MD5 много разных состояний, которые влияют на быстродействие алгоритма.
|
0..n |
0 seed 0..n |
|
|
MurMur3 |
9 |
32 |
|
WangHash |
8 |
31 |
|
xxHash |
8 |
32 |
|
WangDoubleHash |
9 |
|
|
MD5 |
202 |
Оптимизация хеш-функций
Этот инструмент создавался для других целей — свёртки целых сообщений, поэтому на вход они принимают массивы данных. Лучше оптимизировать хеш-функции для задач генерирования случайных чисел, ведь нам достаточно подать два простых числа — зерно и счётчик.
Что нужно сделать для оптимизации:
-
Убрать функцию включения хвоста. Это операция вставки недостающих элементов в конец массива для хеш-функции. Если его длина меньше требуемой для хеширования, недостающие элементы заполняются определёнными значениями, обычно нулями.
-
Перевести обработку данных с типа byte на тип int.
-
Избавиться от конвертирования массива byte в одно число int.
Мы можем взять такую реализацию алгоритма xxHash:
uint h32;
var index = 0;
var len = buf.Length;
if (len >= 16)
{
var limit = len - 16;
var v1 = seed + P1 + P2;
var v2 = seed + P2;
var v3 = seed + 0;
var v4 = seed - P1;
do
{
v1 = SubHash(v1, buf, index);
index += 4;
v2 = SubHash(v2, buf, index);
index += 4;
v3 = SubHash(v3, buf, index);
index += 4;
v4 = SubHash(v4, buf, index); index += 4;
} while (index <= limit);
h32 = Rot32(v1, 1) + Rot32(v2, 7) + Rot32(v3, 12) + Rot32(v4, 18);
}
else
{
h32 = seed + P5;
}
h32 += (uint) len;
while (index <= len — 4)
{
h32 += BitConverter.ToUInt32(buf, index) * P3;
h32 = Rot32(h32, 17) * P4;
index += 4;
}
while (index < len)
{
h32 += buf[index] * P5;
h32 = Rot32(h32, 11) * P1;
index++;
}
h32 ^= h32 >> 15;
h32 *= P2;
h32 ^= h32 >> 13;
h32 *= P3;
h32 ^= h32 >> 16;
return h32;
И уменьшить до такой:
public static uint GetHash(int buf, uint seed)
{
var h32 = seed + P5;
h32 += 4U;
h32 += (uint) buf * P3;
h32 = Rot32(h32, 17) * P4;
h32 ^= h32 >> 15;
h32 *= P2;
h32 ^= h32 >> 13;
h32 *= P3;
h32 ^= h32 >> 16;
return h32;
}Здесь Р1, Р2, Р3, Р4, Р5 — стандартные коэффициенты алгоритма xxHash.
Комбинированные подходы
Комбинированные подходы бывают двух типов:
-
Сочетание хеш-функции и генератора случайных чисел.
-
Иерархические генераторы.
С первым всё предельно просто: берём хеш-функцию и получаем с её помощью зёрна, которые отправляем в другие генераторы. Слева показан результат работы комбинации стандартного Random из библиотеки C#, зёрна которому мы создавали с помощью хеш-функций.
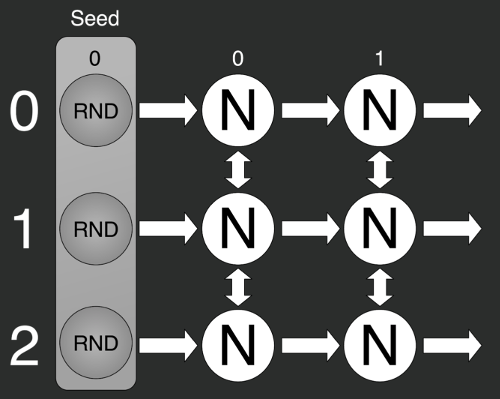
Второй подход гораздо интереснее. Мы его используем в ситуациях, когда нам необходимо генерировать группы последовательностей, например, ботов для тестирования.
Сначала генерируем зёрна, а затем отправляем их в генераторы ботов. Первое число, полученное из генератора, мы используем как индекс для массива из ников игроков. Второе число будет зерном для генерирования истории матчей. Третье у нас используется для генерирования истории турнира. И т.п.
В этой иерархии могут применяться разные генераторы. Например, когда нам необходимо создать какую-то короткую последовательность, мы использовали перемешанный конгруэнтный генератор. А когда нам нужно было создать длинную историю матча, то использовали генератор Unity.
Мы разобрали наиболее популярные алгоритмы генераторов псевдослучайных чисел, рассмотрели альтернативу в виде хеш-функций, узнали, как их оптимизировать и прошлись по комбинированным подходам к генерированию псевдослучайных чисел. Надеюсь, что вам это было полезно!
Время на прочтение
6 мин
Количество просмотров 35K
Представьте, что вам нужно сгенерировать равномерно распределённое случайное число от 1 до 10. То есть целое число от 1 до 10 включительно, с равной вероятностью (10%) появления каждого. Но, скажем, без доступа к монетам, компьютерам, радиоактивному материалу или другим подобным источникам (псевдо) случайных чисел. У вас есть только комната с людьми.
Предположим, что в этой комнате чуть более 8500 студентов.
Самое простое — попросить кого-нибудь: «Эй, выбери случайное число от одного до десяти!». Человек отвечает: «Семь!». Отлично! Теперь у вас есть число. Однако вы начинаете задаваться вопросом, является ли оно равномерно распределённым?
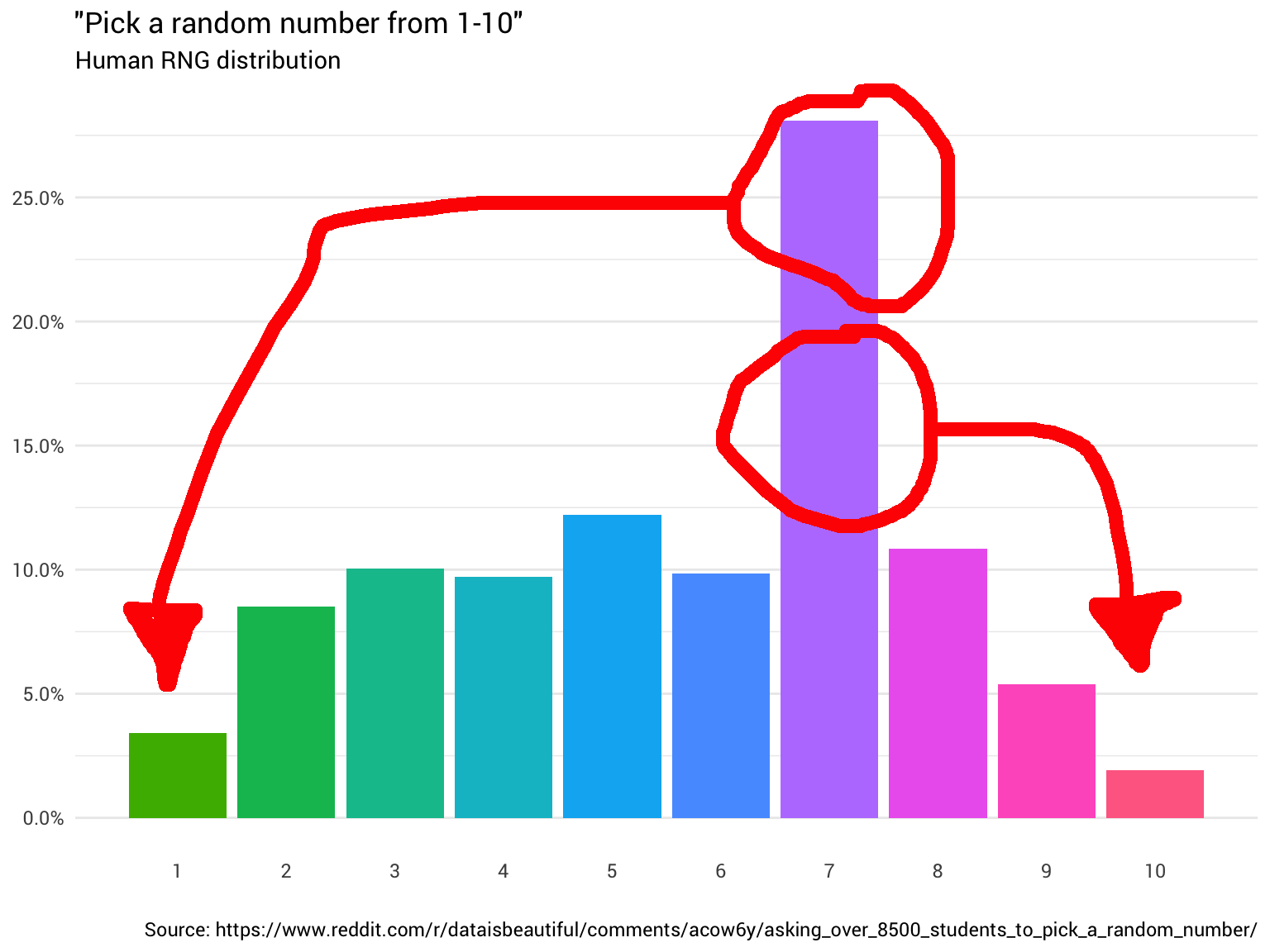
Поэтому вы решили спросить ещё несколько человек. Вы продолжаете их спрашивать и считать их ответы, округляя дробные числа и игнорируя тех, кто думает, что диапазон от 1 до 10 включает 0. В конце концов вы начинаете видеть, что распределение вообще не равномерное:
library(tidyverse)
probabilities <-
read_csv("https://git.io/fjoZ2") %>%
count(outcome = round(pick_a_random_number_from_1_10)) %>%
filter(!is.na(outcome),
outcome != 0) %>%
mutate(p = n / sum(n))
probabilities %>%
ggplot(aes(x = outcome, y = p)) +
geom_col(aes(fill = as.factor(outcome))) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(labels = scales::percent_format(),
breaks = seq(0, 1, 0.05)) +
scale_fill_discrete(h = c(120, 360)) +
theme_minimal(base_family = "Roboto") +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank()) +
labs(title = '"Pick a random number from 1-10"',
subtitle = "Human RNG distribution",
x = "",
y = NULL,
caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/")
Данные с Reddit
Вы хлопаете себя по лбу. Ну конечно, оно не будет случайным. В конце концов, нельзя доверять людям.
Итак, что делать?
Вот бы найти какую-то функцию, которая преобразует распределение «человеческого ГСЧ» в равномерное распределение…
Интуиция тут относительно проста. Нужно всего лишь взять массу распределения оттуда, где она выше 10%, и переместить туда, где она меньше 10%. Так, чтобы все столбцы на графике были одного уровня:
По идее, такая функция должна существовать. Фактически, должно быть много различных функций (для перестановки). В крайнем случае, можно «разрезать» каждый столбец на бесконечно малые блоки и построить распределение любой формы (как кирпичики Lego).
Конечно, такой экстремальный пример немного громоздок. В идеале мы хотим сохранить как можно больше исходного распределения (т. е. сделать как можно меньше измельчений и перемещений).
Как найти такую функцию?
Ну, наше объяснение выше звучит очень похоже на линейное программирование. Из Википедии:
Линейное программирование (LP, также именуется линейной оптимизацией) — метод достижения наилучшего результата… в математической модели, требования которой представлены линейными отношениями… Стандартная форма представляет собой обычную и наиболее интуитивную форму описания задачи линейного программирования. Она состоит из трёх частей:
- Линейная функция, которую необходимо максимизировать
- Проблемные ограничения следующей формы
- Неотрицательные переменные
Аналогично можно сформулировать и проблему перераспределения.
Представление проблемы
У нас есть набор переменных
, каждая из которых кодирует долю вероятности, перераспределённую от целого числа
(от 1 до 10) к целому числу
(от 1 до 10). Поэтому, если
, то нам нужно перенести 20% ответов от семёрки к единице.
variables <-
crossing(from = probabilities$outcome,
to = probabilities$outcome) %>%
mutate(name = glue::glue("x({from},{to})"),
ix = row_number())
variables## # A tibble: 100 x 4 ## from to name ix ## <dbl> <dbl> <glue> <int> ## 1 1 1 x(1,1) 1 ## 2 1 2 x(1,2) 2 ## 3 1 3 x(1,3) 3 ## 4 1 4 x(1,4) 4 ## 5 1 5 x(1,5) 5 ## 6 1 6 x(1,6) 6 ## 7 1 7 x(1,7) 7 ## 8 1 8 x(1,8) 8 ## 9 1 9 x(1,9) 9 ## 10 1 10 x(1,10) 10 ## # … with 90 more rows
Мы хотим ограничить эти переменные таким образом, чтобы все перераспределённые вероятности суммировались в 10%. Другими словами, для каждого
от 1 до 10:
Можем представить эти ограничения в виде списка массивов в R. Позже свяжем их в матрицу.
fill_array <- function(indices,
weights,
dimensions = c(1, max(variables$ix))) {
init <- array(0, dim = dimensions)
if (length(weights) == 1) {
weights <- rep_len(1, length(indices))
}
reduce2(indices, weights, function(a, i, v) {
a[1, i] <- v
a
}, .init = init)
}
constrain_uniform_output <-
probabilities %>%
pmap(function(outcome, p, ...) {
x <-
variables %>%
filter(to == outcome) %>%
left_join(probabilities, by = c("from" = "outcome"))
fill_array(x$ix, x$p)
})Мы также должны убедиться, что сохраняется вся масса вероятностей из исходного распределения. Так что для каждого
в диапазоне от 1 до 10:
one_hot <- partial(fill_array, weights = 1)
constrain_original_conserved <-
probabilities %>%
pmap(function(outcome, p, ...) {
variables %>%
filter(from == outcome) %>%
pull(ix) %>%
one_hot()
})Как уже говорилось, мы хотим максимизировать сохранение исходного распределения. Это наша цель (objective):
maximise_original_distribution_reuse <-
probabilities %>%
pmap(function(outcome, p, ...) {
variables %>%
filter(from == outcome,
to == outcome) %>%
pull(ix) %>%
one_hot()
})
objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums()Затем передаём проблему солверу, например, пакету lpSolve в R, объединив созданные ограничения в одну матрицу:
# Make results reproducible...
set.seed(23756434)
solved <- lpSolve::lp(
direction = "max",
objective.in = objective,
const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)),
const.dir = c(rep_len("==", length(constrain_original_conserved)),
rep_len("==", length(constrain_uniform_output))),
const.rhs = c(rep_len(1, length(constrain_original_conserved)),
rep_len(1 / nrow(probabilities), length(constrain_uniform_output)))
)
balanced_probabilities <-
variables %>%
mutate(p = solved$solution) %>%
left_join(probabilities,
by = c("from" = "outcome"),
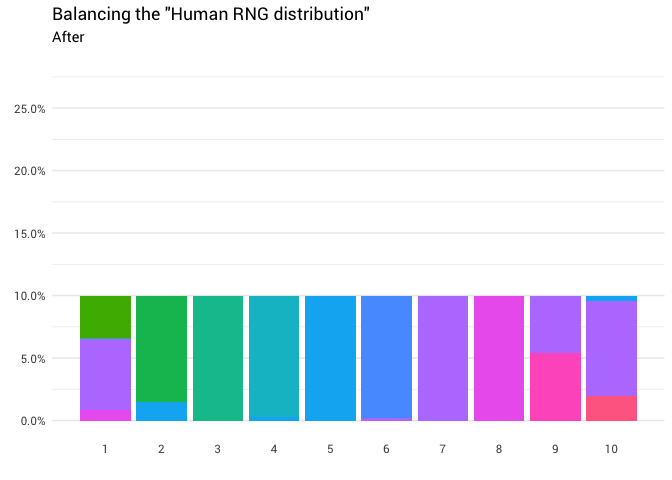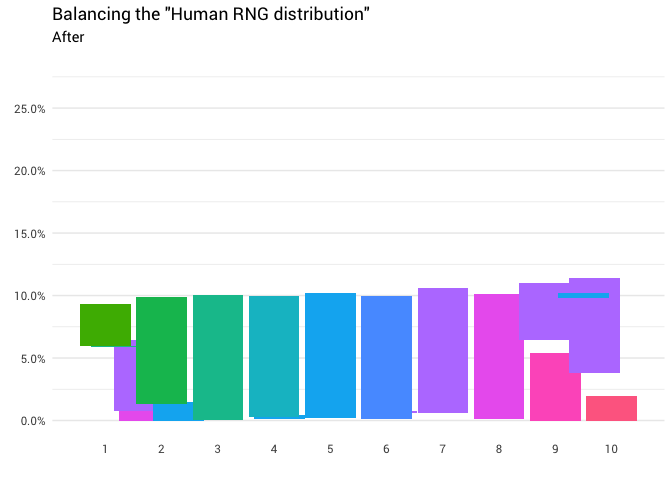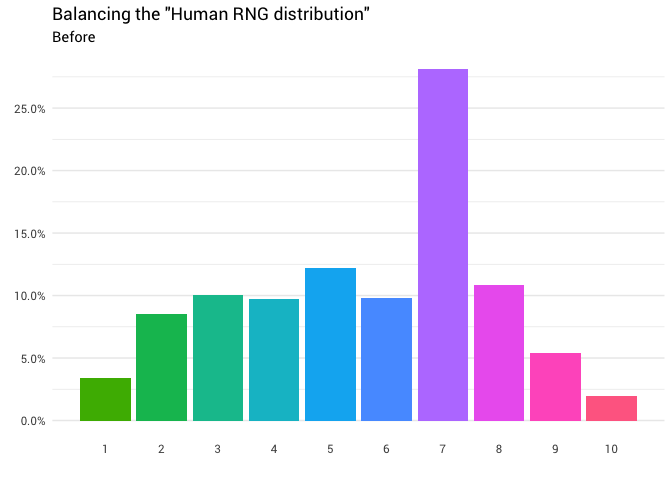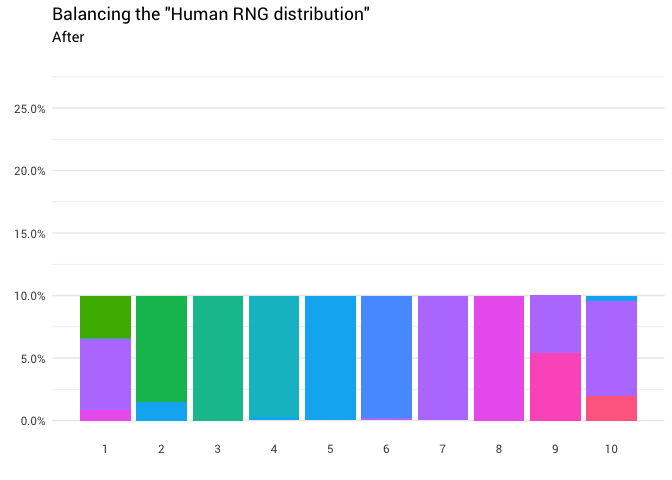
suffix = c("_redistributed", "_original"))Возвращается следующее перераспределение:
library(gganimate)
redistribute_anim <-
bind_rows(balanced_probabilities %>%
mutate(key = from,
state = "Before"),
balanced_probabilities %>%
mutate(key = to,
state = "After")) %>%
ggplot(aes(x = key, y = p_redistributed * p_original)) +
geom_col(aes(fill = as.factor(from)),
position = position_stack()) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(labels = scales::percent_format(),
breaks = seq(0, 1, 0.05)) +
scale_fill_discrete(h = c(120, 360)) +
theme_minimal(base_family = "Roboto") +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank()) +
labs(title = 'Balancing the "Human RNG distribution"',
subtitle = "{closest_state}",
x = "",
y = NULL) +
transition_states(
state,
transition_length = 4,
state_length = 3
) +
ease_aes('cubic-in-out')
animate(
redistribute_anim,
start_pause = 8,
end_pause = 8
)Отлично! Теперь у нас есть функция перераспределения. Давайте поближе посмотрим, как именно движется масса:
balanced_probabilities %>%
ggplot(aes(x = from, y = to)) +
geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) +
geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) +
scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) +
scale_fill_discrete(h = c(120, 360)) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(breaks = 1:10) +
theme_minimal(base_family = "Roboto") +
theme(panel.grid.minor = element_blank(),
panel.grid.major = element_line(linetype = "dotted"),
legend.position = "none") +
labs(title = "Probability mass redistribution",
x = "Original number",
y = "Redistributed number")Эта диаграмма говорит, что примерно в 8% случаев, когда кто-то называет восемь в качестве случайного числа, вам нужно воспринимать ответ как единицу. В остальных 92% случаев он остаётся восьмёркой.
Было бы довольно просто решить задачу, если бы у нас был доступ к генератору равномерно распределённых случайных чисел (от 0 до 1). Но у нас только комната, полная людей. К счастью, если вы готовы примириться с несколькими небольшими неточностями, то из людей можно сделать довольно хороший ГСЧ, не спрашивая более двух раз.
Возвращаясь к нашему исходному распределению, у нас есть следующие вероятности для каждого числа, которые можно использовать для повторного назначения любой вероятности, если необходимо.
probabilities %>%
transmute(number = outcome,
probability = scales::percent(p))## # A tibble: 10 x 2 ## number probability ## <dbl> <chr> ## 1 1 3.4% ## 2 2 8.5% ## 3 3 10.0% ## 4 4 9.7% ## 5 5 12.2% ## 6 6 9.8% ## 7 7 28.1% ## 8 8 10.9% ## 9 9 5.4% ## 10 10 1.9%
Например, когда кто-то даёт нам восемь в качестве случайного числа, нужно определить, должна ли эта восьмёрка стать единицей или нет (вероятность 8%). Если мы спросим другого человека о случайном числе, то с вероятностью 8,5% он ответит «два». Так что если это второе число равно 2, мы знаем, что должны вернуть 1 как равномерно распределённое случайное число.
Распространив эту логику на все числа, получаем следующий алгоритм:
По этому алгоритму вы можете использовать группу людей для получения чего-то близкого к генератору равномерно распределённых случайных чисел от 1 до 10!
Сегодня сложная тема, но мы объясним её просто и понятно. Разговор пойдёт про алгоритмы и немного про математику.
Методы Монте-Карло — это набор методов в математике для изучения случайных процессов. Случайных — это когда что-то в них происходит непредсказуемым образом, например:
- подбрасываем монетку;
- кидаем кубик;
- опускаем жетоны в ячейки со столбиками;
- ловим элементарные частицы;
- считаем столкновения молекул;
- и что угодно ещё, что происходит полностью случайно и что нельзя предсказать заранее.
Смысл методов Монте-Карло в том, чтобы использовать данные случайных событий, чтобы на их основе получить более-менее точные результаты каких-то других вычислений. Они не будут идеально и математически точными, но их уже будет достаточно, чтобы с ними полноценно работать. Иногда это проще и быстрее, чем считать всё по точным формулам.
Пример такого вычисления — построение маршрута в навигаторе. В исходном виде это задача коммивояжёра, которая требует колоссальных вычислительных ресурсов. Но благодаря приближённым методам с ней справится даже не самый мощный телефон. Один из таких методов — метод Монте-Карло.
Своё название метод получил в честь Монте-Карло — района Монако, где находится много казино с рулеткой, самым доступным источником случайных чисел в начале 20-го века.
В чём идея метода
Если совсем примитивно, то работает так:
Вместо того чтобы строить сложную математическую модель, мы берём простую формулу и пуляем в неё случайные числа. Считаем результат по каждому числу и получаем результат с нужной нам точностью. Чем больше случайных чисел — тем точнее результат.
Вот то же самое немного подробнее:
- Выбираем, что мы хотим найти или посчитать — значение формулы, площадь, объём, распределение материала или что-то ещё.
- Смотрим, как это считается в математике, и находим нужные формулы.
- На основе формул составляем критерий проверки — если случайное значение попало в этот критерий, мы его учитываем как совпавшее число, а если не попало — как не совпавшее.
- Запускаем алгоритм, который выдаёт случайные числа, и проверяем каждое по этому критерию.
- Как наберётся достаточное количество случайных чисел — считаем результат. Обычно это соотношение чисел, которые попали в критерий и которые не попали.
Чем больше будет случайных чисел — тем точнее результат.
Плюс этого метода в том, что нам не нужно запрягать весь математический аппарат для решения задачи — достаточно подставлять числа в формулу и смотреть, получилось верное значение или нет.
Как найти число пи методом Монте-Карло
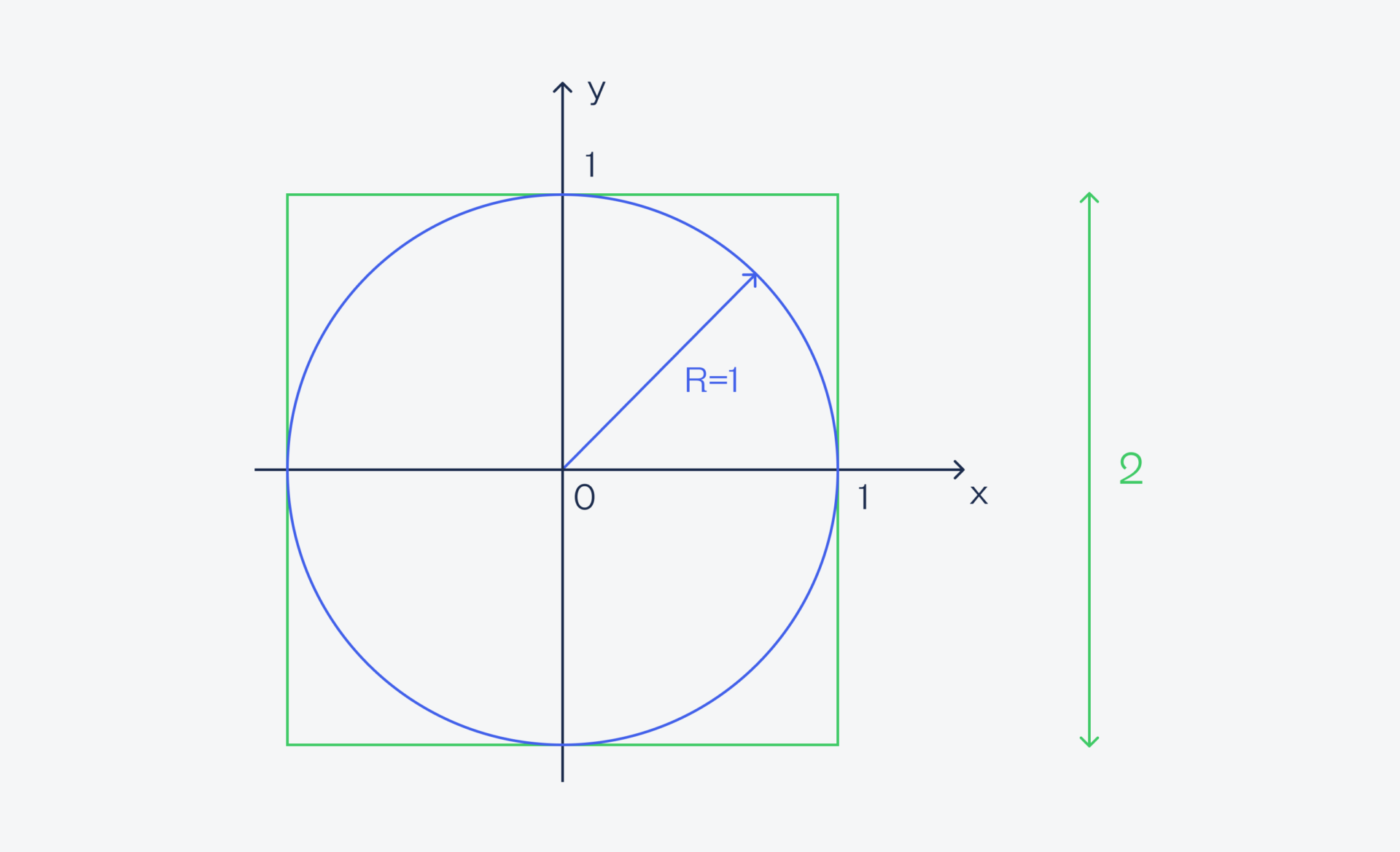
Для примера покажем классическое использование метода Монте-Карло — найдём число пи. Для этого нам понадобится круг, вписанный в квадрат, причём у круга радиус будет равен 1. Это значит, что сторона квадрата равна 2 — это диаметр (или два радиуса) круга:
В этот квадрат мы будем случайным образом кидать песчинки и смотреть, попадут они в круг или нет (но останутся в границах квадрата). Исходя из этого набора данных мы можем посчитать отношение всех песчинок, которые попали в круг, ко всем песчинкам.
Теперь смотрим на формулы:
- площадь квадрата со стороной 2 равна четырём;
- площадь круга радиусом 1 равна πR² → π×1² = π.
Если мы разделим площадь круга на площадь квадрата, то получим π / 4. Но мы ещё не можем по условию посчитать площадь круга, потому что мы не знаем число π. Вместо этого мы можем разделить количество одних песчинок на другие — в этом и суть метода Монте-Карло.
Это соотношение даст нам результат — π / 4. Получается, что если мы умножим этот результат на 4, то получим число π, причём чем больше песчинок мы кинем, тем точнее будет результат.
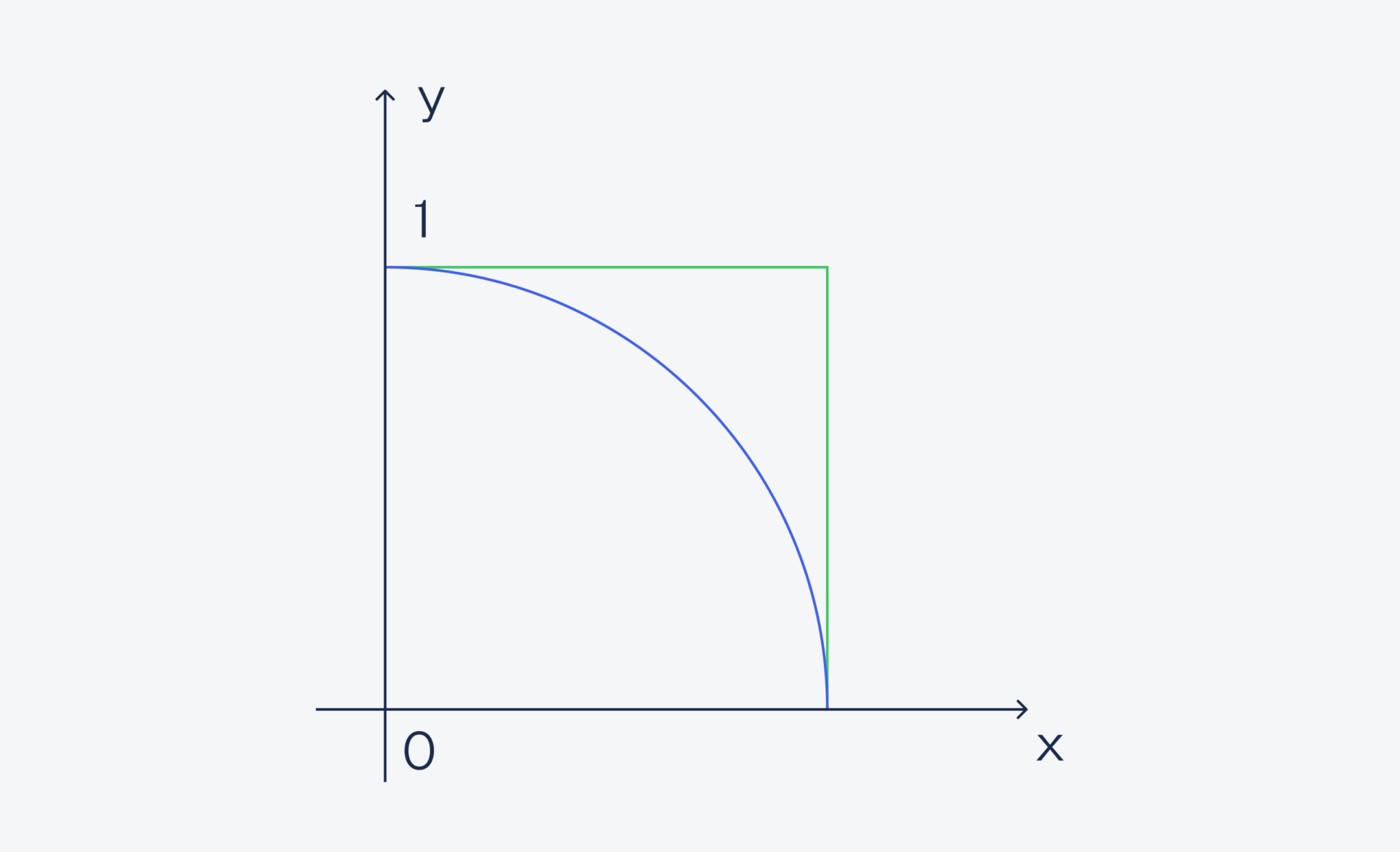
Кидать песчинки будем так: в качестве координат попадания X и Y будем брать случайные числа от 0 до 1. Это значит, что все числа попадут только в один квадрант — правый верхний:
Но так как в этом квадранте ровно четверть круга и ровно четверть квадрата, то соотношение промахов и попаданий будет таким же, как если бы мы бросали песчинки в целый круг и целый квадрат.
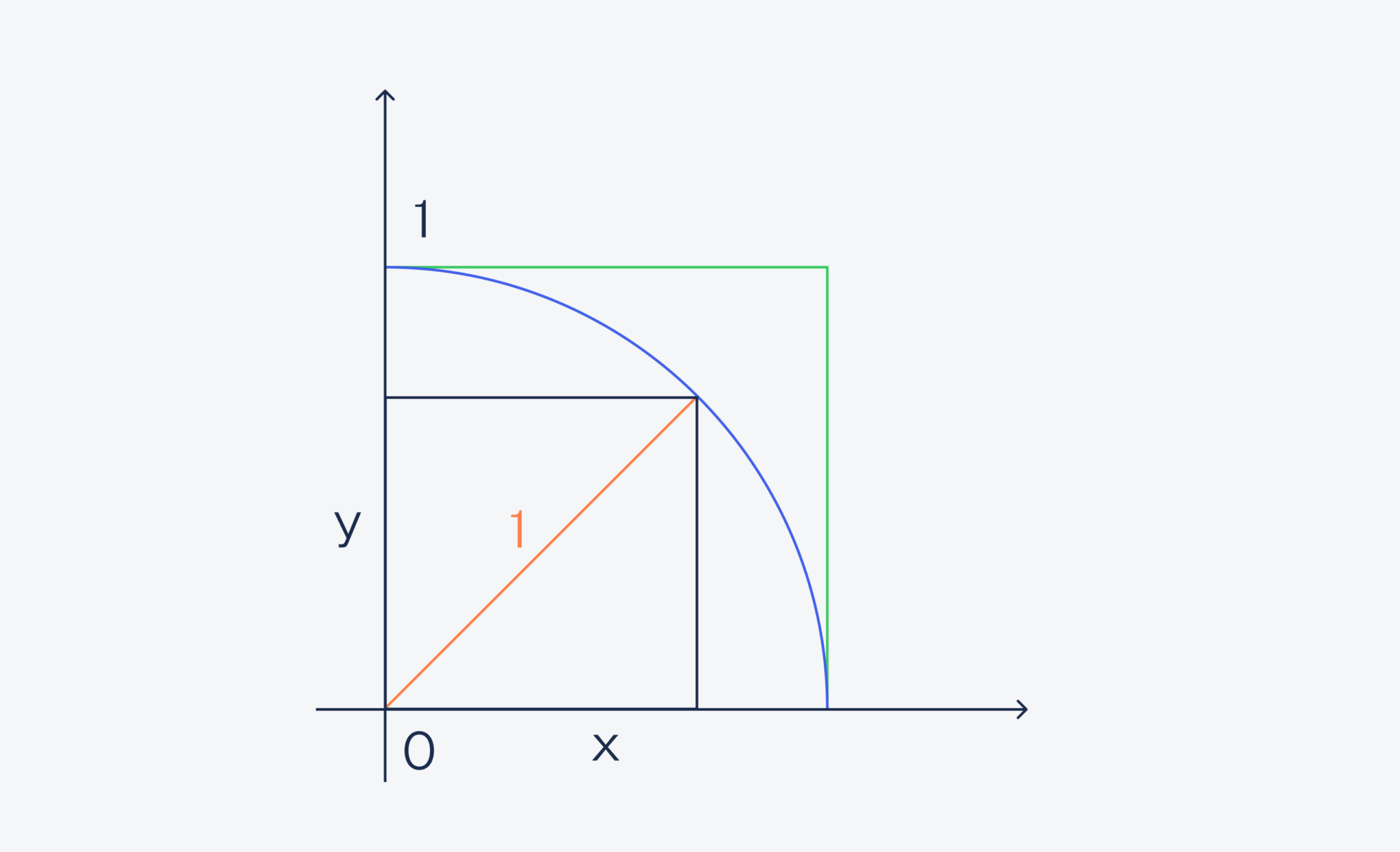
Чтобы проверить, попадает ли песчинка в круг, используем формулу длины гипотенузы: x² + Y² = 1 (так как гипотенуза — это радиус окружности):
Если длина гипотенузы меньше единицы — точка попадает в круг. В итоге мы посчитаем и общее количество точек, и точек, которые попали в круг. Потом мы разделим одно на другое, умножим результат на 4 и получим приближённое значение числа π.
Программируем поиск числа пи по методу Монте-Карло
Алгоритм на языке Python, читайте комментарии, чтобы лучше разобраться в происходящем:
# подключаем модуль случайных чисел
import random
# функция, которая посчитает число пи
def count_pi(n):
# общее количество бросков
i = 0
# сколько из них попало в круг
count = 0
# пока мы не дошли до финального броска
while i < n:
# случайным образом получаем координаты x и y
x = random.random()
y = random.random()
# проверяем, попали мы в круг или нет
if (pow(x, 2) + pow(y, 2)) < 1:
# если попали — увеличиваем счётчик на 1
count += 1
# в любом случае увеличиваем общий счётчик
i += 1
# считаем и возвращаем число пи
return 4 * (count / n)
# запускаем функцию
pi = count_pi(1000000)
# выводим результат
print(pi)Где ещё используется метод Монте-Карло
На методах Монте-Карло основано много полезного:
- моделирование облучения твёрдых тел ионами в физике;
- моделирование поведения разреженных газов
- исследования поведения разных тел при столкновении
- алгоритмы оптимизации и нахождения кратчайшего пути решения
- решение сложных интегралов (или когда их очень много)
- предсказание астрономических наблюдений
- поиск в дереве в различных алгоритмах
- алгоритмы работы некоторых функций квантового компьютера
- моделирование состояния приближённой физической среды
Без них изучать современный мир и совершать новые открытия было бы сложнее.
Что дальше
В следующей части поговорим про отжиг — интересное применение метода Монте-Карло, который имитирует физические процессы. Благодаря отжигу мы можем обучать нейросети и решать сложные комбинаторные задачи.
Вёрстка:
Кирилл Климентьев
Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.
В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.
Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.
Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.
Создание случайных чисел из семени
Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.
Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.
Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.
R(Input) -> Output
Начнём с того, что R — это простая функция, которая всего лишь прибавляет единицу.
R(x) = x + 1
Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, … Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.
R(x) = x + c
Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, … Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало — круг из чисел!
Числовой круг
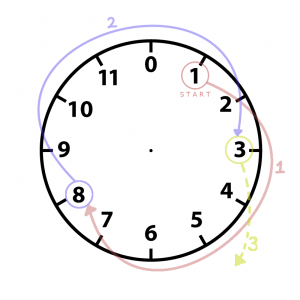
Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.
Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.
Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.
R(x) = (x + c) % m
На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, … что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.
Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.
До сих пор мы делали «прыжки» за счёт добавления, но что если использовать умножение? Умножим х на константу a.
R(x) = (ax + c) % m
Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:
- (а — 1) должно делиться на все простые множители m
- (а — 1) должно делиться на 4, если m делится на 4
Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.
Выбор семени
Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.
Еще один способ — это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.
Конечный результат
Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:
x(n) = (a * x(n - 1) + c) % m
Где начальное значение х — это семя, а — множитель, с — константа, m — оператор остатка от деления.
То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.
В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.
Заключительные замечания
Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.
Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.
На этом всё, спасибо что прочитали!
Оригинал статьи
Библиографическое описание:
Гончарук, В. С. Методы генерации случайных чисел / В. С. Гончарук, Ю. С. Атаманов, С. Н. Гордеев. — Текст : непосредственный // Молодой ученый. — 2017. — № 8 (142). — С. 20-23. — URL: https://moluch.ru/archive/142/40025/ (дата обращения: 25.05.2023).
Случайные числа играют довольно важную роль для программистов разной направленности. Чаще всего случайные числа требуются в задачах моделирования, численного анализа, тестирования, криптографии и теории игр, но существует и множество других весьма специфических задач.
Но для начала давайте разберемся с понятием случайных чисел. Само понятие «случайное число» пришло из такого раздела математики, как теория вероятности, и всегда рассматривается в контексте какой-то последовательности, которая характеризуется тем, что каждое число последовательности не зависит от всех остальных чисел последовательности, то есть случайное число непредсказуемо, никогда нельзя с полной уверенностью предугадать, какое будет следующее число в случайной последовательности. Кроме того, случайные числа должны подчиняться равномерному распределению, то есть вероятность появления каждого числа равновероятна.
Теперь, когда у нас есть понимание, что такое случайные числа и для каких целей они необходимы, стоит вопрос получения какой-то случайной последовательности. Человек очень плох в качестве генератора случайных чисел. Это связано с нашим неверным интуитивным пониманием теории вероятностей. Компьютер справляется с задачей построения последовательности случайных чисел гораздо лучше.
Все генераторы случайных чисел делятся на два вида:
‒ True random number generator (ГНСЧ, генератор настоящих случайных чисел)
‒ Pseudo random number generator (ГПСЧ, генератор псевдослучайных чисел)
Эти два генератора задания случайной последовательности отличаются способом получения случайного числа.
ГНСЧ использует в качестве механизма получения случайного числа некий физический процесс, который сам по себе является непредсказуемым. Если оцифровать такой процесс (например, шумы атмосферы), то можно использовать его для генератора случайных чисел. ГПСЧ в свою очередь использует математические алгоритмы (полностью производимые компьютером) [2].
Рассмотрим сравнительную таблицу 1, которая показывает отличия между ГНСЧ и ГПСЧ.
Таблица 1
Отличия ГНСЧ иГПСЧ
|
ГНСЧ |
ГПСЧ |
|
|
1) Механизм |
Физический процесс |
Математика |
|
2) Равномерное распределение |
✔ |
✔ |
|
3) Независимость |
✔ |
✖ |
|
4) Скорость |
✖ |
✔ |
Стоить отметить, что, используя ГПСЧ, мы вычисляем наши числа по какой-то формуле, то естественно они будут как-то связаны между собой, поэтому псевдо-генераторы не обладают свойством независимости, они всегда связаны между собой, но этот недостаток компенсирует высокая скорость вычисления, так как какой-то физический процесс получает эти числа гораздо медленнее нежели чем, если мы будем вычислять их на процессоре.
Далее рассмотрим один из распространённых методов генерации псевдослучайных чисел — линейный конгруэнтный метод. В большинстве языков программирования именно этот метод используется в стандартной функции получения случайных чисел.
В линейном конгруэнтным методе случайное число вычисляется по следующей рекуррентной формуле: , где
— модуль (
),
— множитель (
),
— приращение (
),
— начальное значение, которое также иногда называют зерном (от англ. seed) (
).
Рассмотрим работу данного алгоритма при следующих значениях: ,
,
,
при 50 итерациях. Результаты вычислений представлены в виде графика на рис. 1.
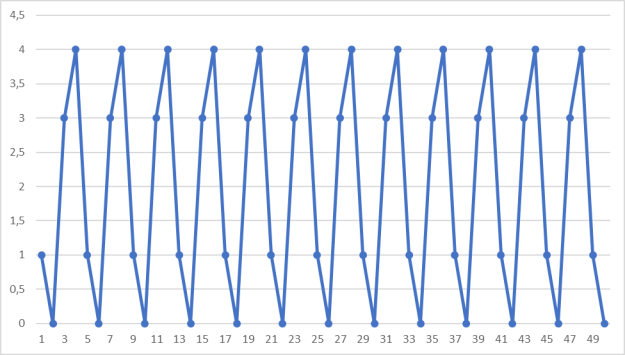
Рис. 1. Пример работы алгоритма при ,
,
,
Как видно из графика, данный метод даёт нам повторяющиеся последовательности, но задача состоит в том, чтобы максимально удлинить уникальную часть последовательности (граница длины уникальной части определяется величиной ).
Теперь пусть (рис. 2).
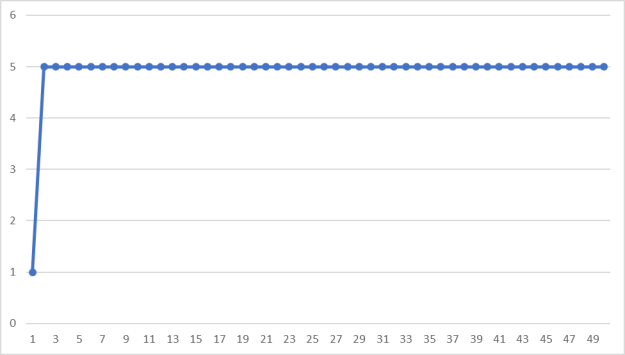
Рис. 2. Пример работы алгоритма при ,
,
,
Как видно, последовательность сразу же начинает повторяться. Это происходит потому, что должно быть простым числом, чтобы периоды были гораздо больше. Вообще говоря, все коэффициенты формулы не должны быть случайными, чтобы полученная в результате последовательность была более случайной.
Теперь в качестве возьмём большое простое число, пусть
(рис. 3).
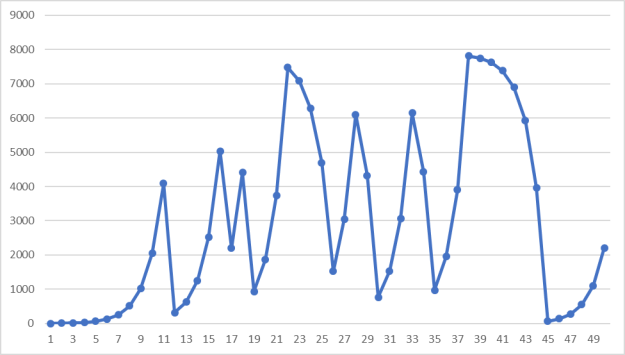
Рис. 3. Пример работы алгоритма при ,
,
,
Как видно, если является большим простым числом, то случайная последовательность ведёт себя вполне непредсказуемо. При удачно подобранных коэффициентах данный метод может давать достаточно случайные числа.
Однако применять данный метод стоит в достаточно простых случаях, так как он не обладает криптографической стойкостью, так как зная четыре подряд идущих числа, криптоаналитик может составить систему уравнений, из которой можно найти ,
и
.
Также существуют более случайные и надёжные модифицированные варианты данного метода генерации последовательностей псевдослучайных чисел. Кроме данного алгоритма применяется и ряд других алгоритмов, которые основаны на другой математике.
Литература:
- Генерация псевдослучайных чисел // habrahabr.ru. URL: https://habrahabr.ru/post/132217/ (дата обращения: 22.02.2017).
- Pseudorandom number generator // en.wikipedia.org. URL: https://en.wikipedia.org/wiki/Pseudorandom_number_generator (дата обращения: 22.02.2017).
- William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. — 2nd ed. — Cambridge University Press, 1992. — P. 277. — ISBN 0–521–43108–5.
Основные термины (генерируются автоматически): число, случайное число, простое число, работа алгоритма, случайная последовательность, Равномерное распределение.