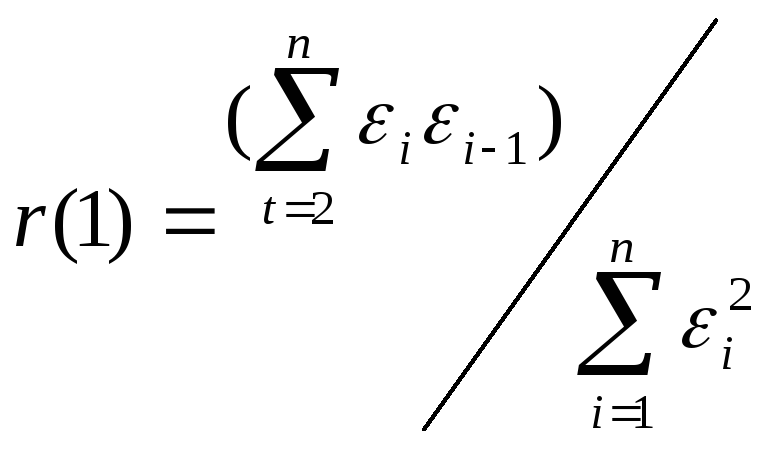Как найти случайный остаток - Исправление недочетов и поиск решений вместе с Examum.ru

Первая предпосылка
МНК– проверка случайного характера
остатков. С этой целью строится график
зависимости остатков от теоретических
значений результативного признака.

Если на графике
получена горизонтальная полоса, то
остатки представляют собой случайные
величины и МНК оправдан, теоретические
значения результативного признака
хорошо аппроксимируют фактические
значения у. возможны следующие случаи:
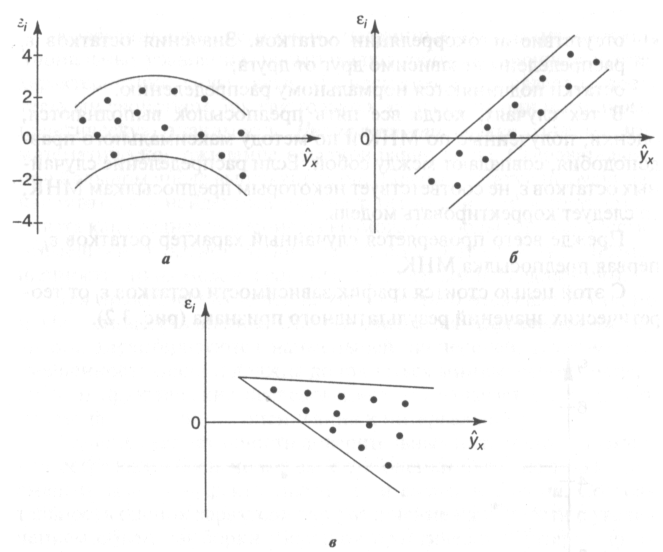
если остатки зависят от теоретических
значений результирующей переменной:

– остатки не
случайны (рис. 3,3а)

– остатки не имеют
постоянной дисперсии (в)

– остатки носят
систематический характер (б), в данном
случае отрацательные значения остатков
соответствуют низким теоретическим
значениям у, а положительные – высоким
значениям. В
случаях а),
б), в) (рис.
3.3) необходимо либо применять другую
функцию, либо вводить дополнительную
информацию и заново строить уравнение
регрессии до тех пор, пока остатки е, не
будут
случайными величинами.

30. Проверка гипотезы о нормальном распределении ряда остатков.

Нормальность
распределения ряда остатков означает
однородность дисперсий наблюдения.
Определяется с помощью R/S-критерия:

; если
нормальный
закон распределения остатков выполняется.

31. D-критерий Дарбина-Уотсона.

Независимость
остатков проверяется с помощью критерия
Дарбина—Уотсона.

Корреляционная
зависимость между текущими уровнями
некоторой переменной и уровнями этой
же переменной, сдвинутыми на несколько
шагов, называется автокорреляцией.

Автокорреляция
случайной составляющей нарушает одну
из предпосылок нормальной линейной
модели регрессии.

Наличие (отсутствие)
автокорреляции в отклонениях проверяют
с помощью критерия Дарбина—Уотсона.
Численное значение коэффициента равно

Значение dw
статистики близко к величине 2(1 — г(1)),
где г(1) — выборочная автокорреляционная
функция остатков первого порядка. Таким
образом, значение статистики Дарбина—Уотсона
распределено в интервале 0—4. Соответственно
идеальное значение статистики — 2
(автокорреляция отсутствует). Меньшие
значения критерия соответствуют
положительной автокорреляции остатков,
большие значения — отрицательной.
Статистика учитывает только
автокорреляцию первого порядка. Оценки,
получаемые по критерию, являются не
точечными, а интервальными. Верхние
(d₂)
и нижние
(d₁)
критические значения, позволяющие
принять или отвергнуть гипотезу об
отсутствии автокорреляции, зависят от
количества уровней динамического ряда
и числа независимых переменных
модели. Значения этих границ для уровня
значимости α = 0,05 даны в специальных
таблицах. При сравнении расчетного
значения dw
статистики с табличным могут возникнуть
такие ситуации: d₂
< dw
< 2
— ряд остатков не коррелирован; dw
< d_}
— остатки
содержат автокорреляцию; d₁
< dw
< d₂
— область
неопределенности, когда нет оснований
ни принять, ни отвергнуть гипотезу о
существовании автокорреляции. Если
d
превышает 2, то это свидетельствует о
наличии отрицательной корреляции. Перед
сравнением с табличными значениями
dw
критерий
следует преобразовать по формуле dw’
= 4 – dw.

Установив наличие
автокорреляции остатков, переходят к
улучшению модели. Если же ситуация
оказалась неопределенной (d₁
< dw<
d₂
) применяют другие критерии. В частности,
можно воспользоваться первым коэффициентом
автокорреляции

Для принятия
решения о наличии или отсутствии
автокорреляции в исследуемом ряду
фактическое значение коэффициента
автокорреляции r(1)
сопоставляется
с табличным (критическим) значением для
5%-ного уровня значимости (вероятности
допустить ошибку при принятии нулевой
гипотезы о независимости уровней ряда).
Если фактическое значение коэффициента
автокорреляции меньше табличного,
то гипотеза об отсутствии автокорреляции
в ряду может быть принята, а если
фактическое значение больше табличного
— делают вывод о наличии автокорреляции
в ряду динамики.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Рассмотрим некоторые методы проверки выполнения предпосылок
Гаусса-Маркова и приемы исследования в случаях, когда они нарушаются.
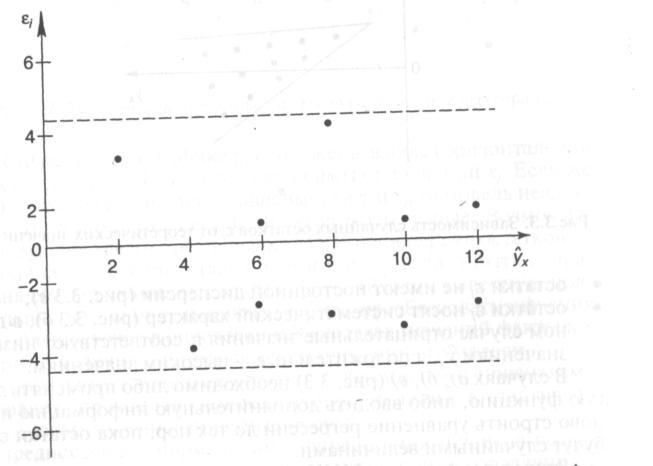
Способ проверки остатков на случайный характер
Для проверки остатков на случайный характер строят график
зависимости случайной компоненты от значений результативного признака:
ε
y
Если значения остатков расположены вблизи горизонтальной прямой
(оси абсцисс), то их можно считать случайными (как на рисунке выше).
На рисунке ниже остатки носят систематический характер:
ε
y
Зависимость регрессионного остатка от значений
результативного признака (систематический характер остатков)
На следующем рисунке дисперсия остатков, соответствующих
большим значениям y, больше, чем дисперсия при малых y, т.е. имеет место
гетероскедастичность остатков:
ε
y
Гетероскедастичность остатков
Кроме того, существует ряд специальных тестов, разработанных для
проверки остатков на гомоскедастичность и отсутствие автокорреляции.
Наиболее известным тестом для проверки на гомоскедастичность
является
тест
Голдфелда-Квандта,
а
для
проверки
остатков
на
автокорреляцию — тест Дарбина-Уотсона. Студентам рекомендуется изучить
их самостоятельно.
Обобщенный МНК
Рассмотрим
гомоскедастичность
отдельно
и
две
отсутствие
важные
предпосылки
автокорреляции
остатков.
МНК:
Взяв
n
наблюдений, для каждого из них можно получить регрессионный остаток ε1,
ε2, …, εn. Каждый из этих остатков сам по себе является случайной
величиной. Для этих случайных величин можно построить ковариационную
матрицу, на диагонали которой будут стоять дисперсии остатков, а
остальные элементы будут представлять собой ковариации между ними
(матрица симметрична относительно главной диагонали):
ε1
ε2
εn
…
ε1  σ2 (ε1 )
Cov(ε1, ε2 )

ε2  Cov(ε1 , ε2 )
σ2 (ε2 )
Ω= 
…
…
…

εn  Cov(ε1 , εn ) Cov(ε2 , εn )
… Cov(ε1 , εn ) 

… Cov(ε2 , εn ) 

…
…

2
…
σ (εn ) 
Если остатки гомоскедастичны, то элементы на главной диагонали
этой матрицы будут равны между собой. Если автокорреляция остатков
отсутствует, то ненулевые элементы этой матрицы могут стоять только на
главной диагонали. Существенное отличие любого другого элемента
матрицы от нуля означает, что регрессионные остатки коррелируют.
Как уже было сказано, гетероскедастичность и автокорреляция
остатков приводят к
тому,
что
оценки, полученные
МНК, будут
неэффективными. Исключить то и другое можно с помощью модификации
МНК – обобщенного метода наименьших квадратов (ОМНК), суть
которого сводится к тому, что при нахождении вектора параметров А
используют не формулу, которую мы ранее получили для матричной формы
МНК, а следующую формулу:
А = (XТΩ-1X)-1XТΩ-1Y,
где Ω-1 – матрица, обратная ковариационной матрице Ω.
Можно доказать, что при использовании этой формулы оценки будут
обладать свойством эффективности (теорема Айткена). Доказательство
можно найти, например, в [Яновский Л.П., Буховец А.Г. Введение в
эконометрику: уч. пособие – 2-е изд., доп. – М.: Кнорус, 2007. – 256 с.].
Исключение гетероскедастичности с помощью ОМНК
Предположим,
что
выполняется
требование
равенства
математического ожидания регрессионного остатка нулю. Тогда дисперсия
регрессионных остатков равна просто ожидаемому квадрату остатка:
σ2(ε) = M(ε – M(ε))2 = M(ε2); σ2(εi) = M(εi2).
Предположим, что требование отсутствия автокорреляции остатков
тоже выполняется. Тогда ковариационная матрица остатков примет вид
диагональной матрицы (ненулевые элементы стоят только на главной
диагонали):
ε1
ε2
ε1  σ2 (ε1 )

ε2  0
σ2 (ε2 )
Ω= 
… …
…

εn  0
…
εn


…
… 
…
… 
… σ2 (εn ) 
…
Пусть остатки гетероскедастичны, т.е. элементы на главной диагонали
матрицы не равны между собой. Применение ОМНК с такой ковариационной
матрицей сведется к тому, что в каждом i–м наблюдении все значения
переменных будут поделены на одно и то же число σ2(εi). Такая модификация
ОМНК называется взвешенным МНК.
Однако в реальных экономических задачах дисперсии регрессионных
остатков для отдельных наблюдений неизвестны, и нет возможности
построить ковариационные матрицы ни в каком виде. Поэтому вместо этих
матриц обычно используют какую-либо их оценку.
Для определения коэффициентов при использовании взвешенного
МНК может быть использован следующий подход. Предположим, что
дисперсии остатков σ2(εi) пропорциональны величине σ2(ε) (дисперсии
генеральной совокупности значений случайной компоненты). Коэффициенты
пропорциональности обозначим Кi, — эти коэффициенты характеризуют
неоднородность дисперсии (способ их нахождения обсудим позже). Получим
для каждого из n наблюдений:
σ2(εi) = σ2(ε) * Кi
В основе применения МНК к линеаризованной функции лежит
соотношение (на примере парной линейной регрессии), которое может быть
n
n
i =1
i =1
2
2
представлено следующим образом: ∑ (ax i + b − y i ) = ∑ ( εi ) . Если в левой
части этого выражения каждое слагаемое в скобках разделить на
K i , то в
результате каждое слагаемое в правой части будет скорректировано на
величину Кi. Поскольку из σ2(εi)/Кi = σ2(ε), можно условно считать, что после
такого преобразования данные будут гомоскедастичны, т.е. иметь общую
дисперсию σ2(ε).
Итак, чтобы применить к парной линейной регрессии ОМНК в случае
гетероскедастичности остатков, необходимо обе части уравнения y = ax + b
разделить на
K i для всех наблюдений:
yi
Ki
=a
xi
Ki
+ b
Ki
, i = 1, n
Чтобы это сделать, исходные данные модели – значения xi и yi, делят
на
K i . Одновременно осуществляют замену переменных
γi =
yi
Ki
; αi =
xi
Ki
; βi = 1
Ki
, i = 1, n
Значения новых переменных γ и α представляют собой значения
показателей, взвешенные на коэффициенты β i = 1
Ki
. В общем случае эти
веса надо задать для каждого наблюдения (каждой пары γi и αi).
После такой замены уравнение регрессии примет вид
γ = a * α + b *β
Полученное
множественной
выражение
(двухфакторной)
представляет
линейной
собой
регрессии,
уравнение
в
которой
результативный признак обозначен γ, а признаки-факторы — α и β. Параметры
регрессии a и b можно найти из системы нормальных уравнений. В данном
случае первое уравнение в системе следует опустить, так как свободный член
регрессии здесь равен нулю (здесь оба параметра — a и b — представляют собой
коэффициенты при переменных). Система примет вид:
a ∑ α 2 + b∑ αβ = ∑ γα

2
 a ∑ αβ + b∑ β = ∑ γβ
где
n
n
n
n
n
i=1
i =1
i =1
∑ α2 =∑ αi ; ∑β2 = ∑βi ; ∑ αβ = ∑ αiβi ; ∑ γα = ∑ γ i αi ;∑ γβ = ∑ γ iβi
2
i=1
2
i=1
Каким образом определяются
коэффициенты
Кi?
Существуют
различные подходы к их определению, и выбор любого из них неизбежно
влияет на значение полученных параметров модели.
Иногда предполагают, что этими коэффициентами являются сами
значения фактора. В многофакторной модели при этом одновременно встает
проблема выбора одного из факторов (того, значения которого будут
использованы при расчете весов). Например, можно взять последний по
порядку фактор в множественной регрессии.
Следует отметить, что при этом, чем меньше значение фактора, тем на
меньшую величину будет поделена величина дисперсии, т.е. весовой
коэффициент 1
Ki
будет больше. Тем самым повышаются веса дисперсий
ошибок в наблюдениях с меньшими значениями. Это говорит о том, что
предположение о пропорциональности между коэффициентами Кi и
значениями фактора может быть вполне обосновано с экономической точки
зрения: большим значениям фактора действительно может соответствовать
большая дисперсия, которую необходимо умножить на меньший вес, чтобы
добиться гомоскедастичности.
Исключение автокорреляции в остатках с помощью ОМНК
Рассмотрим случай автокорреляции остатков для модели, в которой
наблюдения упорядочены во времени. Будем считать, что M(ε) = 0, и остатки
гомоскедастичны.
Возьмем так называемый авторегрессионный процесс первого
порядка, когда каждое последующее значение случайной компоненты
связано с предыдущим линейной зависимостью:
εt = pεt-1 + υt,
где t = 1, 2, …, n – номера последовательных наблюдений;
υt — случайная компонента построенной зависимости1, имеющая
нулевое математическое ожидание и дисперсию σ02, не подверженная
автокорреляции;
p — коэффициент авторегрессии.
Так как величины и независимы, дисперсию суммы можно посчитать
по следующей формуле (постоянный сомножитель выносим за скобки,
возводя в квадрат, по свойству дисперсии):
D(εt) = p2D(εt-1) + D(υt)
Поскольку остатки гомоскедастичны, D(εt) = D(εt-1) = σ2, получим:
σ 2 = p 2σ 2 + σ 02
σ 02
σ =
1 − p2
2
1
Обычно предполагается, что эта случайная величина имеет
нормальное распределение.
Отсюда следует, что |p| < 1 (так как величина дисперсии должна быть
положительной).
Найдем ковариацию2 двух соседних остатков, подставляя вместо εt
выражение (pεt-1 + υt). При этом учтем, что математическое ожидание
каждого из них равно нулю, и что математическое ожидание произведения
независимых случайных величин εt-1 и υt, можно рассчитать, как
произведение математических ожиданий:
Cov( ε t , ε t −1 ) = M ( ε t * ε t −1 ) − 0 = М ( ε t −1 * ( pε t −1 + υt )) =
= М ( pε t −1 ) + М ( ε t −1υ t ) = p * D( ε t −1 ) + M ( ε t −1 * υ t ) = рσ 2
2
Можно
показать,
что
ковариации
любой
пары
остатков
рассчитываются по формуле:
Cov( ε t , ε t − k ) = р k σ2
Тогда ковариационная матрица примет вид:
ε1
ε2
ε1  1
p

ε  p
1
Ω = σ2 2 
… …
…

εn  pn −1 pn −2
…
εn
… pn −1 

n−2
… p 
… … 

… 1 
Если параметр p известен, то для нахождения параметров линейной
функции регрессии можно применить ОМНК.
Покажем, что при этом будет устранена автокорреляция остатков.
Рассмотрим множественную линейную регрессию y = a1x1 + a2x2 +
2
Для расчета ковариации в теории вероятностей можно использовать
следующую формулу: Cov (x,y) = M(x*y) – M(x)*M(y) (рекомендуется
сравнить с формулой, используемой в статистике: Cov( x, y) = xy − x * y .
+ … + amxm + b + ε. Запишем уравнения регрессии для периодов t и (t – 1),
умножив обе части последнего уравнения на p:
yt = a1x1t + a2x2t + … + amxmt + b + εt
pyt-1 = pa1x1 t-1 + pa2x2 t-1 + … + pamxm t-1 + pb + pεt-1
Вычтем из первого уравнения второе, преобразовав результат к
следующему виду:
yt — pyt-1 = a1(x1t — px1 t-1) + a2(x2t – px2 t-1) + … +
+ am(xmt – pxm t-1) + b(1 – p) + εt — pεt-1
Применив формулу (εt = pεt-1 + υt), получим
yt — pyt-1 = a1(x1t — px1 t-1) + a2(x2t – px2 t-1) + … +
+ am(xmt – pxm t-1) + b(1 – p) + υt
В новой модели устранена автокорреляция остатков, так как новые
остатки — υt — независимы.
Для определения неизвестного параметра авторегрессии p можно
использовать различные методы оценки. Проще всего оценить его с
помощью обычного МНК, применяя его к уравнению авторегрессии остатков
εt = pεt-1 + υt. Способ получения оценки дисперсии регрессионных остатков σ2
будет рассмотрен позже. С помощью оценок p и σ2 можно получить оценку
ковариационной матрицы для применения ОМНК. Такой способ нахождения
этой матрицы получил название доступного ОМНК.

Источник

Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.

Одна переменная x известна как предикторная переменная. Другая переменная, y , известна как переменная ответа .

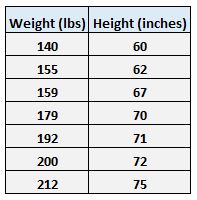
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:

Пусть вес будет предикторной переменной, а рост — переменной отклика.

Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:

На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.

Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным:

Формула для этой линии наилучшего соответствия записывается так:

ŷ = б 0 + б 1 х

где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.

В этом примере линия наилучшего соответствия:

рост = 32,783 + 0,2001*(вес)

Как рассчитать остатки

Обратите внимание, что точки данных на нашей диаграмме рассеяния не всегда точно попадают на линию наилучшего соответствия:

Эта разница между точкой данных и линией называется остатком.Для каждой точки данных мы можем рассчитать остаток этой точки, взяв разницу между ее фактическим значением и прогнозируемым значением из линии наилучшего соответствия.

Пример 1: Расчет остатка

Например, вспомните вес и рост семи человек в нашем наборе данных:

Первая особь имеет вес 140 фунтов. и высотой 60 дюймов.

Чтобы узнать прогнозируемый рост для этого человека, мы можем подставить его вес в уравнение наилучшего соответствия:

рост = 32,783 + 0,2001*(вес)

Таким образом, прогнозируемый рост этого человека:

высота = 32,783 + 0,2001*(140)

высота = 60,797 дюйма

Таким образом, невязка для этой точки данных составляет 60 – 60,797 = -0,797 .

Пример 2: Расчет остатка

Мы можем использовать тот же самый процесс, который мы использовали выше, для вычисления невязки для каждой точки данных. Например, давайте рассчитаем остаток для второго человека в нашем наборе данных:

Второй человек имеет вес 155 фунтов. и высотой 62 дюйма.

рост = 32,783 + 0,2001*(вес)

Таким образом, прогнозируемый рост этого человека:

высота = 32,783 + 0,2001*(155)

высота = 63,7985 дюйма

Таким образом, остаток для этой точки данных составляет 62 – 63,7985 = -1,7985 .

Вычисление всех остатков

Используя тот же метод, что и в предыдущих двух примерах, мы можем рассчитать остатки для каждой точки данных:

Обратите внимание, что некоторые остатки положительны, а некоторые отрицательны. Если мы сложим все остатки, они в сумме дадут ноль.

Это связано с тем, что линейная регрессия находит линию, которая минимизирует общие квадраты остатков, поэтому линия идеально проходит через данные, причем некоторые точки данных лежат над линией, а некоторые — под линией.

Визуализация остатков

Напомним, что невязка — это просто расстояние между фактическим значением данных и значением, предсказанным линией регрессии наилучшего соответствия. Вот как эти расстояния выглядят визуально на диаграмме рассеивания:

Обратите внимание, что некоторые остатки больше других. Кроме того, некоторые остатки положительны, а некоторые отрицательны, как мы упоминали ранее.

Создание остаточного графика

Весь смысл вычисления остатков состоит в том, чтобы увидеть, насколько хорошо линия регрессии соответствует данным.

Большие невязки указывают на то, что линия регрессии плохо соответствует данным, т. е. фактические точки данных не совпадают с линией регрессии.

Меньшие невязки указывают на то, что линия регрессии лучше соответствует данным, т. е. фактические точки данных располагаются близко к линии регрессии.

Одним из полезных типов графика для одновременной визуализации всех остатков является остаточный график. Остаточный график — это тип графика, который отображает прогнозируемые значения в сравнении с остаточными значениями для регрессионной модели.

Этот тип графика часто используется для оценки того, подходит ли модель линейной регрессии для данного набора данных, и для проверки гетероскедастичности остатков.

Ознакомьтесь с этим учебным пособием , чтобы узнать, как создать остаточный график для простой модели линейной регрессии в Excel.

Источник

From Wikipedia, the free encyclopedia

In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.^[1]^[2]^[3]

Introduction[edit]

Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.

A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.

A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:

The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
The difference between the height of each man in the sample and the observable sample mean is a residual.

Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.

One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.

In univariate distributions[edit]

If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have

${displaystyle X_{1},dots ,X_{n}sim Nleft(mu ,sigma ^{2}right),}$

and the sample mean

$overline{X}={X_1 + cdots + X_n over n}$

is a random variable distributed such that:

${displaystyle {overline {X}}sim Nleft(mu ,{frac {sigma ^{2}}{n}}right).}$

The statistical errors are then

${displaystyle e_{i}=X_{i}-mu ,,}$

with expected values of zero,^[4] whereas the residuals are

${displaystyle r_{i}=X_{i}-{overline {X}}.}$

The sum of squares of the statistical errors, divided by σ², has a chi-squared distribution with n degrees of freedom:

${displaystyle {frac {1}{sigma ^{2}}}sum _{i=1}^{n}e_{i}^{2}sim chi _{n}^{2}.}$

However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ² has a chi-squared distribution with only n − 1 degrees of freedom:

${frac 1{sigma ^{2}}}sum _{{i=1}}^{n}r_{i}^{2}sim chi _{{n-1}}^{2}.$

This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.

[edit]

It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:

${displaystyle T={frac {{overline {X}}_{n}-mu _{0}}{S_{n}/{sqrt {n}}}},}$

where ${displaystyle {overline {X}}_{n}-mu _{0}}$ represents the errors, $S_{n}$ represents the sample standard deviation for a sample of size n, and unknown σ, and the denominator term accounts for the standard deviation of the errors according to:^[5]

${displaystyle operatorname {Var} left({overline {X}}_{n}right)={frac {sigma ^{2}}{n}}}$

The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»^[6]

Regressions[edit]

In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.^[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.

However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.^[7]

Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).^[8]

However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:^[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.

Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.

Other uses of the word «error» in statistics[edit]

The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:

The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.

Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).

Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.

The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.

References[edit]

^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
^ ^a ^b A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Bruce, Peter C., 1953- (2017-05-10). Practical statistics for data scientists : 50 essential concepts. Bruce, Andrew, 1958- (First ed.). Sebastopol, CA. ISBN 978-1-4919-5293-1. OCLC 987251007.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.

Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]

External links[edit]

Media related to Errors and residuals at Wikimedia Commons

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Постановка задачи
2 Описание алгоритма
- 2.1 Анализ регрессионных остатков
- 2.2 Оценка значимости признаков
3 Гетероскедастичность
- 3.1 Визуальный анализ
- 3.2 Статистические методы детекции
  - 3.2.1 Тест Уайта
  - 3.2.2 Тест Голдфелда-Кванта
  - 3.2.3 Тест Ансари-Брэдли
- 3.3 Эвристика
4 Вычислительный эксперимент на модельных данных
- 4.1 Три модели
  - 4.1.1 Модель №1 (хорошая)
  - 4.1.2 Модель №2 (плохая, одномерная)
  - 4.1.3 Модель №3 (плохая,многомерная)
- 4.2 Выводы
5 Исходный код
6 См. также
7 Литература

Для получения информации об адекватности построенной модели многомерной линейной регрессии используется анализ регрессионных остатков.

Постановка задачи

Задана выборка $D = { y_i,mathbf{x}_i}_{i=1}^n$ откликов и признаков. Рассматривается множество линейных регрессионных моделей вида:

$y_i=sum_{j=1}^m w_j x_{ij} + varepsilon_i, i=1,dots,n$ . Требуется создать инструмент анализа адекватности модели используя анализ регрессионных остатков и исследовать значимость признаков и поведение остатков в случае гетероскедастичности.

Описание алгоритма

Анализ регрессионных остатков

Анализ регрессионных остатков заключается в проверке нескольких гипотез:

(1)
(2)
(3)
(4)

— независимы

где , , — регрессионные остатки конкретной модели. f_i — отклики посчитанные по модели, а y_i — эмпирические отклики.

Для проверки первой гипотезы воспользуемся критерием знаков.
Проверка второй гипотезы, по сути, является проверкой на гомоскедастичность, то есть на постоянство дисперсии, случай гетероскедастичности будет рассмотрен ниже. Для этого воспользуемся двумя статистическими тестами: тестом Ансари-Брэдли и критерием Голдфелда-Кванта.
Так как тест Ансари-Брэдли фактически осуществляет проверку гипотезы, что у двух предоставленных выборок дисперсии одинаковы, а мы фактически имеем только один вектор остатков, то произведем несколько тестов, сравнивая в каждом две случайные выборки из нашего вектора остатков.
Проверку нормальности распределения осуществим с помощью критерия согласия хи-квадрат, модифицированного для проверки на нормальность, то есть сравнивая данное нам распределение в остатках с нормальным распределением, имеющим моментные характеристики, вычисленные из вектора остатков. Наконец, проверку последнего условия реализуем с помощью статистики Дарбина-Уотсона.

Оценка значимости признаков

Задача состоит в проверке для каждого из признаков, дает ли нам учет этого признака в модели более хорошие результаты, нежели его отсутствие. Оценивать результаты будем с помощью коэффициента детерминации:

$R^2 equiv 1 - {sum_i (y_i - {f}_i)^2over sum_i (y_i-bar{y})^2,$

где y_i — эмпирический отклик, f_i — отклик, посчитанный по модели, и
bar{y} — математическое ожидание y_i .

Гетероскедастичность

Термин гетероскедастичность применяется в ситуации, когда ошибки в различных наблюдениях некоррелированы, но их дисперсии — разные. Соответственно термин гомоскедастичность применяется в случае постоянных дисперсий.

Визуальный анализ

Одним из основных методов предварительного исследования на гетероскедастичность является визуальный анализ графика остатков. Целью данного анализа является нахождение факторов влияющих на изменение дисперсии, номер измерения или значение одного из признаков. Для сравнения приведем несколько примеров.

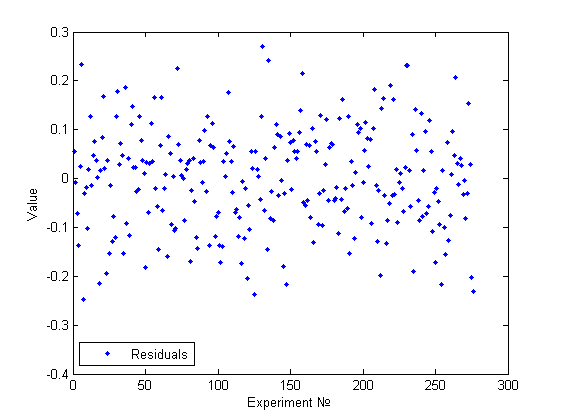
Выше представлена госмоскедастичная модель. Действительно, используя визуальный анализ, не получается найти какие-то признаки непостоянства дисперсии и тем более какие-то зависимости.

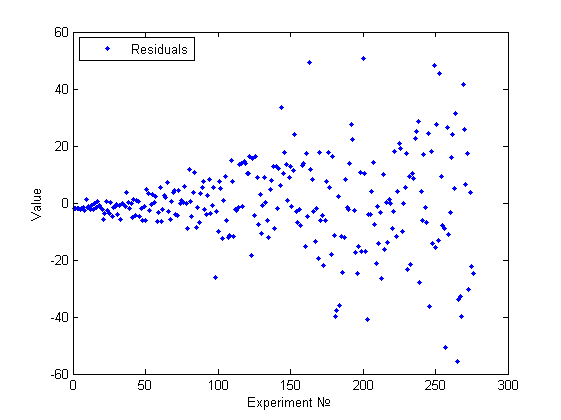
В данном случае визуально можно констатировать факт непостоянства дисперсии и даже связать это изменение с номером эксперимента (или возможно с одним из признаков, если он монотонно изменялся по номеру эксперимента).

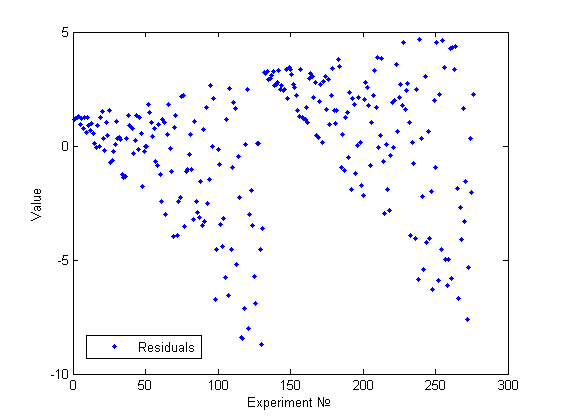
Еще один пример визуально определимой гетероскедастичности.

Статистические методы детекции

Опишем суть нескольких общеупотребительных статистических тестов на гетероскедастичность.
Во всех этих тестах основной гипотезой H_0 является равенство против альтернативной гипотезы H_1 : не H_0 .

Тест Уайта

Содержательный смысл теста в том, что часто гетероскедастичность модели вызвана зависимостью (возможно довольно сложной) дисперсий ошибок от признаков. Реализуя эту идею, Уайт предложил метод тестирования гипотезы H_0 без каких-либо предположений о структуре гетероскедастичности. Сначала к исходной модели применяется обычный метод наименьших квадратов и находятся остатки регрессии . Затем осуществляется регрессия квадратов этих остатков e_t^2 на все признаки, их квадраты, попарные произведения и константу.
Тогда при гипотезе H_0 величина nR^2 асимптотически имеет распределение , где R^2 — коэффициент детерминации, а — число регрессоров второй регрессии.
Плюс данного теста — его универсальность. Минусы : 1) если гипотеза H_0 отвергается, то никаких указаний на функциональную форму гетероскедастичности мы не получаем; 2) несомненным минусом является поиск вслепую вида регрессии(начинаем приближать простыми полиномами второй степени без какой бы то ни было причины на это)

Тест Голдфелда-Кванта

Этот тест применяется, когда есть предположение о прямой зависимости дисперсии ошибок от некоторого признака. Алгоритм метода:

упорядочить данные по убыванию того признака, относительно которого сделано предположение;
Делим наблюдения на три части, причём они должны быть равны или примерно равны, а также первая и третья должны быть одинаковы.
Провести две независимые регрессии для первой части и для последней. Рассчитать выровненные значения и построить соответствующие остатки ( $y_{vyr} -y$ ): и ;
Cоставить cтатистику Фишера . Если кр, следовательно есть гетероскедостичность.

Тест Ансари-Брэдли

Тест получает на вход две выборки размеров n_1 и n_2 и проверяет на равенство дисперсий распределения, из которых они могли быть получены. Алгоритм метода пошагово:

Эвристика

Суть данной эвристики состоит в ранжировании псевдодисперсий и в анализе полученной гистограммы. Под псевдодисперсией будем понимать величины
, где $mean = sum_{i=1}^n varepsilon_i/n$ . Простейший анализ гистограммы, состоящей из 10 интервалов, будем проводить сравнением количества элементов на первых двух интервалах. Это отношение будем сравнивать с некоторой, заранее заданной константой, на основе чего и будем принимать решение о гетероскедастичности. Вот пример гистограммы для гомоскедастичного случая (график его остатков был представлен ранее):

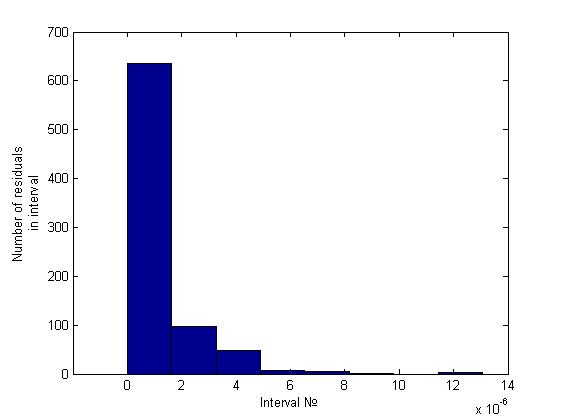
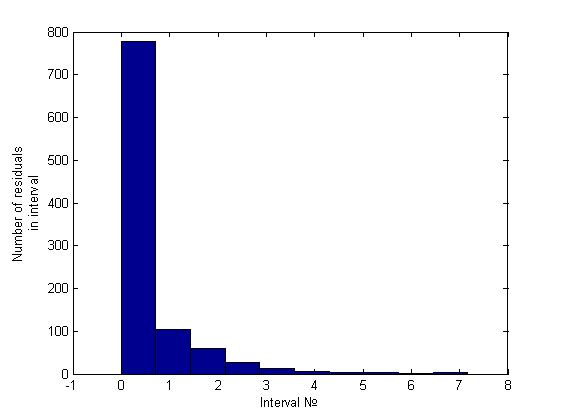
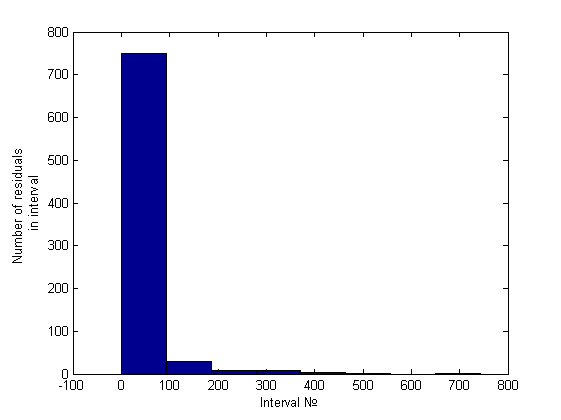
Легко заметить, что порядок отношения первых двух столбцов — около пяти-шести к одному, что же касается гетероскедастичного случая, это отношение будет больше семи (было замечено вплоть до 34) примеры можно посмотреть ниже, в вычислительном эксперименте.

Вычислительный эксперимент на модельных данных

В данном отчете представлены результаты применения созданного инструмента анализа представленной модели с помощью исследования ее регрессионных остатков. Отчет состоит из трех экспериментов, демонстрирующих плюсы и минусы созданного инструмента.

Три модели

Представленные модели были подобраны так, чтобы визуальный анализ регрессионных остатков не давал очевидных результатов. Будем проводить исследование в два этапа — вначале проверяя модель на выполнение основных гипотез, затем исследуя модель на гетероскедастичность с помощью теста Голдфелда-Кванта и несложной эвристики.

Модель №1 (хорошая)

Наша модель : $y_i=sum_{j=1}^m w_j x_{ij} + varepsilon_i, i=1,dots,n$ , где . Таким образом все гипотезы должны выполняться и гетероскедастичность должна отсутствовать.

[A,x,res] = GetGoodExample
[meanst, distab, normchi2, normjb] = ResAnalysis(res)
GoldfeldQuandt(A(:,1:end-1),A(:,end),1)
GoldfeldQuandt(A(:,1:end-1),A(:,end),2)
HistAnalys(res)

Получаем результат:

 % Проверка основных гипотез 
 meanst = 0
 distab = 0.0500
 normchi2 = 0
 normjb = 0
 %Проверка на гетероскедастичность% 
 goldfeldquandt1 = 0
 goldfeldquandt2 = 0
 result = 0

График остатков этой модели уже был приведен выше и не представляет особого интереса.

Модель №2 (плохая, одномерная)

Наша модель : , где . Таким образом, модель очевидным образом гетероскедастична, но визуальным анализом это сложно обнаружить(см.рисунок).

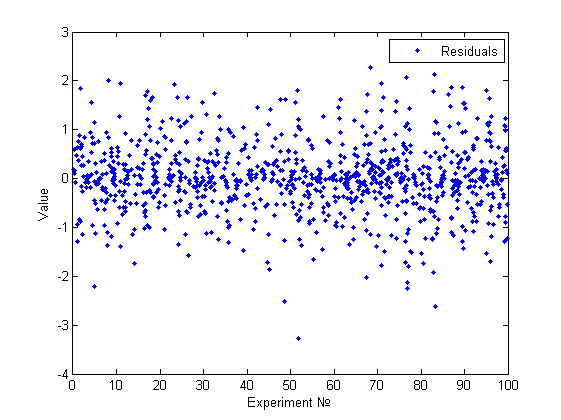
[A,x,res] = GetBadExample
[meanst, distab, normchi2, normjb] = ResAnalysis(res)
GoldfeldQuandt(A(:,1:end-1),A(:,end),1)
HistAnalys(res)

Получаем результат:

 % Проверка основных гипотез 
 meanst = 0
 distab = 0.0340
 normchi2 = 1.0020
 normjb = 1.0020
 %Проверка на гетероскедастичность% 
 goldfeldquandt1 = 0
 result = 1

Нормальность отвергнута. Гетероскедастичность была обнаружена только эвристикой. Приведем гистограмму полученную эвристикой:

Модель №3 (плохая,многомерная)

Наша модель : $y_i=sum_{j=1}^m w_j x_{ij} + ((x_1)^2+x_2)varepsilon_i, i=1,dots,n$ , где . Таким образом, модель очевидным образом гетероскедастична, но снова визуальным анализом это сложно обнаружить(см.рисунок).

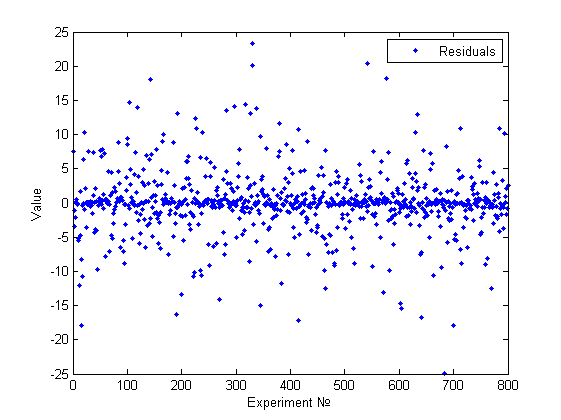
[A,x,res] = GetBadExample1
[meanst, distab, normchi2, normjb] = ResAnalysis(res)
GoldfeldQuandt(A(:,1:end-1),A(:,end),1)
GoldfeldQuandt(A(:,1:end-1),A(:,end),2)
GoldfeldQuandt(A(:,1:end-1),A(:,end),5)
HistAnalys(res)

Получаем результат:

 % Проверка основных гипотез 
 meanst = 0
 distab = 0.0288
 normchi2 = 1.0025
 normjb = 1.0025
 %Проверка на гетероскедастичность% 
 goldfeldquandt1 = 1
 goldfeldquandt2 = 1
 goldfeldquandt5 = 0
 result = 1

Нормальность отвергнута. Гетероскедастичность была обнаружена как эвристикой, так и тестом Голдфелда-Квандта (зависимость от первой и второй и независимость от пятой переменной). Приведем гистограмму полученную эвристикой:

Выводы

Статистические проверки на нормальность показали себя с наилучшей стороны. Эвристика показала хорошие результаты в исследовании на гетероскедастичность. Тест Голдфелда-Квандта не сработал только в одном тесте. Тест Ансари-Брэдли (использовался для проверки на постоянство дисперсии) показал наихудшие результаты, так как с его помощью не удалось различить две существенно разные модели. Это вполне объяснимо: мы применяли этот тест для сравнения дисперсий двух случайных выборок взятых из нашего вектора остатков. Вполне очевидно что результат достаточно не предсказуем вследствие именно этой случайности выборок. В итоге мы получали одинаковые результаты для разных моделей. (причем увеличение числа экспериментов не решает данной проблемы).

Исходный код

Функции анализирующие остатки (реализовано в MATLAB)

См. также

Wikipedia о гетероскедастичности, англ.

Коэффициент детерминации

Анализ регрессионных остатков

Литература

Н.Джонсон, Ф.Лион Статистика и планирование эксперимента в технике и науке, перевод с английского «Мир»,1980. — 610 c.
Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий Эконометрика. Начальный курс:Учеб. — 6 изд.,перераб.и доп. — М.:Дело,2004. — 576 с. ISBN 5-7749-0055-Х
Applied Logistic Regression/ David W. Hosmer,Stanley Lemeshow.-2nd ed. -Wiley-Interscience Publication,2000. — 397 c. ISBN 0-471-35632-8
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с. ISBN 5-9221-0707-0

Данная статья была создана в рамках учебного задания.

Студент: Никита Ивкин

Преподаватель: В.В.Стрижов

Срок: 28 мая 2010

В настоящее время задание завершено и проверено.
Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник

30. Проверка гипотезы о нормальном распределении ряда остатков.

31. D-критерий Дарбина-Уотсона.

Как рассчитать остатки

Пример 1: Расчет остатка

Пример 2: Расчет остатка

Вычисление всех остатков

Визуализация остатков

Создание остаточного графика

Introduction[edit]

In univariate distributions[edit]

[edit]

Regressions[edit]

Other uses of the word «error» in statistics[edit]

See also[edit]

References[edit]

External links[edit]

Материал из MachineLearning.

Содержание

Постановка задачи

Описание алгоритма

Анализ регрессионных остатков

Оценка значимости признаков

Гетероскедастичность

Визуальный анализ

Статистические методы детекции

Тест Уайта

Тест Голдфелда-Кванта

Тест Ансари-Брэдли

Эвристика

Вычислительный эксперимент на модельных данных

Три модели

Модель №1 (хорошая)

Модель №2 (плохая, одномерная)

Модель №3 (плохая,многомерная)

Выводы

Исходный код

См. также

Литература