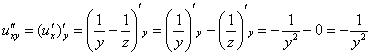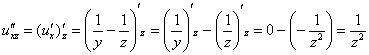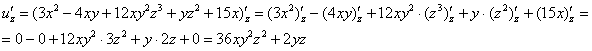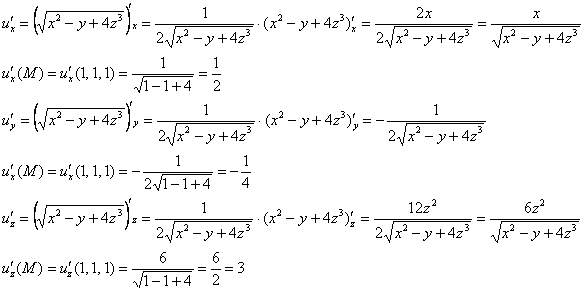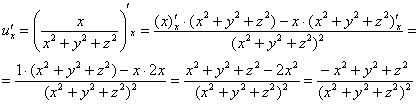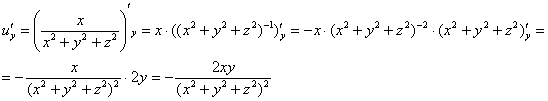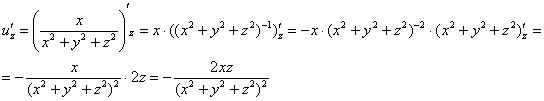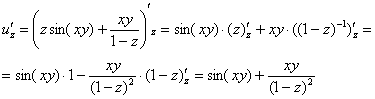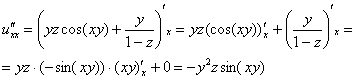Заказать задачи по любым предметам можно здесь от 10 минут
Смешанная частная производная
Как найти?
Постановка задачи
Найти смешанную частную производную второго порядка функции $ z = f(x_1,x_2) $
План решения
Смешанная частная производная второго порядка функции $ z = f(x_1,x_2) $ по переменным $ x_1 $ и $ x_2 $ обозначается: $ frac{partial^2 z}{partial x_1 partial x_2} $ или $ z»_{x_1 x_2} $
Порядок дифференцирования не имеет значения, то есть выполняется свойство:
$$ frac{partial^2 z}{partial x_1 partial x_2} = frac{partial^2 z}{partial x_1 partial x_2} $$
$$ z»_{xy} = z»_{yx} $$
- Фиксируем $ x_2 $. Считая функцию $ z = f(x_1,x_2) $ одной переменной от $ x_1 $ находим её производную $ z’_{x_1} $
- Фиксируем $ x_1 $ и по правилу дифференцирования функции одной переменной находим производную функции $ z = f(x_1,x_2) $ по $ x_2 $ и получаем $ z»_{x_1 x_2} $
Примеры решений
| Пример 1 |
| Найти смешанную частную производную функции $ z(x,y) = ln (x+y) $ |
| Решение |
|
Фиксируем переменную $ x $ и находим производную по $ y $: $$ z’_y = frac{1}{x+y} cdot (x+y)’_y = frac{1}{x+y} $$ Считая переменную $ y $ постоянной дифференцируем функцию $ z’_y $ по $ x $: $$ z»_{yx} = -frac{1}{(x+y)^2} cdot (x+y)’_x = -frac{1}{(x+y)^2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ z»_{xy} = z»_{yx} = -frac{1}{(x+y)^2} $$ |
| Пример 2 |
| Найти смешанную производную функции $ z(x,y) = sin x cos y $ |
| Решение |
|
Фиксируем переменную $ y $ и выполняем дифференцирование по $ x $: $$ z’_x (y = const) = cos x cos y $$ Считаем постоянной $ x $ и находим производную по $ y $: $$ z’_{xy} (x = const) = -cos x sin y $$ |
| Ответ |
| $$ z’_{xy} = z’_{yx} = -cos x sin y $$ |
Частные производные второго порядка
Содержание:
- Примеры с решением
Предположим, что функция 


Частными производными второго порядка функции 
Частных производных второго порядка четыре. Они обозначаются следующим образом:
Аналогично определяются и обозначаются частные производные третьего, четвертого и более высоких порядков. Например, для функции 






Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции 


Аналогично определяются частные производные высших порядков и для функции большего числа переменных.
Если первая производная переменной найдена, получите вторую производную функции, взятую дважды для переменной.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1.
Найти частные производные второго порядка функции
Решение:
Частные производные первого порядка для данной функции имеют вид:
Тогда
Возможно вам будут полезны данные страницы:
Пример 2.
Найти 

Решение:
Имеем

Дифференцируя в обратном порядке, приходим к такому же результату:
В этих двух примерах смешанные частные производные 

Но, вообще говоря, значения смешанных производных зависят от того, в каком порядке производится дифференцирование. Ответ на вопрос, при каких условиях смешанные производные не зависят от того, в каком порядке производится дифференцирование, дает следующая теорема.
Теорема 1. Если производные 




Следствие. Если производные

Аналогичное утверждение справедливо и для частных производных более высокого порядка.
Теорема 2 (Шварц). Если частные производные любого порядка непрерывны в некоторой области, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны в этой области.
Доказательство. Пусть функция 

Возьмем любые точки 



Тогда А запишется в виде







С другой стороны, А можно переписать в виде


Сравнив выражения для А, получим
или
Переходя в этом равенстве к пределу при 


то есть
Методом математической индукции доказанное утверждение можно распространить на частные производные любого порядка.
Лекции:
- Тройной интеграл
- Равномерное распределение
- Признак Даламбера: пример решения
- Производящие функции
- Сложение и вычитание пределов
- Векторы и операции с ними
- Таблица истинности логических выражений
- Элементы векторной алгебры
- Асимптоты графика функции
- Разложение в ряд маклорена
Частные производные высших порядков. Теорема о равенстве смешанных производных
Частные
производныеназывают
частными производными первого порядка.
Их можно рассматривать как функции от
(х;у) є D. Эти функции могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
Аналогично
определяются частные производные 3-го,
4-го и т. д. порядков.
Так,
и т.д.
Частная
производная второго или более высокого
порядка, взятая по различным переменным,
называется
смешанной частной производной.
Таковыми являются, например,
Пример
44.2. Найти частные производные второго
порядка функции z = x4-2x2y3+y5+1.
Решение:
Так както
Оказалось,
что
Этот
результат не случаен.
Имеет место
теорема, которую приведем без
доказательства.
Теорема
44.1 (Шварц). Если частные производные
высшего порядка непрерывны, то смешанные
производные одного порядка, отличающиеся
лишь порядком дифференцирования, равны
между собой.
В
настности, для z=ƒ(х; у) имеем:
Теорема Шварца
Пусть выполнены
условия:
-
функции
определены
в некоторой окрестности точки
. -
непрерывны
в точке
.
Тогда
,
то есть смешанные производные второго
порядка равны в каждой точке, где они
непрерывны.
Теорема Шварца о
равенстве смешанных частных производных
индуктивно распространяется на смешанные
частные производные высших порядков,
при условии, что они непрерывны.
-
Дифференциалы высших порядков
Введем
понятие дифференциала высшего порядка.
Полный дифференциал функции (формула
(44.5)) называют также дифференциалом
первого порядка.
Пусть
функция z=ƒ(х;у) имеет непрерывные частные
производные второго порядка. Дифференциал
второго порядка определяется по формуле
(d2z
= d(dz). Найдем его:
Отсюда:Символически
это записывается так:
Аналогично
можно получить формулу для дифференциала
третьего порядка:
где
Методом
математической индукции можно показать,
что
Отметим,
что полученные формулы справедливы
лишь в случае, когда переменные х и у
функции z = ƒ(х;у) являются независимыми.
Пример
44.4. (Для самостоятельного решения.) Найти
d2z,
если z=х3у2.
Ответ:
d2z=бху2dx2+12х2уdxdy+2х3dy2.
-
Формула Тейлора для функции двух переменных
Формула Тейлора
используется при доказательстве большого
числа теорем в дифференциальном
исчислении.
Говоря нестрого, формула Тейлора
показывает поведение функции в окрестности
некоторой точки.
Теорема:
-
-
Пусть
функция f(x)
имеет n
+ 1 производную
в некоторой окрестности
точки
a,
U(a,ε) -
Пусть
-
Пусть
p —
произвольное положительное число,
тогда:
точка
при
x
< a
или
при
x
> a: -
Это формула
Тейлора с остаточным членом в общей
форме (форма Шлёмильха —
Роша).
$$
то
$$
begin{array}{c}f_{yx}(0,0)=displaystylelim_{xrightarrow0}frac{f_y(x,0)-f_y(0,0)}x=1,\f_{xy}(0,0)=displaystylelim_{yrightarrow0}frac{f_x(0,y)-f_x(0,0)}y=-1.end{array}nonumber
$$
Таким образом, (f_{xy}(0,0)neq f_{yx}(0,0)). (blacktriangle)
Теорема о смешанных производных.
Теорема 1.
Если обе смешанные производные (f_{xy}(x,y)) и (f_{yx}(x,y)) определены в некоторой окрестности точки ((x_0,y_0)) и непрерывны в этой точке, то (f_{xy}(x_0,y_0)=f_{yx}(x_0,y_0)).
Доказательство.
(circ) Пусть смешанные производные определены в прямоугольнике (Pi={(x,y): |x-x_0| < varepsilon, |y-y_0| < eta}) и непрерывны в точке ((x_0,y_0)). Рассмотрим в прямоугольнике (Pi) функцию
$$
omega(x,y)=f(x,y)-f(x_0,y)-f(x,y_0)+f(x_0,y_0).nonumber
$$
При фиксированном (yin (y_0-eta,y_0+eta)) рассмотрим на интервале ((x_0-varepsilon,x_0+varepsilon)) функцию
$$
varphi(t)=f(t,y)-f(t,y_0).
$$
Она дифференцируема на ((x_0-varepsilon,x_0+varepsilon)) и
$$
varphi'(t)=f_x(t,y)-f_x(t,y_0).nonumber
$$
Функцию (omega(x,y)) можно записать в виде
$$
omega(x,y)=varphi(x)-varphi(x_0).nonumber
$$
Применяя формулу конечных приращений Лагранжа, получаем
$$
omega(x,y)=varphi'(x+Theta_1(x-x_0))(x-x_0)=\=Delta[f_x(x_0+Theta_1Delta x,y)-f_x(x_0+Theta_1Delta x,y_0)],quad Delta x=x-x_0,quad 0 <Theta_1 < 1.nonumber
$$
Применяя еще раз формулу конечных приращений Лагранжа, но уже по переменной (y), получаем
$$
omega(x,y)=Delta xDelta y f_{xy}(x_0+Theta_1Delta x, y_0Theta_2Delta y), Delta y=y-y_0, 0 <Theta_2 < 1.label{ref1}
$$
Положим теперь
$$
psi(tau)=f(x,tau)-f(x_0,tau),quad tauin(y_0-eta,y_0+eta).nonumber
$$
Тогда
$$
omega(x,y)=psi(y)-psi(y_0)=frac{partialpsi}{partialtau}(y_0+Theta_3Delta y)Delta y=\=left[frac{partial f}{partial y}(x,y_0+Theta_3Delta y)-frac{partial f}{partial y}(x_0,y_0+Theta_3Delta y)right]Delta y=\=Delta xDelta yf_{xy}(x_0+Theta_4Delta x,y_0+Theta_3Delta y),quad 0 < Theta_3,quadTheta_4 < 1.
$$
При перемножении дифференциальных операторов вида eqref{ref8} нужно пользоваться правилом eqref{ref9}. При этом дифференциалы независимых переменных (dx_1,…,dx_n) перемножаются как вещественные числа.
Частная смешанная производная второго порядка. Расчет
Содержание
- 1 Определение
- 1.1 Для функции двух переменных
- 1.2 Для функции многих переменных
- 1.3 Определение как двойной предел в точке
- 2 Вопросы домена
- 2.1 Для функции двух переменных
- 2.2 Для функции более двух переменных
- 3 факта
Определение
Для функции двух переменных
Предположим, это функция двух переменных, которую мы обозначаем и . Имеются две возможные функции смешанной частной производной второго порядка для , а именно и . В большинстве обычных ситуаций они равны по теореме Клеро о равенстве смешанных частей.
Часто термин смешанная частная производная используется как сокращение для смешанной частной производной второго порядка. Однако смешанная частная производная может также в более общем смысле относиться к более высокой частной производной, которая включает дифференцирование по нескольким переменным.
Ниже приведены все эквивалентные обозначения и определения .
| Имя | Обозначение | Определение в терминах частных производных первого порядка |
|---|---|---|
| Нижний индекс | Определяется как . Более точно: Пусть . Затем, . |
|
| Нотация Лейбница | Определяется как |
Обратите внимание, что порядок, в котором мы пишем и , отличается в обозначениях нижнего индекса и Лейбница, потому что в обозначении нижнего индекса дифференцирование выполняется слева направо (по нижним индексам), тогда как в обозначении Лейбница, дифференцирования проводятся справа налево при упрощении.
Ниже приведены все эквивалентные обозначения и определения .
| Имя | Обозначение | Определение в терминах частных производных первого порядка |
|---|---|---|
| индекс | Определяется как . Более точно: Пусть . Затем, . |
|
| Нотация Лейбница | Определяется как |
Для функции многих переменных
Для функции более чем двух переменных мы можем определить смешанную частную производную второго порядка по двум переменным (в определенном порядке) в одном и том же как для функции двух переменных, где мы рассматриваем остальные переменные как постоянные. Например, для функции трех переменных мы можем рассмотреть шесть смешанных частичных (удерживающих фиксированную), (удерживающих фиксированную), (удерживающих фиксированную).
В общем случае для функции переменных существует множество смешанных частных частей второго порядка, которые мы можем построить.
Определение как двойной предел в точке
Рассмотрим снова случай функции двух переменных. В этом случае частные производные и в точке могут быть выражены как двойные пределы:
Теперь мы используем это:
и:
Подставляя (2) и (3) обратно в (1), получаем, что:
Аналогичный расчет дает следующее:
Как показывает теорема Клеро о равенстве смешанных парциалов, мы можем, при разумных предположениях о существовании и непрерывности, показать, что эти два смешанных парциала второго порядка одинаковы.
Вопросы предметной области
Для функции двух переменных
Предположим, функция двух переменных . Рассмотрим точку в области . Предположим, нас интересует определение существования. Мы можем сказать следующее:
- A необходимое (хотя и не достаточное) условие для существования состоит в том, что существует для везде в открытом интервале, содержащем . Другими словами, существует на линии и рядом с ней. Другими словами, это должно существовать не только в точке, но и в том случае, если мы немного потревожим.
- Основываясь на этом, необходимое (хотя и недостаточное) условие для существования состоит в том, что должно существовать, если мы немного возмущаем и затем немного возмущаем. Заманчиво полагать, что необходимо определить в открытой окрестности точки . Однако это не обязательно так, поскольку нет необходимости, чтобы существовала положительная нижняя граница радиуса -окрестностей для определения при близких к .
Для функции более двух переменных
Предположим, это функция переменных. Рассмотрим точку в области . Рассмотрим смешанный парциал в :
- необходимое (хотя и не достаточное) условие для существования этой смешанной парциальной второго порядка состоит в том, что она должна быть определена в точках, близких к той линии, где мы фиксируем все координаты, кроме и позволяем варьировать. Другими словами, это должно существовать не только в точке, но и в том случае, если мы слегка потревожим.
- Необходимое (хотя и недостаточное) условие для существования этого смешанного частичного второго порядка состоит в том, что оно должно быть определено в точках, близких к плоскости, параллельной плоскости, проходящей через точку. В явном виде должен существовать не только в точке, но и во всех близких к ней точках, получаемых путем слабого возмущения, а затем слабого возмущения.
Факты
- Теорема Клеро о равенстве смешанных парциалов утверждает, что при условии непрерывности (на открытом множестве) обоих смешанных парциалов второго порядка функции двух переменных две смешанные парциалы равны.
Частная смешанная производная второго порядка — исчисление
Содержание
- 1 Определение
- 1.1 Для функции двух переменных
- 1.2 Для функции многих переменных
- 1.3 Определение как двойной предел в точке
- 2 Вопросы домена
- 2.1 Для функции двух переменных
- 2.2 Для функции более двух переменных
- 3 факта
Определение
Для функции двух переменных
Предположим, это функция двух переменных, которую мы обозначаем и . Имеются две возможные функции смешанной частной производной второго порядка для , а именно и . В большинстве обычных ситуаций они равны по теореме Клеро о равенстве смешанных частей. Однако технически они определяются несколько иначе.
Часто термин смешанная частная производная используется как сокращение для смешанной частной производной второго порядка. Однако смешанная частная производная может также в более общем смысле относиться к более высокой частной производной, которая включает дифференцирование по нескольким переменным.
Ниже приведены все эквивалентные обозначения и определения .
| Имя | Обозначение | Определение в терминах частных производных первого порядка |
|---|---|---|
| Нижний индекс | Определяется как . Более точно: Пусть . Затем, . |
|
| Нотация Лейбница | Определяется как |
Обратите внимание, что порядок, в котором мы пишем и , отличается в обозначениях нижнего индекса и Лейбница, потому что в обозначении нижнего индекса дифференцирование выполняется слева направо (по нижним индексам), тогда как в обозначении Лейбница, дифференцирования проводятся справа налево при упрощении.
Ниже приведены все эквивалентные обозначения и определения .
| Имя | Обозначение | Определение в терминах частных производных первого порядка |
|---|---|---|
| индекс | Определяется как . Пусть . Затем, . |
|
| Нотация Лейбница | Определяется как |
Для функции многих переменных
Для функции более чем двух переменных мы можем определить смешанную частную производную второго порядка по двум переменным (в определенном порядке) в одном и том же как для функции двух переменных, где мы рассматриваем остальные переменные как постоянные. Например, для функции трех переменных мы можем рассмотреть шесть смешанных частичных (удерживающих фиксированную), (удерживающих фиксированную), (удерживающих фиксированную).
В общем случае для функции переменных существует множество смешанных частных частей второго порядка, которые мы можем построить.
Определение как двойной предел в точке
Рассмотрим снова случай функции двух переменных. В этом случае частные производные и в точке могут быть выражены как двойные пределы:
Теперь мы используем это:
и:
Подставляя (2) и (3) обратно в (1), получаем, что:
Аналогичный расчет дает следующее:
Как показывает теорема Клеро о равенстве смешанных парциалов, мы можем, при разумных предположениях о существовании и непрерывности, показать, что эти два смешанных парциала второго порядка одинаковы.
Вопросы предметной области
Для функции двух переменных
Предположим, функция двух переменных . Рассмотрим точку в области . Предположим, нас интересует определение существования. Мы можем сказать следующее:
- A необходимое (хотя и не достаточное) условие для существования состоит в том, что существует для везде в открытом интервале, содержащем .
Другими словами, существует на линии и рядом с ней. Другими словами, это должно существовать не только в точке, но и в том случае, если мы немного потревожим.
- Основываясь на этом, необходимое (хотя и недостаточное) условие для существования состоит в том, что должно существовать, если мы немного возмущаем и затем немного возмущаем. Заманчиво полагать, что необходимо определить в открытой окрестности точки . Однако это не обязательно так, поскольку нет необходимости, чтобы существовала положительная нижняя граница радиуса -окрестностей для определения при близких к .
Для функции более двух переменных
Предположим, это функция переменных. Рассмотрим точку в области . Рассмотрим смешанный парциал в :
- необходимое (хотя и не достаточное) условие для существования этой смешанной парциальной второго порядка состоит в том, что она должна быть определена в точках, близких к той линии, где мы фиксируем все координаты, кроме и позволяем варьировать.
Частные производные второго порядка функции трёх переменных
Общий
принцип нахождения частных производных
порядка второго порядка функции трёх
переменных аналогичен принципу нахождения
частных производных 2-го порядка функции
двух переменных. Поэтому, если вы хорошо
проработали урок Частные
производные функции двух переменных,
то будет всё очень просто.
Для
того чтобы найти частные производные
второго порядка, необходимо сначала
найти частные производные первого
порядка
или
в другой записи:
.
Частных
производных второго порядка девять
штук.
Первая
группа – это вторые производные по тем
же переменным:
или
–
вторая производная по «икс»;
или
–
вторая производная по «игрек»;
или
–
вторая производная по «зет».
Вторая
группа – это смешанные частные
производные 2-го порядка, их
шесть:
или
– смешанная производная
«икс по игрек»;
или
– смешанная производная
«игрек по икс»;
или
– смешанная производная
«икс по зет»;
или
– смешанная производная
«зет по икс»;
или
– смешанная производная
«игрек по зет»;
или
– смешанная производная
«зет по игрек».
Как и
для случая функции двух переменных, при
решении задач можно ориентироваться
на следующие равенства смешанных
производных второго порядка:
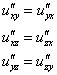
Примечание:
строго говоря, это не всегда так
На
всякий случай несколько примеров, как
правильно читать сиё безобразие
вслух:
–
«у два штриха дважды по игрек»;
–
«дэ два у по дэ зет квадрат»;
–
«у два штриха по икс по зет»;
–
«дэ два у по дэ зет по дэ игрек».
Примеры на нахождение
частных производных 2-го прядка для
функции трёх переменных на практике
встречаются реже. Обычно они не очень
сложные, но довольно большие по объему.
Пример 10
Найти
все частные производные первого и
второго порядка функции трёх переменных
Решение: Сначала
найдем частные производные первого
порядка:
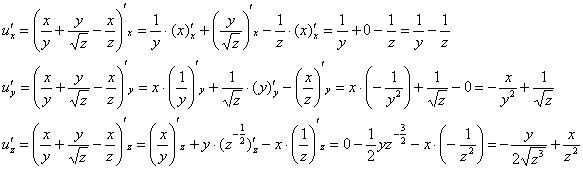
Частные производные
второго порядка рекомендую начинать
искать со смешанных производных,
поскольку это позволит выяснить, а
правильно ли вообще найдены производные
первого порядка.
Берём
найденную производную
и
дифференцируем её по «игрек»:
Берём
найденную производную
и
дифференцируем её по «икс»:
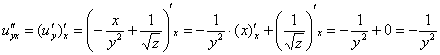
Равенство
выполнено.
Гуд.
Разбираемся
со второй парой смешанных производных.
Берём
найденную производную
и
дифференцируем её по «зет»:
Берём
найденную производную
и
дифференцируем её по «икс»:
–
всё путём.
Аналогично
разбираемся с третьей парой смешанных
производных:
Нормалёк.
После проделанных
трудов гарантированно можно утверждать,
что, во-первых, мы правильно нашли все
частные производные 1-го порядка,
во-вторых, правильно нашли и смешанные
частные производные 2-го порядка.
Осталось
найти ещё три частные производные
второго порядка, вот здесь уже во
избежание ошибок следует максимально
сконцентрировать внимание:

Готово.
Повторюсь, задание не столько сложное,
сколько объемное. Решение можно сократить
и сослаться на равенства смешанных
частных производных, но в этом случае
не будет проверки. Поэтому лучше таки
потратить время и найти все производные
(к тому же это может потребовать
преподаватель), или, в крайнем случае,
выполнить проверку на черновике.
Пример 11
Найти
все частные производные первого и
второго порядка функции трёх переменных
Это пример для
самостоятельного решения.
Решения и ответы:
Пример
2: Решение:
Пример
4: Решение: Найдем
частные производные первого
порядка.
Составим
полный дифференциал первого порядка:
Пример
6: Решение: Вычислим
частные производные первого порядка в
точке
:
Пример
7: Решение: Вычислим
частные производные первого порядка в
точке
:
Пример
9: Решение: Найдем
частные производные первого порядка:
Пример
11: Решение: Найдем
частные производные первого
порядка:
Найдем
частные производные второго
порядка:
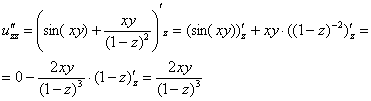
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
08.02.20157.31 Mб91.rtf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #