Как найти смещение колебаний формула

§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы

• Уравнение
гармонических колебаний

где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.

• Угловая частота
колебаний

, или
,

где ν
и
Т — частота и период колебаний.

• Скорость точки,
совершающей гармонические колебания,

• Ускорение при
гармоническом колебании

• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле

где
a₁
и
А₂—
амплитуды
составляющих колебаний; φ₁
и
φ₂—
их
начальные фазы.

•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы

•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по зна­чению
частотами ν₁
и
ν₂,

•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A₁
и A₂
и начальны­ми
фазами φ₁
и φ₂,

Если
начальные фазы φ₁
и
φ₂
составляющих колебаний одинако­вы,
то уравнение траектории принимает вид

т. е. точка движется
по прямой.

В том
случае, если разность фаз
,
уравнение
принимает вид

т. е. точка движется
по эллипсу.

• Дифференциальное
уравнение гармонических колебаний
ма­териальной точки

, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω²).

•
Полная энергия
материальной точки, совершающей
гармони­ческие
колебания,

• Период
колебаний тела, подвешенного на пружине
(пружин­ный
маятник),

где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в ко­торых
выполняется закон Гука (при малой массе
пружины в срав­нении
с массой тела).

Период колебаний
математического маятника

где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника

где J
— момент инерции колеблющегося тела
относительно оси

колебаний;
а
— расстояние центра масс маятника от
оси колебаний;

— приведенная
длина физического маятника.

Приведенные
формулы являются точными для случая
бесконеч­но малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.

Период
крутильных колебаний тела, подвешенного
на упругой нити,

где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.

• Дифференциальное
уравнение затухающих колебаний

, или
,

где r
— коэффициент сопротивления; δ
— коэффициент
затухания:

; ω₀—
собственная угловая частота колебаний
*

• Уравнение
затухающих колебаний

где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.

• Угловая частота
затухающих колебаний

О Зависимость
амплитуды затухающих колебаний от
времени

I

где
А₀
— амплитуда
колебаний в момент t=0.

• Логарифмический
декремент колебаний

где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колеба­ний,
отстоящих по времени друг от друга на
период.

• Дифференциальное
уравнение вынужденных колебаний

, или

,

где

—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F₀
—
ее
амплитудное значение;

•
Амплитуда вынужденных
колебаний

•
Резонансная частота
и резонансная амплитуда

и

Примеры решения
задач

Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если

x(0)= см
и х^,(0)<0.
Построить векторную диаграмму для
мо-­
мента t=0.

Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:

Отсюда
найдем начальную фазу:

*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).

Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента

удовлетворяют
два
значения угла:

Для
того чтобы решить, какое из этих значений
угла φ
удовлет-­
воряет
еще и условию
,
найдем сначала
:

Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем

Так
как всегда A>0
и ω>0,
то условию удовлетворяет
толь­
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза

По
найденному значению φ
постро-­
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-­
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-­
ределить: 1) скорость υ
точки
в мо-­
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
F_max,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ­
ки.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

а
формулу скорости получим, взяв первую
производную по времени от смещения:

(2)

Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квад­рат,
разделим первое на А²,
второе
на A²
ω
²
и сложим:

, или

Решив
последнее уравнение относительно υ,
найдем

Выполнив вычисления
по этой формуле, получим

см/с.

Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — ког­да
направление скорости совпадает с
отрицательным направлением оси
х.

Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением

Повторив
с этим уравнением такое же решение,
получим тот же ответ.

2.
Силу действующую на точку, найдем по
второму закону Нью­тона:

(3)

где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:

, или

Подставив выражение
ускорения в формулу (3), получим

Отсюда максимальное
значение силы

Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем

3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента вре­мени.

Проще
всего вычислить полную энергию в момент,
когда кинети­ческая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии

T_max:

(4)

Максимальную
скорость определим из формулы (2),
положив

:
.
Подставив выражение скорости в фор­-
мулу
(4), найдем

Подставив
значения величин в эту формулу и произведя
вычис­ления, получим

или

мкДж.

Пример
3.
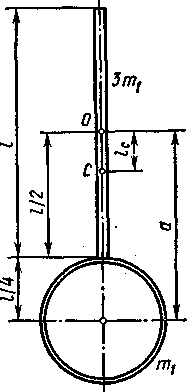
На концах тонкого стержня длиной l
=
1 м и массой m₃=400
г
укреплены шарики малых размеров массами
m₁=200
г
и
m₂=300г.
Стержень
колеблется около горизонтальной оси,
перпен-

дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.

Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_С
— расстояние
от центра масс ма­ятника
до оси.

Момент
инерции данного маятника равен сумме
моментов
инерции шариков J₁
и
J₂
и
стержня J₃:

(2)

Принимая
шарики за материальные точки, вы­разим
моменты их инерции:

Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J₃=
= .
Подставив
полученные выражения
J₁
,
J₂
и

J₃
в формулу (2), найдем общий момент инерции
фи-­
зического маятника:

Произведя
вычисления по этой формуле, найдем

Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:

Расстояние
l_С
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое рас­стояние
l
равно координате центра масс маятника,
т. е.

, или

Подставив
значения величин m₁,
m₂,
m,
l
и произведя вычисле­ния,
найдем

см.

Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:

Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т₁
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т₁.
Горизонтальная
ось Oz

маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.

Решение.
Период
колебаний физического маятника
опреде­ляется
по формуле

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_C
— расстояние
от центра масс
маятника до оси колебаний.

Момент
инерции маятника равен сумме мо­ментов
инерции стержня J₁
и
обруча J₂:

(2).

Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-­
ле
.
В данном случае т=3т₁
и

Момент
инерции обруча найдем, восполь-­
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-­
извольной
оси;
J₀
—
момент
инерции отно-­
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-­
мулу
к обручу, получим

Рис. 6.3

Подставив
выражения J₁
и
J₂
в форму­лу
(2), найдем момент инерции маятника
относительно оси вра­щения:

Расстояние
l_С
от
оси маятника до его центра масс равно

Подставив
в формулу (1) выражения J,
l_с
и массы маятника

, найдем период его колебаний:

После
вычисления по этой формуле получим
T=2,17
с.

Пример
5. Складываются
два колебания одинакового направле-­
ния,
выражаемых уравнениями
;
х₂=
=,
где А₁=1
см,
A₂=2
см,

с,

с, ω
=
=.
1. Определить начальные фазы φ₁
и φ
₂
составляющих коле-

баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:

(2)

Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:

рад и

рад.

2.
Для определения амплитуды А
результирую­щего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим

(3)

где

— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ₂
и φ₁
получим

рад.

Рис. 6.4

Подставим
значения А₁
,
А₂
и

в формулу (3)
и
произведем вычисления:

A=2,65
см.

Тангенс
начальной фазы φ
результирующего колебания опреде-­
лим
непосредственно из рис. 6.4:

, отку-­
да
начальная фаза

Подставим
значения А₁,
А₂,
φ
₁,
φ
₂
и произведем вычисления:

= рад.

Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде

, где A=2,65
см,
,

рад.

Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравне­ния
которых

(1).

(2)

где
a₁=1
см,
A₂=2
см,
.
Найти уравнение траектории точ-­
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.

Решение.
Чтобы
найти уравнение траектории точки,
ис­ключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-

зуемся
формулой
.
В данном случае

, поэтому

Так
как согласно формуле (1)
,
то уравнение траекто-­
рии

(3)

Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.

Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию

см, и составим таблицу:

X , СМ	-1	—0,75	—0,5	0	+0,5	+ 1
у, см	0	±0,707	±1	±1,41	±1,73	±2

Начертив
координатные оси и выбрав масштаб,
нанесем на пло­скость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колеба­ния
в соответствии с уравнениями движе­ния
(1) и (2) (рис. 6.5).

Рис. 6.5

Для
того чтобы указать направление движения
точки, проследим за тем, как из­меняется
ее положение с течением времени. В
начальный момент t=0
координаты точ­ки
равны x(0)=1
см и y(0)=2
см. В по­следующий
момент времени, например при t₁=l
с,
координаты точек изменятся и ста­нут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последую­щий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в мо­мент
t₂
= 2 с колеблющаяся точка достиг­нет
точки D,
она
будет двигаться в обратном направлении.

Задачи

Кинематика
гармонических колебаний

6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с^-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.

6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
коле­баний,
заданных уравнением
,
где ω=2,5π
с^-1,
τ=0,4
с.

6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.

6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.

Оглавление:

• Основные теоретические сведения
  • Гармонические колебания
  • Математический маятник
  • Пружинный маятник
  • Механические волны
  • Электрический контур
  • Переменный ток. Трансформатор
  • Электромагнитные волны

Основные теоретические сведения

Гармонические колебания

К оглавлению…

В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ₀, поэтому φ₀ называют начальной фазой (то есть той стадией, из которой начиналось колебание).

Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

• физические свойства колебательной системы определяют только собственную частоту колебаний ω₀ или период T.
• Такие параметры процесса колебаний, как амплитуда A = x_m и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.е. начальными условиями.
• При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

• Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.
• Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.
• Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.
• Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

Математический маятник

К оглавлению…

Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:

1. Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.
2. Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
3. Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.

Пружинный маятник

К оглавлению…

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.

Циклическая частота колебаний пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную:

А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):

Механические волны

К оглавлению…

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).

• Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
• Поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:

где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.

Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:

Электрический контур

К оглавлению…

В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.

Переменный ток. Трансформатор

К оглавлению…

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Они позволяют наиболее просто и экономно осуществлять передачу, распределение и использование электрической энергии.

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. Он характеризуется переменным напряжением U(t) (индуцированной ЭДС) на его клеммах. В основу работы генератора переменного тока положено явление электромагнитной индукции.

Переменным током называется электрический ток, который изменяется с течением времени по гармоническому закону. Величины U₀, I₀ = U₀/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.

Переменный ток характеризуется действующими значениями силы тока и напряжения. Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток. Для переменного тока действующее значение силы тока может быть рассчитано по формуле:

Аналогично можно ввести действующее (эффективное) значение и для напряжения, рассчитываемое по формуле:

Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

Обратите внимание, что если идет речь о напряжении или силе переменного тока, то (если не сказано иного) имеется в виду именно действующее значение. Так, 220В – это действующее напряжение в домашней электросети.

Конденсатор в цепи переменного тока

Строго говоря, конденсатор ток не проводит (в том смысле, что носители заряда через него не протекают). Поэтому, если конденсатор подключен в цепь постоянного тока, то сила тока в любой момент времени в любой точке цепи равна нулю. При подключении в цепь переменного тока из-за постоянного изменения ЭДС конденсатор перезаряжается. Ток через него по-прежнему не течет, но ток в цепи существует. Поэтому условно говорят, что конденсатор проводит переменный ток. В этом случае вводится понятие сопротивления конденсатора в цепи переменного тока (или емкостного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Оно в корне отличается от привычного нам сопротивления R. Так, на сопротивлении R выделяется теплота (поэтому его часто называют активным), а на емкостном сопротивлении теплота не выделяется. Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.

Катушка индуктивности в цепи переменного тока

При протекании переменного тока в катушке возникает явление самоиндукции, и, следовательно, ЭДС. Из-за этого напряжение и сила тока в катушке не совпадают по фазе (когда сила тока равна нулю, напряжение имеет максимальное значение и наоборот). Из-за такого несовпадения средняя тепловая мощность, выделяющаяся в катушке, равна нулю. В этом случае вводится понятие сопротивления катушки в цепи переменного тока (или индуктивного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и на емкостном сопротивлении, на индуктивном сопротивлении теплота не выделяется. Индуктивное сопротивление связано с явлением самоиндукции в катушке.

Трансформаторы

Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы, на который намотаны две обмотки: первичная и вторичная. Первичная обмотка подсоединяется к источнику переменного тока с некоторым напряжением U₁, а вторичная обмотка подключается к нагрузке, на которой появляется напряжение U₂. При этом, если число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

Электромагнитные волны

К оглавлению…

Электромагнитные волны – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:

где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:

где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

• Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии.
• Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. А вот цепи, в которых протекает переменный ток, т.е. такие цепи в которых носители заряда постоянно меняют направление своего движения, т.е. двигаются с ускорением – являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают.
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0  смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.
Величина  — максимальная скорость колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при гармоническом колебании имеем: ,  а для случая нулевой начальной фазы  (см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени:  — вторая производная от координаты по времени. Тогда: . Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).
Величина  — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы:  (см. график).
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
Сравним выражения для смещения и ускорения при гармонических колебаниях:    и    .
Можно записать:  — т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.
Часто бывает удобно записывать уравнения для колебаний в виде: , где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения.

Источник: https://www.eduspb.com/node/1780

Амплитуда колебаний — определение, характеристика и формулы

Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах. 

Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.

Амплитуда колебаний

Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах. 

За амплитудой можно наблюдать на простом примере пружинного маятника.

 

• В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:
• x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),
• где 

• величина А – это амплитуда свободных движений груза на пружине;
• (ωt + φ0) – это фаза свободных колебаний, где ω — это циклическая частота, а φ0 – это начальная фаза, когда t = 0. 

В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой. 

Период колебаний

1. Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.
2. В физике период обозначают буквой Т и описывают формулами:

Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.

Частота колебаний

Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F. 

• Данная величина описывается выражением:
• v = n/t – количество колебаний за промежуток времени,
• где 

• n – это единица колебаний;
• t – отрезок времени.

В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса. 

Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -1035 Гц при одинаковой скорости.

Циклическая частота

В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой. 

1. Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:
2. ω = 2π/T = 2πν.

Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике. 

• Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:
• WLC = 1/LC.
• Тогда как обычная циклическая резонансная частота выражается:
• VLC = 1/2π*√ LC.

В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.

Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса. 

К ним относят:

• расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
• наибольшее отклонение – амплитуда смещения А;
• фаза колебания – определяет состояние колебательной системы в любой момент времени;
• начальная фаза колебательного процесса – когда t = 0, то φ = φ0.

Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.

Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.

Источник: https://nauka.club/fizika/amplituda-kolebaniy.html

Гармонические колебания

Определение 1

Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.

Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.

Определение 2

Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).

Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.

Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.

Гармонические колебания. Определение

В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.

Определение 3

Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.

Функция x=f(t) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2.1.1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.

Рисунок 2.1.1. Механические колебательные системы.

Механические колебания подразделяют на свободные и вынужденные.

Определение 4

Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.

Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x=xmcos (ωt+φ0), где x– смещение тела от положения равновесия, xm – амплитуда колебаний, ω– циклическая или круговая частота, t – время.

Величина, располагаемая под знаком косинуса, получила название фазы гармонического процесса: φ=ωt+φ0. Если t=0, φ=φ0, тогда φ0 рассматривается в качестве начальной фазы.

Период колебаний Т – это минимальный промежуток времени, через который происходят повторения движения тела. Величина, обратная периоду колебаний, называют частотой колебаний f=1T.

Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах (Г). Связь с циклической частотой ω и периодом T выражается с помощью формулы:

ω=2πf=2πT.

Рисунок 2.1.2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.

Рисунок 2.1.2. Стробоскопическое изображение гармонических колебаний. Начальная фаза φ0=0. Интервал времени между последовательными положениями тела τ = T12.

На графике 2.1.3. показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний xm, или периода Т (частоты f), или начальной фазы φ0.

Рисунок 2.1.3. Во всех трех случаях для синих кривых φ0=0: a – красная кривая отличается от синей только большей амплитудой (x’m>xm); b – красная кривая отличается от синей только значением периода (T’=T2); с – красная кривая отличается от синей только значением начальной фазы  φ0’=-π2 рад.

Гармонический закон

Если колебания совершаются вдоль прямой Ох, тогда направление вектора скорости аналогично. Определение скорости движения тела υ=υx определяют из выражения υ=∆x∆t; ∆t→0.

Отношение ∆x∆t при ∆t→0 математика трактует как вычисление производной функции x(t) за определенное время t. Обозначение принимает вид dx (t)dt, x'(t) или x˙.

Гармонический закон движения записывается в качестве x=xmcos (ωt+φ0). После вычисления производной формула приобретает вид:

υ=x˙(t)=-ωxmsin (ωt+φ0)=ωxmcos ωt+φ0+π2.

Слагаемое +π2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ=ωxmпроизводится при прохождении тела через положение равновесия, то есть x=0. Аналогично определяют ускорение a=ax. Тогда a=∆υ∆t, ∆t→0. Отсюда следует, что a равняется производной функции υ(t) за время t или второй производной функции x(t). Подставив выражения, получим

a=υ˙(t)=x¨(t)=-ω2xmcos (ωt+φ0)=-ω2x(t).

Наличие отрицательного знака указывает на то, что ускорение a(t) имеет противоположный смещению x(t) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия x=0.

На рисунке 2.1.4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.

Рисунок 2.1.4. Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания.

Рисунок 2.1.5. Модель гармонических колебаний.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Источник: https://Zaochnik.com/spravochnik/fizika/mehanicheskie-kolebanija/garmonicheskie-kolebanija/

Механические колебания

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Гармонические колебания

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

• Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
• (1)
• Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

1. (2)
2. (3)
3. Измеряется циклическая частота в рад/с (радиан в секунду).
4. В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
5. .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

.

График гармонических колебаний в этом случае представлен на рис. 2.

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

.

График колебаний представлен на рис. 3.

Уравнение гармонических колебаний

• Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
• . (4)
• Теперь дифференцируем полученное равенство (4):
• . (5)
• Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
• . (6)
• Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
• . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением.

Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

Пружинный маятник

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

1. Тогда соотношение (8) принимает вид:
2. или
3. .
4. Мы получили уравнение гармонических колебаний вида (6), в котором
5. .
6. Циклическая частота колебаний пружинного маятника, таким образом, равна:
7. . (9)
8. Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
9. . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

Математический маятник

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

• Запишем для маятника второй закон Ньютона:
• ,
• и спроектируем его на ось :
• .

Если маятник занимает положение как на рисунке (т. е. ), то:

.

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

1. .
2. Итак, при любом положении маятника имеем:
3. . (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

• ,
• или
• .
• Это — уравнение гармонических колебаний вида (6), в котором
• .
• Следовательно, циклическая частота колебаний математического маятника равна:
• . (12)
• Отсюда период колебаний математического маятника:
• . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Свободные и вынужденные колебания

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

1. Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
2. Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
3. .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний.

Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими.

Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний.

Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе.

При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Источник: https://ege-study.ru/ru/ege/materialy/fizika/mexanicheskie-kolebaniya/

§12. Гармоническое колебательное движение и волны

Решебник Волькенштейн В.С. (1985) — Задача 12. 16

Уравнение колебаний материальной точки массой m = 10 г имеет вид x = 5sin(π/5·t+π/4) см. Найти максимальную силу Fmax, действующую на точку, и полную энергию W колеблющейся точки.

Решебник Волькенштейн В.С. (1985) — Задача 12. 15

Уравнение колебания материальной точки массой m = 16 г имеет вид х = 0,1sin(π/8 · t+π/4). Построить график зависимости от времени t (в пределах одного периода) силы F, действующей на точку. Найти максимальную силу Fmax.

Решебник Волькенштейн В.С. (1985) — Задача 12. 14

Начальная фаза гармонического колебания φ = 0 . При смещении точки от положения равновесия х1 = 2,4 см скорость точки v1 = 3 см/с, а при смещении x2 = 2,8 см ее скорость v2 = 2 см/с. Найти амплитуду А и период Т этого колебания.

Решебник Волькенштейн В.С. (1985) — Задача 12. 13

Написать уравнение гармонического колебательного движения, если максимальное ускорение точки amах = 49,3 см/с2, период колебаний T = 2 с и смещение точки от положения равновесия в начальный момент времени х0 = 25 мм.

Решебник Волькенштейн В.С. (1985) — Задача 12. 12

Точка совершает гармоническое колебание. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза φ = 0.Найти скорость v точки в момент времени, когда смешение точки от положения равновесия х = 25 мм.

Решебник Волькенштейн В.С. (1985) — Задача 12. 11

Уравнение движения точки дано в виде x = sinπ/6·t. Найти моменты времени t, в которые достигаются максимальная скорость и максимальное ускорение.

Решебник Волькенштейн В.С. (1985) — Задача 12. 10

Уравнение движения точки дано в виде х = 2sin(π/2·t+π/4).Найти период колебаний T, максимальную скорость vmах и максимальное ускорение amаx точки.

Решебник Волькенштейн В.С. (1985) — Задача 12. 9

Амплитуда гармонического колебания A = 5 см, период T = 4 с. Найти максимальную скорость vmax колеблющейся точки и ее максимальное ускорение amах.

Решебник Волькенштейн В.С. (1985) — Задача 12. 8

Через какое время от начала движения точка, совершающая колебательное движение по уравнению х = 7sinπ/2·t, проходит путь от положения равновесия до максимального смещения?

Решебник Волькенштейн В.С. (1985) — Задача 12. 7

Начальная фаза гармонического колебания φ = 0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?

Источник: https://zzapomni.com/paragrafy/ss12-garmonicheskoe-kolebatelnoe-dvizhenie-i-volny?page=5

смещение положения равновесия точки

смещение положения равновесия точки

Задача 40713

Написать уравнение синусоидального гармонического колебания, если амплитуда скорости 63 см/с, период колебаний 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найти амплитуду ускорения, частоту колебаний.

Задача 40738

Написать уравнение гармонического колебания, совершаемого по закону косинуса, если амплитуда ускорения 50 см/с2, частота колебаний 50 Гц, смещение точки от положения равновесия в начальный момент времени 25 мм. Найти амплитуду скорости.

Задача 40739

Написать уравнение гармонического колебания, совершаемого по закону косинуса, если амплитуда ускорения 50 м/с2, частота колебаний 50 Гц, смещение точки от положения равновесия в начальный момент времени 0,25 мм. Найти амплитуду скорости.

Задача 26216

Написать уравнение гармонических колебаний с амплитудой 50мм, периодом 4с и начальной фазой П/4. Найти смещение точки от положения равновесия при t = 0 и t = 1,5 с.

Задача 26560

Уравнение незатухающих колебаний дано в виде: У = 4 ·10–2cos6πt, м. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний через 0,01 с после начала колебаний. Скорость распространения колебаний 340 м/с.

Задача 11103

Напишите уравнение гармонического колебания, если амплитуда скорости vm = 63 см/с, период колебаний Т = 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найдите амплитуду ускорения и частоту колебаний. Постройте график зависимости смещения от времени.

Задача 12666

На каком ближайшем расстоянии от источника колебаний с периодом 45 мс через время, равное половине периода после включения источника смещение точки от положения равновесия равно половине амплитуды? Скорость распространения колебаний равна 158 м/с. Считать, что в момент включения источника все точки находятся в положении равновесия.

Задача 14576

Уравнение незатухающих колебаний х = 4sin(600πt) см. Найти смещение x от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01с после начала колебаний. Скорость распространения колебаний v = 300 м/с.

Задача 14932

Плоская монохроматическая волна распространяется вдоль оси Y. Амплитуда волны А = 0,05 м. Считая, что в начальный момент времени смещение точки Р, находящейся в источнике, максимально, определить смещение от положения равновесия точки М, находящейся на расстоянии у = λ/2 от источника колебаний в момент времени t = T/6.

Задача 15330

Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника колебаний, в момент времени Т/6 равно половине амплитуды. Найти длину бегущей волны.

Задача 17372

Начальная фаза гармонического колебания ψ = 0. При смещении точки от положения равновесия х1 = 2,4 см скорость точки v1 = 3 см/с, а при смещении х2 = 2,8 см ее скорость v2 = 2 см/с. Найти амплитуду А и период Т этого колебания.

Задача 19324

На каком расстоянии от источника колебаний, совершаемых по закону синуса, в момент времени t = T/2 смещение точки от положения равновесия равно половине амплитуды? Скорость распространения колебаний 340 м/с. Период колебаний 10–3 с.

Задача 19326

Источник плоских волн совершает колебания по закону x = A cos ωt. Через четверть периода после начала колебаний смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника, равно половине амплитуды. Найти длину бегущей волны.

Задача 19327

Источник плоских волн совершает колебания по закону x = A cos ωt. Какова амплитуда колебаний, если смещение от положения равновесия точки, отстоящей от источника на расстоянии λ/12 для момента времени T/4, равно 0,025 м?

Задача 20380

Определить начальную фазу колебаний, которые происходят по закону косинуса, если максимальная скорость равна 16 см/с, период колебаний 1,4 с, а смещение точки от положения равновесия в начальный момент времени составляет 2,84 см.

Источник: http://reshenie-zadach.com.ua/fizika/1/smeshhenie_polozheniya_ravnovesiya_tochki.php

Амплитуда результирующего колебания равна сумме амплитуд слагаемых колебаний

• Синфазные колебания усиливают друг друга!
• Интересно, что энергия суммарного колебательного движения, пропорциональная квадрату амплитуды, не равна сумме энергий каждого колебания по отдельности, ибо

• 2 Пусть j01 — j02 = (2k -1)p, где k = 0, 1, 2,… В этом случае говорят, что колебания происходят в противофазе. Векторная диаграмма выглядит следующим образом

• Если А1 > А2, то результирующее колебание происходит синфазно с первым колебанием. Но амплитуда результирующего колебания уменьшилась:

В этом случае говорят, что колебания ослабляют друг друга. Очевидно, что при А1 = А2 результирующая амплитуда вообще будет равной нулю. Это означает, что тело не будет двигаться вообще. Колебания погасили друг друга.

3 Во всех остальных случаях, когда колебания не будут синфазными или противофазными, мы будем видеть колебания с амплитудой, большей , но меньшей, чем .

Полученные результаты имеют бесчисленное множество применений. Забегая вперед, скажем, что если, например, в определенном месте пространства происходят звуковые колебания под действием двух источников, то результирующая громкость звука может оказаться меньше, чем громкость, создаваемая каждым источником в отдельности.

Если звуки, создаваемые каждым источником в отдельности, имеют одинаковую интенсивность, то при подходящих условиях эти звуки гасят друг друга, и можно сказать, что «звук + звук = молчание».

Возможны также условия, когда два пучка света, падающие на экран, дают не большую, а меньшую освещенность, чем каждый пучок в отдельности; возможен даже случай, когда «свет + свет = темнота». Но об этом позже…

§ 2 Сложение взаимно перпендикулярных колебаний

Рассмотрим сначала случай, когда материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях, имеющих одну частоту. Проблема заключается в определении траектории точки, которую мы будем в этом случае наблюдать.

Пусть одно колебание происходит по оси ОХ, другое – по OY .

Понятно, что точка описывает плоскую траекторию и уравнения и можно рассматривать как уравнение этой траектории в параметрической форме. Нетрудно видеть, что это — уравнение эллипса, вписанного в прямоугольник со сторонами . Ориентация главных осей эллипса зависит от сдвига фаз . На рисунке показаны частные случаи таких эллипсов:

1. Нетрудно показать, то при сдвиге фаз эллипс вырождается в прямую на рисунке б:
2. Мы будем видеть колебательное движение точки вдоль прямой, проходящей через начало координат, с амплитудой .
3. При получаем траекторию на рисунке в:
4. Траекторией будет эллипс, у которого главные оси совпадают с осями координат так, как показано на рисунке г , если
5. Покажем это
6. Разделив обе части каждого уравнения на А и В соответственно, получаем
7. Возведем каждое уравнение в квадрат и сложим почленно:

Сдвиг по фазе определит в этом случае направление движения точки. Оно будет происходить по часовой стрелке, если , и против часовой стрелки, если .

• Если амплитуды колебаний по осям ОХ и OY будут равны А = В, то эллипс преобразуется в окружность радиуса А = В:
• Важно заметить, что любое равномерное движение по окружности радиуса А с угловой скоростью может быть разложено на два взаимно перпендикулярных гармонических колебания с частотой .
• Движение по эллипсу тоже может быть разложено на два взаимно перпендикулярных колебания.

Более сложной получается траектория точки, совершающей колебания во взаимно перпендикулярных направлениях, если частоты колебаний не равны. В частности, если частоты относятся как целые числа, траектория оказывается замкнутой линией. Такая траектория называются фигурой Лиссажу. Ниже приведены примеры фигур Лиссажу для некоторых значений и .

1. §3 Сложение колебаний с близкими частотами, происходящими вдоль одной прямой
2. Рассмотрим случай сложения двух колебаний одного направления и одинаковой амплитуды, частоты которых и очень мало отличаются друг от друга (

Источник: https://megaobuchalka.ru/5/47822.html