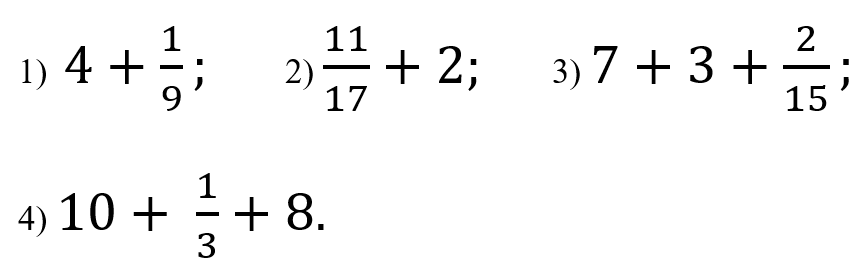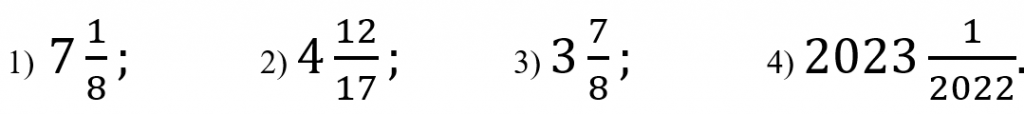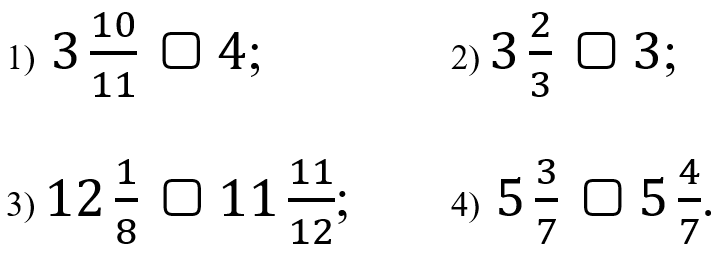Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 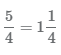
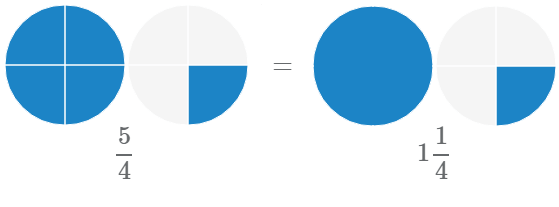
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 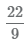
- 1 Разделим числитель на знаменатель 22 ÷ 9, получим 2 целых и 4 в остатке.
- 2 Число 2 будет целой частью смешанного числа.
-
3 Остаток от деления 4 будет числителем дроби, а знаменатель останется прежним, равным 9. В результате получаем
Пример Перевести неправильные дроби  в смешанные числа.
в смешанные числа.
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 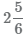
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
Рассмотрим на примерах как переводить смешанные числа в неправильные дроби.
Пример Перевести смешанные числа  в неправильные дроби.
в неправильные дроби.
Пусть $%n$% смешное. Тогда оно имеет не более одного простого делителя, отличного от трёх. Действительно, если $%p$% — такой делитель, то $%p$% и $%p+2$% не делятся на 3, откуда $%p+1$% кратно 3. Но тогда, если $%q$% — второй такой делитель, то $%pq$% также делит $%n$%, но оно при делении на 3 даёт в остатке 1, и число $%pq+2$% не простое.
Таким образом, достаточно рассматривать числа, делящиеся на 3. Легко видеть, что числа вида $%3^k+2$% будут простыми при $%0le kle4$%, а $%3^5+2=245$% составное. Если $%n$% является степенью тройки, то делителей у него не более пяти. Предположим, что есть ещё какой-то простой делитель $%p$% — он может быть всего один.
У чисел $%p+2$%, $%3p+2$%, $%9p+2$%, $%27p+2$% остатки от деления на 5 попарно различны, если $%pne5$% — это сразу ясно из рассмотрения попарных разностей. При $%p=5$% эти числа принимают значения $%7$%, $%17$%, $%47$%, $%137$%, то есть все являются простыми. Отсюда следует, что число $%135$% смешное, и у него имеется $%8$% делителей. Покажем, что это значение максимально, и оно ни на каком другом числе больше не достигается.
Прежде всего, если $%pne5$%, то при остатках от его деления на 5, равных 1, 2, 3, 4, на 5 будут делиться $%3p+2$%, $%9p+2$%, $%p+2$%, $%27p+2$% соответственно, то есть они вместе не могут оказаться простыми. Тогда смешное число $%n$% будет иметь не более 6 делителей. Действительно, других простых делителей больше нет, а $%p^2$% делителем не будет из-за остатка 1 от деления на 3. Остаётся случай $%p=5$%, который мы уже рассмотрели, и здесь осталось заметить, что 81 делителем $%n$% быть не может ввиду того, что $%5cdot81+2=407$% делится на 11.
Таким образом, только на числе $%135$% получается «рекордное» количество делителей, равное $%8$%.
На данном уроке мы продолжим разговор об обыкновенных дробях.
Выясним, какие числа называют смешанными, как их принято записывать и читать.
Эта информация доступна зарегистрированным пользователям
Установим связь между смешанными числами и правильными дробями.
Научимся переводить смешанное число в неправильную дробь.
Рассмотрим обратную операцию перевода неправильной дроби в смешанное число.
Определим расположение смешанных чисел на координатном луче.
Правильной называют дробь, в которой числитель меньше знаменателя, она всегда меньше единицы.
Неправильной называют дробь, в которой числитель больше знаменателя или равен ему, такие дроби всегда больше единицы.
Сегодня речь пойдет о неправильных дробях.
Рассмотрим несколько примеров.
Пример №1.
Разделили три конфеты на троих человек.
Сколько конфет получил каждый?
Эта информация доступна зарегистрированным пользователям
Известно, что обыкновенная дробь (mathbf{frac{m}{n}}) представляет собой математическую операцию деления m— объектов на n-частей, а дробную черту, которая отделяет числитель от знаменателя, применяют как знак деления.
Общее количество конфет (m = 3) разделим на количество человек (n = 3).
Запишем частное в виде дроби.
(mathbf{frac{m}{n} = frac{3}{3}})
В результате получили неправильную дробь, в которой числитель равен знаменателю.
(mathbf{frac{3}{3} = 3 div 3 = 1}) (конф.) получил каждый.
Ответ: каждый получил 1 конфету.
Пример №2.
Разделили поровну шесть конфет между тремя друзьями.
Сколько конфет получил каждый?
Эта информация доступна зарегистрированным пользователям
Общее количество конфет (m = 6) разделим на количество друзей (n = 3).
Запишем частное в виде дроби.
(mathbf{frac{m}{n} = frac{6}{3}})
В итоге получилась неправильная дробь, в которой числитель больше знаменателя.
(mathbf{frac{6}{3} = 6 div 3 = 2}) (конф.) получил каждый из друзей.
Ответ: по 2 конфеты получил каждый из друзей.
В рассмотренных примерах частное двух чисел найти было нетрудно, так как числитель дроби нацело делится на знаменатель.
Рассмотрим еще одну ситуацию.
Пример №3.
Два брата решили разделить поровну пять апельсинов.
Сколько апельсинов достанется каждому из братьев?
Эта информация доступна зарегистрированным пользователям
Общее количество апельсинов (m = 5) разделим на количество братьев (n = 2).
Запишем частное в виде дроби.
(mathbf{frac{m}{n} = frac{5}{2}})
В данном примере мы получили неправильную дробь, в которой числитель хоть и больше знаменателя, но он не делится нацело.
Разделить пять апельсинов на две равные части можно двумя способами.
1. Можно разрезать каждый апельсин на две равные части.
Каждая полученная часть будет равна ½ апельсина.
Эта информация доступна зарегистрированным пользователям
Тогда по одной части от каждого апельсина достанется каждому из братьев.
Оба мальчика получат по пять таких частей: (mathbf{frac{1}{2} + frac{1}{2} + frac{1}{2} + frac{1}{2} + frac{1}{2}})
Эта информация доступна зарегистрированным пользователям
Следовательно, каждый получит (mathbf{frac{5}{2}}) апельсина.
Если внимательно присмотреться к сумме дробей, можно заметить, что две части, т.е. сумма (mathbf{frac{1}{2} + frac{1}{2}}) составляет (mathbf{frac{2}{2}}).
В свою очередь нам известно, что неправильная дробь (mathbf{frac{2}{2}}) равна единице: (mathbf{frac{2}{2} = 2 div 2 = 1}).
Получаем: (mathbf{frac{1}{2} + frac{1}{2} + frac{1}{2} + frac{1}{2} + frac{1}{2} = (frac{1}{2} + frac{1}{2}) + (frac{1}{2} + frac{1}{2}) + frac{1}{2} = 1 + 1 + frac{1}{2} = 2 + frac{1}{2}})
Таким образом получится, что каждому мальчику достанется два апельсина, да еще половинка: (mathbf{2 + frac{1}{2}}) апельсина.
2. Можно поделить поровну сначала целые апельсины.
В таком случае каждому брату достанется по два апельсина.
Затем оставшийся апельсин необходимо разделить поровну на двоих, так каждый получит еще по половине апельсина, т.е. ((mathbf{frac{1}{2}})) его часть.
Эта информация доступна зарегистрированным пользователям
В результате оба брата получат по два целых апельсина, да еще половину: (mathbf{2 + frac{1}{2}}) апельсина.
Сумму (mathbf{A + frac{m}{n}}), где А— это натуральное число, (mathbf{frac{m}{n}})— правильная дробь, можно записать в виде (mathbf{Afrac{m}{n}}).
Такую сокращенную запись называют смешанным числом, оно имеет целую часть (натуральное число) и дробную часть (дробное число).
Дробная часть смешанного числа- это всегда правильная дробь.
Например, представим смешанные числа в виде суммы их целой и дробной части.
(mathbf{1frac{4}{11} = 1 + frac{4}{11}}) (целая часть равна 1, дробная- (mathbf{frac{4}{11}})).
(mathbf{7frac{10}{15} = 7 + frac{10}{15}}) (целая часть равна 7, дробная- (mathbf{frac{10}{15}})).
(mathbf{frac{5}{16} = 0 + frac{5}{16}}) (целая часть отсутствует, т.е. равна 0, дробная- (mathbf{frac{5}{16}})).
А теперь наоборот сумму натурального числа и правильной дроби представим в виде смешанного числа.
Выразим в килограммах 3 килограмма 150 граммов.
Известно, что 1 кг = 1000 г.
Значит 150 г- это часть от килограмма, т.е. часть от 1000 г.
Чтобы узнать какую часть составляет 150 г от 1000 г, необходимо 150 разделить на 1000, получим (mathbf{frac{150}{1000}}).
В итоге имеем 3 килограмма, да еще часть- (mathbf{frac{150}{1000}}) килограмма, получаем (mathbf{3 + frac{150}{1000}}).
Ответ: 3 килограмма 150 граммов- это (mathbf{3frac{150}{1000}}) килограмма.
Запишем определение.
Число, содержащее целую часть (натуральное число) и дробную часть (правильную дробь), называют смешанным числом.
Читают смешанное число следующим образом: произносится сначала целая часть, затем дробная, в соответствии с правилами чтения дробных чисел.
В нашем примере про апельсины выражение (mathbf{2 + frac{1}{2}}) можно записать как (mathbf{2frac{1}{2}}).
Число 2— это целая часть смешанного числа, а число (mathbf{frac{1}{2}}) его дробная часть.
Читается данное число так: «Две целых одна вторая».
Любое смешанное число можно перевести в неправильную дробь.
Выясним взаимосвязь смешанных чисел и неправильных дробей на примере.
Испекли три одинаковые пиццы.
От первой пиццы съели несколько кусочков, в результате от нее осталась часть, равная (mathbf{frac{5}{8}}) всей пиццы.
По сути осталось несъеденными 2 (две) целых да еще (mathbf{frac{5}{8}}) (пять восьмых) пиццы.
Эта информация доступна зарегистрированным пользователям
Если мы сложим эти два числа, то получим сумму (mathbf{2 + frac{5}{8}}).
Выражение (mathbf{2 + frac{5}{8}}) представляет собой ничто иное, как смешанное число (mathbf{2frac{5}{8}}) (две целых пять восьмых).
Общее количество оставшейся пиццы мы можем определить иначе.
Возьмем так же три одинаковые пиццы и разрежем каждую на восемь равных частей.
Теперь вторую и третью пиццу мы можем представить в виде дроби (mathbf{frac{8}{8}}), а остаток от первой запишем как (mathbf{frac{5}{8}}).
Эта информация доступна зарегистрированным пользователям
В результате общее количество несъеденной пиццы будет выражаться суммой:
(mathbf{frac{5}{8} + frac{8}{8} + frac{8}{8} = frac{5 + 8 + 8}{8} = frac{13 + 8}{8} = frac{21}{8}})
При этом ясно, что общее количество оставшейся пиццы, найденное первым способом и вторым, совпадают, значит (mathbf{2frac{5}{8} = frac{21}{8}}).
Запишем алгоритм перевода смешанного числа в неправильную дробь.
Чтобы представить смешанное число в виде неправильной дроби, необходимо:
1. Умножить целую часть смешанного числа на знаменатель его дробной части.
2. К полученному произведению прибавить числитель дробной части.
3. Записать полученный результат суммы в числитель новой дроби.
4. Знаменатель оставить без изменений.
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров.
Пример №1.
Представьте смешанное число (mathbf{6frac{2}{5}}) в виде дроби.
1. Умножим целую часть смешанного числа (число 6) на знаменатель его дробной части (число 5), получим число 30.
6 • 5 = 30
2. К полученному произведению (число 30) прибавим числитель дробной части смешанного числа (число 2), получим число 32.
3. Запишем полученную сумму (число 32) в числитель новой дроби, а знаменатель останется прежним (число 5).
(mathbf{color{red}{6}frac{color{green}{2}}{color{blue}{5}} = frac{color{red}{6} cdot color{blue}{5} + color{green}{2}}{color{blue}{5}} = frac{30 + color{green}{2}}{color{blue}{5}} = frac{32}{color{blue}{5}}})
Получили неправильную дробь (mathbf{frac{32}{5}}).
Ответ: (mathbf{6frac{2}{5} = frac{32}{5}}).
Пример №2.
Представьте смешанное число (mathbf{20frac{1}{3}}) в виде дроби.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
(mathbf{color{red}{20}frac{color{green}{1}}{color{blue}{3}} = frac{color{red}{20} cdot color{blue}{3} + color{green}{1}}{color{blue}{3}} = frac{60 + color{green}{1}}{color{blue}{3}} = frac{61}{color{blue}{3}}})
Получили неправильную дробь (mathbf{frac{61}{3}}).
Ответ: (mathbf{20frac{1}{3} = frac{61}{3}}).
Пример №3.
Представьте смешанное число (mathbf{3frac{3}{4}}) в виде дроби.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
(mathbf{color{red}{3}frac{color{green}{3}}{color{blue}{4}} = frac{color{red}{3} cdot color{blue}{4} + color{green}{3}}{color{blue}{4}} = frac{12 + color{green}{3}}{color{blue}{4}} = frac{15}{color{blue}{4}}})
Получили неправильную дробь (mathbf{frac{15}{4}}).
Ответ: (mathbf{3frac{3}{4} = frac{15}{4}}).
Возможна и обратная операция.
Неправильную дробь, в которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
Чтобы перейти от неправильной дроби к смешенному числу, необходимо выделить целую часть.
Выделить целую часть из неправильной дроби- это значит заменить неправильную дробь равным ей смешанным числом.
Для этого необходимо разделить с остатком числитель неправильной дроби на знаменатель.
При этом неполное частное будет являться целой частью, остаток- числителем, а делитель- знаменателем.
Знаменатель неправильной дроби всегда равен знаменателю дробной части смешенного числа.
Запишем алгоритм выделения целой части из неправильной дроби.
Чтобы перейти от неправильной дроби к смешанному числу, необходимо:
1. Разделить с остатком числитель неправильной дроби на ее знаменатель.
2. Неполное частное будет представлять собой целую часть смешанного числа.
3. Если остаток есть, то его необходимо записать в числитель дробной части смешанного числа, а делитель в знаменатель.
Эта информация доступна зарегистрированным пользователям
Выясним, где на координатном луче находятся смешанные числа.
1. Для того чтобы изобразить на координатном луче смешанное число, важно выбрать правильно длину единичного отрезка.
Единичный отрезок целесообразно устанавливать такой длины, чтобы было удобно его разделить на части, количество которых должно соответствовать числу, стоящему в знаменателе.
2. Далее от начала отсчета нужно отложить определенное количество равных частей, соответствующих числу, стоящему в числителе.
Рассмотрим поясняющий пример.
Отметим на координатном луче точку с координатой (mathbf{2frac{2}{3}}).
(mathbf{2frac{2}{3}})— это смешанное число.
Данное смешанное число содержит правильную дробь со знаменателем 3.
Следовательно, единичный отрезок разобьем на три равные части, каждая такая часть (доля) будет равна (mathbf{frac{1}{3}}) единичного отрезка.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
В таком случае одна часть (доля единичного отрезка) соответствует дроби (mathbf{frac{1}{3}}), две части- это (mathbf{frac{2}{3}}), три части- это 1.
Чтобы изобразить смешанное число (mathbf{2frac{2}{3}}), отсчитываем от начала координат два целых единичных отрезка, а от третьего единичного отрезка возьмем только две его доли из трех.
Отметим точку на координатном луче, назовем ее точка А((mathbf{2frac{2}{3}})).
Переведем смешанное число в неправильную дробь.
(mathbf{color{red}{2}frac{color{green}{2}}{color{blue}{3}} = frac{color{red}{2} cdot color{blue}{3} + color{green}{2}}{color{blue}{3}} = frac{6 + color{green}{2}}{color{blue}{3}} = frac{8}{color{blue}{3}}})
Определим расположение точки с координатой (mathbf{frac{8}{3}}).
Дробь (mathbf{frac{8}{3}}) означает восемь долей единичного отрезка ОЕ.
Отложим от начала координат восемь долей, каждая из которых равна (mathbf{frac{1}{3}}) единичного отрезка.
Попадем в точку с координатой (mathbf{frac{8}{3}}).
В этой же точке мы ранее отметили точку А((mathbf{2frac{2}{3}})).
Смешанное число и соответствующая ему неправильная дробь, у которой числитель больше знаменателя, на координатном луче находятся всегда правее единицы и принадлежат они одной и той же точке координатного луча.
Рассмотрим пример.
Определим расположение точек В((mathbf{1frac{2}{3}})), С((mathbf{2frac{1}{3}})), D((mathbf{frac{12}{3}})) на координатном луче.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Так как знаменатель каждой заданной дроби равен трем, то разобьем единичный отрезок ОЕ на три равные части, каждая часть будет равна (mathbf{frac{1}{3}}) ОЕ.
Эта информация доступна зарегистрированным пользователям
1. Смешанное число (mathbf{1frac{2}{3}}) представляет собой один целый единичный отрезок, да еще две части (доли) из трех от второго единичного отрезка.
Следовательно, точка В((mathbf{1frac{2}{3}})) будет удалена вправо от начала координат на расстояние одного целого единичного отрезка, да еще двух отрезков, каждый из которых равен одной доле единичного отрезка.
В данную точку также мы можем попасть, если от начала координат вправо отсчитаем пять долей единичного отрезка- ((mathbf{frac{5}{3}}))ОЕ.
Таким образом точка с координатой (mathbf{frac{5}{3}}) и точка с координатой (mathbf{1frac{2}{3}}) это одна и та же точка на координатном луче.
Отметим тот факт, что (mathbf{1frac{2}{3}}) смешанное число и соответствующая ему неправильная дробь (mathbf{frac{5}{3}}) больше единицы, и на координатном луче данные точки располагаются правее единицы (правее точки E(1)).
2. Выясним, где на координатном луче будет находиться точка С((mathbf{2frac{1}{3}})).
Смешанное число (mathbf{2frac{1}{3}}) представляет собой два целых единичных отрезка, да еще одну часть (долю) из трех от третьего единичного отрезка.
Отметим точку С((mathbf{2frac{1}{3}})) на координатном луче, для этого отсчитаем вправо от начала координат два целых единичных отрезка и еще одну долю единичного отрезка, равную (mathbf{frac{1}{3}}) ОЕ.
Так же в данную точку можно попасть, если от начала координат вправо отсчитать семь долей единичного отрезка- ((mathbf{frac{7}{3}}))OE.
Точка с координатой (mathbf{frac{7}{3}}) и точка с координатой (mathbf{2frac{1}{3}}) это одна и та же точка на координатном луче.
Смешанное число (mathbf{2frac{1}{3}}) и соответствующая ему неправильная дробь (mathbf{frac{7}{3}}) больше единицы, на координатном луче данные точки располагается правее единицы (правее точки E(1)) и правее найденной нами точки В((mathbf{1frac{2}{3}})).
3. Обозначим на координатном луче точку D с координатой (mathbf{frac{12}{3}}).
(mathbf{frac{12}{3}})- неправильная дробь, в которой числитель больше знаменателя.
Найдем соответствующее этой дроби смешанное число, для этого выделим из дроби (mathbf{frac{12}{3}}) целую часть.
(mathbf{frac{12}{3} = 12 div 3 =4})
Получается, что дробь (mathbf{frac{12}{3}}) равна четырем целым единичным отрезкам.
Дробная часть данного числа отсутствует, т.е. она равна нулю.
(mathbf{frac{12}{3}}) и 4— это одно и то же число, значит (mathbf{frac{12}{3} = 4}).
Отложим от начала координат четыре целых единичных отрезка и обозначим точку D((mathbf{frac{12}{3}})).
Обратите внимание как расположены смешанные числа на координатном луче, чем правее от единицы находится смешанное число, тем оно больше.
Эта информация доступна зарегистрированным пользователям
Читайте также
6*6=36, 6*6*6=216, 6*6*6*6=1296, 6**5=7776, 6**6=46656, 6**7=279936, 6**8=1679616,
5*5=25, 5**3=125, 5**4=625, 5**5=3125, 6**6=15625, 5**7=78125, 5**8=390625…
и так далее.
[Как понимать **?]
Двумя звездочками ** я кратко обозначаю возведение в степень, то есть, многократное умножение числа самого на себя. Это удобно. Например: 4**3 это просто-напросто 4*4*4, а 6**8=6*6*6*6*6*6*6*6.
Так же точно ведет себя и любое число, которое заканчивается на 5 или на 6, при возведении в любую степень. Например:
23423786**23=31777015701265874148423457214899307132892090989199920819277484025607338074233294492804166400591413227935540822413832621915682803707180038127054532163967000996457643769856, а
19578125**31=11089296799830771221957695164400841146651473667631210712354882995182788491789272425372043100187522263659607530027584553788478212271456524373086790515955215925579637141149230092879339405927130446372075311955995857715606689453125
В последнем примере неизменными сохраняются даже две цифры. Не просто 5, а 25.
Мало того: если перемножить любые два числа, заканчивающиеся на 5, то результат будет заканчиваться на 5. И если перемножить любые два числа, заканчивающиеся на 6, то результат будет заканчиваться на 6.
Например: 2235*9865=22048275, а 3450986*34576=119321291936.
Можно задаться вопросом: а какие ещё числа обладают таким свойством? Чтобы проверить это, сначала сообразим вот что: достаточно установить, что число проявляет данное свойство при возведении в квадрат. И тогда можно быть уверенным, что дальше оно уже выполняется автоматически. В самом деле, если пятерку нельзя с первого раза «убить» умножением на пятерку, то это невозможно и ни на каком шаге, сколько бы ты ни старался.
Кроме 5 и 6 есть ещё два числа, обладающих этим свойством. Это очевидные 0 и 1. Например:
12340**2=152275600, а 16741**2=280261081
Причина тут очевидна: когда мы перемножаем числа, то результат для последней цифры зависит только от последних цифр. «Старшие» разряды на него никак не влияют. И это основное свойство арабской системы записи чисел, которое мы в первую очередь используем при обычном школьном «умножении в столбик».
35
45
——-
175
140
——-
1575
Ну, хорошо. А можно подобрать число так, чтобы при возведении в квадрат (а значит, и в любую степень!) сохранялись две последние цифры? Что это за цифры, и сколько таких чисел?
Оказывается, их всего четыре:
00, 01, 25 и 76
Например: 200*200=40000, 2101*2101=4414201, 625*625=390625, 123476*123476
15246322576.
В одном из премеров у нас сохранились не две, а аж три цифры! Оказывается, если число оканчивается на 625, то и любая его степень тоже оканчивается на 625.
Такое совпадение разогревает наш аппетит и хочется спросить: а какие ещё трехзначные числа обладают этим свойством? И сколько этих чисел?
Оказывается, их тоже всего четыре:
000, 001, 376, 625
Ну, а теперь — нам нечего делать в математике, если мы не замечаем закономерности: каждое следующее число такого типа включает в себя предыдущее, так как последние цифры в них сохраняются. Наша первоначальная четверка 0, 1, 5, 6 просто постепенно обрастает «подробностями»:
0, 1, 5, 6
00, 01, 25, 76
000, 001, 625, 376
0000, 0001, 0625, 9376
00000, 00001, 90625, 09376
000000, 000001, 890625, 109376
0000000, 0000001, 2890625, 7109376
00000000, 00000001, 12890625, 87109376
и так далее!
Эти ряды цифр можно сделать сколь угодно длинными.
Согласитесь, свойства двух последних чисел вглядят уже совсем-совем нетривиально! Например:
28367487109376 * 28367487109376 = 804714324900613528187109376,
а 6712890625**3 = 302502322591841220855712890625
Всё это было бы не более чем приколом и случайным совпадением, если бы не было тесно связано с самыми крутыми теоремами самой крутой теорией чисел, на которой и основаны современные системы шифрования.
И эта связь неслучайна! ведь великие математики прошлого (такие как Ферма или Эйлер), создавшие эту теорию, сами были когда-то детьми и странные совпадения вначале их просто забавляли, потом очаровывали, а потом захватили их ум и повели в неведомые выси. Невероятно, но весь необходимый шифрования математический аппарат был полностью придуман или ещё в XVIII веке. Современные математики лишь приладили этот аппарат к компьютеру, разработали алгоритм и научили машинку считать эти вещи.
Но каждый из нас в душе продолжает оставаться ребнком, и у каждого из нас спит в душе маленький Ферма или Эйлер, который так и не вырос в большого Ферма или Эйлера лишь потому, что рядом не оказалось умного и доброго взрослого, который помог бы ребенку ощутить жар холдных чисел. Сегодня мы уже старые, седина в волосах, и поздно начинать — но если бы мы жили как Адам и Ева по несколько веков, то рано или поздно каждый из нас нашел бы время исправить эту досадную оплошность нашего воспитания и вникнуть в идеи великих. Потому что великие — такие же люди, как и мы. И все, что было понятно для них, может быть понятным и для нас. Пусть не в той же мере — люди все-таки отличаются друг от друга по естественным способностям! — но в значительной мере. Естественные способности разных людей отличаются друг от друга в несколько раз, ну от силы в десять раз — но не в тысячу или в сто, как может показаться, когда пытаешься «въехать» в ход мысли того же Эйлера.
Загадчным, таинственным остается момент, когда человеку «приходит в голову». Когда идея зачинается в нашем уме. Откуда она берется? Кто дает нам это таинственное семя? Это тайна, выходящая за пределы нашего разума, та тайна Бессознательного, которой посвящена значительная часть моего ЖЖурнала. И я надеюсь, я уже достаточно убедительно показал, что это НЕ человеческое. А далее уже нет ничего особенно таинственного. Человеческий ум постепенно взращивает это семя и рождает нормальную человеческую идею. Всё, что происходит в это время в уме Эйлера, в принципе могло бы произойти в уме каждого из нас. Ну, может быть, нам понадобилось бы в десять раз больше времени, чем Эйлеру — но не в тысячу и не в сто. Хотя при быстротечности нашей жизни даже десятка может стать критической…
А значит, в чем-то важном мы немногим хуже Эйлера. Он принял семя от Бессознательного, вырастил и родил. А мы принимаем готовый плод, усваиваем его — и он становится нашим. А в чем заключается суть усваивания? В том, чтобы выделить в этом плоде то изначальное семя, из которого Эйлер его произрастил. Увидеть нетривиальность, эвристичность самого первого хода его мысли — но вместе с тем железную логику и последовательность всех последующих ходов.
Двигаясь этим путем, можно воспринять идеи великих, прочувствовать их так же глубоко, как свои собственные идеи. Именно так я всегда поступал, когда мне нужно было усвоить новую теорию. Теория усвоена полностью, если у тебя есть такое чувство, будто ты сам её придумал. С нуля. Усвоить значить внутренне присвоить. А для этого нужно всегда начинать с нуля. Нужно стать на какое-то время маленьким Эйлером, который дивится забавным совпадениям-рифмам: пятью пять — двадцать пять, шестью шесть — тридцать шесть.
Маленькие дети не делятся на гуманитариев и технарей. Они цельны, и эта цельность является началом и концом настоящей мудрости. Я стараюсь сохранять строгий баланс между гуманитарной и технической стороной своего ума. Для меня это инь и ян, и одно без другого немыслимо. И мне бывает больно видеть людей, резко «перекошенных» на одну или другую сторону.
Последнее время я мало общаюсь с «физиками», всё больше с «лириками» — и это понятно и неизбежно, потому что наша физика находится пока в зачаточном состоянии. Мы только-только начали постигать этот мир при помощи матерматики, мы находимся в самом начале пути. Теория Власти — один из первых шагов в направлении вожделенного синтеза, в котором младенческая непосредственность и старческая мудрость сливаются воедино. Простота и цельность миросозерцания.
Физика — в интимном лоне своем, где она зачинает и рождает великие идеи — в самой основе своей — это не наука, а искусство.
Физика — это искусство применять математику для описания реальности.
Но мало того! Сама математика — это самая гуманитарная из всех наук. Ведь это единственная наука, которая изучает чистые продукты человеческого ума. Она черпает вдохновение не из реальности материального мира, а напрямую из идеального мира «Платоновских идей». А если говорить на христианском языке, она через духовную реальность пусть очень отдаленно и слегка, но все-таки прикасается к Божественным логосам бытия.
Потому понятно, что в душной безысходности замкнутого на себя советского мифа строителей коммунизма я не мог не стать физиком или математиком. Гуманитарных наук в СССР просто не было, они были истреблены ещё в 20-е, максимум в 30-е годы. И живой ребенок мог находить утешение лишь в фантастике и удивительной музыке сфер, которая звучала в переливах чисел и геометрических фигур. Здесь ощущалось настоящее, здесь бился пульс реальной жизни, в материальном мире почти полностью задавленный гнетом партийно-советской цензуры.
Лишь через религию вообще, а через Церковь в особенности мне довелось впервые понять, прочувствовать глубину и бездну классической гуманитарной философии, вернуться к той естественной среде обитания, где жила и дышала российская интеллектуальная элита до революции — все эти Менделеевы, Розановы, Булгаковы, Сикорские — для которых не было никакой границы между «естественным» и «гуманитарным», потому что гуманитарное для них было естественно, а естественное — гуманитарно.
Надеюсь, эта небольшая заметка поможет читателю если не понять, то хотя бы почувствовать, в чем состоит амбициозный замысел задуманного мною цикла «Математика для гуманитариев». Как и в каком стиле писать — я пока лишь нащупываю, придумываю на ходу, методом проб и ошибок. И мои читатели-комментаторы активно помогают мне найти верный путь.
Что нужно гуманитарию? Заново ощутить жизнь в той омертвевшей ещё в детстве части ума, которая отвечает за математическое мышление. Что это значит для него? Это значит ощутить прелесть, поэзию, небесную музыку, которая скрыта в формулах. Формулы — это язык, и они не бывают «сухими». «Сухой» в мире смыслов означает «лишенный смысла». Формула суха лишь для того, для кого она бессмысленна, кто не овладел языком, на котором выражена записанная при помощи этих знаков живая человеческая мысль.
Освоить этот язык, понять смысл формул значит открыть для себя целый новый мир! И притом это намного легче, чем выучить французский или там немецкий язык. Язык формул прост, в нём мало слов, но эти слова страшно ёмки. Это не язык Эллочки Людоедки, а скорее немногословные строки Мандельштама:
Из полутёмной залы вдруг
Ты выскользнула в лёгкой шали.
Мы никому не помешали,
Мы не будили спящих слуг.
Концентрация смысла зашкаливает, не правда ли?
Вот, например, малая теорема Ферма. Выглядит угрожающе просто:
An%n=A
Даже проще, чем стих Мандельштама.
А в чем её смысл? Берется некое число, его возводят в какую-то степень (то есть, несколько раз перемножают само на себя), потом делают нечто таинственное (что я обозначил значком процента %) — и в результате получается само же число A, с которого начинали.
Что это? Совпадение?
Нет! говорит Ферма.
Это не совпадение. Это так и должно быть. И можно строго доказать, что иначе и быть не может, говорит Ферма.
И это безумно красиво. И не только красиво, но и полезно. Потому что на этом основаны современные системы шифрования. Когда Ферма создавал свою теорию, не было компьютеров и никому не приходила в голову безумная идея использовать такие вещи для шифрования. Просто потому, то это заняло бы слишком много времени. Трудные, длинные расчеты нужны, чтобы таким способом что-то зашифровать, а потом расшифровать. Но в XX веке появился железный паровоз, который делает такие вещи в два притопа и три прихлопа. Только «объясни» ему, что ты хочешь. Составь программу на понятном для него языке — и посчитает всё, что хочешь, за милую душу.
Тогда, в XVII (!) веке, Ферма просто баловался. Ему было прикольно и интересно понять, случайны ли такие совпадения? Почему пятью пять именно двадцать пять? А сегодня для нас это критически важно, чтобы совпало. Иначе мы зашифровать зашифруем, а расшифровать назад — не сможем.
Но каким надо было обладать гением, чтобы в XVII (!) веке, во время Тридцатилетней войны, доказать теорему, из которой потом (в XVIII веке) великий Эйлер сделает конфетку, скушав которую в XX веке математики сделают готовую шифровальную машинку.
Ферма просто забавлялся. И мы можем позабавиться вместе с ним. Например, я построил на теореме Фрема забавную заметку по теории чисел (см. Если n нечетно, то (n**5 — n) делится на 240 без остатка).
Это очень важно — позабавиться. Это необходимо для обновления. Тут мудрость. И у этой забавной мудрости есть недетский смысловой слой. Если кто имеет мудрость, сочти число зверя, ибо это число человеческое. Уметь считать — полезно, и иногда это критически важно для выживания. Но невозможно научиться считать, если не полюбишь числа. Любовь — основа бытия.
И потому для гуманитария нет никакого другого способа освоить математику, кроме как вернуться в детство и начать просто играть с числами и другими категориями, похожими на числа.
Заметьте! Хотя мы по видимости говорили о числах, на самом деле нас интересовали не сами числа, а только последние цифры в этих числах.
Нам было всё равно, 12476376 или 8764376. По сути, мы просто-напросто отождествляли между собой все числа, оканчивающиеся на заданные цифры. Мы отбрасывали у числа все, что идет впереди. Хотя впереди идет вроде бы самое важное, самые страшные миллиарды и триллионы! Но мы же дети, и нам забавно наблюдать за тем простым и понятным, что стоит в конце. Оно для нас важнее потому, что оно привлекло наше внимание. Мы заметили, что там происходит что-то прикольное и интересное. И мы по-детски непосредственно отбрасываем то, что нам в данный момент неинтересно. Нам пока неважны миллиарды, мы смотрим на гармонию сфер, которая вдруг зазвучала в последних цифрах числа. Она стала пока важной, а прочее неважным. И вот как раз отбрасывание неважного и обозначено в теореме Ферма при помощи значка процента %.
То есть, в переводе на русский язык, формула An%n=A означает: если число А помножить само на себя n раз (А*А*А*…*А) и по определенному правилу отбросить образовавшиеся миллиарды и миллионы, то в остатке получится то же самое число А. Разве это не забавно? А если знаешь, что это ещё и полезно (для правильной расшифровки!), то имеет смысл вникнуть в это внимательнее.
…
Обыкновенные дроби 5 класс
1. Выполни сложение:
2. Запиши число в виде суммы его целой и дробной части:
3. Выделите целую и дробную часть числа:
1) frac{11}{2} ; 2) frac{48}{3} ; 3) frac{29}{4} ; 4) frac{37}{8} ;
5) frac{311}{10} ; 6) frac{259}{17} ; 7) frac{91}{24} ; 
4. Запиши частное в виде дроби и переведи в смешанное число:
1) 19 : 4; 2) 37 : 5; 3) 29 : 7; 4) 85 : 13.
5. Сравни:
6. Начерти координатный луч, взяв за единичный отрезок 3 клетки. Обозначь на нем точки, соответствующие неправильным дробям frac{4}{3} ; frac{7}{3} ; frac{11}{3} ; frac{14}{3} ; frac{19}{3} , предварительно выделив целую и дробную части каждой из них.
7. Сравни:
8. Размести числа frac{38}{7} ; frac{59}{8} ; frac{10}{2} ; frac{14}{3} ; frac{20}{3} в порядке возрастания.
9. Какие натуральные числа удовлетворяют неравенству frac{23}{7} < n < frac{45}{8} .
10. Турист прошел 13 км за 3 часа. Найди скорость туриста.
11. На пошив семи одинаковых платьев мастерская израсходовала 15 м ткани. Хватит ли 2 м ткани на пошив одного платья?

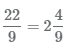
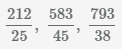 в смешанные числа.
в смешанные числа.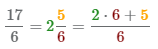
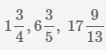 в неправильные дроби.
в неправильные дроби.