На этой странице вы узнаете
- Чем отличаются признаки от свойств?
- Сколько крыс у биссектрисы?
- Гибридом чего будет квадрат?
Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.
Параллелограмм
Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.

Параллелограмм мы видим достаточно часто.


Признаки параллелограмма
У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма:
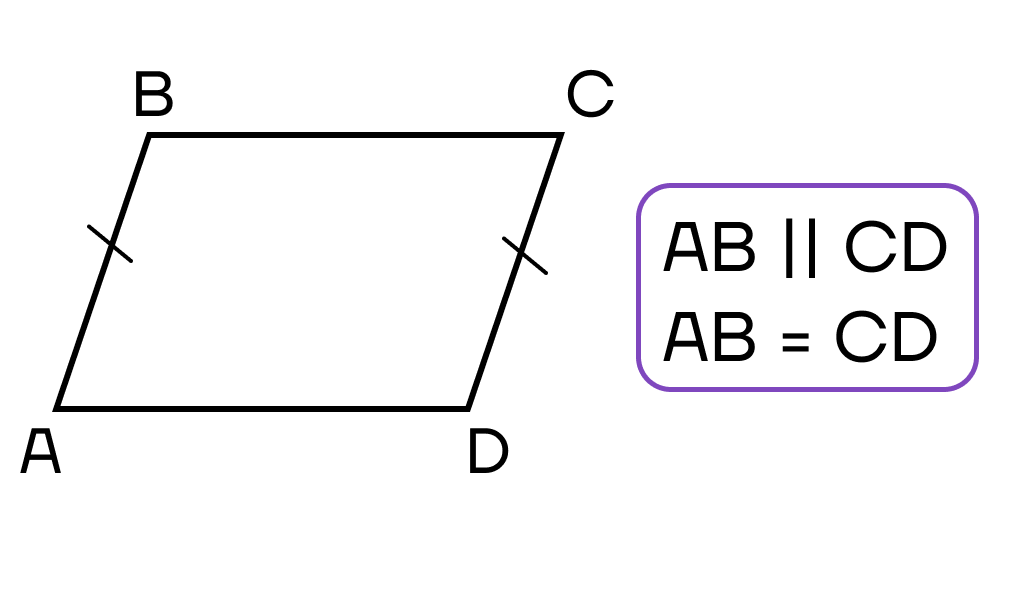
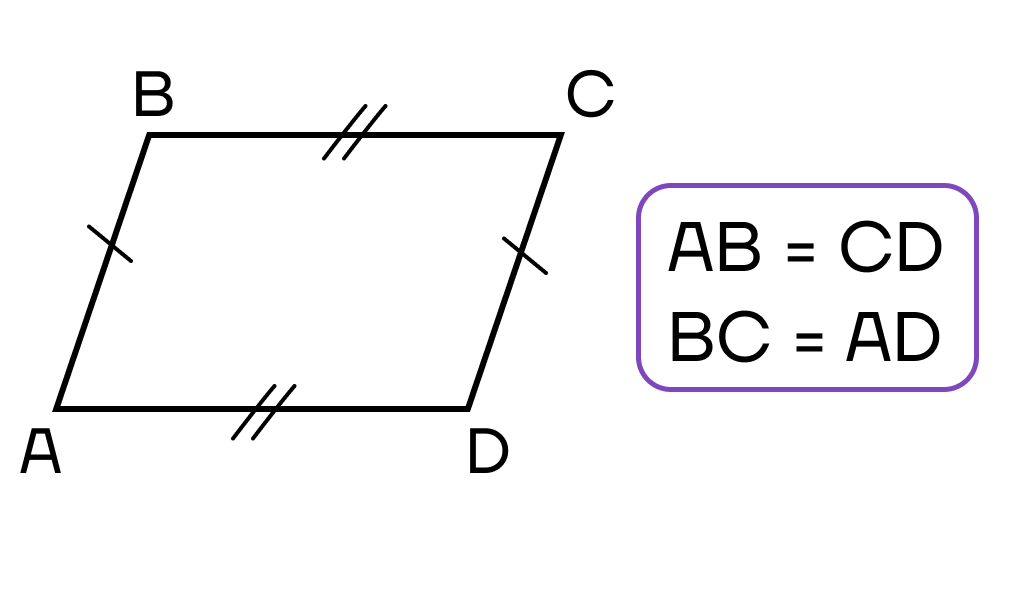
- Две противоположные стороны четырехугольника параллельны и равны.
- Противоположные стороны четырехугольника попарно равны.
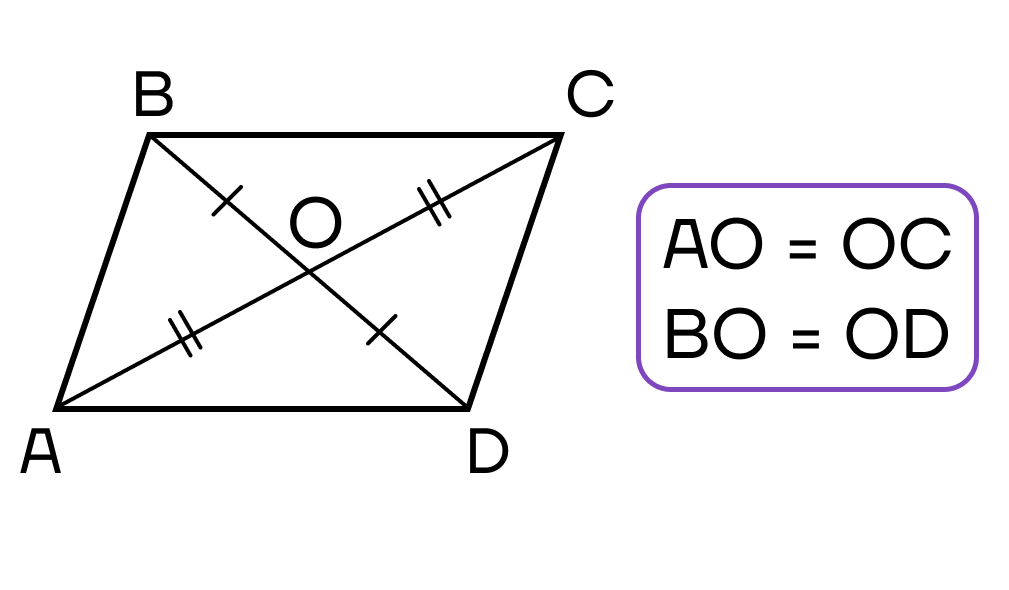
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Свойства параллелограмма
Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников.
Свойства параллелограмма:
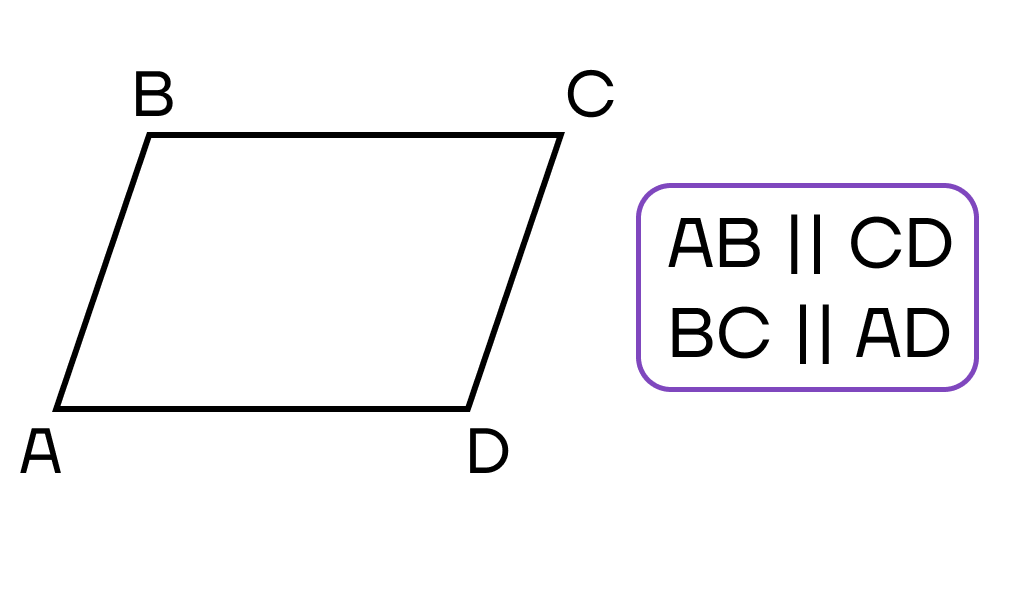
- Противолежащие стороны равны.

- Противолежащие стороны параллельны.
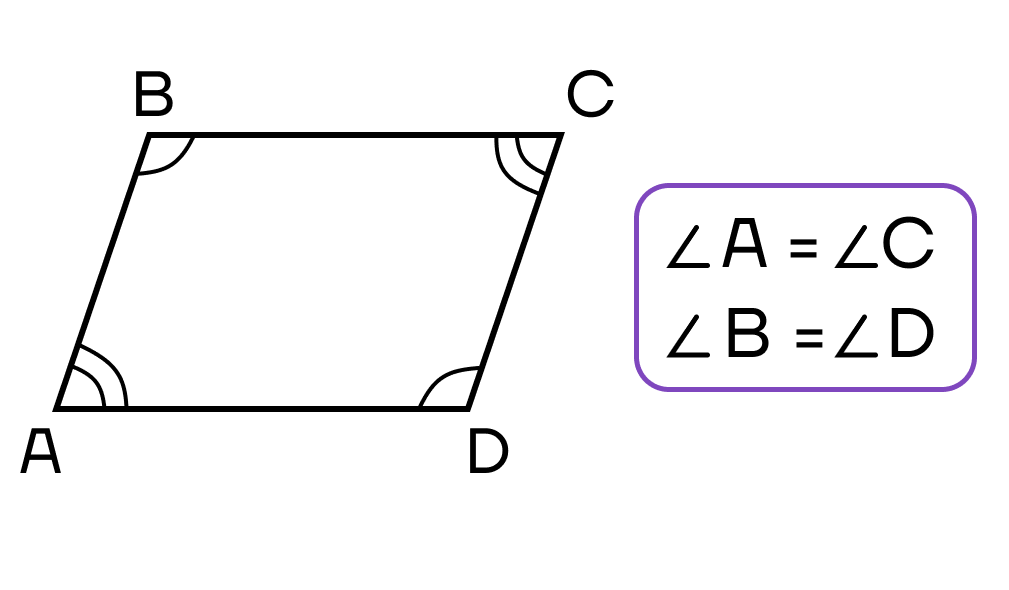
- Противолежащие углы равны.
- Сумма всех углов 3600.
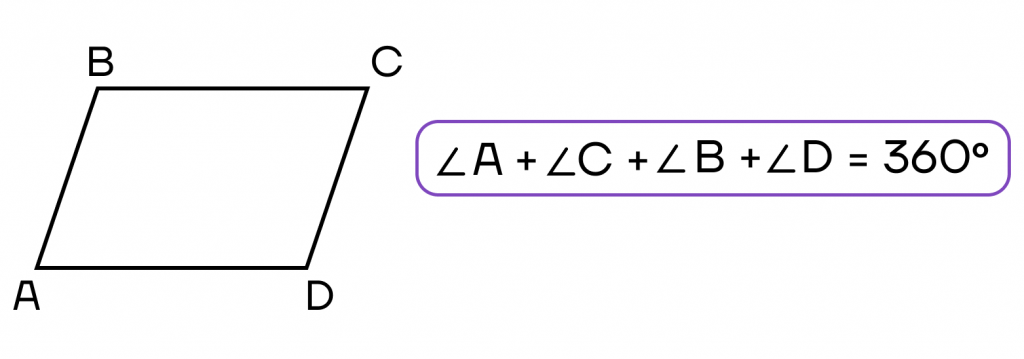
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Сумма углов, прилежащих к любой стороне, равна 1800.
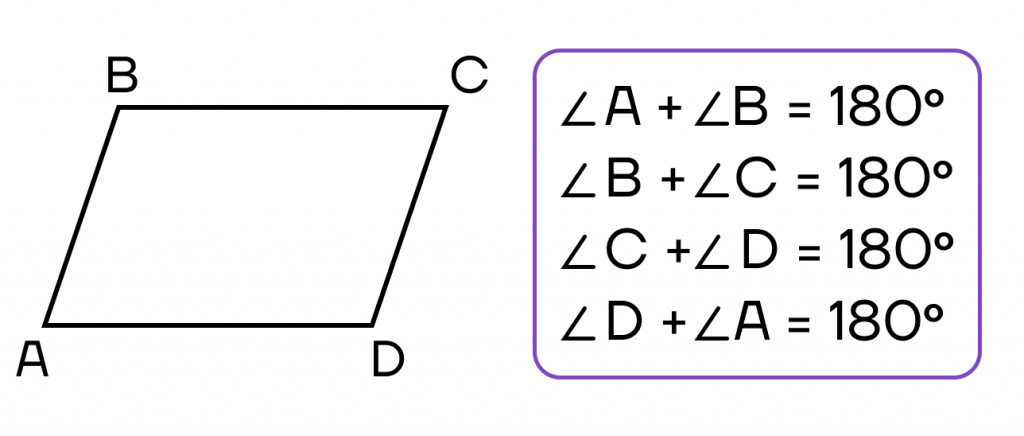
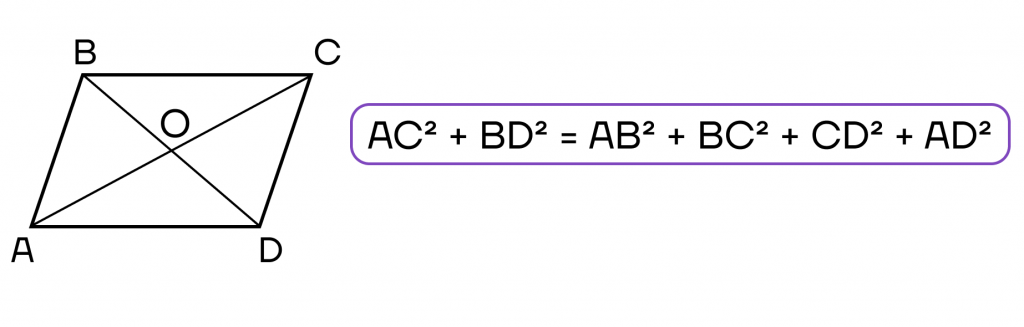
- Сумма квадратов диагоналей равна сумме квадратов всех сторон.
- Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.

- Каждая диагональ делит параллелограмм на два равных треугольника

Биссектриса в параллелограмме
Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”.
Так как у треугольника три угла – соответственно, и крыс-биссектрис тоже три.
Два факта связанные с биссектрисой в параллелограмме:
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
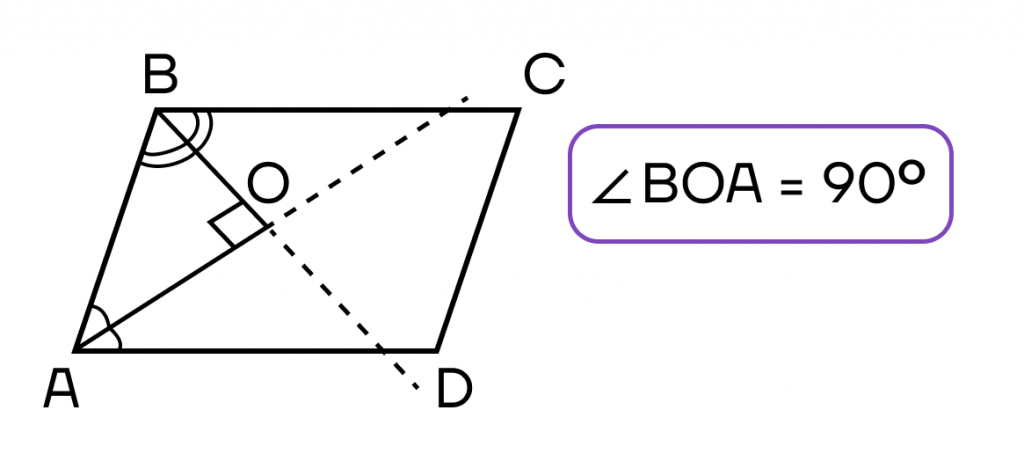
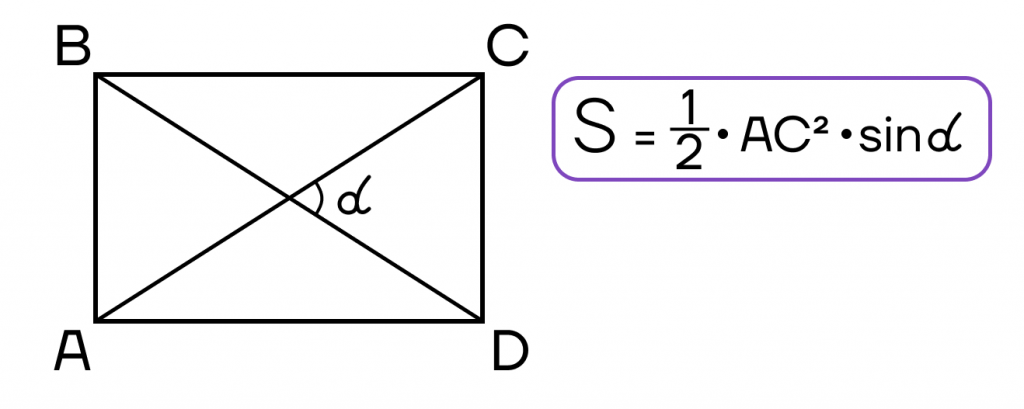
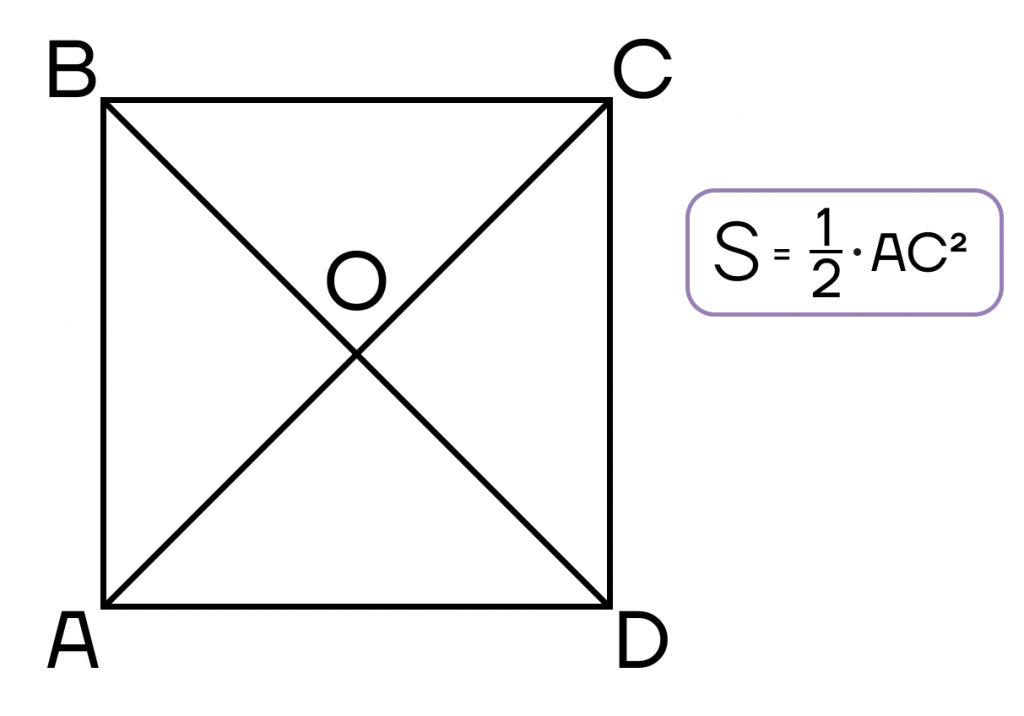
Площадь параллелограмма
Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
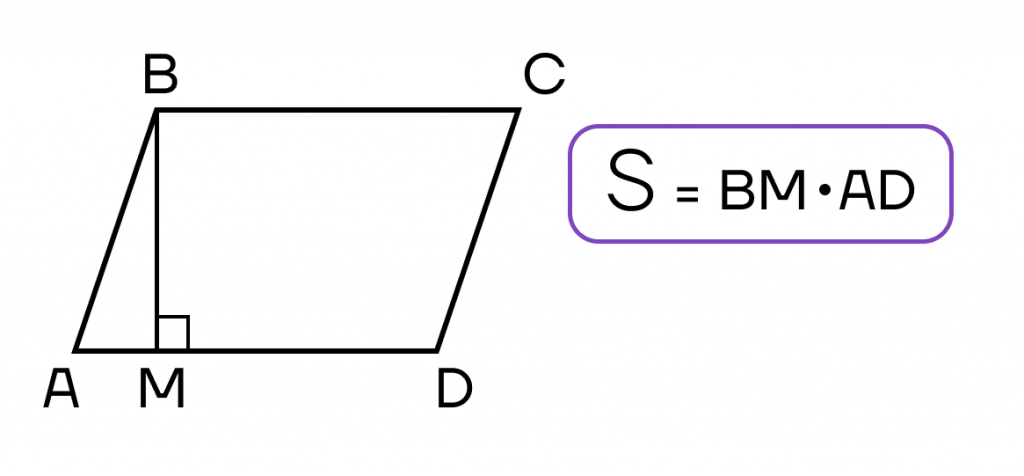
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Прямоугольник
Как параллелограмм связан с прямоугольником?
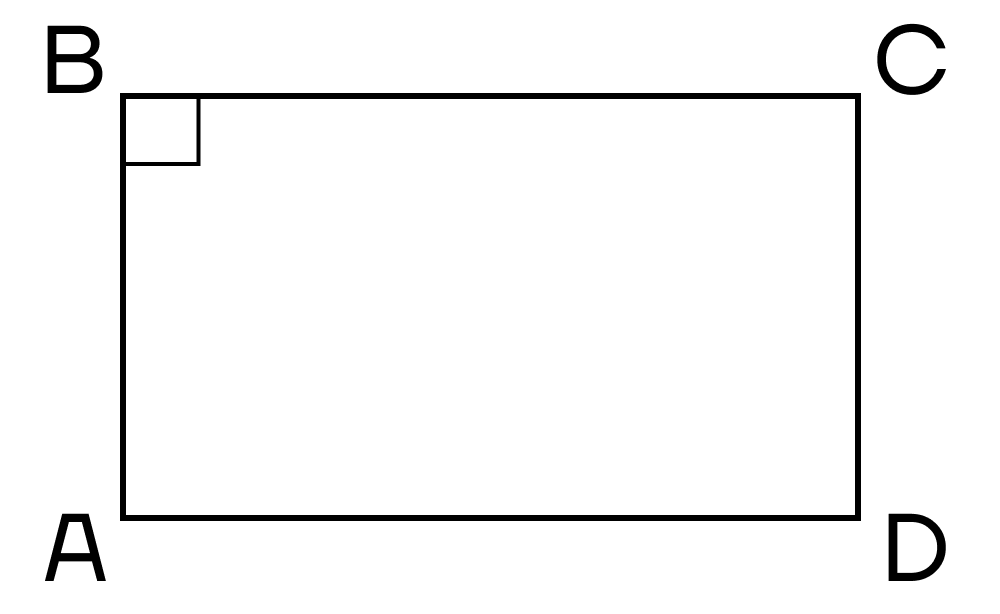
Прямоугольник – это параллелограмм, углы которого по 900.
Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.
В жизни прямоугольником можно назвать дверь, картину или фотографию:
Признаки прямоугольника
- Параллелограмм, имеющий хотя бы один прямой угол.
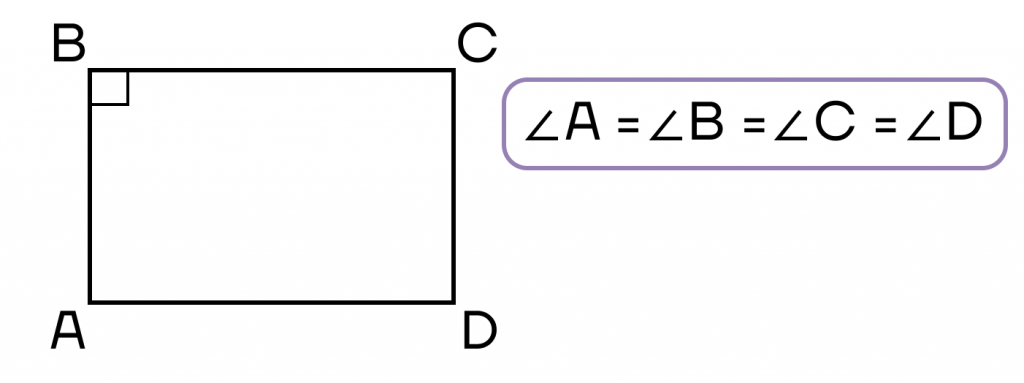
- Параллелограмм, все углы которого равны.
- Параллелограмм, диагонали которого равны.
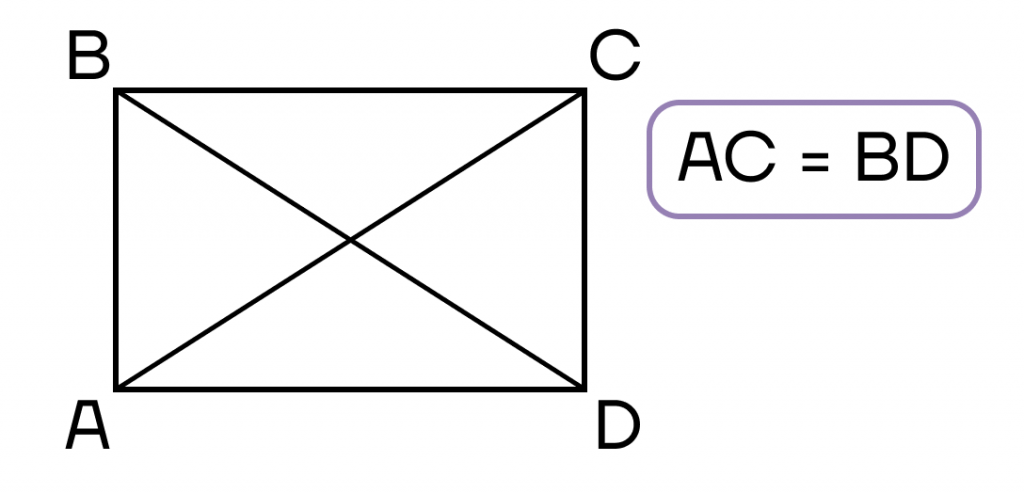
- Четырехугольник, у которого три прямых угла.

Свойства прямоугольника
- Все углы прямые.

- Диагонали равны.

- Стороны прямоугольника одновременно являются и его высотами.
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали.
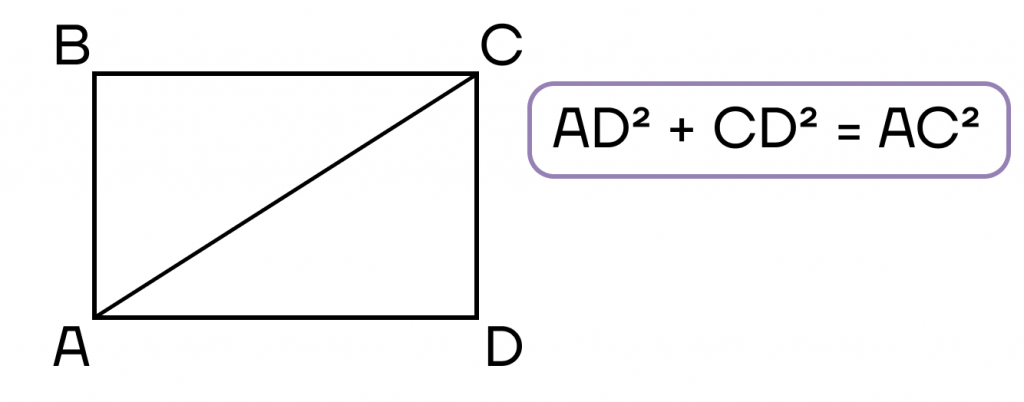
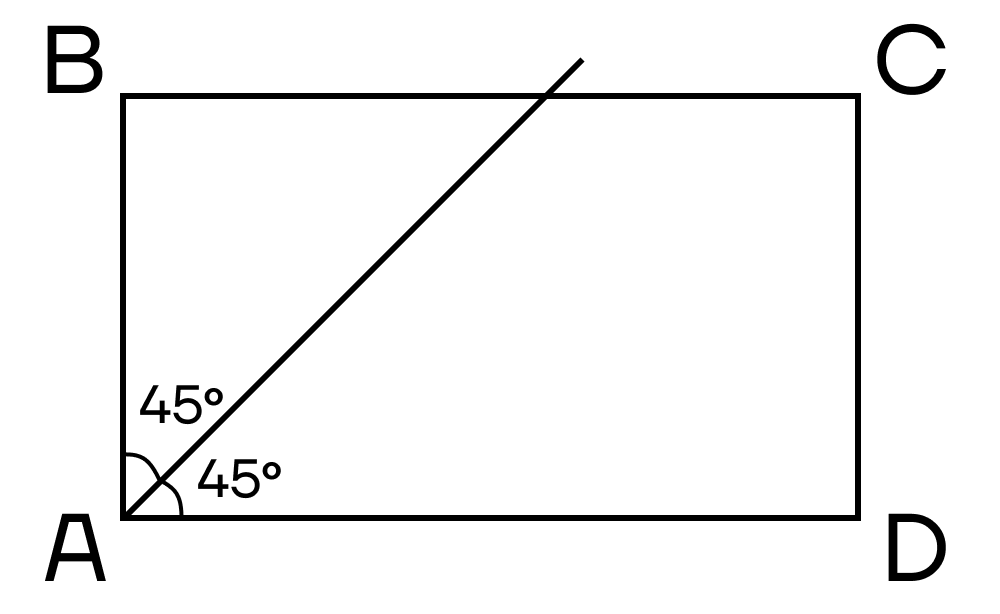
Биссектриса и площадь прямоугольника
Биссектриса делит угол прямоугольника на два угла по 450 и пересекает одну из сторон прямоугольника.
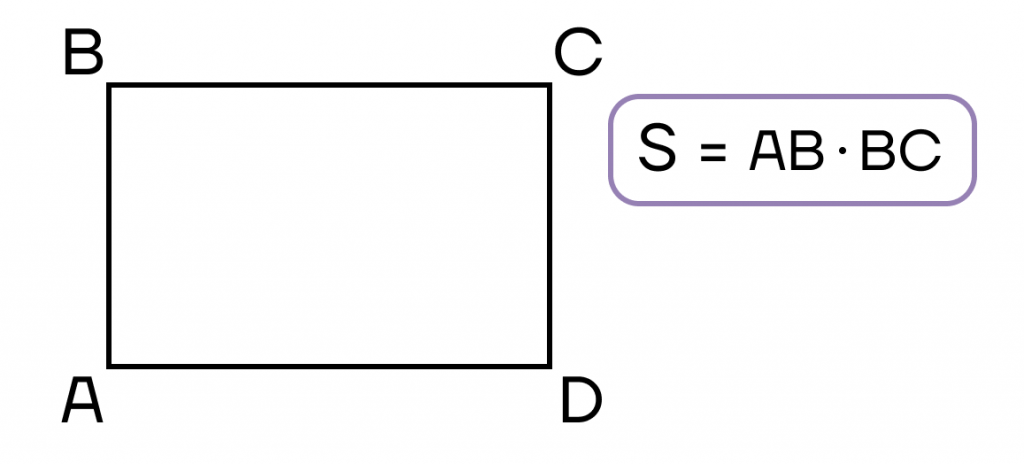
Теперь рассмотрим два способа нахождения площади прямоугольника:
- Площадь прямоугольника равна произведению двух соседних сторон.
- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
Ромб
Пожалуй, это самая неустойчивая фигура.

Ромб – это параллелограмм, у которого все стороны равны.

Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.
А также в игровых наградах:

Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.
Всё о ромбе
Признаки ромба:
- Две смежные стороны параллелограмма равны.
- Диагонали параллелограмма пересекаются под прямым углом.
- Диагональ параллелограмма делит каждый угол пополам.
- Четырехугольник, у которого все стороны равны.
Свойства ромба:
- Все стороны равны.

- Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

- Диагонали являются биссектрисами.

- Высоты в ромбе равны.
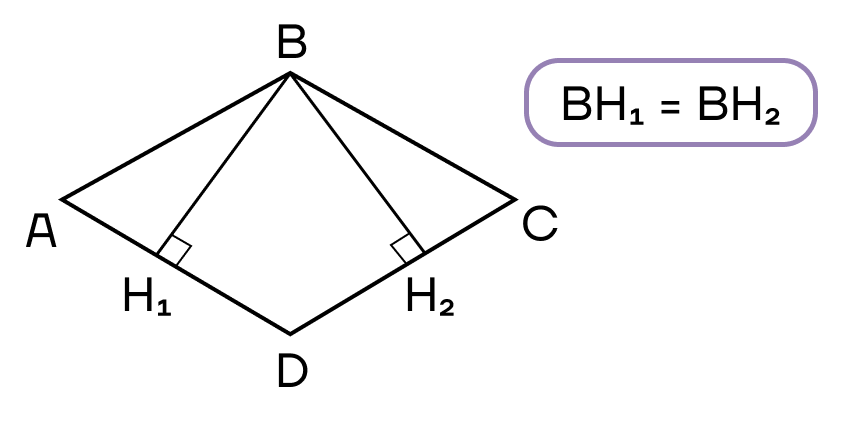
Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.
Как найти площадь ромба?
Для нахождения площади ромба есть три разные формулы:
- Площадь ромба равна произведению стороны и высоты ромба.
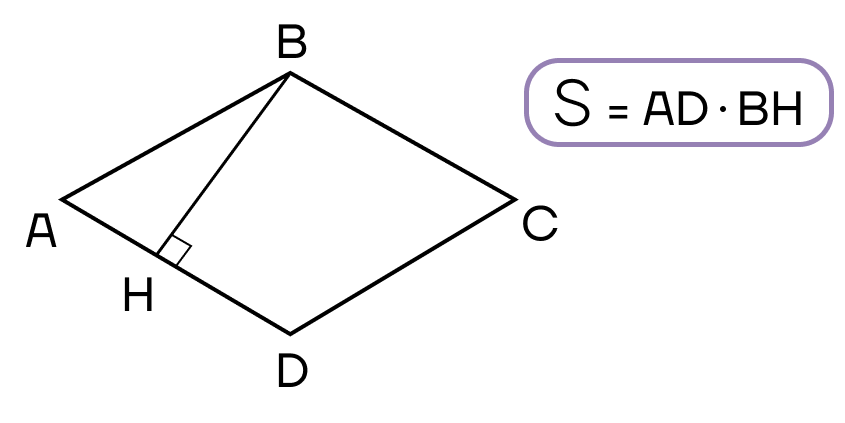
- Площадь ромба равна половине произведения его диагоналей.
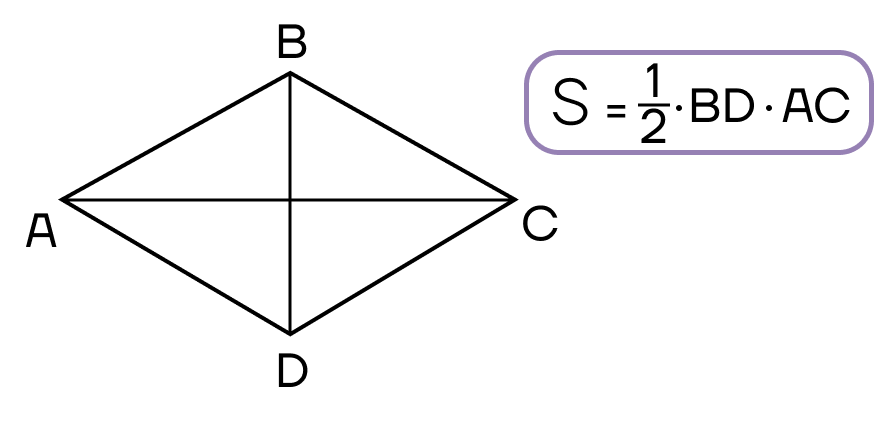
- Площадь ромба равна произведению квадрата стороны на синус угла ромба.
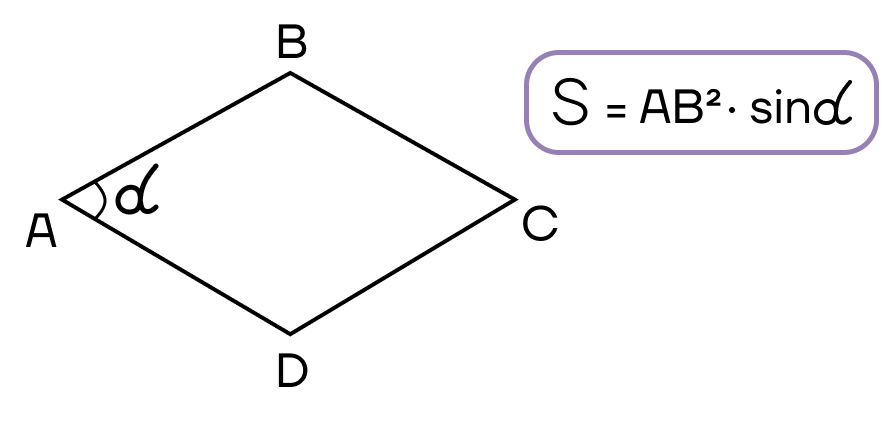
Квадрат
А вот квадрат, наоборот, достаточно устойчив.

Квадрат – это четырехугольник, у которого все углы и стороны равны.
Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб.
Нечто, сочетающее в себе разнородные элементы, называют гибридом. Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.

Квадратом может быть крышка подарочной коробки или окно.


Рассмотрим признаки и свойства данной фигуры.
Всё о квадрате
Признаки квадрата:
- Ромб, у которого хотя бы один угол прямой.
- Ромб, у которого все углы равны.
- Ромб, у которого диагонали равны.
- Четырехугольник, диагонали которого равны и перпендикулярны.
Свойства квадрата:
- Диагональ квадрата равна 2 стороны квадрата.
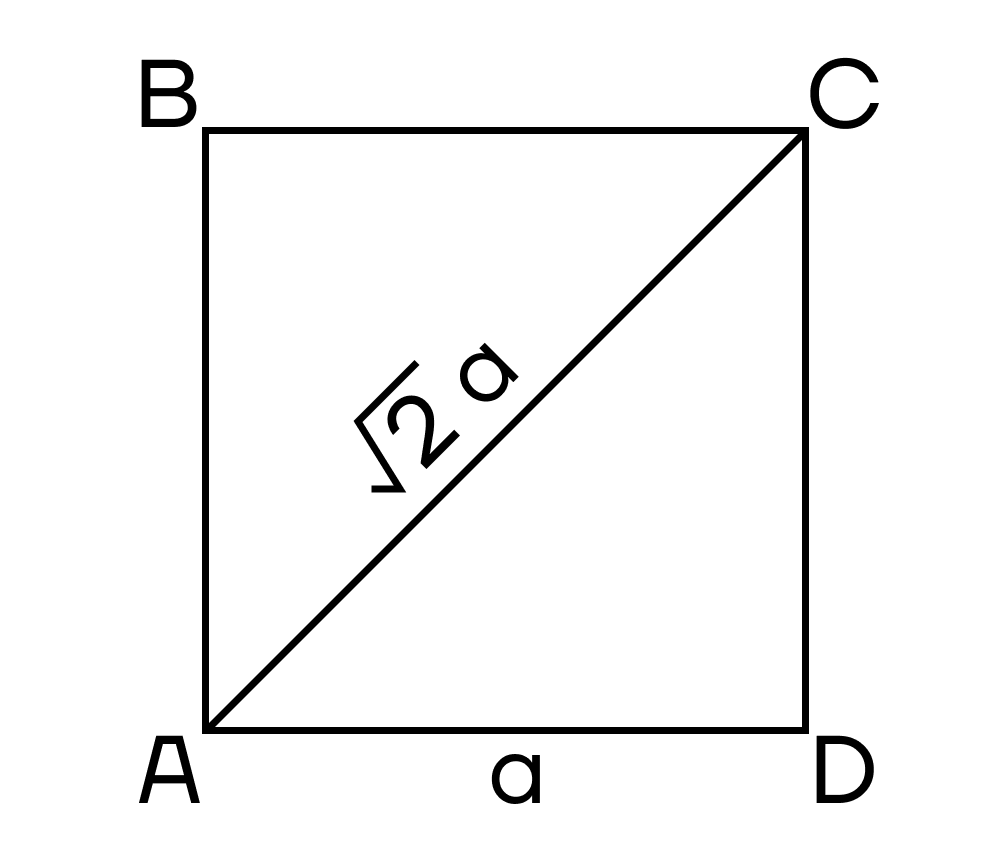
- Диагонали делят квадрат на четыре равных треугольника.

Биссектрисой квадрата, как и у ромба, является диагональ.
Рассмотрим формулы для нахождения площади квадрата:
- Площадь квадрата равна квадрату его стороны.
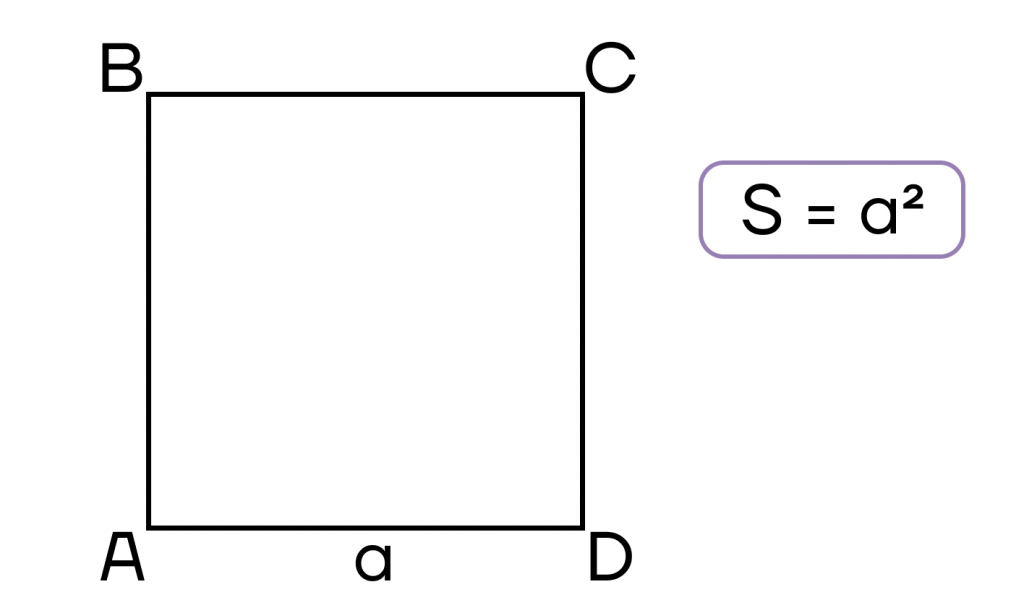
- Площадь квадрата равна половине квадрата диагонали.
Фактчек
- Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
- Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
- Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
- Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.
Проверь себя
Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 300
- 40
- 20
- 10
- 25
Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 600
- 83
- 6
- 63
- 4
Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10
- 30
- 60
- 15
- 25
Задание 4.
У четырехугольника диагонали пересекаются под углом 300, а его стороны попарно параллельны и равны. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3
Определение.
Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны, то есть лежат на параллельных прямых.
Если
ABCD — параллелограмм (по определению).
противолежащие стороны параллелограмма ABCD:
AB и CD; AD и BC
смежные стороны параллелограмма ABCD:
AB и BC; AB и AD; BC и CD; CD и AD;
противолежащие углы параллелограмма ABCD:
∠A и ∠C, ∠B и ∠D
углы параллелограмма ABCD, прилежащие к одной стороне:
∠A и ∠B, ∠C и ∠D, ∠A и ∠D, ∠B и ∠C
Соседние вершины параллелограмма — это вершины, являющиеся концами одной из его сторон.
Соседние вершины параллелограмма ABCD: A и B, C и D, A и D, B и C
Диагонали параллелограмма — это отрезки, соединяющие его противолежащие вершины.
диагонали параллелограмма ABCD: AC и BD
Большинство задач на параллелограмм сводятся к рассмотрению треугольников.
В следующий раз поговорим о свойствах параллелограмма.
Смежные стороны параллелограмма это?
Перед вами страница с вопросом Смежные стороны параллелограмма это?, который относится к
категории Геометрия. Уровень сложности соответствует учебной программе для
учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
План урока:
Понятие многоугольника
Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Теорема Фалеса
Понятие многоугольника
Построим на плоскости отрезок А1А2. Выберем произвольную точку А3, не лежащую на прямой А1А2, и соединим ее с точкой А2. Получится фигура, состоящая из двух отрезков. Можно отметить на плоскости следующую точку А4, не лежащую на прямой А2А3, и также соединить ее с А3. Получим три соединенных друг с другом отрезка. Процесс можно продолжать сколь угодно долго. Фигура, получаемая при таком построении, называется ломанной.
Отрезки А1А2, А2А3 и т.д. называют звеньями ломанной. Если начало и конец ломанной совпадают друг с другом, а ее звенья не пересекаются, то ломанная образует замкнутую фигуру, которая называется многоугольником (иногда используют сокращение многоуг-к):
Для примера покажем замкнутую ломанную, имеющую самопересечения. Она НЕ является многоугольником:
Каждое звено ломанной называется стороной многоуг-ка, а их начальные и конечные точки – это вершины многоугольника. Число сторон многоуг-ка всегда равно количеству его вершин. Если сложить длину всех сторон многоуг-ка, то можно получить величину, которую называют периметром многоугольника.
Задание. Найдите периметр многоугольника, длины сторон которого показаны на рисунке:
Решение. Для нахождения периметра (его обычно обозначают буквой Р) надо просто сложить длины всех сторон:
В общем случае, когда многоуг-к имеет n сторон, его называют n-угольником. В частности, многоуг-к с тремя сторонами называется треугольником, с четырьмя сторонами – четырехугольником и т.д.
Любые две вершины многоуг-ка, которые соединены друг с другом его стороной, называются соседними вершинами. Отрезок, соединяющий любые несоседние вершины многоуг-ка, называется диагональю многоугольника:
Можно заметить, что любой многоуг-к делит плоскость на две области – внутреннюю, ограниченную сторонами многоугольника, и внешнюю.
Выпуклый многоугольник
В рамках школьной геометрии в основном изучают особые многоугольники, которые называются выпуклыми. Они отличаются тем, что полностью лежат с одной стороны от любой прямой, проходящей через соседние вершины многоугольника. Проиллюстрируем понятие выпуклого многоуг-ка с помощью рисунка:
Здесь АВСD – выпуклый многоугольник, так как ни одна из прямых, проходящих через его стороны, не пересекает его. А многоуг-к ЕРМК выпуклым не является, ведь прямые КМ и ЕМ проходят сквозь него и делят многоуг-к на две части.
Есть несколько свойств выпуклого многоугольника, которые иногда используются для того, чтобы дать ему определение. Во-первых, у всякого выпуклого многоуг-ка любая диагональ полностью лежит внутри многоуг-ка. Если же хоть одна диагональ лежит вне площади, ограниченной многоуг-ком, то он является невыпуклым:
Во-вторых, если в выпуклом многоуг-ке любые две точки внутренней области соединить отрезком, то он будет полностью лежать внутри многоуг-ка. У невыпуклого же многоуг-ка обязательно найдутся такие две точки внутренней области, что отрезок, соединяющий их, будет проходить и через внешнюю область. В частности, на рисунке отрезок RQ соединяет две точки выпуклого моногоуг-ка, поэтому он обязательно должен полностью лежать внутри АВСD. Многоугольник ЕРМК является невыпуклым, поэтому обязательно найдутся такие точки Т и Н, что отрезок ТН будет частично «выходить» за пределы внутренней области ЕРМН:
Любые две соседние стороны многоуг-ка образуют угол, который часто именуют той же буквой, что и соответствующую вершину многоуг-ка:
Существует особая формула, которая позволяет находить сумму углов выпуклого многоугольника. Для ее вывода изобразим произвольный выпуклый многоуг-к, у которого n вершин, и построим в нем диагонали, исходящие из одной вершины. В результате мы получим несколько треугольников:
Сначала попытаемся сосчитать количество получившихся диагоналей. Диагонали соединяют вершину А с всеми вершинами, кроме двух соседних (на рисунке это В и F) и самой вершины А. То есть из n вершин только 3 (А, В и F) не могут быть соединены диагональю с А, а остальные (n – 3) точки с ней соединены. Тогда и диагоналей ровно (n – 3).
Теперь посчитаем число получившихся треугольников. Каждая диагональ разбивает одну часть многоугольника на две. Таким образом, треугольников ровно на единицу больше, чем диагоналей, то есть их количество равно (n – 2).
Можно заметить, что сумма углов всех этих получившихся треуг-ков в точности равна сумме углов многоуг-ка. Однако нам уже известно, что сумма углов в треуг-ке равна 180°. Тогда в многоугольнике с n сторонами эта сумма будет равна величине 180°(n– 2).
Задание. Найдите, чему равна сумма углов четырехугольника, пятиугольника и стоугольника.
Решение. У четырехугольника 4 вершины, то есть n = 4. Просто подставляем это значение в формулу:
Аналогично для пятиугольника принимаем n = 5:
Наконец, для стоугольника число n будет равно 100:
Ответ: 360°; 540°; 17640°.
Задание. У выпуклого шестиугольника все углы равны. Чему они равны?
Решение. Если сложить все углы шестиугольника, то получится сумма, равная
Всего углов шесть, поэтому для нахождения каждого угла их сумму следует поделить на 6:
Ответ: 120°.
Задание. Сколько сторон имеет многоугольник, если каждый его угол равен 135°?
Решение. Обозначим число сторон многоугольника буквой n. Сумма всех его углов будет равна величине 180(n– 2). Если все углы равны друг другу, то каждый из них равен
Приравняв эту дробь к 135°, получим уравнение, из которого можно найти n:
Четырехугольник
Частным случаем многоугольника является четырехугольник (четырехуг-ник) – плоская фигура с 4 вершинами. Выше мы уже выяснили, что сумма углов четырехугольника равна 360°. Те стороны четырехуг-ка, которые не являются смежными, называются противоположными.
Задание. Периметр четырехуг-ка равен 80 см. Известно, что его наибольшая сторона больше трех других сторон на 3, 4 и 5 см. Найдите каждую из сторон четырехугольника.
Решение. Обозначим длину наибольшей стороны переменной х. Тогда длины оставшихся сторон будут равны величинам х – 3, х – 4 и х – 5 см. Из условия ясно, что их сумма должна равняться 80 см, поэтому можно составить уравнение:
Итак, наибольшая сторона имеет длину 23 см. Теперь мы можем вычислить и три оставшиеся стороны:
Задание. Один из углов четырехуг-ка равен 135°, а три остальных равны друг другу. Определите величину этих углов.
Решение. Обозначим углы цифрами. Тогда условие задачи можно записать так:
Задание. Углы четырехуг-ка пропорциональны числам 1, 2, 4 и 5. Рассчитайте их величину.
Решение. Условие задачи означает, что наименьший угол, который пропорционален числу 1, меньше трех других углов в 2, 4 и 5 раз. То есть, если обозначить его как х, то тогда другие углы будут равны 2х, 4х и 5х. Тогда можно составить следующее уравнение:
Параллелограмм
Большой интерес для геометрии представляют частные случаи четырехуг-ков, которые обладают особыми свойствами. Одним из них является параллелограмм. Так называют четырехуг-к, у которого противоположные стороны параллельны друг другу.
Задание. АВСD– выпуклый четырехугольник. Известно, что
Можно ли утверждать, что АВСD – это параллелограмм?
Решение. Используем рисунок:
Нам уже известно, что сумма углов четырехуг-ка АВCD равна 360°. На рисунке видно, что сумма углов при каждой стороне одинакова:
Теперь заметим, что прямая АВ– это секущая для АD и BC, причем∠А и ∠Вв таком случае являются односторонними. Но если сумма односторонних углов равна 180°, то прямые должны быть параллельными, то есть АD||BC. Аналогично, рассматривая АD как секущую прямых АВ и СD, и учитывая, что
можно доказать параллельность отрезков АВ и СD.Тогда получается, что противоположные стороны четырехугольника АВCD параллельны. Значит, он является параллелограммом.
Параллелограмм обладает примечательным свойством – его противоположные стороны равны друг другу, также как и противоположные углы.
Докажем эти утверждения. Для этого построим произвольный параллелограмм АВCD и проведем в нем диагональ:
В результате получились два треуг-ка: ∆АВD и ∆ВСD. У них есть общая сторона ВD. Далее заметим, что диагональ ВD является секущей как для параллельных прямых ВС и АD, так и для АВ и CD (параллельны же эти отрезки по определению параллелограмма). Но накрест лежащие углы при параллельных прямых равны, поэтому
Теперь мы видим, что у ∆АВD и ∆ВСD есть равная сторона, а также равны и прилегающие к ней углы. Отсюда делаем вывод, что
Из этого сразу вытекает, что
Также очевидно, что и ∠В = ∠D, ведь они могут быть представлены в виде суммы углов, которые соответственно равны друг другу:
Задание. Периметр параллелограмма равен 48 см. Известно, что одна из его сторон больше другой на 3 см. Найдите все стороны параллелограмма.
Решение. Обозначим меньшую сторону переменной х, тогда большая сторона параллелограмма будет равна х + 3 см. Так как противоположные стороны у параллелограмма одинаковы, то две другие стороны также будут равны х и х + 3 см:
Сложив длины всех сторон и приравняв эту сумму к 48 см, получим уравнение:
Задание. Биссектриса угла М параллелограмма МКНР пересекает сторону КН в точке Е. Известно, что КЕ = 15 см, а ЕН = 9 см. Чему равен периметр МКНР?
Решение: Выполним построение по условию задачи:
Чтобы найти периметр, надо знать длины двух смежных сторон параллелограмма. Проще всего найти КН:
Осталось найти МК. Заметим, что биссектриса МЕ является секущей параллельных КН и МР. Из этого вытекает, что
ведь они накрест лежащие. В свою очередь
ведь биссектриса МЕ разбивает ∠М на два равных угла. Из этих двух равенств получаем, что
Получается, что в∆КЕМ два угла равны. А значит, он равнобедренный, причем основанием является МЕ. Это значит, что
Две смежные стороны нам известны, теперь мы можем найти периметр:
Задание. Известен один из углов параллелограмма, он равен 84°. Найдите все остальные его углы.
Решение. Обозначим параллелограмм буквами АВСD, и пусть
Проще всего найти ∠С, ведь противоположные углы параллелограмма равны:
Сумма углов∠А и ∠В должна равняться 180°, ведь они являются односторонними при параллельных прямых ВС и AD. Это позволяет найти∠В:
Углы∠В и ∠D одинаковы, ведь они являются противоположными в параллелограмме:
Второе свойство параллелограмма связано с его диагоналями.
Докажем это утверждения, построив следующий рисунок:
Пусть диагонали ABСD пересекаются в точке, обозначенной буквой О. Рассмотрим ∆АОB и ∆СОD. Их стороны АВ и CD одинаковы, ведь в параллелограмме АВСD они являются противоположными сторонами. Также как накрест лежащие равны следующие углы:
По 2-ому признаку равенства треуг-ков можно сделать вывод, что
Это как раз и означает, что точка О – это середина диагоналей.
Признаки параллелограмма
Существует несколько признаков, которые позволяют доказать, что тот или иной четырехуг-к является параллелограммом. Рассмотрим первый из них.
Пусть в четырехуг-ке параллельны и равны стороны АB и CD. Проведем диагональ ВD. Она окажется секущей для АВ и СD, поэтому накрест лежащие углы окажутся равными:
Сторона ВD – общая, а АВ = СD по условию. Тогда по 1-ому признаку равенства треуг-ков ∆АВD = ∆CВD. В свою очередь это означает, что
Они являются накрест лежащими уже при отрезках ВС и АD. Отсюда вытекает, что эти отрезки параллельны друг другу. В итоге в четырехуг-ке ABCD параллельными оказываются все противоположные стороны, поэтому он должен быть параллелограммом.
Задание. В параллелограмме АВCD смежные стороны различны, а∠А – острый. Из точек B и D опущены перпендикуляры ВК и DM на диагональ АС. Докажите, что фигура ВМDК – тоже параллелограмм.
Решение. Выполним построение по заданным условиям:
Необходимо доказать, что красная фигура – это параллелограмм. По выведенному нами признаку достаточно показать, что отрезки ВК и MD параллельны и равны. Их параллельность очевидна, ведь эти отрезки перпендикулярны к одной прямой (АС). Равенство отрезков можно доказать, рассмотрев ∆АВК и ∆СМD. Они являются прямоугольными, у них равны гипотенузы АВ и СD (как противоположные стороны в одном параллелограмме), а также
ведь это накрест лежащие углы при параллельных отрезках АВ и CD. В итоге получаем, что
Но тогда ВК = МD. В итоге, с учетом того, что ВК||МD, получаем, что ВМDК – это параллелограмм.
Следующая теорема позволяет определять, является ли фигура параллелограммом, только по длине ее сторон.
Для доказательства используем всё тот же прием: проведем в четырехуг-ке диагональ:
Мы снова получаем равенство треуг-ков
но на этот раз они равны по трем равным сторонам. Отсюда получаем равенство углов:
Из равенства этих углов, являющихся накрест лежащими, следует, что АВ||СDи ВС||АD. Это и значит, что АВСD– параллелограмм.
Задание. Середины смежных сторон параллелограмма соединили друг с другом отрезками. Докажите, что получившаяся таким образом фигура – параллелограмм.
Решение.
Обозначим середины сторон АВСD буквами М, Р, К и Т. Ясно, что
как противоположные стороны одного параллелограмма. Если отрезки равны, то равны и их половины, поэтому можно записать:
Теперь рассмотрим ∆АМТ и ∆СРК. Они равны, ведь у них одинаковы две стороны и угол, лежащий между ними:
Отсюда следует, что МТ = РК. Аналогично можно показать, что ∆МВР = ∆ТDК, из чего вытекает, что МР = ТК.
В итоге получаем, что у МРКТ противоположные стороны попарно равны. А это означает, что МРКТ – это параллелограмм.
Следующий признак параллелограмма связан с диагоналями.
Действительно, пусть в произвольном четырехуг-ке АВСD диагонали пересекаются в точке О, являющейся серединой диагоналей:
Тогда ВО = ОDи АО = ОС. Рассмотрим ∆АОВ и ∆СОD. ∠ВОА = ∠СОD, ведь это вертикальные углы. В итоге у этих треуг-ков равны две стороны, а также угол между ними. Следовательно, ∆АОВ = ∆СОD. Но отсюда следует, что
В итоге у АВСD противоположные стороны одинаковы. Значит, это параллелограмм.
Задание. О – точка, в которой пересекаются диагонали параллелограмма АВСD. М, Р, Н, К – середины отрезков АО, ВО, СО и DO соответственно. Докажите, что МРНК – это параллелограмм.
Решение.
По свойству параллелограмма точка О делит их пополам, то есть на равные отрезки:
Заметим, что диагоналями МРНК являются отрезки РК и МН, причем они пересекаются в точке О. Так как
Можно сказать, что О – середина диагоналей РК и МН. Отсюда вытекает вывод, что МРНК – параллелограмм.
Теорема Фалеса
Свойства параллелограмма помогают доказать одну из древнейших теорем планиметрии – теорему Фалеса. Она названа в честь философа, который считается родоначальником всей древнегреческой науки. Можно сказать, что Фалес – это самый ранний из всех ученых-геометров, чье имя дошло до наших дней. Сформулируем теорему Фалеса:
Здесь на прямой m отложили равные друг другу отрезки А1А2, А2А3,А3А4 и т.д.:
Далее через концы отрезков провели параллельные линии (показаны синим цветом), которые пересекли некоторую прямую n в точках В1, В2,В3 и т.д. Теорема утверждает, что получившиеся при этом отрезки равны между собой:
Для доказательства теоремы нужно рассмотреть два случая. Сначала изучим ситуацию, когда прямые m и n параллельны друг другу:
Рассмотрим четырехуг-к А1В1В2А2. Его противоположные стороны лежат на параллельных прямых:
Тогда этот четырехуг-к по определению оказывается параллелограммом, а в нем, как известно, противоположные стороны одинаковы, то есть
Однако отрезки А1А2, А2А3,А3А4 равны друг другу, следовательно, и равные им отрезки В1В2, В2В3, В3В4 и т. д. будут также равными, что мы и пытаемся доказать.
Более сложным является случай, когда исходные прямые m и n непараллельны друг другу:
В этом случае проведем через В1 отрезок В1С2, параллельный m. При этом точка С2 будет лежать на прямой А2В2. Аналогично проведем отрезки В2С3, В3С4 и т. д. , каждый из которых будет параллельным прямой m:
Рассмотрим фигуры А1В1С2А2, А2В2С3А3, А3В3С4А4 и т. д. Это четырехуг-ки, у каждого из которых противоположные стороны параллельны. Значит, все эти фигуры – параллелограммы. Но у него противоположные стороны одинаковы:
Далее заметим, что прямая n является секущей для параллельных прямых В1С2, В2С3, В3С4 и т.д. Это значит, что можно записать равенство углов:
Эта же прямая является секущей для параллельных прямых А1В1, А2В2 и т. д., поэтому можно записать равенство углов:
Наконец, рассмотрим треуг-ки ∆В1В2С2, ∆В2В3С3, ∆В3В4С4. Только что мы выяснили, что у них есть по два равных угла. Но так как сумма углов в любом треуг-ке равна 180°, то и третьи углы у них также будут равными.
Но тогда эти треуг-ки оказываются равными друг другу, так как у них равны стороны В1С2, В2С3, В3С4 и т.д. Из равенства треуг-ков вытекает и равенство сторон:
Именно это равенство мы и пытались доказать.
Данная теорема может быть очень полезна при практических построениях. Пусть на клетчатом листке бумаги изображен такой треуг-к:
Предположим, требуется найти середину стороны АВ, а также разделить сторону ВС на три равные части. Для этого достаточно провести напротив этих сторон вертикальные линии, которые можно разделить на равные части буквально «по клеточкам». Далее надо просто провести уже горизонтальные линии, которые и разделят стороны АВ и ВС в нужных пропорциях:
Итак, из этого урока мы узнали о понятии выпуклого четырехуг-ка и изучили один из его частных случаев – параллелограмм. В будущем мы познакомимся и с другими видами четырехуг-ков.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
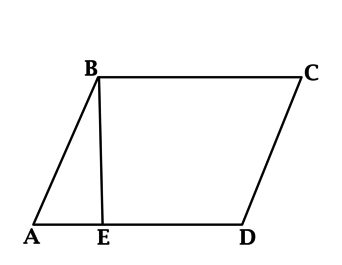
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни