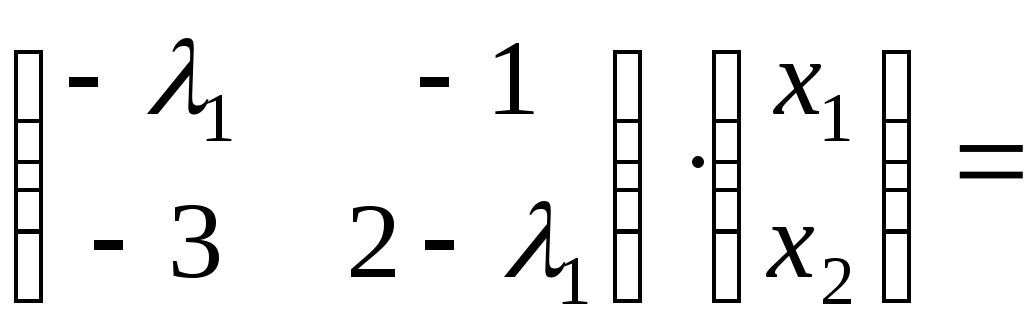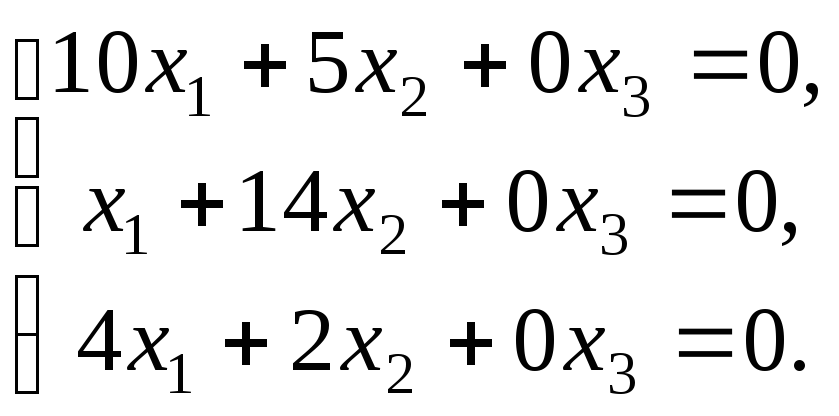Как найти собственное значение оператора заданного матрицей

Собственные
векторы и собственные

значения
линейного оператора

Определение 1.
Собственным
вектором оператора

называют
ненулевой вектор
,
удовлетворяющий равенству:
=.

Определение 2.
Собственным
значением оператора

называют
число
,
для которого выполняется равенство:
=,
где

— ненулевой вектор.

(1)

(2)

Решив последнее
уравнение относительно
,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
,
каждый из которых соответствует
определенному собственному значению.

Рассмотрим несколько
примеров, в каждом из которых будем
выполнять последовательность действий
решения задачи об отыскании собственных
значений и собственных векторов матрицы.

Пример 1.

Найти собственные
значения и собственные векторы матрицы
.
Дать геометрическую интерпретацию
полученного решения.

Решение

1. Матрица имеет
   размерность 22,
   то есть является представлением
   линейного оператора в пространстве
   .
   Собственный вектор матрицы будем искать
   в виде:
   .

2. Составим уравнение
   для отыскания собственных векторов в
   матричном виде:

3. Перепишем
матричное уравнение в виде системы
уравнений:

1. Однородная система
   имеет ненулевые решения тогда и только
   тогда, когда определитель ее главной
   матрицы равен 0. Получаем характеристическое
   уравнение системы и решаем его:

.

Собственные
значения матрицы
:

,

.

1. Найдем собственные
   векторы для каждого собственного
   значения:

; ; ; Пусть , тогда собственное направление матрицы , соответствующее собственному значению , задается множеством векторов: , где .

; ; ; Пусть , тогда собственное направление матрицы , соответствующее собственному значению , задается множеством векторов: , где .

Пример
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.

1. Составим и решим
   характеристическое уравнение
   .

В нашей задаче
.

Тогда характеристическое
уравнение принимает вид:

,
или
,

,

,

— собственные
значения линейного оператора.

1. Найдем собственные
   векторы, соответствующие собственному
   значению
   ,
   решая матричное уравнение:

х=0
или
,
т.е.

.

Полагая в последнем
равенстве
,
получим
.

Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х¹=.

1. Найдем собственные
   векторы, соответствующие собственному
   значению
   ,
   решая матричное уравнение:

х=0
или
,
т.е.

.

Полагая в последнем
равенстве
,
получим
.

Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х²=.

Ответ. Собственному
значению
соответствуют собственные векторы
х¹=,
а собственному значению
собственные векторы

х²=.

Пример
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.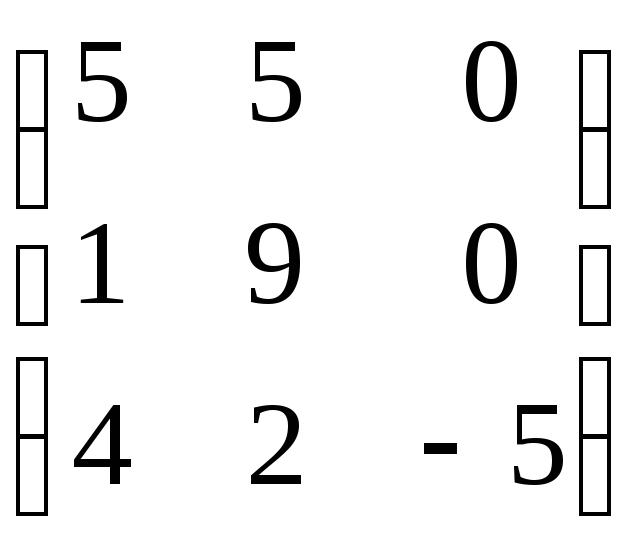

1. Найдем собственные
   значения линейного оператора. Для этого
   составим характеристическое уравнение
   и найдем его корни:

.

,

,

,

,

,

,

,

— собственные значения линейного
оператора.

1. Найдем собственные
   векторы, соответствующие собственному
   значению
   .
   Исходя из соотношения
   х=0
   или в нашем случае

,
запишем систему:

Решая методом
Гаусса, получаем

Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим
,
.

Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х¹=.

1. Найдем собственные
   векторы, соответствующие собственному
   значению
   .
   Исходя из соотношения
   х=0
   или в нашем случае

,
т.е.

Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
,
получим
.

Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х²=.

1. Найдем собственные
   векторы, соответствующие собственному
   значению
   .
   Исходя из соотношения
   х=0
   или в нашем случае

,
т.е.

Решая методом
Гаусса, получаем

,

откуда, система
принимает вид

Полагая
,
получим
.

Таким
образом, собственные векторы,
соответствующие собственному значению
,
имеют вид: Х³=.

Соседние файлы в папке Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #

Нахождение собственных чисел и собственных векторов

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.

Больше:

Выводить десятичную дробь

,

• Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.

• Элементы матриц — десятичные (конечные и периодические) дроби: 1/3, 3,14, -1,3(56) или 1,2e-4; либо арифметические выражения: 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2).

  • decimal (finite and periodic) fractions:

    1/3, 3,14, -1,3(56) или 1,2e-4

  • 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2)

  • matrix literals:

    {{1,3},{4,5}}

  • operators:

    +, -, *, /, , !, ^, ^{*}, ,, ;, ≠, =, ⩾, ⩽, > и <

  • functions:

    sqrt, cbrt, exp, log, abs, conjugate, min, max, gcd, rank, adjugate, inverse, determinant, transpose, pseudoinverse, cos, sin, tan, cot, cosh, sinh, tanh, coth, arccos, arcsin, arctan, arccot, arcosh, arsinh, artanh и arcoth

  • units:

    rad, deg

  • special symbols:

    • pi, e, i — mathematical constants
    • k, n — integers
    • I or E — identity matrix
    • X, Y — matrix symbols
• Используйте ↵ Ввод, Пробел, ←↑↓→, Backspace и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V — для копирования матриц.
• Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
• За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.

Примеры

• Найти собственные векторы ({{-26,-33,-25},{31,42,23},{-11,-15,-4}})

Линейные операторы

Определение

Самый простой линейный оператор — умножение вектора на число (lambda ). Этот оператор просто растягивает все вектора в (lambda ) раз. Его матричная форма в любом базисе — (diag(lambda ,lambda ,…,lambda )). Фиксируем для определенности базис ({e}) в векторном пространстве (mathit{L}) и рассмотрим линейный оператор с диагональной матричной формой в этом базисе, (alpha = diag(lambda _1,lambda _2,…,lambda _n)). Этот оператор, согласно определению матричной формы, растягивает (e_k) в (lambda _k) раз, т.е. (Ae_k=lambda _ke_k) для всех (k=1,2,…,n). С диагональными матрицами удобно работать, для них просто строится функциональное исчисление: для любой функции (f(x)) можно положить (f(diag(lambda _1,lambda _2,…,lambda _n))=diag(f(lambda _1),f(lambda _2),…,f(lambda _n))). Таким образом возникает естественный вопрос: пусть имеется линейный оператор (A), можно ли выбрать такой базис в векторном пространстве, чтобы матричная форма оператора (A) была диагональной в этом базисе? Этот вопрос приводит к определению собственных чисел и собственных векторов.

Определение.
Пусть для линейного оператора (A) существует ненулевой вектор (u) и число (lambda ) такие, что
[
Au=lambda cdot u. quad quad(59)
]
Тогда вектор (u) называют собственным вектором оператора (A), а число (lambda ) — соответствующим собственным числом оператора (A). Совокупность всех собственных чисел называют спектром линейного оператора (A).

Возникает естественная задача: найти для заданного линейного оператора его собственные числа и соответствующие собственные вектора. Эту задачу называют задачей о спектре линейного оператора.

Уравнение для собственных значений

Фиксируем для определенности базис в векторном пространстве, т.е. будем считать, что он раз и навсегда задан. Тогда, как обсуждалось выше, рассмотрение линейных операторов можно свести к рассмотрению матриц — матричных форм линейных операторов. Уравнение (59) перепишем в виде
[
(alpha -lambda E)u=0.
]
Здесь (E) — единичная матрица, а (alpha) — матричная форма нашего линейного оператора (A). Это соотношение можно трактовать как систему (n) линейных уравнений для (n) неизвестных — координат вектора (u). Причем это однородная система уравнений, и нам следует найти ее нетривиальное решение. Ранее было приведено условие существования такого решения — для этого необходимо и достаточно, чтобы ранг системы был меньше числа неизвестных. Отсюда следует уравнение для собственных чисел:
[
det(alpha -lambda E)=0. quad quad(60)
]

Определение. Уравнение (60) называется характеристическим уравнением для линейного оператора (A).

Опишем свойства этого уравнения и его решений. Если его выписывать в явном виде, получим уравнение вида
[
(-1)^nlambda ^n+…+det(A)=0. quad quad(61)
]
В левой части стоит полином по переменной (lambda ). Такие уравнения называются алгебраическими степени (n). Приведем необходимые сведения об этих уравнениях.

Справка об алгебраических уравнениях.

Основная теорема алгебры.
Уравнение (61) имеет решение на комплексной плоскости (mathbb{C}).

Следствие.
Уравнение (61) имеет на комплексной плоскости столько решений, какова его степень (решения учитываются с учетом кратности).

Пример.

Рассмотрим уравнение
[
lambda (lambda-1)^2(lambda+1)^3=0.
]
Это уравнение 6 степени. Оно имеет следующие решения: ( lambda =0), ( lambda =1), ( lambda =-1), причем кратность первого решения равна 1 (такие решения называют простыми корнями), кратность второго решения равна 2, кратность третьего решения равна 3. Решения, кратность которых выше 1, называют кратными . В нашем случае 1+2+3=6. Уравнения степени (n geq 5) невозможно решить с помощью радикалов (теорема Абеля-Руффини). Для уравнений степени (n=2,3,4) такие явные формулы существуют. Однако на практике уравнения высокой степени можно успешно решать с помощью компьютеров. Таким образом, в дальнейшем будем считать, что мы тем или иным способом построили решения уравнения (61).

Собственные вектора

Рассмотрим вопрос о построении собственного вектора, соответствующего известному собственному числу (lambda _k). Для этого обратимся к уравнению
[
(alpha -lambda_k E)u=0.
]
Это уравнение можно понимать как систему линейных уравнений для координат вектора (u) — собственного вектора, соответствующего собственному числу (lambda _k). При этом данная система имеет нетривиальное решение, так как ранг этой системы меньше числа неизвестных. Решая эту систему методом Гаусса, можно определить координаты вектора (u). Перебирая все значения (lambda _k), (k=1,2,…,n), находим соответствующие собственные вектора (u_k).

Пример. Найдем собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе следующей матрицей:
[
A=left ( begin{array}{ccc}5 & -7 & 0 \-3 & 1 & 0 \12 & 6 & -3 end{array} right ).
]
Матрица (A-lambda E) имеет в данном случае вид:
[
A- lambda E=left ( begin{array}{ccc}5 -lambda & -7 & 0 \-3 & 1-lambda & 0 \12 & 6 & -3 -lambdaend{array} right ).
]
Вычисляем определитель (det(A-lambda E)) и выписываем уравнение на собственные значения:
[
det(A-lambda E)=-(lambda +3)(lambda ^2-6lambda -16)=0.
]
Отсюда находим 3 собственных значения: (lambda _1=-3, lambda _2=8, lambda _3=-2). Мы получили 3 собсвенных значения, все они имеют кратность 1, т.е. это
простые собственные числа. Вычислим соответствующие собственные вектора.

1. Рассмотрим (lambda _1=-3). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left( begin{array}{ccc}8 & -7 & 0 \-3 & 4 & 0 \12 & 6 & 0end{array} right) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта система уравнений для 3 неизвестных имеет следующее решение: (u=(0,0,1)^T).

2. Рассмотрим (lambda _2=8). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left ( begin{array}{ccc}-3 & -7 & 0 \-3 & -7 & 0 \12 & 6 & 5 end{array} right ) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта однородная система уравнений для неизвестных (u_1,u_2,u_3) имеет решение: (u=(7, -3, 0)^T).

3. Рассмотрим (lambda _3=-2). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left ( begin{array}{ccc}7 & -7 & 0 \-3 & 3 & 0 \12 & 6 & -1 end{array} right ) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта однородная система уравнений для неизвестных (u_1,u_2,u_3) имеет решение: (u=(1,1,0)^T).

Теорема.
Пусть все собственные числа линейного оператора (A) — простые. Тогда набор собственных векторов, соответствующих этим собственным числам, образует базис векторного пространства.

Итак, в условиях теоремы появляется базис, связанный с данным линейным оператором — базис его собственных векторов. Рассмотрим матричную форму оператора в таком базисе. Как упоминалось выше, (k)-ый столбец этой матрицы — это разложение вектора (Au_k) по базису. Однако по определению (Au_k=lambda _ku_k), так что это разложение (то, что выписано в правой части) содержит только одно слагаемое и построенная матрица оказывается диагональной. В итоге получаем, что в условиях теоремы матричная форма оператора в базисе его собственных векторов равна (diag(lambda _1,lambda _2,…,lambda _n)). Поэтому если необходимо развивать функциональное исчисление для линейного оператора разумно работать в базисе его собственных векторов.

Если же среди собственных чисел линейного оператора есть кратные, описание ситуации становится сложнее и может включать так называемые жордановы клетки. Мы отошлем читателя к более продвинутым руководствам для изучения соответствующих ситуаций.

Предыдущий раздел

Назад

Следующий раздел

Онлайн калькулятор нахождение собственных чисел и собственных векторов — Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.