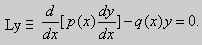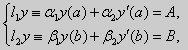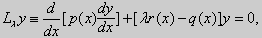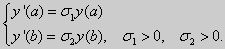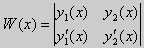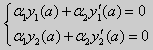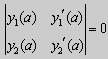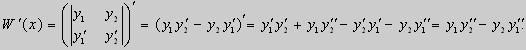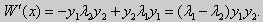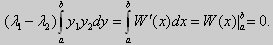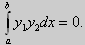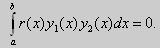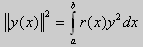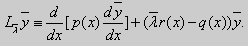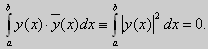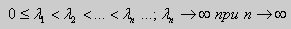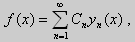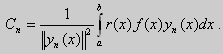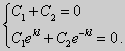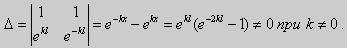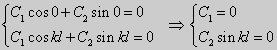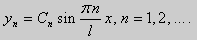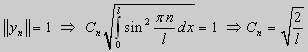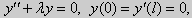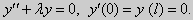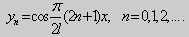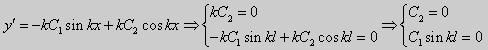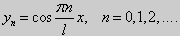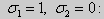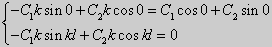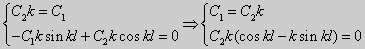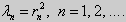
58
При этом значении силы Pкр первоначальная прямолинейная форма равно-
весия сжатого стержня становится неустойчивой.
Пример. Найти собственные значения и собственные функции однородной краевой задачи:
|
y′′ = λy, |
y(0) = y(l) = 0, |
l > 0. |
|
|
Если λ = 0, |
то y =C1x + C2 , |
и граничным условиям удовлетворяет |
|
|
только тривиальное решение |
y ≡ 0. |
Следовательно, |
λ = 0 не является соб- |
|
ственным значением. |
|||
|
При λ > 0 |
общее решение уравнения y′′ = λy |
будет: |
y =C1e
λx + C2e−
λx .
Подставляя это решение в граничные условия, убеждаемся в том, что они удовлетворяются только при y ≡ 0.
Если же λ < 0, то общее решение уравнения имеет вид
y =C1 sin
− λx + C2 cos 
− λx.
Подставляя это выражение в граничные условия, получим
C2 = 0,
C1 sin
− λl = 0.
Чтобы краевая задача имела ненулевые решения, необходимо принять
|
nπ |
2 |
|||||||||
|
sin − λl = 0. Тогда |
− λl = nπ |
и |
, |
n =1,2,… |
||||||
|
λ = − |
l |
|||||||||
Эти значения λ и являются собственными. Соответствующие им собственные функции с точностью до множителя равны
|
y =sin |
nπx |
, |
n =1,2,… |
|
|
l |
||||
Пример. Найти собственные значения и собственные функции однородной краевой задачи для уравнения (2.51) при граничных условиях
y(0) − y(1) = 0, y′(1) = 0.
59
Общее решение уравнения согласно (2.55) имеет вид
Вычисляем |
y = C1 cos λx +C2 sinλx. |
|
|
y (x) = −C1λsinλx +C2λcos λx, |
||
|
′ |
||
|
y(0) = C1, |
y(1) = C1 cos λ +C2 sinλ, |
|
|
′ |
||
|
y (1) = −C1λsinλ +C2λcos λ. |
Подставляя эти величины в граничные условия, после элементарных преобразований получим систему линейных однородных алгебраических уравнений относительно C1 и C2 :
(1− cosλ) C1 −sinλ C2 = 0,
− λsinλ C1 + λcosλ C2 = 0.
Ненулевое решение ее существует тогда и только тогда, когда определитель системы равен нулю:
|
1− cosλ |
−sinλ |
|
|
= 0. |
||
|
− λsinλ |
λcosλ |
Раскрывая этот определитель, получим уравнение относительно параметра
λ :
λ(cosλ −1) = 0,
корни которого являются собственными значениями задачи:
|
λ = 0, |
||
|
λ = 2πn, |
n =1,2,… |
|
|
Легко убедиться, что при λ = 0 y = const. Подставляя λ = 2πn, |
n =1,2,… |
в систему линейных однородных алгебраических уравнений относительно C1 и C2 , находим C2 = 0. Соответствующие собственные функции с точностью до множителя будут y = cos 2πnx.
2.4. Дифференциальные уравнения с переменными коэффициентами
Если коэффициенты ai (x), (i =1,2,…,n) линейного неоднородного уравнения
|
60 |
|
|
y(n) + a1(x) y(n−1) + a2 (x) y(n−2) + an−1(x) y′+ an (x) y = f (x) |
(2.61) |
и его правая часть f(x) представляют собой функции, которые определены и непрерывны на заданном интервале, то рассмотренные выше теоремы о структуре общего решения линейного неоднородного уравнения и соответствующего ему однородного уравнения остаются справедливыми. Остаются в силе также принцип суперпозиции решений для неоднородного уравнения и метод вариации произвольных постоянных. Но при этом нельзя искать фундаментальную систему решений однородного уравнения рассмотренным выше методом.
Одним из простейших линейных дифференциальных уравнений с переменными коэффициентами является уравнение Эйлера.
2.4.1. Уравнение Эйлера
Уравнением Эйлера называется линейное уравнение вида
|
(ax +b)n y(n) + a (ax |
+b)n−1 y(n−1) + a |
2 |
(ax +b)n−2 |
y(n−2) + + |
|
|
1 |
(2.62) |
||||
|
+ an−1(ax +b)y′+ an y |
= f (x), |
||||
где a, b, a1, a2 , , an−1, an — константы. В наиболее распространенном
|
случае, при a =1, b = 0 |
уравнение Эйлера имеет вид |
|
xn y(n) + a1xn−1y(n−1) |
+ a2 xn−2 y(n−2) + + an−1xy′+ an y = f (x). (2.63) |
Как видно, уравнение Эйлера является уравнением с переменными коэффициентами специального вида, но оно приводится к уравнению с постоянными коэффициентами заменой независимой переменной x.
Для уравнения (2.63), полагая
|
x = et , (x > 0) → t = ln x, |
(2.64) |
находим производные разного порядка от функции y по новой переменной t:
|
′ |
dy |
dy dt |
−t |
dy |
−2t d 2 y |
dy |
|||||||||||||||||||
|
y |
= |
= |
= e |
, |
y |
′′ |
= e |
2 − |
, |
||||||||||||||||
|
dx |
dt dx |
dt |
dt |
||||||||||||||||||||||
|
dt |
|||||||||||||||||||||||||
|
3 |
y |
d |
2 |
y |
dy |
||||||||||||||||||||
|
y |
′′′ |
= e |
−3t |
d |
−3 |
+ 2 |
(2.65) |
||||||||||||||||||
|
3 |
2 |
||||||||||||||||||||||||
|
dt |
dt |
, |
|||||||||||||||||||||||
|
dt |
…………………………………
61
и подставляя (2.65) в (2.63), получим уравнение с постоянными коэффициентами относительно функции y(t).
В общем случае, для уравнения(2.62) формулы перехода (2.65) примут
вид:
|
′ |
−t dy |
′′ |
2 |
−2t d 2 y |
dy |
|||||
|
y |
== ae |
, |
y |
= a e |
2 − |
, |
||||
|
dt |
dt |
|||||||||
|
dt |
|
d |
3 |
y |
d |
2 |
y |
dy |
|||||||||
|
y |
′′′ |
= a |
3 |
e |
−3t |
−3 |
+ 2 |
||||||||
|
3 |
2 |
||||||||||||||
|
dt |
dt |
dt |
, |
||||||||||||
…………………………………..
Пример. Решить уравнение
|
x2 y′′+3xy′+ y = 2 + x. |
(2.66) |
Уравнение (2.66) есть уравнение Эйлера второго порядка. Применим замену независимой переменной и производных по формулам (2.64), (2.65). Тогда уравнение примет вид
|
2t |
−2t d 2 y |
dy |
t −t dy |
t |
|||||||
|
e |
e |
+3e e |
+ y = 2 + e |
||||||||
|
2 − |
|||||||||||
|
dt |
dt |
||||||||||
|
dt |
и после упрощений получим линейное неоднородное уравнение с постоянными коэффициентами
|
d 2 y |
+ 2 dy |
+ y = 2 +et . |
(2.67) |
|
|
dt 2 |
||||
|
dt |
Его общее решение
y = y0 + y1 + y2 ,
где y0 — общее решение соответствующего однородного уравнения: y0 = C1e−t +C2 t e−t ,
y1 — частное решение неоднородного уравнения
y2 — частное решение неоднородного уравнения
d 22y + 2 dy + y = 2 , dt dt
d 22y + 2 dy + y = et . dt dt
Эти решения находятся методом подбора (см. выше) и имеют вид
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Краевые задачи для уравнений высших порядков
Рассмотрим для простоты уравнение второго порядка
(1)
Коэффициенты и
будем считать непрерывными в некотором интервале
. Тогда каждое решение
уравнения (1) будет определено во всем этом интервале. В дальнейшем вместо уравнения (1) будем рассматривать уравнение вида
(2)
Уравнения (1) и (2) могут быть преобразованы одно в другое. Уравнение вида (2) называются самосопряженными.
Решение дифференциального уравнения полностью определяется начальными условиями
. Однако во многих физических задачах приходится искать решения, заданные иным способом. Например, может быть поставлена задача: найти решение уравнения (2), принимающее в точках
и
заданные значения
и
. Обычно в таких случаях значения решения ищутся только для
из
. Таким образом, заданные значения
и
находятся на концах интервала, поэтому задачи такого рода называются краевыми (граничными) задачами. В дальнейшем мы положим в основу интервал
(основной интервал), что не уменьшает общности рассуждений.
Весьма общий вид краевых условий для уравнения второго порядка следующий:
(3)
где — заданные постоянные, причем
не равны одновременно нулю.
Если , то краевые условия называются однородными, например:
Вообще говоря, краевые задачи не всегда разрешимы, т.е. не всегда существует такое решение, которое принимает требуемые значения на концах интервала. Например, краевая задача
не имеет ни одного решения. Задача
(4)
имеет ненулевое решение только для целочисленных значений . В самом деле, из общего решения дифференциального уравнения (4)
вытекает, что краевые условия выполнимы в том и только в том случае, если есть квадрат целого числа
. Соответствующими решениями являются функции
.
Как видно из этого примера, если в уравнении (2) есть функция параметра
, то при известных условиях существуют такие значения параметра, для которых однородная краевая задача для уравнения (2) имеет ненулевое решение. Эти значения
называются собственными значениями, а соответствующие им решения краевой задачи — собственными функциями. Последние определяются лишь с точностью до произвольного постоянного множителя. Так для краевой задачи
, числа
и функции
являются соответственно собственными значениями и собственными функциями задачи.
Наряду с простыми собственными значениями, когда одному собственному значению отвечает одна собственная функция (с точностью до постоянного множителя), существуют кратные собственные значения, когда собственному значению отвечают две или более линейно независимые собственные функции.
При решении краевых задач (для линейных однородных дифференциальных уравнений) поступают так: находят общее решение данного дифференциального уравнения
где — линейно независимые решения. Затем требуют, чтобы это решение
удовлетворяло заданным граничным условиям. Это приводит к некоторой линейной системе уравнений для определения
. Разрешая эту систему, если возможно, находят решение данной краевой задачи. При этом, если возникает задача о нахождении собственных значений, условие наличия ненулевого решения у системы, определяющей
, является условием, определяющим собственные значения. Это бывает некоторое вообще трансцендентное уравнение для
.
Пример 1. Решить краевую задачу .
Решение. Общее решение данного уравнения
(5)
отсюда
(6)
Полагая в (6) и
в (5) и учитывая краевые условия, получаем для нахождения значений постоянных
и
неоднородную линейную систему
Определитель этой системы
следовательно, она имеет единственное решение
Подставляя найденные значения и
в (5), получаем решение заданной краевой задачи
или
Пример 2. Найти собственные значения и собственные функции краевой задачи
(7)
(8)
Решение. Обшее решение уравнения (7)
(9)
отсюда
(10)
Полагая (9) и
в (10) и учитывая краевые условия (8), получаем для нахождения
и
однородную линейную систему
(11)
Система (11) будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю; приравняв его нулю, получаем уравнение для нахождения собственных значений данной краевой задачи:
или
Так как по условию , то
, а значит собственные значения
Им соответствуют (с точностью до постоянного множителя , который можно положить равным единице) собственные функции
являющиеся решениями краевой задачи (7)–(8).
Замечание. Собственные значения рассмотренных выше задач образуют возрастающую числовую последовательность. Если же коэффициенты дифференциального уравнения имеют особую точку на границе основной области или если основная область бесконечна, например вся числовая ось, то спектр, т.е. совокупность собственных значений, может обладать иной структурой. В частности, могут встретиться спектры, содержащие все числа какого-либо интервала значений , так называемые непрерывные спектры. Например, пусть требуется решить уравнение
для интервала
при «краевых условиях»:
ограничено на бесконечности. Очевидно, в этом случае всякое неотрицательное число
является собственным значением с собственными функциями
и
.
При решении задач математической физики, приводящих к задачам на определение собственных значений, часто получаются дифференциальные уравнения вида
но такие, что в концевых точках основной области могут иметь место особенности дифференциального уравнения, например, обращение в ноль коэффициента . Для этих особых точек из самого характера задачи возникают условия, например, непрерывности или ограниченности решения или обращение его в бесконечность не выше заданного порядка. Эти условия играют роль краевых условий. Типичным примером является уравнение Бесселя
(12)
которое появляется в задачах математической физики. Здесь и сделанное выше предположение, что
во всей основной области
здесь уже не выполняется, так как
. Точка
является особой точкой для уравнения Бесселя.
Требование, чтобы решение было ограничено в этой точке, будет специального вида краевым условием для уравнения Бесселя: найти решение уравнения (12), ограниченное при и, например, обращающееся в ноль при
.
Пример 3. Решить краевую задачу функция
ограничено при
.
Решение. Данное уравнение является уравнением Эйлера. Его общее решение имеет вид
По условию решение должно быть ограниченным при
. Это требование будет выполнено, если в общем решении положить
. Тогда будем иметь
. Краевое условие
дает
. Следовательно, искомое решение
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Лекция 4. Краевые задачи для дифференциальных уравнений.
Задача Штурма-Лиувилля.
Будем рассматривать однородное линейное уравнение второго порядка
Ly ≡ a2(x)y» + a1(x)y’ + a0(x)y = 0.
Его можно записать по-другому:
|
|
(15) |
Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида
|
|
(16) |
где α1, α2, β1, β2, A, B — заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).
Наряду с уравнением (15) рассмотрим уравнение
|
|
(17) |
содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.
Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде
{Lλy = 0, l1y = 0, l2y = 0}.
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у{х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет вид
Из множества краевых условий вида (16) ограничимся тремя частными случаями:
1) краевые условия первого рода
2) краевые условия второго рода
3) краевые условия третьего рода
|
|
(21) |
Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.
Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.
Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.
Доказательство. Напомним, что определителем Вронского функций у = y1(x) и у = у2(x) называется определитель вида
Рассмотрим однородные краевые условия общего вида (16). Пусть у1(x) и у2(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства
Числа α1, и α2 не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю:
Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0.
Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0.
Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.
Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y1(x) и у2(x) — линейно зависимые функции.
Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны.
Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у1 и у2 и продифференцируем его:
Так как у1 и у2 — решения уравнения (18) при λ = λ1 и λ = λ2, соответственно, то получим
Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь
По условию λ1 — λ2 ≠0, следовательно 
Функции y1(x) 
0 и у2(х) 0, поэтому 
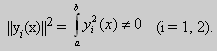
Значит, y1(x) и у2(х) на отрезке [а, b] ортогональны.
Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y1(x) и у2(х) ортогональны на отрезке [а, b] с весом r(x), если
Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму:
Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.
Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2).
Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.
Доказательство. Предположим, что задача Штурма-Лиувилля {Lλy = 0, l1y = 0, l2y = 0} имеет комплексное собственное значение λ = α + βi,β ≠ 0. Пусть ему соответствует собственная функция у(х) (вообще говоря, тоже комплекснозначная). Так как все коэффициенты уравнения и краевых условий имеют действительные значения, то
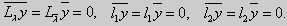
Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае
Значит число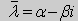 
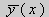
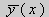
также является собственным значением той же задачи Штурма-Лиувилля и ему соответствует собственная функция 
. Так как в силу свойства 2 функции y(x) и ортогональны на [а, b], то
Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением.
Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля {Lλ y = 0, l1 y = 0, l2 y = 0} имеет бесконечное число собственных значений λ 1, λ2, … λn, … Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам
Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l1f = 0 и l2f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям yn(х) задачи Штурма-Лиувилля {Lλ y = 0, l1 y = 0, l2 y = 0} :
где коэффициенты Фурье Сn вычисляются по формулам:
Эта теорема применяется при решении уравнений математической физики методом Фурье.
Решение задач Штурма-Лиувилля
Задачу Штурма-Лиувилля в общем виде мы, конечно, решить не сможем. Однако некоторые частные случаи удается разобрать до конца и получить формулы для собственных значений и собственных функций. Разберем эти случаи.
Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится.
Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ < 0, 2) λ = 0, 3) λ > 0. В первом случае обозначим λ = — k2. Тогда характеристическое уравнение r2 — k2 = 0 будет иметь действительные различные корни r1 = k, r2 = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C1ekx + C2e-kx. Подставим краевые условия в общее решение и получим
Определитель этой системы равен
Следовательно, система имеет только нулевое (тривиальное) решение C1 = C2 = 0. Значит, при λ < 0 данная задача не имеет собственных значений. Если λ = 0, то общее решение уравнения y» = 0 записывается в виде y = C1x + C2. При подстановке краевых условий получим: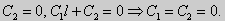 
Поэтому, точка λ = 0 также не является собственным значением задачи. Наконец, в третьем случае обозначим λ = k2 и получим характеристическое уравнение r2 + k2 = 0. Оно имеет комплексные корни r1 = ki и r2 = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C1cos kx + C2sin kx. Подставим краевые условия в общее решение:
|
|
(22) |
Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть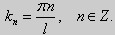 
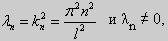
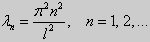
Так как 
то можно ограничиться только положительными значениями n = 1, 2, … . Таким образом, собственные значения данной задачи имеют вид 
При этих значениях алгебраическая система (22) имеет решения:C1 = 0, C2 — любое действительное число. Подставим эти значения в общее решение дифференциального уравнения и получим собственные функции задачи 
Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:
По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:
|
|
(23) |
и
|
|
(24) |
Эти задачи так же, как и предыдущая, при λ 
0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C1cos kx +C2sin kx, где 
После подстановки у в краевые условия, получим:
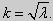
а) для задачи (23)
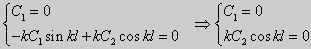
b)для задачи (24)
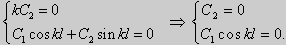
Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно,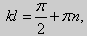 
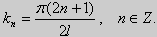
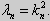
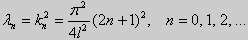
то есть 
Отрицательные значения n можно не рассматривать, так как 
Таким образом, собственные значения у этих задач одинаковые 
Собственные функции задачи (23) имеют вид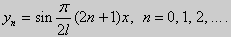 
А у задачи (24) они другие:
|
|
Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода
|
y» + λy = 0, y'(0) = y'(l) = 0. |
(25) |
Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ < 0 не имеет собственных значений. А вот λ = 0 является собственным числом. В самом деле, при λ = 0 общее решение уравнения имеет вид y = C1x + C2. После подстановки у в краевые условия (25) получим: C1 = 0, C2 — любое действительное число. Следовательно, функция у = 1 является собственной функцией задачи. Другие собственные значения и собственные функции получаются при λ > 0. В этом случае, общее решение уравнения имеет вид y = C1cos kx + C2sin kx,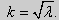 
Найдем производную этой функции и подставим в нее краевые условия (25):
Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или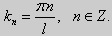 
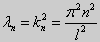
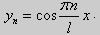
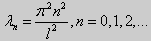
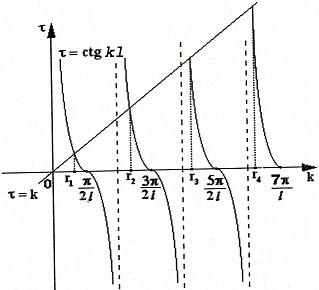
Таким образом, числа 
также являются собственными значениями задачи. Собственные функции при этих значениях имеют вид 
. Окончательно, задача (25) имеет собственные значения 
и собственные функции 
Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда 
|
y» + λy = 0, y'(0) = y(0), y'(l) = 0. |
(26) |
При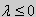 
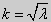
задача (26) не имеет собственных значений и собственных функций. Доказательство этого проводится так же, как и для краевых условий первого рода. При λ > 0 общее решение уравнения записывается в виде y = C1coskx + C2sinkx, где 
. После дифференцирования этой функции и подстановки её производной и самой функции в краевые условия (26) будем иметь:
или
|
|
(27) |
Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда
coskl — ksinkl = 0
или
Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через rn, n = 1,2, … . Тогда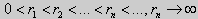 
при 
Рис.13
Численными методами можно найти приближенные значения rn. Из системы (27) при k = rn получим C1n = rnC2n , где C2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид
yn = C2n (rn cos rnx + sin rnx).
Они являются собственными функциями краевой задачи (26) с собственными значениями 
$begingroup$
For simplicity let me call $lambda=mu^2$. The equation for the eigenvalues can be written as
$$
mu=-frac{k}{ell}tan(ell,mu).
$$
$mu=0$ is a solution that gives$yequiv0$, so it is not an eigenvalue. If you draw the graph of $mu$ and $-(k/ell)tan(ell,mu)$, it becomes cleat that there is a solution
$$
mu_kinBigl(frac{(2,k-1),pi}{2,ell},frac{(2,k+1),pi}{2,ell}Bigr),quad k=1,2,3dots
$$
To find the numerical values of $mu_k$ you will have to resort to numerical methods. From the picture is also clear that
$$
lim_{ktoinfty}mu_k-frac{(2,k-1),pi}{2,ell}=0.
$$
answered Nov 13, 2014 at 14:46
Julián AguirreJulián Aguirre
75.6k2 gold badges56 silver badges114 bronze badges
$endgroup$
Собственная функция — краевая задача
Cтраница 1
Собственные функции краевой задачи образуют систему ортогональных функций.
[1]
Собственные функции краевых задач Дирихле и Неймана на прямоугольнике для эллиптического уравнения синус — Гордон.
[2]
Собственные значения и собственные функции краевой задачи ( 56) определяются методом разделения переменных.
[3]
Тогда при 0 х к разложение по собственным функциям краевой задачи (5.1) — (5.3) ведет себя в отношении сходимости так же, как и обычный тригонометрический ряд Фурье.
[4]
Вынужденные колебания в распределенной системе конечной длины представляются в виде разложения по собственным функциям краевой задачи. Если частота внешней силы совпадает с одной из собственных частот системы, происходит резонансное увеличение амплитуды колебаний.
[5]
Для этого воспользуемся методом Фурье, который заключается в том, что решение смешанной задачи ищется в виде ряда по собственным функциям соответствующей эллиптической краевой задачи.
[6]
Значения параметра Л, при которых задача (4.11) имеет нетривиальные решения, называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями краевой задачи на собственные значения.
[7]
Тем самым известные из теории интегральных уравнений свойства собственных значений и собственных функций интегрального уравнения Фредгольма второго рода с симметричным ядром дают возможность сделать заключение о свойствах собственных значений и собственных функций краевой задачи Штурма-Лиувилля.
[8]
На практике при постановке задачи расчета температурного поля прямоугольных нагревательных плит часто оказывается, что функция распределения плотности источников тепла ( о ( х, у) при разложении ее в ряд по собственным функциям краевой задачи дает ряд с хорошей абсолютной сходимостью, так что с достаточной для инженерных расчетов точностью оказывается возможным пренебречь всеми членами ряда, за исключением нескольких первых членов.
[9]
В заключение главы IV, посвященной методу Фурье, заметим следующее. Часто изложение этого метода состоит в построении решения краевой задачи ( и тем самым в доказательстве существования решения) с помощью решений специального вида стоячих волн. Однако полученные нами формулы для коэффициентов разложения решений симметричных консервативных задач дают возможность выписать явные выражения для решений по начальным данным, если известны собственные функции краевой задачи для соответствующей системы обыкновенных дифференциальных уравнений.
[10]
Страницы:
1