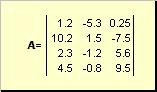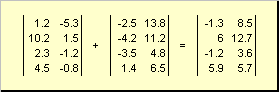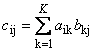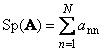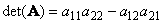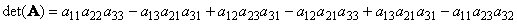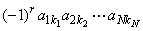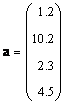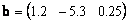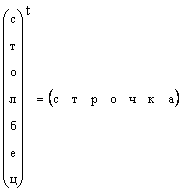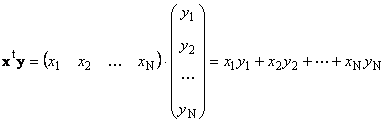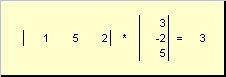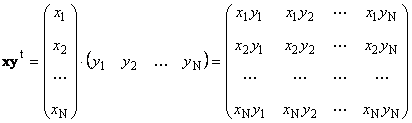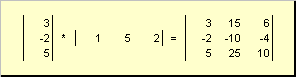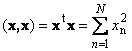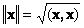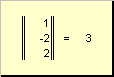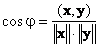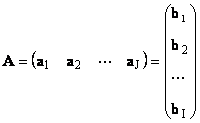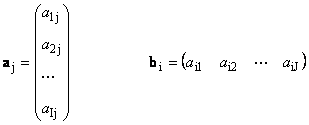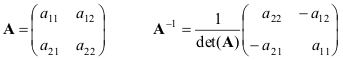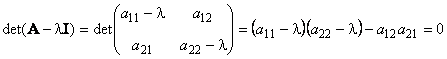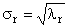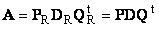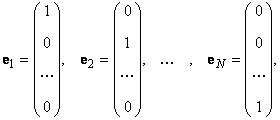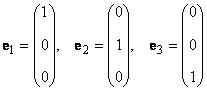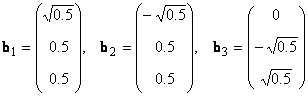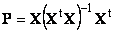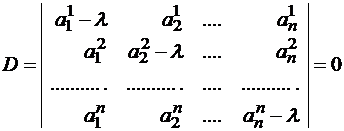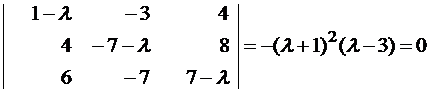Как найти собственные углы

Угол между векторами.

Формула вычисления угла между векторами

cos α =	a · b
| a |·| b |

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5

Найдем угол между векторами:

cos α =	a · b	=	24	=	24	= 0.96
| a | · | b |	5 · 5	25

Решение: Найдем скалярное произведение векторов:

a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α =	a · b	=	40	=	40	=	4	= 0.8
| a | · | b |	5√ 2 · 5√ 2	50	5

Примеры вычисления угла между векторами для пространственных задач

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6

Найдем угол между векторами:

cos α =	a · b	=	28	=	14
| a | · | b |	5 · 6	15

Решение: Найдем скалярное произведение векторов:

a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

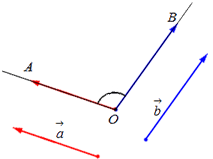
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

1. Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

1. Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Содержание

В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.

Текст разбит на две части названные — «Базовые сведения» и «Дополнительная информация». В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.

Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.

Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x ( a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2 ) = x (C 1 )+ x (C 2 ). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера — хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии — это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 . x n , характеризующих набор концентраций C 1 ,C 2 , . C m веществ, присутствующих в изучаемой системе.

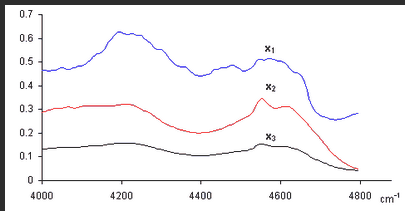
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на Рис. 1, где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый ( x 1 ) и второй ( x 2 ) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?

Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Базовые сведения

1.1 Матрицы

Матрицей называется прямоугольная таблица чисел, например

Матрицы обозначаются заглавными полужирными буквами ( A ), а их элементы — соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как < a ij , i = 1. I ; j = 1. J >. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.

Пара чисел I и J называется размерностью матрицы и обознается как I × J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.

1.2. Простейшие операции с матрицами

Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —

Рис. 3 Умножение матрицы на число

Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,

Рис. 4 Сложение матриц

В результате умножения на число и сложения получается матрица той же размерности.

Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A + O = A , A − A = O и 0 A = O .

Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A ‘ или индексом A t . Таким образом, если A = < a ij , i = 1. I ; j = 1. J >, то A t = < a ji , j = 1. J ; i = 1. I >. Например

Рис. 5 Транспонирование матрицы

Очевидно, что ( A t ) t = A , ( A + B ) t = A t + B t .

1.3. Умножение матриц

Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I × K , и матрицы B , размерностью K × J , называется матрица C , размерностью I × J , элементами которой являются числа

Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц —

Рис.6 Произведение матриц

Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца ( c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B

Рис.7 Элемент произведения матриц

Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = ( AB ) C = A ( BC ). Кроме того, оно еще и дистрибутивно, т.е. A ( B + C ) = AB + AC . Очевидно, что AO = O .

1.4. Квадратные матрицы

Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.

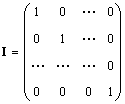
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.

Очевидно AI = IA = A .

Матрица называется диагональной , если все ее элементы, кроме диагональных ( a ii ) равны нулю. Например

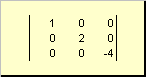
Рис. 8 Диагональная матрица

Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i > j . Например

Рис. 9 Верхняя треугольная матрица

Аналогично определяется и нижняя треугольная матрица.

Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например

Рис. 10 Симметричная матрица

Матрица A называется ортогональной , если

Матрица называется нормальной если

1.5. След и определитель

Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,

Рис. 11 След матрицы

Sp(α A ) = α Sp( A ) и

Sp( A + B ) = Sp( A )+ Sp( B ).

Можно показать, что

Sp( A ) = Sp( A t ), Sp( I ) = N ,

Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

В случае матрицы ( N × N ) определитель вычисляется как сумма 1·2·3· . · N = N ! слагаемых, каждый из которых равен

Индексы k 1 , k 2 . k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, . , N ). Вычисление определителя матрицы — это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,

Рис. 12 Определитель матрицы

Отметим только очевидные свойства:

det( I ) = 1, det( A ) = det( A t ),

det( AB ) = det( A )det( B ).

1.6. Векторы

Если матрица состоит только из одного столбца ( J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например

Можно рассматривать и матрицы, состоящие из одной строки, например

Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.

Размерностью вектора называется число его элементов.

Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.

В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .

1.7. Простейшие операции с векторами

Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами

Два вектора x и y называются колинеарными , если существует такое число α, что

1.8. Произведения векторов

Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = ( x 1 , x 2 . x N ) t и y = ( y 1 , y 2 . y N ) t . Руководствуясь правилом перемножения «строка на столбец», мы можем составить из них два произведения: x t y и xy t . Первое произведение

называется скалярным или внутренним . Его результат — это число. Для него также используется обозначение ( x , y ) = x t y . Например,

Рис. 14 Внутреннее (скалярное) произведение

называется внешним . Его результат — это матрица размерности ( N × N ). Например,

Рис. 15 Внешнее произведение

Векторы, скалярное произведение которых равно нулю, называются ортогональными .

1.9. Норма вектора

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение

Рис. 16 Норма вектора

Вектор единичной длины (|| x || = 1) называется нормированным. Ненулевой вектор ( x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = || x || ( x/ || x ||) = || x || e . Здесь e = x/ || x || — нормированный вектор.

Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

1.10. Угол между векторами

Скалярное произведение определяет и угол φ между двумя векторами x и y

Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.

1.11. Векторное представление матрицы

Каждую матрицу A размера I × J можно представить как набор векторов

Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A

1.12. Линейно зависимые векторы

Векторы одинаковой размерности ( N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 . x K и столько же чисел α α 1 , α 2 . α K . Вектор

y = α 1 x 1 + α 2 x 2 +. + α K x K

называется линейной комбинацией векторов x k .

Если существуют такие ненулевые числа α k ≠ 0, k = 1. K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2 x 2 = 0

1.13. Ранг матрицы

Рассмотрим набор из K векторов x 1 , x 2 . x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе

имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.

Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.

Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.

rank( A ) = rank( A t ).

1.14. Обратная матрица

Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями

Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является

det( A ) ≠ 0 или rank( A ) = N .

Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы

Приведем формулы для простейшего случая — матрицы 2×2

Если матрицы A и B невырождены, то

1.15. Псевдообратная матрица

Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что

Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.

Если число столбцов меньше числа строк, то

A + =(A t A) −1 A t

Рис. 1 7a Псевдообращение матрицы

Если же число столбцов больше числа строк, то

A + =A t (AA t ) −1

1.16. Умножение вектора на матрицу

Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка — слева x t A . Если размерность вектора J , а размерность матрицы I × J то в результате получится вектор размерности I . Например,

Рис. 18 Умножение вектора на матрицу

Если матрица A — квадратная ( I × I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что

A (α 1 x 1 + α 2 x 2 ) = α 1 Ax 1 + α 2 Ax 2 .

Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .

2. Дополнительная информация

2.1. Системы линейных уравнений

Пусть A — матрица размером I × J , а b — вектор размерности J . Рассмотрим уравнение

относительно вектора x , размерности I . По сути — это система из I линейных уравнений с J неизвестными x 1 . x J . Решение существует в том, и только в том случае, когда

rank( A ) = rank( B ) = R ,

где B — это расширенная матрица размерности I ×( J+1 ), состоящая из матрицы A , дополненной столбцом b , B = ( A b ). В противном случае уравнения несовместны.

Если R = I = J , то решение единственно

Если R I , то существует множество различных решений, которые можно выразить через линейную комбинацию J − R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A ( N × N ) имеет нетривиальное решение ( x ≠ 0 ) тогда и только тогда, когда det( A ) = 0. Если R = rank( A ) N , то существуют N − R линейно независимых решений.

2.2. Билинейные и квадратичные формы

Если A — это квадратная матрица , а x и y — вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой , определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.

2.3. Положительно определенные матрицы

Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0 ,

Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.

2.4. Разложение Холецкого

Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой

Рис. 19 Разложение Холецкого

2.5. Полярное разложение

Пусть A — это невырожденная квадратная матрица размерности N × N . Тогда существует однозначное полярное представление

где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:

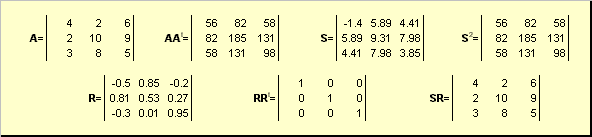
S 2 = AA t или S = ( AA t ) ½ и R = S −1 A = ( AA t ) −½ A .

Рис. 20 Полярное разложение

Если матрица A вырождена, то разложение не единственно — а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .

2.6. Собственные векторы и собственные значения

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A , если

где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.

2.7. Собственные значения

У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Рис. 21 Собственные значения

Набор собственных значений λ 1 . λ N матрицы A называется спектром A .

Спектр обладает разнообразными свойствами. В частности

det( A ) = λ 1 ×. ×λ N , Sp( A ) = λ 1 +. +λ N .

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.

2.8. Собственные векторы

У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений

Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.

2.9. Эквивалентные и подобные матрицы

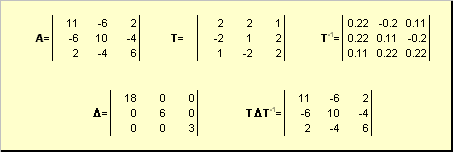
Две прямоугольные матрицы A и B одной размерности I × J эквивалентны , если существуют такие квадратные матрицы S , размерности I × I , и T , размерности J × J , что

Эквивалентные матрицы имею один и тот же ранг.

Две прямоугольные матрицы A и B одной размерности N × N подобны , если существует такая невырожденная матрица T , что

Матрица T называется преобразованием подобия.

Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.

2.10. Приведение матрицы к диагональному виду

Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —

Здесь Λ = diag(λ 1 . λ N ) — это диагональная матрица, элементами которой являются собственные значения матрицы A , а T — это матрица, составленная из соответствующих собственных векторов матрицы A , т.е. T = ( v 1 . v N ).

Рис. 23 Приведение к диагональному виду

2.11. Разложение по сингулярным значениям (SVD)

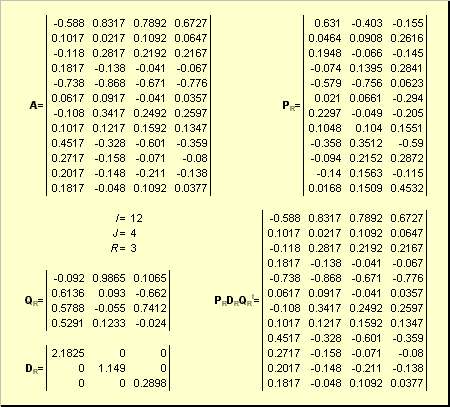
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —

.

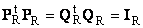
Здесь P R — матрица, образованная R ортонормированными собственными векторами p r матрицы AA t , соответствующим R наибольшим собственным значениям λ r ;

AA t p r = λ r p r ;

Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;

A t Aq r = λ r q r .

D R = diag (σ 1 . σ R ) — положительно определенная диагональная матрица , элементами которой являются σ 1 ≥. ≥σ R ≥0 — сингулярные значения матрицы A , равные квадратным корням из собственных значений матрицы A t A —

Рис. 24 SVD разложение

Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что

2.12. Линейное пространство

Рассмотрим все возможные векторы размерности N . Это множество называется линейным пространством размерности N и обозначается R N . Так как в R N включены все возможные векторы, то любая линейная комбинация векторов из R N будет также принадлежать этому пространству.

2.13. Базис линейного пространства

Любой набор из N линейно независимых векторов называется базисом в пространстве R N . Простейший пример базиса — это набор векторов

в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = ( x 1 , x 2 . x N ) t может быть представлен как линейная комбинация x = x 1 e 1 + x 2 e 2+ . + x N e N базисных векторов.

Базис, составленный из попарно ортогональных векторов, называется ортогональным , а если базисные вектора еще и нормированы, то этот базис называется ортонормированным .

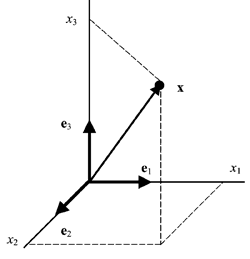
2.14. Геометрическая интерпретация

Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N -мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = ( x 1 , x 2 . x N ) t можно изобразить точкой в этом пространстве с координатами ( x 1 , x 2 . x N ).

Рис. 25 Координатное пространство

2.15. Множественность базисов

В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса

можно установить и другой ортонормированный базис, например

Каждый базис можно представить матрицей B = ( b 1 . b N ), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T , т.е. B 2 = TB 1 .

2.16. Подпространство

Пусть имеется набор из K линейно независимых векторов x 1 , x 2 . x K в пространстве R N . Рассмотрим все возможные линейные комбинации этих векторов

x = α 1 x 1 + α 2 x 2 +. + α K x K

О получившимся множестве Q говорят, что оно является линейной оболочкой или что оно натянуто на векторы x 1 , x 2 . x K . По определению линейного пространства это множество Q само является линейным пространством размерности K . При этом оно принадлежит пространству R N , поэтому Q называется линейным подпространством R K в пространстве R N .

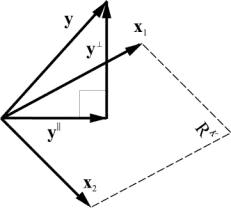
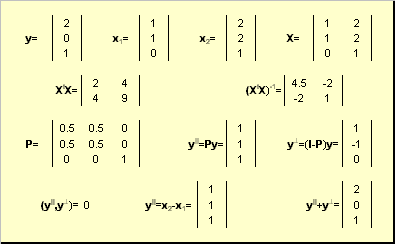
2.17. Проекция на подпространство

Рассмотрим подпространство R K , натянутое на векторы X = ( x 1 , x 2 . x K ) в пространстве R N . Матрица базиса X имеет размерность ( N × K ). Любой вектор y из R N может быть спроецирован на подпространство R K , т.е. представлен в виде

где вектор y || принадлежит R K , а вектор y ⊥ ортогонален y || .

Рис. 26 Проекция на подпространство

Проекцию y || можно представить как результат действия проекционной матрицы P

Проекционная матрица определяется как

Рис. 27 Проекционное разложение

Заключение

Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.

Методы решения задач о собственных
значениях и векторах матриц

Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math]. Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math], удовлетворяющий условию

[math]Acdot X= lambdacdot X,qquad mathsf{(2.1)}[/math]

называется собственным вектором матрицы [math]A[/math]. Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math].

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

[math](A-lambda E)cdot X=0quad (Xne 0).qquad mathsf{(2.2)}[/math]

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math]) при условии [math]|A-lambda E|=0[/math]. Это равенство есть характеристическое уравнение:

где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math], а соответствующие каждому собственному значению [math]lambda_i,~ i=1,ldots,n[/math], ненулевые векторы [math]X^i[/math], удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_{i}|lambda_i(A)|[/math] и [math]min_{i}|lambda_i(A)|[/math]. Величина [math]rho(A)[/math] называется спектральным радиусом.

Замечания

1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math], то вектор [math]mu X^i[/math], где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math].

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]lambda_i,~ i=overline{1,n}[/math], действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

---

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math], вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math], при которых [math]P_n(lambda_i)=0~ (i=overline{1,n})[/math]. Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,~ i=overline{1,n}[/math]. Эти решения [math]X^i[/math], определенные с точностью до произвольной константы, образуют систему [math]n[/math], вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math]. Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math]. Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

[math](A-lambda_iE)cdot X^i=0,quad i=1,2,ldots,n[/math]

и найти собственные векторы [math]X^i[/math].

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname{rang}(A-lambda_iE)=r<n[/math] и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb{R}^{2times 2}[/math], где [math]A=begin{pmatrix}3&-2\-4&1end{pmatrix}[/math].

Решение

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin{pmatrix}2&-1&1\-1&2&-1\0&0&1end{pmatrix}[/math].

Решение

---

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_{i}bigl|lambda_i(A)bigr|[/math].

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,~ i=1,ldots,n[/math], и собственные значения матрицы [math]A[/math] таковы, что

[math]rho(A)= bigl|lambda_1(A)bigr|> bigl|lambda_2(A)bigr|geqslant ldotsgeqslant bigl|lambda_n(A)bigr|.[/math]

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^{1(0)}[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math].

2. Найти [math]X^{1(1)}=AX^{1(0)},~ lambda_1^{(1)}= frac{x_i^{1(1)}}{x_i^{1(0)}}[/math], где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math], и положить [math]k=1[/math].

3. Вычислить [math]X^{1(k+1)}=Acdot X^{1(k)}[/math].

4. Найти [math]lambda_1^{(k+1)}= frac{x_i^{1(k+1)}}{x_i^{1(k)}}[/math], где [math]x_i^{1(k+1)}, x_i^{1(k)}[/math] — соответствующие координаты векторов [math]X^{1(k+1)}[/math] и [math]X^{1(k)}[/math]. При этом может быть использована любая координата с номером [math]i,~ 1leqslant ileqslant n[/math].

5. Если [math]Delta= bigl|lambda_1^{(k+1)}- lambda_1^{(k)}bigr|leqslant varepsilon[/math], процесс завершить и положить [math]lambda_1cong lambda_1^{k+1}[/math]. Если [math]Delta>varepsilon[/math], положить [math]k=k+1[/math] и перейти к пункту 3.

---

Замечания

1. Процесс последовательных приближений

[math]begin{aligned}&X^{1(1)}= AX^{1(0)},quad X^{1(2)}= AX^{1(1)}= A^{2}X^{1(0)},quad ldots,\ &X^{1(k)}= AX^{1(k-1)}= AA^{k-1}X^{1(0)}= A^kX^{1(0)},quad ldots end{aligned}[/math]

сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^{1(k)}[/math] стремится к собственному вектору [math]X^1[/math]. Действительно, разложим [math]X^{1(0)}[/math] по всем собственным векторам: [math]textstyle{X^{1(0)}= sumlimits_{i=1}^{n} c_iX^i}[/math]. Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math], то

[math]begin{aligned}& AX^{1(0)}= X^{1(1)}= sumlimits_{i=1}^{n} c_i lambda_iX^i,quad AX^{1(1)}= A^2X^{1(0)}= X^{1(2)}= sumlimits_{i=1}^{n} c_i lambda_i^2X^i,quad ldots\ &A^kX^{1(0)}= X^{1(k)}= sumlimits_{i=1}^{n} c_i lambda_i^kX^i= lambda_1^k! left[c_1X^1+ c_2{left(frac{lambda_2}{lambda_1}right)!}^k X^2+ ldots+ c_n{left(frac{lambda_n}{lambda_1}right)!}^k X^nright]!. end{aligned}[/math]

При большом [math]k[/math] дроби [math]{left(frac{lambda_2}{lambda_1}right)!}^k, ldots, {left(frac{lambda_n}{lambda_1}right)!}^k[/math] малы и поэтому [math]A^kX^{1(0)}= c_1lambda_1^kX^1[/math], то есть [math]X^{1(k)}to X^1[/math] при [math]ktoinfty[/math]. Одновременно [math]lambda_1= limlimits_{ktoinfty} frac{x_{i}^{1(k+1)}}{x_{i}^{1(k)}}[/math].

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^{(k+1)}[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

[math]lambda_1= lambda_2= ldots= lambda_s[/math] и [math]bigl|lambda_1bigr|> bigl|lambda_kbigr|[/math] при [math]k>s[/math].

4. При неудачном выборе начального приближения [math]X^{1(0)}[/math] предел отношения [math]frac{x_i^{1(k+1)}}{x_i^{1(k)}}[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac{lambda_2}{lambda_1}[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.

7. Используя [math]lambda_1[/math], можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac{x_i^{1(k+1)}- lambda_1 x_i^{1(k)}}{x_i^{1(k)}- lambda_1 x_i^{1(k-1)}}~ (i=1,2,ldots,n)[/math]. Эта формула дает грубые значения для [math]lambda_2[/math], так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j~(j=3,4,ldots,n)[/math].

8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac{X^{1(k)}}{|X^{1(k)}|_1}[/math].

Пример 2.3. Для матрицы [math]A=begin{pmatrix}5&1&2\ 1&4&1\ 2&1&3 end{pmatrix}[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math].

Решение

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin{pmatrix}2&-1&1\ -1&2&-1\ 0&0&3 end{pmatrix}[/math] и соответствующий собственный вектор.

Решение

---

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb{R}^{ntimes n}[/math] с помощью ортогональной матрицы [math]H[/math].

Напомним, что две матрицы [math]A[/math] и [math]A^{(i)}[/math] называются подобными ([math]Asim A^{(i)}[/math] или [math]A^{(i)}sim A[/math]), если [math]A^{(i)}=H^{-1}AH[/math] или [math]A=HA^{(i)}H^{-1}[/math], где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^{T}=H^{T}H=E[/math], т.е. [math]H^{T}=H^{-1}[/math]. В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^{(i)}[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]

[math]operatorname{tr}A= sum_{i=1}^{n}a_{ii}= sum_{i=1}^{n} lambda_i(A)= operatorname{tr}A^{(i)}.[/math]

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^{(0)}=A[/math]. На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_{ij}^{(k)},~ ine j[/math], определяется ортогональная матрица [math]H^{(k)}[/math], приводящая этот элемент [math]a_{ij}^{(k+1)}[/math] (а также и [math]a_{ji}^{(k+1)}[/math]) к нулю. При этом на каждой итерации в качестве [math]a_{ij}^{(k+1)}[/math] выбирается наибольший по модулю. Матрица [math]H^{(k)}[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^{(k)}[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_{ii}^{(k)}= cosvarphi^{(k)}[/math] и [math]h_{jj}^{(k)}=cosvarphi^{(k)}[/math], а остальные элементы нулевые, за исключением [math]h_{ij}^{(k)}=-sinvarphi^{(k)}[/math], [math]h_{ji}^{(k)}=sinvarphi^{(k)}[/math] ([math]h_{ij}[/math] -элементы матрицы [math]H[/math]).

Угол поворота [math]varphi^{(k)}[/math] определяется по формуле

где [math]|2varphi^{(k)}|leqslant frac{pi}{2},~ i<j[/math] ([math]a_{ij}[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math]).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^{(k)})[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^{(k+1)})< sigma(A^{(k)})[/math]. Однако элементы [math]a_{ij}^{(k)}[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность [math]sigma(A^{(1)})> sigma(A^{(2)})> ldots> sigma(A^{(k)})>ldots[/math]. Поэтому [math]sigma(A^{(k)})to0[/math] при [math]ktoinfty[/math]. Это и означает сходимость метода. При этом [math]A^{(k)}to Lambda= operatorname{diag}(lambda_1,ldots,lambda_n)[/math].

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]{vec{i},vec{j}}[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

[math]begin{cases}vec{i},’= vec{i}cos varphi+ vec{j}sin varphi,\[2pt] vec{j},’=-vec{i}sin varphi+ vec{j}cos varphi. end{cases}[/math]

Таким образом, для компонент [math]vec{i},’,, vec{j},'[/math] будем иметь [math]bigl(vec{i},’,vec{j},’bigr)= bigl(vec{i},vec{j}bigr)cdot! begin{pmatrix} cos varphi&-sin varphi\ sin varphi& cos varphiend{pmatrix}[/math]. Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin{pmatrix} cos varphi&-sin varphi\ sin varphi& cos varphiend{pmatrix}[/math]. Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

---

Алгоритм метода вращений

1. Положить [math]k=0,~ A^{(0)}=A[/math] и задать [math]varepsilon>0[/math].

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^{(k)}[/math] максимальный по модулю элемент [math]a_{ij}^{(k)},~ i<j[/math].

Если [math]|a_{ij}^{(k)}|leqslant varepsilon[/math] для всех [math]ine j[/math], процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^{(k)})=a_{ii}^{(k)},~ i=1,ldots,n[/math].

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

[math]nu_k= H^{(0)}cdot H^{(1)}cdot H^{(2)}cdot ldotscdot H^{(k-1)}= bigl( X^1,X^2,X^3,ldots,X^nbigr).[/math]

Если [math]bigl|a_{ij}^{(k)}bigr|>varepsilon[/math], процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^{(k)}= frac{1}{2} operatorname{arctg} frac{2a_{ij}^{(k)}}{a_{ii}^{(k)}-a_{jj}^{(k)}}[/math].

4. Составить матрицу вращения [math]H^{(k)}[/math].

5. Вычислить очередное приближение [math]A^{(k+1)}= bigl(H^{(k)}bigr)^T A^{(k)} H^{(k)}[/math].Положить [math]k=k+1[/math] и перейти к пункту 2.

Замечания

1. Используя обозначение [math]overline{P}_k= frac{2a_{ij}^{(k)}}{a_{ii}^{(k)}-a_{jj}^{(k)}}[/math], можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

[math]sinvarphi^{(k)}= operatorname{sign}overline{P}_kcdot sqrt{frac{1}{2}!left(1-frac{1}{sqrt{1+overline{P}_{k}^{;2}}}right)},,qquad cosvarphi^{(k)}= sqrt{frac{1}{2}!left(1+ frac{1}{sqrt{1+overline{P}_{k}^{;2}}}right)},.[/math]

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin{pmatrix} 2&1\1&3 end{pmatrix}[/math] методом вращений найти собственные значения и собственные векторы.

Решение

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin{pmatrix}5&1&2\ 1&4&1\ 2&1&3 end{pmatrix}[/math].

Решение

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

6

Занятие 5 (Фдз 6).

Собственные значения и собственные
векторы линейного оператора.

5.1. Определение собственного вектора и
собственного значения линейного
оператора, их геометрический смысл.
Главные направления линейного оператора.
Примеры нахождения собственных векторов
и собственных значений линейного
оператора.

5.1. Собственным вектором
линейного оператора

называется такой элемент
,
что
,
при этом число

называется собственным числом
линейного оператора
.
Нулевой элемент

пространства

исключается из множества собственных
векторов по той причине, что

и
.
Другими словами, элемент

не выявляет каких-либо различий у
различных линейных операторов.

Если

— векторное пространство, то собственный
вектор приобретает ясный геометрический
смысл:

— собственный вектор оператора

тогда и только тогда, когда его образ

параллелен вектору

(т.к.
).

Если

— собственный вектор оператора

,
то вектор

при любом значении постоянной

также является собственным вектором
оператора

с тем же собственным значением
,
которое отвечает вектору
.
Действительно,

.

Таким образом, собственный вектор

с собственным значением

оператора

определяет в пространстве

прямую, образованную векторами

и называемую главным направлением
оператора

с собственным значением
.

Одной из основных задач теории линейных
операторов является задача по нахождении
собственных значений, собственных
значений и главных направлений заданного
линейного оператора.

Пример 1. Найти собственные
значения, собственные векторы, главные
направления линейного оператора
,
действующего в линейном пространстве

векторов на декартовой плоскости

следующим образом:

проектирует векторы на ось
.

Решение.

Собственные векторы и отвечающие им
собственные значения заданного линейного
оператора легко определяются, исходя
из геометрического смысла собственного
вектора и геометрии действия оператора.

Рассмотрим единичные векторы

на осях

и

соответственно. Эти векторы образуют
базис пространства
.

— собственный вектор оператора

с собственным значением
.

— собственный вектор оператора

с собственным значением
.

Главными направлениями оператора

являются:

ось

(с собственным значение
)
и ось
(с
собственным значением
).

Пример 2. Найти собственные
значения, собственные векторы, главные
направления линейного оператора
,
действующего в линейном пространстве

векторов на декартовой плоскости

следующим образом:

поворачивает каждый вектор

на угол

против часовой стрелки вокруг начала
координат – точки
.

Решение.

Собственные векторы у этого оператора
есть только при двух значениях угла
:

и
.

1) Если
,
то заданный оператор

является тождественным отображением.

.
Следовательно, любой ненулевой вектор
плоскости

является собственным вектором линейного
оператора

с собственным значением
,
и любая прямая, проходящая через начало
координат, будет главным направлением
оператора

с собственным значением
.

2) Если
,
то оператор

осуществляет отображение по закону:

.
Следовательно, любой ненулевой вектор
плоскости

является собственным вектором линейного
оператора

с собственным значением
,
и любая прямая, проходящая через начало
координат, служит главным направлением
оператора

с собственным значением
.

3) Если
,
то такой оператор поворота векторов
не имеет ни одного собственного вектора.
В этом случае,
вектор

не параллелен вектору
,
и значит, не существует числа

такого, что
.

Пример 3. Найти собственные
значения, собственные векторы, главные
направления линейного оператора
,
действующего в линейном пространстве

векторов декартова пространства

следующим образом:

проектирует каждый вектор

на плоскость
.

Решение.

Также как и в примерах выше, собственные
векторы и отвечающие им собственные
значения заданного линейного оператора
легко находятся из геометрического
смысла собственного вектора.

1) Если вектор

лежит на плоскости

(или параллелен этой плоскости), то
.
Значит, любой такой вектор является
собственным вектором линейного оператора
,
с собственным значением
.
Указанные векторы

имеют координаты
.

Соответственно, главными направлениями
с собственным значением

является множество всех прямых в
плоскости
,
проходящих через начало координат.

2) Другими собственными векторами
рассматриваемого оператора будут все
векторы
,
параллельные оси
.
Для них
,
т.е. векторы

— собственные векторы линейного оператора

с собственным значением
.
Указанные векторы

имеют координаты
.

Соответственно, главным направлением
со значением

является ось
.

Других собственных векторов, отличных
от указанных выше, у оператора

нет.

Пример 4. Найти собственные
значения и собственные векторы линейного
оператора
,
действующего в линейном пространстве

векторов декартова пространства

следующим образом:

зеркально отражает каждый вектор
пространства от плоскости
.

Решение.

1) Любой вектор
,
направленный перпендикулярно плоскости
,
при зеркальном отражении от этой
плоскости изменяет свое направление
на противоположное, не меняя при этом
своей длины. Т.е.
.
Следовательно, все такие векторы

— собственные векторы с собственным
значением
.
Из уравнения плоскости легко находится
вектор
,
перпендикулярный этой плоскости. Т.к.

параллелен
,
то
,
где
.
Таким образом, множество всех собственных
векторов линейного оператора

с собственным значением

образуют векторы с координатами
,
где
.

2) Теперь рассмотрим векторы
,
лежащие в (или параллельные) плоскости
.
Эти векторы при зеркальном отражении
от указанной плоскости не меняются,
т.е.
.
Значит векторы

— собственные векторы линейного оператора

с собственным значением
.

Других собственных векторов у заданного
линейного оператора нет.

Пример 5. Найти собственные
значения и собственные векторы линейного
оператора
,
действующего в линейном пространстве

векторов декартова пространства

следующим образом:

поворачивает каждый вектор на

вокруг прямой
,
проходящей через начало координат
.

Решение.

Рассмотрим сначала векторы
,
лежащие на заданной прямой. Эти векторы
параллельны направляющему вектору
,
и значит, имеют координаты
,
где
.

Под действием оператора

векторы

переходят в себя, т.е.
.

Следовательно, векторы

— собственные векторы линейного оператора

с собственным значением
.

Другими собственными векторами оператора

будут векторы
,
перпендикулярные прямой
.
Под действием

векторы

переходят в векторы
,
т.е.
.

Следовательно, векторы

— собственные векторы линейного оператора

с собственным значением
.

Если обозначить координаты векторов

через
,
то возможные значения этих координат
найдутся из условия ортогональности
векторов

и
,
и будут представлять ненулевые решения
уравнения
.

Пример 6. Найти собственные
значения и собственные векторы линейного
оператора
,
действующего в линейном пространстве

векторов декартова пространства

следующим образом:

проектирует каждый вектор на прямую
.

Решение.

Векторы
,
лежащие на прямой
,
являются собственными векторами
оператора

с собственным значением
.
Оператор

не меняет эти векторы.
.

Векторы
,
перпендикулярные прямой
,
проектируются в точку (т.е. нулевой
вектор) на этой прямой.
.
Следовательно, векторы

— собственные векторы линейного оператора

с собственным значением
.

Пример 7. Найти собственные значения
и собственные векторы линейного
оператора,
где
,
и оператор

действует по правилу
,
где
.

Решение.

Данный линейный оператор рассматривался
в примере 4 занятия 4. Там установлено,
что

.

Согласно определению собственного
вектора линейного оператора ненулевая
матрица

будет собственной матрицей (вектором)
оператора
,
если
,
т.е. когда
.

Из 1-го и 4-го уравнений полученной системы
видно, что
,
либо
.

Рассмотрим первый случай:
.
Из уравнений системы выводим

,
где
.

Следовательно, собственными матрицами
линейного оператора

со значением

являются все матрицы из ядра

этого оператора.

Рассмотрим второй случай:
.
Теперь из уравнений системы выводим

.

(*)

Здесь в свою очередь: либо
;
либо
.

1) Если
,
то из системы (*) находим:
,
где
.
Учитывая, что в рамках второго случая
,
заключаем: матрицы вида

являются собственными матрицами
линейного оператора

с собственным значением
.

2) Если же
,
то из системы (*) находим:
.
В результате получили нулевую матрицу
,
которая по определению не включается
в множество собственных векторов
линейного оператора
.

Других собственных матриц у линейного
оператора

нет.

__________________________________________________________________

Домашнее задание.

1. Исходя из геометрии действия линейного
оператора, найти собственные векторы
и собственные значения следующих
линейных операторов:

1.1. Оператора проектирования векторов
на плоскость
;

1.2. Оператора отражения векторов от оси
;

1.3. Оператора поворота векторов на

вокруг оси
.

2. Используя определение собственного
вектора и собственного значения оператора
найти собственные векторы и собственные
значения следующих линейных операторов.

2.1.
,
,
.

2.2.
,
,

.

2.3.
,

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Дифференциальные уравнения собственный вектор

СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. СВЯЗЬ С УРАВНЕНИЯМИ n-ГО ПОРЯДКА. МЕТОД СОБСТВЕННЫХ ВЕКТОРОВ

Дадим основные определения, связанные с системами линейных дифференциальных уравнений.

1. Если система к дифференциальных уравнений, связывающая независимую переменную х и к функций уДх), . у_А(х), разрешена относительно старших производных этих функций yf A) (x), . у[ Рк х), т.е. имеет вид

то она называется канонической, причем число п = р₁ + р₂ +. + р_к называется порядком системы.

Каноническая система (17.33) при р_х = р₂ = . = p_k = 1, т.е. система дифференциальных уравнений 1-го порядка

называется нормальной системой порядка п.

• 2. Решением системы (17.34) на интервале а ^

Пример 17.35. Решить систему уравнений У У7 сведя

ее к одному уравнению второго порядка.

? Выразим у₂ из первого уравнения: у₂ = 4у _{, =} или = .Получаем

собственный вектор = f^l и соответствующее корню Х _{ке ь .}

Если же для кратного корня X кратности к имеется только т линейно независимых собственных векторов, и т 2t :

Приравнивая коэффициенты при одинаковых степенях /, получаем

Итак, общее решение исходной системы имеет вид

Описанный метод нахождения решения системы линейных однородных дифференциальных уравнений (17.41) носит название метод собственных векторов.

Пример 17.43. Найти частное решение системы дифференциальных уравнений

удовлетворяющее начальному условию х(0) = 0, у(0) = 1, z(0) = -2.

• -Х -1 1
• ? Характеристическое уравнение 1 1 — X -1=0 имеет
• 2 -1 -X

Для корня Х _{(i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.}

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)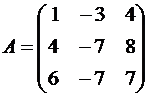
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Методы решения задач о собственных
значениях и векторах матриц

Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math] . Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math] , удовлетворяющий условию

называется собственным вектором матрицы [math]A[/math] . Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math] .

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math] ) при условии [math]|A-lambda E|=0[/math] . Это равенство есть характеристическое уравнение:

где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]lambda_i,

i=1,ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_|lambda_i(A)|[/math] и [math]min_|lambda_i(A)|[/math] . Величина [math]rho(A)[/math] называется спектральным радиусом .

1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]mu X^i[/math] , где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math] .

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]lambda_i,

i=overline<1,n>[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math] , при которых [math]P_n(lambda_i)=0

(i=overline<1,n>)[/math] . Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,

i=overline<1,n>[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math] . Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math] . Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

и найти собственные векторы [math]X^i[/math] .

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname(A-lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb^<2times 2>[/math] , где [math]A=begin3&-2\-4&1end[/math] .

1. Запишем уравнение (2.5): [math]|A-lambda E|= begin3-lambda&-2\-4& 1-lambda end= lambda^2-4 lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(lambda)equiv lambda^2-4 lambda-5=0[/math] .

2. Находим его корни (собственные значения): [math]lambda_1=5,

3. Составим систему [math](A-lambda_iE)X^i=0,

i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:

Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=mu[/math] , то [math]x_1^1=-mu[/math] . В результате получаем [math]X^1= bigl^T= bigl<mu(-1;1)bigr>^T[/math] .

Для [math]lambda_2=-1[/math] имеем

Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=mu[/math] , то [math]x_2^2=2mu[/math] . В результате получаем [math]X^2= bigl^T= bigl<mu(1;2)bigr>^T[/math] , где [math]mu[/math] — произвольное действительное число.

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin2&-1&1\-1&2&-1\0&0&1end[/math] .

1. Запишем характеристическое уравнение (2.5):

2. Корни характеристического уравнения: [math]lambda_<1,2>=1[/math] (кратный корень), [math]lambda_3=3[/math] — собственные значения матрицы.

3. Найдем собственные векторы.

Для [math]lambda_<1,2>=1[/math] запишем систему [math](A-lambda_<1,2>E)cdot X^<1,2>=0colon[/math]

Поскольку [math]operatorname(A-lambda_<1,2>E)=1[/math] , в системе имеется одно независимое уравнение

x_3^<1,2>=3[/math] , получаем [math]x_1^<1,2>=1[/math] и собственный вектор [math]X^1= begin1&1&0end^T[/math] .

x_3^<1,2>=1[/math] , получаем [math]x_1^<1,2>=-1[/math] и другой собственный вектор [math]X^2= begin-1&0&1end^T[/math] . Заметим, что оба собственных вектора линейно независимы.

Для собственного значения [math]lambda_3=3[/math] запишем систему [math](A-lambda_3E)cdot X^3=0colon[/math]

Поскольку [math]operatorname(A-lambda_3E)=2[/math] , то выбираем два уравнения:

x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=begin-1&1&0 end^T[/math] .

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_bigl|lambda_i(A)bigr|[/math] .

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,

i=1,ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^<1(0)>[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .

lambda_1^<(1)>= frac>>[/math] , где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math] , и положить [math]k=1[/math] .

4. Найти [math]lambda_1^<(k+1)>= frac>>[/math] , где [math]x_i^<1(k+1)>, x_i^<1(k)>[/math] — соответствующие координаты векторов [math]X^<1(k+1)>[/math] и [math]X^<1(k)>[/math] . При этом может быть использована любая координата с номером [math]i,

1leqslant ileqslant n[/math] .

5. Если [math]Delta= bigl|lambda_1^<(k+1)>— lambda_1^<(k)>bigr|leqslant varepsilon[/math] , процесс завершить и положить [math]lambda_1cong lambda_1^[/math] . Если varepsilon»>[math]Delta>varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.

1. Процесс последовательных приближений

сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^<1(k)>[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^<1(0)>[/math] по всем собственным векторам: [math]textstyle= sumlimits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math] , то

При большом [math]k[/math] дроби [math]<left(frac<lambda_2><lambda_1>right)!>^k, ldots, <left(frac<lambda_n><lambda_1>right)!>^k[/math] малы и поэтому [math]A^kX^<1(0)>= c_1lambda_1^kX^1[/math] , то есть [math]X^<1(k)>to X^1[/math] при [math]ktoinfty[/math] . Одновременно [math]lambda_1= limlimits_ frac^<1(k+1)>>^<1(k)>>[/math] .

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^<(k+1)>[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

4. При неудачном выборе начального приближения [math]X^<1(0)>[/math] предел отношения [math]frac>>[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac<lambda_2><lambda_1>[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.

7. Используя [math]lambda_1[/math] , можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac— lambda_1 x_i^<1(k)>>— lambda_1 x_i^<1(k-1)>>

(i=1,2,ldots,n)[/math] . Эта формула дает грубые значения для [math]lambda_2[/math] , так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j

8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac><|X^<1(k)>|_1>[/math] .

Пример 2.3. Для матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math] .

1. Выбирается начальное приближение собственного вектора [math]X^<(0)>= begin 1&1&1 end^T[/math] . Положим [math]k=0[/math] .

5. Так как varepsilon»>[math]bigl|lambda_1^<(2)>— lambda_1^<(1)>bigr|= 0,!75> varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.

Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= begin 2838& 1682& 1888end^T[/math] .

Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим

Согласно замечаниям, в качестве собственного значения [math]lambda_1[/math] матрицы можно взять не только отношение

а также их среднее арифметическое [math]frac<6,!9559+6,!728+6,!8905><3>approx 6,!8581[/math] .

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin2&-1&1\ -1&2&-1\ 0&0&3 end[/math] и соответствующий собственный вектор.

1. Зададим начальное приближение [math]X^<1(0)>= begin1&-1&1 end^T[/math] и [math]varepsilon=0,!0001[/math] .

Выполним расчеты согласно методике (табл. 10.11).

В результате получено собственное значение [math]lambda_1cong 3,!00003[/math] и собственный вектор [math]X^1= begin 88573&-88573&1end^T[/math] или после нормировки

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .

Напомним, что две матрицы [math]A[/math] и [math]A^<(i)>[/math] называются подобными ( [math]Asim A^<(i)>[/math] или [math]A^<(i)>sim A[/math] ), если [math]A^<(i)>=H^<-1>AH[/math] или [math]A=HA^<(i)>H^<-1>[/math] , где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^<-1>[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^<(i)>[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]

[math]operatorname

A= sum_^a_= sum_^ lambda_i(A)= operatornameA^<(i)>.[/math]

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^<(0)>=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^<(k)>,

ine j[/math] , определяется ортогональная матрица [math]H^<(k)>[/math] , приводящая этот элемент [math]a_^<(k+1)>[/math] (а также и [math]a_^<(k+1)>[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^<(k+1)>[/math] выбирается наибольший по модулю. Матрица [math]H^<(k)>[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^<(k)>[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^<(k)>= cosvarphi^<(k)>[/math] и [math]h_^<(k)>=cosvarphi^<(k)>[/math] , а остальные элементы нулевые, за исключением [math]h_^<(k)>=-sinvarphi^<(k)>[/math] , [math]h_^<(k)>=sinvarphi^<(k)>[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).

Угол поворота [math]varphi^<(k)>[/math] определяется по формуле

где [math]|2varphi^<(k)>|leqslant frac<pi><2>,

i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^<(k)>)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^<(k+1)>) . Однако элементы [math]a_^<(k)>[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^<(2)>)> ldots> sigma(A^<(k)>)>ldots»>[math]sigma(A^<(1)>)> sigma(A^<(2)>)> ldots> sigma(A^<(k)>)>ldots[/math] . Поэтому [math]sigma(A^<(k)>)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^<(k)>to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

Алгоритм метода вращений

1. Положить [math]k=0,

A^<(0)>=A[/math] и задать 0″>[math]varepsilon>0[/math] .

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^<(k)>[/math] максимальный по модулю элемент [math]a_^<(k)>,

Если [math]|a_^<(k)>|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^<(k)>)=a_^<(k)>,

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

Если varepsilon»>[math]bigl|a_^<(k)>bigr|>varepsilon[/math] , процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^<(k)>= frac<1> <2>operatorname frac<2a_^<(k)>>^<(k)>-a_^<(k)>>[/math] .

4. Составить матрицу вращения [math]H^<(k)>[/math] .

5. Вычислить очередное приближение [math]A^<(k+1)>= bigl(H^<(k)>bigr)^T A^ <(k)>H^<(k)>[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.

1. Используя обозначение [math]overline

_k= frac<2a_^<(k)>>^<(k)>-a_^<(k)>>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.

1. Положим [math]k=0,

2°. Выше главной диагонали имеется только один элемент [math]a_=a_<12>=1[/math] .

3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:

4°. Сформируем матрицу вращения:

5°. Выполним первую итерацию:

Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^<2>a_^<(0)>= sum_^<2>a_^<(0)>=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2. Максимальный по модулю наддиагональный элемент [math]|a_<12>|= 4,!04620781325cdot10^ <-12>. Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .

1. Положим [math]k=0,

2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_<13>^<(0)>=2[/math] . Так как varepsilon=0,!001″>[math]a_<13>=2> varepsilon=0,!001[/math] , то процесс продолжается.

3°. Находим угол поворота:

4°. Сформируем матрицу вращения: [math]H^<(0)>= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .

5°. Выполним первую итерацию: [math]A^<(1)>= bigl(H^<(0)>bigr)^T A^<(0)>H^<(0)>= begin 6,!236&1,!376&2,!33cdot10^<-6>\ 1,!376&4&0,!325\ 2,!33cdot10^<-6>&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2(1). Максимальный по модулю наддиагональный элемент [math]a_<12>^<(1)>=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_<12>^<(1)>> varepsilon=0,!001[/math] , процесс продолжается.

3(1). Найдем угол поворота:

4(1). Сформируем матрицу вращения: [math]H^<(1)>= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .

5(1). Выполним вторую итерацию: [math]A^<(2)>= bigl(H^<(1)>bigr)^T A^<(1)>H^<(1)>= begin 6,!891& 2,!238cdot10^<-4>&0,!14\ 2,!238cdot10^<-4>& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.

2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_<23>^<(2)>=0,!293> varepsilon=0,!001[/math] .

3(2). Найдем угол поворота:

4(2). Сформируем матрицу вращения [math]H^<(2)>= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .

5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:

2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_<13>^<(3)>= 0,!138>varepsilon[/math] .

3(3). Найдем угол поворота:

4(3). Сформируем матрицу вращения: [math]H^<(3)>= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .

5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:

2(4). Так как varepsilon»>[math]a_<12>^<(4)>=0,!025>varepsilon[/math] , процесс повторяется

3(4). Найдем угол поворота

4(4). Сформируем матрицу вращения: [math]H^<(4)>= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .

5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:

2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^<-4>bigr| , процесс завершается.

Собственные значения: [math]lambda_1cong a_<11>^<(5)>= 6,!895,,

lambda_3cong a_<33>^<(5)>=1,!707,,[/math] . Для нахождения собственных векторов вычислим

X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

источники:

http://mathhelpplanet.com/static.php?p=metody-resheniya-zadach-o-sobstvennykh-znacheniyakh-i-vektorakh-matritsy

http://mathdf.com/dif/ru/