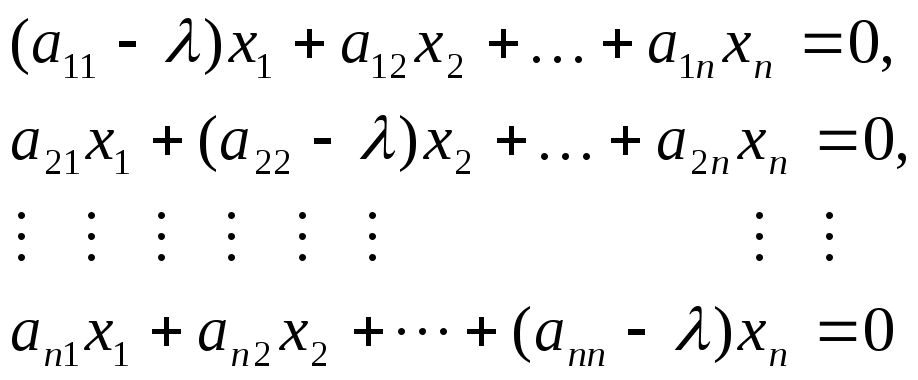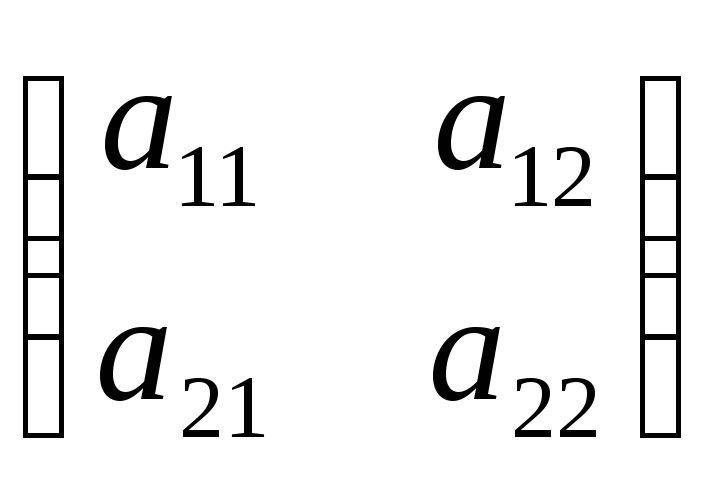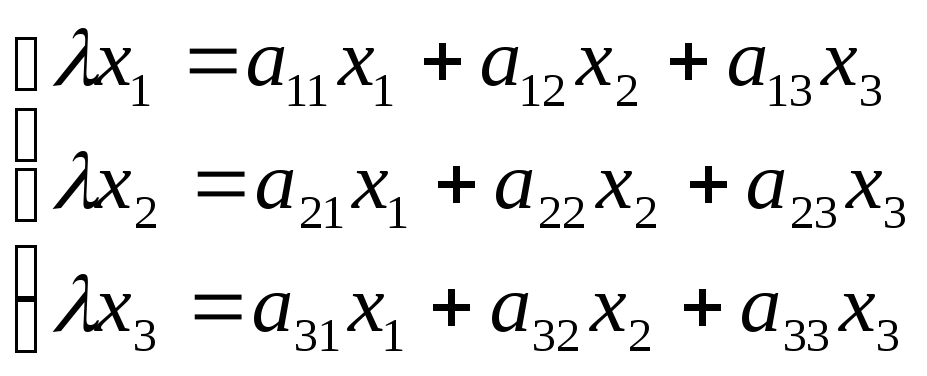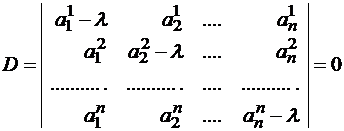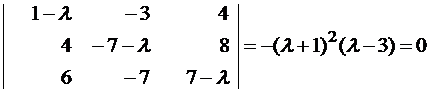Как найти собственные векторы линейного преобразования - Исправление недочетов и поиск решений вместе с Examum.ru

Определение:ПустьL– заданноеn—мерное линейное пространство. Ненулевой
векторLназываетсясобственным векторомлинейного преобразования А, если
существует такое число,
что выполняется равенство:

A(7.1)

При этом число называетсясобственным значением
(характеристическим числом)линейного
преобразования А, соответствующего
вектору.

Перенеся правую часть (7.1) в левую и
принимая во внимание соотношение
,
перепишем (7.1) в виде

(7.2)

Уравнение (7.2) эквивалентно системе
линейных однородных уравнений:

(7.3)

Для существования ненулевого решения
системы линейных однородных уравнений
(7.3) необходимо и достаточно, чтобы
определитель коэффициентов этой системы
равнялся нулю, т.е.

|A-λE|=(7.4)

Этот определитель
является многочленом n-ой степени
относительно λ и называется
характеристическим многочленомлинейного преобразования А, а уравнение
(7.4) —характеристическим уравнением
матрицы А.

Определение:Если линейное
преобразование А в некотором базисе,,…,имеет матрицу А =,
то собственные значения линейного
преобразования А можно найти как корни₁,₂,
… ,_nхарактеристического уравнения:

Рассмотрим
частный случай. Пусть А – некоторое
линейное преобразование плоскости,
матрица которого равна.
Тогда преобразование А может быть задано
формулами:

;

в некотором
базисе
.

Если
преобразование А имеет собственный
вектор с собственным значением ,
то А.

или

Т.к. собственный
вектор
ненулевой,
то х₁и х₂не равны нулю
одновременно. Т.к. данная система
однородна, то для того, чтобы она имела
нетривиальное решение, определитель
системы должен быть равен нулю. В
противном случае по правилу Крамера
система имеет единственное решение –
нулевое, что невозможно.

Полученное
уравнение является характеристическим
уравнением линейного преобразования
А.

Таким образом,
можно найти собственный вектор
(х₁,
х₂) линейного преобразования А с
собственным значением,
где- корень
характеристического уравнения, а х₁и х₂– корни системы уравнений
при подстановке в нее значения.

Понятно, что
если характеристическое уравнение не
имеет действительных корней, то линейное
преобразование А не имеет собственных
векторов.

Следует
отметить, что если
—
собственный вектор преобразования А,
то и любой вектор ему коллинеарный –
тоже собственный с тем же самым собственным
значением.

Действительно,.
Если учесть, что векторы имеют одно
начало, то эти векторы образуют так
называемоесобственное направление
илисобственную прямую.

Т.к.
характеристическое уравнение может
иметь два различных действительных
корня ₁и₂,
то в этом случае при подстановке их в
систему уравнений получим бесконечное
количество решений. (Т.к. уравнения
линейно зависимы). Это множество решений
определяет двесобственные прямые.

Если характеристическое уравнение
имеет два равных корня₁=₂=,
то либо имеется лишь одна собственная
прямая, либо, если при подстановке в
систему она превращается в систему
вида:
.
Эта система удовлетворяет любым значениям
х₁и х₂. Тогда все векторы
будут собственными, и такое преобразование
называетсяпреобразованием подобия.

Пример.Найти характеристические
числа и собственные векторы линейного
преобразования с матрицей А =
.

Запишем
линейное преобразование в виде:

Составим характеристическое уравнение:

²— 4+ 4 = 0;

Корни
характеристического уравнения: ₁=₂= 2;

Получаем:

Из системы
получается зависимость: x₁
– x₂ =0. Собственные векторы для первого корня
характеристического уравнения имеют
координаты:(t;
t)гдеt— параметр.

Собственный
вектор можно записать:
.

Рассмотрим
другой частный случай. Если—
собственный вектор линейного преобразования
А, заданного в трехмерном линейном
пространстве, а х₁, х₂, х₃– компоненты этого вектора в некотором
базисе,
то

где - собственное значение (характеристическое
число) преобразования А.

Если матрица
линейного преобразования А имеет вид:

,
то

Характеристическое
уравнение:

Раскрыв
определитель, получим кубическое
уравнение относительно .
Любое кубическое уравнение с действительными
коэффициентами имеет либо один, либо
три действительных корня.

Тогда любое
линейное преобразование в трехмерном
пространстве имеет собственные векторы.

Пример.Найти характеристические
числа и собственные векторы линейного
преобразования А, матрица линейного
преобразования А =.

Пример.Найти характеристические числа и
собственные векторы линейного
преобразования А, матрица линейного
преобразования А =.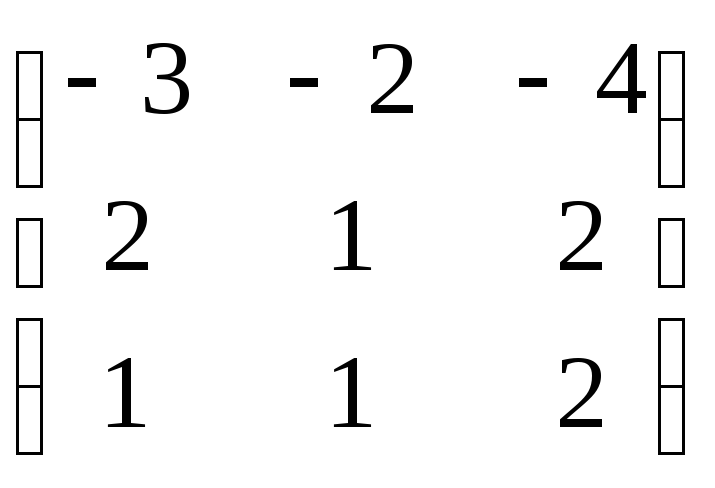

Составим
характеристическое уравнение:

-(3 + )((1
-)(2 -)
– 2) + 2(4 — 2- 2) — 4(2 — 1
+) = 0

-(3 + )(2
-- 2+²— 2) + 2(2 — 2)
— 4(1 +) = 0

-(3 + )(²— 3) + 4 — 4- 4 — 4= 0

-3²+ 9-³+ 3²— 8= 0

-³+= 0

₁= 0;₂= 1;₃= -1;

Для ₁= 0:

Если принять
х₃= 1, получаем х₁= 0, х₂= -2

Собственные
векторы
t,
гдеt– параметр.

Аналогично
можно найти
идля₂и₃.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение: Пусть L – заданное n — мерное линейное пространство. Ненулевой вектор L называется Собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:

При этом число l называется Собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору .

Определение: Если линейное преобразование А в некотором базисе ,,…, имеет матрицу А = , то собственные значения линейного преобразования А можно найти как корни l1, l2, … ,ln уравнения:

Это уравнение называется Характеристическим уравнением, а его левая часть — Характеристическим многочленом линейного преобразования А.

Следует отметить, что характеристический многочлен линейного преобразования не зависит от выбора базиса.

Рассмотрим Частный случай. Пусть А – некоторое линейное преобразование плоскости, матрица которого равна . Тогда преобразование А может быть задано формулами:

;

В некотором базисе .

Если преобразование А имеет собственный вектор с собственным значением l, то А.

или

Т. к. собственный вектор Ненулевой, то х1 и х2 не равны нулю одновременно. Т. к. данная система однородна, то для того, чтобы она имела нетривиальное решение, определитель системы должен быть равен нулю. В противном случае по правилу Крамера система имеет единственное решение – нулевое, что невозможно.

Полученное уравнение является Характеристическим уравнением линейного преобразования А.

Таким образом, можно найти собственный вектор (х1, х2) линейного преобразования А с собственным значением l, где l — корень характеристического уравнения, а х1 и х2 – корни системы уравнений при подстановке в нее значения l.

Понятно, что если характеристическое уравнение не имеет действительных корней, то линейное преобразование А не имеет собственных векторов.

Следует отметить, что если — собственный вектор преобразования А, то и любой вектор ему коллинеарный – тоже собственный с тем же самым собственным значением l.

Действительно, . Если учесть, что векторы имеют одно начало, то эти векторы образуют так называемое Собственное направление Или Собственную прямую.

Т. к. характеристическое уравнение может иметь два различных действительных корня l1 и l2, то в этом случае при подстановке их в систему уравнений получим бесконечное количество решений. (Т. к. уравнения линейно зависимы). Это множество решений определяет две Собственные прямые.

Если характеристическое уравнение имеет два равных корня l1 = l2 = l, то либо имеется лишь одна собственная прямая, либо, если при подстановке в систему она превращается в систему вида: . Эта система удовлетворяет любым значениям х1 и х2. Тогда все векторы будут собственными, и такое преобразование называется Преобразованием подобия.

Пример. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А = .

Запишем линейное преобразование в виде:

Составим характеристическое уравнение:

L2 — 8l + 7 = 0;

Корни характеристического уравнения: l1 = 7; l2 = 1;

Для корня l1 = 7:

Из системы получается зависимость: X1 – 2X2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (T; 0,5T) где T— параметр.

Для корня l2 = 1:

Из системы получается зависимость: X1 + X2 = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (T; —T) где T— параметр.

Полученные собственные векторы можно записать в виде:

Пример. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А = .

Запишем линейное преобразование в виде:

Составим характеристическое уравнение:

L2 — 4l + 4 = 0;

Корни характеристического уравнения: l1 = l2 = 2;

Получаем:

Из системы получается зависимость: X1 – X2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (T; T) где T— параметр.

Собственный вектор можно записать: .

Рассмотрим другой Частный случай. Если — собственный вектор линейного преобразования А, заданного в трехмерном линейном пространстве, а х1, х2, х3 – компоненты этого вектора в некотором базисе , то

Где l — собственное значение (характеристическое число) преобразования А.

Если матрица линейного преобразования А имеет вид:

, то

Характеристическое уравнение:

Раскрыв определитель, получим кубическое уравнение относительно l. Любое кубическое уравнение с действительными коэффициентами имеет либо один, либо три действительных корня.

Тогда любое линейное преобразование в трехмерном пространстве имеет собственные векторы.

Пример. Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования А = .

Составим характеристическое уравнение:

(1 — l)((5 — l)(1 — l) — 1) — (1 — l — 3) + 3(1 — 15 + 3l) = 0

(1 — l)(5 — 5l — l + l2 — 1) + 2 + l — 42 + 9l = 0

(1 — l)(4 — 6l + l2) + 10l — 40 = 0

4 — 6l + l2 — 4l + 6l2 — l3 + 10l — 40 = 0

-l3 + 7l2 – 36 = 0

-l3 + 9l2 — 2l2 – 36 = 0

-l2(l + 2) + 9(l2 – 4) = 0

(l + 2)(-l2 + 9l — 18) = 0

Собственные значения: l1 = -2; l2 = 3; l3 = 6;

1) Для l1 = -2:

Если принять х1 = 1, то Þ х2 = 0; x3 = -1;

Собственные векторы:

2) Для l2 = 3:

Если принять х1 = 1, то Þ х2 = -1; x3 = 1;

Собственные векторы:

3) Для l3 = 6:

Если принять х1 = 1, то Þ х2 = 2; x3 = 1;

Собственные векторы:

Пример. Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования А = .

Составим характеристическое уравнение:

-(3 + l)((1 — l)(2 — l) – 2) + 2(4 — 2l — 2) — 4(2 — 1 + l) = 0

-(3 + l)(2 — l — 2l + l2 — 2) + 2(2 — 2l) — 4(1 + l) = 0

-(3 + l)(l2 — 3l) + 4 — 4l — 4 — 4l = 0

-3l2 + 9l — l3 + 3l2 — 8l = 0

-l3 + l = 0

L1 = 0; l2 = 1; l3 = -1;

Для l1 = 0:

Если принять х3 = 1, получаем х1 = 0, х2 = -2

Собственные векторы ×t, где t – параметр.

Для самостоятельного решения: Аналогично найти И для l2 и l3.

< Предыдущая		Следующая >

Источник

Собственные векторы и значения линейного оператора (преобразования)

Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного линейного пространства . Ненулевой вектор boldsymbol{s} линейного пространства , удовлетворяющий условию

mathcal{A}(boldsymbol{s})=lambdacdot boldsymbol{s},

(9.5)

называется собственным вектором линейного преобразования mathcal{A} . Число lambda в равенстве (9.5) называется собственным значением преобразования . Говорят, что собственный вектор соответствует (принадлежит) собственному значению lambda . Если пространство вещественное (комплексное), то собственное значение lambda — действительное (комплексное) число.

Множество всех собственных значений линейного преобразования называется его спектром.

Поясним геометрический смысл собственных векторов. Ненулевой вектор s является собственным для преобразования mathcal{A} , если его образ mathcal{A} (boldsymbol{s}) коллинеарен прообразу . Другими словами, если — собственный вектор, то преобразование имеет одномерное инвариантное подпространство operatorname{Lin}(boldsymbol{s}) . Справедливо и обратное утверждение.

В самом деле, пусть собственный вектор boldsymbol{s} соответствует некоторому собственному значению lambda . Любой вектор boldsymbol{v} из operatorname{Lin}(boldsymbol{s}) имеет вид boldsymbol{v}=alpha boldsymbol{s} , где alpha — любое число из заданного поля. Найдем образ этого вектора

mathcal{A}(boldsymbol{v})= mathcal{A}(alpha boldsymbol{s})= alphacdot mathcal{A}(boldsymbol{s})= alphacdot lambdacdot boldsymbol{s}in operatorname{Lin} (boldsymbol{s}).

Следовательно, mathcal{A}(boldsymbol{v})in operatorname{Lin}(boldsymbol{s}) для любого вектора boldsymbol{v}in operatorname{Lin}(boldsymbol{s}) , т.е. подпространство инвариантно относительно преобразования . Размерность подпространства operatorname{Lin} (boldsymbol{s}) равна единице, так как boldsymbol{s}ne boldsymbol{o} по определению.

Обратное утверждение доказывается, проводя рассуждения в обратном порядке.

Связь собственных векторов линейного преобразования (оператора) и его матрицы

Ранее рассматривались собственные векторы и собственные значения матрицы. Напомним, что собственным вектором квадратной матрицы n-го порядка называется ненулевой числовой столбец $s=begin{pmatrix}s_1&cdots&s_{n}end{pmatrix}^T$ , удовлетворяющий условию (7.13):

Acdot s=lambdacdot s.

(9.6)

Число lambda в (9.6) называется собственным значением матрицы . При этом считалось, что собственное значение lambda и числа s_i~(i=1,ldots,n) принадлежат полю комплексных чисел.

Эти понятия связаны с собственными векторами и собственными значениями линейного преобразования.

Теорема 9.3 о собственных векторах линейного преобразования и его матрицы. Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного линейного пространства с базисом $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ . Тогда собственное значение lambda и координатный столбец {s} собственного вектора boldsymbol{s} преобразования mathcal{A} являются собственным значением и собственным вектором матрицы этого преобразования, определенной относительно базиса $boldsymbol{e}_1,ldots, boldsymbol{e}_n$ , т.е.

mathcal{A}(boldsymbol{s})=lambdacdot boldsymbol{s}quad Rightarrowquad Acdot s=lambdacdot s, где $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n,~ s=begin{pmatrix}s_1&cdots& s_nend{pmatrix}^T.$

Обратное утверждение справедливо при дополнительных условиях: если столбец $s=begin{pmatrix} s_1&cdots&s_nend{pmatrix}^T$ и число lambda являются собственным вектором и собственным значением матрицы , причем числа s_1,ldots,s_n,lambda принадлежат тому же числовому полю, над которым определено линейное пространство , то вектор $boldsymbol{s}=s_1 boldsymbol{e}_1+ ldots+s_n boldsymbol{e}_n$ и число lambda являются собственным вектором и собственным значением линейного преобразования mathcal{A}colon Vto V с матрицей в базисе $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ .

В самом деле, условие (9.5) в координатной форме имеет вид (9.6), что совпадает с определением (7.13) собственного вектора матрицы. Наоборот, из равенства (9.6) следует равенство (9.5) при условии, что векторы $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n$ и lambdacdot boldsymbol{s} определены, т.е. числа s_1,ldots,s_n, lambda принадлежат тому же числовому полю, над которым определено линейное пространство.

Напомним, что нахождение собственных значений матрицы сводится к решению ее характеристического уравнения Delta_A(lambda)=0 , где Delta_A(lambda)=det(A-lambda E) — характеристический многочлен матрицы . Для линейного преобразования введем аналогичные понятия.

Характеристическим многочленом линейного преобразования mathcal{A}colon Vto V n-мерного линейного пространства называется характеристический многочлен $Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ матрицы этого преобразования, найденной относительно любого базиса пространства .

Уравнение $Delta_{mathcal{A}}(lambda)=0$ называется характеристическим уравнением линейного преобразования.

Преобразование mathcal{A}-lambdamathcal{E} называется характеристическим для линейного преобразования mathcal{A}colon Vto V .

Замечания 9.4

1. Характеристический многочлен линейного преобразования не зависит от базиса, в котором найдена матрица преобразования.

В самом деле, матрицы $mathop{A}limits_{(boldsymbol{e})}$ и $mathop{A}limits_{(boldsymbol{f})}$ линейного преобразования mathcal{A} в базисах $(boldsymbol{e})= (boldsymbol{e}_1,ldots, boldsymbol{e}_n)$ и $(boldsymbol{f})=(boldsymbol{f}_1,ldots,boldsymbol{f}_n)$ являются, согласно (9.4), подобными: $mathop{A}limits_{(boldsymbol{f})}=S^{-1}mathop{A}limits_{(boldsymbol{e})}S$ , где — матрица перехода от базиса к базису . Как показано ранее, характеристические многочлены подобных матриц совпадают (см. свойство 3). Поэтому для характеристического многочлена преобразования mathcal{A} можно использовать обозначение $Delta_{mathcal{A}}(lambda)$ , не указывая матрицу этого преобразования.

2. Из теоремы 9.3 следует, что любой комплексный (действительный, рациональный) корень характеристического уравнения является собственным значением линейного преобразования mathcal{A}colon Vto V линейного пространства , определенного над полем комплексных (действительных, рациональных) чисел.

3. Из теоремы 9.3 следует, что любое линейное преобразование комплексного линейного пространства имеет одномерное инвариантное подпространство, так как это преобразование имеет собственное значение (см. пункт 2), а следовательно, и собственные векторы. Таким подпространством является, например, линейная оболочка любого собственного вектора. У преобразования вещественного линейного пространства одномерных инвариантных подпространств может и не быть, если все корни характеристического уравнения комплексные (но не действительные).

Теорема 9.4 об инвариантных подпространствах линейного оператора вещественного пространства. У всякого линейного преобразования вещественного линейного пространства существует одномерное или двумерное инвариантное подпространство.

Действительно, составим матрицу линейного преобразования mathcal{A}colon Vto V n-мерного вещественного линейного пространства в произвольном базисе $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ . Элементы этой матрицы — действительные числа. Следовательно, характеристический многочлен $Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ — это многочлен степени с действительными коэффициентами. Согласно следствиям 3, 4 основной теоремы алгебры, такой многочлен может иметь действительные корни и пары комплексных сопряженных корней.

Если lambda=lambda_1 — действительный корень характеристического уравнения, то и соответствующий собственный вектор $s=begin{pmatrix}s_1&cdots&s_nend{pmatrix}^T$ матрицы также действительный. Поэтому он определяет собственный вектор $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n$ линейного преобразования (см. теорему 9.3). В этом случае существует одномерное инвариантное относительно mathcal{A} подпространство operatorname{Lin}(boldsymbol{s}) (см. геометрический смысл собственных векторов).

Если lambda=alphapmbeta i — пара комплексных сопряженных корней (betane0) , то собственный вектор sne o матрицы также с комплексными элементами: $s=begin{pmatrix}x_1+y_1i&cdots& x_n+y_n i end{pmatrix}^T$ . Его можно представить в виде s=x+yi , где x,,y — действительные столбцы. Равенство (9.6) при этом будет иметь вид

Acdot(x+yi)= (alpha+beta i)cdot(x+yi).

Выделяя действительную и мнимую части, получаем систему

$begin{cases}Ax=alpha x-beta y,\ Ay=beta x+alpha y.end{cases}$

(9.7)

Покажем, что столбцы {x} и {y} линейно независимы. Рассмотрим два случая. Если x=o , то из первого уравнения (9.7) следует, что y=o , так как betane0 . Тогда s=o , что противоречит условию sne o . Предположим, что xne o и столбцы и пропорциональны, т.е. существует такое действительное число gamma , что y=gamma x . Тогда из системы (9.7) получаем $begin{cases}Ax=(alpha-betagamma)x,\ gamma Ax=(beta-alphagamma)x. end{cases}$ Прибавляя ко второму уравнению первое, умноженное на (-gamma) , приходим к равенству [(beta+alphagamma)-gamma(alpha-betagamma)]x=o . Так как xne o , то выражение в квадратных скобках равно нулю, т.е. (beta+alphagamma)- gamma(alpha- betagamma)= beta(1+gamma^2)=0 . Поскольку betane0 , то gamma^2=-1 . Этого не может быть, так как gamma — действительное число. Получили противоречие. Таким образом, столбцы и линейно независимы.

Рассмотрим подпространство operatorname{Lin}(boldsymbol{x},boldsymbol{y}) , где $boldsymbol{x}= x_1 boldsymbol{e}_1+ldots+x_n boldsymbol{e}_n,~ boldsymbol{y}= y_1 boldsymbol{e}_1+ldots+ y_n boldsymbol{y}_n$ . Это подпространство двумерное, так как векторы линейно независимы (как показано выше, их координатные столбцы x,y линейно независимы). Из (9.7) следует, что $begin{cases}mathcal{A}(boldsymbol{x})=alpha boldsymbol{x}-beta boldsymbol{y},\ mathcal{A}(boldsymbol{y})=beta boldsymbol{x}+alpha boldsymbol{y},end{cases}$ т.е. образ любого вектора, принадлежащего operatorname{Lin}(boldsymbol{x},boldsymbol{y}) , также принадлежит . Следовательно, — двумерное подпространство, инвариантное относительно преобразования mathcal{A} , что и требовалось доказать.

Нахождение собственных векторов и значений линейного оператора (преобразования)

Для нахождения собственных векторов и собственных значений линейного преобразования mathcal{A}colon Vto V вещественного линейного пространства следует выполнить следующие действия.

1. Выбрать произвольный базис $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ линейного пространства и найти в этом базисе матрицу преобразования mathcal{A} .

2. Составить характеристический многочлен преобразования $mathcal{A}colon, Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ .

3. Найти все различные действительные корни lambda_1,ldots,lambda_k характеристического уравнения $Delta_{mathcal{A}}(lambda)=0$ . Комплексные (но не действительные) корни характеристического уравнения следует отбросить (см. пункт 2. замечаний 9.4).

4. Для корня lambda=lambda_1 найти фундаментальную систему $varphi_1, varphi_2,ldots,varphi_{n-r}$ решений однородной системы уравнений (A-lambda_1E)x=o , где $r=operatorname{rg}(A-lambda_1E)$ . Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы.

5. Записать линейно независимые собственные векторы преобразования mathcal{A} , отвечающие собственному значению lambda_1:

$begin{matrix} boldsymbol{s}_1=varphi_{1,1}boldsymbol{e}_1+ ldots+ varphi_{n,1}boldsymbol{e}_n,\ boldsymbol{s}_2=varphi_{1,2}boldsymbol{e}_1+ ldots+ varphi_{n,2}boldsymbol{e}_n,\ vdots\ boldsymbol{s}_{n-r}=varphi_{1,n-r} boldsymbol{e}_1+ ldots+varphi_{n,n-r}boldsymbol{e}_n. end{matrix}$

Для нахождения совокупности всех собственных векторов, отвечающих собственному значению lambda_1 , образовать ненулевые линейные комбинации

$boldsymbol{s}= C_1 boldsymbol{s}_1+C_2 boldsymbol{s}_2+ldots+ C_{n-r}boldsymbol{s}_{n-r},$

где $C_1,C_2,ldots,C_{n-r}$ — произвольные постоянные, не равные нулю одновременно.

Повторить пункты 4, 5 для остальных собственных значений lambda_2,ldots,lambda_k линейного преобразования mathcal{A} .

Для нахождения собственных векторов линейного преобразования комплексного линейного пространства нужно в пункте 3 определить все корни характеристического уравнения и, не отбрасывая комплексные корни, выполнить для них пункты 4,5.

Примеры собственных векторов линейных операторов (преобразований)

1. Для нулевого преобразования mathcal{O}colon Vto V любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим нулевому собственному значению lambda=0 , так как mathcal{O}(boldsymbol{s})=0cdot boldsymbol{s}~ forall boldsymbol{s}in V .

2. Для тождественного преобразования mathcal{E}colon Vto V любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим единичному собственному значению lambda=1 , так как mathcal{E} (boldsymbol{s})=1cdot boldsymbol{s}~ forall boldsymbol{s}in V .

3. Для центральной симметрии $mathcal{Z}_{boldsymbol{o}}colon Vto V$ любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим собственному значению lambda=-1 , так как $mathcal{Z}_{boldsymbol{o}} (boldsymbol{s})=(-1)cdot boldsymbol{s}~ forall boldsymbol{s}in V$ .

4. Для гомотетии $mathcal{H}_{lambda}colon Vto V$ любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим собственному значению lambda (коэффициенту гомотетии), так как $mathcal{H}_{lambda} (boldsymbol{boldsymbol{s}})= lambdacdot boldsymbol{s}~ forall boldsymbol{s}in V$ .

5. Для поворота $mathcal{R}_{varphi}colon V_2to V_2$ плоскости (при varphinepi k,~ kinmathbb{Z} ) собственных векторов нет, так как при повороте на угол, не кратный , образ каждого ненулевого вектора неколлинеарен прообразу. Здесь рассматривается поворот вещественной плоскости, т.е. двумерного векторного пространства над полем действительных чисел.

6. Для оператора дифференцирования $mathcal{D}colon P_n(mathbb{R})to P_n(mathbb{R})$ любой ненулевой многочлен нулевой степени (не равный тождественно нулю) является собственным вектором, соответствующим нулевому собственному значению lambda=0 , так как mathcal{D}(s(x))=0cdot s(x) forall s(x)equiv text{const} . Любой многочлен ненулевой степени не является собственным вектором, так как многочлен не пропорционален своей производной: mathcal{D}(s(x))=s'(x)ne lambdacdot s(x) , поскольку они имеют разные степени.

7. Рассмотрим оператор $Pi_{L_1}colon Vto V$ проектирования на подпространство L_1 параллельно подпространству L_2 . Здесь V=L_1oplus L_2, $Pi_{L_1}(boldsymbol{v}_1+ boldsymbol{v}_2)=boldsymbol{v}_1$ для $boldsymbol{v}=boldsymbol{v}_1+boldsymbol{v}_2,$ $boldsymbol{v}_1in L_1,~ boldsymbol{v}_2in L_2$ . Для этого оператора любой ненулевой вектор $boldsymbol{v}_1in L_1$ является собственным, соответствующим собственному значению lambda=1 , так как $Pi_{L_1}(boldsymbol{v}_1)=1cdot boldsymbol{v}_1$ , а любой ненулевой вектор $boldsymbol{v}_2in L_2$ является собственным, соответствующим собственному значению lambda=0 , так как $Pi_{L_2}(boldsymbol{v}_2)=0cdot boldsymbol{v}_2$ . Другие векторы не являются собственными, так как равенство $Pi_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1= lambda(boldsymbol{v}_1+boldsymbol{v}_2)$ возможно либо при $boldsymbol{v}_1=boldsymbol{o}$ , либо при $boldsymbol{v}_2= boldsymbol{o}$ .

8. Рассмотрим оператор $mathcal{Z}_{L_1}colon Vto V$ отражения на подпространство L_1 параллельно подпространству L_2 . Здесь V=L_1oplus L_2 $mathcal{Z}_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1- boldsymbol{v}_2$ , для $boldsymbol{v}=boldsymbol{v}_1+boldsymbol{v}_2,$ $boldsymbol{v}_1in L_1,~ boldsymbol{v}_2in L_2$ . Для этого оператора любой ненулевой вектор $boldsymbol{v}_1in L_1$ является собственным, соответствующим собственному значению lambda=1 , так как $mathcal{Z}_{L_1} (boldsymbol{v}_1)= 1cdot boldsymbol{v}_1$ , а любой ненулевой вектор $boldsymbol{v}_2in L_2$ является собственным, соответствующим собственному значению lambda=-1 , так как $mathcal{Z}_{L_2} (boldsymbol{v}_2)= (-1)cdot boldsymbol{v}_2$ . Другие векторы не являются собственными, так как равенство $mathcal{Z}_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1- boldsymbol{v}_2= lambda(boldsymbol{}_1+ boldsymbol{v}_2)$ возможно либо при $boldsymbol{v}_1=boldsymbol{o}$ , либо при $boldsymbol{v}_2= boldsymbol{o}$ .

9. В пространстве V_3 радиус-векторов пространства, отложенных от фиксированной точки , рассмотрим поворот на угол varphinepi k,~ kinmathbb{Z} , вокруг оси ell , заданной радиус-вектором vec{ell} . Любой ненулевой вектор, коллинеарный вектору , является собственным, отвечающим собственному значению lambda=1 . Других собственных векторов у этого преобразования нет.

Пример 9.1. Найти собственные значения и собственные векторы оператора дифференцирования $mathcal{D}colon T_1to T_1$ , преобразующего пространство тригонометрических многочленов (частоты omega=1 ):

а) с действительными коэффициентами $T_1=T_1(mathbb{R})= operatorname{Lin} (sin{t},cos{t})$ ;

б) с комплексными коэффициентами $T_1=T_1(mathbb{C})= operatorname{Lin} (sin{t},cos{t})$ .

Решение. 1. Выберем стандартный базис $e_1(t)=sin{t},~ e_2(t)=cos{t}$ и составим в этом базисе матрицу оператора mathcal{D}:

$D=begin{pmatrix}0&-1\ 1&0 end{pmatrix}!.$

2. Составим характеристический многочлен преобразования $mathcal{D}colon, Delta_{mathcal{D}}(lambda)= begin{vmatrix}-lambda&-1\ 1&-lambdaend{vmatrix}= lambda^2+1.$ .

3. Характеристическое уравнение lambda^2+1=0 имеет комплексные сопряженные корни lambda_1=i,~ lambda_2=-i . Действительных корней нет, поэтому преобразование mathcal{D} вещественного пространства $T_1(mathbb{R})$ (случай (а)) не имеет собственных значений, а следовательно, и собственных векторов. Преобразование комплексного пространства $T_1(mathbb{C})$ (случай (б)) имеет комплексные собственные значения lambda_1,,lambda_2 .

4(1). Для корня lambda_1=i находим фундаментальную систему varphi_1 решений однородной системы уравнений (D-lambda_1 E)x=o:

$begin{pmatrix}-i&-1\ 1&-iend{pmatrix}!cdot! begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Приведем матрицу системы к ступенчатому виду, умножая первое уравнение на {i} и вычитая его из второго уравнения:

$begin{pmatrix}-i&-1\ 1&-i end{pmatrix}sim begin{pmatrix}1&-i\ 1&-i end{pmatrix}sim begin{pmatrix}1&-i\ 0&0end{pmatrix}!.$

Выражаем базисную переменную x_1 через свободную: x_1=ix_2 . Полагая x_2=1 , получаем x_1=i , т.е. $varphi=begin{pmatrix}i&1 end{pmatrix}^T$ .

5(1). Записываем собственный вектор, отвечающий собственному значению $lambda_1= icolon, s_1(t)=icdotsin{t}+1cdotcos{t}$ . Совокупность всех собственных векторов, отвечающих собственному значению lambda_1=i , образуют ненулевые функции, пропорциональные s_1(t) .

4(2). Для корня lambda_2=-i аналогично находим фундаментальную систему (состоящую из одного вектора) $varphi_2=begin{pmatrix}-i&1 end{pmatrix}^T$ решений однородной системы уравнений (D-lambda_2E)x=o:

$begin{pmatrix}i&-1\ 1&i end{pmatrix}!cdot! begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

5(2). Записываем собственный вектор, отвечающий собственному значению $lambda_2=-icolon, s_2(t)=-icdotsin{t}+1cdotcos{t}$ . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные s_2(t) .

См. также Свойства собственных векторов линейных операторов (преобразований)

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 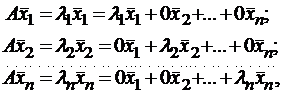тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)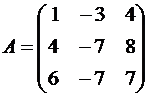
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Собственные векторы и значения линейного оператора (преобразования)

Пусть — линейное преобразование n-мерного линейного пространства . Ненулевой вектор линейного пространства , удовлетворяющий условию

называется собственным вектором линейного преобразования . Число в равенстве (9.5) называется собственным значением преобразования . Говорят, что собственный вектор соответствует (принадлежит) собственному значению . Если пространство вещественное (комплексное), то собственное значение — действительное (комплексное) число.

Множество всех собственных значений линейного преобразования называется его спектром .

Поясним геометрический смысл собственных векторов. Ненулевой вектор s является собственным для преобразования , если его образ коллинеарен прообразу . Другими словами, если — собственный вектор, то преобразование имеет одномерное инвариантное подпространство . Справедливо и обратное утверждение.

В самом деле, пусть собственный вектор соответствует некоторому собственному значению . Любой вектор из имеет вид , где — любое число из заданного поля. Найдем образ этого вектора

Следовательно, для любого вектора , т.е. подпространство инвариантно относительно преобразования . Размерность подпространства равна единице, так как по определению.

Обратное утверждение доказывается, проводя рассуждения в обратном порядке.

Связь собственных векторов линейного преобразования (оператора) и его матрицы

Ранее рассматривались собственные векторы и собственные значения матрицы. Напомним, что собственным вектором квадратной матрицы n-го порядка называется ненулевой числовой столбец , удовлетворяющий условию (7.13):

Число в (9.6) называется собственным значением матрицы . При этом считалось, что собственное значение и числа принадлежат полю комплексных чисел.

Эти понятия связаны с собственными векторами и собственными значениями линейного преобразования.

Теорема 9.3 о собственных векторах линейного преобразования и его матрицы. Пусть — линейное преобразование n-мерного линейного пространства с базисом . Тогда собственное значение и координатный столбец собственного вектора преобразования являются собственным значением и собственным вектором матрицы этого преобразования, определенной относительно базиса , т.е.

Обратное утверждение справедливо при дополнительных условиях: если столбец и число являются собственным вектором и собственным значением матрицы , причем числа принадлежат тому же числовому полю, над которым определено линейное пространство , то вектор и число являются собственным вектором и собственным значением линейного преобразования с матрицей в базисе .

В самом деле, условие (9.5) в координатной форме имеет вид (9.6), что совпадает с определением (7.13) собственного вектора матрицы. Наоборот, из равенства (9.6) следует равенство (9.5) при условии, что векторы и определены, т.е. числа принадлежат тому же числовому полю, над которым определено линейное пространство.

Напомним, что нахождение собственных значений матрицы сводится к решению ее характеристического уравнения , где — характеристический многочлен матрицы . Для линейного преобразования введем аналогичные понятия.

Характеристическим многочленом линейного преобразования n-мерного линейного пространства называется характеристический многочлен матрицы этого преобразования, найденной относительно любого базиса пространства .

Уравнение называется характеристическим уравнением линейного преобразования .

Преобразование называется характеристическим для линейного преобразования .

В самом деле, матрицы и линейного преобразования в базисах и являются, согласно (9.4), подобными: , где — матрица перехода от базиса к базису . Как показано ранее, характеристические многочлены подобных матриц совпадают (см. свойство 3). Поэтому для характеристического многочлена преобразования можно использовать обозначение , не указывая матрицу этого преобразования.

2. Из теоремы 9.3 следует, что любой комплексный (действительный, рациональный) корень характеристического уравнения является собственным значением линейного преобразования линейного пространства , определенного над полем комплексных (действительных, рациональных) чисел.

Действительно, составим матрицу линейного преобразования n-мерного вещественного линейного пространства в произвольном базисе . Элементы этой матрицы — действительные числа. Следовательно, характеристический многочлен — это многочлен степени с действительными коэффициентами. Согласно следствиям 3, 4 основной теоремы алгебры, такой многочлен может иметь действительные корни и пары комплексных сопряженных корней.

Если — действительный корень характеристического уравнения, то и соответствующий собственный вектор матрицы также действительный. Поэтому он определяет собственный вектор линейного преобразования (см. теорему 9.3). В этом случае существует одномерное инвариантное относительно подпространство (см. геометрический смысл собственных векторов).

Если — пара комплексных сопряженных корней , то собственный вектор матрицы также с комплексными элементами: . Его можно представить в виде , где — действительные столбцы. Равенство (9.6) при этом будет иметь вид

Выделяя действительную и мнимую части, получаем систему

Покажем, что столбцы и линейно независимы. Рассмотрим два случая. Если , то из первого уравнения (9.7) следует, что , так как . Тогда , что противоречит условию . Предположим, что и столбцы и пропорциональны, т.е. существует такое действительное число , что . Тогда из системы (9.7) получаем Прибавляя ко второму уравнению первое, умноженное на , приходим к равенству . Так как , то выражение в квадратных скобках равно нулю, т.е. . Поскольку , то . Этого не может быть, так как — действительное число. Получили противоречие. Таким образом, столбцы и линейно независимы.

Рассмотрим подпространство , где . Это подпространство двумерное, так как векторы линейно независимы (как показано выше, их координатные столбцы линейно независимы). Из (9.7) следует, что т.е. образ любого вектора, принадлежащего , также принадлежит . Следовательно, — двумерное подпространство, инвариантное относительно преобразования , что и требовалось доказать.

Нахождение собственных векторов и значений линейного оператора (преобразования)

Для нахождения собственных векторов и собственных значений линейного преобразования вещественного линейного пространства следует выполнить следующие действия.

1. Выбрать произвольный базис линейного пространства и найти в этом базисе матрицу преобразования .

2. Составить характеристический многочлен преобразования .

3. Найти все различные действительные корни характеристического уравнения . Комплексные (но не действительные) корни характеристического уравнения следует отбросить (см. пункт 2. замечаний 9.4).

4. Для корня найти фундаментальную систему решений однородной системы уравнений , где . Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы.

5. Записать линейно независимые собственные векторы преобразования , отвечающие собственному значению

Для нахождения совокупности всех собственных векторов, отвечающих собственному значению , образовать ненулевые линейные комбинации

где — произвольные постоянные, не равные нулю одновременно.

Повторить пункты 4, 5 для остальных собственных значений линейного преобразования .

Примеры собственных векторов линейных операторов (преобразований)

1. Для нулевого преобразования любой ненулевой вектор является собственным, соответствующим нулевому собственному значению , так как .

2. Для тождественного преобразования любой ненулевой вектор является собственным, соответствующим единичному собственному значению , так как .

3. Для центральной симметрии любой ненулевой вектор является собственным, соответствующим собственному значению , так как .

4. Для гомотетии любой ненулевой вектор является собственным, соответствующим собственному значению (коэффициенту гомотетии), так как .

5. Для поворота плоскости (при ) собственных векторов нет, так как при повороте на угол, не кратный , образ каждого ненулевого вектора неколлинеарен прообразу. Здесь рассматривается поворот вещественной плоскости, т.е. двумерного векторного пространства над полем действительных чисел.

6. Для оператора дифференцирования любой ненулевой многочлен нулевой степени (не равный тождественно нулю) является собственным вектором, соответствующим нулевому собственному значению , так как . Любой многочлен ненулевой степени не является собственным вектором, так как многочлен не пропорционален своей производной: , поскольку они имеют разные степени.

7. Рассмотрим оператор проектирования на подпространство параллельно подпространству . Здесь для . Для этого оператора любой ненулевой вектор является собственным, соответствующим собственному значению , так как , а любой ненулевой вектор является собственным, соответствующим собственному значению , так как . Другие векторы не являются собственными, так как равенство возможно либо при , либо при .

8. Рассмотрим оператор отражения на подпространство параллельно подпространству . Здесь , для . Для этого оператора любой ненулевой вектор является собственным, соответствующим собственному значению , так как , а любой ненулевой вектор является собственным, соответствующим собственному значению , так как . Другие векторы не являются собственными, так как равенство возможно либо при , либо при .

9. В пространстве радиус-векторов пространства, отложенных от фиксированной точки , рассмотрим поворот на угол , вокруг оси , заданной радиус-вектором . Любой ненулевой вектор, коллинеарный вектору , является собственным, отвечающим собственному значению . Других собственных векторов у этого преобразования нет.

Пример 9.1. Найти собственные значения и собственные векторы оператора дифференцирования , преобразующего пространство тригонометрических многочленов (частоты ):

а) с действительными коэффициентами ;

б) с комплексными коэффициентами .

Решение. 1. Выберем стандартный базис и составим в этом базисе матрицу оператора

2. Составим характеристический многочлен преобразования .

3. Характеристическое уравнение имеет комплексные сопряженные корни . Действительных корней нет, поэтому преобразование вещественного пространства (случай (а)) не имеет собственных значений, а следовательно, и собственных векторов. Преобразование комплексного пространства (случай (б)) имеет комплексные собственные значения .

4(1). Для корня находим фундаментальную систему решений однородной системы уравнений

Приведем матрицу системы к ступенчатому виду, умножая первое уравнение на и вычитая его из второго уравнения:

Выражаем базисную переменную через свободную: . Полагая , получаем , т.е. .

5(1). Записываем собственный вектор, отвечающий собственному значению . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные .

4(2). Для корня аналогично находим фундаментальную систему (состоящую из одного вектора) решений однородной системы уравнений

5(2). Записываем собственный вектор, отвечающий собственному значению . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные .

Найти собственные векторы дифференцирование

Найдем такие вектора (называются собственными векторами) v
и такие числа — значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.

Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.

Где учитесь?

Для правильного составления решения, укажите:

источники:

http://mathhelpplanet.com/static.php?p=sobstvennye-vektory-i-znacheniya-linyeinogo-operatora

http://www.kontrolnaya-rabota.ru/s/matrix/sobstvennyie/

Источник