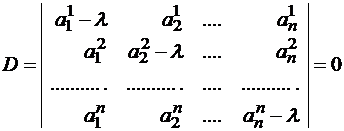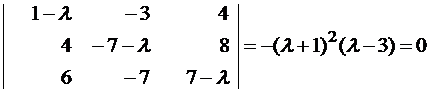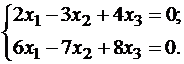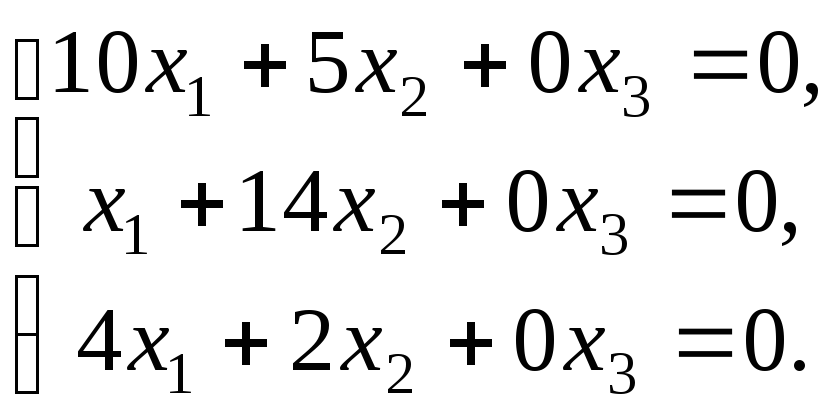Как найти собственные векторы матрицы линейного оператора - Исправление недочетов и поиск решений вместе с Examum.ru

Собственные числа и собственные векторы линейного оператора

Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.

Пусть дано линейное пространство R_n и действующий в нем линейный оператор A; в этом случае оператор A переводит R_n в себя, то есть A:R_n
→ R_n.

Определение. Ненулевой вектор x называется собственным вектором оператора A, если оператор A переводит x в коллинеарный ему вектор, то есть A·x = λ·x. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x.

Отметим некоторые свойства собственных чисел и собственных векторов.

1. Любая линейная комбинация собственных векторов x₁, x₂, …, x_m оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.

2. Собственные векторы x₁, x₂, …, x_m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m
линейно независимы.

3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x₁, x₂, …, x_n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 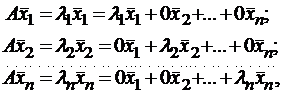тогда .

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.

Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе {ε_i} (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Пусть дан вектор x=(x₁, x₂, …, x_n), где x₁, x₂, …, x_n — координаты вектора x относительно базиса {ε₁, ε₂, …, ε_n} и x — собственный вектор линейного оператора A, соответствующий собственному числу λ, то есть A·x=λ·x. Это соотношение можно записать в матричной форме

x·(A-λ·E). (*)

Уравнение (*) можно рассматривать как уравнение для отыскания x, причем x ≠ 0, то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A — λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A — λE) = 0.

Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1)

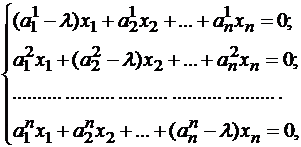
где — матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Получили уравнение для нахождения собственных чисел.

Это уравнение называется характеристическим уравнением, а его левая часть — характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.

Пусть λ₁, λ₂, …, λ_n — вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример №1. Линейный оператор A действует в R₃ по закону A·x=(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, .., x_n — координаты вектора x в базисе e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.

Решение. Строим матрицу этого оператора:

A·e₁=(1,4,6)

A·e₂=(-3,-7,-7)

A·e₃=(4,8,7)

.

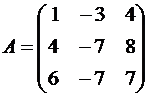
Составляем систему для определения координат собственных векторов:

(1-λ)x₁-3x₂+4x₃=0

x₁-(7+λ)x₂+8x₃=0

x₁-7x₂+(7-λ)x₃=0

Составляем характеристическое уравнение и решаем его:

λ_1,2 = -1, λ₃ = 3.

Подставляя λ = -1 в систему, имеем:

или

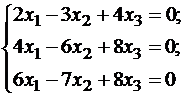
Так как 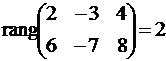, то зависимых переменных два, а свободное одно.

Пусть x₁ — свободное неизвестное, тогда 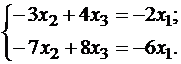Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как n — r = 3 — 2 = 1.

Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: (x₁, 2x₁, x₁)=x₁(1,2,1), где x₁ — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x₁ = 1: x₁=(1,2,1).

Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: x₂=(1,2,2).

В пространстве R₃ базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R₃ составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.

Пример №2. Дана матрица .

1. Доказать, что вектор x=(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.

2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.

1. Если A·x=λ·x, то x — собственный вектор

Вектор (1, 8, -1) — собственный вектор. Собственное число λ = -1.

Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.

Собственные векторы ищем из системы:

(2-λ)x₁+3x₃=0;

10x₁-(3+λ)x₂-6x₃=0;

-x₁-(2+λ)x₃=0;

Характеристическое уравнение: ;

(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ² — 1) = 0

λ₁ = -3, λ₂ = 1, λ₃ = -1.

Найдем собственный вектор, отвечающий собственному числу λ = -3:

5x₁+3x₃=0;

10x₁-6x₃=0;

-x₁+x₃=0;

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x₁ = x₃ = 0. x₂ здесь может быть любым, отличным от нуля, например, x₂ = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:

Если λ = 1, то получаем систему

Ранг матрицы равен двум. Последнее уравнение вычеркиваем.

Пусть x₃ — свободное неизвестное. Тогда x₁ = -3x₃, 4x₂ = 10x₁ — 6x₃ = -30x₃ — 6x₃, x₂ = -9x₃.

Полагая x₃ = 1, имеем (-3,-9,1) — собственный вектор, отвечающий собственному числу λ = 1. Проверка:

Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R₃. Таким образом, в базисе f₁=(1,8,-1), f₂=(0,1,0), f₃=(-3,-9,1) матрица A имеет вид:

.

Не всякую матрицу линейного оператора A:R_n→ R_n можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i^k=a_kⁱ.

Замечания.

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Перейти к онлайн решению своей задачи

Источник

Собственные
векторы и собственные

значения
линейного оператора

Определение 1.
Собственным
вектором оператора

называют
ненулевой вектор
,
удовлетворяющий равенству:
=.

Определение 2.
Собственным
значением оператора

называют
число
,
для которого выполняется равенство:
=,
где

— ненулевой вектор.

(1)

(2)

Решив последнее
уравнение относительно
,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
,
каждый из которых соответствует
определенному собственному значению.

Рассмотрим несколько
примеров, в каждом из которых будем
выполнять последовательность действий
решения задачи об отыскании собственных
значений и собственных векторов матрицы.

Пример 1.

Найти собственные
значения и собственные векторы матрицы
.
Дать геометрическую интерпретацию
полученного решения.

Решение

Матрица имеет
размерность 22,
то есть является представлением
линейного оператора в пространстве
.
Собственный вектор матрицы будем искать
в виде:
.
Составим уравнение
для отыскания собственных векторов в
матричном виде:

3. Перепишем
матричное уравнение в виде системы
уравнений:

Однородная система
имеет ненулевые решения тогда и только
тогда, когда определитель ее главной
матрицы равен 0. Получаем характеристическое
уравнение системы и решаем его:

Собственные
значения матрицы
:

Найдем собственные
векторы для каждого собственного
значения:

;

Пусть
,
тогда собственное направление матрицы
,
соответствующее собственному значению
,
задается множеством векторов:

,
где
.

;

,
где
.

Пример
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.

Составим и решим
характеристическое уравнение
.

В нашей задаче
.

Тогда характеристическое
уравнение принимает вид:

,
или
,

— собственные
значения линейного оператора.

Найдем собственные
векторы, соответствующие собственному
значению
,
решая матричное уравнение:

х=0
или
,
т.е.

Полагая в последнем
равенстве
,
получим
.

Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х¹=.

Найдем собственные
векторы, соответствующие собственному
значению
,
решая матричное уравнение:

х=0
или
,
т.е.

Полагая в последнем
равенстве
,
получим
.

Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х²=.

Ответ. Собственному
значению
соответствуют собственные векторы
х¹=,
а собственному значению
собственные векторы

х²=.

Пример
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.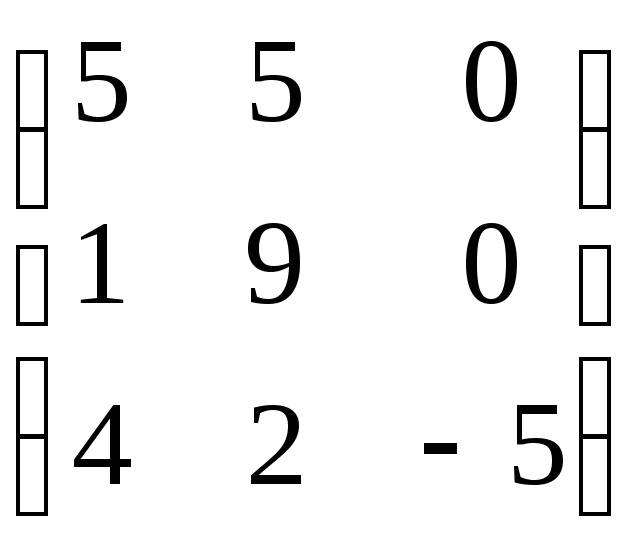

Найдем собственные
значения линейного оператора. Для этого
составим характеристическое уравнение
и найдем его корни:

,

— собственные значения линейного
оператора.

Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

,
запишем систему:

Решая методом
Гаусса, получаем

Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим
,
.

Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х¹=.

Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

,
т.е.

Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
,
получим
.

Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х²=.

Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

,
т.е.

Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
,
получим
.

Таким
образом, собственные векторы,
соответствующие собственному значению
,
имеют вид: Х³=.

Соседние файлы в папке Математика

Источник

Собственные векторы и значения линейного оператора (преобразования)

Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного линейного пространства . Ненулевой вектор boldsymbol{s} линейного пространства , удовлетворяющий условию

mathcal{A}(boldsymbol{s})=lambdacdot boldsymbol{s},

(9.5)

называется собственным вектором линейного преобразования mathcal{A} . Число lambda в равенстве (9.5) называется собственным значением преобразования . Говорят, что собственный вектор соответствует (принадлежит) собственному значению lambda . Если пространство вещественное (комплексное), то собственное значение lambda — действительное (комплексное) число.

Множество всех собственных значений линейного преобразования называется его спектром.

Поясним геометрический смысл собственных векторов. Ненулевой вектор s является собственным для преобразования mathcal{A} , если его образ mathcal{A} (boldsymbol{s}) коллинеарен прообразу . Другими словами, если — собственный вектор, то преобразование имеет одномерное инвариантное подпространство operatorname{Lin}(boldsymbol{s}) . Справедливо и обратное утверждение.

В самом деле, пусть собственный вектор boldsymbol{s} соответствует некоторому собственному значению lambda . Любой вектор boldsymbol{v} из operatorname{Lin}(boldsymbol{s}) имеет вид boldsymbol{v}=alpha boldsymbol{s} , где alpha — любое число из заданного поля. Найдем образ этого вектора

mathcal{A}(boldsymbol{v})= mathcal{A}(alpha boldsymbol{s})= alphacdot mathcal{A}(boldsymbol{s})= alphacdot lambdacdot boldsymbol{s}in operatorname{Lin} (boldsymbol{s}).

Следовательно, mathcal{A}(boldsymbol{v})in operatorname{Lin}(boldsymbol{s}) для любого вектора boldsymbol{v}in operatorname{Lin}(boldsymbol{s}) , т.е. подпространство инвариантно относительно преобразования . Размерность подпространства operatorname{Lin} (boldsymbol{s}) равна единице, так как boldsymbol{s}ne boldsymbol{o} по определению.

Обратное утверждение доказывается, проводя рассуждения в обратном порядке.

Связь собственных векторов линейного преобразования (оператора) и его матрицы

Ранее рассматривались собственные векторы и собственные значения матрицы. Напомним, что собственным вектором квадратной матрицы n-го порядка называется ненулевой числовой столбец $s=begin{pmatrix}s_1&cdots&s_{n}end{pmatrix}^T$ , удовлетворяющий условию (7.13):

Acdot s=lambdacdot s.

(9.6)

Число lambda в (9.6) называется собственным значением матрицы . При этом считалось, что собственное значение lambda и числа s_i~(i=1,ldots,n) принадлежат полю комплексных чисел.

Эти понятия связаны с собственными векторами и собственными значениями линейного преобразования.

Теорема 9.3 о собственных векторах линейного преобразования и его матрицы. Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного линейного пространства с базисом $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ . Тогда собственное значение lambda и координатный столбец {s} собственного вектора boldsymbol{s} преобразования mathcal{A} являются собственным значением и собственным вектором матрицы этого преобразования, определенной относительно базиса $boldsymbol{e}_1,ldots, boldsymbol{e}_n$ , т.е.

mathcal{A}(boldsymbol{s})=lambdacdot boldsymbol{s}quad Rightarrowquad Acdot s=lambdacdot s, где $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n,~ s=begin{pmatrix}s_1&cdots& s_nend{pmatrix}^T.$

Обратное утверждение справедливо при дополнительных условиях: если столбец $s=begin{pmatrix} s_1&cdots&s_nend{pmatrix}^T$ и число lambda являются собственным вектором и собственным значением матрицы , причем числа s_1,ldots,s_n,lambda принадлежат тому же числовому полю, над которым определено линейное пространство , то вектор $boldsymbol{s}=s_1 boldsymbol{e}_1+ ldots+s_n boldsymbol{e}_n$ и число lambda являются собственным вектором и собственным значением линейного преобразования mathcal{A}colon Vto V с матрицей в базисе $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ .

В самом деле, условие (9.5) в координатной форме имеет вид (9.6), что совпадает с определением (7.13) собственного вектора матрицы. Наоборот, из равенства (9.6) следует равенство (9.5) при условии, что векторы $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n$ и lambdacdot boldsymbol{s} определены, т.е. числа s_1,ldots,s_n, lambda принадлежат тому же числовому полю, над которым определено линейное пространство.

Напомним, что нахождение собственных значений матрицы сводится к решению ее характеристического уравнения Delta_A(lambda)=0 , где Delta_A(lambda)=det(A-lambda E) — характеристический многочлен матрицы . Для линейного преобразования введем аналогичные понятия.

Характеристическим многочленом линейного преобразования mathcal{A}colon Vto V n-мерного линейного пространства называется характеристический многочлен $Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ матрицы этого преобразования, найденной относительно любого базиса пространства .

Уравнение $Delta_{mathcal{A}}(lambda)=0$ называется характеристическим уравнением линейного преобразования.

Преобразование mathcal{A}-lambdamathcal{E} называется характеристическим для линейного преобразования mathcal{A}colon Vto V .

Замечания 9.4

1. Характеристический многочлен линейного преобразования не зависит от базиса, в котором найдена матрица преобразования.

В самом деле, матрицы $mathop{A}limits_{(boldsymbol{e})}$ и $mathop{A}limits_{(boldsymbol{f})}$ линейного преобразования mathcal{A} в базисах $(boldsymbol{e})= (boldsymbol{e}_1,ldots, boldsymbol{e}_n)$ и $(boldsymbol{f})=(boldsymbol{f}_1,ldots,boldsymbol{f}_n)$ являются, согласно (9.4), подобными: $mathop{A}limits_{(boldsymbol{f})}=S^{-1}mathop{A}limits_{(boldsymbol{e})}S$ , где — матрица перехода от базиса к базису . Как показано ранее, характеристические многочлены подобных матриц совпадают (см. свойство 3). Поэтому для характеристического многочлена преобразования mathcal{A} можно использовать обозначение $Delta_{mathcal{A}}(lambda)$ , не указывая матрицу этого преобразования.

2. Из теоремы 9.3 следует, что любой комплексный (действительный, рациональный) корень характеристического уравнения является собственным значением линейного преобразования mathcal{A}colon Vto V линейного пространства , определенного над полем комплексных (действительных, рациональных) чисел.

3. Из теоремы 9.3 следует, что любое линейное преобразование комплексного линейного пространства имеет одномерное инвариантное подпространство, так как это преобразование имеет собственное значение (см. пункт 2), а следовательно, и собственные векторы. Таким подпространством является, например, линейная оболочка любого собственного вектора. У преобразования вещественного линейного пространства одномерных инвариантных подпространств может и не быть, если все корни характеристического уравнения комплексные (но не действительные).

Теорема 9.4 об инвариантных подпространствах линейного оператора вещественного пространства. У всякого линейного преобразования вещественного линейного пространства существует одномерное или двумерное инвариантное подпространство.

Действительно, составим матрицу линейного преобразования mathcal{A}colon Vto V n-мерного вещественного линейного пространства в произвольном базисе $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ . Элементы этой матрицы — действительные числа. Следовательно, характеристический многочлен $Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ — это многочлен степени с действительными коэффициентами. Согласно следствиям 3, 4 основной теоремы алгебры, такой многочлен может иметь действительные корни и пары комплексных сопряженных корней.

Если lambda=lambda_1 — действительный корень характеристического уравнения, то и соответствующий собственный вектор $s=begin{pmatrix}s_1&cdots&s_nend{pmatrix}^T$ матрицы также действительный. Поэтому он определяет собственный вектор $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n$ линейного преобразования (см. теорему 9.3). В этом случае существует одномерное инвариантное относительно mathcal{A} подпространство operatorname{Lin}(boldsymbol{s}) (см. геометрический смысл собственных векторов).

Если lambda=alphapmbeta i — пара комплексных сопряженных корней (betane0) , то собственный вектор sne o матрицы также с комплексными элементами: $s=begin{pmatrix}x_1+y_1i&cdots& x_n+y_n i end{pmatrix}^T$ . Его можно представить в виде s=x+yi , где x,,y — действительные столбцы. Равенство (9.6) при этом будет иметь вид

Acdot(x+yi)= (alpha+beta i)cdot(x+yi).

Выделяя действительную и мнимую части, получаем систему

$begin{cases}Ax=alpha x-beta y,\ Ay=beta x+alpha y.end{cases}$

(9.7)

Покажем, что столбцы {x} и {y} линейно независимы. Рассмотрим два случая. Если x=o , то из первого уравнения (9.7) следует, что y=o , так как betane0 . Тогда s=o , что противоречит условию sne o . Предположим, что xne o и столбцы и пропорциональны, т.е. существует такое действительное число gamma , что y=gamma x . Тогда из системы (9.7) получаем $begin{cases}Ax=(alpha-betagamma)x,\ gamma Ax=(beta-alphagamma)x. end{cases}$ Прибавляя ко второму уравнению первое, умноженное на (-gamma) , приходим к равенству [(beta+alphagamma)-gamma(alpha-betagamma)]x=o . Так как xne o , то выражение в квадратных скобках равно нулю, т.е. (beta+alphagamma)- gamma(alpha- betagamma)= beta(1+gamma^2)=0 . Поскольку betane0 , то gamma^2=-1 . Этого не может быть, так как gamma — действительное число. Получили противоречие. Таким образом, столбцы и линейно независимы.

Рассмотрим подпространство operatorname{Lin}(boldsymbol{x},boldsymbol{y}) , где $boldsymbol{x}= x_1 boldsymbol{e}_1+ldots+x_n boldsymbol{e}_n,~ boldsymbol{y}= y_1 boldsymbol{e}_1+ldots+ y_n boldsymbol{y}_n$ . Это подпространство двумерное, так как векторы линейно независимы (как показано выше, их координатные столбцы x,y линейно независимы). Из (9.7) следует, что $begin{cases}mathcal{A}(boldsymbol{x})=alpha boldsymbol{x}-beta boldsymbol{y},\ mathcal{A}(boldsymbol{y})=beta boldsymbol{x}+alpha boldsymbol{y},end{cases}$ т.е. образ любого вектора, принадлежащего operatorname{Lin}(boldsymbol{x},boldsymbol{y}) , также принадлежит . Следовательно, — двумерное подпространство, инвариантное относительно преобразования mathcal{A} , что и требовалось доказать.

Нахождение собственных векторов и значений линейного оператора (преобразования)

Для нахождения собственных векторов и собственных значений линейного преобразования mathcal{A}colon Vto V вещественного линейного пространства следует выполнить следующие действия.

1. Выбрать произвольный базис $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ линейного пространства и найти в этом базисе матрицу преобразования mathcal{A} .

2. Составить характеристический многочлен преобразования $mathcal{A}colon, Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ .

3. Найти все различные действительные корни lambda_1,ldots,lambda_k характеристического уравнения $Delta_{mathcal{A}}(lambda)=0$ . Комплексные (но не действительные) корни характеристического уравнения следует отбросить (см. пункт 2. замечаний 9.4).

4. Для корня lambda=lambda_1 найти фундаментальную систему $varphi_1, varphi_2,ldots,varphi_{n-r}$ решений однородной системы уравнений (A-lambda_1E)x=o , где $r=operatorname{rg}(A-lambda_1E)$ . Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы.

5. Записать линейно независимые собственные векторы преобразования mathcal{A} , отвечающие собственному значению lambda_1:

$begin{matrix} boldsymbol{s}_1=varphi_{1,1}boldsymbol{e}_1+ ldots+ varphi_{n,1}boldsymbol{e}_n,\ boldsymbol{s}_2=varphi_{1,2}boldsymbol{e}_1+ ldots+ varphi_{n,2}boldsymbol{e}_n,\ vdots\ boldsymbol{s}_{n-r}=varphi_{1,n-r} boldsymbol{e}_1+ ldots+varphi_{n,n-r}boldsymbol{e}_n. end{matrix}$

Для нахождения совокупности всех собственных векторов, отвечающих собственному значению lambda_1 , образовать ненулевые линейные комбинации

$boldsymbol{s}= C_1 boldsymbol{s}_1+C_2 boldsymbol{s}_2+ldots+ C_{n-r}boldsymbol{s}_{n-r},$

где $C_1,C_2,ldots,C_{n-r}$ — произвольные постоянные, не равные нулю одновременно.

Повторить пункты 4, 5 для остальных собственных значений lambda_2,ldots,lambda_k линейного преобразования mathcal{A} .

Для нахождения собственных векторов линейного преобразования комплексного линейного пространства нужно в пункте 3 определить все корни характеристического уравнения и, не отбрасывая комплексные корни, выполнить для них пункты 4,5.

Примеры собственных векторов линейных операторов (преобразований)

1. Для нулевого преобразования mathcal{O}colon Vto V любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим нулевому собственному значению lambda=0 , так как mathcal{O}(boldsymbol{s})=0cdot boldsymbol{s}~ forall boldsymbol{s}in V .

2. Для тождественного преобразования mathcal{E}colon Vto V любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим единичному собственному значению lambda=1 , так как mathcal{E} (boldsymbol{s})=1cdot boldsymbol{s}~ forall boldsymbol{s}in V .

3. Для центральной симметрии $mathcal{Z}_{boldsymbol{o}}colon Vto V$ любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим собственному значению lambda=-1 , так как $mathcal{Z}_{boldsymbol{o}} (boldsymbol{s})=(-1)cdot boldsymbol{s}~ forall boldsymbol{s}in V$ .

4. Для гомотетии $mathcal{H}_{lambda}colon Vto V$ любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим собственному значению lambda (коэффициенту гомотетии), так как $mathcal{H}_{lambda} (boldsymbol{boldsymbol{s}})= lambdacdot boldsymbol{s}~ forall boldsymbol{s}in V$ .

5. Для поворота $mathcal{R}_{varphi}colon V_2to V_2$ плоскости (при varphinepi k,~ kinmathbb{Z} ) собственных векторов нет, так как при повороте на угол, не кратный , образ каждого ненулевого вектора неколлинеарен прообразу. Здесь рассматривается поворот вещественной плоскости, т.е. двумерного векторного пространства над полем действительных чисел.

6. Для оператора дифференцирования $mathcal{D}colon P_n(mathbb{R})to P_n(mathbb{R})$ любой ненулевой многочлен нулевой степени (не равный тождественно нулю) является собственным вектором, соответствующим нулевому собственному значению lambda=0 , так как mathcal{D}(s(x))=0cdot s(x) forall s(x)equiv text{const} . Любой многочлен ненулевой степени не является собственным вектором, так как многочлен не пропорционален своей производной: mathcal{D}(s(x))=s'(x)ne lambdacdot s(x) , поскольку они имеют разные степени.

7. Рассмотрим оператор $Pi_{L_1}colon Vto V$ проектирования на подпространство L_1 параллельно подпространству L_2 . Здесь V=L_1oplus L_2, $Pi_{L_1}(boldsymbol{v}_1+ boldsymbol{v}_2)=boldsymbol{v}_1$ для $boldsymbol{v}=boldsymbol{v}_1+boldsymbol{v}_2,$ $boldsymbol{v}_1in L_1,~ boldsymbol{v}_2in L_2$ . Для этого оператора любой ненулевой вектор $boldsymbol{v}_1in L_1$ является собственным, соответствующим собственному значению lambda=1 , так как $Pi_{L_1}(boldsymbol{v}_1)=1cdot boldsymbol{v}_1$ , а любой ненулевой вектор $boldsymbol{v}_2in L_2$ является собственным, соответствующим собственному значению lambda=0 , так как $Pi_{L_2}(boldsymbol{v}_2)=0cdot boldsymbol{v}_2$ . Другие векторы не являются собственными, так как равенство $Pi_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1= lambda(boldsymbol{v}_1+boldsymbol{v}_2)$ возможно либо при $boldsymbol{v}_1=boldsymbol{o}$ , либо при $boldsymbol{v}_2= boldsymbol{o}$ .

8. Рассмотрим оператор $mathcal{Z}_{L_1}colon Vto V$ отражения на подпространство L_1 параллельно подпространству L_2 . Здесь V=L_1oplus L_2 $mathcal{Z}_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1- boldsymbol{v}_2$ , для $boldsymbol{v}=boldsymbol{v}_1+boldsymbol{v}_2,$ $boldsymbol{v}_1in L_1,~ boldsymbol{v}_2in L_2$ . Для этого оператора любой ненулевой вектор $boldsymbol{v}_1in L_1$ является собственным, соответствующим собственному значению lambda=1 , так как $mathcal{Z}_{L_1} (boldsymbol{v}_1)= 1cdot boldsymbol{v}_1$ , а любой ненулевой вектор $boldsymbol{v}_2in L_2$ является собственным, соответствующим собственному значению lambda=-1 , так как $mathcal{Z}_{L_2} (boldsymbol{v}_2)= (-1)cdot boldsymbol{v}_2$ . Другие векторы не являются собственными, так как равенство $mathcal{Z}_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1- boldsymbol{v}_2= lambda(boldsymbol{}_1+ boldsymbol{v}_2)$ возможно либо при $boldsymbol{v}_1=boldsymbol{o}$ , либо при $boldsymbol{v}_2= boldsymbol{o}$ .

9. В пространстве V_3 радиус-векторов пространства, отложенных от фиксированной точки , рассмотрим поворот на угол varphinepi k,~ kinmathbb{Z} , вокруг оси ell , заданной радиус-вектором vec{ell} . Любой ненулевой вектор, коллинеарный вектору , является собственным, отвечающим собственному значению lambda=1 . Других собственных векторов у этого преобразования нет.

Пример 9.1. Найти собственные значения и собственные векторы оператора дифференцирования $mathcal{D}colon T_1to T_1$ , преобразующего пространство тригонометрических многочленов (частоты omega=1 ):

а) с действительными коэффициентами $T_1=T_1(mathbb{R})= operatorname{Lin} (sin{t},cos{t})$ ;

б) с комплексными коэффициентами $T_1=T_1(mathbb{C})= operatorname{Lin} (sin{t},cos{t})$ .

Решение. 1. Выберем стандартный базис $e_1(t)=sin{t},~ e_2(t)=cos{t}$ и составим в этом базисе матрицу оператора mathcal{D}:

$D=begin{pmatrix}0&-1\ 1&0 end{pmatrix}!.$

2. Составим характеристический многочлен преобразования $mathcal{D}colon, Delta_{mathcal{D}}(lambda)= begin{vmatrix}-lambda&-1\ 1&-lambdaend{vmatrix}= lambda^2+1.$ .

3. Характеристическое уравнение lambda^2+1=0 имеет комплексные сопряженные корни lambda_1=i,~ lambda_2=-i . Действительных корней нет, поэтому преобразование mathcal{D} вещественного пространства $T_1(mathbb{R})$ (случай (а)) не имеет собственных значений, а следовательно, и собственных векторов. Преобразование комплексного пространства $T_1(mathbb{C})$ (случай (б)) имеет комплексные собственные значения lambda_1,,lambda_2 .

4(1). Для корня lambda_1=i находим фундаментальную систему varphi_1 решений однородной системы уравнений (D-lambda_1 E)x=o:

$begin{pmatrix}-i&-1\ 1&-iend{pmatrix}!cdot! begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Приведем матрицу системы к ступенчатому виду, умножая первое уравнение на {i} и вычитая его из второго уравнения:

$begin{pmatrix}-i&-1\ 1&-i end{pmatrix}sim begin{pmatrix}1&-i\ 1&-i end{pmatrix}sim begin{pmatrix}1&-i\ 0&0end{pmatrix}!.$

Выражаем базисную переменную x_1 через свободную: x_1=ix_2 . Полагая x_2=1 , получаем x_1=i , т.е. $varphi=begin{pmatrix}i&1 end{pmatrix}^T$ .

5(1). Записываем собственный вектор, отвечающий собственному значению $lambda_1= icolon, s_1(t)=icdotsin{t}+1cdotcos{t}$ . Совокупность всех собственных векторов, отвечающих собственному значению lambda_1=i , образуют ненулевые функции, пропорциональные s_1(t) .

4(2). Для корня lambda_2=-i аналогично находим фундаментальную систему (состоящую из одного вектора) $varphi_2=begin{pmatrix}-i&1 end{pmatrix}^T$ решений однородной системы уравнений (D-lambda_2E)x=o:

$begin{pmatrix}i&-1\ 1&i end{pmatrix}!cdot! begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

5(2). Записываем собственный вектор, отвечающий собственному значению $lambda_2=-icolon, s_2(t)=-icdotsin{t}+1cdotcos{t}$ . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные s_2(t) .

См. также Свойства собственных векторов линейных операторов (преобразований)

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 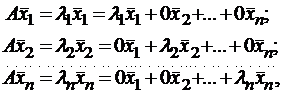тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)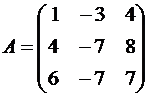
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

5.1.3. Собственные числа и собственные векторы матрицы

Вектор Х называется Собственным вектором матрицы А, если найдется такое число L, что выполняется равенство: АХ = LХ, то есть результатом применения к Х линейного оператора, задаваемого матрицей А, является умножение этого вектора на число L. Само число L называется Собственным числом матрицы А.

Подставив в формулы (3) X’J = LXj, получим систему уравнений для определения координат собственного вектора:

Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

Получим уравнение для определения собственных чисел L, называемое Характеристическим уравнением. Кратко его можно представить так:

Поскольку в его левой части стоит определитель матрицы А-LЕ. Многочлен относительно L | A — LE| называется Характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

1) Характеристический многочлен линейного преобразования не зависит от выбора базиса.

(см. (11.4)), но Следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A—LE| не изменяется при переходе к новому базису.

2) Если матрица А линейного оператора является Симметрической (т. е. АIj=Aji), то все корни характеристического уравнения (11.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов Х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

Доказательство этого свойства следует из определения собственных векторов.

2) Если собственные значения оператора А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

Найдем собственные числа и собственные векторы матрицы

Составим характеристическое уравнение:

Найдем координаты собственных векторов, соответствующих каждому найденному значению L. Из (5) следует, что если Х(1)=<X1,X2,X3> – собственный вектор, соответствующий L1=-2, то

Совместная, но неопределенная система. Ее решение можно записать в виде Х(1)=(A,0,-A), где А – любое число. В частности, если потребовать, чтобы |X(1)|=1,

Подставив в систему (5) L2=3, получим систему для определения координат второго собственного вектора — X(2)=(Y1,Y2,Y3):

Спектральная кластеризация

Дата публикации Feb 21, 2019

Введение

В этом посте мы рассмотрим тонкости спектральной кластеризации для графиков и других данных. Кластеризация является одной из главных задач в машинном обучении без учителя. Цель состоит в том, чтобы назначить немаркированные данные группам, где, возможно, аналогичные точки данных будут назначены в одну группу.

Спектральная кластеризация — это метод с корнями в теории графов, где этот подход используется для идентификации сообществ узлов в графе на основе соединяющих их ребер. Этот метод является гибким и позволяет кластеризовать не графовые данные.

Спектральная кластеризация использует информацию из собственных значений (спектра) специальных матриц, построенных из графика или набора данных. Мы узнаем, как построить эти матрицы, интерпретировать их спектр и использовать собственные векторы для назначения наших данных кластерам.

Собственные векторы и собственные значения

Критическим для этой дискуссии является концепция собственных значений и собственные векторы. Для матрицы A, если существует вектор x, который не является всеми 0 и скалярным λ, таким, что Ax = λx, то x называется собственным вектором A с соответствующим собственным значением λ.

Мы можем думать о матрице A как о функции, которая отображает векторы на новые векторы. Большинство векторов окажутся где-то совершенно разными, когда к ним будет применен A, но собственные векторы меняются только по величине. Если вы проведете линию через начало координат и собственный вектор, то после отображения собственный вектор все равно попадет на линию. Величина, по которой вектор масштабируется вдоль линии, зависит от λ.

Мы можем легко найти собственные значения и собственные векторы матрицы, используя numpy в Python:

Собственные векторы являются важной частью линейной алгебры, потому что они помогают описать динамику систем, представленных матрицами. Существует множество приложений, в которых используются собственные векторы, и мы будем использовать их непосредственно здесь для выполнения спектральной кластеризации.

диаграммы

Графики являются естественным способом представления многих типов данных. Граф — это набор узлов с соответствующим набором ребер, которые соединяют узлы. Края могут быть направленными или ненаправленными и даже иметь веса, связанные с ними.

Сеть роутеров в интернете легко представить в виде графика. Маршрутизаторы — это узлы, а ребра — это соединения между парами маршрутизаторов. Некоторые маршрутизаторы могут разрешать трафик только в одном направлении, поэтому границы могут быть направлены в направлении направления трафика. Веса на краях могут представлять полосу пропускания, доступную вдоль этого края. При такой настройке мы могли бы затем запросить график, чтобы найти эффективные пути для передачи данных от одного маршрутизатора к другому по сети.

Давайте использовать следующий неориентированный граф в качестве рабочего примера:

Этот граф имеет 10 узлов и 12 ребер. Он также имеет два соединенных компонента <0,1,2,8,9>и <3,4,5,6,7>. Связанный компонент — это максимальный подграф узлов, у всех из которых есть пути к остальным узлам подграфа.

Связанные компоненты кажутся важными, если наша задача — назначить эти узлы сообществам или кластерам. Простая идея — сделать каждый связанный компонент отдельным кластером. Это кажется разумным для нашего примера графа, но возможно, что весь граф может быть связан, или что связанные компоненты очень велики. Могут также быть меньшие структуры в связанном компоненте, которые являются хорошими кандидатами для сообществ. Вскоре мы увидим важность идеи связанного компонента для спектральной кластеризации.

Матрица смежности

Мы можем представить наш примерный граф в виде матрицы смежности, где индексы строк и столбцов представляют узлы, а записи представляют отсутствие или наличие ребра между узлами. Матрица смежности для нашего примера графа выглядит следующим образом:

В матрице мы видим, что строка 0, столбец 1 имеет значение 1. Это означает, что существует ребро, соединяющее узел 0 с узлом 1. Если ребра были взвешены, веса ребер были бы в этой матрице вместо только 1 и 0. Так как наш график не направлен, записи для строки i, col j будут равны записи в строке j, col i. Последнее, что следует отметить, это то, что диагональ этой матрицы равна 0, поскольку ни один из наших узлов не имеет ребер.

Степень Матрица

Степень узла — это количество ребер, соединенных с ним. В ориентированном графе мы могли бы говорить о степени и степени, но в этом примере у нас просто есть степень, так как ребра идут в обе стороны. Глядя на наш график, мы видим, что узел 0 имеет степень 4, поскольку он имеет 4 ребра. Мы также можем получить степень, взяв сумму строки узла в матрице смежности.

Матрица степеней — это диагональная матрица, где значение на входе (i, i) является степенью узла i Давайте найдем матрицу степеней для нашего примера:

Сначала мы взяли сумму по оси 1 (строки) нашей матрицы смежности, а затем поместили эти значения в диагональную матрицу. Из матрицы степеней мы легко видим, что узлы 0 и 5 имеют 4 ребра, в то время как остальные узлы имеют только 2.

График лапласианский

Теперь мы собираемся вычислить граф Лапласа. Лапласиан — это просто еще одно матричное представление графа. У него есть несколько прекрасных свойств, которыми мы воспользуемся для спектральной кластеризации. Чтобы вычислить нормальный лапласиан (есть несколько вариантов), мы просто вычитаем матрицу смежности из нашей матрицы степеней:

Диагональ лапласиана — это степень наших узлов, а вне диагонали — вес отрицательного края. Это представление, которое мы ищем для выполнения спектральной кластеризации.

Собственные значения графа лапласиана

Как уже упоминалось, лапласиан обладает некоторыми прекрасными свойствами. Чтобы понять это, давайте рассмотрим собственные значения, связанные с лапласианом, когда я добавлю ребра в наш граф:

Мы видим, что когда граф полностью отключен, все десять наших собственных значений равны 0. Когда мы добавляем ребра, некоторые из наших собственных значений увеличиваются. Фактически, число собственных значений 0 соответствует числу связанных компонент в нашем графе!

Посмотрите внимательно, как добавлен этот последний край, соединяя два компонента в один. Когда это происходит, все собственные значения, кроме одного, были отменены:

Первое собственное значение равно 0, потому что у нас есть только один связный компонент (весь граф связен). Соответствующий собственный вектор всегда будет иметь постоянные значения (в этом примере все значения близки к 0,32).

Первое ненулевое собственное значение называется спектральной щелью. Спектральная щель дает нам некоторое представление о плотности графика. Если бы этот граф был плотно связан (все пары из 10 узлов имели ребро), то спектральный разрыв был бы 10.

Второе собственное значение называется значением Фидлера, а соответствующий вектор является вектором Фидлера. Значение Фидлера приблизительно соответствует минимальному срезу графа, необходимому для разделения графа на два связанных компонента. Напомним, что если бы в нашем графе уже было два связанных компонента, то значение Фидлера было бы равно 0. Каждое значение в векторе Фидлера дает нам информацию о том, какой стороне разреза принадлежит этот узел. Давайте раскрасим узлы в зависимости от того, положительна ли их запись в векторе Филдера:

Этот простой трюк разделил наш график на две группы! Почему это работает? Помните, что нулевые собственные значения представляют связанные компоненты. Собственные значения около нуля говорят нам, что существует почти разделение двух компонентов. Здесь у нас есть одно преимущество: если бы его не было, у нас было бы два отдельных компонента. Таким образом, второе собственное значение мало.

Подводя итог, что мы знаем до сих пор: первое собственное значение 0, потому что у нас есть один связанный компонент. Второе собственное значение около 0, потому что мы на расстоянии одного края от двух соединенных компонентов. Мы также видели, что вектор, связанный с этим значением, говорит нам, как разделить узлы на эти приблизительно связанные компоненты.

Возможно, вы заметили, что следующие два собственных значения также довольно малы. Это говорит нам о том, что мы «близки» к четырем отдельным подключенным компонентам. В общем, мы часто ищем первый большой разрыв между собственными значениями, чтобы найти число кластеров, выраженных в наших данных. Видите разрыв между собственными значениями четыре и пять?

Наличие четырех собственных значений перед разрывом указывает на то, что, вероятно, существует четыре кластера. Векторы, связанные с первыми тремя положительными собственными значениями, должны дать нам информацию о том, какие три разреза необходимо сделать на графике, чтобы назначить каждый узел одному из четырех приближенных компонентов. Давайте построим матрицу из этих трех векторов и выполним кластеризацию K-средних для определения назначений:

График был сегментирован на четыре квадранта, причем узлы 0 и 5 произвольно назначены одному из их связанных квадрантов. Это действительно круто, и это спектральная кластеризация!

Подводя итог, мы сначала взяли наш граф и построили матрицу смежности. Затем мы создали лапласиан графа, вычтя матрицу смежности из матрицы степеней. Собственные значения лапласиана указывали на наличие четырех кластеров. Векторы, связанные с этими собственными значениями, содержат информацию о том, как сегментировать узлы. Наконец, мы выполнили K-средства для этих векторов, чтобы получить метки для узлов. Далее мы увидим, как это сделать для произвольных данных.

Спектральная кластеризация произвольных данных

Посмотрите на данные ниже. Точки нарисованы из двух концентрических кругов с добавлением шума Нам бы хотелось, чтобы алгоритм позволял группировать эти точки в два круга, которые их генерировали.

Эти данные не в форме графика. Итак, во-первых, давайте просто попробуем алгоритм обрезки печенья, такой как K-Means. K-Means найдет два центроида и пометит точки, в зависимости от того, к какому центроиду они ближе всего. Вот результаты:

Очевидно, K-Means не собирался работать. Он действует на евклидовом расстоянии и предполагает, что скопления примерно сферические. Эти данные (и часто данные реального мира) нарушают эти предположения. Давайте попробуем решить эту проблему с помощью спектральной кластеризации.

График ближайших соседей

Есть несколько способов обработать наши данные как график. Самый простой способ — построить граф k-ближайших соседей. Граф k-ближайших соседей обрабатывает каждую точку данных как узел в графе. Затем ребро рисуется от каждого узла до его k ближайших соседей в исходном пространстве. Как правило, алгоритм не слишком чувствителен к выбору k. Меньшие числа, такие как 5 или 10, обычно работают довольно хорошо.

Посмотрите на изображение данных еще раз и представьте, что каждая точка связана со своими 5 ближайшими соседями. Любая точка во внешнем кольце должна быть в состоянии следовать по пути вдоль кольца, но во внутреннем круге не будет никаких путей. Довольно легко увидеть, что этот график будет иметь два связанных компонента: внешнее кольцо и внутренний круг.

Поскольку мы разделяем эти данные только на два компонента, мы должны использовать наш векторный метод Фидлера ранее. Вот код, который я использовал для спектральной кластеризации этих данных:

И вот результаты:

Другие подходы

Граф ближайших соседей — хороший подход, но он основан на том факте, что «близкие» точки должны принадлежать одному кластеру. В зависимости от ваших данных, это может быть не так. Более общий подход заключается в построении аффинной матрицы. Матрица сходства похожа на матрицу смежности, за исключением того, что значение для пары точек показывает, насколько эти точки похожи друг на друга. Если пары точек сильно различаются, то сродство должно быть 0. Если точки идентичны, то сродство может быть 1. Таким образом, сродство действует как вес для ребер нашего графа.

Как решить, что означает совпадение двух точек данных, является одним из наиболее важных вопросов в машинном обучении. Часто знание предметной области — лучший способ построить меру подобия. Если у вас есть доступ к экспертам по доменам, задайте им этот вопрос.

Есть также целые поля, посвященные изучению того, как строить метрики подобия непосредственно из данных. Например, если у вас есть некоторые помеченные данные, вы можете обучить классификатор, чтобы предсказать, похожи ли два входа или нет, основываясь на том, имеют ли они одинаковую метку. Затем этот классификатор можно использовать для присвоения сходства парам немаркированных точек.

Вывод

Мы рассмотрели теорию и применение спектральной кластеризации для графов и произвольных данных. Спектральная кластеризация — это гибкий подход для поиска кластеров, когда ваши данные не соответствуют требованиям других распространенных алгоритмов.

Сначала мы сформировали график между нашими точками данных. Края графика отражают сходство точек. Собственные значения графа лапласиана могут затем использоваться для поиска наилучшего числа кластеров, а собственные векторы могут использоваться для поиска фактических меток кластеров.

Я надеюсь, что вам понравился этот пост, и вы нашли спектральную кластеризацию полезной в вашей работе или исследовании.

источники:

http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/5-1-3-sobstvennye-chisla-i-sobstvennye-vektory-matritcy

http://www.machinelearningmastery.ru/spectral-clustering-aba2640c0d5b/

Источник

Собственные числа и вектора матриц. Методы их нахождения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Пусть число $lambda$ и вектор $xin L, xneq 0$ таковы, что $$Ax=lambda x.qquadqquadqquadqquadqquad(1)$$ Тогда число $lambda$ называется собственным числом линейного оператора $A,$ а вектор $x$ собственным вектором этого оператора, соответствующим собственному числу $lambda.$

В конечномерном пространстве $L_n$ векторное равенство (1) эквивалентно матричному равенству $$(A-lambda E)X=0,,,,, Xneq 0.qquadqquadquadquad (2)$$

Отсюда следует, что число $lambda$ есть собственное число оператора $A$ в том и только том случае, когда детерминант $det(A-lambda E)=0,$ т. е. $lambda$ есть корень многочлена $p(lambda)=det(A-lambda E),$ называемого характеристическим многочленом оператора $A.$ Столбец координат $X$ любого собственного вектора соответствующего собственному числу $lambda$ есть нетривиальное решение однородной системы (2).

Примеры.

Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.

4.134. $A=begin{pmatrix}2&-1&2\5&-3&3\-1&0&-2end{pmatrix}.$

Решение.

Найдем собственные вектора заданного линейного оператора. Число $lambda$ есть собственное число оператора $A$ в том и только том случае, когда $det(A-lambda E)=0.$ Запишем характеристическое уравнение:

$$A-lambda E=begin{pmatrix}2&-1&2\5&-3&3\-1&0&-2end{pmatrix}-lambdabegin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=$$ $$=begin{pmatrix}2-lambda&-1&2\5&-3-lambda&3\-1&0&-2-lambdaend{pmatrix}.$$

$$det(A-lambda E)=begin{vmatrix}2-lambda&-1&2\5&-3-lambda&3\-1&0&-2-lambdaend{vmatrix}=$$ $$=(2-lambda)(-3-lambda)(-2-lambda)+3+2(-3-lambda)+5(-2-lambda)=$$ $$=-lambda^3-3lambda^2+4lambda+12+3-6-2lambda-10-5lambda=-lambda^3-3lambda^2-3lambda-1=0.$$

Решим найденное уравнение, чтобы найти собственные числа.

$$lambda^3+3lambda^2+3lambda+1=(lambda^3+1)+3lambda(lambda+1)=$$ $$=(lambda+1)(lambda^2-lambda+1)+3lambda(lambda+1)=(lambda+1)(lambda^2-lambda+1+3lambda)=$$ $$=(lambda+1)(lambda^2+2lambda+1)=(lambda+1)^3=0Rightarrow lambda=-1.$$

Собственный вектор для собственного числа $lambda=-1$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A+E)X=0, Xneq 0$$

$$(A+E)X=begin{pmatrix}2+1&-1&2\5&-3+1&3\-1&0&-2+1end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}3x_1-x_2+2x_3\5x_1-2x_2+3x_3\-x_1-x_3end{pmatrix}=0.$$

Решим однородную систему уравнений:

$$left{begin{array}{lcl}3x_1-x_2+2x_3=0\ 5x_1-2x_2+3x_3=0\-x_1-x_3=0end{array}right.$$

Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}3&-1&2\5&-2&3\-1&0&-1end{pmatrix}$ методом окаймляющих миноров:

Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}3&-1\5&-2end{vmatrix}=-6+5=-1neq 0.$

Рассмотрим окаймляющий минор третьего порядка: $begin{vmatrix}3&-1&2\5&-2&3\-1&0&-1end{vmatrix}=6+3-4-5=0;$

Таким образом ранг матрицы $A$ равен двум.

Выберем в качестве базисного минор $M=begin{vmatrix}3&-1\5&-2end{vmatrix}=-1neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}3x_1-x_2+2с=0\ 5x_1-2x_2+3с=0end{array}right.Rightarrowleft{begin{array}{lcl}3x_1-x_2=-2c\5x_1-2x_2=-3cend{array}right.$$

По правилу Крамера находим $x_1$ и $x_2:$

$Delta=begin{vmatrix}3&-1\5&-2end{vmatrix}=-6+5=-1;$

$Delta_1=begin{vmatrix}-2c&-1\-3c&-2end{vmatrix}=4c-3c=c;$

$Delta_2=begin{vmatrix}3&-2c\5&-3cend{vmatrix}=-9c+10c=c;$

$x_1=frac{Delta_1}{Delta}=frac{c}{-1}=-c;$ $x_2=frac{Delta_2}{Delta}=frac{c}{-1}=-c.$

Таким образом, общее решение системы $X(c)=begin{pmatrix}-c\-c\cend{pmatrix}.$

Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}-1\-1\1end{pmatrix}.$

С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$

Ответ: $lambda=-1;$ $X=cbegin{pmatrix}-1\-1\1end{pmatrix}, cneq 0.$

{jumi[*3]}

4.143. $A=begin{pmatrix}0&-1&0\1&1&-2\1&-1&0end{pmatrix}.$

Решение.

$$A-lambda E=begin{pmatrix}0&-1&0\1&1&-2\1&-1&0end{pmatrix}-lambdabegin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=$$ $$=begin{pmatrix}-lambda&-1&0\1&1-lambda&-2\1&-1&-lambdaend{pmatrix}.$$

$$det(A-lambda E)=begin{vmatrix}-lambda&-1&0\1&1-lambda&-2\1&-1&-lambdaend{vmatrix}=$$ $$=-lambda(1-lambda)(-lambda)+2-lambda+2lambda=$$ $$=-lambda^3+lambda^2+lambda+2=0.$$

Решим найденное уравнение, чтобы найти собственные числа.

$$-lambda^3+lambda^2+lambda+2=(lambda-2)(-lambda^2-lambda-1)=0Rightarrow lambda=2.$$

Собственный вектор для собственного числа $lambda=2$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-2E)X=0, Xneq 0$$

$$(A-2E)X=begin{pmatrix}-2&-1&0\1&-1&-2\1&-1&-2end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}-2x_1-x_2\x_1-x_2-2x_3\x_1-x_2-2x_3end{pmatrix}=0.$$

Решим однородную систему уравнений:

$$left{begin{array}{lcl}-2x_1-x_2=0\ x_1-x_2-2x_3=0\x_1-x_2-2x_3=0end{array}right.$$

Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}-2&-1&0\1&-1&-2\1&-1&-2end{pmatrix}$ методом окаймляющих миноров:

Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}-2&-1\1&-1end{vmatrix}=2+1=3neq 0.$

Рассмотрим окаймляющий минор третьего порядка: $begin{vmatrix}-2&-1&0\1&-1&-2\1&-1&-2end{vmatrix}=0;$

Таким образом ранг матрицы $A$ равен двум.

Выберем в качестве базисного минор $M=begin{vmatrix}-2&-1\1&-1end{vmatrix}=3neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}-2x_1-x_2=0\ x_1-x_2-2с=0end{array}right.Rightarrowleft{begin{array}{lcl}-2x_1-x_2=0\x_1-x_2=2cend{array}right.$$

По правилу Крамера находим $x_1$ и $x_2:$

$Delta=begin{vmatrix}-2&-1\1&-1end{vmatrix}=2+1=3;$

$Delta_1=begin{vmatrix}0&-1\2c&-1end{vmatrix}=2c;$

$Delta_2=begin{vmatrix}-2&0\1&2cend{vmatrix}=-4c;$

$x_1=frac{Delta_1}{Delta}=frac{2c}{3};$ $x_2=frac{Delta_2}{Delta}=frac{-4c}{3}.$

Таким образом, общее решение системы $X(c)=begin{pmatrix}frac{2c}{3}\-frac{4c}{3}\cend{pmatrix}.$

Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}frac{2}{3}\-frac{4}{3}\1end{pmatrix}.$

С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$ Переобозначив постоянную, $alpha=3c,$ получаем собственный вектор $X=alphabegin{pmatrix}2\-4\3end{pmatrix}, alphaneq 0.$

Ответ: $lambda=2;$ $X=alphabegin{pmatrix}2\-4\3end{pmatrix}, alphaneq 0.$

Домашнее задание.

Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.

4.135. $A=begin{pmatrix}0&1&0\-4&4&0\-2&1&2end{pmatrix}.$

Ответ: $lambda=2;$ $X=c_1begin{pmatrix}1\2\0end{pmatrix}+c_2begin{pmatrix}0\0\1end{pmatrix}, $c_1$ и $ c_2$ не равны одновременно нулю.

4.142. $A=begin{pmatrix}1&-3&1\3&-3&-1\3&-5&1end{pmatrix}.$

Ответ: $lambda_1=-1,$ $X(lambda_1)=cbegin{pmatrix}1\1\1end{pmatrix};$ $lambda_2=2,$ $X(lambda_2)=cbegin{pmatrix}4\1\7end{pmatrix};$ $lambda_3=-2,$ $X(lambda_3)=cbegin{pmatrix}2\3\3end{pmatrix}, cneq 0.$

{jumi[*4]}

Источник