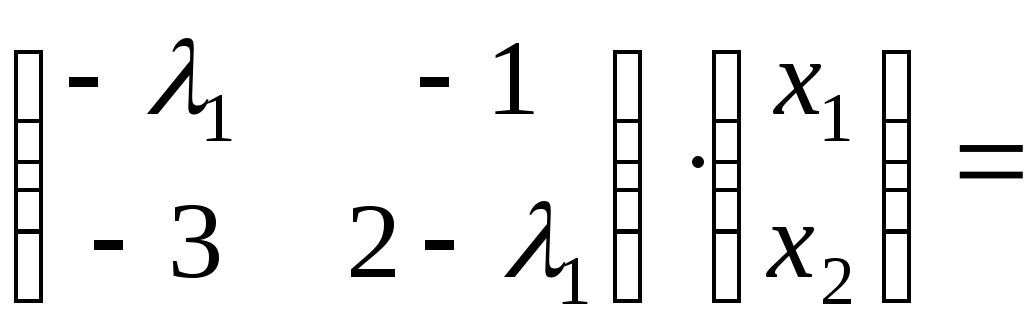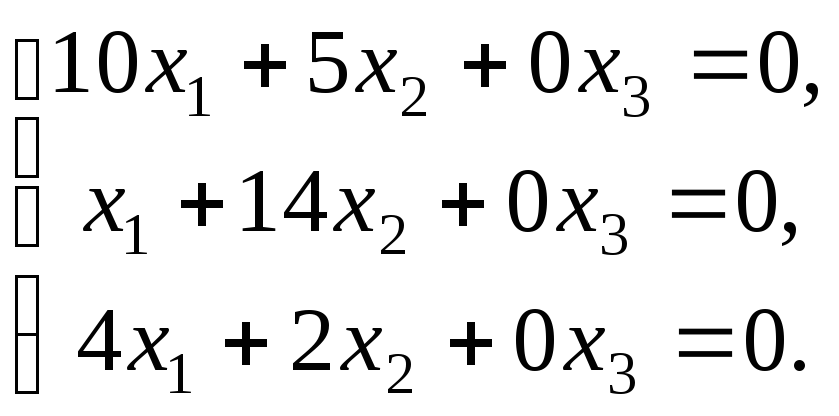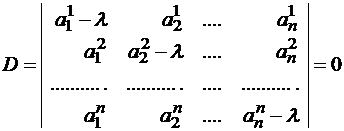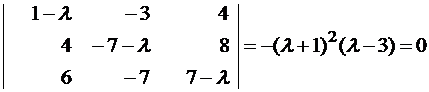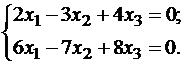Собственные
векторы и собственные
значения
линейного оператора
Определение 1.
Собственным
вектором оператора
называют
ненулевой вектор
,
удовлетворяющий равенству:
=
.
Определение 2.
Собственным
значением оператора
называют
число
,
для которого выполняется равенство:
=
,
где
— ненулевой вектор.
|
|
(1) |
|
|
(2) |
Решив последнее
уравнение относительно
,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
,
каждый из которых соответствует
определенному собственному значению.
Рассмотрим несколько
примеров, в каждом из которых будем
выполнять последовательность действий
решения задачи об отыскании собственных
значений и собственных векторов матрицы.
Пример 1.
Найти собственные
значения и собственные векторы матрицы
.
Дать геометрическую интерпретацию
полученного решения.
Решение
-
Матрица имеет
размерность 22,
то есть является представлением
линейного оператора в пространстве
.
Собственный вектор матрицы будем искать
в виде:
.
-
Составим уравнение
для отыскания собственных векторов в
матричном виде:
3. Перепишем
матричное уравнение в виде системы
уравнений:
-
Однородная система
имеет ненулевые решения тогда и только
тогда, когда определитель ее главной
матрицы равен 0. Получаем характеристическое
уравнение системы и решаем его:
.
Собственные
значения матрицы
:
,
.
-
Найдем собственные
векторы для каждого собственного
значения:
|
Пусть
|
Пусть
|
П
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.
-
Составим и решим
характеристическое уравнение
.
В нашей задаче
.
Тогда характеристическое
уравнение принимает вид:
,
или
,
,
,
— собственные
значения линейного оператора.
-
Найдем собственные
векторы, соответствующие собственному
значению
,
решая матричное уравнение:
х=0
или

т.е.
.
Полагая в последнем
равенстве
,
получим
.
Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х1=.
-
Найдем собственные
векторы, соответствующие собственному
значению
,
решая матричное уравнение:
х=0
или

т.е.
.
Полагая в последнем
равенстве
,
получим
.
Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х2=.
Ответ. Собственному
значению
соответствуют собственные векторы
х1=,
а собственному значению
собственные векторы
х
.
П
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=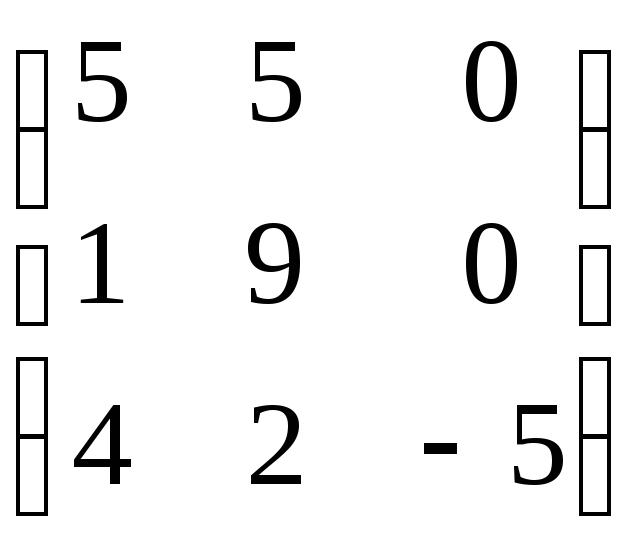
-
Найдем собственные
значения линейного оператора. Для этого
составим характеристическое уравнение
и найдем его корни:

,
,
,
,
,
,
,
— собственные значения линейного
оператора.
-
Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

запишем систему:
Решая методом
Гаусса, получаем
Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим
,
.
Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х1=.
-
Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

т.е.
Решая методом
Гаусса, получаем
откуда, система
принимает вид
Полагая
,
получим
.
Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х2=
-
Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

т.е.
Решая методом
Гаусса, получаем

откуда, система
принимает вид
Полагая
,
получим
.
Т
образом, собственные векторы,
соответствующие собственному значению
,
имеют вид: Х3=
Соседние файлы в папке Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Собственные числа и собственные векторы линейного оператора
Наиболее просто устроены матрицы диагонального вида 
Пусть дано линейное пространство Rn и действующий в нем линейный оператор A; в этом случае оператор A переводит Rn в себя, то есть A:Rn
→ Rn.
Определение. Ненулевой вектор x называется собственным вектором оператора A, если оператор A переводит x в коллинеарный ему вектор, то есть A·x = λ·x. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x.
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x1, x2, …, xm оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x1, x2, …, xm оператора A с попарно различными собственными числами λ1, λ2, …, λm
линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x1, x2, …, xn, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 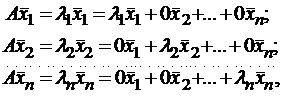

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе {εi} (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Пусть дан вектор x=(x1, x2, …, xn), где x1, x2, …, xn — координаты вектора x относительно базиса {ε1, ε2, …, εn} и x — собственный вектор линейного оператора A, соответствующий собственному числу λ, то есть A·x=λ·x. Это соотношение можно записать в матричной форме
x·(A-λ·E). (*)
Уравнение (*) можно рассматривать как уравнение для отыскания x, причем x ≠ 0, то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A — λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A — λE) = 0.
Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:
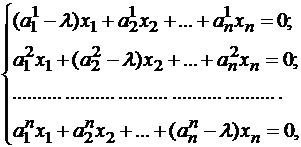
где 
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Получили уравнение для нахождения собственных чисел.
Это уравнение называется характеристическим уравнением, а его левая часть — характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.
Пусть λ1, λ2, …, λn — вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.
Пример №1. Линейный оператор A действует в R3 по закону A·x=(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, .., xn — координаты вектора x в базисе e1=(1,0,0), e2=(0,1,0), e3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A·e1=(1,4,6)
A·e2=(-3,-7,-7)
A·e3=(4,8,7)
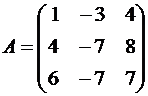
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
λ1,2 = -1, λ3 = 3.
Подставляя λ = -1 в систему, имеем:
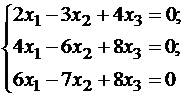
Так как 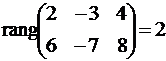
Пусть x1 — свободное неизвестное, тогда 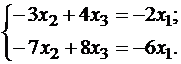

Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: (x1, 2x1, x1)=x1(1,2,1), где x1 — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: x1=(1,2,1).
Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: x2=(1,2,2).
В пространстве R3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.
Пример №2. Дана матрица 
1. Доказать, что вектор x=(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A·x=λ·x, то x — собственный вектор
Вектор (1, 8, -1) — собственный вектор. Собственное число λ = -1.
Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.
Собственные векторы ищем из системы:
(2-λ)x1+3x3=0;
10x1-(3+λ)x2-6x3=0;
-x1-(2+λ)x3=0;
Характеристическое уравнение: 
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 — 1) = 0
λ1 = -3, λ2 = 1, λ3 = -1.
Найдем собственный вектор, отвечающий собственному числу λ = -3:
5x1+3x3=0;
10x1-6x3=0;
-x1+x3=0;
Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x1 = x3 = 0. x2 здесь может быть любым, отличным от нуля, например, x2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:
Если λ = 1, то получаем систему
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.
Пусть x3 — свободное неизвестное. Тогда x1 = -3x3, 4x2 = 10x1 — 6x3 = -30x3 — 6x3, x2 = -9x3.
Полагая x3 = 1, имеем (-3,-9,1) — собственный вектор, отвечающий собственному числу λ = 1. Проверка:
Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R3. Таким образом, в базисе f1=(1,8,-1), f2=(0,1,0), f3=(-3,-9,1) матрица A имеет вид:

Не всякую матрицу линейного оператора A:Rn→ Rn можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.
Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой aik=aki.
Замечания.
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Перейти к онлайн решению своей задачи
Нахождение собственных чисел и собственных векторов
Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.
Больше:
Выводить десятичную дробь
,
- Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.
-
Элементы матриц — десятичные (конечные и периодические) дроби:
1/3,3,14,-1,3(56)или1,2e-4; либо арифметические выражения:2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2).-
decimal (finite and periodic) fractions:
1/3,3,14,-1,3(56)или1,2e-4 -
2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2) -
matrix literals:
{{1,3},{4,5}} -
operators:
+,-,*,/,,!,^,^{*},,,;,≠,=,⩾,⩽,>и< -
functions:
sqrt,cbrt,exp,log,abs,conjugate,min,max,gcd,rank,adjugate,inverse,determinant,transpose,pseudoinverse,cos,sin,tan,cot,cosh,sinh,tanh,coth,arccos,arcsin,arctan,arccot,arcosh,arsinh,artanhиarcoth -
units:
rad,deg -
special symbols:
pi,e,i— mathematical constantsk,n— integersIorE— identity matrixX,Y— matrix symbols
-
- Используйте ↵ Ввод, Пробел, ←↑↓→, Backspace и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V — для копирования матриц.
- Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
- За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.
Примеры
- Найти собственные векторы
({{-26,-33,-25},{31,42,23},{-11,-15,-4}})
Собственные числа и вектора матриц. Методы их нахождения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пусть число $lambda$ и вектор $xin L, xneq 0$ таковы, что $$Ax=lambda x.qquadqquadqquadqquadqquad(1)$$ Тогда число $lambda$ называется собственным числом линейного оператора $A,$ а вектор $x$ собственным вектором этого оператора, соответствующим собственному числу $lambda.$
В конечномерном пространстве $L_n$ векторное равенство (1) эквивалентно матричному равенству $$(A-lambda E)X=0,,,,, Xneq 0.qquadqquadquadquad (2)$$
Отсюда следует, что число $lambda$ есть собственное число оператора $A$ в том и только том случае, когда детерминант $det(A-lambda E)=0,$ т. е. $lambda$ есть корень многочлена $p(lambda)=det(A-lambda E),$ называемого характеристическим многочленом оператора $A.$ Столбец координат $X$ любого собственного вектора соответствующего собственному числу $lambda$ есть нетривиальное решение однородной системы (2).
Примеры.
Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.
4.134. $A=begin{pmatrix}2&-1&2\5&-3&3\-1&0&-2end{pmatrix}.$
Решение.
Найдем собственные вектора заданного линейного оператора. Число $lambda$ есть собственное число оператора $A$ в том и только том случае, когда $det(A-lambda E)=0.$ Запишем характеристическое уравнение:
$$A-lambda E=begin{pmatrix}2&-1&2\5&-3&3\-1&0&-2end{pmatrix}-lambdabegin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=$$ $$=begin{pmatrix}2-lambda&-1&2\5&-3-lambda&3\-1&0&-2-lambdaend{pmatrix}.$$
$$det(A-lambda E)=begin{vmatrix}2-lambda&-1&2\5&-3-lambda&3\-1&0&-2-lambdaend{vmatrix}=$$ $$=(2-lambda)(-3-lambda)(-2-lambda)+3+2(-3-lambda)+5(-2-lambda)=$$ $$=-lambda^3-3lambda^2+4lambda+12+3-6-2lambda-10-5lambda=-lambda^3-3lambda^2-3lambda-1=0.$$
Решим найденное уравнение, чтобы найти собственные числа.
$$lambda^3+3lambda^2+3lambda+1=(lambda^3+1)+3lambda(lambda+1)=$$ $$=(lambda+1)(lambda^2-lambda+1)+3lambda(lambda+1)=(lambda+1)(lambda^2-lambda+1+3lambda)=$$ $$=(lambda+1)(lambda^2+2lambda+1)=(lambda+1)^3=0Rightarrow lambda=-1.$$
Собственный вектор для собственного числа $lambda=-1$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A+E)X=0, Xneq 0$$
$$(A+E)X=begin{pmatrix}2+1&-1&2\5&-3+1&3\-1&0&-2+1end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}3x_1-x_2+2x_3\5x_1-2x_2+3x_3\-x_1-x_3end{pmatrix}=0.$$
Решим однородную систему уравнений:
$$left{begin{array}{lcl}3x_1-x_2+2x_3=0\ 5x_1-2x_2+3x_3=0\-x_1-x_3=0end{array}right.$$
Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}3&-1&2\5&-2&3\-1&0&-1end{pmatrix}$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}3&-1\5&-2end{vmatrix}=-6+5=-1neq 0.$
Рассмотрим окаймляющий минор третьего порядка: $begin{vmatrix}3&-1&2\5&-2&3\-1&0&-1end{vmatrix}=6+3-4-5=0;$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=begin{vmatrix}3&-1\5&-2end{vmatrix}=-1neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}3x_1-x_2+2с=0\ 5x_1-2x_2+3с=0end{array}right.Rightarrowleft{begin{array}{lcl}3x_1-x_2=-2c\5x_1-2x_2=-3cend{array}right.$$
По правилу Крамера находим $x_1$ и $x_2:$
$Delta=begin{vmatrix}3&-1\5&-2end{vmatrix}=-6+5=-1;$
$Delta_1=begin{vmatrix}-2c&-1\-3c&-2end{vmatrix}=4c-3c=c;$
$Delta_2=begin{vmatrix}3&-2c\5&-3cend{vmatrix}=-9c+10c=c;$
$x_1=frac{Delta_1}{Delta}=frac{c}{-1}=-c;$ $x_2=frac{Delta_2}{Delta}=frac{c}{-1}=-c.$
Таким образом, общее решение системы $X(c)=begin{pmatrix}-c\-c\cend{pmatrix}.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}-1\-1\1end{pmatrix}.$
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$
Ответ: $lambda=-1;$ $X=cbegin{pmatrix}-1\-1\1end{pmatrix}, cneq 0.$
{jumi[*3]}
4.143. $A=begin{pmatrix}0&-1&0\1&1&-2\1&-1&0end{pmatrix}.$
Решение.
Найдем собственные вектора заданного линейного оператора. Число $lambda$ есть собственное число оператора $A$ в том и только том случае, когда $det(A-lambda E)=0.$ Запишем характеристическое уравнение:
$$A-lambda E=begin{pmatrix}0&-1&0\1&1&-2\1&-1&0end{pmatrix}-lambdabegin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=$$ $$=begin{pmatrix}-lambda&-1&0\1&1-lambda&-2\1&-1&-lambdaend{pmatrix}.$$
$$det(A-lambda E)=begin{vmatrix}-lambda&-1&0\1&1-lambda&-2\1&-1&-lambdaend{vmatrix}=$$ $$=-lambda(1-lambda)(-lambda)+2-lambda+2lambda=$$ $$=-lambda^3+lambda^2+lambda+2=0.$$
Решим найденное уравнение, чтобы найти собственные числа.
$$-lambda^3+lambda^2+lambda+2=(lambda-2)(-lambda^2-lambda-1)=0Rightarrow lambda=2.$$
Собственный вектор для собственного числа $lambda=2$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-2E)X=0, Xneq 0$$
$$(A-2E)X=begin{pmatrix}-2&-1&0\1&-1&-2\1&-1&-2end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}-2x_1-x_2\x_1-x_2-2x_3\x_1-x_2-2x_3end{pmatrix}=0.$$
Решим однородную систему уравнений:
$$left{begin{array}{lcl}-2x_1-x_2=0\ x_1-x_2-2x_3=0\x_1-x_2-2x_3=0end{array}right.$$
Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}-2&-1&0\1&-1&-2\1&-1&-2end{pmatrix}$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}-2&-1\1&-1end{vmatrix}=2+1=3neq 0.$
Рассмотрим окаймляющий минор третьего порядка: $begin{vmatrix}-2&-1&0\1&-1&-2\1&-1&-2end{vmatrix}=0;$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=begin{vmatrix}-2&-1\1&-1end{vmatrix}=3neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}-2x_1-x_2=0\ x_1-x_2-2с=0end{array}right.Rightarrowleft{begin{array}{lcl}-2x_1-x_2=0\x_1-x_2=2cend{array}right.$$
По правилу Крамера находим $x_1$ и $x_2:$
$Delta=begin{vmatrix}-2&-1\1&-1end{vmatrix}=2+1=3;$
$Delta_1=begin{vmatrix}0&-1\2c&-1end{vmatrix}=2c;$
$Delta_2=begin{vmatrix}-2&0\1&2cend{vmatrix}=-4c;$
$x_1=frac{Delta_1}{Delta}=frac{2c}{3};$ $x_2=frac{Delta_2}{Delta}=frac{-4c}{3}.$
Таким образом, общее решение системы $X(c)=begin{pmatrix}frac{2c}{3}\-frac{4c}{3}\cend{pmatrix}.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}frac{2}{3}\-frac{4}{3}\1end{pmatrix}.$
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$ Переобозначив постоянную, $alpha=3c,$ получаем собственный вектор $X=alphabegin{pmatrix}2\-4\3end{pmatrix}, alphaneq 0.$
Ответ: $lambda=2;$ $X=alphabegin{pmatrix}2\-4\3end{pmatrix}, alphaneq 0.$
Домашнее задание.
Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.
4.135. $A=begin{pmatrix}0&1&0\-4&4&0\-2&1&2end{pmatrix}.$
Ответ: $lambda=2;$ $X=c_1begin{pmatrix}1\2\0end{pmatrix}+c_2begin{pmatrix}0\0\1end{pmatrix}, $c_1$ и $ c_2$ не равны одновременно нулю.
4.142. $A=begin{pmatrix}1&-3&1\3&-3&-1\3&-5&1end{pmatrix}.$
Ответ: $lambda_1=-1,$ $X(lambda_1)=cbegin{pmatrix}1\1\1end{pmatrix};$ $lambda_2=2,$ $X(lambda_2)=cbegin{pmatrix}4\1\7end{pmatrix};$ $lambda_3=-2,$ $X(lambda_3)=cbegin{pmatrix}2\3\3end{pmatrix}, cneq 0.$
{jumi[*4]}