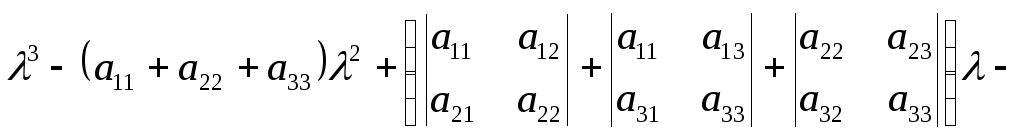Как найти собственные значения собственные векторы матрицы - Исправление недочетов и поиск решений вместе с Examum.ru

Собственные векторы и собственные значения матрицы

Пусть — числовая квадратная матрица n-го порядка. Матрица A-lambda E называется характеристической для , а ее определитель $Delta_{A}(lambda)=det(A-lambda E)$ характеристическим многочленом матрицы

$A-lambda E=begin{pmatrix}a_{11}-lambda&cdots&a_{1n}\ vdots&ddots& vdots\ a_{n1}&cdots&a_{nn}-lambdaend{pmatrix}!,quad Delta_{A}(lambda)=det(A-lambda E)= begin{vmatrix} a_{11}-lambda&cdots&a_{1n}\ vdots&ddots&vdots\ a_{n1}&cdots&a_{nn}-lambdaend{vmatrix}!.$

(7.12)

Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.

Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец $x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}$ , удовлетворяющий условию

Acdot x=lambdacdot x,

(7.13)

называется собственным вектором матрицы . Число lambda в равенстве (7.13) называется собственным значением матрицы . Говорят, что собственный вектор соответствует {принадлежит) собственному значению lambda .

Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде (A-lambda E)x=o , где — единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему линейных алгебраических уравнений с неизвестными x_1,x_2,ldots,x_n:

$begin{cases}(a_{11}-lambda)x_1+a_{12}x_2+ldots+a_{1n}x_n=0,\ a_{21}x_1+(a_{22}-lambda)x_2+ldots+a_{2n}x_n=0,\ cdotscdotscdotscdotscdots\ a_{n1}x_1+a_{2n}x_2+ldots+(a_{nn}-lambda)x_n=0. end{cases}$

(7.14)

Поскольку нас интересуют только нетривиальные решения (xne o) однородной системы, то определитель матрицы системы должен быть равен нулю:

$det(A-lambda E)=begin{vmatrix}a_{11}-lambda&a_{12}&cdots&a_{1n}\ a_{21}&a_{22}-lambda&cdots&a_{2n}\ vdots&vdots&ddots&vdots\ a_{n1}&a_{n2}& cdots&a_{nn}-lambda end{vmatrix}=0.$

(7.15)

В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена $Delta_{A}(lambda)=det(A-lambda E)$ матрицы . Уравнение $Delta_{A}(lambda)=0$ называется характеристическим уравнением матрицы . Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде

$Delta_{A}(lambda)= det(A-lambda E)= a_{n}(lambda-lambda_1)^{n_1}cdot (lambda-lambda_2)^{n_2}cdotldotscdot(lambda-lambda_k)^{n_k},$

где lambda_1,lambda_2,ldots,lambda_k — корни многочлена кратности n_1,n_2,ldots,n_k соответственно, причем n_1+n_2+ldots+n_k=n . Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.

Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.

Действительно, если число lambda — собственное значение матрицы , которому соответствует собственный вектор xne o , то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число lambda удовлетворяет характеристическому уравнению (7.15). Наоборот, если lambda — корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е. operatorname{rg}(A-lambda E)<n .В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец xne o , удовлетворяющий условию (7.14). Значит, lambda — собственное значение матрицы .

Свойства собственных векторов

Пусть — квадратная матрица n-го порядка.

1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.

В самом деле, пусть s_1 и s_2 — собственные векторы, соответствующие собственным значениям lambda_1 и lambda_2 , причем lambda_1ne lambda_2 . Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:

alpha_1cdot s_1+alpha_2cdot s_2=o.

(7.16)

Надо показать, что это равенство возможно только в тривиальном случае, когда alpha_1=alpha_2=0 . Действительно, умножая обе части на матрицу и подставляя As_1=lambda_1s_1 и As_2=lambda_2s_2 имеем

A(alpha_1s_1+alpha_2s_2)=oquad Leftrightarrowquad alpha_1As_1+ alpha_2As_2= oquad Leftrightarrowquad alpha_1 lambda_1s_1+alpha_2 lambda_2s_2=o.

Прибавляя к последнему равенству равенство (7.16), умноженное на (-lambda_2) , получаем

alpha_1cdotlambda_1cdot s_1-alpha_2cdotlambda_2cdot s_2=oquad Leftrightarrowquad alpha_1cdot(lambda_1-lambda_2)cdot s_1=o.

Так как s_1ne o и lambda_1ne lambda_2 , делаем вывод, что alpha_1=0 . Тогда из (7.16) следует, что и alpha_2=0 (поскольку s_2ne o ). Таким образом, собственные векторы s_1 и s_2 линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.

2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.

Действительно, если собственному значению lambda соответствуют собственные векторы s_1,ldots,s_k , то из равенств S_i=lambda s_i, i=1,ldots,k , следует, что вектор s=alpha_1s_1+ldots+alpha_ks_k также собственный, поскольку:

As=A(alpha_1s_1+ldots+alpha_ks_k)= alpha_1lambda s_1+ldots+alpha_klambda s_k=lambda(alpha_1s_1+ldots+alpha_ks_k)=lambda s.

3. Пусть $(A-lambda E)^{+}$ — присоединенная матрица для характеристической матрицы . Если lambda_0 — собственное значение матрицы , то любой ненулевой столбец матрицы $(A-lambda E)^{+}$ является собственным вектором, соответствующим собственному значению .

В самом деле, применяя формулу (7.7) имеем $(A-lambda E)(A-lambda E)^{+}=Delta_k(lambda)cdot E$ . Подставляя корень lambda_0 , получаем $(A-lambda_0E)(A-lambda_0E)^{+}=O$ . Если — ненулевой столбец матрицы $(A-lambda_0E)^{+}$ , то (A-lambda_0E)s=oLeftrightarrow As=lambda_0s . Значит, — собственный вектор матрицы .

Замечания 7.5

1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.

2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений lambda_1,lambda_2, ldots,lambda_k записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем

(A-lambda_1E)cdot x=o,quad (A-lambda_2E)cdot x=o,quad ldots,quad (A-lambda_kE)cdot x=o.

Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.

3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.

4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).

5. Для простого корня lambda=lambda_0 характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы (A-lambda_0E) по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы , является собственным вектором.

Нахождение собственных векторов и собственных значений матрицы

Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.

1. Составить характеристический многочлен матрицы Delta_A(lambda)=det(A-lambda E) .

2. Найти все различные корни lambda_1,lambda_2,ldots,lambda_k характеристического уравнения Delta_A(lambda)=0 (кратности n_1,n_2,ldots,n_k (n_1+n_2+ldots+n_k=n) корней определять не нужно).

3. Для корня lambda-lambda_1 найти фундаментальную систему $varphi_1,varphi_2,ldots,varphi_{n-r}$ решений однородной системы уравнений

(A-lambda_1E)cdot x=o , где $r=operatorname{rg}(A-lambda_1E)$

Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).

4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению lambda_1:

$s_1=C_1varphi_1,quad s_2=C_2varphi_2,quad ldots,quad s_{n-r}=C_{n-r}varphi_{n-r},$

(7.17)

где $C_1,C_2,ldots,C_{n-r}$ — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению lambda_1 , образуют ненулевые столбцы вида $s=C_1varphi_1+C_2varphi_2+ldots+C_{n-r}varphi_{n-r}$ . Здесь и далее собственные векторы матрицы будем обозначать буквой .

Повторить пункты 3,4 для остальных собственных значений lambda_1,lambda_2,ldots,lambda_k .

Пример 7.8. Найти собственные значения и собственные векторы матриц:

$A=begin{pmatrix}1&-2\3&8end{pmatrix}!,quad B=begin{pmatrix}1&-4\ 1&1 end{pmatrix}!,quad C=begin{pmatrix}1&1&1\1&1&1\1&1&1end{pmatrix}!.$

Решение. Матрица . 1. Составляем характеристический многочлен матрицы

$Delta_{A}(lambda)=begin{vmatrix}1-lambda&-2\3&8-lambdaend{vmatrix}= (1-lambda)(8-lambda)+6=lambda^2-9 lambda+8+6= lambda^2-9 lambda+14.$

2. Решаем характеристическое уравнение: $lambda^2-9 lambda+14=0~Rightarrow~! left[!begin{gathered}lambda_1=2,\ lambda_2=7.end{gathered}right.$ .

3(1). Для корня lambda_1=2 составляем однородную систему уравнений (A-lambda_1E)x=o:

$begin{pmatrix}1-2&-2\ 3&8-2 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-1&-2\ 3&6 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-1&-2!!&vline!!&0\ 3&6!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2!!&vline!!&0\ 3&6!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}!.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=-2x_2 . Полагая x_2=1 , получаем решение $varphi_1= begin{pmatrix}-2\1end{pmatrix}$ .

4(1). Записываем собственные векторы, соответствующие собственному значению lambda_1=2colon~ s_1=C_1cdotvarphi_1 , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы $begin{pmatrix}-1&-2\3&6end{pmatrix}$ , то есть $begin{pmatrix}2\-1 end{pmatrix}$ . Умножив этот столбец на (-1), получим varphi_1 .

3(2). Для корня lambda_2=7 составляем однородную систему уравнений (A-lambda_2E)x=o:

$begin{pmatrix}1-7&-2\ 3&8-7 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-6&-2\ 3&1 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-6&-2!!&vline!!&0\ 3&1!!&vline!!&0end{pmatrix}sim begin{pmatrix}3&1!!&vline!!&0\ -6&-2!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&1/3!!& vline!!&0\ -6&-2!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&1/3!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}!.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: $x_1=-frac{1}{3}x_2$ . Полагая x_2=1 , получаем решение $varphi_2=begin{pmatrix}-1/3\1end{pmatrix}$ .

4(2). Записываем собственные векторы, соответствующие собственному значению lambda_2=7colon~ s_2=C_2cdotvarphi_2 , где C_2 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-6&-2\3&1end{pmatrix}$ , т.е. $begin{pmatrix}1\-3 end{pmatrix}$ . Поделив его на (- 3), получим varphi_2 .

Матрица . 1. Составляем характеристический многочлен матрицы

$Delta_{B}(lambda)= begin{vmatrix}1-lambda&-4\1&1-lambdaend{vmatrix}= (1-lambda)^2+4=lambda^2-2 lambda+1+4= lambda^2-2 lambda+5.$

2. Решаем характеристическое уравнение: $lambda^2-2 lambda+5=0~Rightarrow~! left[! begin{gathered}lambda_1=1+2i,\ lambda_2=1-2i.end{gathered}right.$ .

3(1). Для корня lambda_1=1+2i составляем однородную систему уравнений (B-lambda_1E)x=o

$begin{pmatrix}1-(1+2i)&-4\ 1&8-1-(1+2i) end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-2i&-4\ 1&-2i end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-2i&-4!!&vline!!&0\ 1&-2i!!&vline!!&0end{pmatrix}sim begin{pmatrix} 1&-2i!!&vline!!&0\ -2i&-4!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&-2i!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=2i,x_2 . Полагая x_2=1 , получаем решение $varphi_1= begin{pmatrix}2i\1 end{pmatrix}$ .

4(1). Записываем собственные векторы, соответствующие собственному значению lambda_1= 1+2icolon~ s_1=C_1cdotvarphi_1 , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-2i&-4\1&-2iend{pmatrix}$ , то есть $begin{pmatrix}-2i\ -1 end{pmatrix}$ . Умножив этот столбец на (-1), получим varphi_1 .

3(2). Для корня lambda_2=1-2i составляем однородную систему уравнений (B-lambda_2E)x=o:

$begin{pmatrix}1-(1-2i)&-4\ 1&8-1-(1-2i) end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}2i&-4\ 1&2i end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}2i&-4!!&vline!!&0\ 1&2i!!&vline!!&0end{pmatrix}sim begin{pmatrix} 1&2i!!&vline!!&0\ 2i&-4!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2i!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=-2i,x_2 . Полагая x_2=1 , получаем решение $varphi_2= begin{pmatrix}-2i\1 end{pmatrix}$ .

4(2). Записываем собственные векторы, соответствующие собственному значению lambda_2=1-2icolon~ s_2=C_2cdotvarphi_2 , где C_2 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}2i&-4\1&2iend{pmatrix}$ , т.е. $begin{pmatrix}2i\-1 end{pmatrix}$ . Умножив его на (-1), получим varphi_2 .

Матрица 1. Составляем характеристический многочлен матрицы

$Delta_{C}(lambda)= det(C-lambda E)= begin{vmatrix}1-lambda&1&1\1&1-lambda&1\ 1&1&1-lambda end{vmatrix}= (1-lambda)^3+2-3(1-lambda)= -lambda^3+3 lambda^2.$

2. Решаем характеристическое уравнение: $-lambda^3+3 lambda^2=0~Rightarrow~! left[! begin{gathered}lambda_1=3,\ lambda_2=0end{gathered}right.$ .

3(1). Для корня lambda_1=3 составляем однородную систему уравнений (C-lambda_1E)x=o:

$begin{pmatrix}1-3&1&1\ 1&1-3&1\ 1&1&1-3end{pmatrix}!cdot! begin{pmatrix} x_1\x_2\x_3end{pmatrix}=begin{pmatrix}0\0\0end{pmatrix}quad Leftrightarrowquad begin{cases}-2x_1+x_2+x_3=0,\ x_1-2x_2+x_3=0,\ x_1+x_2-2x_3=0.end{cases}$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):

$begin{gathered}begin{pmatrix}C-lambda_1Emid oend{pmatrix}= begin{pmatrix} -2&1&1!!&vline!!&0\ 1&-2&1!!&vline!!&0\ 1&1&-2!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&1&-2!!&vline!!&0\ -2&1&1!!&vline!!&0\ 1&-2&1!!&vline!!&0 end{pmatrix}sim\[2pt] simbegin{pmatrix} 1&1&-2!!&vline!!&0\ 0&3&-3!!&vline!!&0\ 0&-3&3!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&1&-2!!&vline!!&0\ 0&1&-1!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&0&-1!!&vline!!&0\ 0&1&-1!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}!.end{gathered}$

Ранг матрицы системы равен 2 (r=2) , число неизвестных n=3 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисные переменные x_1,x_2 через свободную $x_3colon begin{cases}x_1=x_3,\x_2=x_3,end{cases}$ и, полагая x_3=1 , получаем решение $varphi=begin{pmatrix}1\1\1end{pmatrix}$ .

4(1). Все собственные векторы, соответствующие собственному значению lambda_1=3 , вычисляются по формуле s=C_1cdotvarphi , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-2&1&1\1&-2&1\1&1&-2end{pmatrix}$ , то есть $begin{pmatrix}3\3\3end{pmatrix}$ , так как

$A_{11}=(-1)^{1+1}begin{vmatrix} -2&1\1&-2 end{vmatrix} =3;quad A_{12}=(-1)^{1+2} begin{vmatrix} 1&1\1&-2 end{vmatrix}= 3;quad A_{13}=(-1)^{1+3}begin{vmatrix}1&-2\ 1&1 end{vmatrix}=3.$

Разделив его на 3, получим varphi .

3(2). Для собственного значения lambda_2=0 имеем однородную систему Cx=o . Решаем ее методом Гаусса:

$begin{pmatrix}Cmid oend{pmatrix}= begin{pmatrix}1&1&1!!&vline!!&0\ 1&1&1!!&vline!!&0\ 1&1&1!!&vline!!&0 end{pmatrix}sim begin{pmatrix}1&1&1!!& vline!!&0\ 0&0&0!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}!.$

Ранг матрицы системы равен единице (r=1) , следовательно, фундаментальная система решений состоит из двух решений (n-r=2) . Базисную переменную x_1 , выражаем через свободные: x_1=-x_2-x_3 . Задавая стандартные наборы свободных переменных x_2=1,~x_3=0 и x_2=0,~ x_3=1 , получаем два решения

$varphi_1=begin{pmatrix}-1\1\0end{pmatrix}!,qquad varphi_2=begin{pmatrix}-1\0\1 end{pmatrix}!.$

4(2). Записываем множество собственных векторов, соответствующих собственному значению lambda_2=0colon~ s=C_1varphi_1+C_2varphi_2 , где C_1,C_2 — произвольные постоянные, не равные нулю одновременно. В частности, при C_1=0, C_2=-1 получаем $s_1=begin{pmatrix}1&0&-1end{pmatrix}^T$ ; при C_1=0,~C_2=-1colon $s_2=begin{pmatrix}1&-1&0end{pmatrix}^T$ . Присоединяя к этим собственным векторам собственный вектор $s_3=begin{pmatrix}1&1&1 end{pmatrix}^T$ , соответствующий собственному значению lambda_1=3 (см. пункт 4(1) при C_1=1 ), находим три линейно независимых собственных вектора матрицы

$s_1=begin{pmatrix}1\0\-1end{pmatrix}!,qquad s_2=begin{pmatrix}1\-1\0 end{pmatrix}!,qquad s_3=begin{pmatrix}1\1\1end{pmatrix}!.$

Заметим, что для корня lambda_2=0 собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы равно нулю.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

В этой главе
рассматриваются вопросы о собственных
векторах и собственных значениях
произвольной квадратной матрицы,
симметрической матрицы и подобных
матриц.

1. Основные понятия.

Определение.
Вектор
,
называетсясобственным
вектором
квадратной матрицы
,
если существует такое число,
что

.
При
этом числоназываетсясобственным
значением
матрицы
,
соответствующим собственному вектору.

Уравнение
может быть записано в виде

Определение.
Если
— собственное значение матрицы,
асоответствующий ему собственный вектор,
тоназываютсобственной
парой матрицы
.

● Пример 1.
Показать,
что вектор
является собственным вектором матрицы.
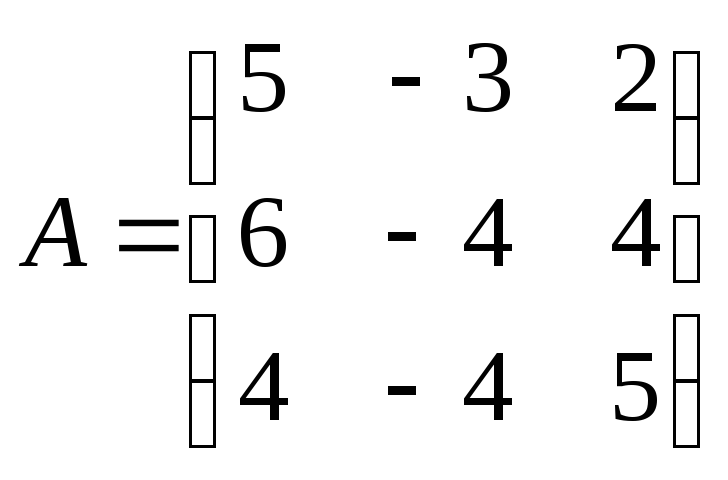
Найти
соответствующее ему собственное
значение.

Решение.

Так как
(),
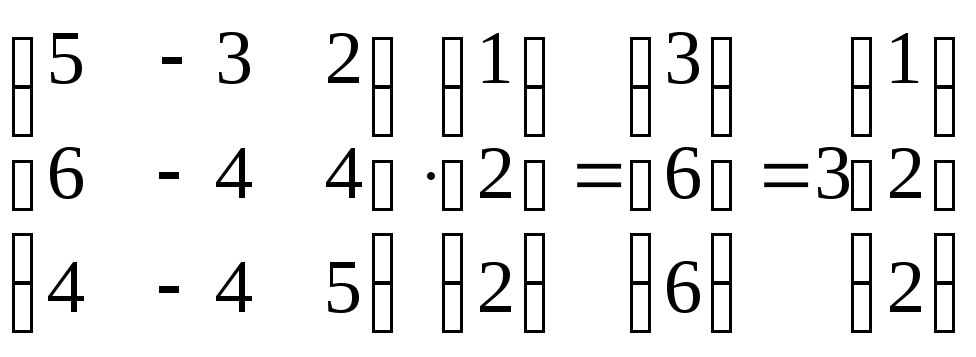
то—
собственный вектор матрицы,
соответствующий собственному значению.●

● Пример 2.
Показать,
что если
— собственная пара матрицы,
то— собственная пара матрицы.

Решение.
Действительно,

,
т.е.
.
Из последнего следует, что— собственная пара матрицы.●

● Пример 3.
При каких
ивекторявляется собственным вектором матрицы?

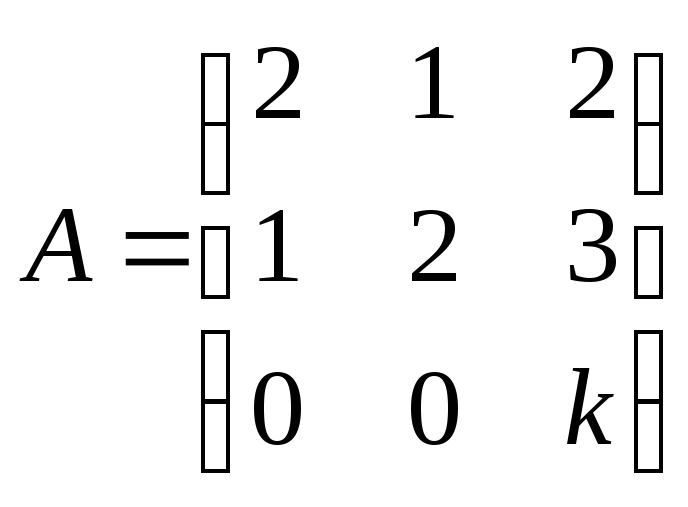
Решение.
Найдем вектор
..

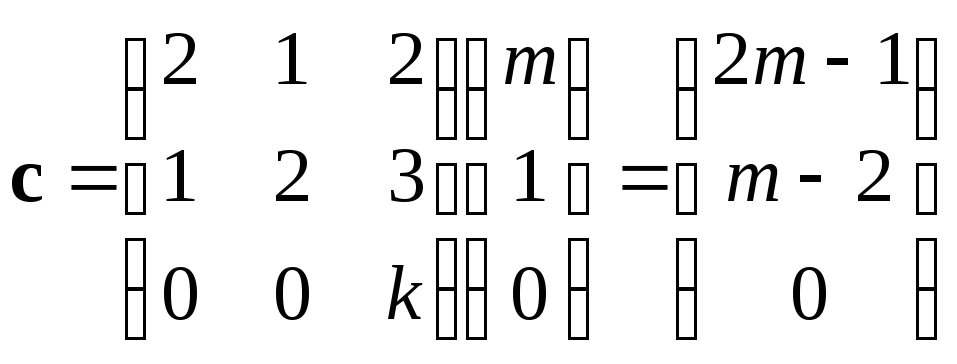
Если —
собственный вектор матрицы
,
то,
откуда.
Из последнего имеемии.

Ответ:
при
и произвольномвекторсобственный вектор матрицы.

● Пример 4.
Существует
ли
,
при котором—
собственный вектор матрицы?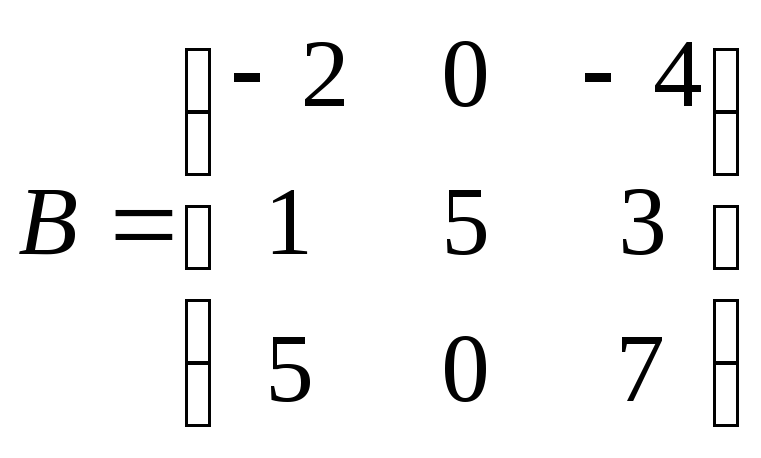
Если существует, указать соответствующую
собственную пару.

Решение.
Вычислим произведение

Если
—
собственная пара матрицы,
то

Из последнего
равенства имеем
Откуда,,.

—
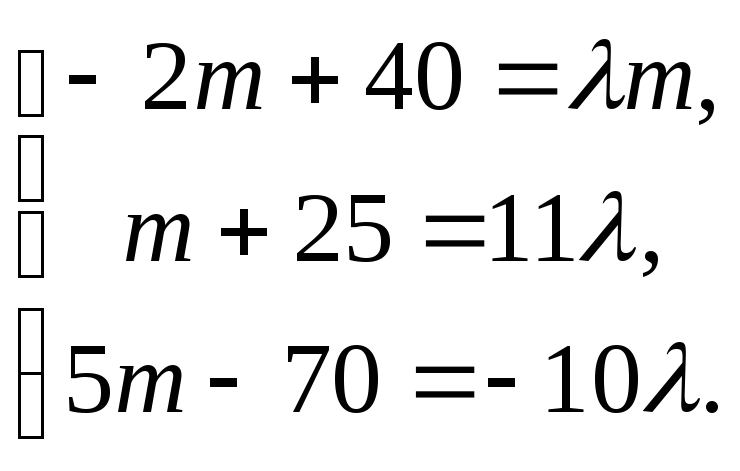
собственная пара матрицы.●

2. Свойства собственных векторов.

1)
Если —
собственный вектор матрицы
,
а—
соответствующее ему собственное
значение, то при любомвектортакже является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.

►Действительно,
.◄

Замечание. Любой
собственный вектор матрицы определяет
целое направление
собственных векторов этой матрицы с
одним и тем же собственным значением.

2)
Собственные векторы матрицы, соответствующие
различным
её собственным значениям, линейно
независимы.

►Доказательство.
Пусть
и—
собственные пары матрицы,
где.

Предположим, что
илинейно зависимые векторы.

Если
илинейно зависимы, то хотя бы один из
этих векторов можно представить в виде
линейной комбинации другого (пусть).

Тогда
,
откуда следует, что.
Так как,
то.

Полученное
противоречие доказывает утверждение.◄

3)
Если
илинейно независимые собственные векторы
матрицы,
соответствующие одному и тому же
собственному значению,
то любая нетривиальная линейная
комбинация этих векторов()
также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.

►Действительно,
,

что и требовалось доказать.◄

4)
Если матрица
диагональная
,
то ее собственные значения совпадают
с диагональными элементами этой матрицы
(),
а единичный векторявляется собственным вектором,
соответствующим собственному значению.

►Действительно,
◄

3 Нахождение собственных значений и собственных векторов.

Собственные
значения и собственные векторы матрицы
удовлетворяют матричному уравнению.

Если
собственный вектор матрицы
,
то однородная системаимеет нетривиальное решение, поэтому(порядок
матрицыи.
Последнее
уравнение позволяет найти собственные
значения матрицы.

Определение.
Многочлен
называютхарактеристическим многочленомматрицы.

Определение.
Уравнение

называется
характеристическим
уравнением
матрицы
.

Корни характеристического
уравнения
матрицы
являются собственными значениями
матрицы.

Характеристическое
уравнение матрицы
может быть записано в виде.

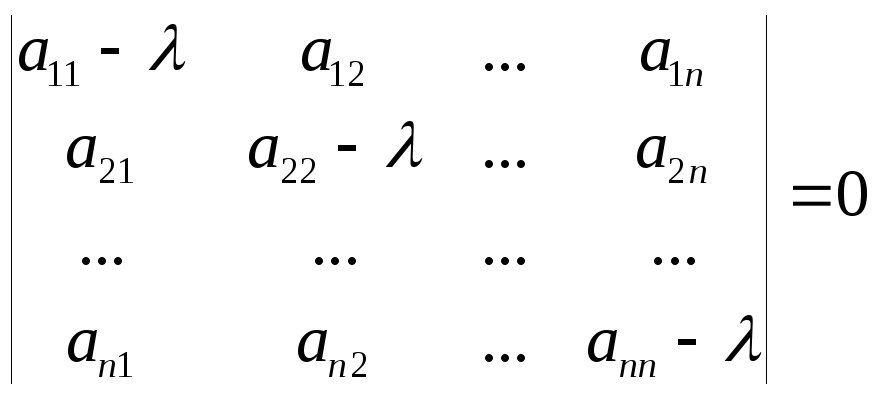
Определение.
Множество всех собственных значений
квадратной матрицы называется спектром
этой
матрицы.

Спектр матрицы
-го
порядка содержитсобственных значений матрицы, которые
могут быть как действительными, так и
комплексными, простыми так и кратными.

Для матрицы
характеристическое уравнениеможет быть может быть преобразовано к
виду
.

,
поэтому характеристическое уравнение
матрицы
имеет вид

. (8.1)

При этом

,(8.2)

.(8.3)

Уравнение
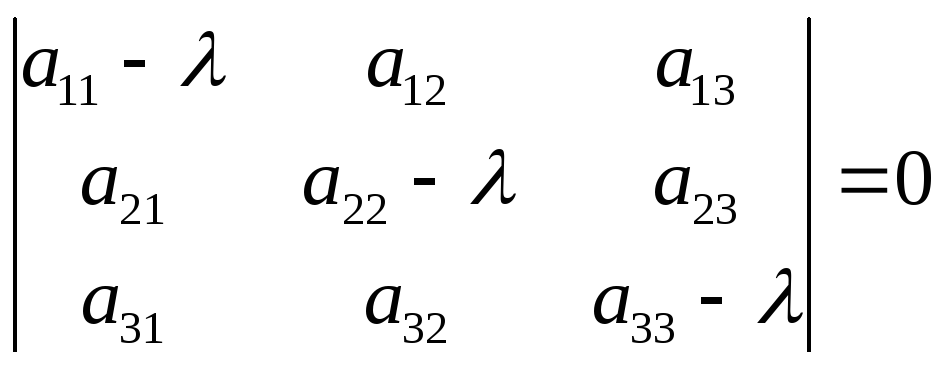
является характеристическим уравнением
матрицы.Это
уравнение может быть представлено в
виде

или

,
(8.4)

где
,
аминоры определителя.

Если
,икорни характеристического уравнения
(8.4), то это уравнение может быть записано
в виде

. (8.5)

Сравнивая уравнения
(8.4) и (8.5), можно записать следующее:

,(8.6)

,(8.7)

.(8.8)

Собственные векторы
матрицы
,
соответствующие собственному значению,
удовлетворяют матричному уравнению,
которое может быть записана в форме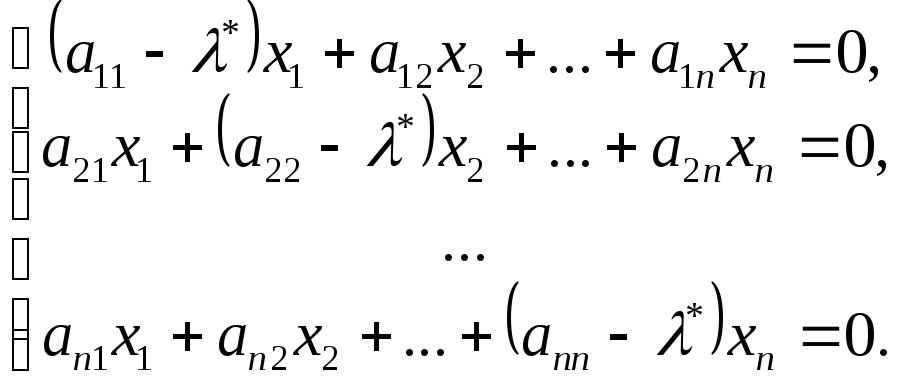Так
как ранг матрицы этой системы меньше
числа неизвестных (=0),
то система имеет бесконечное множество

решений, каждое
ненулевое
из которых является собственным вектором,
соответствующим собственному значению
.

● Пример 5.
Найти собственные значения и собственные
векторы матрицы
.

Решение.
— характеристическое уравнение для
данной матрицы, откуда,и.

Для нахождения
собственных векторов, соответствующих
собственному
значению
,
имеем системуэквивалентную уравнению.
Векторявляется решением этого уравнения, а
привектор— искомый собственный вектор.

Для
нахождения собственных векторов,
соответствующих собственному значению
,
имеем системуиз которой следует, что векторприявляется собственным вектором,
соответствующим собственному значению.

Ответ.
,при;,при.

● Пример 6.

Найти собственные
пары матрицы
.

Решение.
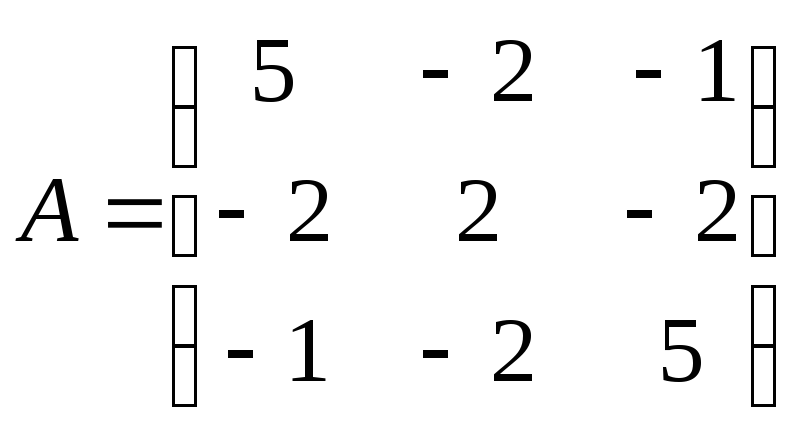
— характеристическоеуравнение
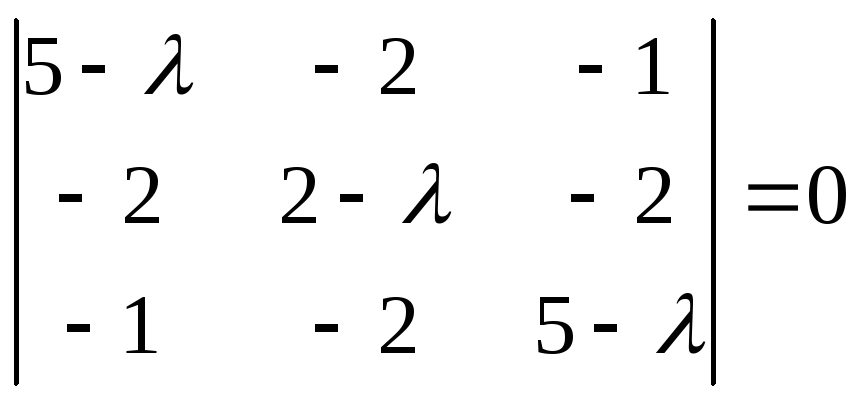
матрицы
,
которое может быть записано в виде,
где,,,,(проверьте).

—
характеристическое уравнение матрицы
,
корни которого.

Собственные
векторы, соответствующие собственному
значению
,
находим из системы.
Приимеем систему
которая
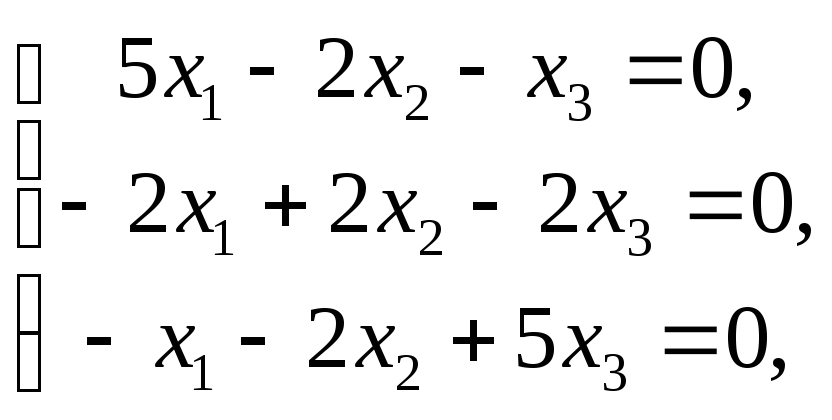
равносильна системе
решение
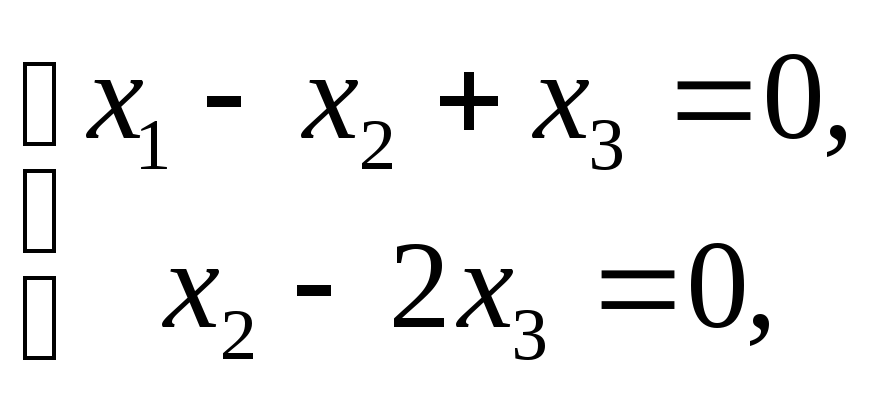
которой
.

При
векторявляется собственным вектором матрицы,
соответствующим собственному значению.

При
для нахождения собственных векторов
имеем систему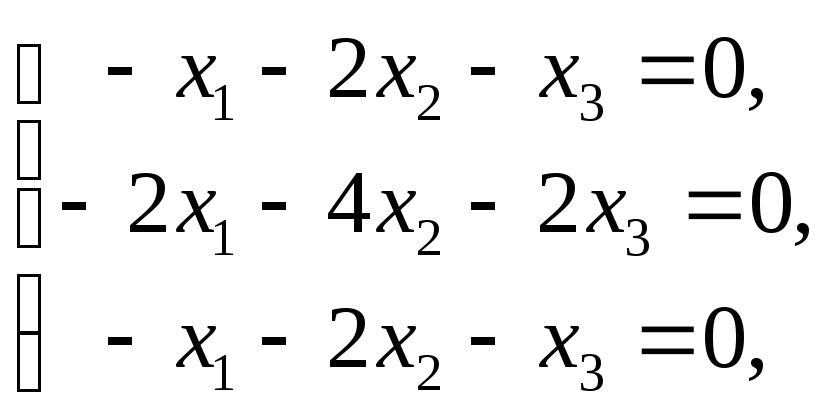которая равносильна одному уравнению.

При любых
ивекторесть решение уравнения,
а при

является собственным
вектором, который соответствует
собственному значению
.

Ответ:
при;при.

● Пример 7.
Найти собственные значения и собственные
векторы матрицы
.

Решение.
Характеристическое уравнение для
указанной матрицы имеет вид
,
откудаи.

Для нахождения
собственных векторов, соответствующих
собственному значению
,
имеем системуиз которой следуетпри.

Ответ.
,при;,при.

● Пример 8.

Доказать, что если
собственная
пара невырожденной матрицы
,
то
—собственная
пара матрицы
.

►Так матрица
невырожденная (),
то существует.
Произведение собственных значений
матрицыравно,
а так как,
то собственное значение.

— собственная
пара матрицы
,
поэтому.Умножив
последнее равенство слева на
,
имеем,
откуда,и.
Последнее равенство означает, что
—
собственная
пара матрицы
.◄

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Download Article

The matrix equation involves a matrix acting on a vector to produce another vector. In general, the way acts on is complicated, but there are certain cases where the action maps to the same vector, multiplied by a scalar factor.

Eigenvalues and eigenvectors have immense applications in the physical sciences, especially quantum mechanics, among other fields.

Steps

1

Understand determinants. The determinant of a matrix when is non-invertible. When this occurs, the null space of becomes non-trivial — in other words, there are non-zero vectors that satisfy the homogeneous equation ^[1]
2

Advertisement
3
4
5
Solve the characteristic polynomial for the eigenvalues. This is, in general, a difficult step for finding eigenvalues, as there exists no general solution for quintic functions or higher polynomials. However, we are dealing with a matrix of dimension 2, so the quadratic is easily solved.
- ${begin{aligned}&(lambda -5)(lambda +2)=0\&lambda =5,-2end{aligned}}$
6
Substitute the eigenvalues into the eigenvalue equation, one by one. Let’s substitute $lambda _{{1}}=5$ first.^[3]
- $(A-5I){mathbf {x}}={begin{pmatrix}-4&4\3&-3end{pmatrix}}$
- The resulting matrix is obviously linearly dependent. We are on the right track here.
7

Row-reduce the resulting matrix. With larger matrices, it may not be so obvious that the matrix is linearly dependent, and so we must row-reduce. Here, however, we can immediately perform the row operation $R_{{2}}to 4R_{{2}}+3R_{{1}}$ to obtain a row of 0’s.^[4]
8

Obtain the basis for the eigenspace. The previous step has led us to the basis of the null space of — in other words, the eigenspace of with eigenvalue 5.

Add New Question

Question

Why do we replace y with 1 and not any other number while finding eigenvectors?

For simplicity. Eigenvectors are only defined up to a multiplicative constant, so the choice to set the constant equal to 1 is often the simplest.
Question

How do you find the eigenvectors of a 3×3 matrix?

Alphabet

Community Answer

First, find the solutions x for det(A — xI) = 0, where I is the identity matrix and x is a variable. The solutions x are your eigenvalues. Let’s say that a, b, c are your eignevalues. Now solve the systems [A — aI | 0], [A — bI | 0], [A — cI | 0]. The basis of the solution sets of these systems are the eigenvectors.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

The determinant of a triangular matrix is easy to find — it is simply the product of the diagonal elements. The eigenvalues are immediately found, and finding eigenvectors for these matrices then becomes much easier.^[5]
- Beware, however, that row-reducing to row-echelon form and obtaining a triangular matrix does not give you the eigenvalues, as row-reduction changes the eigenvalues of the matrix in general.

Thanks for submitting a tip for review!

References

About This Article

Thanks to all authors for creating a page that has been read 109,584 times.

Did this article help you?

Источник