Как найти сокращенную днф функции

Сокращенная ДНФ

Определение:

Сокращенная ДНФ (англ. reduced disjunctive normal form) — форма записи функции, обладающая следующими свойствами: любые два слагаемых различаются как минимум в двух позициях, ни один из конъюнктов не содержится в другом.

Например:
содержится в .

Функцию можно записать с помощью сокращенной ДНФ не единственным способом.

Запишем функцию (медиана) в виде совершенной ДНФ:
.
Известно, что это выражение равносильно следующему:
.
Вынесем в каждой скобке общий конъюнкт (например, в первой .
Так как , то такой конъюнкт не влияет на значение выражения, и его можно опустить.
Получим в итоге формулу .

Минимальная ДНФ

Определение:

Минимальная ДНФ (англ. minimal disjunctive normal form) — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных.

Каждая минимальная ДНФ является сокращенной, но не каждая сокращенная — минимальна.
Например, запись является минимальной ДНФ для медианы (она же сокращенная, как видно в примере выше); а запись — не минимальная, но сокращенная ДНФ.

Минимизация ДНФ

Рассмотрим несколько способов минимизации дизъюнктивных нормальных форм:

Визуализация гиперкубами

Этот способ работает при количестве переменных не больше трёх (в противном необходимо вводить четвёртое или следующие за ним измерения для представления фигур).
Сначала мы рисуем куб в системе отсчёта (названия координатных осей соответствуют названиям переменных). Затем каждую вершину обрабатываем следующим образом:

Описание алгоритма	Пример
Если у нас конъюнкт, переменные в котором равны соответствующим координатам вершины, то в эту вершину мы помещаем закрашенный чёрным кружок.	Вершине с координатами соответствует конъюнкт , он равен единице при и )
В противном случае мы помещаем в вершину закрашенный белый кружок.	Для такой ДНФ: мы получим следующий гиперкуб (см. рисунок)
Далее обработка гиперкуба идёт следующим образом: пока у нас есть незакрашенные вершины, мы выбираем грань, либо вершину, либо ребро, на которых больше всего закрашенных чёрным вершин и ещё не обработанных вершин.
Если в данном гиперкубе есть грань, все вершины на которой закрашены чёрным, то мы можем записать её в качестве конъюнкта, где будет только переменная с неизменяющейся соответствующей ей координатой.	Грань, на которой лежат закрашенные вершины и мы можем записать как конъюнкт .
Теперь мы смотрим, остались ли на рёбрах куба закрашенные и не отмеченные нами в ДНФ вершины. Если — да, то рёбра с такими вершинами мы можем записать в качестве конъюнкта, где будут только переменные с неизменяющимися соответствующим им координатами	Ребро, соединяющее закрашенные вершины и мы можем записать как конъюнкт .
И если после такой обработки у нас остались свободные вершины, мы просто переписываем координаты каждой такой вершины в отдельный конъюнкт, равный .	Вершину мы бы переписали как конъюнкт .

В итоге нашу изначальную ДНФ можно записать как .

Карты Карно

Построим следующую таблицу , где — число переменных:

Теперь для каждого конъюнкта мы помечаем соответствующую ему ячейку таблицы.

Теперь покрываем прямоугольниками (длины сторон которых — степени двойки ()) те ячейки карт Карно, которые содержат в себе единицу (на каждом ходу мы выбираем такой прямоугольник, чтобы он покрывал наибольшее количество ещё не покрытых клеток) до тех пор, пока не покроем все такие ячейки.

Для карт Карно на примере это выглядело бы так:

После этого записываем каждый прямоугольник в виде конъюнкта, в котором будут указаны только те переменные, которые одинаковы для всех ячеек этого прямоугольника.

То есть, в этом примере получаем: 

Метод Квайна

Этот метод основан на применении двух основных операций:

• Операция попарного неполного склеивания:

• Операция элементарного поглощения:

(где — некоторая элементарная конъюнкция, то есть конъюнкт, в который каждая из переменных входит не более одного раза)

Например:

Пусть , тогда:

• Операция попарного неполного склеивания:

• Операция элементарного поглощения:

Метод состоит в последовательном выполнении всех возможных склеиваний и затем всех поглощений частей СДНФ пока это может быть осуществимо.

Описание алгоритма

• Исходным является множество пар вида или
• Выполняются все возможные операции неполного попарного склеивания для элементарных конъюнкций длины (где — число аргументов).
• Выполняются все возможные операции элементарного поглощения для элементарных конъюнкций длины (общая часть «» имеет длину )
• В результате получилось множество элементарных конъюнкций, разделяемых на два подмножества (по длине):
  • подмножество элементарных конъюнкций длины (оставшиеся)
  • подмножество элементарных конъюнкций длины
• Если множество элементарных конъюнкций длины не пусто, то заново выполняются операции неполного попарного склеивания и элементарного поглощения для конъюнкций длины и так далее.

Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания.
После выполнения этого алгоритма будет получена сокращенная (но еще не минимальная) форма.

Переход от сокращённой формы к минимальной осуществляется с помощью специальной таблицы.
Члены СДНФ заданной функции вписываются в столбцы, а в строки — члены сокращённой формы. Отмечаются столбцы членов СДНФ, которые поглощаются отдельными элементами сокращённой формы.

Члены сокращённой формы, не подлежащие исключению, образуют ядро. Такие члены определяются по вышеуказанной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только этим членом.

Для получения минимальной формы достаточно выбрать из членов сокращённой формы, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих членов, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра.

Пример

Функция от четырёх аргументов задана следующей таблицей:

Набор
Значение исходной функции

Проведём операции неполного склеивания и поглощения:

№	Элементарная конъюнкция	Поглощение

№ склеивания	Результат

На данном шаге все элементы вида или участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому элементы сокращённой ДНФ на этом шаге не получены.

№	Элементарная конъюнкция	Поглощение

№ склеивания	Результат

На данном этапе получаем элементы сокращённой ДНФ и

№	Элементарная конъюнкция	Поглощение

Обе элементарные конъюнкции на данном шаге являются элементами сокращённой ДНФ.

В результате выполнения алгоритма мы получаем следующую сокращённую ДНФ:

Переход от сокращённой формы к минимальной:

• Единицы ДНФ, покрываемые элементами или обозначаются «+». Пары и , попадающие в ядро помечаются «*».
• Единицы функции, которые покрываются только каким-то одним конъюнктом из системы элементов сокращённой ДНФ, помечаются “>”.
• Единицы функции, покрываемые ядром, но не покрываемые только каким-то одним конъюнктом из системы элементов сокращённой ДНФ помечаются “>>”.

На основе этой таблицы получим ядро , которое является также и минимальной ДНФ.

См. также

• ДНФ
• КНФ

Источники информации

• Минимизация логических функций методом Куайна — Википедия
• Метод Квайна
• Карта Карно — Википедия
• Минимизация булевых функций в классе ДНФ
• Минимизация ДНФ методом Квайна

6.1 Сокращенная и тупиковая ДНФ

6.2 Метод импликантных матриц

Цель данного раздела – изложение основных методов построения минимальных дизъюнктивно нормальных форм.

6.1 Сокращенная и тупиковая ДНФ. В разделе 3 было показано, что любая булева функция может быть представлена дизъюнктивной нормальной формой. Следует отметить, что дизъюнктивная нормальная форма часто допускает упрощение. При этом путем различных тождественных преобразований получится дизъюнктивная нормальная форма, эквивалентная исходной, но содержащая меньшее число вхождений символов.

Дизъюнктивная нормальная форма называется Минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей дизъюнктивными нормальными формами.

Заметим, что если некоторый символ в формуле, скажем , встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.

Основной вопрос данного параграфа – это как для произвольной булевой функции построить ей минимальную дизъюнктивную нормальную форму. Эта задача называется Проблемой минимизации булевых функций.

Существует тривиальный алгоритм построения минимальной ДНФ для произвольной булевой функции . Для этого все ДНФ, составленные из символов упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение . Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции .

Число различных ДНФ, составленных из переменных , равно .

Прежде чем доказать данное утверждение, приведем следующее определение.

Конъюнкция называется Элементарной, если при .

Число R называется Рангом элементарной конъюнкции. В случае r=0 конъюнкция называется Пустой и Полагается равной 1.

Так как каждая из N переменных либо не входит в элементарную, либо входят в нее с отрицанием, либо без отрицания, то число элементарных конъюнкций, составленных из равно . Ясно, что число различных ДНФ, составленных из переменной , равно числу подмножеств множества, из элементов, т. е. .

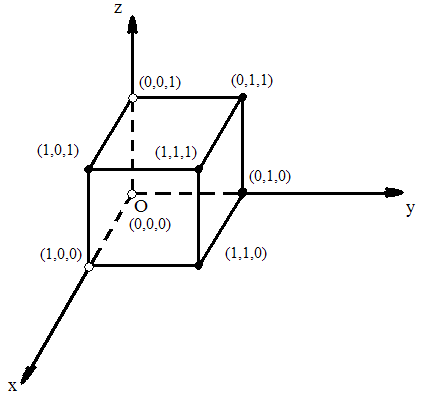
Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций.

Обозначим через множество всех точек , где . Ясно, что — множество всех вершин единичного n-мерного куба.

Сопоставим каждой булевой функции Подмножество Из , определенное следующим образом:

Например, функции

X	Y	Z
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Соответствует подмножество

Вершин трехмерного единичного куба

Данное соответствие является взаимно однозначным и обладает следующими свойствами:

1) булевой функции Соответствует подмножество ;

2) булевой функции соответствует подмножество ;

3) булевой функции соответствует подмножество .

Докажем утверждение 2. Пусть

Отсюда .

Тогда .

А это значит, что .

Отсюда .

Пусть ДНФ, где — элементарные конъюнкции. Подмножество называется интервалом R-го ранга, если оно соответствует элементарной конъюнкции К R-го ранга. Как показано выше, . Итак, с каждой ДНФ функции F связано покрытие такими интервалами , что .

Пусть — ранг интервала . Тогда совпадает с числом букв в ДНФ функции .

Теперь ясно, что задача построения минимальной ДНФ сводится к отысканию такого покрытия подмножества интервалами , чтобы число было наименьшим.

Интервал , содержащий , называется Максимальным для булевой функции, если не существует интервала , такого, что .

Заметим, что соотношение выполняется тогда и только тогда, когда элементарная конъюнкция получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.

Очевидно, что каждый интервал из содержится в некотором максимальном интервале. Если — список всех максимальных интервалов подмножества , то нетрудно видеть, что .

ДНФ булевой функции f, соответствующая покрытию подмножества всеми максимальными интервалами, называется Сокращенной ДНФ функции F.

Ясно, что сокращенная ДНФ для любой булевой функции f определяется однозначно.

Пример 1. Пусть . Обозначим , , . Найдем соответствующие этим конъюнкциям интервалы , , .

Изобразим эти интервалы

Очевидно, что и — все максимальные интервалы. Интервал не является максимальным, ибо . Следовательно, покрытию подмножества соответствует сокращенная ДНФ функции , равная .

Данный геометрический подход дает и метод построения сокращенной ДНФ.

Теперь рассмотрим аналитический метод построения сокращенной ДНФ – метод Блейка. Этот метод основан на следующей теореме.

Теорема 1. Если в произвольной ДНФ булевой функции F произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получиться сокращенная ДНФ функции F.

Следовательно, чтобы найти сокращенную ДНФ, надо к произвольной ДНФ данной функции применить правило обобщенного склеивания до тех пор, пока это возможно, а затем правило поглощения.

Пример 2. Найти сокращенную ДНФ для функции . Применяя правило обобщенного склеивания, получаем: .

Затем правило поглощения и находим сокращенную ДНФ: .

Рассмотрим еще один метод построения сокращенной ДНФ – метод Нельсона. Этот метод основан на следующей теореме.

Теорема 2. Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции.

Пример 3. Найти сокращенную ДНФ для функции

После раскрытия скобок с помощью дистрибутивного закона, получаем:

.

Так как , , то имеем:

.

Далее, применяя правило поглощения, получаем сокращенную ДНФ:

.

Рассмотрим табличный метод построения сокращенной ДНФ. Этот метод основан на составлении прямоугольной таблицы (минимизирующей карты).

Минимизирующие карты для булевых функций от трех и от четырех переменных изображены на следующих таблицах.

Z X y	0	1
00
01
11
10

X4 X3 X1 X2	0 0	0 1	1 1	1 0
0 0
0 1
1 1
1 0

Объединяя соседние клетки, соответствующие единичным значениям булевой функции f в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.

Пример 4. Найти сокращенную ДНФ для функции, заданной следующей таблицей.

X4 X3 X1 X2	0 0	0 1	1 1	1 0
0 0	1	1	0	1
0 1	0	1	1	0
1 1	1	1	1	0
1 0	0	1	0	0

В данной таблице объединены клетки в максимальные интервалы

.

Этим интервалам соответствуют элементарные конъюнкции

, , , ,

Следовательно, сокращенная ДНФ для данной функции имеет вид:

Построение сокращенной ДНФ есть только первый этап решения задачи минимизации булевой функции. В общем случае сокращенная ДНФ не является минимальной. Следующая теорема устанавливает связь между минимальной и сокращенной ДНФ.

Теорема 3. Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций.

Доказательство этого утверждения следует из того факта, что покрытие подмножества , отвечающее минимальной ДНФ, состоит только из максимальных интервалов. Действительно, если бы покрытие содержало не максимальный интервал, то его можно было бы заменить объемлющим максимальным интервалом. В результате этого сумма рангов интервалов данного покрытия уменьшилась бы, что противоречит предположению о минимальности ДНФ.

Покажем, что в классе монотонных функций понятия минимальной и сокращенной ДНФ совпадают.

Теорема 4. Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции.

Пусть К – элементарная конъюнкция, входящая в сокращенную ДНФ. Предположим, что К содержит отрицание переменных. Обозначим через произведение всех переменных, входящих в К без отрицания. Пусть – набор переменных, в которых всем переменным, входящим в , приписано значение 1, а всем остальным – значение 0. Ясно, что при этом наборе значение функции Равно 1. Элементарная конъюнкция обращается в 1 при всех наборах . Очевидно, что при этих наборах значение функции также равно 1. Следовательно, .

Получили противоречие с максимальностью интервала . Итак, сокращенная ДНФ булевой функции Не содержит отрицаний переменных.

Пусть — любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами . Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция обращалась в этой вершине в 1, то не содержала бы, во-первых, букв , и, во-вторых, букв . Поэтому в конъюнкцию могли бы входить лишь буквы , причем не все. Но тогда . Получили противоречие с максимальностью интервала . Следовательно, для любого максимального интервала существует вершина куба , которая покрывается только этим интервалом. Поэтому из покрытия соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.

Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. Действительно, в сокращенной ДНФ

Элементарная конъюнкция поглощается дизъюнкцией остальных элементарных конъюнкций, т. е. .

Ввиду этого введем следующее определение.

Покрытие области истинности булевой функции максимальными интервалами называется Неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции , соответствующая неприводимому покрытию, называется Тупиковой.

Теорема 5. Всякая минимальная ДНФ является тупиковой.

Доказательство этого утверждения следует из того, что покрытие, соответствующее минимальной ДНФ, является неприводимым.

Заметим, что булева функция может обладать несколькими различными минимальными ДНФ. Существуют также тупиковые ДНФ, не являющиеся минимальными ДНФ. Соответствующие примеры будут разобраны ниже.

Из того, что минимальная ДНФ является тупиковой, следует общая схема решения задачи минимизации булевых функций.

1. Выделяются все максимальные интервалы, и строится сокращенная ДНФ.

2. Строятся все тупиковые ДНФ.

3. Среди всех тупиковых ДНФ выделяются все минимальные ДНФ.

Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем:

1) для булевой функции строим сокращенную ДНФ;

2) для каждой вершины из выделяем в сокращенной ДНФ функции F все такие элементарные конъюнкции , что ;

3) составляем выражение вида

(*)

4) применяем к выражению вида (*) законы дистрибутивности и поглощения. В результате получаем .

Теперь каждая ДНФ является тупиковой ДНФ функции .

Рассмотрим работу данного алгоритма на следующем примере.

Пример 5. Рассмотрим булеву функцию, заданную следующей таблицей:

X	Y	Z
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Найдем сокращенную ДНФ данной функции по методу Нельсона. Для этого составим КНФ данной функции .

Применяя законы дистрибутивности, получаем:

.

Обозначим , , , , , .

Составляем выражение (*)

Преобразуем данное выражение к виду

= =.

Таким образом, имеет шесть тупиковых ДНФ:

Две из них и являются минимальными.

6.2 Метод импликантных матриц. Для булевой функции находим сокращенную ДНФ . Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются , а в горизонтальные .

			…		…
…
				+
…

Для каждой находим набор такой, что .

Клетку импликантной матрицы, образованную пересечением I-строки и J-столбца отметим крестиком.

Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число , которые совместно накрывают крестиками все столбцы импликантной матрицы.

Пример 6. Найти минимальные ДНФ для функции

.

Из предыдущего примера следует, что сокращенная ДНФ для данной функции . Очевидно, что

.

Строим импликантную матрицу

	(0,0,1)	(0,1,0)	(0,1,1)	(1,0,0)	(1,0,1)	(1,1,0)
				+	+
				+		+
		+	+
		+				+
	+		+
	+				+

Отсюда видно, что данная функция имеет два минимальные ДНФ:

; .

Вопросы для самоконтроля.

1. Дайте определение основных логических операций булевой алгебры.

2. Дайте определение булевой функции.

3. Что такое таблицы истинности булевой функции?

4. Каково число булевых функций от переменных?

5. Какие булевы функции называются элементарными?

6. Дайте определение формулы алгебры логики.

7. Какие формулы алгебры логики называются равносильными?

8. Сформулируйте законы алгебры логики.

9. Какая формула алгебры логики называется двойственной к данной формуле алгебры логики?

10. Сформулируйте принцип двойственности.

11. Сформулируйте теорему о разложении и следствие из нее.

12. Дайте определение СДНФ.

13. Приведите алгоритмы построения СДНФ.

14. Дайте определение СКНФ.

15. Приведите алгоритмы построения СКНФ.

16. Дайте определение ДНФ.

17. Как найти ДНФ?

18. Дайте определение КНФ.

19. Как найти КНФ?

20. Какая формула алгебры логики называется тождественно истинной?

21. Какая формула алгебры логики называется тождественно ложной?

22. Какая формула алгебры логики называется выполнимой?

23. Что называется проблемой разрешимости?

24. Сформулируйте методы решения проблемы разрешения.

25. Что называется алгеброй Жегалкина?

26. Сформулируйте законы алгебры Жегалкина.

27. Что называется полиномом Жегалкина?

28. Сформулируйте алгоритмы построения полиномов Жегалкина.

29. Какая система булевых функций называется полной?

30. Что называется замыканием множества булевых функций?

31. Какой класс булевых функций называется замкнутым?

32. Дайте определение пяти важнейших замкнутых классов.

33. Сформулируйте теорему о полноте.

34. Сформулируйте алгоритм Поста.

35. Какая система булевых функций называется несократимой?

36. Каково максимальное возможное число функций в несократимой полной системе булевых функций?

37. Что такое релейно-контактная схема?

38. Почему любую булеву функцию можно изобразить в виде релейно-контактной схемы?

39. В чем состоит проблема анализа релейно-контактных схем?

40. В чем состоит проблема синтеза релейно-контактных схем?

41. Что такое логические элементы?

42. Приведите геометрическое изображение логических элементов.

43. Что такое логическая схема?

44. Что Вы понимаете под двоичным сумматором?

45. Какая ДНФ называется минимальной?

46. Чему равно число всех ДНФ от переменных?

47. Сформулируйте тривиальный алгоритм построения МДНФ?

48. Что такое элементарная конъюнкция?

49. Что такое ранг элементарной конъюнкции?

50. Что называется интервалом элементарной конъюнкции?

51. Какой интервал называется максимальным?

52. Что называется областью истинности булевой функции?

53. Сформулируйте теорему об области истинности булевой функции.

54. Что называется покрытием области истинности булевой функции?

55. Какое число элементов содержится в интервале?

56. Какая ДНФ называется сокращенной?

57. В чем состоит геометрическая интерпретация задачи минимизации булевой функции?

58. Сформулируйте геометрический метод построения сокращенной ДНФ.

59. Сформулируйте метод Нельсона построения сокращенной ДНФ.

60. Сформулируйте метод Блейка построения сокращенной ДНФ.

61. Сформулируйте метод карт Карно построения сокращенной ДНФ.

62. Какая связь между МДНФ и сокращенной ДНФ?

63. Какое покрытие области истинности булевой функции называется неприводимым.

64. Какая ДНФ называется тупиковой?

65. Какая связь между МДНФ и тупиковой ДНФ?

66. Сформулируйте алгоритм построения всех тупиковых ДНФ.

67. Как строится импликантная матрица?

68. Сформулируйте алгоритм нахождения МДНФ методом импликантных матриц.

< Предыдущая		Следующая >

Материал из eSyr’s wiki.

Перейти к: навигация, поиск

[править] По заданной ФАЛ построить ее сокращенную ДНФ, ДНФ Квайна, ДНФ сумма тупиковых, все тупиковые ДНФ

[править] Определения

[править] Функция алгебры логики

Функция алгебры логики — функция, переводящая вектор из n-элементов множества B = {0, 1} в элемент множества B. То есть, для каждого набора нулей и единиц у функции определено значение, равное нулю или единице.

[править] Построение сокращённой ДНФ

[править] Определения

[править] Буква x^σ

Есть алфавит X(n) = {x₁, … x_n}. Буква x_i^σ есть x_i, если σ = 1, и x̅_i, если σ = 0.

[править] Конъюнкция ранга r

Конъюнкция ранга r K = x_i1^σ₁…x_ir^σ_r, 0 ≤ r ≤ n; K = 0 при r = 0.

[править] Элементарная конъюнкция

Элементарная конъюнкция — конъюнкция, у которой все переменные в буквах различны: x_ik^σ_l ≠ x_il^σ_l при k ≠ l

[править] Импликанта

Элементарная конъюнкция К называется импликантой f, если K ∨ f = f.

[править] Простая импликанта

Импликанта К функции f называется простой импликантой, если при вычёркивании любой буквы K получается элементарная конъюнкция, которая не является импликантой f.

[править] Сокращённая ДНФ

Сокращённая ДНФ — дизъюнкция всех простых импликант f

[править] Геометрический метод (с использованием единичного куба)

• Рисуем единичный куб (для 6 и более переменных это уже затруднительно)

Единичный куб для двух переменных	Единичный куб для трёх переменных	Единичный куб для четырёх переменных
Единичный куб для пяти переменных

• Отмечаем все грани максимальной размерности, во всех точках которых функция равна единице
• Отмечаем все грани размерности на единицу меньше, во всех точках которых функция равна единице
• …
• Отмечаем все вершины, в которых функция равна единице

Таким образом, мы наглядно получаем максимальные грани, видим местоположение ядровых точек и т. п.

[править] Пример

Построить сокращённую ДНФ для функции f = (0110 1111). С использованием единичного куба.

Решение.
Размеченный куб представлен справа. Как видно из иллюстрации, можно выделить следующие максимальные грани:

• (1 − −) → x₁
• (− 1 0) → x₂x₃
• (− 0 1) → x₂x₃

В результате получим сокращённую ДНФ x₁ ∨ x₂x₃ ∨ x₂x₃

[править] Метод Блейка

Пусть у нас имеется произвольная ДНФ функции f. Определим два преобразования:

• xA ∨ xB → xA ∨ xB ∨ AB
• A ∨ AB → A

Тогда, если сначала применять к имеющейся ДНФ первое преобразование, пока это возможно, а потом — второе, то получим сокращённую ДНФ.

[править] Пример

Построить сокращённую ДНФ по имеющейся ДНФ

x1x2x3 ∨ x1x2x3 ={применяем первое правило}= x1x2x3 ∨ x1x2x3 ∨ x1x3 ={применяем второе правило дважды}= x1x3

[править] Метод Нельсона

Метод Нельсона использует КНФ функции f. Для построения сокращённой ДНФ по КНФ достаточно раскрыть скобки и привести подобные методом поглощения (A ∨ AB → A)

[править] Пример

Построить сокращённую ДНФ по имеющейся КНФ
f(x₁,x₂,x₃)=(x₃ ∨ x₁)(x₁ ∨ x₂ ∨ x₃)

f = x₃x₁ ∨ x₃x₂ ∨ x₃x₃ ∨ (x₁x₁) ∨ x₁x₂ ∨ x₁x₃
= x₃ ∨ x₃x₁ ∨ x₃x₂ ∨ x₁x₃ ∨ x₁x₂
= x₃ ∨ x₁x₂

[править] Метод с использованием карт Карно

Данный метод удобен для функций от 4 переменных (его также можно использовать для функций от 3 переменных, но для них обычно используются другие методы). Он основан на нахождении блоков единиц на построенной специальном образом карте значений функции. Карта строится следующим образом: по вертикали выписываются переменные x₁, x₂; по горизонатли — x₃, x₄. Пары переменых выписываются в порядке (00), (01), (11), (10). После чего в таблицу заносятся значения функции для данных значений переменных. Рассмотрим построение карты для функции f = (f₀₀₀₀f₀₀₀₁f₀₀₁₀f₀₀₁₁ f₀₁₀₀f₀₁₀₁f₀₁₁₀f₀₁₁₁ f₁₀₀₀f₁₀₀₁f₁₀₁₀f₁₀₁₁ f₁₁₀₀f₁₁₀₁f₁₁₁₀f₁₁₁₁):

	x3	0	0	1	1
x4	0	1	1	0
x1	x2
0	0		f0000	f0001	f0011	f0010
0	1		f0100	f0101	f0111	f0110
1	1		f1100	f1101	f1111	f1110
1	0		f1000	f1001	f1011	f1010

Далее на полученной карте находим все максимально возможные блоки единиц вида 2^k × 2^l; k, l ∈ N, учитывая тот факт, что карта закольцована. Блоки могут пересекаться, но не должны включать друг друга. Далее для каждого блока выписывается вектор, в котором в случае, если переменная в пределах этого блока меняла значение, знак «–», если же не меняет, то её значение в пределах блока. Для позиций вектора i, в которых стоит знак σ ∈ {0, 1}? в ЭК добавляется x_i^σ. Дизъюнкция всех полученных ЭК и есть сокращённая ДНФ.

[править] Пример

Найдём сокращённую ДНФ для функции f = (1010 0110 0111 1101) методом карт Карно.

Решение
Строим карту:

На основании карты получаем следующие блоки:

• (0 0 − 0) = x₁x₂x₄
• (0 − 1 0) = x₁x₃x₄
• (− 0 1 0) = x₂x₃x₄
• (− 1 0 1) = x₂x₃x₄
• (1 1 0 −) = x₁x₂x₃
• (1 0 1 −) = x₁x₂x₃
• (1 − − 1) = x₁x₄

В результате получаем сокращённую ДНФ x₁x₂x₄ ∨ x₁x₃x₄ ∨ x₂x₃x₄ ∨ x₂x₃x₄ ∨ x₁x₂x₃ ∨ x₁x₂x₃ ∨ x₁x₄

нужно обьединить в прямоугольник единицу (с координатами [1;1]) с единицей ,у которой координаты [4;1]
нужно обьединить в прямоугольник единицу (с координатами [4;1]) с единицей ,у которой координаты [4;4]
прокомментировал getbraine e-mail v000du@gmail.com

[править] Построение сокращенной ДНФ по совершенной ДНФ при помощи алгоритма Квайна

Алгоритм Квайна построения сокращенной ДНФ по совершенной ДНФ:
0) i:=1
1)Пока возможно к слагаемым ранга n-i+1 применять неполное склеивание:

   xK v (not x)K = xK v (not x)K v K

2)пока возможно поглощение
3) i++; if (i<=n) goto 1

[править] Построение ДНФ Квайна

ДНФ, которую получают путем выбрасывания всех простых импликант, соответствующих максимальным граням, которые покрываются ядром, называется ДНФ Квайна.

Алгоритм построения ДНФ Квайна:

1. получить сокращенную ДНФ;

2. найти ядровые грани;

3. удалить импликанты, покрываемые ядром.

Полученная ДНФ, является ДНФ Квайна.

[править] Построение ДНФ ΣT (суммы тупиковых)

см ниже

[править] Построение всех тупиковых ДНФ

Пусть мы ищем все тупиковые решения для ФАЛ f. Выпишем таблицу M(таблицу Квайна), в которой столбцам соответствуют элементы из N_f (наборы, на которых функция принимает значение 1), строкам соответствуют максимальные грани. В ячейке стоит 1, если грань, соответствующая строке содержит набор, соответствующий столбцу.

Затем выписываем КНФ функции покрытия следующим образом:

Пусть каждой строке соответствует некоторая переменая y_i.

Для каждого столбца, переменные, соотвествующие строкам в которых в данном столбце стоит 1, запишем через логическое или. Функция покрытия равна произведению таких сумм для каждого столбца.

[править] Пример

Есть функция g: N_g = {α₁ = (100), α₂ = (110), α₃ = (010), α₄ = (011), α₅ = (001), α₆ = (101) }.

Множество максимальных граней = {N₁,…,N₆}, где N_i={α_i,α_i+1}, причем α₇=α₁.

Таблица Квайна:

ФАЛ покрытия: F(y) = (y₆ ∨ y₁)(y₁ ∨ y₂)(y₂ ∨ y₃)(y₃ ∨ y₄)(y₄ ∨ y₅)(y₅ ∨ y₆).

Раскрывая скобки и приводя подобные, получаем:

F(y) = y₁y₃y₅ ∨ y₂y₄y₆ ∨ y₁y₂y₄y₅ ∨ y₂y₃y₅y₆ ∨ y₁y₃y₄y₅.

Это соответствет тупиковым покрытиям 1 = N₁N₃N₅; 2 = N₂N₄N₆; и т.д.

[править] Пример

Построить все тупиковые ДНФ для ФАЛ f = (1010 0110 0111 1101).

Решение.

Сокращённая ДНФ для данной функции есть x₁x₂x₄ ∨ x₁x₃x₄ ∨ x₂x₃x₄ ∨ x₂x₃x₄ ∨ x₁x₂x₃ ∨ x₁x₂x₃ ∨ x₁x₄ (как было получено ранее). Выпишем все точки, где ЭК принимают значение, равное единице, следующим образом:

ЭК	x1x2x4	∨	x1x3x4	∨	x2x3x4	∨	x2x3x4	∨	x1x2x3	∨	x1x2x3	∨	x1x4
αi	α1 = (0000) α2 = (0010)		α2 = (0010) α3 = (0110)		α2 = (0010) α4 = (1010)		α5 = (0101) α6 = (1101)		α7 = (1100) α6 = (1101)		α4 = (1010) α8 = (1011)		α9 = (1001) α8 = (1011) α6 = (1101) α10 = (1111)

Построим таблицу (таблицу Квайна), у которой по строкам указаны ЭК, а по столбцам — точки, где функция принимает значение, равное единице. На пересечении ЭК и точки будет стоять значение ЭК в этой точке (фактически, входит ли данная точка в характеристическое множество данной ЭК, или нет). Для наглядности, единицы выделены.

	α1	α2	α3	α4	α5	α6	α7	α8	α9	α10
K1 = x1x2x4	1	1	0	0	0	0	0	0	0	0
K2 = x1x3x4	0	1	1	0	0	0	0	0	0	0
K3 = x2x3x4	0	1	0	1	0	0	0	0	0	0
K4 = x2x3x4	0	0	0	0	1	1	0	0	0	0
K5 = x1x2x3	0	0	0	0	0	1	1	0	0	0
K6 = x1x2x3	0	0	0	1	0	0	0	1	0	0
K7 = x1x4	0	0	0	0	0	1	0	1	1	1

Далее, определим ядровые точки, то есть те α_i, у которых в столбце только одна единица. Таковыми являются α₁, α₃, α₅, α₇, α₉, α₁₀. Соответственно, ядровыми гранями являются те грани, которые соответствуют конъюнкциям, которым принадлежат ядровые вершины (смотрим на строки, в которых хотя бы для одного из выбранных столбцов α_i стоит единица), то есть K₁, K₂, K₄, K₅, K₇. Дизъюнкция этих конъюнкций есть пересечение тупиковых.

Для нахождения всех тупиковых ДНФ построим КНФ, элементарныё дизъюнкции которой будут состоять из БП, соответствующих тем конъюнкциям, в которые входит рассматриваемая точка α_i (то есть, всего дизъюнкций столько же, сколько есть точек, где функция принимает единичное значение, причём первая дизъюнкция будет содержать те БП, которые соответствуют тем ЭК, которым принадлежит α₁ (в данном примере это K₁), вторая — те, которые соответствуют ЭК, которым принадлежит α₂ (K₁, K₂, K₃), и так далее):

K₁ & (K₁ ∨ K₂ ∨ K₃) & K₂ & (K₃ ∨ K₆) & K₄ & (K₄ ∨ K₅ ∨ K₇) & K₅ & (K₆ ∨ K₇) & K₇ & K₇

После раскрытия и приведения подобных получим ДНФ, состоящих из ЭК, которые будут соответствовать тупиковым ДНФ, причём БП в ЭК будут соответствовать ЭК, входящим в тупиковую ДНФ:

K₁ & (K₁ ∨ K₂ ∨ K₃) & K₂ & (K₃ ∨ K₆) & K₄ & (K₄ ∨ K₅ ∨ K₇) & K₅ & (K₆ ∨ K₇) & K₇ & K₇ = K₁K₂K₄K₅K₇ & (K₁ ∨ K₂ ∨ K₃) & (K₃ ∨ K₆) & (K₄ ∨ K₅ ∨ K₇) & (K₆ ∨ K₇) = K₁K₂K₄K₅K₃K₇ ∨ K₁K₂K₄K₅K₆K₇

ДНФ K₁K₂K₃K₄K₅K₇ ∨ K₁K₂K₄K₅K₆K₇ соответствует тупиковым ДНФ

K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 ∨ K7	x1x2x4 ∨ x1x3x4 ∨ x2x3x4 ∨ x2x3x4 ∨ x1x2x3 ∨ x1x4
K1 ∨ K2 ∨ K4 ∨ K5 ∨ K6 ∨ K7	x1x2x4 ∨ x1x3x4 ∨ x2x3x4 ∨ x1x2x3 ∨ x1x2x3 ∨ x1x4