1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы и
,
и противоположно направленные им векторы, например:
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам .
А теперь рассмотрим произвольный вектор либо
и поставим задачу найти
единичный вектор , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора
разделить на его длину:
либо
,
или, что то же самое – умножить каждую координату вектора на
. То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
либо
Задача 10
Найти единичные векторы, коллинеарные векторам а) , б)
. Выполнить проверку.
Решение: а) вычислим длину вектора и найдём
сонаправленный единичный вектор:
, от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
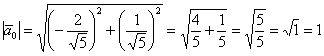
Второй вектор очевиден: , как очевидна и его
длина .
Ответ:
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Вспомним для начала основные понятия и формулы.
Пусть даны две точки: А(x1; x2) и B(y1; y2). Рассмотрим отрезок AB.
Длина отрезка АВ – это расстояние между точками A и B, его величина вычисляется по следующей формуле:
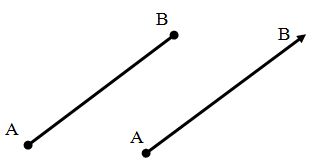
Рассмотрим теперь вектор AB. Напомню, что вектор – это направленный отрезок, то есть для него указано, какая из двух точек A и B является началом, а какая – концом. На рисунке ниже слева изображен отрезок AB, а справа – вектор AB с началом в точке A и концом в точке B.
Координаты вектора AB вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора. Например, для нашего вектора AB это будет выглядеть так: AB(x2 – x1; y2 – y1).
Замечу, что модулем вектора AB называется длина отрезка AB.
Вспомним как найти координаты середины отрезка AB. Для этого есть простая формула:
x = (x1 + x2)/2, y = (y1 + y2)/2.
До этого момента мы рассматривали координаты на плоскости, а что, если речь пойдет о пространстве? Тут, оказывается, тоже все просто.
Пусть даны две точки A(x1; x2; x3) и B(y1; y2; y3).
Формула для вычисления длины отрезка AB, расположенного в пространстве будет выглядеть так:
А координаты середины отрезка AB найдем по формуле
x = (x1 + x2)/2, y = (y1 + y2)/2, z = (z1 + z2)/2.
И еще одна полезная формула: если вектор задан своими координатами, например, MN(x1; x2; x3), то его модуль вычисляется по формуле:
Чтобы сложить два или более векторов, нужно сложить их соответствующие координаты, например,
(x1; x2; x3) + (y1; y2; y3) = (x1 + y1; x2 + y2; x3 + y3).
Чтобы умножить вектор на число, нужно умножить каждую его координату на это число, например,
5 · (x1; x2; x3) = (5 · x1; 5 · x2; 5 · x3).
Скалярным произведением двух векторов а и b называется число
a · b = |a»b| · сos (a, b),
Чтобы вычислить скалярное произведение векторов, заданных координатами, например, MN(x1; x2; x3) и PK(y1; y2; y3), можно воспользоваться следующей формулой:
MN · PK = x1 · y1 + x2 · y2 + x3 · y3.
Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
На практике коллинеарность векторов (x1; x2) и (y1; y2) проще всего проверить, используя следующее свойство: коллинеарные векторы имеют пропорциональные координаты, то есть существует число p, такое, что (x1; x2) = p · (y1; y2).
Существуют также такие понятия, как сонаправленные векторы и противоположно направленные векторы. Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону, соответственно, противоположно направленные векторы – это коллинеарные векторы, которые направлены в разные стороны.
Теперь давайте рассмотрим несколько задач на эту тему.
Задача 1.
Доказать, что треугольник с вершинами A(6; -4; 2), B(3; 2; 3) и C(3; -5; -1) прямоугольный.
Решение.
Вполне очевидно, что для доказательства этой задачи достаточно показать, что один из углов треугольника ABC равен 90 градусов. Вспомним формулу для вычисления скалярного произведения через модули соответствующих векторов и косинус угла между ними, преобразуем ее и воспользуемся для нахождения угла.
сos (a, b) = a · b/|a»b|.
Для начала нам понадобятся координаты всех векторов, задающих стороны треугольника, их модули и всевозможные скалярные произведения. Вычисляем их.
Координаты векторов:
AB(3 – 6; 2 – (-4); 3 – 2) = AB(-3; 6; 1);
BC(3 – 3; -5 – 2; -1 – 3) = BC(0; -7; -4);
CA(6 – 3; -4 – (-5); 2 – (-1)) = CA(3; 1; 3).
Модули:
|AB| =
|BC| =
|CA| =
Скалярные произведения:
AB · BC = (-3) · 0 + 6 · (-7) + 1 · (-4) = 0 – 42 – 4 = -46;
BC · CA = 0 · 3 + (-7) · 1 + (-4) · 3 = 0 – 7 – 12 = -19;
AB · CA = (-3) · 3 + 6 · 1 + 1 · 3 = -9 + 6 + 3 = 0.
Теперь легко заметить, что угол между векторами AB и CA равен 90 градусов, так как
сos (AB, CA) = AB · CA / |AB»CA| = 0.
А, значит, угол А треугольника ABC равен 90 градусов, то есть треугольник ABC – прямоугольный, что и требовалось доказать.
Задача 2.
Даны точки А(0; 1; 2), B(1; 2; 4), C(-1; -1; 3) и D(1; 0; 0). Точки M и N – середины отрезков AC и BD. Найдите вектор MN и его модуль.
Решение.
Для начала найдем координаты точек M и N.
M((0 – 1)/2; (1 – 1)/2; (2 + 3)/2) = M(-1/2; 0; 5/2);
N((1 + 1)/2; (2 + 0)/2; (4 + 0)/2) = N(1; 1; 2).
Теперь найдем координаты вектора MN:
MN(1 – (-1/2); 1 – 0; 2 – 5/2) = MN(3/2; 1; -1/2).
Осталось найти модуль вектора MN.
|MN| =
Задача 3.
При каких значениях x векторы (x3 – 1)a и 2xa сонаправлены, где a – вектор, не равный нулевому вектору?
Решение.
Для того чтобы данные векторы были сонаправлены, необходимо, чтобы коэффициенты (x3 – 1) и 2x имели одинаковый знак, а значит, чтобы выполнялось следующее неравенство: (x3 – 1) · 2x > 0. Решим его методом интервалов и найдем соответствующие x.
Получим x € (-∞; 0) U (1; +∞).
Если бы в задаче требовалось узнать, при каких x данные векторы будут противоположно направлены, мы бы потребовали, чтобы у коэффициентов (x3 – 1) и 2x были различные знаки.
Задача 4.
Даны координаты вершин четырехугольника: A(2; -2), B(-3; 1), C(7; 7) и D(7; 1). Доказать, что ABCD – трапеция.
Решение.
Так как трапеция – это четырехугольник, у которого одна пара противолежащих сторон параллельна, то для доказательства нам достаточно показать, что векторы BC и AD – коллинеарны, то есть лежат на параллельных прямых. Найдем для начала их координаты.
BC(7 – (-3); 7 – 1) = BC(10; 6);
AD(7 – 2; 1 – (-2)) = AD(5; 3).
Заметим, что координаты векторов пропорциональны: (10; 6) = 2 · (5; 3). Это и указывает на то, что данные векторы коллинеарны, а, значит, ABCD – трапеция.
Остались вопросы? Не знаете, как выполнять действия над векторами?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Определение вектора
Вектором (от лат. vector – «переносчик») называется направленный отрезок, имеющий длину и определенное направление. Графически векторы изображаются в виде направленных отрезков прямой определенной длины (см. Рис. 1).
Рис. 1. Вектор
Вектор, начало которого есть точка , а конец – точка
, обозначается
(см. Рис. 1). Также векторы обозначают одной маленькой буквой, например
.
Коллинеарные векторы. Сонаправленные и противоположно направленные векторы
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых: (см. Рис. 2).
Рис. 2. Коллинеарные векторы
Два коллинеарных вектора и
называются сонаправленными векторами, если их направления совпадают:
(см. Рис. 2).
Два коллинеарных вектора и
называются противоположно направленнымивекторами, если их направления противоположны:
(см. Рис. 2).
Равные векторы
Векторы и
называются равными, если они сонаправлены и их абсолютные величины равны (см. Рис. 3).
, если: 1.
2.
Рис. 3. Равные векторы
Умножение вектора на число
Произведение ненулевого вектора начисло – это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа (см. Рис. 4).
Рис. 4. Произведение вектора на число
Сложение векторов
(см. Рис. 5)
Рис. 5. Сложение векторов
Координаты коллинеарных векторов
Даны два коллинеарных вектора и
(см. Рис. 6), причем
.
Рис. 6. Коллинеарные векторы
– это коэффициент пропорциональности (число), для нахождения этого числа необходимо:
1. Если и
– это сонаправленные векторы:
2. Если и
– это противоположно направленные векторы:
Задание произвольного вектора на плоскости
На плоскости для задания произвольного вектора необходимы две координаты и пара неколлинеарных векторов.
Теорема
Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом, то есть для любых неколлинеарных ,
и для любого
найдется единственная пара действительных чисел
таких, что
.
Доказательство теоремы
Дано: ,
(см. Рис. 7)
Доказать:
1. ,
2. равенство верно для единственной пары чисел
.
Рис. 7. Иллюстрация к доказательству
Доказательство
1. Из точки проведем прямую (параллельно
), на пересечении с осью
получим точку
(см. Рис. 8). Вектор
будет равен:
Рис. 8. Иллюстрация к доказательству
Вектор коллинеарен вектору
, следовательно, найдется такое число
, которое при умножении на вектор
даст нам вектор
.
Вектор коллинеарен вектору
, следовательно, найдется такое число
, которое при умножении на вектор
даст нам вектор
.
Следовательно:
То есть существует такая пара чисел , что:
.
2. Методом от противного докажем, что пара чисел единственна.
Имеем: для
Предположим, что существует другая пара чисел такая, что
. Вычтем из первого равенства второе:
Пусть , то есть
. Тогда:
Получили, что векторы и
коллинеарные:
, а это противоречит условию (
). Следовательно,
.
Аналогично доказывается, что . Таким образом:
Что и требовалось доказать.
Теорему можно сформулировать также следующим образом:
Неколлинеарные векторы и
образуют систему координат
. Любой третий вектор
однозначно представляется в виде линейной комбинации векторов
и
:
.
Пара действительных чисел – это координаты вектора. То есть вектор
имеет координаты
.
Задача 1
В системе координат с координатными и
построить заданный
с координатами
.
Решение
Вектора и
задают ось
и
. Необходимо построить вектор
:
Эта запись означает:
Рис. 9. Иллюстрация к задаче
Отложим на оси вектор
(см. Рис. 9). На оси
отложим вектор
. Проведем из точки
прямую, параллельную оси
, а из точки
– прямую, параллельную оси
. На пересечении этих прямых будет находиться точка
. Вектор
– это искомый вектор.
Если задана система координат, то под координатами точки на плоскости подразумеваются координаты вектора, проведенного из начала координат в эту точку. Например, в задаче 1 точка имеет координаты
.
Задача 2
Построить с координатами
.
Решение
Векторы и
задают ось
и
. Необходимо построить вектор
:
Эта запись означает:
Рис. 10. Иллюстрация к задаче
Отложим на оси вектор
(см. Рис. 10). На оси
отложим вектор
. Проведем из конца вектора
прямую, параллельную оси
, а из конца вектора
– прямую, параллельную оси
. На пересечении этих прямых будет находиться точка
. Вектор
– это искомый вектор.
Задача 3
Выписать координаты вектора.
Дано:
Решение
Координатами вектора являются числа
.
Ответ: .
Задача 4
Найти недостающие координаты и
, если известно, что
.
Решение
Данное равенство означает, что это один и тот же разложенный по векторам вектор, но записанный иначе. Следовательно, этому вектору соответствует единственная пара . Поэтому:
Ответ: ;
.
Задача 5
Найти и
, если
.
Решение
Нулевой вектор равен:
Следовательно, можно записать
Поэтому:
Ответ: ;
.
Список литературы
1. Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л.С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт ru.onlinemschool.com (Источник)
2. Интернет-сайт mathprofi.ru (Источник)
3. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Задачи 911, 913 – Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия, 7-9 (Источник)
2. Какие векторы называют равными?
3. Построить с координатами
.
Равные вектора
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
 |
| рис. 1 |
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Проверим равенство компонентов векторов
ax = bx = 1
ay = by => 8 = 2 n => n = 8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторов
a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Проверим равенство компонентов векторов
ax = bx = 1
ay = by = 2
az = bz => 4 = 2 n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Векторы на плоскости и в пространстве — основные определения
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Длину вектора A B → принято обозначать так A B → .
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .
Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
Равные векторы
В различных школьных учебниках определение равных векторов даётся по-разному.
В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.
Два вектора называются равными, если они совмещаются параллельным переносом.
(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).
Например, изображенные на рисунке
Равенство векторов обозначают так:
(Свойства равных векторов)
1) Равные векторы сонаправлены и имеют равные длины.
2) Равные векторы имеют равные координаты.
3) От любой точки можно отложить вектор, равный данному, и притом только один.
1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.
2) Пусть дан вектор
с началом в точке A(x1; y1) и концом в точке B(x2; y2).
По определению равных векторов, вектор
равный данному, получен из
Если этот параллельный перенос задан формулами
Найдём координаты каждого из векторов:
То есть координаты равных векторов
Что и требовалось доказать.
Таким образом, координаты задают длину и направление вектора, но не фиксируют его.
3) Пусть даны вектор
и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор
При таком параллельном переносе вектор
переходит в вектор
По определению равных векторов,
Что и требовалось доказать.
На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).
Например,
отложенный от точки C, равен вектору
(Признаки равенства векторов)
1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.
2) Если у векторов соответствующие координаты равны, то векторы равны.
1) Пусть векторы
сонаправлены и имеют одинаковые длины.
Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор
переводит в вектор
По определению равных векторов,
Что и требовалось доказать.
2) Пусть векторы
Параллельный перенос, заданный формулами
переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы
А это означает, что
Что и требовалось доказать.
В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.
Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.
http://zaochnik.com/spravochnik/matematika/vektory/vectory_na_ploskosti_i_v_prostranstve/
§ 1. Векторы.
.
Векторы. Основные понятия. Правила
действия с векторами.
Основные
понятия, связанные с векторами, в
стереометрии те же, что и в планиметрии.
Определение.
Вектором
называется направленный отрезок, т.е.
вектор однозначно определяется
направлением и длиной.
Любая
точка пространства может рассматриваться
как нулевой
вектор.
Определение.
Длиной
вектора
называется расстояние от начала вектора
до его конца
Определение.
Два ненулевых вектора называются
коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Коллинеарные
векторы могут быть сонаправленными
или противоположно
направленными.
Теорема.
Если векторы
и
коллинеарны и вектор
– ненулевой, то существует число k
такое, что .
Определение.
Два ненулевых вектора называются
противоположными,
если их длины равны и они противоположно
направлены.
Определение.
Векторы называются равными,
если они сонаправлены и их длины равны.
Определение.
Векторы называются взаимно
перпендикулярными
(ортогональными),
если угол между ними равен 90°.
К
известным правилам сложения векторов
(правила треугольника, параллелограмма,
многоугольника (или ломаной)) в пространстве
добавляется правило
параллелепипеда:
.
|
D Ad Bd Od
Cd |
Правила
сложения векторов:
① ;
② ;
③ .
Вычитание
векторов .
Правила
умножения вектора на число:
① β
· (λ
·
)
= (β
· λ)
·;
② 1
·
= ;
③ -1
·
= ;
④ (β
+ λ)·
= β
·
+ λ
· ;
⑤ λ
· ()
= λ
·
+ λ
· .
Теорема.
Любой вектор на плоскости можно разложить
единственным образом по двум неколлинеарным
векторам.
;
числа x,
y
называют коэффициентами разложения.
.
Компланарные векторы.
Определение.
Векторы называются компланарными,
если они параллельны одной плоскости
или лежат в одной плоскости. Другими
словами, векторы компланарны, если при
откладывании их от одной точки они будут
лежать в одной плоскости.
Очевидно,
что любые два вектора компланарны; три
вектора, два из которых коллинеарны,
также компланарны.
|
Векторы Векторы |
A1
C1
B1
B
C
A |
Теорема.
Любой вектор можно разложить по трём
данным некомпланарным векторам, причём
коэффициенты разложения определяются
единственным образом.
.
.
Скалярное произведение векторов.
Основные формулы.
Скалярное
произведение векторов вычисляется по
формуле
, где φ – угол между векторами
и .
Законы
скалярного произведения:
① ;
;
③;
④
и
перпендикулярны.
Из
определения скалярного произведения
получаем формулу для нахождения косинуса
угла между векторами:
.
Если
,
то угол φ
– острый;
Если
,
то угол φ
– тупой;
Если
,
то угол φ
– прямой.
§ 2. Координаты в пространстве.
.
Прямоугольная система координат в
пространстве.
Если
через точку пространства проведены три
попарно перпендикулярные прямые, на
каждой из которых выбрано направление
и выбрана единица измерения отрезков,
то говорят, что задана прямоугольная
система координат
в пространстве.
|
Оси Ox Oy Oz Координатные Вся |
z
x
y
O
|
Каждой
точке М
пространства сопоставляется тройка
чисел, которые называются её координатами.
Координатные
(базисные) векторы:
единичный
вектор оси абсцисс;
единичный
вектор оси ординат;
единичный
вектор оси аппликат.
Очевидно,
что координатные векторы не коллинеарны,
поэтому любой вектор
можно разложить по координатным векторам:
,
причём коэффициенты разложения x,
y,
z
определяются единственным образом и
называются координатами вектора.
Применяют
запись: .
Каждая
координата вектора равна разности
соответствующих координат его конца и
начала.
.
Правила
действий с векторами в координатах.
Основные формулы.
– Каждая
координата суммы двух или более векторов
равна сумме соответствующих координат
этих векторов.
– Каждая
координата разности двух векторов равна
разности соответствующих координат
этих векторов.
– Каждая
координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.
Длина
вектора :
.
Скалярное
произведение
векторов
и :
.
Косинус
угла
между векторами
и :
.
Условие
перпендикулярности
(ортогональности) векторов
и :
.
Условие
коллинеарности
векторов
и :
.
Расстояние
между точками
М1
и М2
:
|M1M2|
= .
Пусть
С
(x;
y;
z)
— середина
отрезка
M1M2.
Тогда координаты точки С:
;
;
.
-
Вопросы
и задачи
-
Точки
М
и К
– середины рёбер В1С1
и А1D1
параллелепипеда ABCDA1B1C1D1
соответственно. Укажите все пары:
а)
сонаправленных векторов;
б)
противоположно направленных векторов;
в)
равных векторов.
-
На
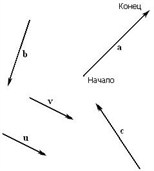
плоскости даны векторыи
.
Построить векторы: 3,
+,
.
-
ABCD
– параллелограмм,,
.
Выразить через
и
векторы,
,
,
.
-
Упростите
выражение: а);
б);
в);
г).
-
Даны
точки А, В, С и D.
Представьте вектор
в виде алгебраической суммы следующих
векторов: а),
,
;
б),
,
;
в),
,
.
-
Упростите
выражение: а);б)
;в)
.
-
Упростите:
а);
б).
-
Докажите,
что в параллелепипедеABCDA1B1C1D1
+
= 2.
-
Дан
параллелепипед ABCDA1B1C1D1.
Какие из следующих трёх векторов
компланарны: а);
б),
,
;
в);
г),
?
-
Дан
параллелепипед ABCDA1B1C1D1.
а) Разложите вектор
по векторам.
б) Разложите векторпо
векторам,
и.
-
Докажите,
что если М – точка пересечения медиан
треугольника АВС,
а О
– произвольная точка пространства, то
.
-
Даны
точки А (3; -1; 0), В (0; 0; -7), С (2; 0; 0), D(-
4; 0; 3), E
(0; -1; 0), F(1;
2; 3), G
(0; 5; -7), H
(-;
;
0). Какие из этих точек лежат на: а) оси
абсцисс; б) оси ординат; в) оси аппликат;
г) плоскости Oxy;
д) плоскости Оyz;
е) плоскости Оxz? -
Найдите
координаты проекций точек А (2; -3; 5), В
(3; -5;)
и С ()
на: а) координатные плоскости Оxz,
Oxy
и Oyz;
б) оси координат Ох,
Оу
и Оz. -
Даны
координаты четырёх вершин куба
ABCDA1B1C1D1:
А (0; 0; 0), В (0; 0; 1), D
(0; 1; 0) и А1
(1; 0; 0). Найдите координаты остальных
вершин куба. -
В
кубе ABCDA1B1C1D1
D
(0; 0; 0), C
(2; 0; 0), A1
(0; 2; 2). Найдите координаты остальных
вершин куба. -
Даны
точки А (1; 4; -3), В (-1; 0; -2). Найдите координаты
вектораи
его длину. -
Даны
три точки А (1; 0; 2), В (-1; -1; 0), С (1; 2; 0). Найти
векторы,
,
,
.
-
Даны
три точки А (2; 1; 0), В (-1; 3; 1), С (-1; 3; -4). Найти
векторы,
,
.
-
Даны
векторы
(5; 1; -1) и
(9; 0; -4). Найти вектор
и его длину. -
Даны
векторы
(5; 0; 1) и
(-7; 4; -2). Найти вектор
и его длину. -
Запишите
координаты векторов:,
,
,
,
,
.
-
Даны
векторы,
,
,
.
Запишите разложения этих векторов по
координатным векторам,
,
.
-
Даны
векторы
и.
Найти векторы;
;
;
.
-
Даны
векторы
и.
Найти векторы;
;
;
.
-
Даны
векторы,
,
и.
Найдите координаты векторов: а);
б);
в);
г);
д);
е);
ж);
з).
-
Даны
векторы(5;
-1; 1),
(-2; 1; 0),(0;
0,2; 0) и
().
Найдите координаты векторов: а);
б);
в);
г);
д);
е);
ж);
з) 2;
и) -3;
к) -6;
л);
м) 0,2.
-
Даны
векторы,
и
.
Найдите координаты векторови
.
-
Найдите
координаты векторов, противоположных
следующим векторам:,
,
,
,
,
).
-
Коллинеарны
ли векторы: а)
и
;
б)
и
;
в)
и
;
г)
и
;
д)
и
?
-
Найдите
значения m
и n,
при которых следующие векторы коллинеарны:
а)
и;
б)
и.
-
Даны
два вектора
и.
Найти x
и z,
если
||.
-
Даны
два вектора
и.
Найти k
и m,
если
||.
-
Определить,
при каких значениях х
векторы (х³
— 1)·
и 2х
являются сонаправленными, если.
-
Определить,
при каких значениях m
векторы (m²
— m
— 2)·
и m³·
противоположно направлены, если.
-
Даны
три последовательные вершины
параллелограмма: А (3; -1; 4), В (0; -2; 5) и
С (1; 2; 2). Найти четвёртую вершину
параллелограмма. -
Даны
три последовательные вершины
параллелограмма: А (2; 3; 4), В (1; -3; 7) и
С (4; 3; 7). Найти четвёртую вершину
параллелограмма. -
Даны
точки А (3; -1; 2), В (1; 2; -1), С (-1; 1; -3) и D
(3; -5; 3). Доказать, что ABCD
– трапеция. -
Найти
такое число m,
при котором векторы,
и
являются
компланарными. -
Установить,
являются ли компланарными следующие
векторы:
а)
(2; 3; -1); (1;
-1; 3); (1;
9; -11);
б)
(3; -2; 1);
(2; 1; 2);
(3; -1; -2);
в)
(2; -1; 2);
(1; 2; -3);
(3; -4; 7).
-
Компланарны
ли векторы: а),
и
;
б),
и
;
в)
,
и
;
г),
и
;
д),
и
(-1; 2; 4);
е),
и
?
-
Дан
куб ABCDA1B1C1D1.
Найдите угол между векторами: а)и
;
б)
и
;
в)
и
;
г)
и
;
д)
и
;
е)и
;
ж)
и
;
з)
и
.
-
Даны
векторы
(1; -1; 2),
(-1; 1; 1) и
(5; 6; 2). Вычислите,
,
,
,
.
-
Даны
векторы
(3; -1; 1),
(-5; 1; 0) и
(-1; -2; 1).Выясните, какой угол (острый,
прямой или тупой между векторами: а)
и;
б)
и;
в)
и.
-
Даны
векторы
и.
При каком значении mвекторы
и
перпендикулярны? -
Даны
точки А (0; 1; 2), В (;
1; 2), С (;
2; 1) и D
(0; 2; 1). Докажите, что ABCD
– квадрат. -
Вычислите
углы между вектором
и координатными векторами. -
Даны
точки А (1; 3; 0), В (2; 3; -1) и С (1; 2; -1). Вычислите
угол между векторами
и.
-
Найдите
углы, периметр и площадь треугольника,
вершинами которого являются точки А
(1; -1; 3), В (3; -1; 1) и С (-1; 1; 3). -
Найти
,
если ||
= 3; ||
= 4 и угол между
и
равен.
-
Найти
,
если ||
= 1; ||
= 2 и угол между
и
равен.
-
Найти
,
если ||
= 2; ||
= 3 и вектор.
-
Найти
,
если ||
= 3; ||
= 4; угол между
и
равен.
-
Найти
угол между векторами
и.
-
Дан
треугольник с вершинами в точках А (3;
-2; 1), В (3; 0; 2) и С (1; 2; 5). Найти угол,
образованный медианой BD
и стороной АС. -
Даны
вектора
и.
Найти угол, образованный векторами
и.
-
Найти
площадь параллелограмма, построенного
на векторахи
,
если векторыи
составляют угол 30° и.
-
Найти
площадь треугольника с вершинами А (2;
3; 1), В (4; 4; 0) и С (3; 1; -1). -
Точки
А (4; -3; 7), В (5; 3;и D
(10; -4; 6) являются вершинами ромба ABCD.
Найти длину диагонали АС.
П

Греческий
алфавит.
|
Α |
α |
альфа |
Ι |
ι |
йота |
Ρ |
ρ |
ро |
|
Β |
β |
бета |
Κ |
κ |
каппа |
Σ |
σ |
сигма |
|
Γ |
γ |
гамма |
Λ |
λ |
лямбда |
Τ |
τ |
тау |
|
Δ |
δ |
дельта |
Μ |
μ |
мю |
Υ |
υ |
ипсилон |
|
Ε |
ε |
эпсилон |
Ν |
ν |
ню |
Φ |
φ |
фи |
|
Ζ |
ζ |
дзета |
Ξ |
ξ |
кси |
Χ |
χ |
хи |
|
Η |
η |
эта |
Ο |
ο |
омикрон |
Ψ |
ψ |
пси |
|
Θ |
θ |
тета |
Π |
π |
пи |
Ω |
ω |
омега |
Латинский
алфавит.
|
A |
a |
а |
J |
j |
жи |
S |
s |
эс |
|
B |
b |
бе |
K |
k |
ка |
T |
t |
тэ |
|
C |
c |
це |
L |
l |
эль |
U |
u |
у |
|
D |
d |
де |
M |
m |
эм |
V |
v |
вэ |
|
E |
e |
э |
N |
n |
эн |
W |
w |
дубль-вэ |
|
F |
f |
эф |
O |
o |
о |
X |
x |
икс |
|
G |
g |
же |
P |
p |
пэ |
Y |
y |
игрек |
|
H |
h |
аш |
Q |
q |
ку |
Z |
z |
зет |
|
I |
i |
и |
R |
r |
эр |
Квадраты
натуральных чисел от 11 до 99.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
|
2 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
|
3 |
961 |
1024 |
1089 |
1156 |
1225 |
1296 |
1369 |
1444 |
1521 |
|
4 |
1681 |
1764 |
1849 |
1936 |
2025 |
2116 |
2209 |
2304 |
2401 |
|
5 |
2601 |
2704 |
2809 |
2916 |
3025 |
3136 |
3249 |
3364 |
3481 |
|
6 |
3721 |
3844 |
3969 |
4096 |
4225 |
4356 |
4489 |
4624 |
4761 |
|
7 |
5041 |
5184 |
5329 |
5476 |
5625 |
5776 |
5929 |
6084 |
6241 |
|
8 |
6561 |
6724 |
6889 |
7056 |
7225 |
7396 |
7569 |
7744 |
7921 |
|
9 |
8281 |
8464 |
8649 |
8836 |
9025 |
9216 |
9409 |
9604 |
9801 |
Факториалы.
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
n! |
1 |
1 |
2 |
6 |
24 |
120 |
720 |
5040 |
40320 |
362880 |
3628800 |
Степени.
|
n |
2n |
3n |
4n |
5n |
6n |
7n |
8n |
9n |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
3 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
|
4 |
16 |
81 |
256 |
625 |
1296 |
2401 |
4096 |
6561 |
|
5 |
32 |
243 |
1024 |
3125 |
7776 |
16807 |
32768 |
59049 |
|
6 |
64 |
729 |
4096 |
15625 |
46656 |
117649 |
262144 |
531441 |
|
7 |
128 |
2187 |
16384 |
78125 |
279936 |
823543 |
2097152 |
4782969 |
|
8 |
256 |
6561 |
65536 |
390625 |
1679616 |
5764801 |
16777216 |
43046721 |
|
9 |
512 |
19683 |
262144 |
1953125 |
10077696 |
40353607 |
134217728 |
387420489 |
|
10 |
1028 |
59049 |
1048576 |
9765625 |
60466176 |
282475249 |
1073741824 |
3486784401 |
Некоторые
сведения из курса планиметрии.
.
Площади
фигур.
Площадь
треугольника.
|
|
A
B
C
c
b
a |
Следствия
из формулы (1):
(
ha—
высота, проведённая к стороне a)
Площадь
квадрата со стороной a:
Площадь
прямоугольника со сторонами a
и b:
|
Площадь
|
a
b hb ha |
|
Площадь |
a
a h |
|
Площадь
|
a
b h N M |
Площадь
круга радиуса R:
Длина
окружности радиуса R:
Площади
подобных фигур относятся как квадрат
коэффициента подобия.
.
Теорема косинусов.
|
|
A
B
C
c
b
a |
.
Теорема синусов.
V.
Четыре
замечательных точки треугольника.
-
Медианы
треугольника пересекаются в одной
точке (центр тяжести) и делятся в
отношении 2 : 1, считая от вершины.Медиана
делит треугольник на два равновеликих.
Три медианы делят треугольник на
шесть равновеликих треугольников.
AM
BM
CM
A1
C1
B1
O
Высоты
треугольника пересекаются в одной точке
( ортоцентр).
Биссектрисы
треугольника
пересекаются в одной точке, которая
является центром окружности, вписанной
в данный треугольник.
Серединные
перпендикуляры к
сторонам треугольника пересекаются в
одной точке, которая является центром
окружности, описанной около данного
треугольника.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

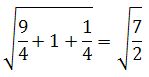







































 и D
и D




























