Онлайн-калькулятор соотношений поможет вам определить одинаковые коэффициенты, указав три из четырех частей двух соотношений. Кроме того, этот калькулятор соотношений лучше всего подходит для нахождения пятой и шестой частей из трех соотношений, давая любые четыре части. Наш решатель соотношений выполняет следующие семь операций как с двумя, так и с тремя отношениями.
- Найдите эквивалент отношения
- Сделайте соотношение больше
- Сделайте соотношение меньше
- Упростить соотношение
- Упростите соотношение до формы “1: n: m”
- Упростите соотношение до формы “n: 1: m”
- Упростите соотношение до формы “n: m: 1”
Прежде чем мы собираемся использовать этот калькулятор соотношений, мы должны знать основное определение, формулу соотношения и то, как найти соотношение вручную. Продолжайте читать, чтобы получить краткие сведения о том, как делать соотношения.
Кроме того, вы можете попробовать наш онлайн-калькулятор пропорций, который поможет вам легко решить проблему пропорций разными методами.
Читать дальше!
Что такое коэффициент?
Его можно определить как «сравнение двух конкретных чисел, очень часто представленных в виде дробей». Просто он показывает, сколько одной части отношения содержится в другой части. Наш искатель соотношений разработан для вычисления этого контраста и определения взаимосвязи между числами.
как посчитать соотношение чисел (шаг за шагом):
Отношение состоит из двух частей: числитель и знаменатель, как и дробь. Если у нас есть два отношения, и мы хотим вычислить соотношение для недостающего значения в соотношении, просто выполните следующие действия:
- Запишите отношения в виде дроби и вставьте любую переменную (x или y) в пропущенное значение
- Установите дроби равными друг другу
- Используя перекрестное умножение, сгенерируйте уравнение
- Найдите недостающую переменную
- Наконец, попробуйте калькулятор соотношений, чтобы проверить свой ответ.
Вы можете воспользоваться нашим онлайн-калькулятором дробей, чтобы сложить, вычесть, умножить или разделить две или три дроби. Здесь у нас есть ручной пример, чтобы прояснить понимание:
Пример:
У нас есть 6 кусочков пиццы, из которых съедаются 2. Теперь мы хотим знать, сколько кусочков можно съесть из 54 кусочков пиццы?
Решение:
Шаг 1:
Запишите соотношение в виде дроби как:
Съеденный ломтик / всего ломтик = 2/6
Съеденный ломтик / всего ломтик = x / 54
Шаг 2:
Приравняйте дроби друг к другу:
2/6 = х / 54
Шаг 3:
Крестным умножением:
6х = 54 * 2
х = 54 * 2/6
х = 108/6
х = 18
Мы рекомендуем вам использовать наш калькулятор соотношений, если вы собираетесь решать комплексные отношения больших чисел.
Как использовать онлайн-калькулятор соотношений:
Наш калькулятор – точный инструмент для упрощения и поиска неизвестного значения в соотношении. Вам просто нужно придерживаться следующих пунктов для расчета соотношений:
Проведите по!
Входы:
- Прежде всего, нажмите вкладку, чтобы выбрать, сколько соотношений вы хотите выполнить
- вычисления. Это может быть A: B или A: B: C
- Затем выберите метод расчета из раскрывающегося списка этого калькулятора.
- Затем введите в поля в соответствии с выбранными входными параметрами.
- Как только вы закончите, нажмите кнопку расчета
Выходы:
Калькулятор показывает:
- Отсутствующие значения
- Упрощение соотношения
- Визуальное представление отношения (круговая диаграмма)
Заметка:
Этот калькулятор соотношений не даст вам значений, которые вам не нужны; он даст вам результат в соответствии с входными параметрами.
Что такое золотое сечение?
Когда две величины имеют то же отношение, что и отношение их суммы к большей из двух величин, то это соотношение называется золотым сечением. Например, если величины выражены в x и y, то золотое сечение между x и y равно (x + y) / x = x / y.
Конечное примечание:
К счастью, вы узнали о том, как рассчитать соотношение соотношения вручную и с помощью калькулятора. Соотношение используется везде, от приготовления пищи до строительства дома. Это очень полезно для образования K-12 и во многих других областях науки, таких как механика, бизнес и бухгалтеры, еда и многие другие. Когда дело доходит до решения отношений для комплексных чисел, просто используйте онлайн-калькулятор соотношений, который поможет вам найти недостающее значение в соотношении и выполнить упрощение отношения по вашему желанию.
Other Langauges: Ratio Calculator, Oran Hesaplama, Kalkulator Rasio, Kalkulator Współczynnika, Verhältnis Berechnen, 比率 計算, 비율계산기, Výpočet Poměru, Calculadora Razão, Calcul Ratio, Calcolo Rapporto, حساب النسبة, Suhde Laskuri, Forhold Lommeregner.
Calculate, simplify, scale, or compare ratios using the ratio calculator below.
How to Calculate Ratios
A ratio is a comparison of the size of one number to another number. Ratios can compare the size of an object, a quantity, an angle, or another unit of measure.
A ratio is expressed as one number to another number and is denoted in the form A:B, where the first term is separated from the second term with a colon (:). For example, the ratio of 3 to 2 can be written as 3:2.
Ratios are widely used in our everyday world. In addition to mathematics, ratios are used in financial calculations, for instance when comparing someone’s debt-to-income (how much you owe to how much income you have). Ratios are also used in in photography or video applications for comparing aspect ratios or even architecture and engineering to scale dimensions. Furthermore, ratios can be used for things like the lottery to express the odds of winning.
How to Solve a Ratio in a Proportion
A proportion is an equation showing two equivalent ratios. Given a proportion with one ratio and one part of an equivalent ratio, it is possible to solve the proportion’s missing value.
Start by finding the decimal value for the complete ratio. Divide the left side of the ratio by the right side, or use our ratio to decimal calculator.
Transform the incomplete ratio into a fraction by placing the left side on top of the right side. Thus, the left side becomes the numerator and the right becomes the denominator.
Next, form an equation for the proportion with the decimal on one side and the fraction on the other side. The decimal comes from dividing the numerator by the denominator.
decimal value = known value / unknown value
Finally, solve the equation to find the missing value in the second ratio of the proportion.
For example, let’s solve for x in the proportion 6:4 = 12:x
Start by converting 6:4 to decimal form
6:4 = 6 / 4 = 1.5
Next, put 12:x into fraction form
12:x = 12 / x
Then, position the converted values into an equation representing the proportion and solve
1.5 = 12 / x
12 / 1.5 = x
8 = x
The resulting proportion is thus 6:4 = 12:8
How to Compare Ratios
How do you know if two ratios are equivalent or if one is larger than the other? The answer is to compare them using a two simple steps.
The first step is to convert both ratios to decimal by dividing the left of each ratio by the right of each ratio.
Then, compare the decimal values to determine if the ratios are equal or if one is larger than the other.
For example, let’s compare 3:2 and 5:3
Start by converting to decimal form
3:2 = 3 / 2 = 1.5
5:3 = 5 / 3 = 1.67
Then compare the decimal values
1.5 < 1.67
Thus, 3:2 is less than 5:3
How to Reduce a Ratio
Ratios can be reduced just like a fraction can be reduced. In fact, the process of simplifying a ratio is the exact same as simplifying a fraction.
To reduce a ratio, find the greatest common factor of the left and right sides. The greatest common factor is the largest number that can be evenly divided into both the numbers on the left and right sides.
Then, divide the left and right sides by the greatest common factor. The result is a reduced ratio in the simplest form. This reduced ratio is equivalent to the original ratio.
For example, let’s reduce 6:4
Start by finding the greatest common factor of both 6 and 4
- Factors of 6: 1, 2, 3, 6
- Factors of 4: 1, 2, 4
The greatest common factor of both 6 and 4 is 2
Divide the left and right side by the common factor
6 / 2 = 3
4 / 2 = 2
6:4 = 3:2
Thus, the reduced ratio is 3:2 shown by the proportion 6:4 = 3:2
How to Scale a Ratio
Ratios can be scaled larger or smaller in the same proportion to the original. To scale it, simply multiply the left and right sides by the scaling factor.
For example, let’s scale 7:4 by a factor of 2
Multiply the numbers on the left and right side by 2
7 × 2 = 14
4 × 2 = 8
Thus the scaled ratio is 14:8
How to Convert a Ratio to a Percentage
We’ve shown how to convert a ratio to a decimal and to a fraction, but did you know that you can also convert a ratio to a percentage? You can convert a ratio to a percentage in a few easy steps.
First, convert the ratio to a decimal by dividing the left side by the right side.
Then, convert the decimal to percentage by multiplying it by 100. Don’t forget to add the percent symbol (%).
For example, let’s convert 3:2 to a percentage
Convert 3:2 to a decimal
3:2 = 3 ÷ 2 = 1.5
Multiply the decimal value to 100
1.5 × 100 = 150%
Thus, 3:2 converted to a percentage is 150%. You can also use our ratio to percentage conversion calculator to convert more easily.
Frequently Asked Questions
What is a ratio in math?
A ratio is an ordered pair of numbers that does not equal 0. For example: if there are 3 dogs and 4 cats you would write 3:4 as the ratio.
How do you identify a ratio question on a test?
Ratio questions usually compare two units. For example: A pet shop has 20 animals. There are 12 dogs and 8 cats. What is the ratio for dogs to cats?
12:8 or 12 to 8 or 12/8
Is the order of numbers important in a ratio?
Yes! The ratio 5:4 represents a different relationship than 4:5.
When would you use a ratio?
You would use ratios to compare one value to another.
What are three ways to write a ratio?
1 to 2, 1:2, 1/2
Соотношение 1: упростить
:
Соотношение 2: сравнить
:
Результат упрощения
Результат сравнения
Вы можете использовать этот инструмент для получения наиболее упрощенного соотношения или для сравнения двух одинаковых соотношений.
Соотношение
Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом». Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».
Что такое соотношение?
Соотношение определяется как сравнение двух величин в одних и тех же единицах измерения, которое показывает, сколько одного количества присутствует в другом количестве. Коэффициенты можно разделить на два типа. Одно из них — соотношение части к части, а другое — соотношение части к целому. Соотношение частей к частям показывает, как связаны две различные сущности или группы. Например, соотношение мальчиков и девочек в классе составляет 12: 15, тогда как соотношение частей к целому обозначает соотношение между определенной группой и целым. Например, из каждых 10 человек 5 любят читать книги. Таким образом, соотношение части к целому составляет 5: 10, что означает, что каждые 5 человек из 10 любят читать книги.
Формула соотношения
Мы используем формулу соотношения при сравнении соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».
Форма дроби, представляющая это соотношение, — a/b. Чтобы еще больше упростить соотношение, мы следуем той же процедуре, которую используем для упрощения дроби. a:b = a/b. Давайте разберемся в этом на примере.
Пример. В классе из 50 учеников 23 девочки, а остальные мальчики. Найдите соотношение количества мальчиков к количеству девочек.
Общее количество студентов = 50; Количество девушек = 23.
Общее количество мальчиков = Общее количество учеников — Общее количество девочек
= 50 — 23
= 27
Таким образом, желаемое соотношение (Количество мальчиков: Количество девочек) равно 27:23.
Расчет коэффициентов
Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления пышных блинов необходимо 15 стаканов муки и 20 стаканов сахара, давайте рассчитаем соотношение муки и сахара, используемых в рецепте.
- Шаг 1: Найдите величины обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 15/20.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 может быть упрощено до 3/4.
- Шаг 4: Поэтому соотношение муки к сахару можно выразить как 3:4.
Используйте бесплатный онлайн-калькулятор коэффициентов, чтобы проверить свои ответы при расчете коэффициентов.
Как упростить соотношения?
Соотношение выражает, сколько требуется одного количества по сравнению с другим количеством. Два термина в соотношении могут быть упрощены и выражены в их низшей форме. Соотношения, выраженные в их наименьших выражениях, легко понять и могут быть упрощены так же, как мы упрощаем дроби. Чтобы упростить соотношение, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, давайте упростим соотношение 18:10.
- Шаг 1: Запишите заданное соотношение a:b в виде дроби a/b. Записав соотношение в виде дроби, мы получим 18/10.
- Шаг 2: Найдите наибольший общий коэффициент ‘a’ и ‘b’. В этом случае GCF из 10 и 18 равен 2.
- Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, мы получаем, (18÷2)/(10÷2) = 9/5.
- Шаг 4: Представьте эту дробь в форме соотношения, чтобы получить результат. Таким образом, упрощенное соотношение составляет 9:5.
Используйте бесплатный онлайн-калькулятор коэффициентов упрощения, чтобы проверить свои ответы.
Советы и рекомендации по соотношению:
- В случае, если оба числа «a» и «b» равны в соотношении a: b, то a: b = 1.
- Если a > b в соотношении a : b, то a : b > 1.
- Если a < b в соотношении a : b, то a : b < 1.
- Перед их сравнением необходимо убедиться в том, что единицы измерения двух величин одинаковы.
Эквивалентные Соотношения
Эквивалентные соотношения аналогичны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) данного соотношения умножаются или делятся на одно и то же число, отличное от нуля, это дает эквивалентное соотношение. Например, когда антецедент и следствие соотношения 1:3 умножаются на 3, мы получаем, (1 × 3) : (3 × 3) или 3: 9. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Аналогично, когда оба члена соотношения 20:10 делятся на 10, это дает 2:1. Здесь 20:10 и 2:1 являются эквивалентными соотношениями. Бесконечное число эквивалентных соотношений любого заданного соотношения может быть найдено путем умножения предшествующего и последующего на положительное целое число.
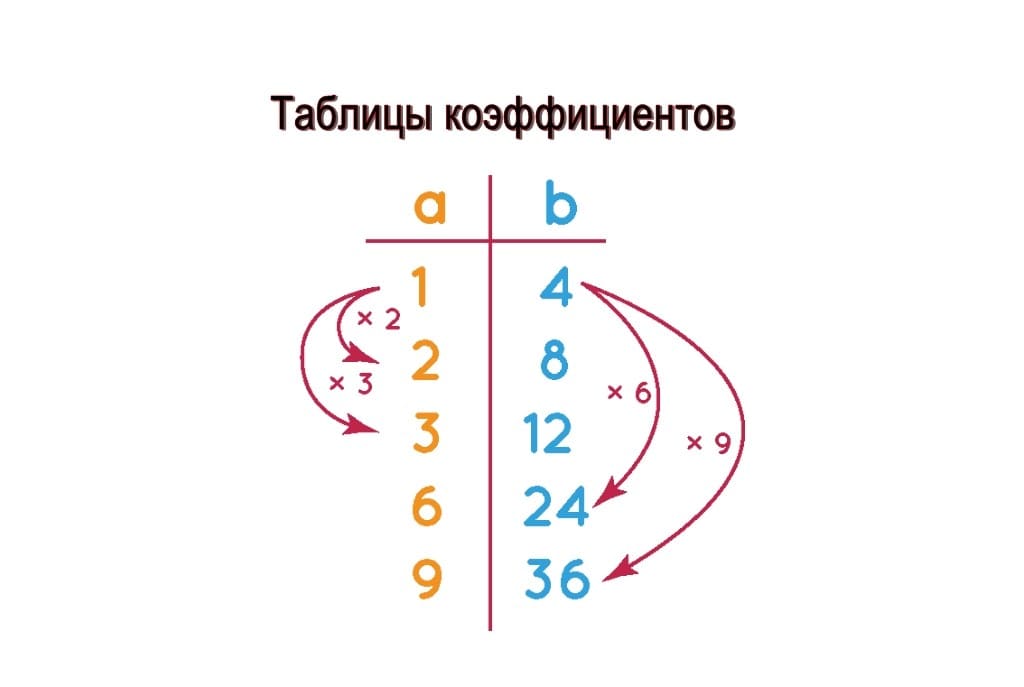
Таблица коэффициентов
Таблица коэффициентов — это список, содержащий эквивалентные коэффициенты любого заданного соотношения в структурированном виде. В следующей таблице соотношений приведено соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные соотношения связаны друг с другом умножением числа. Эквивалентные соотношения получаются путем умножения или деления двух членов соотношения на одно и то же число. В примере, показанном на рисунке, давайте возьмем соотношение 1:4 и найдем четыре эквивалентных соотношения, умножив оба члена соотношения на 2, 3, 6 и 9. В результате мы получаем 2:8, 3:12, 6:24, и 9:36.
Используйте бесплатный онлайн-калькулятор эквивалентных коэффициентов, чтобы проверить свои ответы.
Примеры соотношения
-
Пример 1. В школьном зале 49 мальчиков и 28 девочек. Выразите соотношение числа мальчиков к числу девочек.
Решение:
Учитывая, что количество мальчиков = 49, а количество девочек = 28. GCF 49 и 28 равен 7. Теперь, для упрощения, разделите два термина на их GCF, который равен 7. Это означает, (49 ÷ 7)/(28 ÷ 7) = 7/4. Следовательно, соотношение числа мальчиков к числу девочек = 7:4.
-
Пример 2: В музыкальном классе 30 учеников. 10 из них были взрослыми, а остальные — детьми. Каково соотношение числа детей к общему числу учащихся в музыкальном классе?
Решение:
Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно 20. Отношение общего числа детей к общему числу учащихся в музыкальном классе = 20: 30, что в упрощенном виде дает 2:3.
-
Пример 3: Упростите заданное соотношение, 87:75.
Решение:
Чтобы упростить данное соотношение, мы сначала найдем GCF 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшей форме равно 29:25.
Как ваш ребенок может овладеть математическими понятиями?
Математическое мастерство приходит с практикой и пониманием того, «Почему» стоит за «Что». Почувствуйте разницу в математике.
FAQ по соотношению
Что такое соотношение в математике?
Соотношение может быть определено как соотношение или сравнение между двумя числами одной и той же единицы измерения, чтобы проверить, насколько одно число больше другого. Например, если количество баллов, набранных в тесте, равно 7 из 10, то отношение полученных баллов к общему количеству баллов записывается как 7:10.
Каковы способы написания соотношения?
Соотношение может быть записано путем разделения двух величин с помощью двоеточия (:) или оно может быть записано в дробной форме. Например, если есть 4 яблока и 8 дынь, то соотношение яблок и дынь можно записать как 4: 8 или 4/8, что может быть дополнительно упрощено как 1: 2.
Как рассчитать Соотношение между двумя числами?
Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления крема для глазури необходимо 14 чашек сливочного масла и 28 чашек сахара, каково соотношение масла и сахара?
- Шаг 1: Обратите внимание на количество обоих ингредиентов, для которых мы определяем соотношение. В данном случае это 14 и 28.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 14/28.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 14/28 может быть упрощено до 1/2.
- Шаг 4: Поэтому соотношение сливочного масла к сахару можно выразить как 1:2.
Как найти эквивалентные соотношения?
Два коэффициента считаются эквивалентными, если при упрощении они представляют одно и то же значение. Эта концепция аналогична эквивалентным дробям. Например, когда соотношение 1: 4 умножается на 2, это означает умножение обоих членов в соотношении на 2. Таким образом, мы получаем, (1 × 2)/ (4 × 2) = 2/8 или 2: 8. Здесь 1:4 и 2:8 являются эквивалентными соотношениями. Аналогично, соотношение 30: 10 при делении на 10 дает соотношение 3:1. Здесь 30:10 и 3:1 являются эквивалентными соотношениями. Таким образом, эквивалентные соотношения можно найти с помощью операции умножения или деления в зависимости от чисел.
Что такое Таблица коэффициентов?
Таблица коэффициентов показывает список эквивалентных коэффициентов, которые получаются либо путем умножения, либо деления обеих величин на одно и то же значение. Например, если таблица коэффициентов начинается с соотношения 1 : 3, то последующие строки будут иметь 2:6, 3:9, 4:12, и так далее. Когда эти соотношения упрощены, они представляют одно и то же значение, то есть 1:3.
Что такое Золотое сечение?
Золотое сечение — это отдельное число, значение которого приблизительно равно 1,618. Символом для этого является греческая буква «phi», представленная как ϕ. Это особый атрибут, который используется в искусстве, геометрии и архитектуре, потому что считается, что золотое сечение создает наиболее приятную и красивую форму.Это также известно как божественная пропорция, которая существует между двумя величинами, и соотношение для расчета золотого сечения представлено как ϕ = a /b = (a + b)/a = 1,61803398875… где a и b — размеры двух величин, а a — большее между ними.
Почему важны Коэффициенты?
Соотношения важны, потому что они позволяют нам выражать величины таким образом, чтобы их было легче интерпретировать. Это инструмент, который используется для сравнения размеров двух или более величин по отношению друг к другу. Например, если в классе 30 девочек и 20 мальчиков. Мы можем представить количество девочек к числу мальчиков с помощью соотношения, которое в данном случае равно 3: 2.
Какова формула соотношения?
Формула соотношения используется для сравнения соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».
Что такое Соотношение и Пропорция?
Соотношение — это соотношение или сравнение между двумя величинами одной и той же единицы измерения, чтобы проверить, насколько одно число больше другого. Он записывается как a/b или a: b, где b не равно нулю. Пропорция — это равенство двух соотношений. Пропорции используются для записи эквивалентных соотношений, которые помогают решить неизвестные величины. Например, пропорция выражается следующим образом: a: b = c: d
Как сравнить коэффициенты?
Существуют различные методы сравнения коэффициентов. Например, давайте сравним 1: 2 и 2: 3 с помощью метода LCM.
- Шаг 1: Запишите соотношения в виде дроби. Здесь это означает 1/2 и 2/3.
- Шаг 2: Уменьшите фракции по отдельности. Здесь обе фракции 1/2 и 2/3 уже находятся в их уменьшенной форме.
- Шаг 3: Теперь сравните 1/2 и 2/3, найдя LCM (наименьшее общее кратное) знаменателей. LCM 2 и 3 равно 6.
- Шаг 4: Сделайте знаменатели равными, умножив числитель и знаменатель первой дроби на 3, то есть, (1 × 3)/(2 × 3) = 3/6. Затем умножьте числитель и знаменатель второй дроби на 2, то есть, (2 × 2)/(3 × 2) = 4/6.
- Шаг 5: Теперь 3/6 и 4/6 можно легко сравнить. Это показывает, что 4/6 больше, чем 3/6. Следовательно, 2:3 > 1:2.
Как преобразовать соотношения в дроби?
Соотношения могут быть записаны в виде дробей очень простым способом. Предшествующее записывается как числитель, а последующее записывается как знаменатель. Например, если мы возьмем соотношение 3: 5. Здесь 3 — это предшествующее, а 5 — последующее. Итак, мы можем записать это как 3/5.
Как преобразовать дроби в соотношения?
Дроби могут быть записаны в виде соотношений после упрощения. Это означает, что мы сначала уменьшаем данную дробь до ее наименьших членов, а затем записываем числитель в качестве предшествующего, а знаменатель — в качестве последующего. Например, доля 16/48 сначала будет уменьшена до 1/3, а затем она может быть выражена в виде соотношения 1:3.
Как перевести коэффициенты в десятичные дроби?
Соотношения можно легко преобразовать в десятичные дроби, записав соотношение в виде дроби, а затем дробь преобразуется в десятичную дробь путем деления числителя на знаменатель. Например, 3:7 может быть записано как 3/7. Теперь 3/7 = 0,428.
Как преобразовать коэффициенты в проценты?
Коэффициенты можно преобразовать в проценты, выполнив следующие действия. Например, давайте преобразуем 5: 6 в виде процента.
- Шаг 1: Запишите соотношение в виде дроби. Здесь 5: 6 может быть записано как 5/6.
- Шаг 2: Умножьте эту дробь на 100 и добавьте символ процента. В этом случае 5/6 × 100 = 83,33%.
Загрузить PDF
Загрузить PDF
Соотношение (в математике) — это взаимосвязь между двумя или более числами одного рода. Соотношения сравнивают абсолютные величины или части целого. Соотношения вычисляются и записываются по-разному, но основные принципы одинаковы для всех соотношений.
-
1
Использование соотношений. Соотношения используются как в науке, так и в повседневной жизни для сравнения величин. Простейшие соотношения связывают только два числа, но есть соотношения, сравнивающие три или более значения. В любой ситуации, в которой присутствует более одной величины, можно записать соотношение. Связывая некоторые значения, соотношения могут, например, подсказать, как увеличить количество ингредиентов в рецепте или веществ в химической реакции.[1]
-
2
Определение соотношений. Соотношение — это взаимосвязь между двумя (или более) значениями одного рода. Например, если для приготовления торта необходимы 2 стакана муки и 1 стакан сахара, то соотношение муки к сахару равно 2 к 1.
- Соотношения могут быть использованы и в тех случаях, когда две величины не связаны друг с другом (как в примере с тортом). Например, если в классе учатся 5 девочек и 10 мальчиков, то соотношение девочек к мальчикам равно 5 к 10. Эти величины (число мальчиков и число девочек) не зависят друг от друга, то есть их значения изменятся, если кто-то уйдет из класса или в класс придет новый ученик. Соотношения просто сравнивают значения величин.
-
3
Обратите внимание на разные способы представления соотношений. Соотношения могут быть представлены словами или при помощи математических символов.[2]
- Очень часто соотношения выражены словами (как показано выше). Особенно такая форма представления соотношений применяется в повседневной жизни, далекой от науки.
- Также соотношения можно выразить через двоеточие. При сравнении двух чисел в соотношении вы будете использовать одно двоеточие (например, 7:13); при сравнении трех и более значений ставьте двоеточие между каждой парой чисел (например, 10:2:23). В нашем примере с классом вы можете выразить соотношение девочек и мальчиков так: 5 девочек : 10 мальчиков. Или так: 5:10.
- Реже соотношения выражаются при помощи наклонной черты. В примере с классом оно может быть записано так: 5/10. Тем не менее это не дробь и читается такое соотношение не как дробь; более того, запомните, что в соотношении цифры не представляют собой часть единого целого.
Реклама
-
1
Упростите соотношение. Соотношение можно упростить (аналогично дробям), разделив каждый член (число) соотношения на наибольший общий делитель. Однако при этом не упустите из виду исходных значений соотношения.[3]
- В нашем примере в классе 5 девочек и 10 мальчиков; соотношение равно 5:10. Наибольший общий делитель членов соотношения равен 5 (так как и 5, и 10 делятся на 5). Разделите каждое число соотношения на 5 и получите соотношение 1 девочка к 2 мальчикам (или 1:2). Однако при упрощении соотношения помните об исходных значениях. В нашем примере в классе не 3 ученика, а 15. Упрощенное соотношение сравнивает количество мальчиков и количество девочек. То есть на каждую девочку приходится 2 мальчика, но в классе не 2 мальчика и 1 девочка.
- Некоторые соотношения не упрощаются. Например, соотношение 3:56 не упрощается, так как у этих чисел нет общих делителей (3 — простое число, а 56 не делится на 3).
-
2
Используйте умножение или деление для увеличения или уменьшения соотношения. Распространены задачи, в которых необходимо увеличить или уменьшить два значения, пропорциональных друг другу. Если вам дано соотношение и нужно найти соответствующее ему большее или меньшее соотношение, умножьте или разделите исходное соотношение на некоторое данное число.[4]
- Например, пекарю нужно утроить количество ингредиентов, данных в рецепте. Если по рецепту соотношение муки к сахару составляет 2 к 1 (2:1), то пекарь умножит каждый член соотношения на 3 и получит соотношение 6:3 (6 чашек муки к 3 чашкам сахара).
- С другой стороны, если пекарю необходимо уполовинить количество ингредиентов, данных в рецепте, то пекарь разделит каждый член соотношения на 2 и получит соотношение 1:½ (1 чашка муки к 1/2 чашке сахара).
-
3
Поиск неизвестного значения, когда даны два эквивалентных соотношения. Это задача, в которой необходимо найти неизвестную переменную в одном соотношении при помощи второго соотношения, которое эквивалентно первому. Для решения таких задач пользуйтесь умножением крест-накрест. Запишите каждое соотношение в виде обыкновенной дроби, поставьте между ними знак равенства и перемножьте их члены крест-накрест.[5]
- Например, дана группа учеников, в которой 2 мальчика и 5 девочек. Каково будет число мальчиков, если число девочек увеличить до 20 (пропорция сохраняется)? Во-первых, запишите два соотношения — 2 мальчика:5 девочек и х мальчиков:20 девочек. Теперь запишите эти соотношения в виде дробей: 2/5 и х/20. Перемножьте члены дробей крест-накрест и получите 5x = 40; следовательно, х = 40/5 = 8.
Реклама
-
1
Избегайте сложения и вычитания в текстовых задачах на соотношение. Многие текстовые задачи выглядят примерно так: «В рецепте необходимо использовать 4 клубня картофеля и 5 корнеплодов моркови. Если вы хотите добавить 8 клубней картофеля, то сколько понадобится моркови, чтобы соотношение осталось неизменным?» При решении подобных задач ученики часто допускают ошибку, прибавляя одинаковое количество ингредиентов к исходному числу. Однако, чтобы сохранить соотношение, нужно использовать умножение. Вот примеры правильного и неправильного решения:
- Неверно: «8 — 4 = 4 — так мы добавили 4 клубня картофеля. Значит, нужно взять 5 корнеплодов моркови и к ним добавить еще 4… Стоп! Соотношения так не вычисляют. Стоит попробовать снова».
- Верно: «8 ÷ 4 = 2 — значит, мы умножили количество картофеля на 2. Соответственно, 5 корнеплодов моркови тоже нужно умножить на 2. 5 x 2 = 10 — в рецепт нужно добавить 10 корнеплодов моркови».
-
2
Преобразуйте члены в те же единицы измерения. Некоторые текстовые задачи специально усложняют, добавляя разные единицы измерения. Преобразуйте их, прежде чем вычислять соотношение. Вот пример задачи и решения:
- У дракона есть 500 грамм золота и 10 килограмм серебра. Каково соотношение золота к серебру в сокровищнице дракона?
- Граммы и килограммы — разные единицы измерения, их нужно преобразовать. 1 килограмм = 1000 грамм, соответственно, 10 килограмм = 10 килограмм x 1000 грамм/1 килограмм = 10 x 1000 грамм = 10 000 грамм.
- У дракона в сокровищнице 500 грамм золота и 10 000 грамм серебра.
- Соотношение золота к серебру равно: 500 грамм золота/10 000 грамм серебра = 5/100 = 1/20.
-
3
Записывайте единицы измерения после каждой величины. В текстовых задачах гораздо проще распознать ошибку, если записывать единицы измерения после каждого значения. Помните, что величины с одними и теми же единицами измерения в числителе и знаменателе сокращаются. Сократив выражение, вы получите верный ответ.
- Пример: дано 6 коробок, в каждой третьей коробке находится 9 шариков. Сколько всего шариков?
- Неверно: 6 коробок x 3 коробки/9 шариков = … Стоп, ничего нельзя сократить. Ответ будет таким: «коробки x коробки / шарики». Он не имеет смысла.
- Верно: 6 коробок x 9 шариков/3 коробки = 6 коробок * 3 шарика/1 коробку = 6 коробок * 3 шарика/1 коробку = 6 * 3 шарика/1 = 18 шариков.
Реклама
Источники
Об этой статье
Эту страницу просматривали 225 631 раз.
Была ли эта статья полезной?
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com