Трапеция, ее свойства, формулы площади, высоты, сторон.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция (понятие, определение)
Видеоурок “Трапеция”
Виды трапеций
Элементы трапеции: основания, боковые стороны, средняя линия и высота
Свойства трапеции
Свойства равнобедренной трапеции
Формулы трапеции
Трапеция (понятие, определение):
Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.
Рис. 1. Трапеция
Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
@ https://youtu.be/Q4EpXexoMrM
Виды трапеций:
Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.
Рис. 2. Равнобедренная трапеция
Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.
Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.
Рис. 3. Прямоугольная трапеция
Элементы трапеции: основания, боковые стороны, средняя линия и высота:
Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.
Рис. 4. Трапеция
AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.
AD – большее основание трапеции, BC – меньшее основание трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.
Рис. 5. Трапеция и срединная линия
Расстояние между основаниями трапеции называется высотой трапеции.
Рис. 6. Трапеция
Высота трапеции (h) определяется формулой:
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
Свойства трапеции:
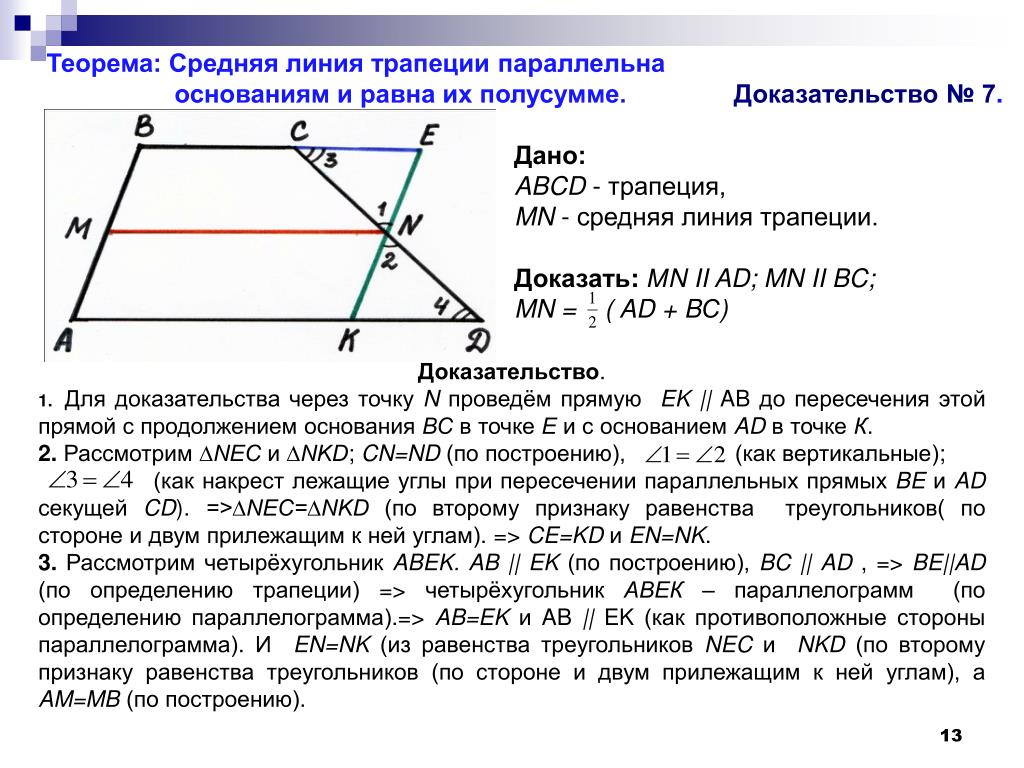
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Рис. 7. Трапеция и срединная линия
MN || BC, MN || AD,
l = (a + b) / 2
2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
Рис. 8. Трапеция
MN = (b – a) / 2
3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° .
Рис. 9. Трапеция
4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
Рис. 9. Трапеция
5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

AB = BK
6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Рис. 11. Трапеция
∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2
7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
Рис. 12. Трапеция
AB + CD = AD + BC
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Рис. 13. Трапеция
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
Рис. 14. Трапеция
MN = (AB + CD) / 2,
MN = (AD + BC) / 2
8. Диагонали трапеции делят ее на 4 треугольника.
Два из них, прилежащие к основаниям, подобны.
Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.
Рис. 15. Трапеция
Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции. k = AD / BC. Отношение площадей этих подобных треугольников есть k2.
Треугольники ABO и CDO имеют одинаковую площадь.
9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.
Рис. 16. Трапеция
BC : AD = OC : AO = OB : DO
10. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c 2 + d 2
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия, UV – отрезок, который соединяет основания трапеции
12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:
где b – большее основание трапеции, a – меньшее основание трапеции, S1 и S2 – площади образованных трапеций, в результате разделения средней линией.
Рис. 18. Трапеция
S1 – площадь трапеции MBCN,
S2 – площадь трапеции AMND
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Формулы трапеции:
Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d1 и d2 – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.
Формулы для определения сторон трапеции:
Через среднюю линию и одно из оснований трапеции:
a = 2m – b
b = 2m – a
Через высоту и углы при нижнем основании трапеции:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
Через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
Через высоту и углы при нижнем основании трапеции:
Формулы для определения средней линии трапеции:
Через длины оснований трапеции:
Через площадь и высоту трапеции:
Формулы для определения высоты трапеции:
Через сторону и прилегающий угол при нижнем основании трапеции:
h = c·sin α = d·sin β
Через диагонали трапеции и углы между ними:
Через диагонали трапеции, углы между ними и среднюю линию трапеции:
Через площадь и длины оснований трапеции:
Через площадь и длину средней линии трапеции:
Формула для определения периметра трапеции:
P = a + b + c + d
Формулы для определения площади трапеции:
Через основания и высоту трапеции:
Через среднюю линию и высоту трапеции:
S = m · h
Через диагонали трапеции и угол между ними:
Через все стороны трапеции:
С помощью формулы Герона для трапеции:
Как называется объемная трапеция?
Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.
В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.
Квадрат
Овал
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/Q4EpXexoMrM
Коэффициент востребованности
6 632
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a(d 2 — c2) |
| a — b |
| d2 = | √ | c2 + ab — | a(c2 — d 2) |
| a — b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
a — большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО
ОБРАЗОВАНИЯ
город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка
к ОГЭ и ЕГЭ.
«Формулы
и свойства трапеции»
Методическая разработка
учителя
математики
Снегуровой Амины Мугиновны
2018 год.
Оглавление
Введение 3
1.
Определения 4
2.
Частные случаи трапеции 5
3.
Свойства произвольной трапеции 6-7
4.
Свойства равнобедренной трапеции 8-10
5. Свойства
биссектрисы угла трапеции 10-12
6.
Свойства треугольников, образованных диагоналями трапеции 12-13
7.
Формулы нахождения диагоналей трапеции 13-14
8.
Трапеция и окружность 14-17
9.
Дополнительные построения в трапеции 17-23
10. Для
тех, кому интересно. Теоремы. 23-27
11.
Задачи с решениями.27-35
12. Список используемой литературы .
Введение
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются
задачи на трапецию, решение которых требует от учащихся знаний
«непрограммных» свойств трапеции. (Программными считаются свойство средней
линии трапеции, свойства диагоналей и углов
равнобедренной
трапеции.) Свойства, необходимые для решения задач, отсутствуют в
учебниках или перенесены в задачи и не воспринимаются как теоретические
положения.
Какими же замечательными свойствами обладает трапеция?
Как решать геометрические задачи, требующие глубоких знаний? Трапеция
обладает рядом интересных и полезных для решения задач свойствами. Если
овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает
объективная возможность для решения задач повышенной сложности.
В планиметрии существует целый класс таких задач,
к которым традиционные методы (метод цепочек равных треугольников, метод
геометрических преобразований, векторный метод и др.) либо вовсе не применимы,
либо дают сложные и громоздкие решения. Во многих случаях решать такого рода
задачи помогает введение в чертеж дополнительных линий – так называемое
дополнительное построение. В одних случаях эти построения напрашиваются сами
собой, в других они не так очевидны и требуют от решающего достаточно большого
опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно
достраивать до фигуры другого типа, можно с многоугольной фигурой связывать
окружность, а можно целью дополнительного построения ставить выделение на
чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в
большинстве случаев позволяет решать, казалось бы, сложные геометрические
задачи просто, понятно и красиво.
В этой
разработке собраны формулы, свойства и подсказки для решения задач связанных с
трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные
стороны
называются её основаниями, а две другие стороны — боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.

Kаждый
из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В
формулах используются следующие обозначения:
a,
b — основания трапеции
c,
d — боковые стороны трапеции
d1
d2 — диагонали трапеции
α
β — углы при большем основании трапеции
h—
высота.
2.Частные
случаи трапеции.
Прямоугольной
трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна
основаниям.
У
нее два прямых угла при меньшей боковой стороне.
Эта
сторона одновременно является и высотой трапеции.
произвольная
Трапецией
называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У
равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при
основании равны.
Трапеция,
у которой боковые стороны равны, называется равнобедренной
(равнобокой,
равнобочной).
3.Свойства произвольной
трапеции.
1. Во всякой трапеции сумма углов , прилежащих к
одной ее боковой стороне, равна 1800.


основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.

MК =
3.Четыре замечательные
точки трапеции:
Во всякой трапеции середины
оснований, точка пересечения диагоналей и точка пересечения продолжений боковых
сторон лежат на одной прямой.

4. Во всякой трапеции если
сумма углов при большем основании равна 900, то боковые стороны
лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины
оснований, равна полуразности оснований.
5.
Свойства отрезка, соединяющего основания трапеции

соединяющий основания всякой трапеции, и проходящий через точку пересечения
диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований
трапеции.
Если провести отрезок, концы которого лежат на основаниях
трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то
соотношение составляющих его отрезков от стороны основания до точки пересечения
диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.

провести отрезок, параллельный основаниям трапеции и проходящий через точку
пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей
трапеции пополам, то есть КО=ОМ
*Длина отрезка,
проходящего через точку пересечения диагоналей трапеции и параллельного
основаниям, равна
KM = .
 |
|||
7.Во всякой трапеции с основаниями a и b отрезок, параллельный
основаниям, концы которого лежат на боковых сторонах, равен среднему
геометрическому оснований, если он делит трапецию на две трапеции, подобные
между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный
основаниям, концы которого лежат на боковых сторонах, равен среднему
квадратичному оснований, если он делит трапецию на две трапеции равной площади
(равновеликие).

9.Сумма
квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс
удвоенное произведение ее оснований.
d12
+ d22
= c2 + d2+
2ab, d— боковая сторона. d1 и
d2 –
диагонали.
Свойства
равнобедренной трапеции.
Трапеция является равнобедренной
тогда и только тогда, когда
*углы, прилежащие к одному
основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;

AC = BD
*отрезки диагоналей, соединяющих точку пересечения
с концами одного основания, равны; BO = OC, AO = OD.

описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.

большее основание на отрезки, один из которых равен полуразности оснований, а
другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны,
то
1)квадрат ее диагонали равен половине квадрата суммы
оснований, а также удвоенному квадрату высоты и удвоенному квадрату
средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4)
площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны,
равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).


диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через
точку пересечения диагоналей, в
равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две
равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины
оснований, перпендикулярна им и является осью симметрии трапеции.


*отрезки, последовательно соединяющие середины смежных сторон
равнобедренной трапеции, образуют ромб.

MNKE – ромб,
то есть
MN=NK=KE=
ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его
боковой стороны плюс произведение оснований: d2
= c2 + a b

равнобедренной трапеции с радиусом вписанной окружности равным r и углом при
основании α:
S =
Свойства
биссектрисы угла трапеции.
*биссектриса угла отсекает
от трапеции равнобедренный треугольник.



*точка пересечения биссектрис
тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то
меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от
трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под
прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой
стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то
боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее
боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой
боковой стороне острого угла.
Если в условии задачи сказано, что основание трапеции равно ее боковой
стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее
угла.
*если меньшее основание трапеции равно ее
боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой
боковой стороне острого угла.

трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой
прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции
равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла,
прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции
равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла,
прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее
большей боковой стороне, диагональ является биссектрисой прилежащего к этой
боковой стороне острого угла.
* если большее основание прямоугольной трапеции
равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к
этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции
равно ее боковой стороне, то диагональ является биссектрисой острого угла
трапеции.
* если большее основание равнобедренной трапеции
равно ее боковой стороне, то диагональ является биссектрисой тупого угла
трапеции.
Свойства
треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой
пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются
вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD
и BC (основания трапеции параллельны между собой) и секущей прямой AC,
следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим
углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для
решения задач по геометрии подобие треугольников используется следующим
образом.
*Если
нам известны значения длин двух соответствующих элементов подобных
треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда
длины всех остальных элементов соотносятся между собой точно таким же
значением.
*В подобных треугольниках
длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы
вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис,
медиан (проведенных из равных углов) подобных треугольников равны отношению
соответствующих сторон (лежащих против равных углов) или равны коэффициенту
подобия.
*Площади подобных
треугольников относятся как квадраты соответствующих сторон или равно квадрату
коэффициента подобия.

образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции
AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных
сторон у данных треугольников могут быть совершенно различны, но площади
треугольников, образованных боковыми сторонами и точкой пересечения диагоналей
трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего
основания, то они пересекутся в одной точке с прямой, соединяющей середины
оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами,
углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения
задач по геометрии на тему «диагонали трапеции»

Далее, в формулах используются следующие обозначения:
a, b —
основания трапеции
c, d —
боковые стороны трапеции
d1 d2 —
диагонали трапеции
α β —
углы при большем основании трапеции
h— высота
Формулы нахождения диагоналей трапеции
через основания, боковые стороны и углы при основании

Эта группа формул отражает одно из основных свойств диагоналей
трапеции:
*Сумма квадратов диагоналей трапеции равна
сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем
теорему косинусов.
*Данная
формула получена путем преобразования предыдущей формулы. Квадрат второй
диагонали переброшен через знак равенства, после чего из левой и правой части
выражения извлечен квадратный корень.
*Эта формула
нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что
в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна
разности квадратов оснований
d12
— d22
= a2 –
b2
*Если
диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего
середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали
прямоугольника равны.
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя
линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность,
является средним геометрическим её оснований
h2
= a ∙ b
2)
Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна
средней линии. Площадь трапеции определяется произведением средней линии на
высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной
окружности или двум ее радиусам.
MK —
высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной
окружности является точкой пересечения биссектрис углов трапеции.
. CF =m,
FD =n, OF = r.

как сумма
внутренних односторонних углов при параллельных прямых AD и BC и секущей CD
равна 1800.
Отсюда
радиус вписанной в трапецию окружности выражается через длины отрезков, как
которые боковая сторона делится точкой касания, как r = .
А так как
высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через
длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно
описать окружность, то проекция диагонали на большее основание, равна боковой
стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько
путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда,
когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма
ее оснований равна сумме боковых сторон.
AB+CD=AD+BC

проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в
окружность? Четырехугольник можно вписать в окружность тогда и только тогда,
когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать
в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как
радиус окружности, описанной около из одного из двух треугольников, на которые
трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это
зависит от угла между диагональю трапеции и ее боковой стороной.

перпендикулярна ее боковой стороне, то центр окружности, описанной около
трапеции, лежит на середине ее большего основания. Радиус описанной около
трапеции окружности в этом случае равен половине ее большего основания:

боковой стороной острый угол, центр окружности, описанной около трапеции, лежит
внутри трапеции.
3) Если
диагональ трапеции образует с боковой стороной тупой угол, центр описанной
около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по
следствию из теоремы синусов. Из треугольника ACD

Из треугольника ABC
Другой вариант найти радиус описанной окружности —

угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и
ACF:
При решении задач на трапецию, вписанную в окружность, можно
также использовать то, что вписанный угол равен половине соответствующего ему
центрального угла. Например,

Использовать углы COD и CAD можно и для нахождения площади
трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции
(четырехугольника) взаимно перпендикулярны, то сумма квадратов его
противоположных сторон равна квадрату диаметра описанной окружности или
удвоенному квадрату боковой стороны:
a2
+ b2
= 4R2
= 2c2.

вписанной в нее окружности и основание перпендикуляра, опущенного из другой
вершины на основание, лежат на одной прямой.
Дополнительные построения
как прием при решении задач
Дополнительные
построения являются эффективным методом решения геометрических задач. Наиболее
часто используются при решении задач:
1.
Опускание высот из концов одного основания на другое основание
2.
Проведение через вершины трапеции прямой, параллельной боковой стороне, не
содержащей эту вершину
3.
Проведение через середину меньшего основания прямых, параллельных боковым
сторонам
4.
Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей
эту вершину .
5.
Продолжение боковых сторон до пересечения.
Рассмотрим
каждое их них.
При
решении задач на отыскание площади дополнительным построением считается
построение ее высоты или высот. Если построение высоты не помогает решить
задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом
найти площадь полученного треугольника, который будет равновеликим исходной
трапеции.
1.
Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей
эту вершину.
При
дополнительном построении, когда переносится диагональ, образуется треугольник,
площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите
площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим
CF // BD и
получим SACF = SABCD.
Почему?
ABC
= CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит,
для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF
= АD + ВС — сумма оснований трапеции. По условию задачи средняя линия
трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF.
Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172
= 82 + 152
289
= 64 + 225.
289
= 289.
ACF
– прямоугольный. SACF = AC*CF
= 8*15 = 60. SABCD=
60.
Если ACF
разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2.
Продолжение боковых сторон до пересечения.
Свойства трапеции,
достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то
точка пересечения сторон будет совпадать с прямой линией, которая
проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до
треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной
в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является,
одновременно, медианой построенного треугольника.
*Если ABCD равнобедренная трапеция, то KL
является биссектрисой, медианой и высотой одновременно.
Это
дополнительное построение позволяет перейти от трапеции к треугольнику. Если
сумма углов при большем основании равна 900, топродолжив боковые
стороны мы получим прямоугольный треугольник.
Задача.
В
трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна
900. Найдите радиус окружности, проходящей через точки А и В и
касающейся прямой CD, если АВ = 18.
Решение.
Центром
О данной окружности будет точка пересечения серединного
перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD
из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые
стороны трапеции и получим прямоугольный треугольник АМD.
KMNO – прямоугольник, где KM = MN
= NO =КО = R.
BMC
AMD.
=
, то есть
и x
= 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное
построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого —
одно из оснований и высота трапеции) и два прямоугольных треугольника (в
которых один из катетов – высота трапеции, а гипотенузы – боковые стороны
трапеции)
Построение
1 Построение 2

Задача. Найдите площадь трапеции с основаниями 8 и 13 и
боковыми сторонами 3 и 4.

Решение.
Проведем ВН и СM — высоты и получим ABD (египетский
треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту
трапеции: h= 2S:5 = 2*6:5=
2,4.
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение
через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4
делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в
треугольник.


5. Проведение через вершины трапеции прямой, параллельной боковой
стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см
и 12 см. Найдите высоту трапеции.
Решение.
Пусть АВСД трапеция, заданная в условии.
Проведем
через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД
в точке М.
Тогда
АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так
как 92+122=152, то, применив обратную теорему
Пифагора, приходим к выводу, что СМ перпендикулярна СД.
Заметим,
что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают.
Для определения искомой высоты применим метод площадей. Пусть искомая высота
равна х. Тогда для определения х составим уравнение, дважды вычислив площадь
треугольника МСД:
.
Решив
это уравнение находим: х=7,2. Ответ: 7,2.
Задача.
Боковые стороны AB и CD трапеции ABCD равны 15 и 12
соответственно. Найдите градусную величину угла D, если одно из оснований
трапеции на 9 больше другого.
Решение.
Из вершины угла проведем
прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на
параллелограмм и треугольник. Противоположные стороны параллелограмма равны,
значит, длина стороны треугольника равна разности длин оснований трапеции. Данный
треугольник определен по трем сторонам. По теореме косинусов определим искомый
угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию,
искомый угол прямой.

Для
тех, кому интересно.



Теорема.
Задачи с решениями.
Пример
1.Найдите площадь равнобедренной трапеции, описанной около окружности с
радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD —
равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
1.
AB = CD = 10 по условию.
2.
AB + CD = AD + BC по свойству вписанной
окружности.
3.
AD + BC = 10 + 10 = 20.
4.
FE = 2r = 2 · 4 = 8.
5.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20
· 8 = 20/2 · 8 = 10 · 8 = 80.
Пример
2.Основания трапеции
равны 10 м и 31 м, а
боковые стороны —
20 м и 13 м. Найдите
высоту трапеции.
Решение.
Пусть HK
= BC = 10 м, BH
= CK = x, AH
= y, тогда KD
= 21 – y
По
теореме Пифагора:x2 +
y2 =
132x2 +
(21 – y)2 =
202x2 +
y2 =
169 (1)
x2 +
441 – 42y + y2 =
400 (2)
Вычтем
из (2) уравнения (1):441 – 42y =
23142y = 210y
= 5AH = 5 м
По
теореме Пифагора:BH2 =
AB2 –
AH2BH2 =
132 – 52BH2 =
169 – 25BH2 =
144
BH
= 12
Пример
3.Большее основание трапеции равно 24. Найдите длину меньшего основания, если
расстояние между серединами диагоналей равно 4.
Решение.

Пример
4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите
площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны
соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие
треугольников.
Квадраты соответствующих
сторон относятся как площади треугольников.
Введем параметры
треугольников: стороны оснований и высоты треугольников.
Площади трапеции и
треугольников определим по известным формулам.
Решение.

Пример
5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны
боковым сторонам. Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и
перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников
по катету и гипотенузе: ABD
= ACD,
поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для
определения боковой стороны трапеции.
Высоту трапеции определим из
равенства площадей.
Проекцию боковой стороны на
большее основание легче определить из подобия треугольников, чем по теореме
Пифагора.
Длину средней линии в равнобокой
трапеции можно определять как разность большего основания и проекции боковой
стороны на основание.
Площадь трапеции находим как
площадь прямоугольника АМСК, который получим, если достроим трапецию.

Пример
6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9.
Найдите длину отрезка, соединяющего середины оснований трапеции.

Задача решается построением.
Достроим прямоугольники и
используем свойство прямоугольника: диагонали прямоугольника равны и в точке
пересечения делятся пополам.
Длина средней линии равна
полусумме длин оснований.
Длина отрезка, соединяющая
середины оснований, равна полусумме длин диагоналей двух построенных
треугольников.
Пример
7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного
основаниям и заключенного между боковыми сторонами, который делит трапецию на
две равновеликие части.
Анализ.
Провести из вершины тупого
угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей
трапеций.
Определить отношение при
подобии треугольников.
Рациональные алгебраические
преобразования приведут к результату.
Решение.
Пример
11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона
трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон
трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине
средней линии.
Применяем теорему Пифагора для
нахождения высоты трапеции.
Площадь трапеции определяем по
доступной формуле.

Пример
8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно
вписать окружность, а средняя линия делит ее на части, площади которых
относятся как 5: 11. Найдите длину большего основания трапеции.

Трапеция является описанной.
Сумма длин оснований равна
сумме боковых сторон.
Средняя линия делит трапецию
на две трапеции, высоты которых равны.
Задача сводится к системе
уравнений.
Длина средней линии равна
половине суммы длин боковых сторон.
Пример
9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите
среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.

Трапеция равнобедренная.
Длина средней линии равна
боковой стороне.
Площадь трапеции определяется
произведением средней линии на высоту трапеции.
Опустим высоту трапеции из
тупого угла. Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту
трапеции через боковую сторону.

Пример
10.В прямоугольной трапеции, описанной около окружности, большая боковая
сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание
трапеции.
Анализ.
Необходимо использовать
свойство сторон четырехугольника, описанной около окружности: сумма длин
противоположных сторон равна между собой.
Кроме того, длина средней
линии равна полусумме длин сторон оснований.
Проведем из вершины тупого
угла высоту трапеции.
Воспользуемся теоремой
Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример
11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь
равна ,
вписана окружность. Найдите радиус этой окружности.

Анализ.
Важное положение, что трапеция
является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны
равна длине средней линии.
Введем параметр боковой
стороны, из прямоугольного треугольника по заданному углу определим высоту
трапеции, которая является диаметром вписанной окружности. Площадь трапеции
определяется как произведение средней линии на высоту трапеции.
.
Пример
12.Найдите площадь равнобедренной трапеции, у которой большее основание равно
13, средняя линия равна 8, а биссектриса тупого угла является диагональю
трапеции.
Анализ.
При проведении биссектрисы
тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой
стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем
высоту трапеции.
Площадь трапеции находим по
формул.
Список используемой литературы
1.
2.
3.
От двух до пяти, Или о равных отрезках в трапеции
Наш разговор посвящен равным отрезкам в трапеции. Некоторые из этих отрезков весьма знамениты, с другими мы где-то (возможно, на олимпиадах) встречались. Третьи и вовсе могут нам показаться незнакомыми. Но все вместе они являют любопытную коллекцию важных, полезных, подчас непростых задач. В основном нас ожидают встречи с двумя и тремя равными отрезками, но в целом их насчитывается от двух до пяти. Итак, начинаем!..
Задача 1. Докажите, что x = y, где EF AD (рис. 1).
Доказательство. Треугольники AEK и ABC подобны и
(1)
Аналогично, треугольники DFN и DCB подобны и
(2)
Сравнив (1) и (2), получаем: x = y.
Задача 2. Покажите, что x = y, где EF AD (L — точка пересечения продолжений боковых сторон трапеции ABCD и лежит на EF (рис. 2)).
При помощи одной линейки постройте отрезок, равный
Решение. Поскольку треугольники BLE и BAD, CLF и CDA подобны, то после составления пропорций, как и в задаче 1, получим: x = y. Далее:
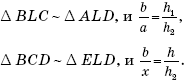 |
(3) (4) |
Сложим левые и правые части равенств (3) и (4). С учетом того, что h1 + h = h2, получим: или bx + ab = ax, откуда
Значит, отрезок EF и есть тот отрезок, который необходимо построить при помощи одной линейки. Остается показать, как через данную точку L построить прямую, параллельную двум данным
( BC и AD), пользуясь только линейкой.
Такое построение предложено на рисунке 3 с указанием порядка проведения линий. Дополнительные комментарии представляются излишними.
Задача 3. Найдите отношение оснований трапеции ABCD, если x = y, где x = LO, y = OM (рис. 4).
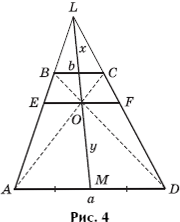
Решение. Поскольку LO = OM, то (средняя линия в треугольнике ALD). С другой стороны, EF — один из самых знаменитых отрезков в трапеции ABCD, и
(покажите!). Тогда имеем:
или 4b = a + b, откуда
Задача 4. Под каким углом пересекаются боковые стороны трапеции, если x = y (рис. 5), где x — отрезок, соединяющий середины диагоналей, y — отрезок, соединяющий середины оснований.
Решение. KG NM и KG = NM — они параллельны и равны
AB как средние линии соответственно в треугольниках ABC и ABD. Значит, KGNM — параллелограмм. Но поскольку x = y, то это параллелограмм с равными диагоналями, то есть прямоугольник. Следовательно, ∠ KGN = 90°. Тогда и угол между прямыми AB и CD также равен 90°.
Задача 5. Для оснований трапеции ABCD справедливо равенство a2 = b2 + ab. Докажите, что x = y, или BO = DN, где CK AB (рис. 6).
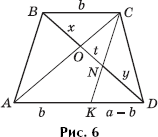
Доказательство. Равенство a2 = b2 + ab равносильно пропорции Треугольники BOC и DOA подобны, и
Треугольники DNK и BNC подобны, и
Поскольку
то
Имеем:
x2 + xt = y2 + yt,
или
(x – y)(x + y + t) = 0.
Однако x + y + t > 0, поэтому x = y.
Задача 6. В трапеции ABCD x = y = z, ∠ACD = 90°(рис. 7). Найдите углы трапеции.
Решение. Пусть ∠1 = ∠2 = α. Тогда ∠2 = ∠3 = α
(внутренние накрест лежащие при BC AD). Значит, ∠A = ∠D = 2α. Из треугольника ACD
α + 2α = 90°, откуда α = 30°.
Ответ: 60° и 120°.
Статья опубликована при поддержке интернет-сайта «ЕГЭ по математике ОНЛАЙН». Электронный онлайн курс ЕГЭ по математике 2016 — базовый и профильный уровень, расширенный доступ бесплатно, индивидуальные рекомендации, демонстрационный вариант ЕГЭ 2015 года. Пройти тест Вы сможете на сайте, который располагается по адресу: егэ-по-математике.онлайн.
Задача 7. Пересеките трапецию ABCD прямой, параллельной основаниям так, чтобы ее отрезок, лежащий внутри трапеции, делился диагоналями на три равные части.
Решение. Пусть M — середина основания AD, AC и BD — диагонали (рис. 8). Пусть также
K = BM ∩ AC. Проведем через K прямую EF параллельно AD. При этом EK = KN = NF, или
x = y = z. Действительно, x = y, так как AM = MD,
а x = z — по задаче 1.
Замечание. Существуют два отрезка, отвечающих требованиям задачи. Кроме отрезка EF, это будет еще и отрезок QT (рис. 9). Он строится так же, как и отрезок EF, но берется F — середина основания BC.
Задача 8. ABCD — равнобокая трапеция с перпендикулярными диагоналями AC и BD. Известно, что ортоцентр треугольника ABD делит пополам его высоту AO. Проведя не более одной линии, разделите диагональ BD на три равные части (рис. 10).
Решение. Поскольку трапеция равнобокая, то около нее можно описать окружность. Пусть H — ортоцентр треугольника ABD и AH = HO. C — точка, симметричная ортоцентру H относительно BD (так как она лежит на описанной окружности треугольника ABD). Тогда OC = OH = AH. Диагонали AC и BD равны. Остается из точки O раствором циркуля, равным BO, сделать засечку на диагонали BD — получим точку N. При этом BO = ON = ND.
Задача 9. Существует ли трапеция ABCD, в которой EF — средняя линия и x = y = z = t (рис. 11)?
Решение. Так как EF — средняя линия трапеции ABCD, то она делит любой отрезок между основаниями трапеции пополам, то есть y + z = t. Но, согласно условию, y + z = 2t. Противоречие. Такой трапеции, где x = y = z = t, как на рисунке 11, не существует.
Задача 10. При каком отношении оснований трапеции x = y = z = t = q (рис. 12)?
Решение. Пусть BK = k и DN = n. Равные по условию отрезки обозначим через x. Треугольники KT3B и NT3D подобны, (по двум углам). Тогда
Треугольники KT1B и NT1A подобны, и
откуда
Далее, треугольники KT2C и NT2A подобны и
Имеем:
откуда Стало быть,
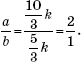
Еще несколько задач на равные отрезки в трапециях предложим вниманию читателей для самостоятельного решения.
Задача 11. Покажите, что (рис. 13).
Задача 12. Диагонали трапеции делят ее среднюю линию на три равные части. Найдите отношение оснований. Ответ: 2 : 1.
Задача 13. Основания трапеции ABCD равны a и b. EF и QT параллельны основаниям, при этом x = y = z (рис. 14). Найдите EF и QT.
Ответ:
Задача 14. При помощи одной линейки на основании AD трапеции ABCD постройте точки K и N такие, что AK = KN = ND.
Задача 15. (Санкт-Петербургские олимпиады.) На боковых сторонах трапеции ABCD нашлись точки K и N такие, что KN не параллелен основаниям и при этом x = y = z (рис. 15).
Найдите отношение оснований.
Задача 16. Дано: x = y. Докажите, что z = t (рис. 16).
Задача 17. В трапеции ABCD x = y = z (рис. 17). При каком отношении оснований площадь трапеции будет наибольшей?
Филипповский Г.
Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными.
Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые.
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h1h2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Площадь трапеции
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции
Содержание главы:
- Площадь трапеции
- Высота трапеции
- Трапеция (задачи про основания)
- Диагонали трапеции
- Прямоугольная трапеция
- Равнобокая (равнобедренная) трапеция
- Углы равнобокой (равнобедренной) трапеции
- Высота равнобедренной трапеции
- Равнобокая трапеция
- Равнобокая трапеция (часть 2)
- Трапеция, описанная вокруг окружности
0
Ромб |
Описание курса
| Площадь трапеции
Все о трапеции для подготовки к ОГЭ и ЕГЭ
Трапеция
и все-все-все
Для
начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.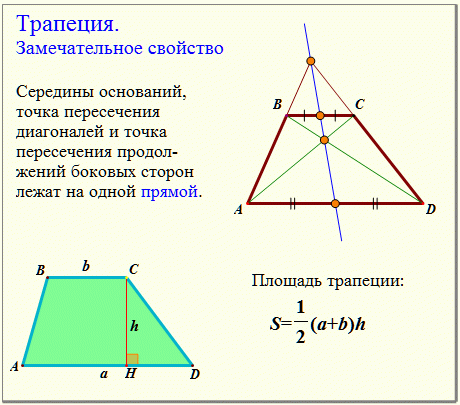
Итак,
трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу
(это основания). И две не параллельны – это боковые стороны.
В
трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены
средняя линия и диагонали. А также из любого угла трапеции возможно провести
биссектрису.
Про
различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас
и поговорим.
Свойства
диагоналей трапеции
Чтобы
было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и
проведите в ней диагонали.
1. Если
вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и
соедините их, получится отрезок. Одно из свойств диагоналей трапеции
заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно
получив, разделив разность оснований на два: ХТ = (a – b)/2.
2. Перед
нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте
рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с
основаниями трапеции.
треугольников выражается через отношение оснований трапеции:
k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k2.
3. Все
та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы
будем рассматривать треугольники, которые отрезки диагоналей образовали
совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО
являются равновеликими – их площади одинаковые.
4. Еще
одно свойство трапеции включает в себя построение диагоналей. Так, если
продолжить боковые стороны АК и МЕ в направлении меньшего основания, то
рано или поздно они пересекутся к некоторой точке. Дальше, через середины
оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения
диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон
и середины оснований Х и Т.
5. Через
точку пересечения диагоналей проведем отрезок, который соединит основания
трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка
пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ
= КМ/АЕ.
6. А
теперь через точку пересечения диагоналей проведем параллельный основаниям
трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части.
Найти длину отрезка можно по формуле 2ab/(a + b).
Свойства
средней линии трапеции
Среднюю
линию проведите в трапеции параллельно ее основаниям.
1. Длину
средней линии трапеции можно вычислить, если сложить длины оснований и
разделить их пополам: m = (a + b)/2.
2. Если
провести через оба основания трапецию любой отрезок (высоту, к примеру),
средняя линия разделит его на две равных части.
Свойство
биссектрисы трапеции
Выберите
любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей
трапеции АКМЕ.
Выполнив построение самостоятельно, вы легко убедитесь –
биссектрисой отсекается от основания (или его продолжения на прямой за
пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства
углов трапеции
1. Какую
бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в
паре всегда составляет 1800: α +
β = 1800 и γ + δ = 1800.
2. Соединим
середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при
основаниях трапеции. Если сумма углов при любом из них составляет 900 ,
длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной
пополам: ТХ = (АЕ – КМ)/2.
3. Если
через стороны угла трапеции провести параллельные прямые, те разделят
стороны угла на пропорциональные отрезки.
Свойства
равнобедренной (равнобокой) трапеции
1. В
равнобедренной трапеции равны углы при любом из оснований.
2. Теперь
снова постройте трапецию, чтобы проще было представить, о чем речь.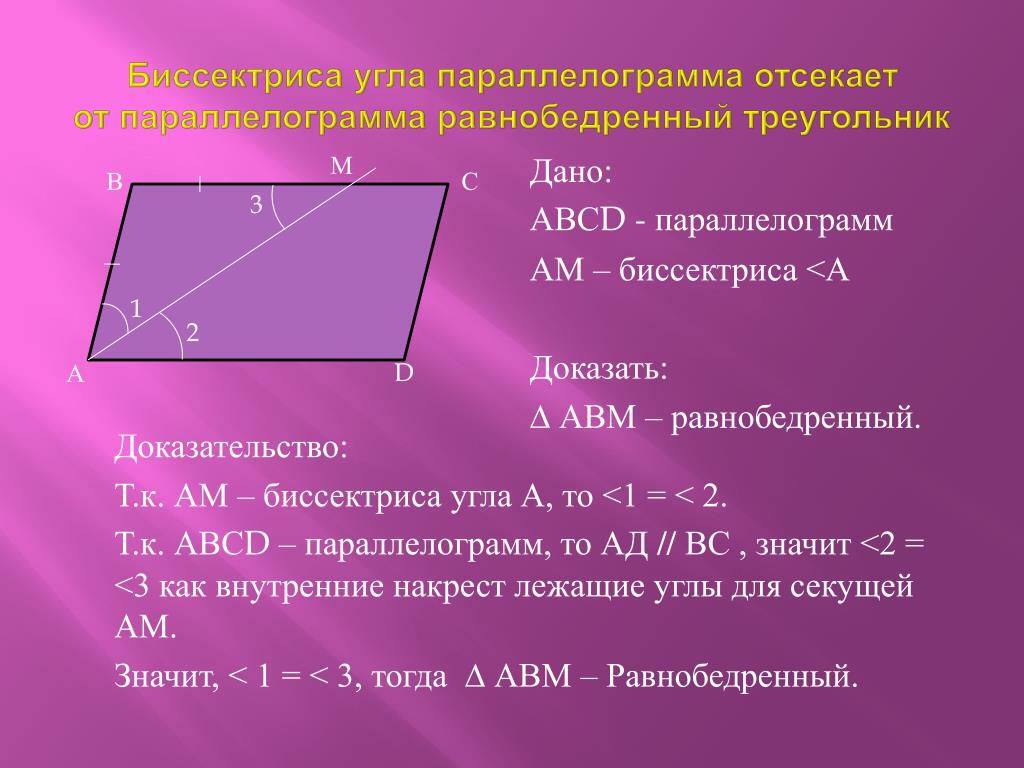
внимательно на основание АЕ – вершина противоположного основания М проецируется
в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки
проекции вершины М и средняя линия равнобедренной трапеции – равны.
3. Пару
слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также
одинаковы углы наклона этих диагоналей к основанию трапеции.
4. Только
около равнобедренной трапеции можно описать окружность, поскольку сумма
противолежащих углов четырехугольника 1800 –
обязательное условие для этого.
5. Из
предыдущего пункта следует свойство равнобедренной трапеции – если возле
трапеции можно описать окружность, она является равнобедренной.
6. Из
особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее
диагонали пересекаются под прямым углом, то длина высоты равна половине суммы
оснований:
h = (a + b)/2.
7. Снова
проведите отрезок ТХ через середины оснований трапеции – в равнобедренной
трапеции он является перпендикуляром к основаниям.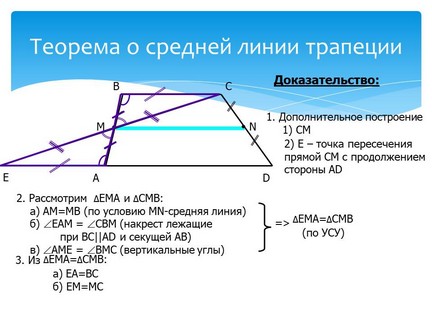
симметрии равнобедренной трапеции.
8. На
этот раз опустите на большее основание (обозначим его a) высоту из
противолежащей вершины трапеции. Получится два отрезка. Длину одного можно
найти, если длины оснований сложить и разделить пополам: (a + b)/2.
Второй получим, когда из большего основания вычтем меньшее и полученную
разность разделим на два: (a – b)/2.
Свойства
трапеции, вписанной в окружность
Раз
уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе
подробней. В частности на том, где находится центр окружности по отношению к
трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и
начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
1. Расположение
центра окружности определяется углом наклона диагонали трапеции к ее боковой
стороне. Например, диагональ может выходить из вершины трапеции под прямым
углом к боковой стороне. В таком случае большее основание пересекает центр
описанной окружности точно посередине (R = ½АЕ).
2. Диагональ
и боковая сторона могут встречаться и под острым углом – тогда центр окружности
оказывается внутри трапеции.
3. Центр
описанной окружности может оказаться вне пределов трапеции, за большим ее
основанием, если между диагональю трапеции и боковой стороной – тупой угол.
4. Угол,
образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол)
составляет половину того центрального угла, который ему соответствует:МАЕ =
½МОЕ.
5. Коротко
про два способа найти радиус описанной окружности. Способ первый: посмотрите
внимательно на свой чертеж – что вы видите? Вы без труда заметите, что
диагональ разбивает трапецию на два треугольника. Радиус можно найти через
отношение стороны треугольника к синусу противолежащего угла, умноженному на
два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно
расписать для любой из сторон обоих треугольников.
6. Способ
второй: находим радиус описанной окружности через площадь треугольника,
образованного диагональю, боковой стороной и основанием трапеции: R =
АМ*МЕ*АЕ/4*SАМЕ.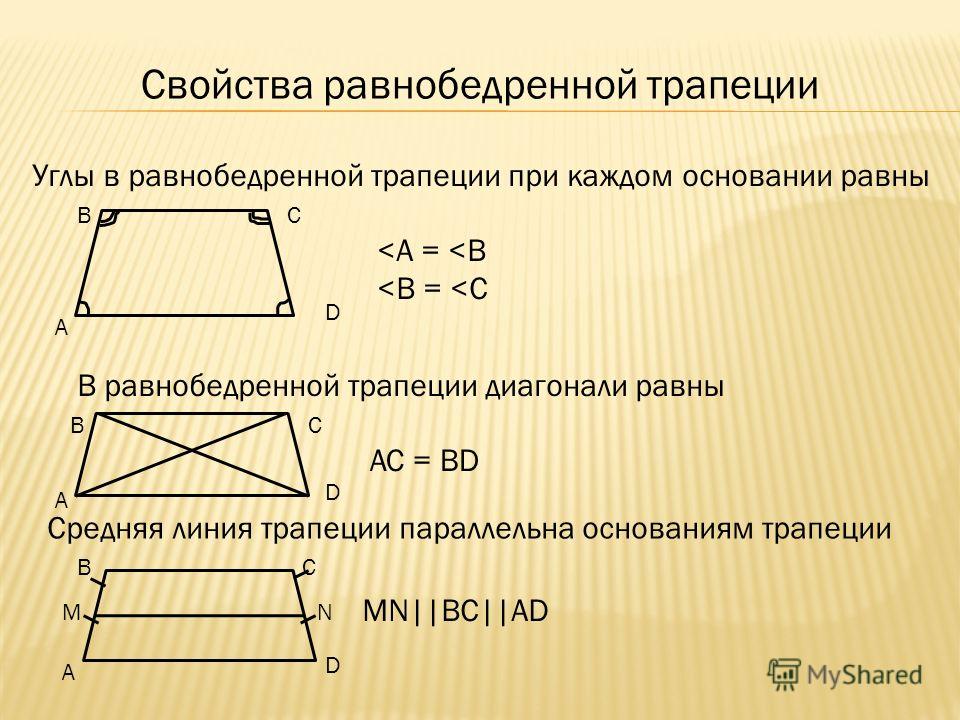
Свойства
трапеции, описанной около окружности
Вписать
окружность в трапецию можно, если соблюдается одно условие. Подробней о нем
ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
1. Если
в трапецию вписана окружность, длину ее средней линии можно без труда найти,
сложив длины боковых сторон и разделив полученную сумму пополам: m = (c
+ d)/2.
2. У
трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме
длин боковых сторон: АК + МЕ = КМ + АЕ.
3. Из
этого свойства оснований трапеции вытекает обратное утверждение: окружность можно
вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
4. Точка
касания окружности с радиусом r, вписанной в трапецию, разбивает боковую
сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по
формуле: r = √ab.
5. И
еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас
есть старая-добрая трапеция АКМЕ, описанная около окружности.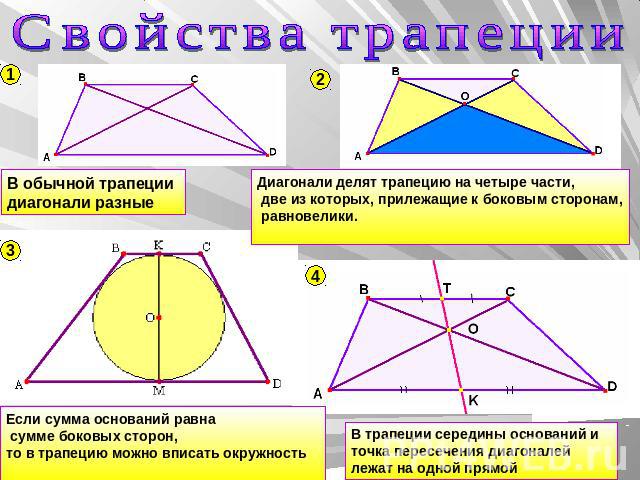
диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и
боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны
трапеции), совпадают с радиусами вписанной окружности. А высота трапеции –
совпадает с диаметром вписанной окружности.
Свойства
прямоугольной трапеции
Прямоугольной
называют трапецию, один из углов которой является прямым. И ее свойства
проистекают из этого обстоятельства.
1. У
прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
2. Высота
и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет
вычислять площадь прямоугольной трапеции (общая формула S = (a + b) *
h/2) не только через высоту, но и через боковую сторону, прилежащую к
прямому углу.
3. Для
прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей
трапеции.
Доказательства
некоторых свойств трапеции
Равенство
углов при основании равнобедренной трапеции:
·
Вы уже наверное и сами догадались, что тут нам снова потребуется
трапеция АКМЕ – начертите равнобедренную трапецию.
прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный
четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА =
МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК ||
МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда
АКМ = 1800 — МЕТ = 1800 —
КАЕ = КМЕ.
Что и
требовалось доказать.
Теперь
на основании свойства равнобедренной трапеции (равенства диагоналей) докажем,
что трапеция АКМЕ является равнобедренной:
·
Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм
КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ
– равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ ||
КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас
получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ –
общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что
АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача
для повторения
Основания
трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует
угол 1500 с меньшим основанием.
найти площадь трапеции.
Решение: Из
вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать
углы трапеции.
Углы
АЕМ и КАН являются односторонними. А это значит, в сумме они дают 1800.
Поэтому КАН = 300 (на
основании свойства углов трапеции).
Рассмотрим
теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без
дополнительных доказательств). Из него найдем высоту трапеции КН – в
треугольнике она является катетом, который лежит напротив угла в 300.
Поэтому КН = ½АВ = 4 см.
Площадь
трапеции находим по формуле: SАКМЕ =
(КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см2.
Послесловие
Если
вы внимательно и вдумчиво изучили этот материал, не поленились с карандашом в
руках начертить трапеции для всех приведенных свойств и разобрать их на
практике, материал должен был неплохо вами усвоиться.
Конечно,
информации тут много, разнообразной и местами даже запутанной: не так уж сложно
перепутать свойства описанной трапеции со свойствами вписанной.
убедились, что разница огромна.
Теперь
у вас есть подробный конспект всех общих свойств трапеции. А также
специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им
очень удобно пользоваться, чтобы готовиться к контрольным и ЕГЭ, ОГЭ.
трапеция и ее теоремы
Введение в геомантию
Пожалуйста, включите JavaScript
Введение в геомантию
Мы в ask-math считаем, что образовательный материал должен быть бесплатным для всех. Пожалуйста, используйте содержимое этого веб-сайта для более глубокого понимания концепций. Кроме того, мы создали и разместили видеоролики на нашем YouTube.
Мы также предлагаем индивидуальные / групповые занятия / помощь в выполнении домашних заданий по математике с 4 по 12 классы по алгебре, геометрии, тригонометрии, предварительному исчислению и исчислению для учащихся из США, Великобритании, Европы, Юго-Восточной Азии и ОАЭ.
Также приветствуются связи со школами и учебными заведениями.
Пожалуйста, свяжитесь с нами по [email protected] / Whatsapp +919998367796 / Skype id: anitagovilkar.abhijit
Мы также будем рады разместить видео в соответствии с вашими требованиями. Напишите нам.
В этом разделе мы обсудим некоторые трапеции и их теоремы.
Трапеция – это четырехугольник, по крайней мере, с одной парой параллельных сторон. АБ || CD. (если есть две пары параллельных прямых, то это параллелограмм)
Если непараллельные стороны трапеции равны, то она называется равнобедренной трапецией.
Теорема 1. Трапеция равнобедренная тогда и только тогда, когда углы при основании равны.
Дано: ABCD — равнобедренная трапеция. AD = ВС и АВ || CD.
Докажите, что: ↑C = ♂
0045
| Заявления | Причины |
1) ABCD — трапеция. |
1) Дано |
| 2) AB || CD | 2) Дано |
| 3) AD = BC | 3) Дано |
| 4) DA || CE | 4) По конструкции |
| 5) ADCE является параллелограммом. | 5) По свойствам параллелограмма. |
| 6) DA = CE и DC = AE | 6) По свойствам параллелограмма. |
| 7) BC = CE | 7) BC = AD и AD = CE (переходное свойство) |
 ∠CEB ≅ &CBE ∠CEB ≅ &CBE |
 Если BC ≅ CE, то противоположные им углы равны. Если BC ≅ CE, то противоположные им углы равны. |
| 9) ∠DAB ≅ ∠ABC | 9) свойство параллелограмма и линейной пары углов |
| 10) ∠A + ∠D = 180 и ∠B + 1002 ∠90 на внутренних углах 180 те же стороны трансверсали являются дополнительными. | |
| 11) ∠A + ∠D = ∠C + ∠B | 11) Транзитивность (правые стороны одинаковы, поэтому левые равны) |
| 12) ∠D = ∠C | 12) Сверху (∠A = ∠B) |
Пример: В трапеции QRS и.
Решение:
PQ||RS и PS = QR, поэтому трапеция PQRS является равнобедренной трапецией.
В равнобедренной трапеции углы при основании равны.(трапеция и ее теоремы)
∠S = ∠R и ∠P = ∠Q
Но ∠S = 60 0
∴ ∠R = 60 0
Пусть ∠P = ∠Q = x
Сумма всех углов четырехугольника равна 360.
∴ ∠P + ∠Q + ∠S + ∠R = 360
x + x + 60 + 60 = 360
2x +120 = 360
2x = 360 -120
2x = 240
∴ x = 240/2
x = 120
тнаг.
Теоремы
1. Трапеция равнобедренная тогда и только тогда, когда углы при основании равны.
2. Трапеция равнобедренная тогда и только тогда, когда диагонали конгруэнтны.
3.
Медиана (или середина) трапеции параллельна каждому основанию, и ее длина составляет половину суммы длин оснований.
Никогда не предполагайте, что трапеция равнобедренная, если вы не получили (или не можете доказать) эту информацию.
Практика
1) В трапеции ABCD,AB|| CD и ВС = AD. Если m∠C=65 0 , то найти m∠D.
2) PQRS — трапеция, в которой PQ || РС. Если ∠P = ∠Q = 40, найдите величины двух других углов.
3) В трапеции ABCD ∠B= 120 0 Найти m∠C.
4) В четырехугольнике HELP, если EP = LH, то какой это четырехугольник?
5) В четырехугольнике углы относятся как 4:5:3:6. Найдите величины каждого угла.
6) Если три угла трапеции равны 130 0 ,120 0 ,50 0 и 2x 0 . Найдите х и четвертый угол.
7) Нарисуйте равнобедренную трапецию с именем PQRS, PS||QR и PQ = SR.
Четырехугольник
• Введение в четырехугольник
• Типы четырехугольника
• Свойства четырехугольника
• Параллелограмм и его теоремы
• Rectangle and its Theorems
• Square and its Theorems
• Rhombus and its Theorems
• Trapezoid and its Theorems
• Kite and its Theorems
• Mid Point Theorem
Geometry
Home Page
- Домашняя страница
- Видео по математике
- Чувство чисел
- Алгебра
- Бизнес-математика
- Геометрия
- Измерение
- Статистика
- Тригонометрия
- 75 Измерения
- 750275
- 11th grade math
- Hindi Numbers
- Formula 1
- Ask Experts
- f UN zONE
- Link Partners
- About us/Disclaimer
- Contact Us
- Privacy Policy
- Math Blog
- CBSE Sample Papers
сообщите об этом объявлении
сообщите об этом объявлении
сообщите об этом объявлении
Свойства трапеций: определение и теорема
Ключевые понятия
- Дайте определение трапеции.
- Объясните свойства трапеции.
- Решение задач на основе свойств воздушного змея.
Трапеция
Четырехугольник, имеющий только одну пару параллельных сторон, называется трапецией .
- Трапеция, у которой непараллельные стороны равны, равна равнобедренной трапеции .
Свойство трапеции, связанное с углами при основании
Теорема 1:
В равнобедренной трапеции каждая пара углов при основании конгруэнтна.
Дано: ABCD — трапеция, где AB∥CD.
Чтобы доказать: ∠ADC = ∠BCD и ∠BAD = ∠ABC
Доказательство:
Проведите перпендикулярные линии AE и BF между параллельными сторонами трапеции.
в ΔAED и ΔBFC,
AD = BC [Isosceles Trapezoid]
AE = BF [Расстояние между параллельными линиями всегда будет равным]
omaEB = ♂ = 90 ° [AEʇCD и BFʇCD]
Если у двух прямоугольных треугольников гипотенузы равны по длине, а пара более коротких сторон равна по длине, то треугольники конгруэнтны.
∴ ΔAED ≌ ΔBFC [правостороннее правило конгруэнтности]
Мы знаем, что соответствующие части конгруэнтных треугольников равны.
Отсюда, ↑ADC = Ϫbcd
и ↑EAD = ♂фбк
Теперь, ▲BAD = ↑BAE + тий hTEAD
потряно РАД
∠BAD = ∠ABC
Следовательно, каждая пара углов при основании равнобедренной трапеции конгруэнтна.
Свойство трапеции, связанное с длиной диагоналей
Теорема 2:
Диагонали равнобедренной трапеции конгруэнтны.
Приведено: в трапециевии ABCD, AB∥CD и AD = BC
, чтобы доказать: AC = BD
Доказательство:
в ΔAdc и ΔBCD,
AD = BCESESIS ISOSCZESIOD].
↑ADC = ↑BCD [базовые углы Isockeles Trapezoid]
CD = CD [Common]
Следовательно, ΔAed ≌ ΔBFC [SAS -правило]
Мы знаем, что соответствующие части конгруэнтных треурианцев равны.
Итак, AC = BD
Следовательно, диагонали равнобедренной трапеции равны.
Свойство трапеции, связанное с длиной диагоналей
Теорема 3:
В трапеции средний сегмент параллелен основаниям, а длина среднего сегмента равна половине суммы длин оснований.
Дано: В трапеции ABCD AB∥CD, X — середина AD, Y — середина BC.
Чтобы доказать: XY = 1/2 × (AB+CD)
Доказательство: Постройте BD так, чтобы середина BD проходила через XY.
В ΔADB X — это середина AD, а M — середина DB.
Итак, XM — это середина ΔADB.
Мы знаем, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и имеет длину, равную половине длины третьей стороны. [Теорема о среднем отрезке]
∴ XM ∥ AB и XM = 1/2 × AB …(1)
В ΔBCD Y — середина BC, а M — середина BD.
Итак, MY — это середина ΔBCD.
∴ MY ∥ CD и MY = 1/2 × CD …(2) [Теорема о среднем отрезке]
Поскольку XM ∥ AB и MY ∥ CD, то XY
Теперь XY=XM+MY
/
2 × AB + 1/2 × CD
XY = 1/2 × (AB+CD)
Воздушный змей
Воздушный змей — это два равных четырехугольника, четыре стороны которых можно сгруппировать в группы.
(или)
Параллелограмм также имеет две пары сторон одинаковой длины, но они противоположны друг другу в воздушном змее .
- Только одна диагональ воздушного змея делит пополам другую диагональ.
Свойство воздушного змея, связанное с углом между диагоналями
Теорема:
Диагонали воздушного змея перпендикулярны.
Дано: В змее WXYZ, XY=YZ, WX=ZW
Доказать: XZ Ʇ WY
Доказательство: Проведите диагонали XZ и WY. Пусть диагонали пересекаются в O.
в ΔWxy и ΔWzy,
Wx = WZ [соседние стороны кайта]
xy = zy [соседние стороны кайта]
Wy = YW [Рефлексивное свойство]
δ ΔWxy ≌ ≌ ≌ wxy ≌. ΔWZY [правило конгруэнтности SSS]
Мы знаем, что соответствующие части конгруэнтных треугольников равны.
Итак, ∠XYW= ∠ZYW …(1)
в Δoxy и Δozy,
xy = ZY [соседние стороны Kite]
OY = yo [рефлексивное свойство]
↑xyw = ↑zyw [из (1)]
δ Δoxy Δozy [SAS urduence rule].



























































































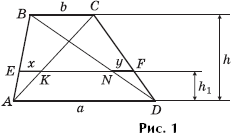
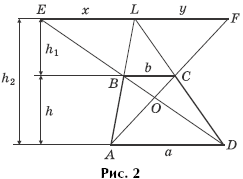
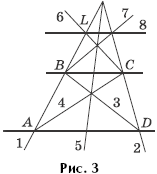
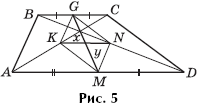
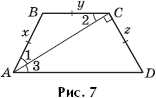
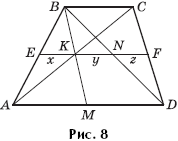
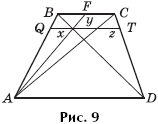
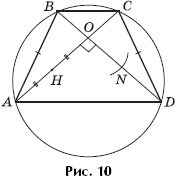
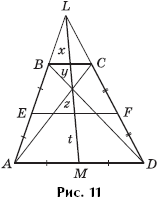
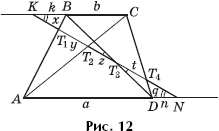
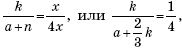
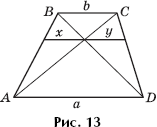
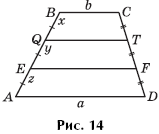
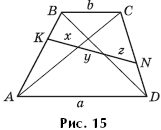
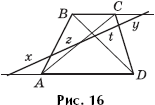
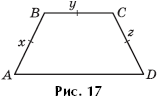
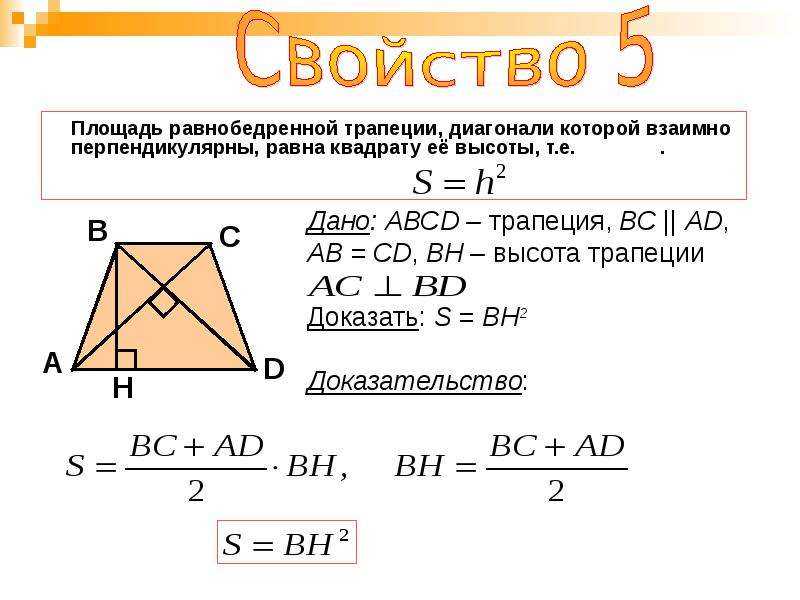 Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции