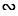Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Основные сведения об отношении площадей подобных треугольников
Понятие подобия треугольников
Два треугольника называются подобными, если их углы попарно равны, а стороны, лежащие напротив соответственных углов пропорциональны.
A B / K L = B C / L M = A C / K M = k , ∠ A = ∠ K , ∠ B = ∠ L , ∠ C = ∠ M ⇒ Δ A B C
Отношение длин подобных треугольников называют коэффициентом подобия (k).
Также пропорциональные стороны подобных треугольников могут быть названы сходственными сторонами.
В подобных треугольниках, кроме сторон, подобны и другие величины: биссектрисы, медианы, высоты и т.д.
Теорема об отношении площадей подобных треугольников
Формулировка теоремы: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
В геометрии существует три признака подобия треугольников:
1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.
Свойства подобных треугольников:
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных элементов равно коэффициенту подобия.
Доказательство теоремы
Докажем теорему об отношении площадей подобных треугольников.
Теорема: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство: изобразим подобные треугольники Δ A B C
Из подобия треугольников по определению следует: A B / K L = B C / L M = A C / K M = k .
Воспользуемся следующей теоремой: если у двух треугольников равны углы (∠A=∠K), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем в виде формулы:
Что и требовалось доказать.
Примеры решения задач
Площади подобных треугольников ΔABC и ΔA1B1C1 равны соответственно 200 см² и 50 см². Сторона A1B1=5 см. Найдите сходственную ей сторону AB треугольника ABC.
По теореме об отношении площадей подобных треугольников: S a b c / S a 1 b 1 c 1 = k ² ⇒ 200 / 50 = k ² ⇒ k = 2 .
A B / A 1 B 1 = 2 , A B = A 1 B 1 * 2 , A B = 5 * 2 = 10 с м .
ΔABC и ΔA1B1C1 — подобны. Сходственные стороны AC и A1C1 соответственно равны 13 см и 0,1 м.
Найдите отношение периметров ΔABC и ΔA1B1C1.
A 1 C 1 = 0 , 1 м = 10 с м
A C / A 1 C 1 = 13 / 10 = 1 , 3 ⇒ P a b c / P a 1 b 1 c 1 = 1 , 3
Задача для самостоятельной работы
Треугольники Δ A B C
Δ K L M подобны. Площадь ΔABC равна 500 см², площадь ΔKLM равна 125 см². Сторона AC равна 18 см, найти сходственную ей сторону KM.
Проверьте, насколько верный или неверный ваш ответ.
Советуем составить краткий конспект для подготовки к уроку.
Отношение площадей подобных треугольников
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»
http://wika.tutoronline.ru/geometriya/class/8/osnovnye-svedeniya-ob-otnoshenii-ploshhadej-podobnyh-treugolnikov
http://interneturok.ru/lesson/geometry/8-klass/podobnye-treugolniki/otnoshenie-ploschadey-podobnyh-treugolnikov
Данные в задаче треугольники подобны, так как их стороны пропорциональны
15:5=24:8=36:12
Признак 3 подобия
Два треугольника подобны, если три стороны одного треугольника пропорциональны сторонам другого треугольника.
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
15:5=3
k=3
Отношение площадей данных треугольников равно
k²=9
Отношение площадей = 9:1
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Отношение площадей подобных треугольников
Теорема
Доказательство
Дано: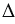 
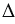
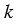
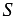
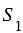
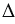
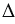
АВС
А1В1С1, 
— коэффициент подобия, 
и 
— площади АВС и А1В1С1.
Доказать: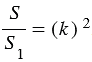 
.
Доказательство:
1. АВСА1В1С1, следовательно, 
А =А1, значит, 
(т.к. площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих равные углы). При этом, из подобия треугольников АВС и А1В1С1 следует то, что 
, значит, 
и 
, тогда, 
.
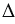
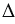
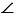
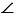
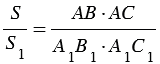
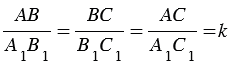
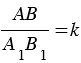
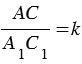
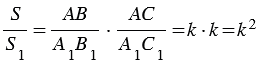
Теорема доказана.
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 543,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 544,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 545,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 546,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1077,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1143,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1209*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1308,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
math-public:otnoshenie_ploshchadej_treugolnikov_s_ravnymi_ehlementami
Содержание
Отношение площадей треугольников с равными элементами
Теорема
-
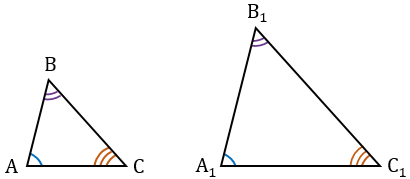
Если высоты двух треугольников равны, то их площади относятся, как основания.
-
Если основания двух треугольников равны, то их площади относятся, как высоты, проведенные к этим основаниям.
-
Если угол одного треугольника равен углу другого треугольника, то их площади относятся, как произведения сторон, заключающих равные углы.
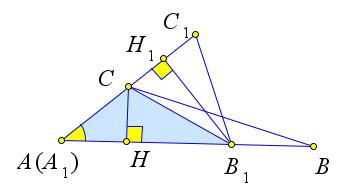
Докажем первый пункт теоремы.
Рассмотрим треугольники $triangle ABC$ и $triangle A_1B_1C_1$ в которых высоты $BH$ и $B_1H_1$ равны.
Тогда $dfrac{S_{ABC}}{S_{A_1B_1C_1}}=dfrac{frac{1}{2}BHcdot
AC}{dfrac{1}{2}B_1H_1cdot A_1C_1}=dfrac{AC}{A_1C_1}$.
Докажем второй пункт теоремы.
Рассмотрим треугольники $triangle ABC$ и $triangle A_1B_1C_1$ в которых основания $AC$ и $A_1C_1$ равны.
Тогда $dfrac{S_{ABC}}{S_{A_1B_1C_1}}=dfrac{dfrac{1}{2}BHcdot
AC}{dfrac{1}{2}B_1H_1cdot A_1C_1}=dfrac{BH}{B_1H_1}$.
Докажем третий пункт теоремы.
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$ в которых углы $A$ и $A_1$ равны.
Докажем, что их площади относятся как произведения сторон, заключающих эти углы.
Наложим треугольник $A_1B_1C_1$ на треугольник $ABC$ так, чтобы вершина $A_1$ совместилась с вершиной $A$, а стороны $A_1B_1$ и $A_1C_1$ наложились соответственно на лучи $AB$ и $AC$.
Треугольники $ABC$ и $AB_1C$ имеют общую высоту $CH$, поэтому
$dfrac{S_{ABC}}{S_{AB_1C}}=dfrac{AB}{AB_1}$.
Треугольники $AB_1C$ и $AB_1C_1$ имеют общую высоту $B_1H_1$, поэтому
$dfrac{S_{AB_1C}}{S_{AB_1C_1}}=dfrac{AC}{AC_1}$.
Перемножая полученные равенства, находим: $dfrac{S_{ABC}}{S_{A_1B_1C_1}}=dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1}$.
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки,
пропорциональные двум другим его сторонам.
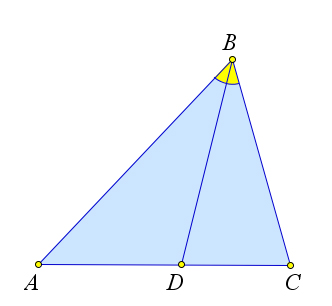
Доказательство
Рассмотрим треугольник $ABC$, в котором проведена биссектриса $BD$.
Докажем, что $dfrac{AD}{DC}=dfrac{AB}{BC}$.
Действительно, так как у треугольников $ABD$ и $BDC$ высота,
проведенная из вершины $B$, общая, то $S_{ABD}:S_{BDC}=AD:DC$.
Кроме того у этих треугольников есть равные углы, следовательно их площади
относятся, как произведения сторон: $S_{ABD}:S_{BDC}=dfrac{ABcdot
BD}{BDcdot BC}=dfrac{AB}{BC}$.
Сравнивая полученные равенства для отношения площадей, получаем: $dfrac{AD}{DC}=dfrac{AB}{BC}$.
Теорема об инцентре
-
Инцентр делит биссектрису $l_c$ в отношении $(a+b):c$
-
Все биссектрисы треугольника пересекаются в одной точке.
Доказательство
Докажем первый пункт теоремы
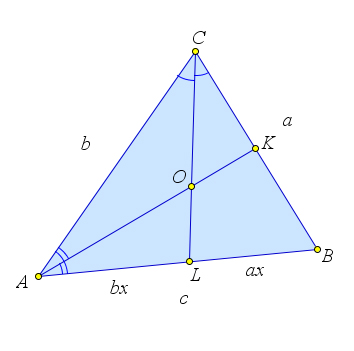
Рассмотрим треугольник $ABC$, в котором проведены биссектрисы $AK$ и $CL$.
Пусть $BC=a, AC=b, AB=c$.
Пусть $AK$ пересекает $CL$ в точке $O$.
По теореме $AL:LB=b:a$.
Тогда $AL=ccdotdfrac{b}{a+b}$
Кроме того в треугольнике $ACL$, $AO$ – биссектриса.
Тогда $CO:OL=b:AL=b:left(dfrac{bc}{a+b}right)=dfrac{a+b}{c}$.
Докажем второй пункт теоремы
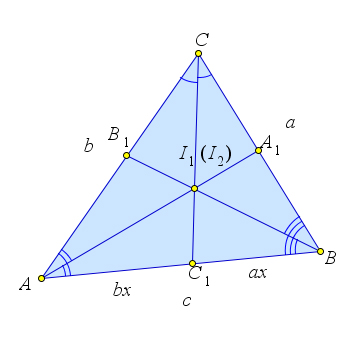
Рассмотрим треугольник $ABC$, в котором проведены биссектрисы $AA_1$, $BB_1$ и $CC_1$.
Пусть $BC=a, AC=b, AB=c$.
Пусть $AA_1cap CC_1=I_1$, $BB_1cap CC_1=I_2$.
Тогда по теореме $CI_1:I_1C_1=dfrac{a+b}{c}$ и $CI_2:I_2C_1=dfrac{a+b}{c}$.
А это означает, что точки $I_1$ и $I_2$ совпадают (так как они обе лежат на отрезке $CC_1$).
Таким образом все биссектрисы пересекаются в одной точке.
Доптеоремы
О шести треугольниках и медианах
О боковых треугольниках трапеции
О произведении площадей в четырехугольнике с диагоналями и следствие для трапеции
· Последнее изменение: 2019/11/18 18:08 —
labreslav
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Отношение площадей подобных треугольников
Теорема об отношении площадей подобных треугольников
Для подобных треугольников 
и 
с коэффициентом подобия 
справедлива следующая теорема:
ТЕОРЕМА
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Обозначим через 
и 
площади треугольников и с коэффициентом подобия . Так как 
, то
![[frac{S}{S_1 } =frac{ABcdot AC}{A_1 B_1 cdot A_1 C_1 } ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eef9da9698297d86af926eba48b980b2_l3.png "Rendered by QuickLaTeX.com")
Из свойств подобных треугольников следует, что 
. Тогда
![[frac{S}{S_1 } =k^2 ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ce5aa3d22b953f13908c20ad4f095d3c_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.