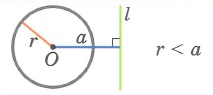
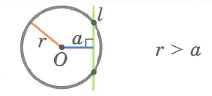
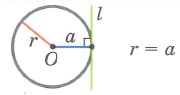
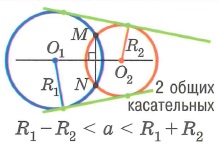
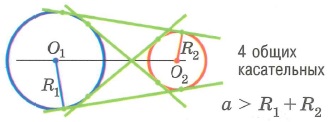
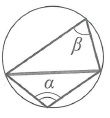
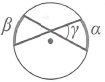
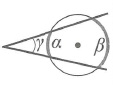
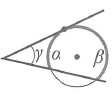
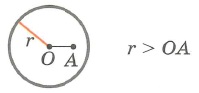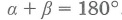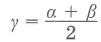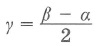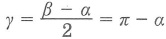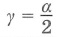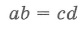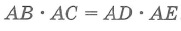Треугольник. Соотношения между сторонами треугольника и радиусами вписанного и описанного кругов.
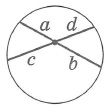
По двум сторонам a и b треугольника ABC и радиусу R описанного круга вычислить третью сторону x треугольника.
Применяя к этому четырехугольнику теорему Птоломея будем иметь:
откуда легко найдем x .
Задача будет иметь другое решение, если предположим, что стороны a и b лежат по одну сторону от центра. Применяя к этому случаю теорему Птоломея, мы получим следующее уравнение:
Теорема.
Произведение двух сторон треугольника равно:
1. произведению диаметра описанного круга на высоту, проведенную к третьей стороне.
2. квадрату биссектрисы угла, заключенного между этими сторонами, сложенному с произведением отрезков третьей стороны.
1.Обозначим стороны треугольника ABC через a, b и с, высоту, опущенную на сторону a через ha , а радиус описанного круга через R.Проведем диаметр AD и соединим D с B.
Треугольники ABD и AEC подобны, потому что углы B и E прямые и D= С , как углы вписанные, опирающиеся на одну и ту же дугу.
Из этой формулы легко определить величину радиуса R описанного круга.
По первой теореме мы имеем: bс = 2Rha , где b и с есть две стороны треугольника, ha — высота, опущенная на третью сторону треугольника, и R — радиус описанного круга.
Из этого равенства выводим:
Исключим из этой формулы высоту ha: для этого умножим числитель и знаменатель дроби на a. Тогда, заменив произведение ha a удвоенной площадью треугольника (которую обозначим S), получим:
,
Чтобы найти радиус r внутреннего вписанного круга рассмотрим треугольник АВС со вписанной в него окружностью. Отметим центр вписанной окружности и примем во внимание, что прямые OA, OB и OС разделяют данный треугольник на три других треугольника, у которых основаниями служат стороны данного треугольника, а высотой — радиус r.
Поэтому: S=1/2ar + 1/2br + 1/2cr = r ½ (a+b+c) = rp.
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
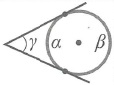
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
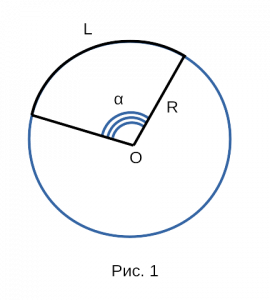
Сторона окружности
Определение стороны окружности
Сторона окружности — это длина дуги окружности.
Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.
На рисунке 1, изображена окружность,
обладающая следующими величинами:
- O — точка, являющаяся
центром окружности; - R — радиус
окружности; - α — центральный
угол окружности; - L — сторона
окружности;
Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:
Ⅰ. Умножить радиус окружности на π,
получившееся разделить на 180 градусов.
Ⅱ. Полученный результат умножить на угол.
Также, все это можно сделать, зная одну из
известных формул стороны окружности:
Формулы стороны окружности
Ⅰ. Через диаметр и центральный угол
Сторону окружности L, можно найти, разделив
произведение половины диаметра и π на 180 градусов.
Затем умножить полученное значение на угол.
Ⅱ. Через площадь и центральный угол
Эта формула, примечательна тем, что
для нахождения длины, не обязательно
знать радиус — главное знать площадь.
Ⅲ. Через периметр и центральный угол
Самая краткая запись формулы
стороны окружности.
Пример решения задач по теме сторона окружности
Возьмем для удобства π равное 3.14.
Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?
Решение:
( L = frac<frac<6> <180>cdot pi> <180>cdot 180 = frac<3 pi> <180>cdot 180 = 3pi = 9.42 )
Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?
Решение:
( L = frac<100> <180>cdot 60 = 0.55 cdot 60 = 33 )
http://skysmart.ru/articles/mathematic/teorema-sinusov
http://colibrus.ru/storona-okruzhnosti/
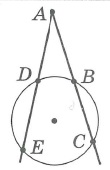
Метрические соотношения в окружности
Оценка 4.7
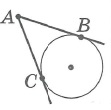
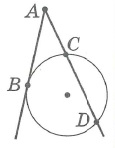
друзья всем привет мы продолжаем наш разговор о геометрии в рамках проекта наука в регионы на прошлом семинаре мы с вами говорили о касательной к окружности и порешали довольно большое количество задач сегодня мы делаем большой шаг вперед и говорим уже о метрических соотношениях в окружности и построим наш урок подобно тому как было в прошлый раз сначала сформулирует три фундаментальных факта а затем опираясь на них мы с вами прорешаем довольно большое количество задач начинаем итак первый факт носит имя теорема о касательный секущей квадрат отрезка касательной равен произведению всей секущей на ее внешняя часть по всей секущие понимается отрезок соединяющий точку из которой секущая проведена и вторая точка пересечения с окружностью этот факт мы с вами уже доказывали в прошлый раз он напрямую следовал из подобие треугольников a pc и а д б кто не видел пожалуйста пересмотреть второй факт говорит нам о том что произведение секущей на ее внешнюю часть это постоянная величина в частности на нашей картинке а d умножить на a c будет равно а f умножить на а и почему же это так да безумно просто давайте я рядышком незаметно проведу касательную а.б. тогда всему 1 факта а d умножить на отца равно а b квадрат но то же самое можно сказать и про пару а.ф. они а b квадрат равно f умножить на а и ну и таким образом часто бывает удобно пользоваться именно этой теоремой теоремой о постоянстве произведения секущие на ее внешнюю часть надеюсь никаких вопросов здесь не возникает ну и наконец третий теорема это теорема об отрезках пересекающихся хорд ей мы также будем сегодня пользоваться поэтому я вам и я сейчас аккуратно напомню пусть есть две хорды ab и cd пересекаются эти хорда в точке а тогда произведение отрезков на которое хорда делится этой точкой будут соответственно равны а умножить на b равно а умножить на а да откуда же берется этот факт но безумно просто соединим от c и d b отрезками мы тогда совершенно очевидно что треугольник у отца будет подобен треугольнику а б д просто-напросто по двум углам один вертикальный а второй как угол опирающийся на одну и ту же дугу например вот этот угол бы равен этому ну и таким образом если это подобие расписать то вот этот результат получается моментально буквально в один клик по этому доказательство всех этих утверждений совсем несложные что-то у нас уже была и давайте используя вот эту скромную базу фактов будем решать задачи которых они будут ключевыми вперед примерно родин в равнобедренном треугольнике a b c основания отца равно 4 а боковые стороны а bbc равно 6 кроме того проведена биссектриса cd эту самую точку d проведена окружность которая касается стороны отца в ее середине я отметил это что m равно 2 и пересекает пересекает отрезочек а.д. в точке ну а нам собственно нужно найти длину отрезка да и ну что же давайте решать эту задачу первое начнём мы с того что не имеет непосредственного отношения к теме нашего сегодняшнего занятия однако должно быть вам прекрасно известно начнем мы со свойство биссектрисы вы прекрасно знаете что биссектриса делит третью сторону на отрезке пропорциональные боковым сторонам у меня на картиночке получилось немного не так но у меня это и не совсем биссектриса надо было опустите немножечко пониже тогда была бы еще более наглядно тем не менее науку не перевернуть и безусловно мы скажем что а.б. так относится к db как отца относятся к bc то есть две трети иными словами можно сказать что а b равно 2 3 db кроме того мы знаем с вами что а d + db вместе а д д б вместе дают всю сторону то есть дают 6 откуда мы с вами получаем что две третьих до b плюс д.б. это 5 3 d b равно 6 откуда db равно ну давайте посчитаем 18 5 18 5 ну что ж знаем отрезок db ну и можно было сразу даже найти отрезок а д а до я получается равен 6 лет у нас 35 35 минус 18 5 12 5 итак нашли отрезочек а.д. а нам надо найти отрезочек d и как его можно найти ну мы смогли например найти отрезок да ей если бы знали длину отрезка ае но тогда просто из ада вышли бы это самое а.е. а откуда можно найти а.е. но несомненно а е является внешней частью касательной секущей а.д. и вот здесь как раз ключом и станет наш с вами первый факт а именно а m в квадрате квадрат отрезка касательной равен произведению секущей ада на ее внешняя часть ребята здесь я пожалуй становлюсь и отмечу что секущей является именно а.д. очень часто в работах ребят даже по проверке олимпиады физтех это просто невероятно частая ошибка ребята считают секущей а.б. причем 10 . b когда мы говорим о металлических соотношениях для этой окружности совершенно не причем все секущие являются повторюсь отрезок соединяющий точку из которых секущая выходит и вторую точку пересечения с окружностью будьте внимательны но мы получаем с вами что 4 равно 12 5 умножить на а е ну откуда а если я не ошибаюсь равно 5 третьих самом деле пятерочки уйду то 12 на 3 будет равно 4 ну и таким образом не осталось всего лишь навсего третье действие третье действие которое будет стоять буквально в следующем для того чтобы найти дает мне нужно из ада да я равна из ада вычесть а я то есть из 12 5 вычесть 5 третьих вы соответственно 36 1536 15х минус 25 15 получается 11 15 это правильный ответ 1115 вот такая нехитрая задача просто в качестве некоторого стартового упражнения во первых вспомнили свойство биссектрисы а во-вторых ключом стала как раз теорема о касательный и секущей едем дальше в 1 1976 году на вступительных экзаменах на кистях предлагалась следующая задача прямоугольный треугольник a b c угол c прямой соответственно угольники известно что отношения отсек а.б. это 4 к 5 и кроме того проведена окружность центр который лежит накатить и отце центр . а эта окружность касается гипотенуза в точке м пересекает катет bc в точке p известно также что bp относится к pc как две третьих а нам требуется с вами найти отношение радиус этой окружности к отрезку bc катету pc то есть ни одна длина не дано даны только отношений зная эти отношения нужно найти отношение радиуса соответственно к стороне bc ну что ж давайте начнем с того что некоторым образом попробуем формализовать все то что у нас есть в частности 1 нам дано такое отношение ни о каком подобие пока что говорить не приходится в этом смысле очень удобно просто напросто заказать что ну окей давайте от c будет равно 4 x aa b будет равно 5x тогда я даже не хочу это подробно расписывать по теореме пифагора однозначно следует чтобы все это просто-напросто 3x это самый известный египетский треугольник 345 ну хорошо bc равно 3x но с другой стороны мы с вами из условия знаем чтобы c делится свою очередь на два отрезка давайте а прямо условия немножечко перепишу в частности мы знаем что bp это две третьих паца аж такой bc это под а + б.п. давайте это запишем скажем что это просто-напросто pc + п п п п то две третьих пациент то есть посмотрите мы еще в 1 клик с вами узнали что опять третьих по c равно 3 икс откуда прямо следует что под сайта 9x на 59 x на 5 а отрезочек bp получается 6 x на 5 самом деле соотношению них будет два к трём а в сумме они будут давать 15 x на 5 то есть три икс то есть давайте отметим наше достижение к текущему моменту мы знаем что вот это 6 x на 5 мы знаем что вот эта 9 x на 5 мы знаем что а.б. это 5x мы знаем что отца целиком и to 4x ну хорошо выразили все отрезки в задаче через соответственно ну кроме б м а м через x и но что же делать дальше с одной стороны не понятно с другой стороны ну очень бы хотелось воспользоваться теоремой соответственно касательно секущей но касательно у меня есть б.м. а вот секущей ты нет мы медведь с другой стороны никакой проблемы ребятки в том чтобы просто напросто продлить отрезать чек cb до пересечения до 2 пересечения с окружности давайте назовем эту точку и здесь нам потребуется еще один факт о котором мы кстати не говорили факт довольно очевидный если у вас диаметр перпендикулярен какой-то хорде то он безусловно будет делить ее пополам этот факт и сейчас доказывает не буду просто на пальцах покажу откуда он берется но у вас ведь вот этот треугольничек будет несомненно равнобедренным а дальше из равенства вписанных уголочков можно будет показать что от сайта биссектриса ну а раз о цвета биссектриса а треугольник равнобедренный то это и соответственно и медиана и высота то есть все это довольно просто показывается итак мы с вами продлили в два раза отрезочек pc получается и получаем что qc наше дополнительное построение это тоже 9 x на 5 повторюсь так как диаметр перпендикулярных орды давайте это отдельно запишем хорде делит ее пополам делит ее на 2 тоже значит отрезочек куца это тоже 9 x на 5 и я уже ребятки могу воспользоваться теоремой о касательной секущей а значит смогу найти еще отрезочек mb ну что ж мы с вами получаем третий пункт мы получаем что mv квадрат есть не что иное как вся секущая а сколько это будет давайте посчитаем 9 до 9 да еще шесть это 24 x на 5 умножить на ее внешнюю часть на 6 x на 5 24 умножить на 6 это 144 следовательно это 144 x в квадрате на 25 откуда мы с вами и отрезочек mbs могли спокойно сейчас выразить через x cam бета 12 x на 5 mb это 12 x на 5 ну соответственно язык а м это 13 x на 5 потому что это просто-напросто 5 икс минус 12 x на 5 все что могли расписали через одну и ту же переменную но где же та ниточка за которую нужно потянуть чтобы найти ответ давайте во-первых сделаем то что давно бы пора сделать проведем этот самый радиус он у нас в явном виде в задаче присутствует это вот этот отрезочек о.м. это вот этот отрезочек о.м. ну и смотрите друзья получили мы прямоугольный треугольник а ма-а-ма-а ну и вот это просто-напросто радиус и нам надо радиус чем-то связать ну и тут смотрите какая не хит какую нехитрую модели вам предлагаю можно конечно было бы рассмотреть подобные треугольники вот этот треугольник будет подобен большому треугольнику из подобие все это расписать нам можно наверно поступить еще проще смотрите с одной стороны четвертый пункт соответственно тангенс вообще говорят что нам надо сделать я немножечко упускаю суть нам достаточно р выразить через x потому что бы с этому выразили через x этот рикс одохар выразить просто через xado задача будет решена собственно для этого давайте заметим следующие с одной стороны тангенс угла а из большого треугольника это просто-напросто bc делить на отце то есть три четверти это давайте я подпишу из треугольника об отце а с другой стороны из треугольника amo и этот же тангенс будет равен чему ребятки р делить на 13 5 x то есть r вверх пойдет от этого деления пятерочка а здесь соответственно будет просто напросто 13 таким образом ну и x конечно 13x таким образом мы с вами р из этого равенства спокойно можем выразить r равно 39 x делить на 20 ну все что нам остается это на эти отношения радиуса kbc но радиус much rice указ выразили bc мы через x выразили поэтому остается только формальное действие р делить на b c равно иксы сократятся и надо будет 39 двадцатых поделить на вот эту троечку еще раз ирма через x выразили bc мы через x выразили и получается ответ 1320 их совершенно верный ответ вот такая друзья мои не сложная задача здесь важно было просто не отчаиваться и все-таки настоять на вот этой теореме о касательной и секущей для этого пришлось там отрезочек pc в два раза продлить в два раза надеюсь понятно почему повторюсь диаметр перпендикулярных орды деле то ее пополам ну а в остальном вот эта часть была очень технически мы просто выражали все через x ну а дальше снова ключом то стала что ключом стала теорема касательной секущей благодаря именно этой теореме мы нашли отрезок mb соответственно отрезок а.м. ну а дальше можно либо было через подобие либо через вот этот общий угол выразить р через x что мы собственно и сделали надеюсь никаких вопросов не по примеру один не по примеру два нет и мы с вами более менее отработали дарема касательно секущей однако впереди нас ждет еще очень много примеров пример под номером три параллелограмме abcd угол b c d вот этот тупой угол равен 120 градусам а одна из сторон а d равна 8 окружность проходит через точку а касается стороны cd точки к и пересекает сторону а.б. в точке м да так что это расстояние точки причине даже равно 2 то есть м д равно 2 больше ничего не дано найти нас просят радиус вот этой окружностью ну что же давайте решать эту задачу задача кажется очень уж содержательными я буду решать ее просто путем некоторых последовательных действий а в конце прокомментирую почему они были именно такие чему сводился смысл всех этих действий и как действовать в подобных ситуациях в принципе давайте просто подумаем даже что мы можем сделать уже вот мы знаем что отрезок md равен двум значит отрезочек а.м. например равен 6 но все лады вместе равно 8 ну прямо-таки напрашивается теорема правильно а касательно и секущей и так первое действие по теореме о касательные секущей у нас к d в квадрате равно m умножить на а д то есть равно 16 ну чтож уже неплохо нашли что когда у нас с вами равно четырем давайте отмечать то что мы находим по ходу желтеньким мелочком что мы ещё знаем с вами ребятки ну знаем мы с вами например вот этот уголочек ведь сумма односторонних углов 180 а значит уголочек а dc это просто 60 градусов давайте прямо здесь а в скобочках это по мячу угол а dc можно для себя считать просто таким условие 60 градусов о чём это нам говорит что это позволяет нам построить но давайте отрезочек к м соединим и в треугольнички mdk мы с вами можем кое-что сделать а что мы можем сделать но мы знаем две стороны мы знаем угол между ними а это значит мы можем например найти в сторону м.к. ну что ж по теореме косинусов которая вам прекрасно известно уж то что а теорему косинусов восточно загрузили по теореме косинусов мы получаем что м к квадрат равно a к d квадрат плюс md квадрат минус 2 к днд косинус 60 градусов значит получается что м к квадрат равно когда квадрат 16 16 + 4 а сразу пишу 20 минус двоечка и косинус 60 самоликвидируется косинус 60 это 1 2 и получается соответственно к d умножить на md это у нас с вами это у нас с вами просто напросто 8 то есть получается что м к у нас с вами равно 12 но замечательно кмк квадрат простите значит м к у нас с вами будет равно просто-напросто чему ну просто напросто 2 корня из 3 ну что ж замечательным знаем отрезок cam cam это два корня из трёх ну что ж дальше что же дальше друзья мои что же дальше на дальше давайте с вами рассуждать откуда мы в принципе могли бы с вами найти вот этот радиус окружности ведь центр нам здесь явно не задан таким образом радиус на картинке просто не присутствует и вот оказывается что в этом случае спасает теорема синусов она гласит о том что она синус альфа не только равно скажем б на синус бета но и равно еще doom радиусом описанной окружности тоже тот факт который вы должны знать из базовой школьной программы в этом смысле для того чтобы воспользоваться этой обобщенной теоремы синусов нужно выбрать треугольник для которого данная окружность является описанной но у меня такой треугольник всего лишь навсего один этот треугольник а к м этот треугольник а к м соответственно в этом треугольнике я знаю две стороны я знаю что m равно 8 я знаю что м к равно 2 корня из 3 и чего же мне не хватает друзья а мне не хватает знаний какого-то угла либо угла com либо угла а кому потому что если бы я знал какой то из этих углов а точнее синус какого-то из этих углов я бы тогда сразу по теореме синусов смог бы найти радиус ну что же давайте соображать какой из этих углов будет легче искать вот я утверждаю что намного легче будет найти угол в пару к отрезку к м то есть намного легче найти будет угол а к м давайте такой волне со чертой я его обозначу а почему вы будет найти проще ребятки да потому что на картинке не единственный а потому что друзья мои угол а к м будет равен какому углу мкд вспоминайте почему по теореме об угле между касательной и хордой у вас вот касательная cd вот corteco и и вспоминаете что мы говорили в прошлый раз уголочек между острый уголочек между касательной и хордой ravens песчаному углу на нее опирающимся таким образом давайте это зафиксируем и скажем что по теореме об угле между касательной и хордой угол касательная хорда мы можем сразу сказать что углы но и частности их синус и синус угла какого com будет равен синусу какого угла мкд ну а как же друзья мои а можно найти синус угла мкд да очень просто по теореме синусов треугольники mdk в треугольнике mdk по теореме синусов мы получаем что два корня из трёх так относится к синусу 60 градусов синусу 60 градусов то есть к корню из 3 пополам как соответственно что md относится к синусу угла мкд то есть как двоечка относится к синусу угла мкд ну и здесь соответственно посмотрите корень из 3 и корень из 3 просто-напросто сокращается четверочка у нас с вами просто напросто пойдет наверх и получается что двоечка будет наверх и получается что синус угла мкд равен оказался 1 2 то есть углам когда это оказалось 30 градусов это оказался прямоугольный треугольник ну что ж процессе так бывает в процессе так бывает на самом деле тут можно было сделать бы и раньше если бы мы заметили что этот угол 60 а получившийся один из отрезок ав равен половине другого отрезочек а уже здесь можно было бы это заметить однако лишним то что мы сделали совершенно точно не будет и даже если получилось бы не так красиво мы с вами что нашли мы с вами нашли синус угла мкд а он же является синусом угла com по теореме об угле между касательной и хордой и все что нам с вами осталось это пятое действие сказать что в треугольнике а к м у нас с вами к м так относится к синусу угла com как два радиуса это просто-напросто теорема синусов или как их ещё называют обобщенная теорема синусов ну что ж остается просто подставить сюда два корня из трёх сюда соответственно одну вторую и получается что 4 корня из 3 равно 2n откуда мы с вами получаем что r равно двум корням из 3 и это опять же друзья мои правильный ответ если мы нигде не ошиблись в арифметике а здесь этого не произошло давайте проверим еще раз два корня из трёх синус com равен синус мкд равен 1 2 это получается 4 корня из 3 делим на 2 получается два корня из трёх вот такая вот довольно нехитрая задача которая однако вместила себя теорема касательной секущей которая дала всему старт теорему косинусов теорему синусов обобщенную теорему синусов и даже теорема об угле между касательной и хордой как вы видите еще раз давали теперь я повторю спектр своих рассуждений мне нужно было как найти радиус вот этой окружности а это можно сделать из ты центр не задан явно скорее всего при помощи обобщенный теоремы синусов то есть надо выбрать было треугольник для которого то окружность является описанной и выбрать в этом треугольнике пару сторона и противолежащий угол и соответственно первые действия наши были направлены на то чтобы чуть больше узнали про этот треугольник частности мы узнали что к m равно 2 корня из 3 ну а дальнейшее было в общем то было в общем-то делом техники было в общем-то делом техники и мы с вами заметили по теореме об угле между касательной и хордой что вот этот сеанс такой же как этот синус по теореме синусов легко его нашли из маленького треугольника мдк и по обобщенный теорему синусов треугольники окоем записали ответ сзади интересно можно было бы еще даже по другому немного рассуждать а именно посмотрите если мы какой-то момент заметили что этот угол прямой то получается что прямой угол опирается на диаметра к это диаметр и можно было бы просто напросто по теореме коши по теореме пифагора это дело искать то просто вот так красиво совпало условия а то решение которые привели мы работу любое в менее приятных ситуациях и никакой дополнительной красоты не требовала ну что же едем дальше 1 1989 год подарил абитуриентам московского физтеха вот такую замечательные задач дан треугольник a b c и окружность построена на стороне отца этого треугольника как на диаметре известно что это окружность пересекает сторону bc в точке м то есть в середине а сторону абэ пересекает в точке d так что а д равно 3 от а.б. ну а найти нужно друзья мои площадь этого треугольника bc ну что же давайте рассуждать самом деле сейчас окажется очень и очень просто тут важно сделать один очень качественный первый шаг пока неясно чего talkie ваются да здесь есть некоторое отношение да мы знаем сторону отце подобие никакой не рассмотреть чтобы использовать это отношение непонятно с какой стороны подступиться однако достаточно было просто взять и соединить точки и а отрезком тогда я надеюсь многим из вас станет очевидно одна простая вещь угол опирающийся на диаметр есть какой совершенно верно есть прямой угол и все задачи сейчас пойдет просто влет первый факт угол а mc равен 90 градусов так как опирается на диаметр ну а теперь посмотрите получается что а м это не только медиана как по условию но еще и высота треугольника a pc ну а это значит что треугольник a b c какой друзья мои совершенно верно на равнобедренной треугольник a b c у нас с вами равнобедренный таким образом а b равно ация равно единичке а это значит например что а d равно 1 3 п равно 1 3 просто а d равно 1 3 а д б равно двум третям замечательно нашли еще кое что то есть и такое простое замечание что на диаметр нас опирается прямой угол позволил нам сделать вид что треугольник был равнобедренной и в миг найти отрезочек а.д. отрезочек db оказался равным соответственно две третьих мы вот здесь к нашему разговору наконец-то подключается 2 теоретических факты которым мы говорили здесь в явном виде напрашивается теорема об отрезках секущих давайте ее запишем и так оказывается что b умножить на b равно b c умножить на бмп а умножить на b да это просто 2 девятых а что такое bc ведь . м это середина поэтому bc это просто 23 . б.м. то есть получается что это 2pm квадрат двоечки сокращаются и получается чтобы м это единичка делить на корень из 3 вот так вот теорема секущих дала нам еще один важный результат вот это единичка на корень из 3 замечательно ну соответственно mc это тоже единичка на корень из 3 нашли еще и сторону bc то есть основания это равно этого равнобедренного треугольника но что же нам остается друзья остается там получается найти высоту а м а да по полу произведения основания на высоту мы сможем дать ответ на вопрос задачи но откуда можно найти а.м. ну конечно например из теоремы пифагора в треугольнике ну скажем а mc итак третье действие и получается у нас с вами что а м квадрат в треугольнике mc по теореме пифагора получается что отцы квадрат или давайте сразу выразим а м квадрат равно квадрат гипотенузы это единичка минус квадрат катета одна треть и следовательно m равно корень из двух третей ну и все что нам остается это дать ответ задачи четвертый пункт мы с вами получаем что площадь треугольника a b c равна 1 2 умножить на m умножить на b c равно 1 2 на корень из двух третей и умножить получается на что ребятки на единичку они на единичку получается она что у нас с вами bc это 2 на корень из 3 2 на корень из 3 ну соответственно что же получается получается что двоечки сокращаются и получается что площадь это корень из 2 на 3 и правильный ответ вот такая задачка довольно красиво и со дна вспомнили что диаметр виден из точки на окружности под прямым углом ну и соответственно это обстоятельство дало нам пищу для размышлений а дальше уж код вступила теорема секущих когда видите две таких секущих и какие-то отрезочек и вам известны но это конечно же отличный повод воспользоваться теоремой которые по существу ничего нового в себе не несет теорема касательно секущие просто примененная два раза однако часто она дает довольно хорошие результаты и пример номер четыре вступительные на кистях 89 там очень яркое подтверждение ну давайте решим заключительные задачки на факт номер три и закончен наш сегодняшний семинар давайте решим заключительно сегодня пример номер пять мы посвятим есть еще одно занятие окружности мы там порешаем побольше задач а пока такая немножко шутливое устная задача в окружности проведены две хорды abcd и делится они . м соответственно отрезать кеа m равно 4-ем b равно единичке и cm равно двоечке также отмечен центр окружности и нас просят найти чему равен угол о м с но повторюсь ребятки это чистой воды факт номер три теорема об отрезках пересекающихся хорд и сподоби от этих треугольников mc а и мвд сразу же следует что первое действие а m умножить на m b будет равно m умножить на m д это позволит нам найти отрезочек м д мы получаем что 4 умножить на 1 равно 2 умножить на md следовательно md равно 2m d равно двум давайте путники мелочком это отметим но причем тут казалось бы угол у mc shon непонятно откуда же его искать а оказывается достаточно вспомнить факт который мы однажды уже использовали в задаче номер два если у вас вот эти хор дачки вот эти отрезки хор датчик равны 2 и 2 то получается что о м который является несомненно частью диаметра делит эту большую хорду cd пополам ну а если диаметр делит хорду пополам то он не что правильно перпендикулярен так и запишем 2 cm равно mb следовательно о м перпендикулярен cd ну и таким образом угол о mc оказывается равным 90 градусов давайте еще раз прокомментирует обстоятельства берется она из вот этого равнобедренного треугольника т.д. затем показывается что в этом треугольнике это будет не только медиана но еще и биссектриса из простейших слов свойств углов ну а значит и высота верно и обратное то что мы использовали в пример номер два что если бы это была перпендикуляром то она поделила пополам ну соответственно просто потому что в равнобедренном треугольнике медиана биссектриса высота проведённая к основанию это одно и то же таким образом вот вам вся задача из отрезков касательных из отрезков пересекающийся хорд показали что md равно двум а раз этот отрезок равен этому отрезку то они делились пополам перпендикулярным диаметром ну и таким образом получается угол обзора мин 90 градусов повторюсь я надеюсь что мы с вами сможем выкроить еще одно занятие посвященной окружностью потому что задача осталось еще очень много в частности третий факт оказался сегодня подсвечен только вот этой совсем уж устной задачей но тем ни менее надеюсь что сегодня вам было полезно мы посмотрели на очень насыщенные задачки на метрические соотношения в окружности эта теорема касательно секущей теорема о постоянстве произведения секущую внешняя часть и наконец теорема об отрезках пересекающихся хор я ж на этом с вами сегодня прощаюсь и до встречи на следующих занятиях
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
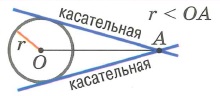
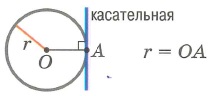
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности.
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
M N – диаметр.
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
∪ A B = ∪ C D = α
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l = 2 π R
Длина дуги окружности, на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
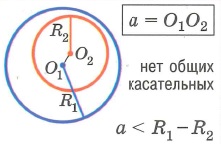
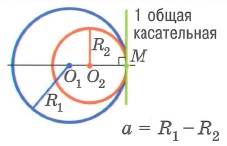
Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Коды баннеров проекта DPVA.ru Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator
|
Предложу следующее подробное доказательство. Оно состоит из 2 частей.
1 Часть: Если дана одна сторона (фиксированная) треугольника вписанного в окружность, то максимальная площадь будет у равнобедренного треугольника с данным основанием, и высотой проходящей через центр окружности. Смотрим рисунок
Проведем произвольную хорду AB (это будет фиксированная сторона). Знаем, что площадь треугольника S=a•h/2. Так как a=AB -фиксированное, то площадь будет большей у треугольника с большей высотой.
Рассмотрим множество перпендикуляров к AB — это множество перпендикулярных хорд. Самой большой будет по определению — диаметр и пересечет хорду AB в середине (точка N). Теперь сравним две части диаметра до хорды AB: CN = CO + ON > R (к радиусу прибавили отрезок)
Противоположная часть, будет меньше радиуса (от радиуса отняли отрезок)
Так же сравнивая СN и часть DM произвольной перпендикулярной хорды к AB. Видим, что CN > DM. Так как проведя через D перпендикуляр к DM, получим хорду, которая пересечет CN образуя прямоугольник, отсекая на CN сторону равную DM.
2 часть
Итак треугольник должен быть равнобедренным и высота к основанию проходит через центр окружности. Определим теперь размер основания данного треугольника.
Смотрим рисунок.
Для определения используем способ мат. анализа. Определим некую зависимость (функцию) площади и найдем максимум функции.
Проведем радиусы в вершины треугольника. Получим, что площадь S: ∆ABC состоит из трех площадей: S₁: ∆OBC; S₂: ∆OCA; S₃: ∆OAB; S = S₁+S₂+S₃
Причем S₁ = S₂, так как ∆ABC — р/б и ∆OBC = ∆OCA
Площадь треугольника равна половине произведения сторон на синус угла между ними:
Тогда: S₁ = S₂ = (R•R•sinα)/2; S₃ = (R•R•sinx)/2, При этом 2α+x = 360˚: α=180˚- x/2 и 0˚< x ≤ 180˚
S = R²•sin(180˚-x/2) + (R²•sin(x))/2, так как R=1, получаем функцию от x
S(x) = sin(x/2) + sin(x)/2, при 0˚< x ≤ 180˚
Чтобы найти точки экстремумов посчитаем производную и приравняем к 0
S'(x) = (sin(x/2))’ + (sin(x)/2)’ = cos(x/2)/2 + cosx/2 = 0
cos(x/2) = -cos(x), при х ∈ (0; π]
Решением будет х = 2π/3 = 120˚ (это точка экстремума)
Проверим теперь значение функции на концах отрезка и в точке экстремума
S(0) = 0
S(180˚) = 1
S(120˚) = √3/2 + √3/4 = 3√3/4 ≈ 1,299 — максимум
Таким образом получается x = 120˚ будет при максимальной площади треугольника, но тогда α = 120˚
А равные центральные углы опираются на равные хорды. Таким образом AB=AC=BC — ∆ABC — равносторонний при максимальной площади.





















 главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности