Как найти соотношение углов в треугольнике

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин :-)

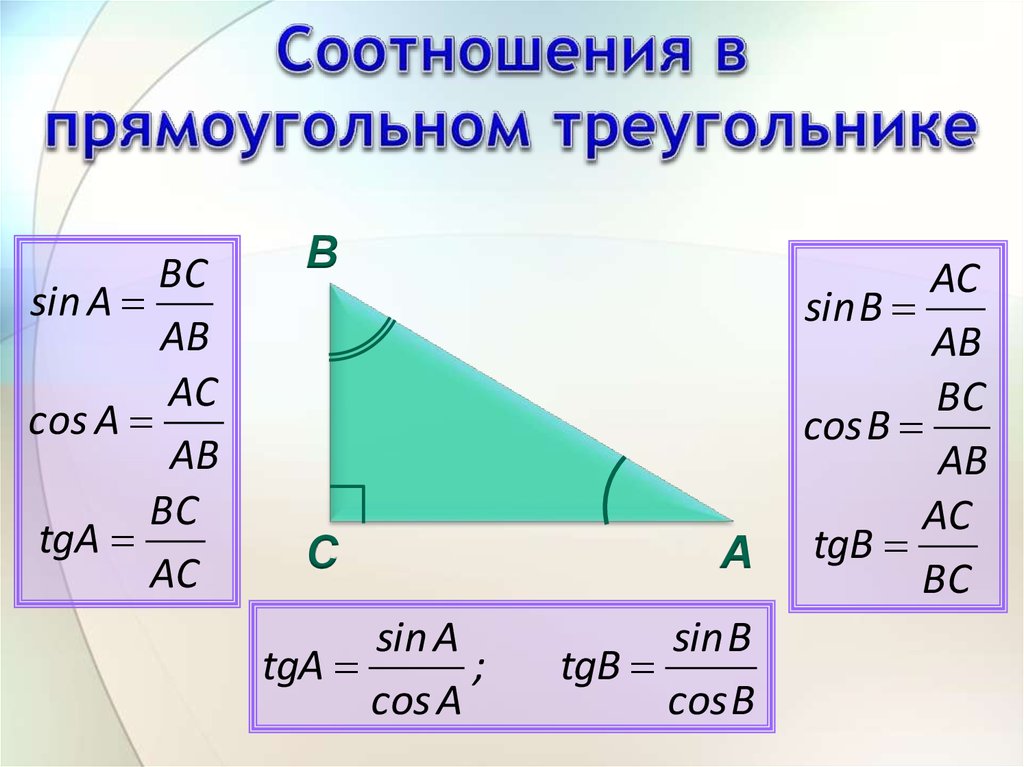
Развёрнутый, прямой, острый и тупой углы

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается a.

Угол A обозначается соответствующей греческой буквой alpha.

Гипотенуза и катеты

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет a, лежащий напротив угла alpha, называется противолежащим (по отношению к углу alpha). Другой катет b, который лежит на одной из сторон угла alpha, называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A =genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A =genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin displaystyle alpha = frac{a}{c} sin{}^2 alpha +cosdisplaystyle {}^2 alpha =1 alpha + beta = 90 ^{circ} 
cos displaystyle alpha = frac{b}{c} 1+tg displaystyle {}^2 alpha =frac{1}{cos ^2 alpha} cosalpha = sin beta
tg displaystyle alpha = frac{a}{b} 1+ctg displaystyle {}^2 alpha =frac{1}{sin ^2 alpha} sinalpha = cosbeta
ctg displaystyle alpha = frac{b}{a} tgalpha = ctgbeta

Давайте докажем некоторые из них.

  1. Сумма углов любого треугольника равна 180^{circ}. Значит, сумма двух острых углов прямоугольного треугольника равнa 90^{circ}.
  2. С одной стороны, sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c} как отношение противолежащего катета к гипотенузе. С другой стороны, cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}, поскольку для угла beta катет а будет прилежащим. Получаем, что cos beta =sin alpha. Иными словами, cos left( 90^{circ}-A right) = sin A.
  3. Возьмем теорему Пифагора: a^2+b^2=c^2. Поделим обе части на c^2, получаем displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 , то есть sin ^2 A+cos^2 A=1.
    Мы получили основное тригонометрическое тождество.
  4. Поделив обе части основного тригонометрического тождества на cos^2 A, получим: 1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }. Это значит, что если нам дан тангенс острого угла alpha, то мы сразу можем найти его косинус. Аналогично,1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна 180^{circ}.

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: a^2+b^2=c^2.

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от 0^{circ} до 90^{circ}.

varphi 0 genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6} genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4} genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3} genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}
sinvarphi 0 displaystyle frac{1}{2} displaystyle frac{sqrt{2}}{2} displaystyle frac{sqrt{3}}{2} 1
cosvarphi 1 displaystyle frac{sqrt{3}}{2} displaystyle frac{sqrt{2}}{2} displaystyle frac{1}{2} 0
tgvarphi 0 genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}} 1 sqrt{3} −
ctgvarphi − sqrt{3} 1 genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}} 0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и A_1B_1C_1 — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и A_1B_1C_1 подобны по первому признаку подобия треугольников, поэтому displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .

Из этих равенств следует, что displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} , т. е. sin А = sin A_1.

Аналогично, displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1}, т. е. cos А = cosA_1, и displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1}, т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен 90^{circ}, sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку A+B = 90^{circ}, sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол C равен 90^{circ}, AB=5, sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.

Найдите AC.

Решение:

sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.

Отсюда

BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.

Найдем AC по теореме Пифагора.

AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен 90^circ , AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против angle C. Значит, sin A displaystyle = frac{BC}{AB}= frac{5}{13}.

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А displaystyle = frac{AC}{AB}=frac{AC}{13}.

Длину катета АС найдем по теореме Пифагора: AC^2+BC^2=AB^2.

Тогда AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.

cos⁡ А displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;

tg A displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен 90^circ , AC = 2, sin A= displaystyle frac{sqrt{17}}{17} .

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17}, displaystyle frac{a}{c} = frac{sqrt{17}}{17} , displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.

По теореме Пифагора a^2+b^2=c^2, получим

a^2+2^2=(sqrt{17} a)^2;

a^2+4=17a^2;

16a^2=4, displaystyle a= frac{1}{2}=0,5;

BC = 0,5.

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен 90^circ , AC = 4, tg A = displaystyle frac{33}{4sqrt{33}} . Найдите AB.

Решение:

AC = b = 4, tg A displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},

displaystyle frac{a}{4}=frac{33}{4sqrt{33}}, displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},

AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен 90^ circ, CH – высота, AB = 13, tg A = displaystyle frac{1}{5} . Найдите AH.

Решение:

AВ = с = 13, tg A = displaystyle frac{a}{b}=frac{1}{5} , тогда b = 5a.

По теореме Пифагора triangleABC: a^2+b^2=c^2,

a^2+(5a)^2=13^2,

26 a^2=169,

displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}}, тогда displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.

triangle AHC approx triangle ACB (по двум углам), следовательно displaystyle frac{AH}{AC}=frac{AC}{AB} , откуда

displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен 90^circ,

CH – высота, BC = 3, sin A = displaystyle frac{1}{6} .

Найдите AH.

Решение:

Так как sin A = displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6}, тогда displaystyle frac{3}{c} = frac{1}{6} , c = АВ = 18.

sin A = displaystyle frac{a}{c} = cos⁡ B = displaystyle frac{1}{6} .

Рассмотрим triangle BHC:

{cos B= }displaystyle frac{BH}{BC} = displaystyle frac{1}{6} , получим displaystyle frac{BH}{3}=displaystyle frac{1}{6},

тогда BH = displaystyle frac{3}{6}=displaystyle frac{1}{2} = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90{}^circ, CH — высота, BC = 3, cos A = displaystyle frac{sqrt{35}}{6}.

Найдите АH.

Решение:

Так как для triangle АВС: cos A = displaystyle frac{AC}{AB}= sin В = displaystyle frac{sqrt{35}}{6},

а для triangle ВНС: sin В = displaystyle frac{CH}{BC} = displaystyle frac{sqrt{35}}{6} , откуда СН = displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},

По теореме Пифагора найдем ВН:

BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=

=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для triangle АВС получим:

{CH}^2=AH cdot BH, тогда AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90{}^circ, CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= displaystyle frac{a}{c} = displaystyle frac{BC}{AB} = {cos B}.

Рассмотрим triangle BHC : {cos B= }displaystyle frac{BH}{BC}.

ВС найдем по теореме Пифагора:

ВС= sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,

тогда {cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28, а значит и sin A = {cos B }= 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90{}^circ, CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = displaystyle frac{a}{c} = displaystyle frac{BC}{AB} = ; cos A = displaystyle frac{b}{c} = displaystyle frac{AC}{AB} = {sin B },

тогда tg A = displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB, который найдем из triangle BHC:

ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90{}^circ, CH — высота, BН = 12, tg A = displaystyle frac{2}{3}. Найдите АН.

Решение:

По определению tg A= displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.

Для triangle BHC: ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3} , значит displaystyle frac{12}{CH}=displaystyle frac{2}{3}, СН = displaystyle frac{12 cdot 3}{2}=18.

Для triangle АHC: tg A= displaystyle frac{CH}{AH}=displaystyle frac{2}{3}, то displaystyle frac{18}{AH}=displaystyle frac{2}{3}, AH = displaystyle frac{18 cdot 3}{2}=27.

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90{}^circ, CH — высота, BН = 12, sin A = displaystyle frac{2}{3}. Найдите АВ.

Решение:

Так как cos В = displaystyle frac{BC}{AB} = sin A = displaystyle frac{2}{3}.

Из triangle СВН имеем cos В = displaystyle frac{HB}{BC} = displaystyle frac{2}{3}, тогда ВС = displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.

В triangle АВС имеем sinA = displaystyle frac{BC}{AB} = displaystyle frac{2}{3}, тогда AВ = displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90{}^circ, из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из triangle ВСН:

HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=

sqrt{8 cdot 32}= sqrt{8 cdot 2 cdot 16}=16.

sin В = displaystyle frac{CH}{BC} = displaystyle frac{12}{20}=displaystyle frac{3}{5}.

Для triangle АВС: cos A = displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5}, получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = displaystyle frac{AC}{AB}=displaystyle frac{3}{5}, то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора {AC}^2+{BC}^2= {AB}^2, получим {(3x)}^2+{(20)}^2= {(5x)}^2
{25x}^2-{9x}^2= {20}^2 ,

{16x}^2= {20}^2,

x^2= {left(displaystyle frac{20}{4}right)}^2,
х = 5 ( так как хtextgreater 0). Значит, AC=15, AB=25.

2-й способ.

triangle HBC approx triangle CBA (по двум углам), значит displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB} или displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,

k = displaystyle frac{16}{20}=displaystyle frac{4}{5} , тогда displaystyle frac{12}{AC}=displaystyle frac{4}{5}, АС = displaystyle frac{12 cdot 5}{4}=15; displaystyle frac{20}{AB}=displaystyle frac{4}{5}, АВ = displaystyle frac{20 cdot 5}{4}=25.

3-й способ.

{CH}^2=AH cdot HB (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда {12}^2=AH cdot 16, АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)} = sqrt{5cdot 45}=sqrt{5cdot 5cdot 9}=15.

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного triangle ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}= sqrt{900}=30;

cos C = displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.

Для triangle АВС: sin А = displaystyle frac{BC}{AC} = cos C = displaystyle frac{3}{5}.

Для triangle АНВ: sin А = displaystyle frac{BH}{AB} = displaystyle frac{3}{5}, то displaystyle frac{24}{AB} = displaystyle frac{3}{5}, АВ = displaystyle frac{24 cdot 5}{3}=40.

Из основного тригонометрического тождества найдем

cos A = sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = displaystyle frac{7}{25}.

Найдите площадь треугольника.

Решение:

В прямоугольном triangle АСЕ sin А = displaystyle frac{CE}{AC},

значит CE=AC cdot sinA=50 cdot displaystyle frac{7}{25} = 14.

Второй катет найдем, используя теорему Пифагора: AE= sqrt{{AC}^2-{CE}^2};

AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.

Площадь прямоугольного треугольника равна S = displaystyle frac{1}{2}ab,

поэтому S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin angle ACK. Результат округлите до сотых.

Решение:

triangle CAK approx triangle BAC ( angle A-общий, angle AKC=angle ACB=90{}^circ ),

значит angle ACK=angle ABC, sin angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.

Найдем АС по теореме Пифагора из triangle САВ:

AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=

=sqrt{(13-12)(13+12)}=sqrt{25}= 5.

Тогда sin angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = displaystyle frac{12}{13}. Найдите высоту СН.

Решение:

Так как АС = ВС, то triangle АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = displaystyle frac{1}{2}AB=36.

Поскольку triangle АСН — прямоугольный,

cos A = displaystyle frac{AH}{AC}= displaystyle frac{12}{13}, то есть displaystyle frac{36}{AC}= displaystyle frac{12}{13} Rightarrow АС = displaystyle frac{36 cdot 13}{12}=39.

По теореме Пифагора {AH}^2+{CH}^2={AC}^2, тогда

CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=

=sqrt{(39-36)(39+36)}=sqrt{3cdot 3cdot 25}=15.

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90{}^circ, sin A = displaystyle frac{11}{14}, AC = 10sqrt{3}. Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = displaystyle frac{BC}{AB}= displaystyle frac{11}{14}, то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора AC^2+{BC}^2={AB}^2;

{(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;

{(14x)}^2-{(11x)}^2 = 3 cdot 100;

(14х- 11х)(14х + 11х) = 3 cdot 100;

3cdot 25 x^2 = 3 cdot 100.

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством {sin}^2A+{cos}^2A=1;

cos A = sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.

По определению cos A = displaystyle frac{AC}{AB}, значит displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.

Так как АС=10sqrt{3}, то displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14}, откуда АВ = displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}} = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, angle DAO=angle BAO = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = displaystyle frac{1}{2} AC=2sqrt{3}, а катет ВО = displaystyle frac{1}{2}BD =2.

Поэтому tgalpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}}, откуда alpha =30{}^circ .

angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .

Ответ: {60}^circ, {120}^circ, {60}^circ, {120}^circ .

Часто в задачах встречаются треугольники с углами 90^{circ},, 30^{circ} и 60^{circ} или с углами 90^{circ},, 45^{circ} и 45^{circ}. Основные соотношения для них запоминайте наизусть!

Прямоугольные треугольники с углами 30, 60, 90 и 45, 45, 90 градусов

Для треугольника с углами 90^{circ},, 30^{circ} и 60^{circ} катет, лежащий напротив угла в 30^{circ}, равен половине гипотенузы.

Треугольник с углами 90^{circ},, 45^{circ} и 45^{circ} — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90{}^circ, угол А равен 30{}^circ, АВ = 2sqrt{3} .

Найдите высоту CH.

Решение:

Рассмотрим triangle АВС:

По свойству катета, лежащего против угла {30}^circ, имеем ВС = displaystyle frac{1}{2} АВ = sqrt{3}.

В triangle BHC: angle BHC=90{}^circ ,; angle B=60{}^circ , то angle HCB=30{}^circ , следовательно, ВН = displaystyle frac{1}{2} BC = displaystyle frac{sqrt{3}}{2}.

По теореме Пифагора найдем НС:

HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=

=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90{}^circ, CH — высота, АВ = 2, angle A=30{}^circ . Найдите АH.

Решение:

Из triangle АВС найдем ВС = displaystyle frac{1}{2} АВ = 1 (по свойству катета, лежащего против угла 30{}^circ),

angle A=30{}^circ , то angle B=60{}^circ .

Из triangle ВСН: angle BHC=90{}^circ , angle B=60{}^circ , то angle HCB=30{}^circ , следовательно,

ВН = displaystyle frac{1}{2} ВС = displaystyle frac{1}{2}.

АН = АВ — НВ = 2 — displaystyle frac{1}{2} = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Треугольник

О многоугольнике с тремя сторонами

Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.

Таким образом, два ключевых элемента образуют рассматриваемую фигуру:

  • вершина;
  • сторона.

И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.

Соотношения между сторонами и углами треугольника

На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.

Существование фигуры

Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.

Математика

Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.

Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:

  1. Остроугольные. В них все три угловые меры меньше 90 °. При этом возможны случаи взаимного их равенства, то есть каждый будет составлять 60 °. Такие треугольники называются равносторонними или правильными. Равны могут быть между собой также два угла, это будет уже равнобедренный треугольник, у которого боковые стороны имеют одинаковую длину.
  2. Тупоугольные. Поскольку сумма составляет 180 °, то по определению в рассматриваемом многоугольнике не может быть больше одного тупого угла. Тупоугольные фигуры могут иметь либо произвольный тип, когда все их отрезки различаются, либо являться равнобедренными.
  3. Прямоугольные. Это специальный тип треугольников, о котором известно многое, и который разграничивает два предыдущих типа. В них один угол равен 90 °, а два других являются острыми.

Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.

Важные линии

Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:

Урок геометрии

  1. Медиана — делящий на две равные по площади части исходный треугольник. Отрезок проводится из вершины к середине противоположной стороны.
  2. Биссектриса. Ею называют отрезок, который на две половины делит угол при произвольной вершине.
  3. Высота. Этот элемент проводится также из вершины, но по отношению к противоположной стороне он является перпендикуляром. Таким образом, высота делит исходную фигуру на два прямоугольных геометрических объекта, которые в общем случае между собой не равны.
  4. Медиатриса — это серединный перпендикуляр, то есть он сочетает свойства медианы и высоты, однако, через вершину треугольника он может не проходить. Медиатрисами пользуются при построении описанной окружности.
  5. Средняя линия — это отрезок, который посередине пересекает две стороны треугольника. Его длина всегда будет в два раза меньше стороны фигуры, которой он параллелен. Средняя линия приводит к созданию подобной исходной фигуры, которая в два раза меньше.

Для правильных, равнобедренных и прямоугольных треугольников некоторые из названных отрезков могут совпадать друг с другом, а также со сторонами фигуры. Например, в прямоугольном треугольнике две малые стороны (катеты) также являются высотами.

Соотношение отрезков и углов

Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.

Большие и меньшие длины

Геометрия

Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.

Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.

Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.

Рассмотренные теоремы приводят к двум важным следствиям:

  1. Против равных сторон лежат равные углы, и наоборот. Следствие актуально для равносторонних и равнобедренных фигур.
  2. Гипотенуза в треугольнике с прямым углом является самой длинной стороной, поскольку она лежит напротив самого большого угла.

Рассмотренные теоремы и их следствия активно используются при изучении подобных фигур. Поскольку напротив равных углов двух треугольников лежат соответствующие им длины отрезков, то последние будут попарно относиться друг к другу с определенным коэффициентом подобия.

Теоремы косинусов и синусов

Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:

c 2 = a 2 + b 2 — 2*a*b*cos©.

Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.

Соотношения между сторонами и углами треугольника математика

Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:

a/sin (A) = b/sin (B) = c/sin©.

Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).

Прямоугольный треугольник

Урок математики

Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:

c 2 = a 2 + b 2 .

Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:

sin (45 °) = a/c = ½ 0,5.

Это соотношение можно получить также из теоремы Пифагора.

Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:

sin (30 °) = ½ = a/c.

Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.

Таким образом, в любом треугольнике существует прямая пропорциональность между длиной стороны и противолежащим ей углом. Для количественного решения задач по геометрии с этой фигурой следует пользоваться выражениями синусов, косинусов и теоремой Пифагора.

Источник

1

Анато­лий-тдр5
[15.3K]

3 года назад 

Из известного отношения внутренних углов легко найти сами эти углы.

2x+3x+4x=180°, 9x=180°, x=20°. Тогда внутренние углы: 40°, 60°, 80°.

Дополнительные им внешние углы: 140°, 120°, 100°.

Их соотношение будет равно 140:120:100=7:6:5.

Ответ: 7:6:5

автор вопроса выбрал этот ответ лучшим

комментировать

в избранное

ссылка

отблагодарить

Источник

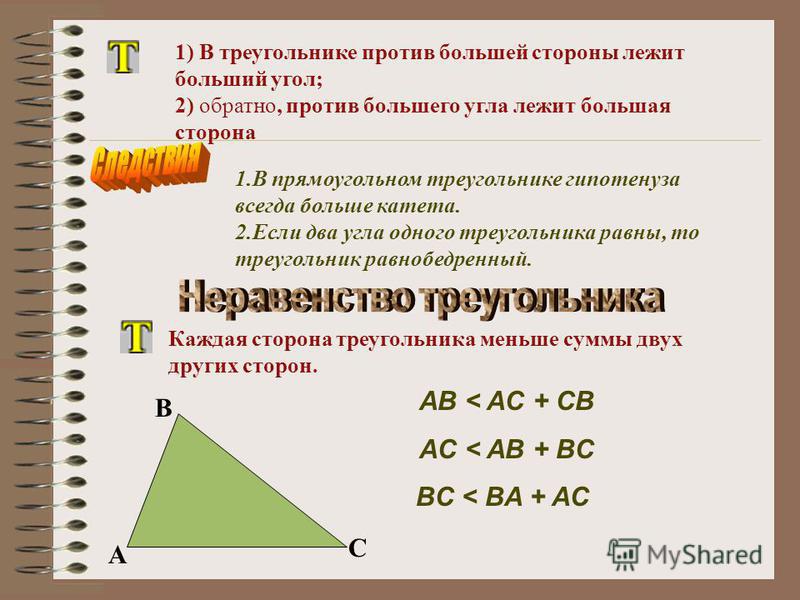
В треугольнике против большей стороны лежит больший угол.

Lenki_malas1.png
 

Доказательство

Пусть дан треугольник (ABC), в котором (AB>AC). Необходимо доказать, что

∠

 (C >)

∠

 (B).

На стороне (AB) отметим точку (D) такую, что (AD=AC). Это возможно, ведь по условию (AC < AB).

Обозначим

∠

(ACD=)

∠

(1),

∠

(ADC=)

∠

(2). Точка (D) лежит между (A) и (B), поэтому 

∠

(1<)

∠

(C).

Треугольник (ADC) — равнобедренный, углы при основании равны,

∠

 (1 =)

∠

 (2). Значит,  

∠

(2<)

∠

(C).

Угол

∠

(2=)

∠

(BCD +)

∠

(B) как внешний угол треугольника (BCD), значит

∠

 (2 >)

∠

 (B). Но 

∠

(2<)

∠

(C), поэтому

∠

 (C >)

∠

 (B).

Справедлива и обратная теорема.

В треугольнике против большего угла лежит большая сторона.

Следствия

Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

Следствие 2. Если три угла треугольника равны, то треугольник равносторонний.

Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.

Неравенство треугольника

Каждая сторона треугольника меньше суммы двух других сторон.

Lenki_malas2.png

Доказательство

Рассмотрим треугольник (ABC) и докажем, что (AB < AC + BC).

Продолжим сторону (AC) и отложим отрезок (CD = BC).

Треугольник (BCD) — равнобедренный, следовательно,

∠

 (1 = )

∠

 (2).

В треугольнике (ABD) очевидно, что

∠

 (ABD >)

∠

 (1), а это значит, что 

∠

 (ABD >)

∠

 (2).

Так как против большего угла лежит большая сторона, (AB < AD), а (AD = AC + BC), значит, (AB < AC + BC).

Следствие 4. Для любых трёх точек (A), (B) и (C), не лежащих на одной прямой, справедливы неравенства:
(AB < AC + CB,  AC < AB + BC,  BC < AB + AC).

Источник

Теорема о соотношениях между сторонами и углами треугольника / Соотношения между сторонами и углами треугольника / Справочник по геометрии 7-9 класс

  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Соотношения между сторонами и углами треугольника
  5. Теорема о соотношениях между сторонами и углами треугольника

Теорема:

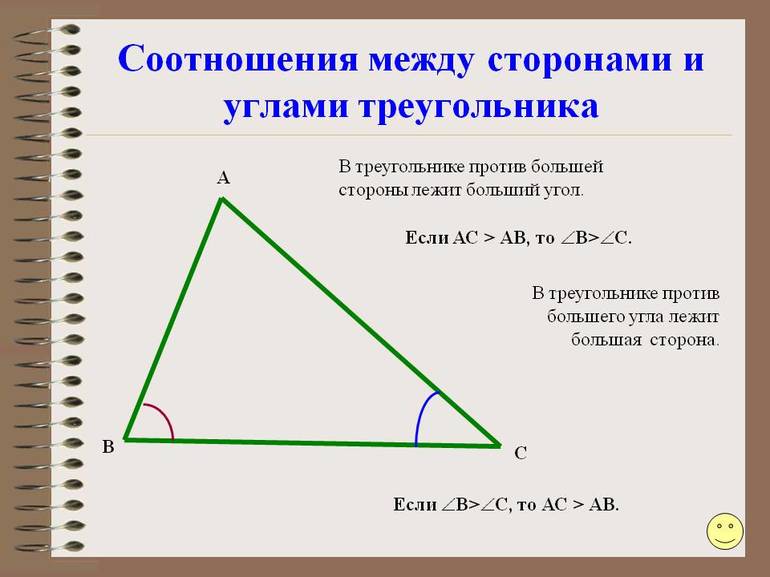
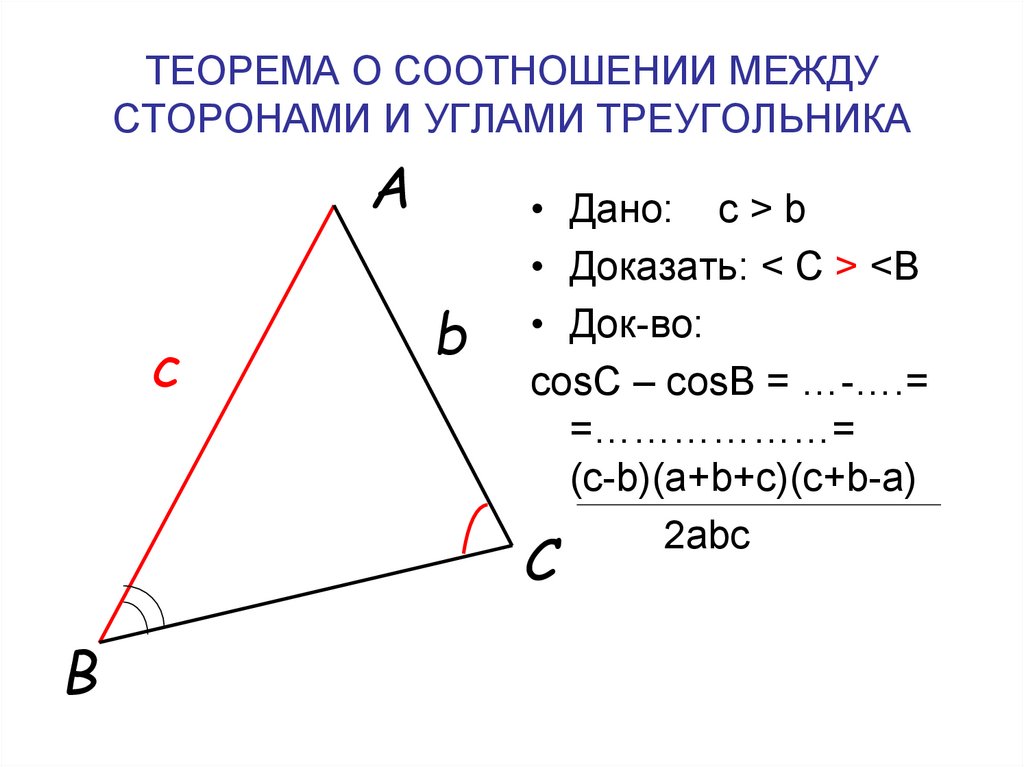
В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.

Доказательство:

1) Дано: АВС, АВАС.

   Доказать: СВ.

   Доказательство:

Отложим на стороне АВ отрезок АD, равный стороне АС.


АDАВ, т.к. по построению АD = АС, а по условию АСАВ, значит, точка D лежит между точками А и В. Следовательно, 1 является частью С, т.е. С1. Угол 2 внешний угол DBC, поэтому 2В. АDС — равнобедренный с основанием DC, т.к. по построению АD = АС, следовательно, 1 =2 (углы при основании).

Итак, С1,


1 =2, значит, С2, при этом 2В, следовательно, СВ.

2) Дано: АВС, СВ.

   Доказать: АВАС.

   Доказательство:

Предположим, что это не так. Тогда возможны два варианта:

  1. либо АВ = АС, тогда АВС — равнобедренный с основанием ВС, значит, С =В (как углы при основании), что противоречит условию: С
    В.
  2. либо АВАС, тогда СВ, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: СВ.  

Значит, наше предположение неверно, следовательно, АВАС. Что и требовалось доказать.

Следствие 1

В прямоугольном треугольнике гипотенуза больше катета.

Доказательство:

Дано: АВС, ВС — гипотенуза, А — прямой.

Доказать: ВСАС, ВС


АВ.

Доказательство:

АВС — прямоугольный, А — прямой, следовательно, углы В и С острые, тогда АВ и АС, значит, ВСАС, ВСАВ (в треугольнике против большего угла лежит большая сторона). Что и требовалось доказать.

Следствие 2

Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

Доказательство:

Дано: АВС

, В =С.

Доказать: АС = АВ.

Доказательство:

Предположим, что одна из сторон будет больше, т.е. АСАВ, тогда и угол лежащий против этой стороны будет больше, т.е. ВС (в треугольнике против большей стороны лежит больший угол), а это противоречит условию: В =С, следовательно, наше предположение неверно, значит АС = АВ.

Итак, в АВС равны две стороны (АС = АВ), следовательно, данный треугольник —


равнобедренный.

Что и требовалось доказать

.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Теорема о сумме углов треугольника

Остроугольный, прямоугольный и тупоугольный треугольники

Неравенство треугольника

Некоторые свойства прямоугольных треугольников

Признаки равенства прямоугольных треугольников

Уголковый отражатель

Расстояние от точки до прямой

Расстояние между параллельными прямыми

Построение треугольника по двум сторонам и углу между ними

Построение треугольника по стороне и двум прилежащим к ней углам

Построение треугольника по трем его сторонам

Соотношения между сторонами и углами треугольника

Правило встречается в следующих упражнениях:

7 класс

Задание 240,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 253,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 256,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 7,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 15,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 336,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 339,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1038,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1079,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Соотношение между сторонами и углами треугольника

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи
из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Предварительные сведения

2. Соотношение сторон и углов в треугольнике

3. Неравенство треугольника

4. Пример задачи

Предварительные сведения

Вначале рассмотрим непосредственно понятие треугольника.

Определение 1

Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками
(рис. 1).

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершин, а также три стороны.

Соотношение сторон и углов в треугольнике

Введем следующую теорему.

Теорема 1

В произвольном треугольнике напротив его большей стороны всегда лежит его больший угол.

Доказательство.

Пусть на рисунке 1 сторона $EF$ — большая сторона треугольника. Тогда нам нужно доказать, что угол $G$ будет большим углом в этом треугольнике.

Отметим на большей стороне отрезок $FK=FG$ (рис. 2).

Так как $EF$ — большая сторона треугольника, то, очевидно, точка K будет лежать на этой стороне. Из этого следует, что

$∠G>∠KGF$

Угол $FKG$ будет внешним углом для треугольника $EKG$. Значит, по теореме о внешнем угле, имеем

$∠GKF=∠E+∠KGE$

Следовательно

$∠GKF>∠E$

Так как треугольник $GKF$ равнобедренный, то $∠GKF=∠KGF$

Из этого всего следует, что

$∠G>∠E$

Аналогично доказывается, что $∠G>∠F$.

Теорема доказана.

Эта теорема имеет обратную теорему. Сформулируем и докажем ее.

Теорема 2

В произвольном треугольнике напротив его большего угла всегда лежит его большая сторона.

Доказательство.

Пусть на рисунке 1 угол $G$ больший угол треугольника. Тогда нам нужно доказать, что сторона $EF$ — большая сторона в этом треугольнике.

Предположим противное, что сторона $EF$ не является большей стороной. Тогда возможны следующие два случая развития событий.

  1. Сторона $EF$ равняется стороне $FG$.

    В этом случае треугольник $EFG$ будет равнобедренным и тогда $∠E=∠G$, что противоречит начальному условию теоремы.

  2. Сторона $EF$ меньше стороны $FG$.

    В этом случае, по теореме 1 будем иметь, что $∠G

Следовательно, сторона $EF$ – большая сторона в этом треугольнике.

Теорема доказана.

Из этих двух теорем можно вывести два следствия. Приведем их также в виде теорем и докажем.

Теорема 3

Гипотенуза любого прямоугольного треугольника является большей стороной в этом треугольнике.

Доказательство.

Так как прямоугольный треугольник имеет один прямой и два острых угла, то прямой угол будет в нем большим. Тогда, по теореме 2, напротив прямого угла и будет находиться большая сторона. Она и будет, по определению прямоугольного треугольника, являться гипотенузой.

Теорема доказана.

Теорема 4

Если в произвольном треугольнике будут два угла равны между собой, то такой треугольник будет равнобедренным.

Доказательство.

Из теорем 1 и 2 будет очевидно, что стороны напротив равных углов будут также равными. Следовательно, по определению равнобедренного треугольника, такой треугольник будет являться равнобедренным.

Теорема доказана.

Отметим, что последняя теорема также называется признаком равнобедренного треугольника.

Неравенство треугольника

Приведем и докажем теперь теорему, которую называют неравенством треугольника.

Теорема 5

Сумма любых двух сторон в произвольном треугольника будет больше, чем его третья сторона.

Доказательство.

Рассмотрим произвольный треугольник $ABC$. Докажем, что

$BC+AC

В этом случае треугольник $BCD$ будет равнобедренным, значит, $∠CBD$ будет равняться $∠D$. Тогда, очевидно, что $∠ABD>∠D$. Следовательно, по теореме 2, $AD>AB$. Из равенства

$AD=AC+CD=AC+CB$

Получим, что

$AB

Теорема доказана.

Пример задачи

Пример 1

Сравнить стороны треугольника $ABC$, если $∠A

Решение.

Для решения используем теорему 2.

Получим, что

$BC

Сообщество экспертов Автор24

Автор этой статьи
Дата последнего обновления статьи: 11.07.2022

Выполнение любых типов работ по
геометрии

Решение задач по геометрии
Контрольная работа на тему теорема синусов и косинусов
Реферат по геометрии
Отчеты по практике по геометрии
Курсовые работы по геометрии
Контрольная работа по геометрии
Дипломная работа по геометрии

Подбор готовых материалов по теме

Дипломные работы
Курсовые работы
Выпускные квалификационные работы
Рефераты
Сочинения
Доклады
Эссе
Отчеты по практике
Решения задач
Контрольные работы

Соотношения между сторонами и углами треугольника с примерами

Соотношения между сторонами и углами треугольника:

Можно заметить, что в треугольнике длины сторон связаны с величинами противолежащих углов следующим образом: большей стороне соответствует больший противолежащий угол, а меньшей стороне — меньший. Так, в треугольнике ABC сторона АС — большая, сторона АВ — средняя, сторона ВС — меньшая,

Эта гипотеза находит подтверждение в следующей теореме.

Теорема (о соотношениях между сторонами и углами в треугольнике).

В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона.

Теорема состоит из двух утверждений. Докажем каждое из них.

1) В треугольнике против большей стороны лежит больший угол.

Дано: АВС, АВ > ВС (рис. 247).

Доказать: C >A.

Доказательство:

На большей стороне ВА от вершины В отложим отрезок BD, равный меньшей стороне ВС, и проведем отрезок CD. Получим равнобедренный ADBC, у которого углы при основании равны, то естьBDC =BCD. НоBDC — внешний для треугольника ADC, и поэтомуBDC большеA. Значит, иBCD большеA. А так какC большеBCD, тоC подавно большеA. Утверждение доказано.

2) В треугольнике против большего угла лежит большая сторона.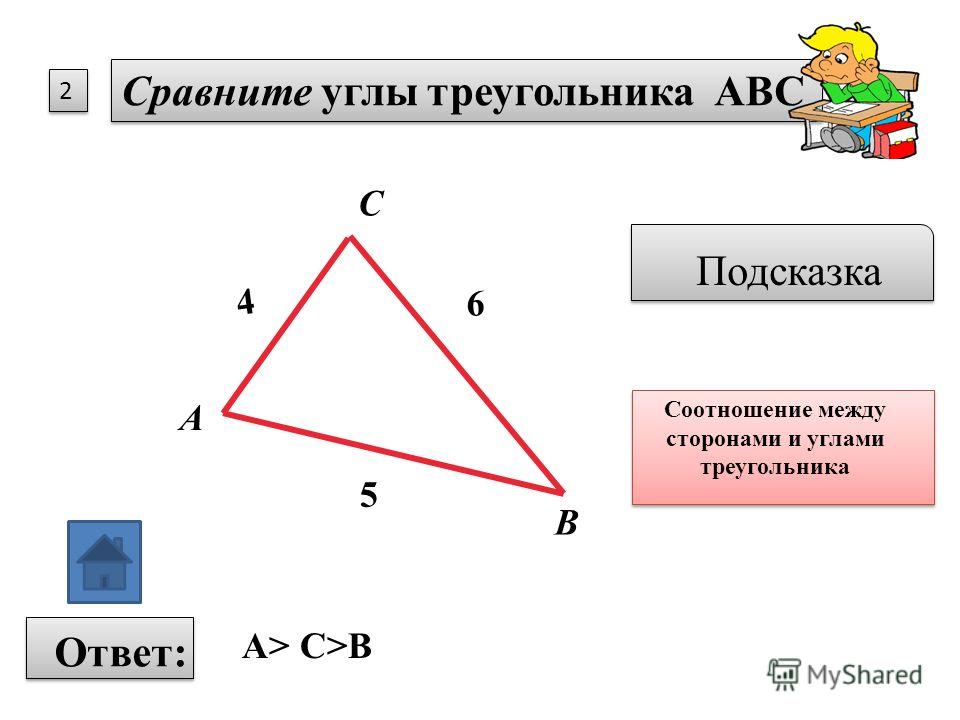

Дано: АВС, C >A (рис. 248).

Доказать: АВ > ВС.

Доказательство:

Применим метод доказательства от противного. ПустьC >A, а АВ C A. Получили противоречие с условием. Если АВ = ВС, то АВС — равнобедренный, и тогда     A =C. Снова получили противоречие. Следовательно, АВ > ВС. Утверждение доказано.

Следствие 1.

Катет прямоугольного треугольника меньше гипотенузы.

Следствие 1 справедливо, так как катет лежит против острого угла, а гипотенуза — против прямого, который больше острого (рис. 249).

Определение. Если АС — перпендикуляр к прямой , точка В принадлежит прямой а и не совпадает с точкой С, то отрезок АВ называется наклонной, проведенной из точки А к прямой (рис. 250). Точка В называется основанием наклонной. Отрезок ВС, соединяющий основание наклонной и основание перпендикуляра, называется проекцией наклонной АВ на прямую .

Следствие 2.

Если из одной точки к прямой проведены перпендикуляр и наклонная, то перпендикуляр и проекция наклонной меньше этой наклонной.

Следствие 2 справедливо, поскольку в прямоугольном треугольнике катет меньше гипотенузы.

Определение. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую.

Если точка лежит на прямой, то это расстояние равно нулю.

Из следствия 2 вытекает, что длина перпендикуляра, опущенного из данной точки на прямую, — это кратчайшее расстояние от данной точки до точек прямой.

На рисунке 251, а расстояние от точки М до прямой равно длине перпендикуляра МК.

Расстояние от вершины А треугольника ABC до прямой ВС, содержащей противоположную сторону, равно высоте АК треугольника (рис. 251, б).

В математике за расстояние между фигурами принимается наименьшее расстояние между точками этих фигур.

Пример:

Отрезок AM — перпендикуляр к прямой .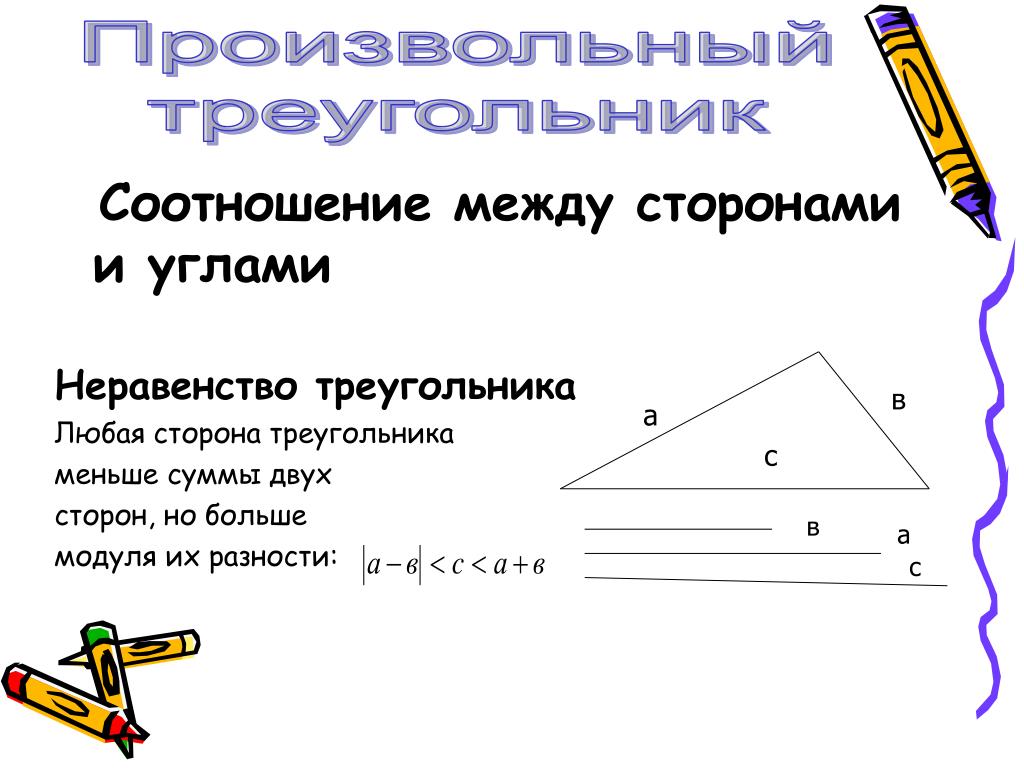 Точки В и С лежат на прямой а по одну сторону от точки М (рис. 252). Доказать, что если СМ

Доказательство:

Так как АМС — прямоугольный, то ACM — острый. Тогда смежный к немуACB — тупой. В треугольнике ABC угол АСВ — больший, поэтомуACB >ABC. Так как в треугольнике против большего угла лежит большая сторона, то АС

Замечание. Решите данную задачу при условии, что точки В и С лежат на прямой по разные стороны от точки М. Тогда будет доказано свойство: «Если наклонные проведены из одной точки к одной прямой, то большей проекции соответствует большая наклонная, а меньшей — меньшая».

Пример:

Дан равнобедренный прямоугольный треугольник с гипотенузой 12 см. Найти расстояние от вершины прямого угла до прямой, содержащей гипотенузу.

Решение:

Пусть в АВС АС=ВС, С=90о, АВ=12 см (рис.253). По свойству равнобедренного треугольника А =В = 45о.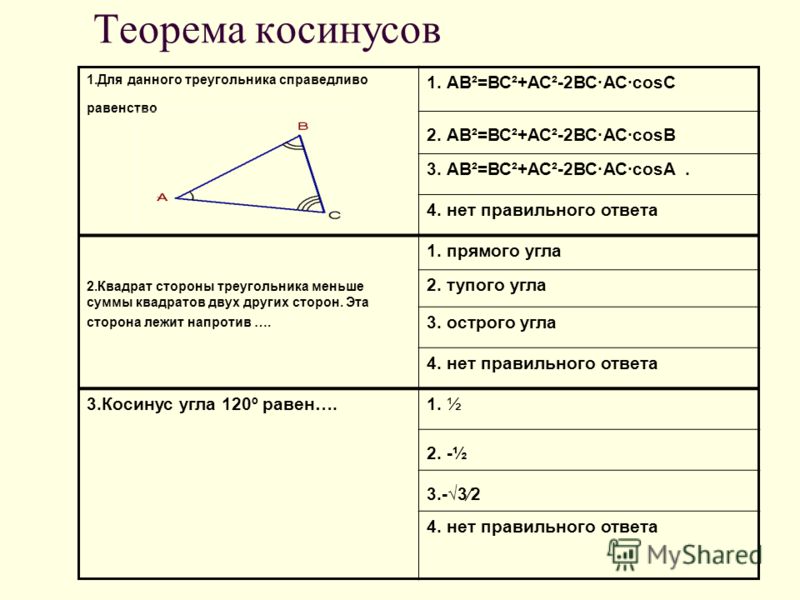 Проведем высоту СК. Длина отрезка СК — искомое расстояние. В равнобедренном треугольнике АСВ высота СК, опущенная на основание АВ, будет медианой и биссектрисой.

Поэтому АК=КВ=АВ=6 см, АСК=АСВ=45о.

В прямоугольном АСК АСК=САК=45о. Поэтому АСК — равнобедренный и СК=АК=6 см.

Ответ: 6 см.

Замечание. В дальнейшем будем пользоваться тем, что высота равнобедренного прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Сумма градусных мер углов треугольника. Внешний угол треугольника

Докажем теорему о сумме градусных мер углов треугольника.

Теорема 1 (теорема о сумме градусных мер углов треугольника). Сумма градусных мер углов треугольника равна 180°.

Доказательство.

1) Пусть ABC — произвольный треугольник. Докажем, что A + B + C= 180°.

2) Проведем через вершину В прямую а, параллельную стороне АС (рис. 103, а).

3) Углы 1 и 4 являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых АС и а секущей AB, значит, 1= 4 (теорема 3, глава 4, § 2).

4) Углы 3 и 5 являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых АС и а секущей ВС, следовательно, 3 = 5.

5) Сумма градусных мер углов 4, 2 и 5 равна градусной мере развернутого угла с вершиной в точке B, т. е. 4+2+5= 180°. Но так как 1 = 4 и 3 = 5, то получаем: 3+2+1= 180°, т. е. A + B + C = 180°.

Теорема доказана.

Например, пусть ABC и ADC — два треугольника, имеющие общую сторону АС и лежащие в разных полуплоскостях с границей АС, тогда ABC + BCD + CDA + DAB = 360° (рис.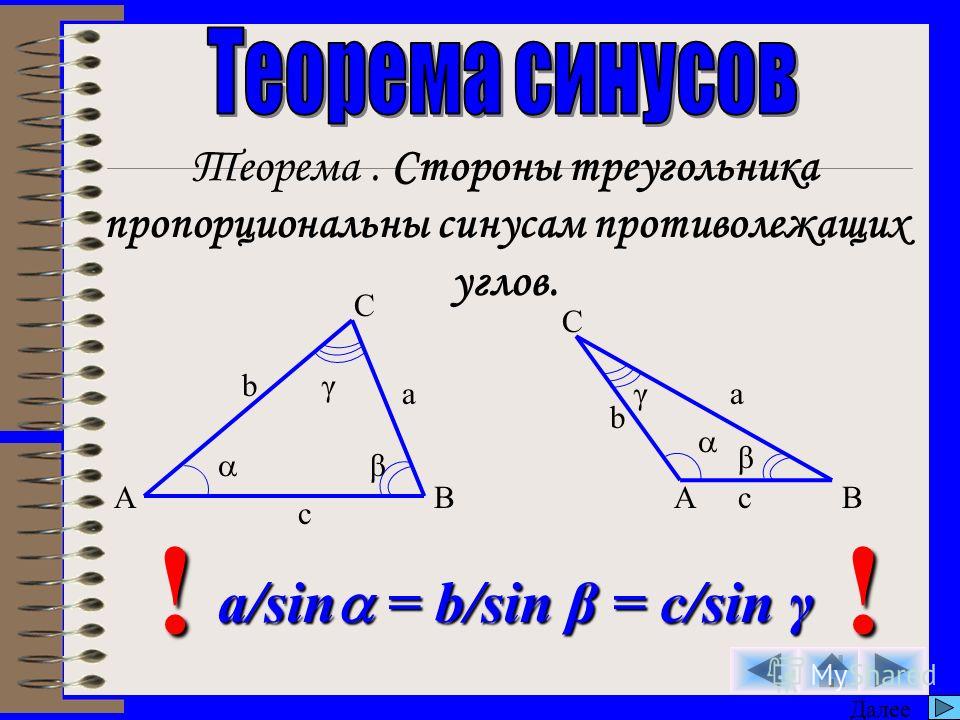 103, б). Действительно,ABC + BCD + CDA + DAB = ABC + (I + 2) + CDA + (3 + 4) = (ABC + 1 + 3) + (CDA +2 + 4) = 180° + 180° = 360°.

Определение. Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника.

Например, 1 — внешний угол треугольника ABC, смежный с углом ВСА, a 2 — внешний угол, смежный с углом ВАС (рис. 104, а).

Теорема 2 (о внешнем угле треугольника). Градусная мера внешнего угла треугольника равна сумме градусных мер двух углов треугольника, не смежных с ним.

Доказательство.

1) Пусть ABC — произвольный треугольник. Докажем, например, что градусная мера внешнего угла 4 равна сумме градусных мер не смежных с ним углов 1 и 2 (рис. 104, б).

2) Так как сумма градусных мер углов 3 и 4 равна градусной мере развернутого угла, то 3 + 4 = 180°, а по теореме о сумме градусных мер углов треугольника (l + 2) +3 = 180°, следовательно, 4 = 1 + 2.

Теорема доказана.

Из теоремы о сумме градусных мер углов треугольника следует, что если в треугольнике один из углов прямой или тупой, то сумма градусных мер двух других углов не больше 90°, следовательно, каждый из них острый. Отсюда вытекает, что в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

Треугольник называется остроугольным, если все его углы острые (рис. 105, а). Треугольник называется тупоугольным, если один из его углов тупой (рис. 105, б). Треугольник называется прямоугольным, если один из его углов прямой (рис. 105, в).

Из определения прямоугольного треугольника и теоремы о сумме градусных мер углов треугольника следует, что сумма градусных мер острых углов прямоугольного треугольника равна 90°.

Стороны прямоугольного треугольника имеют специальное название. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами. Например, на рисунке 105, в изображен прямоугольный треугольник ABC с прямым углом С. Сторона AB этого треугольника является гипотенузой, а стороны АС и ВС — катетами.

Две модели прямоугольного треугольника получаются, если лист бумаги, имеющий форму прямоугольника, разрезать, как показано на рисунке 106, а.

На рисунке 106, б, в изображены прямоугольные треугольники А1AD и DCC1, которые содержатся соответственно в гранях AА1D1D  и DD1C1C  прямоугольного параллелепипеда.

Закон синусов — Открытый справочник по математике

Закон синусов — Открытый справочник по математике

Открытый справочник по математике

Главная
Контакт
О
Тематический указатель

В любом треугольнике отношение длины стороны к синусу противоположного ей угла

одинаков для всех трех сторон. Как формула:

Попробуйте это
Перетащите любую вершину треугольника.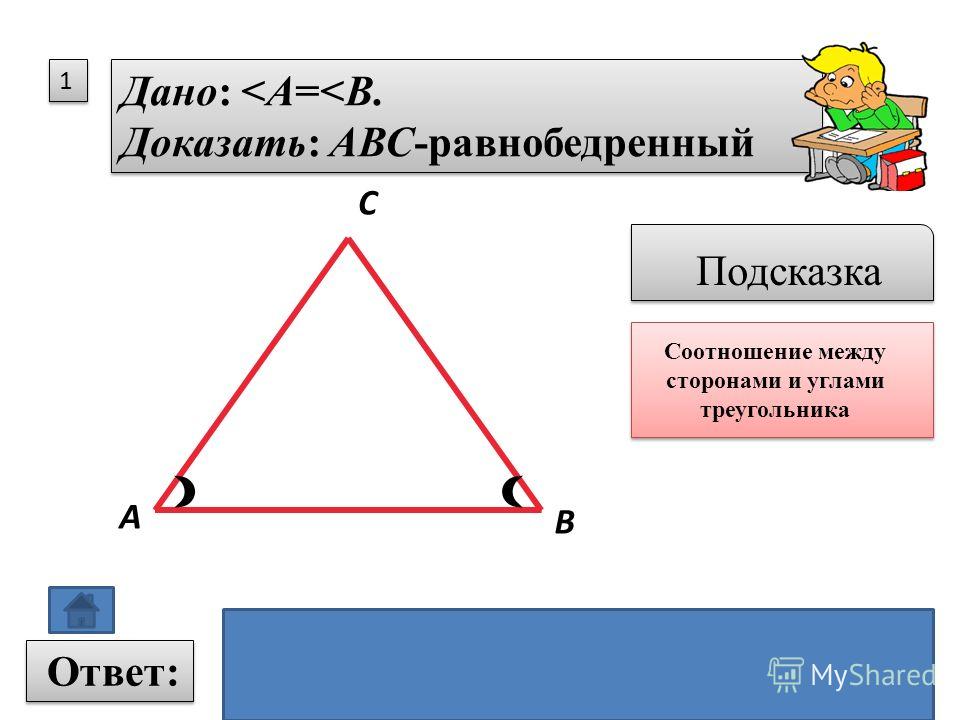 Обратите внимание, что отношение стороны к синусу противоположного ей угла одинаково для всех трех сторон.

См. также Закон косинусов.

Закон синусов гласит, что в любом треугольнике отношение длины любой стороны к синусу противоположного угла одинаково.
для всех трех сторон треугольника.
Это верно для любого треугольника , а не только для прямоугольных треугольников.

Нажмите «сброс» на схеме выше.
Обратите внимание, что сторона «а» имеет длину 25,1, а противолежащий ей угол А равен 67°.
Синус 67° равен 0,921, поэтому отношение 25,1 к 0,921 равно 27,27.
Если вы повторите это для трех других сторон, вы обнаружите, что они имеют такое же соотношение,
обозначенный здесь буквой с .

Когда вы перетащите приведенный выше треугольник, вы увидите, что, хотя это соотношение варьируется, оно всегда одинаково для всех трех сторон треугольника.

Записывается как формула

Формально закон синусов записывается как
где А — угол, противолежащий стороне а, В — угол, противолежащий стороне b, и С — угол, противолежащий стороне с.

Для чего он используется?

Треугольник имеет три стороны и три угла.
Закон синусов — один из инструментов, который позволяет нам
решить треугольник.
То есть, зная некоторые из этих шести мер, мы можем найти остальные.
В зависимости от того, что вам дано для начала, вам может понадобиться использовать этот инструмент в сочетании с другими, чтобы полностью решить треугольник.

Когда его использовать?

Вы можете использовать закон синусов, если вы уже знаете

  1. Одна сторона и противоположный ей угол и
  2. Одна или несколько других сторон или углов

Первый позволяет вычислить отношение «Закон синусов» s .
Затем мы можем использовать это отношение, чтобы найти другие стороны и углы, используя другие данные.

Пример

На рисунке ниже нам даны сторона b и угол B, которые противоположны друг другу, поэтому мы можем
используйте их для расчета коэффициента (ов) по закону синусов
для этого конкретного треугольника:
Обратите внимание, здесь нам также дана длина стороны c. Итак, поскольку мы знаем отношение закона синусов для этого треугольника (s — 21,78), мы можем найти противоположный угол C:

Теперь мы знаем оба угла B и C, поэтому, используя тот факт, что
если сумма внутренних углов треугольника равна 180°, то можно найти третий угол А:

Используя тот же принцип, что и выше, мы знаем, что
поэтому мы решаем это для a , последней неизвестной стороны:
Теперь мы решили треугольник, так как теперь мы знаем все три стороны и все три угла.

Соединение по окружности

Оказывается, отношение «Закона синусов» также является диаметром стороны треугольника.
круг,
это окружность, проходящая через все три вершины треугольника.
Иногда это формально записывается как
где r — радиус описанной окружности — радиус треугольника
окружность

Резюме

Итак, если нам даны одна сторона и противоположный ей угол, мы можем найти соотношение «закон синусов» для треугольника. Затем, используя это
отношение и другие заданные элементы, мы можем решить треугольник.

Доказательство

См. Доказательство закона синусов.

Что попробовать

На рисунке выше

  1. нажмите «скрыть подробности», затем измените форму треугольника, перетащив его вершины.
  2. Решите треугольник по закону синусов.

Когда закончите, нажмите «показать детали», чтобы подтвердить свой ответ.

Другие темы треугольника

Общий

  • Определение треугольника
  • Гипотенуза
  • Уголки внутренние треугольные
  • Наружные треугольные углы
  • Теорема о внешнем угле треугольника
  • Теорема Пифагора
  • Доказательство теоремы Пифагора
  • Пифагоровы тройки
  • Треугольник, описанный вокруг окружности
  • Треугольник вписанный в окружность
  • Медианы треугольника
  • Высота треугольника
  • Средняя линия треугольника
  • Неравенство треугольника
  • Соотношение сторона/угол

Периметр/площадь

  • Периметр треугольника
  • Площадь треугольника
  • Формула Герона
  • Площадь равностороннего треугольника
  • Площадь методом «боковой угол сторона»
  • Площадь треугольника с фиксированным периметром

Типы треугольников

  • Прямоугольный треугольник
  • Равнобедренный треугольник
  • Разносторонний треугольник
  • Равносторонний треугольник
  • Равноугольный треугольник
  • Тупоугольный треугольник
  • Остроугольный треугольник
  • Треугольник 3-4-5
  • 30-60-90 треугольник
  • 45-45-90 треугольник

Треугольные центры

  • В центре треугольника
  • Центр окружности треугольника
  • Центроид треугольника
  • Ортоцентр треугольника
  • Линия Эйлера

Конгруэнтность и подобие

  • Конгруэнтные треугольники

Решение треугольников

  • Решение треугольника
  • Закон синусов
  • Закон косинусов

Тесты и упражнения с треугольниками

  • Викторина типа треугольник
  • Проблема с мячиком
  • Сколько треугольников?
  • Спутниковые орбиты

(C) 2011 Copyright Math Open Reference.

Все права защищены

Калькулятор отношения треугольников

Автор Анна Щепанек, доктор философии

Отзыв от Davide Borchia

Последнее обновление: 06 июня 2022 г.

  • Как использовать этот калькулятор соотношения треугольников?
  • Инструменты Omni, относящиеся к соотношению углов
  • Часто задаваемые вопросы

    • Мы создали этот калькулятор соотношения треугольников, чтобы вы могли легко находить недостающие углы в треугольниках, используя соотношения . Мы обсудим математическую формулу отношения треугольников, а также проведем вас через 90 209 примеров 90 210 решения отношения углов треугольника.

    Формула отношения треугольников

    Если мы имеем дело с отношением углов треугольника, нам нужно запомнить формулу, которая говорит, что сумма углов в треугольнике равна прямому углу, т. е. 180° :

    α + β + γ = 180° .

    Как использовать эту формулу? Если вы знаете, что ваши углы находятся в соотношении a:b:c , вы можете записать их как x , bx , cx , где x неизвестно. И, согласно вышеприведенной формуле, получаем:

    ax + bx + cx = 180°

    Отсюда можно определить сначала неизвестное х , а затем углы: х , х , сх . В следующем разделе мы переведем эти соображения в пошаговое руководство о том, как найти недостающие углы в треугольниках с помощью соотношений.

    Как найти недостающие углы в треугольниках с помощью соотношений?

    Если вы знаете, что углы находятся в соотношении a:b:c и хотите определить углы:

    1. Запишите неизвестные углы как x , bx , cx .
    2. Используйте тот факт, что они составляют прямой угол: ax + bx + cx = 180° .
    3. Упростите уравнение: (a + b + c)x = 180° .
    4. Вычислить x = 180°/(a + b + c) .
    5. Используйте x , чтобы определить недостающие углы как x , bx , cx .
    6. Если вам нужно еще и отношение сторон, используйте закон синусов.

    Давайте вместе рассмотрим примеры, чтобы увидеть, как все это работает на практике:

    Пример 1

    Соотношение углов теперь выглядит как 2:3:4 .

    Запишите углы как 2x , 3x , 4x , и запишите уравнение для их суммы как 2x + 3x + 4x = 180° . После упрощения получаем 9x = 180° и тогда x = 20° . В результате 2x = 40° , 3x = 60° , 4x = 80° . Это означает, что недостающие углы равны 40° , 60° , 80° .

    Пример 2

    Допустим, углы находятся в соотношении 1:1:2 .

    Запишем углы как х , х , 2х . Поскольку их сумма равна 180° , мы получаем: х+х+2х = 180° . Следовательно, 4x = 180° , что означает, что x = 45° . Очень легко мы получаем 2x = 90° , поэтому недостающие углы равны 45° , 45° , 90° . В частности, это прямоугольный треугольник!

    Как использовать этот калькулятор соотношения треугольников?

    Наш калькулятор соотношения треугольников может работать двумя способами:

    • введите соотношение углов и получите углы ; или
    • введите углы и получите отношение углов .

    Обязательно проверьте обе возможности!

    💡 Чтобы облегчить вам жизнь, если вы введете два угла, наш калькулятор соотношения треугольников автоматически определит третий.

    В качестве бонуса мы также расскажем вам отношение длин сторон . Если вам нужно преобразовать длину стороны в углы, перейдите к калькулятору треугольника SSS.

    Существует два известных соотношения углов треугольников: 1:2:3 и 1:1:2 . Оба эти треугольника прямоугольные, а последний еще и равнобедренный (и мы с ним уже встречались!). Подробнее о них читайте здесь:

    • 30 60 90 треугольник
    • 45 45 90 треугольник

    Часто задаваемые вопросы

    Как найти отношение углов в треугольнике?

    Чтобы найти отношение углов треугольника:

    1. Возьмите углы треугольника: α , β и γ .
    2. Запишите их как α:β:γ . Это ваш коэффициент! . Но вы можете захотеть упростить .
    3. Разделите все три числа на их наибольший общий делитель .
    4. Например, если ваше отношение равно 30:60:90 , разделите все три числа на тридцать: 1:2:3 .

    Каковы углы треугольника с отношением 3 : 4 : 5?

    1. Запишите свои углов, используя данное отношение как 3x , 4x , 5x .
    2. Сумма углов в треугольнике представляет собой прямой угол: 3x + 4x + 5x = 180° .
    3. Решите это уравнение для x . Получаем х = 15° .
    4. недостающих углов равны 3x = 45° , 4x = 60° , 5x = 75° .

    Анна Щепанек, PhD

    Отношение углов x : y : z

    Углы

    Отношение длин сторон

    Введите данные для получения результатов!

    Посмотреть 18 похожих калькуляторов треугольников 🔺

    30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… еще 15

    30-60-90 Треугольник — правила, формулы, теоремы, стороны, примеры

    908 Треугольник -60-90 является особым прямоугольным треугольником, так как углы треугольника находятся в соотношении 1:2:3. Существуют различные типы треугольников, такие как тупоугольные, равнобедренные, остроугольные, равносторонние и так далее. Но только несколько типов треугольников считаются особыми треугольниками. Эти треугольники особенные, поскольку их стороны и углы постоянны и предсказуемы. Их свойства можно использовать для решения различных задач геометрии или тригонометрии. А 30-60-90-треугольник — произносится как «тридцать шестьдесят девяносто» — действительно является одним из таких очень особых типов треугольников.

    В этом уроке мы рассмотрим концепцию треугольника 30-60-90 и узнаем все о нем, включая его формулу, определение, стороны, площадь и правила, применимые к этому треугольнику.

    1. Что такое треугольник 0-60-90?
    2. 30-60-90 Стороны треугольника
    3. 30-60-90-Теорема о треугольнике
    4. 30-60-90 Треугольная защита
    5. 30-60-90 Правило треугольника
    6. Площадь треугольника 30-60-90
    7. Часто задаваемые вопросы по треугольнику 30-60-90

    Что такое треугольник 30-60-90?

    30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3. Здесь под прямоугольным треугольником понимается любой треугольник, содержащий угол 90°. Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°. Вот несколько вариантов треугольника 30-60-90. Треугольники ABC и PQK составляют 30-60-90 треугольников.

    Здесь в треугольнике ABC ∠ C = 30°, ∠ A = 60° и ∠ B = 90° и в треугольнике PQK ∠ P = 30°, ∠ K = 60° и ∠ Q = 90°

    30-60-90 Стороны треугольника

    Треугольник 30-60-90 является особым треугольником, поскольку длины его сторон всегда находятся в постоянном соотношении друг с другом.

    В приведенном ниже треугольнике ABC 30-60-90 ∠ C = 30°, ∠ A = 60° и ∠ B = 90°. Мы можем понять отношения между каждой из сторон из следующих определений:

    • Сторона, лежащая против угла 30°, AB = y, всегда будет наименьшей, так как 30° — наименьший угол в этом треугольнике
    • Сторона, противоположная углу 60°, BC = y × √ 3 = y √ 3 будет средней длиной, потому что 60° — средний угол в градусах в этом треугольнике
    • На стороне, противоположной углу 90°, гипотенуза AC = 2y будет наибольшей стороной, поскольку 90° является наибольшим углом.

    Стороны треугольника 30-60-90 всегда находятся в соотношении 1:√3:2. Это также известно как формула треугольника 30-60-90 для сторон y: y√3: 2y. Давайте изучим вывод этого соотношения в разделе доказательства треугольника 30-60-90. Эту формулу можно проверить с помощью теоремы Пифагора.

    Рассмотрим несколько примеров треугольника 30-60-90 градусов со следующими длинами сторон:

    Здесь, в треугольнике 30-60-90 DEF

    ∠ F = 30°, ∠ D = 60° и ∠ E = 90°

    • Сторона, противоположная углу 30°, DE = y = 2
    • Сторона, противоположная углу 60°, BC = y √ 3 = 2 √ 3
    • Сторона, противоположная углу 90°, гипотенуза AC = 2y = 2 × 2 = 4

    Здесь, в треугольнике 30-60-90 PQR

    ∠ R = 30°, ∠ P = 60° и ∠ Q = 90°

    • Сторона, противоположная углу 30°, AB = y = 7
    • Сторона, противоположная углу 60°, BC = y √ 3 = 7 √ 3
    • Сторона, противоположная углу 90°, гипотенуза AC = 2y = 2 × 7 = 14

    30-60-90-Теорема о треугольнике

    Формулировка теоремы 30-60-90-треугольника дается как

    Утверждение: Длина гипотенузы в два раза больше длины самой короткой стороны, а длина другой стороны в √3 раза больше длины самой короткой стороны в треугольнике 30-60-90.

    Формула треугольника 30-60-90

    Вышеупомянутая теорема может быть математически записана как Формула треугольника 30-60-90 в виде 1:√3:2, что является отношением трех сторон треугольника 30-60-. 90-треугольник. Другая формула для этого особого треугольника 1:2:3, которая является отношением трех углов треугольника 30-60-90.

    30-60-90-Triangle Proof

    Рассмотрим равносторонний треугольник ABC с длиной стороны, равной ‘a’.

    Теперь проведем перпендикуляр из вершины A на сторону BC в точке D треугольника ABC. Перпендикуляр в равностороннем треугольнике делит другую сторону пополам.

    Треугольники ABD и ADC — это два треугольника 30-60-90. Оба треугольника подобны и прямоугольные треугольники. Следовательно, мы можем применить теорему Пифагора, чтобы найти длину AD.

    (AB) 2 = (AD) 2 + (BD) 2

    A 2 = (AD) 2 + (A/2) 2

    A 2

    9 0002

    + (A/2) 2

    + (A/2) 2

    2 +. — (a/2) 2 = (AD) 2

    3a 2 /4 = (AD) 2

    (a √ 3)/2 = AD 90a (a √ 3)/2 = AD 90a √ 3)/2

    BD = a/2

    AB = a

    Эти стороны также подчиняются тому же соотношению a/2 : (a√3)/2: a

    Умножить на 2 и разделить на ‘ а’,

    (2а)/(2а) : (2а√3)/(2а): (2а/а)

    Получаем 1:√3:2. Это теорема треугольника 30-60-90.

    30-60-90 Правило треугольника

    В треугольнике 30-60-90 меру любой из трех сторон можно узнать, зная меру хотя бы одной стороны треугольника. Это называется правилом треугольника 30-60-90. В приведенной ниже таблице показано, как найти стороны треугольника 30-60-90, используя правило треугольника 30-60-90:

    База дана Дан перпендикуляр Гипотенуза дана

    Предполагается, что основание BC треугольника равно ‘a’.

    Предполагается, что перпендикуляр DE треугольника равен ‘a’.

    Предполагается, что гипотенуза PR треугольника равна ‘a’.

    Перпендикуляр треугольника ABC равен AB = (a /√3)

    Гипотенуза треугольника ABC равна AC = (2a)/√3

    Основание треугольника DEF равно EF = √3a.

    Гипотенуза треугольника DEF равна DF = 2a.

    Основание треугольника PQR равно QR = (√3a)/2.

    Перпендикуляр треугольника PQR равен PQ = (a/2).

    Площадь треугольника 30-60-90

    Формула для вычисления площади треугольника: = (1/2) × основание × высота. В прямоугольном треугольнике высота есть перпендикуляр треугольника. Таким образом, формула для вычисления площади прямоугольного треугольника = (1/2) × основание × перпендикуляр

    Давайте узнаем, как применить эту формулу, чтобы найти площадь треугольника 30-60-90.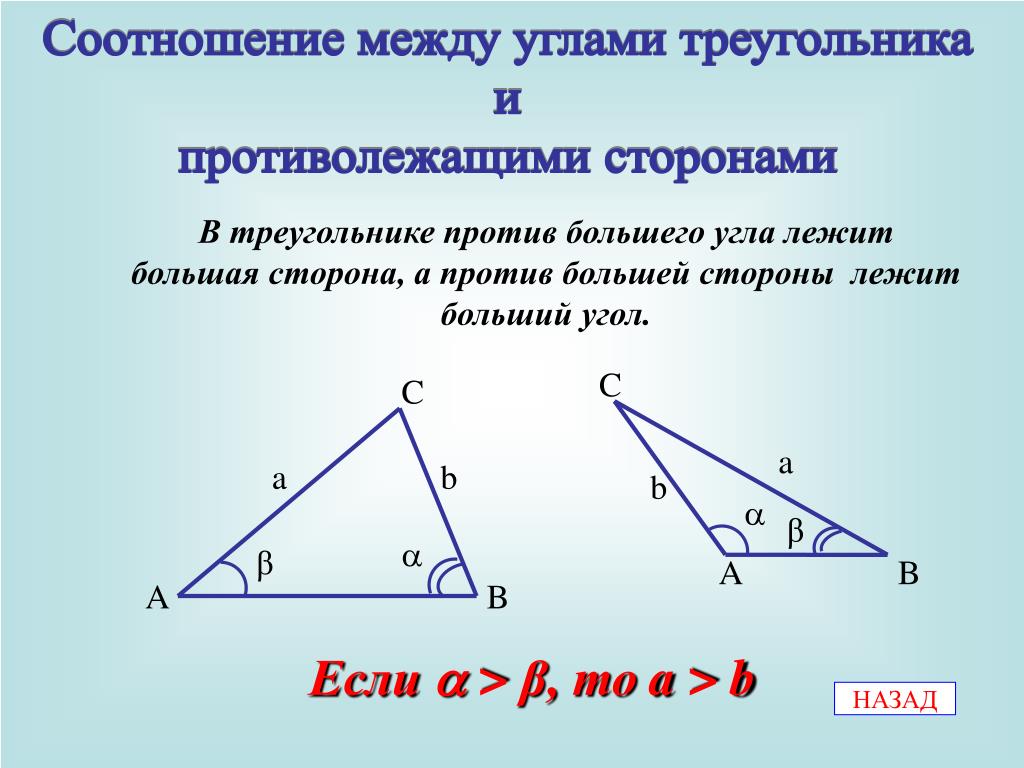

    Основание BC треугольника принимается равным а, а гипотенуза треугольника ABC равна АС. В предыдущем разделе мы узнали, как найти гипотенузу, зная основание.

    Применим изученную формулу.

    Таким образом, перпендикуляр треугольника = a/√3

    Площадь треугольника = (1/2) × основание × перпендикуляр

    Площадь = 1/2 × a × a/√3

    Таким образом, площадь треугольника 30-60-90, когда основание (сторона средней длины) обозначена как «а», составляет: Треугольники

  • Равнобедренные треугольники
  • Тупоугольные треугольники
  • Остроугольный треугольник
  • Периметр треугольника

    • Важные примечания о треугольнике 30-60-90

    Вот несколько моментов, которые следует помнить при изучении треугольника 30-60-9.0 треугольников:

    • Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3, а стороны в соотношении 1:√3:2
    • Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°
    • Все стороны треугольника 30-60-90 можно вычислить, если известна любая сторона. Это называется правилом треугольника 30-60-90.

    Часто задаваемые вопросы по телефону 30-60-90 Треугольник

    Что такое треугольник 30-60-90?

    Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3. Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°.

    Каков периметр треугольника 30-60-90?

    Периметр треугольника 30 60 90 с наименьшей стороной, равной а, является суммой всех трех сторон. Две другие стороны равны a√3 и 2a. Периметр треугольника равен а+а√3+2а = 3а+а√3 = а√3(1+√3).

    Есть ли какие-нибудь советы по запоминанию правил треугольника 30-60-90?

    Этот метод можно использовать для запоминания правила треугольника 30-60-90. Можно запомнить его как 1, 3, 2; это может напоминать соотношение сторон, все, что нужно помнить, это то, что средний член равен √3

    .

    Каковы длины сторон треугольника 30-60-90?

    Стороны треугольника 30-60-90 имеют заданный узор. Сторона, противоположная углу 30°, y всегда будет наименьшей, так как 30° — наименьший угол в этом треугольнике. Сторона, противоположная углу 60°, y√3, будет средней длиной, потому что 60° — это средний угол в градусах в этом треугольнике. Сторона, лежащая напротив 9.Угол 0 °, 2y будет наибольшей стороной, потому что 90 ° — самый большой угол.

    Каковы правила для треугольника 45-45-90?

    Треугольник 45-45-90 имеет прямой угол и два угла по 45 градусов. Две стороны треугольника 45-45-90 всегда равны, а гипотенуза треугольника всегда противоположна прямому углу.

    В чем сходство между треугольниками 30-60-90 и треугольниками 45-45-90?

    Вот некоторые сходства между треугольником 30-60-90 и треугольником 45-45-9.0 треугольник: оба треугольника не остроугольные, оба треугольники прямоугольные, оба треугольники не тупоугольные, квадрат гипотенузы равен сумме квадратов двух других сторон обоих треугольников и сумме внутренних углов треугольника.

    Источник

    Понравилась статья? Поделить с друзьями:
  • Dishonored 2 как найти вентиль
  • Как интровертам найти друг друга
  • На телефоне не высвечивается кто звонит как исправить
  • Интернет пишет днс сервер не отвечает как исправить
  • Как найти угол между стенами