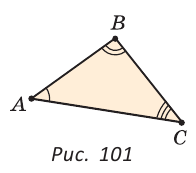
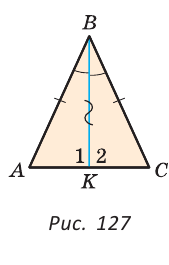
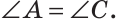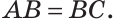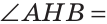Соответственные углы
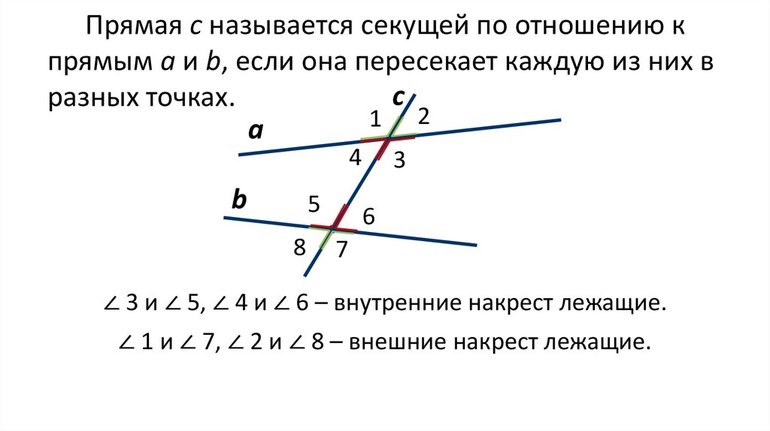
Соответственные углы — вид углов, образованный при пересечении двух прямых секущей.
Один из пары соответственных углов лежит во внутренней области между прямыми, другой — во внешней, причем оба угла находятся по одну сторону от секущей.
При пересечении двух прямых секущей образуется четыре пары соответственных углов.
∠1 и ∠5
∠2 и ∠6
∠3 и∠7
∠4 и ∠8
— соответственные углы при прямых a и b и секущей c.
Наибольший интерес в геометрии представляют соответственные углы при параллельных прямых.
Свойство параллельных прямых
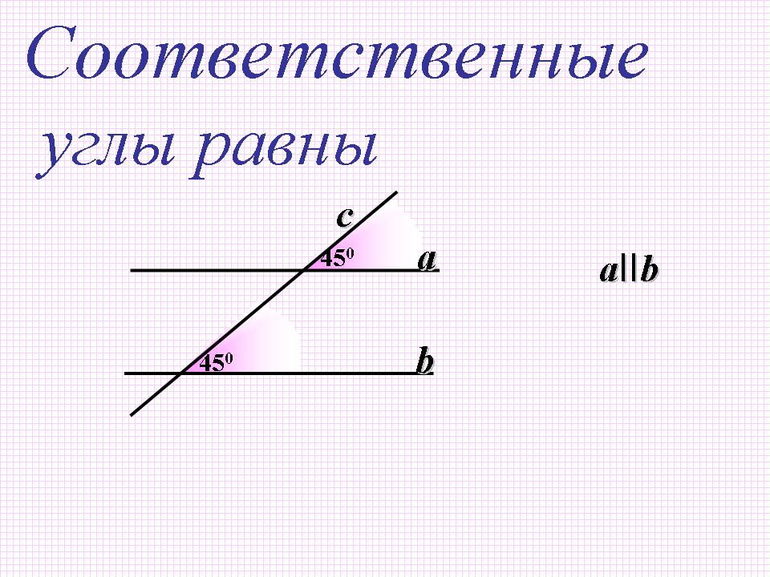
Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
∠1 = ∠2
(как соответственные углы при при a ∥ b и секущей c).
Всего при параллельных прямых и секущей образуется четыре пары равных соответственных углов:
∠1 = ∠5
∠2 = ∠6
∠3 = ∠7
∠4 =∠8
Признак параллельных прямых
Если соответственные углы равны, то прямые параллельны.
∠1 = ∠2
А так как эти углы — соответственные при прямых при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Равенство соответственных углов используется, в частности, для доказательства равенства треугольников и подобия треугольников.
Соответственные углы — определение, основные свойства и признаки
Базисные понятия
Угол — простая фигура в геометрии, образуемая двумя лучами, следующими из некоторой точки. Эту точку определяют как его вершину. Название «угол» может относиться к части плоскости, объединяющей все лучи, исходящие из вершины фигуры. Такое обозначение может также иметь угловая мера, чаще всего определяемая в градусах.
В геометрии существует несколько критериев, позволяющих выделить разные типы угловых фигур. Они бывают тупыми и острыми, смежными или вертикальными. Для углов, образуемых в результате пересечения секущей линией двух прямых, в качестве такого критерия берется свойство взаимных соотношений формируемых при этом фигур. При рассмотрении произвольного геометрического рисунка, образованного двумя прямыми линиями и секущей, можно увидеть 4 пары соответственных, по 2 пары внутренних и внешних накрест лежащих или односторонних угловых фигур. Все эти элементы могут быть как тупоугольными, так и остроугольными.
Углы, образующиеся при пересечении прямых
Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией. Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий.
Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:
- Накрест лежащие внутренние углы — это разносторонние по отношению к секущей объекты внутри области, сформированной прямыми. Если обе фигуры лежат за пределами двух прямых по противоположные стороны от секущей, то такие угловые элементы называются внешними накрест лежащими.
- В отличие от предыдущих противолежащих фигур, односторонние углы расположены на одной стороне: внутри области, образованной двумя прямыми (внутренние), или во внешних областях (наружные).
- Соответственные по определению являются парными фигурами, образующимися по одну сторону от линии, пересекающей две других, с аналогичных сторон обеих прямых. Один из углов пары расположен между прямыми и является внутренним, а другой лежит вне этой зоны, поэтому считается внешним.
Более наглядное представление об этом типе углов можно получить, если секущую изобразить в виде направленного вектора. Парные угловые элементы расположены в одном направлении относительно прямых, пересеченных третьей линией.
Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.
Соответственные углы при параллельных прямых
Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.
Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:
- Отметим отрезок на секущей, начало и конец которого, точки C и D, находятся в местах пересечения секущей с прямыми a и b.
- Через среднюю точку K отрезка опустим перпендикуляр к прямой a. Точки его пересечения с прямыми обозначим как A и B. Сформированные отрезками треугольники CKA и DKB являются прямоугольными, а отрезки AK и BK — сторонами, прилежащими к прямоугольным вершинам. Каждый из этих катетов одновременно является высотой треугольника, проведенной из остроугольной вершины.
- Для доказательства следует учитывать равенство вертикальных ∠CKA и ∠DKB, ∠BDK и ∠АСК равны по условию равенства соответственных углов с учетом того, что вертикальные углы с вершинами в точках C и D равны, CK и KD — два равных отрезка по условию.
- Таким образом, в треугольниках CKA и DKB сторона и прилежащие к ней углы имеют равные величины, что соответствует одному из признаков равенства треугольников.
- Поскольку AB перпендикулярен прямой a и отрезку AC, то CKA — прямоугольный треугольник, и это дает основание считать, что равный ему треугольник DKB также прямоугольный, из чего следует перпендикулярность отрезка AB по отношению к прямой b.
- Было доказано, что две прямые перпендикулярны к третьей прямой, и это подтверждает их параллельность.
Доказательство можно развернуть и в обратном направлении. Параллельные линии при пересечении третьей прямой формируют одинаковые по величине соответственные углы. Это утверждение известно как свойство параллельных линий.
Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.
Доказательство подобия треугольников
Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.
Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:
- Возьмем два треугольника ABC и A1B1C1, в которых равны два угла. Из этого следует, что величина третьего угла также одинакова в обеих фигурах. Требуется доказать подобие треугольников.
- Отметим точку A2 на AB таким образом, чтобы величина BA2 совпала с A1B1. Через A2 параллельно основанию AC проведем прямую, проходящую через BC в точке B2.
- Треугольники A2BC2 и A1B1C1 равны, что подтверждается одинаковыми величинами сторон A1B1, BA2 и углов B, B1 (по построению или условию), а также равенством углов A, A1 как соответственных при параллельных линиях.
- Поскольку, согласно лемме, параллельная стороне треугольника прямая отсекает от него подобный треугольник, то A2BC2 подобен ABC. Из этого следует подобие треугольников ABC и A1B1C1.
Подобного рода рассуждения и доказательства, учитывающие свойства соответственных угловых фигур, учитываются при решении разного рода задач.
В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.
Треугольники. Признаки равенства треугольников
Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .
Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.
Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.
Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.
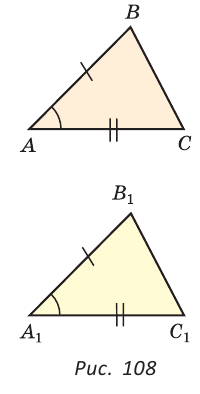
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A1B1C1. Треугольник ABC можно наложить на треугольник A1B1C1 так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.
Вышеизложенное можно сформулировать так:
Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A1B1C1 обозначается так:
Первый признак равенства треугольников
Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1C1 (Рис.3). Пусть AB=A1B1, AС=A1С1 и ∠A=∠A1. Докажем, что .
Второй признак равенства треугольников
Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1С1 (Рис.4). Пусть AB=A1B1, ∠A=∠A1, ∠B=∠B1. Докажем, что .
Третий признак равенства треугольников
Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1С1. Пусть AB=A1B1, AC=A1C1 и BC=B1C1. Докажем, что . Приложим треугольник ABC к треугольнику A1B1С1 так, чтобы вершина A совмещалась с вершиной A1, вершина B совмещалась с вершиной B1, а вершины С и С1 находились по разные стороны от прямой A1B1.
Возможны три варианта: луч CC1 проходит внутри угла ACB(Рис.6); луч CC1 совпадает с одной из сторон угла ACB (Рис.7); луч CC1 проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.
Имеем AC=A1C1, BC=B1C1 ∠ACB=∠A1C1B1 и по первому признаку равенства треугольников . Теорема доказана.
Вариант 2 (Рис.7). Так как по условию теоремы AC=A1C1 и BC=B1C1, то треугольник BСС1 равнобедренный. Тогда ∠1=∠2. Имеем: AC=A1C1, BC=B1C1, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.
Вариант 3 (Рис.8). Так как по условию теоремы AC=A1C1 и BC=B1C1, то треугольники AСС1 и BСС1 равнобедренные. Тогда ∠1=∠2 и и, следовательно:
Имеем AC=A1C1, BC=B1C1 и по первому признаку равенства треугольников . Теорема доказана.
Задачи и решения
Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).
Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .
Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T
Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .
http://nauka.club/matematika/geometriya/sootvetstvenny%D0%B5-ugl%D1%83.html
http://matworld.ru/geometry/treugolniki.php
Соответственные углы — вид углов, образованный при пересечении двух прямых секущей.
Один из пары соответственных углов лежит во внутренней области между прямыми, другой — во внешней, причем оба угла находятся по одну сторону от секущей.
При пересечении двух прямых секущей образуется четыре пары соответственных углов.
∠1 и∠5
∠2 и∠6
∠3 и∠7
∠4 и∠8
— соответственные углы при прямых a и b и секущей c.
Наибольший интерес в геометрии представляют соответственные углы при параллельных прямых.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
Если a ∥ b, то
∠1 =∠2
(как соответственные углы при при a ∥ b и секущей c).
Всего при параллельных прямых и секущей образуется четыре пары равных соответственных углов:

∠2 =∠6
∠3 =∠7
∠4 =∠8
Признак параллельных прямых
Если соответственные углы равны, то прямые параллельны.

А так как эти углы — соответственные при прямых при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Равенство соответственных углов используется, в частности, для доказательства равенства треугольников и подобия треугольников.
Базисные понятия
Угол — простая фигура в геометрии, образуемая двумя лучами, следующими из некоторой точки. Эту точку определяют как его вершину. Название «угол» может относиться к части плоскости, объединяющей все лучи, исходящие из вершины фигуры. Такое обозначение может также иметь угловая мера, чаще всего определяемая в градусах.
В геометрии существует несколько критериев, позволяющих выделить разные типы угловых фигур. Они бывают тупыми и острыми, смежными или вертикальными. Для углов, образуемых в результате пересечения секущей линией двух прямых, в качестве такого критерия берется свойство взаимных соотношений формируемых при этом фигур. При рассмотрении произвольного геометрического рисунка, образованного двумя прямыми линиями и секущей, можно увидеть 4 пары соответственных, по 2 пары внутренних и внешних накрест лежащих или односторонних угловых фигур. Все эти элементы могут быть как тупоугольными, так и остроугольными.
Углы, образующиеся при пересечении прямых
Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией. Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий.
Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:
- Накрест лежащие внутренние углы — это разносторонние по отношению к секущей объекты внутри области, сформированной прямыми. Если обе фигуры лежат за пределами двух прямых по противоположные стороны от секущей, то такие угловые элементы называются внешними накрест лежащими.
- В отличие от предыдущих противолежащих фигур, односторонние углы расположены на одной стороне: внутри области, образованной двумя прямыми (внутренние), или во внешних областях (наружные).
- Соответственные по определению являются парными фигурами, образующимися по одну сторону от линии, пересекающей две других, с аналогичных сторон обеих прямых. Один из углов пары расположен между прямыми и является внутренним, а другой лежит вне этой зоны, поэтому считается внешним.
Более наглядное представление об этом типе углов можно получить, если секущую изобразить в виде направленного вектора. Парные угловые элементы расположены в одном направлении относительно прямых, пересеченных третьей линией.
Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.
Соответственные углы при параллельных прямых
Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.
Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:
- Отметим отрезок на секущей, начало и конец которого, точки C и D, находятся в местах пересечения секущей с прямыми a и b.
- Через среднюю точку K отрезка опустим перпендикуляр к прямой a. Точки его пересечения с прямыми обозначим как A и B. Сформированные отрезками треугольники CKA и DKB являются прямоугольными, а отрезки AK и BK — сторонами, прилежащими к прямоугольным вершинам. Каждый из этих катетов одновременно является высотой треугольника, проведенной из остроугольной вершины.
- Для доказательства следует учитывать равенство вертикальных ∠CKA и ∠DKB, ∠BDK и ∠АСК равны по условию равенства соответственных углов с учетом того, что вертикальные углы с вершинами в точках C и D равны, CK и KD — два равных отрезка по условию.
- Таким образом, в треугольниках CKA и DKB сторона и прилежащие к ней углы имеют равные величины, что соответствует одному из признаков равенства треугольников.
- Поскольку AB перпендикулярен прямой a и отрезку AC, то CKA — прямоугольный треугольник, и это дает основание считать, что равный ему треугольник DKB также прямоугольный, из чего следует перпендикулярность отрезка AB по отношению к прямой b.
- Было доказано, что две прямые перпендикулярны к третьей прямой, и это подтверждает их параллельность.
Доказательство можно развернуть и в обратном направлении. Параллельные линии при пересечении третьей прямой формируют одинаковые по величине соответственные углы. Это утверждение известно как свойство параллельных линий.
Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.
Доказательство подобия треугольников
Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.
Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:
- Возьмем два треугольника ABC и A1B1C1, в которых равны два угла. Из этого следует, что величина третьего угла также одинакова в обеих фигурах. Требуется доказать подобие треугольников.
- Отметим точку A2 на AB таким образом, чтобы величина BA2 совпала с A1B1. Через A2 параллельно основанию AC проведем прямую, проходящую через BC в точке B2.
- Треугольники A2BC2 и A1B1C1 равны, что подтверждается одинаковыми величинами сторон A1B1, BA2 и углов B, B1 (по построению или условию), а также равенством углов A, A1 как соответственных при параллельных линиях.
- Поскольку, согласно лемме, параллельная стороне треугольника прямая отсекает от него подобный треугольник, то A2BC2 подобен ABC. Из этого следует подобие треугольников ABC и A1B1C1.
Подобного рода рассуждения и доказательства, учитывающие свойства соответственных угловых фигур, учитываются при решении разного рода задач.
В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.
Содержание:
Если на плоскости отметить три точки А, В и С, не лежащие на одной прямой, и соединить их отрезками, то получим треугольник ABC. Можно сказать, что треугольник — это трехзвенная замкнутая ломаная. Обозначают:
Определения
Определение. Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает.
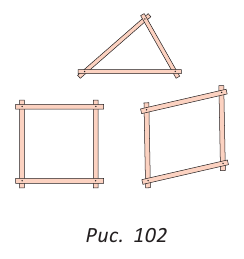
Если соединить концами три деревянных планки, то получится треугольник, который нельзя подвергнуть деформации — он будет сохранять свою форму. Тогда как четырехугольник может менять свою форму (рис. 102)? Это свойство «жесткости» треугольника широко используется в технике, производстве, строительстве.
Равные треугольники
Равные треугольники можно совместить наложением так, что соответственно совпадут все три стороны и все три угла (рис. 103). В совпавших, то есть в равных треугольниках, против равных сторон лежат равные углы, а против равных углов — равные стороны. Если 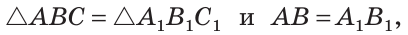
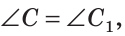
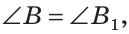
Для совмещения равных отрезков достаточно совпадения их концов, а для совмещения равных треугольников — совпадения их вершин.
Виды треугольников
Если у треугольника все три стороны имеют разную длину, то такой треугольник называется разносторонним.
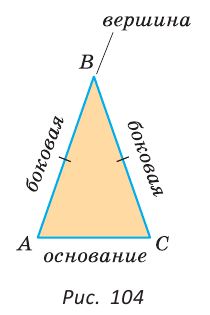
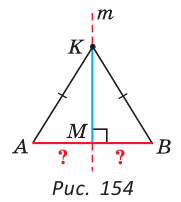
Треугольник, у которого две стороны равны, называется равнобедренным. Его равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника (рис. 104).
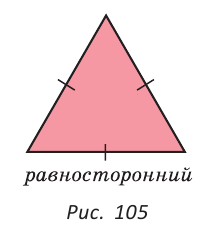
Если у треугольника равны все три стороны, то он называется равносторонним (рис. 105). Равносторонний треугольник является также и равнобедренным, где любую пару сторон можно принять за боковые стороны.
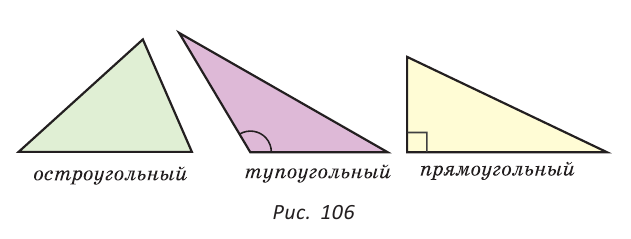
По величине углов треугольники делятся на остроугольные (у них все углы острые), тупоугольные (есть тупой угол) и прямоугольные (есть прямой угол) (рис. 106).
Подведем итоги.
Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает.
Периметром треугольника (многоугольника) называется сумма длин его сторон.
Равными треугольниками называются треугольники, которые можно совместить наложением.
Равнобедренным треугольником называется треугольник, у которого две стороны равны.
Равносторонним треугольником называется треугольник, у которого все стороны равны.
Свойство равных треугольников. В равных треугольниках против равных сторон лежат равные углы, а против равных углов — равные стороны.
Замечание. Называя или записывая равные треугольники, стараются соблюдать последовательность соответствующих вершин. Во многих случаях это удобно. Однако делать это необязательно. Обе записи: 





Первый и второй признаки равенства треугольников
При выяснении равны ли треугольники нет необходимости устанавливать равенство всех их соответствующих элементов путем наложения или измерения. Следующие две теоремы гарантируют равенство треугольников при равенстве некоторых сторон и углов.
Теорема (первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Дано: АВ =А1В1, АС =А1С1, 
Доказать: 

Доказательство:
Наложим треугольник ABC на треугольник А1В1С1 так, чтобы совпали равные углы А и А1, луч АВ совпал с лучом А1В1, а луч АС совпал с лучом А1С1. Так как отрезки АВ и А1В1 равны, то они совпадут при наложении, и вершина В совпадет с вершиной В1. Аналогично совпадут равные отрезки АС и A1C1, вершина С совпадет с вершиной C1. Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, 

Говорят, что две стороны и угол между ними задают треугольник однозначно.
Теорема (второй признак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано:
AC =А1С1, 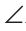
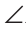
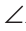
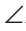
Доказать: 

Доказательство:
Наложим треугольник ABC на треугольник А1В1С1 так, чтобы совпали равные стороны АС и А1С1, угол А совпал с равным углом А1, а угол С — с равным углом Сх. Тогда луч АВ совпадет с лучом А1В1, луч СВ — с лучом С1В1, а вершина В совпадет с вершиной В1 (точка В будет принадлежать и прямой
А1В1, и прямой С1В1, и поэтому совпадет с точкой их пересечения В1). Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, 

Говорят, что сторона и два прилежащих к ней угла задают треугольник однозначно
Пример №1
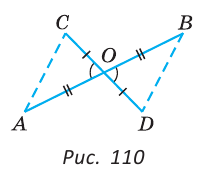
Отрезки АВ и CD пересекаются в их серединах. Доказать, что расстояния между точками А и С, В и D равны.
Доказательство:
Пусть О — точка пересечения отрезков АВ и CD (рис. 110). Рассмотрим 


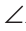
Возможно краткое оформление решения задачи.
Пример №2
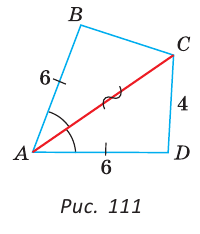
Дана простая замкнутая ломаная ABCD, у которой АВ =AD = 6 см, CD -4 см и луч АС является биссектрисой угла BAD. Найти длину ломаной ABCD.
Решение:
У треугольников ABC и ADC сторона АС — общая (рис. 111), AB=AD по условию, 

Эти треугольники равны по 1-му признаку равенства треугольников.
Отсюда ВС = CD как соответствующие (соответственные) стороны в двух равных треугольниках.
Длина ломаной ABCD:
Ответ: 20 см.
Пример №3
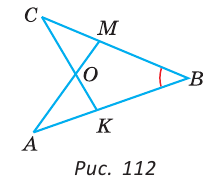
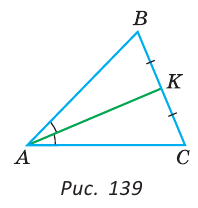
На сторонах угла В отложены отрезки: ВА = ВС, КА-МС (рис. 112). Доказать, что 

Доказательство:
Рассмотрим треугольники АВМ и СВК. У них 


Пример №4
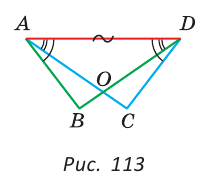
На рисунке 113 



Доказательство:
Так как 



Так как 









Высота, медиана и биссектриса треугольника
У треугольника, помимо трех сторон, трех вершин и трех углов, имеются также и другие элементы — высота, медиана и биссектриса.
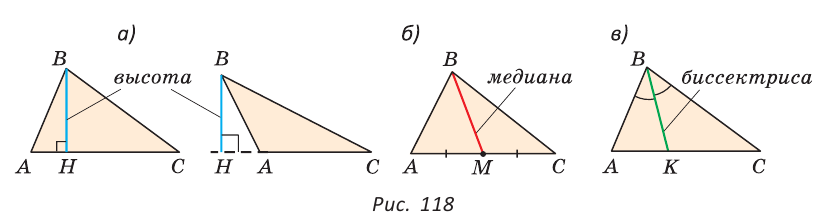
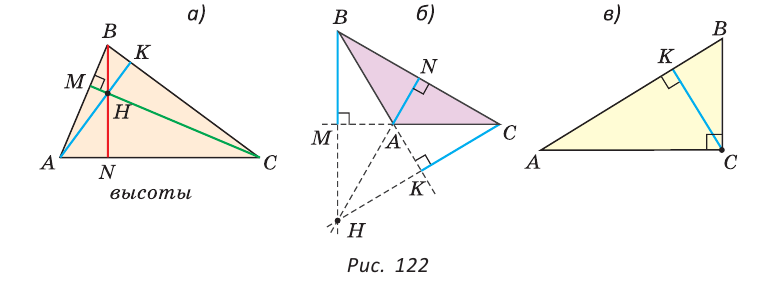
Определение. Высотой треугольника (рис. 118, а) называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на ее продолжение (отрезок ВН).
Определение. Медианой треугольника (рис. 118, б) называется отрезок, который соединяет вершину треугольника с серединой противоположной стороны (отрезок ВМ).
Определение. Биссектрисой треугольника (рис. 118, в) называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой пересечения биссектрисы с противоположной стороной (отрезок ВК).
В равных треугольниках равны соответствующие высоты, медианы и биссектрисы.
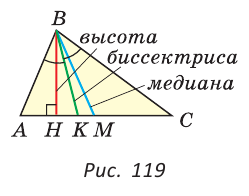
Если треугольник не равнобедренный, то высота, медиана и биссектриса, проведенные из одной вершины треугольника, не совпадают (рис. 119).
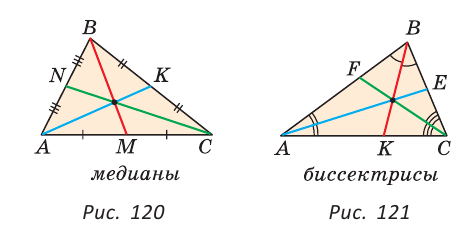
Поскольку у треугольника три вершины, то у него и три высоты, три медианы, три биссектрисы. Позже мы докажем, что высоты треугольника (или их продолжения) пересекаются в одной точке. Это же касается медиан треугольника (рис. 120) и его биссектрис (рис. 121).
Если треугольник остроугольный (рис. 122, а), то точка пересечения его высот находится внутри треугольника ABC. Если треугольник тупоугольный или прямоугольный (рис. 122, б, в), то продолжения высот пересекаются соответственно вне треугольника или в вершине прямого угла.
Точки пересечения высот, биссектрис и медиан называются замечательными точками треугольника.
Геометрия 3D
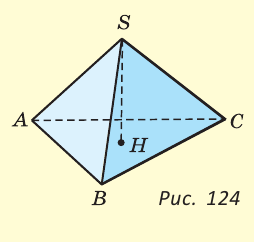
Тетраэдром или треугольной пирамидой называется многогранник, у которого все четыре грани — треугольники. Любую его грань можно принять за основание, а противолежащую вершину — за вершину пирамиды. Если точка S — вершина, а треугольник ABC — основание пирамиды, то перпендикуляр SH к плоскости ABC является высотой тетраэдра (рис. 124).
Равнобедренный треугольник
Определение. Треугольник называется равнобедренным, если у него две стороны равны.
Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника.
Рассмотрим некоторые свойства равнобедренного треугольника и один из его признаков.
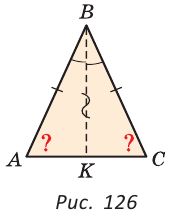
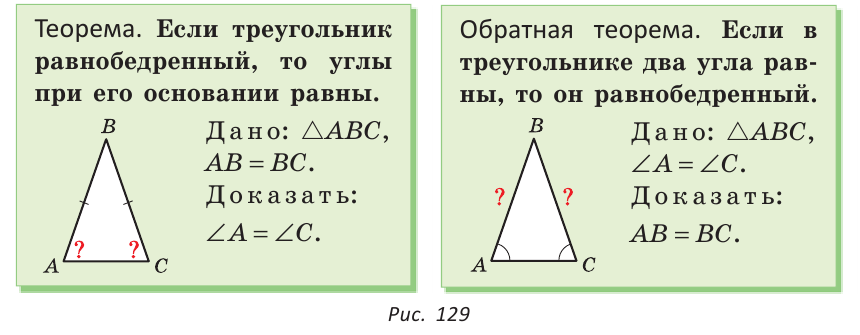
Теорема (о свойстве углов при основании). В равнобедренном треугольнике углы при основании равны.
Дано: 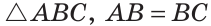
Доказать:
Доказательство:
Проведем биссектрису ВК треугольника ABC. Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК — общая, АВ = ВС по условию, углы АВК и СВК равны по определению биссектрисы. Из равенства этих треугольников следует, что 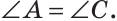
Теорема (о свойстве биссектрисы равнобедренного треугольника).
В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой.
Дано: 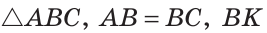
Доказать: ВК — медиана и высота.
Доказательство:
Треугольники АВК и СВК равны по двум сторонам и углу между ними (см. предыдущую теорему). Из равенства треугольников следует, что АК=КС и 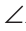
Замечание. Поскольку из вершины треугольника можно провести только одну биссектрису, одну высоту и одну медиану, то теорему можно сформулировать так: «Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают». То есть если по условию задачи дана высота равнобедренного треугольника, проведенная к основанию, то согласно данной теореме она является биссектрисой и медианой. Аналогично, если дана медиана равнобедренного треугольника, проведенная к основанию, то она является высотой и биссектрисой.
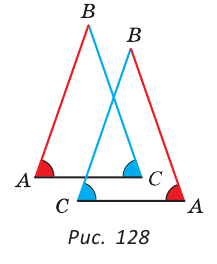
Теорема (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.
Дано:
Доказать:
Доказательство:
Мысленно перевернем треугольник ABC обратной стороной (рис. 128) и наложим перевернутый треугольник на треугольник ABC так, чтобы их стороны АС совпали, угол С совпал с углом А, угол А совпал с углом С.
Тогда перевернутый треугольник совместится с данным, и сторона ВС совместится со стороной АВ. Следовательно, АВ = ВС, т. е. 
Доказанный признак равнобедренного треугольника является теоремой, обратной теореме о свойстве углов при основании равнобедренного треугольника (рис. 129).
Напомним, что любая теорема состоит из условия — того, что дано, и заключения — того, что нужно доказать. У теоремы, обратной данной, условием является заключение данной теоремы, а заключением — условие данной.
Пример №5
Доказать, что в равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.
Доказательство:
Пусть в 


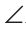
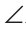



Замечание. Вторым способом доказательства будет рассмотрение

Пример №6
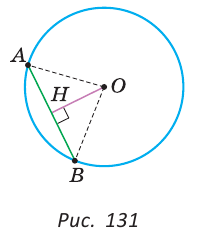
Доказать, что перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду пополам.
Доказательство:
Пусть О — центр окружности, АВ — хорда, ОН — перпендикуляр к хорде АВ (рис. 131).
Отрезки OA и ОВ равны как радиусы. Поэтому треугольник АОВ — равнобедренный, а ОН — его высота, проведенная к основанию. Мы знаем, что высота равнобедренного треугольника, проведенная к основанию, является и медианой. А медиана делит сторону треугольника пополам, то есть АН = НВ. Что и требовалось доказать.
Признаки равнобедренного треугольника
Вы уже знаете один признак равнобедренного треугольника: «Если в треугольнике два угла равны, то треугольник равнобедренный». Докажем еще три признака равнобедренного треугольника, связанных с его высотой, медианой и биссектрисой.
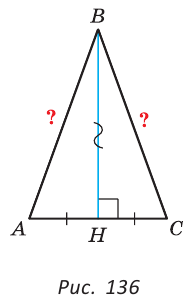
Теорема. Если в треугольнике высота является медианой, то треугольник равнобедренный.
Дано: ВН — высота и медиана 
Доказать: АВ = ВС.
Доказательство:
Рассмотрим 

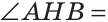
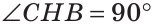
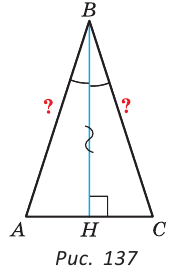
Теорема. Если в треугольнике высота является биссектрисой, то треугольник равнобедренный.
Дано: ВН — высота и биссектриса 
Доказать: АВ = ВС (рис. 137).
Доказательство:
Рассмотрим 

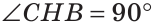
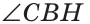
Теорема. Если в треугольнике медиана является биссектрисой, то треугольник равнобедренный.
Дано: ВМ — медиана и биссектриса 
Доказать: АВ = ВС (рис. 138).
Доказательство:
Продлим медиану ВМ на ее длину за точку М. Получим МВХ = ВМ. Треугольники АМВ1 и СМВ равны по двум сторонам и углу между ними (МВ1 = ВМ по построению; AM = МС, так как ВМ — медиана; 






Замечание. Прием продления (продолжения) медианы часто используется при решении геометрических задач.
Пример №7
В треугольнике ABC с периметром 54 см медиана АК перпендикулярна стороне ВС, а высота ВМ составляет равные углы со сторонами ВА и ВС. Найти стороны треугольника ABC.
Решение:
Так как медиана АК является и высотой, то 


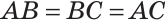
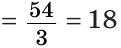
Ответ: 18 см.
Пример №8
Биссектриса АК треугольника АБС делит сторону ВС пополам. Периметр треугольника ABC равен 36 см, периметр треугольника АКС равен 30 см. Найти длину биссектрисы АК.
Решение:
Из условия следует, что биссектриса АК является и медианой 
Тогда 


Ответ: 12 см
Геометрия 3D
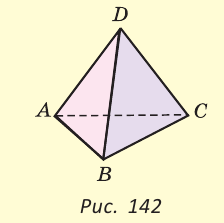
У правильной треугольной пирамиды DABC в основании лежит равносторонний треугольник ABC, а боковые грани ADB, ADC, BDC — равные равнобедренные треугольники с общей вершиной D (рис. 142).
У правильной четырехугольной пирамиды в основании лежит квадрат MNKE, а боковые грани МРЕ, MPN, NPK, ЕРК — равные равнобедренные треугольники с общей вершиной Р (рис. 143).
Третий признак равенства треугольников
Вам уже известны два признака равенства треугольников. Рассмотрим еще один.
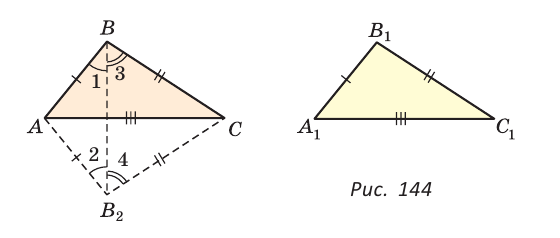
Теорема (третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Дано: АВ=А1В1, ВС = В1С1, АС=А1С1 (рис. 144).
Доказать: 

Доказательство:
Приложим треугольник А1В1С1 к треугольнику ABC так, чтобы у них совместились равные стороны А1С1 и АС, а вершины В1 и В оказались в разных полуплоскостях относительно прямой АС. Треугольник А1В1С1 займет положение треугольника АВ2С. Проведем отрезок ВВ2. Так как АВ2=АВ и В2С = ВС, то треугольники АВВ2 и СВВ2 — равнобедренные. Откуда 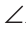
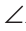
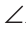
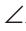
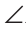


Замечание. Чтобы отрезок ВВ2 проходил внутри треугольника ABC, следует прикладывать треугольники большей стороной.
Говорят, что три стороны задают треугольник однозначно.
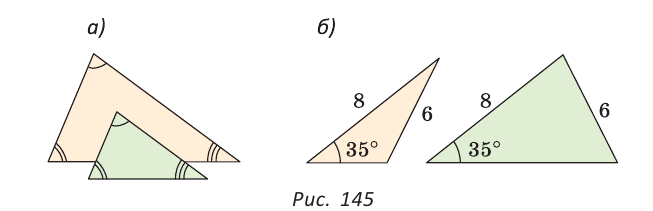
Итак, теперь вы знаете три признака равенства треугольников. Можно сформулировать и другие признаки равенства треугольников, в которых неизбежно будет присутствовать соответственное равенство каких-то трех элементов двух треугольников. Однако не любые три элемента задают треугольник. Так, например, если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники не обязательно равны. То же касается треугольников, у которых соответственно равны две стороны и угол, противолежащий одной из этих сторон.
На рисунке 145, а, б вы видите пары таких неравных треугольников.
Пример №9
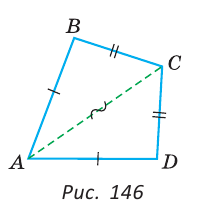
У простой замкнутой ломаной ABCD AB=AD, BC = DC. Доказать, что 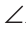
Доказательство:
Проведем отрезок АС (рис. 146).
Треугольники ABC и ADC равны по 3-му признаку равенства треугольников (AB=AD и BC = DC по условию, сторона АС — общая). Поэтому 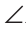
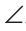
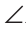
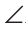
Пример №10
Доказать равенство треугольников по двум сторонам и медиане между ними.
Доказательство:
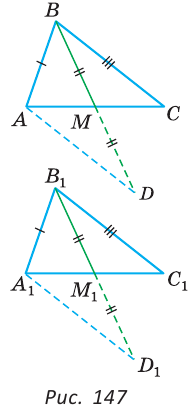
Пусть АВ =А1В1, ВС = В1С1, ВМ = В1М1, где ВМ и В1М1 — медианы (рис. 147).
Нужно доказать, что 




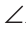










Пример №11
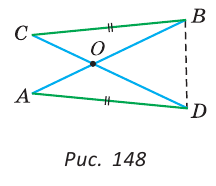
Два равных отрезка АВ и CD пересекаются в точке О и AD = BC. Доказать, что ВО = DO.
Доказательство:
Соединим точки В и D отрезком (рис. 148).
Треугольники ABD и CDB равны по трем сторонам (сторона BD — общая, AB=CD и AD=СВ по условию). Из равенства треугольников следует, что 


Серединный перпендикуляр к отрезку
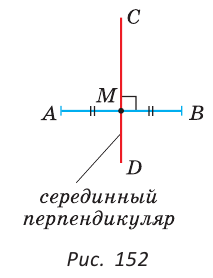
Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Прямая CD — серединный перпендикуляр к отрезку АВ, то есть 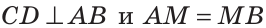
Теорема (о серединном перпендикуляре).
Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.
1) Дано: 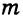
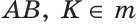
Доказать: КА = КВ.
Доказательство:
По определению серединного перпендикуляра 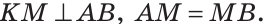

2) Дано: 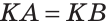
Доказать: 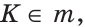
Доказательство:
Проведем в равнобедренном 
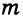
Теорема доказана.
Геометрическим местом точек плоскости (или пространства) называется множество всех точек плоскости (или пространства), обладающих общим свойством.
Из доказанной теоремы следует, что серединный перпендикуляр к отрезку — это геометрическое место точек плоскости, равноудаленных от концов отрезка.
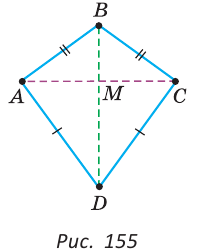
Пример №12
В четырехугольнике (рис. 155) ABCD AB=BC, AD=DC.
Доказать, что AC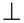
Доказательство:
1-й способ. Из равенства треугольников ABD и CBD по трем сторонам следует, что 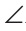
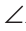
2-й способ. Точки В и D равноудалены от концов отрезка АС, поэтому они лежат на серединном перпендикуляре к отрезку АС. Так как через две точки проходит единственная прямая, то BD — серединный перпендикуляр к отрезку АС. Отсюда AC
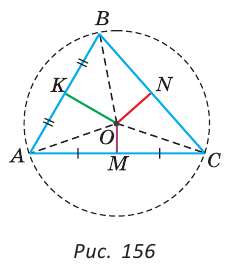
Пример №13 (1-я замечательная точка треугольника).
Доказать, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство:
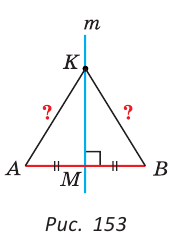
Пусть два серединных перпендикуляра к сторонам АС и АВ пересекаются в точке О (рис. 156).
Точка О лежит на серединном перпендикуляре ОМ, поэтому ОА = ОС. Точка О лежит на серединном перпендикуляре ОК, поэтому ОА = ОВ. Отсюда ОВ = ОС. Поскольку точка О равноудалена от концов отрезка ВС, то она лежит на серединном перпендикуляре к отрезку ВС. Таким образом, третий серединный перпендикуляр пройдет через точку О, и все три серединных перпендикуляра к сторонам треугольника пересекутся в одной точке.
Замечания.
- 1. Если ножку циркуля поставить в точку О и построить окружность радиусом OA, то она пройдет через все вершины треугольника в силу того, что OA = OB = ОС. Такая окружность называется описанной около треугольника. В данной задаче мы доказали, что центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров к его сторонам.
- 2. Точка пересечения серединных перпендикуляров к сторонам треугольника — это еще одна замечательная точка треугольника помимо уже известных вам точек пересечения биссектрис, медиан, высот.
Напомню:
Три признака равенства треугольников:
- По двум сторонам и углу между ними.
- По стороне и двум прилежащим к ней углам.
- По трем сторонам.
Запомните:
- Углы при основании равнобедренного треугольника равны.
- Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является его высотой и медианой.
- Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
- Если высота треугольника является его медианой или биссектрисой, или медиана является его биссектрисой, то треугольник равнобедренный (признаки равнобедренного треугольника).
- Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
- Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке (1-я замечательная точка треугольника).
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
|
Что такое соответственные углы? Они равны между собой? Чему равна сумма двух соответственных углов при параллельных прямых? Соответственные углы образуются при пересечении секущей двух прямых. Также образуются односторонние и накрест лежащие углы. Соответственные углы при параллельных прямых равны между собой, при непараллельных — не равны. Сумма соответственных углов (при параллельных) равна 360 минус удвоенный односторонний угол к любому из соответственных, взятых для расчета. Геометрически соответственные углы находятся по одну сторону от секущей, и …если представить секущую в виде вектора, имеющего направление… в одном направлении относительно точек пересечения секущей с параллельными прямыми. автор вопроса выбрал этот ответ лучшим Возьмем две произвольные прямые на плоскости, их пересекает третья прямая, называемая секущей ( все три прямые лежат в одной плоскости ). При пересечении двух прямых секущей и образуются соответственные углы. При пересечении двух прямых секущей образуется восемь углов. Разберемся, какие из них являются соответственными с помощью рисунка. Но сначала замечу, что в геометрии при решении различных задач, чаще рассматривается вариант, когда две прямые, пересекаемые третьей, параллельны между собой. В этом случае образуемые при пересечении углы обладают рядом свойств. На рисунке мы видим две параллельные прямые a и b, которые пересекает секущая c. Соответственными в данном случае являются: 2 и 6, 3 и 7, 4 и 8, 1 и 5. Соответственные углы, образуемые при пересечении двух параллельных прямых третьей, равны: 2=6, 3=7, 4=8, 1=5. Углы, одной стороной которых является секущая и находящиеся по одну сторону от секущей, называются односторонними, например углы 1 и 6 будут односторонними. На рисунке также хорошо видно, что углы с вершиной в одной точке 1, 2 и 5, 6 составляют угол 180 градусов, то есть 1+2=180, 5+6=180. Поскольку 2=6, то совершенно очевидно, что 1=5. Углы с вершиной в одной точке 1, 2, 3, 4 и 5, 6, 7, 8 составляют угол 360 градусов, то есть 1+2+3+4=360, 5+6+7+8+=360. Если известен односторонний угол 1, то то сумма соответственных углов 2+6= 360 — 2х1. Если выразить это словами, то сумма соответственных углов равна разности между 360 градусами и удвоенным односторонним углом. При изучении параллельных прямых можно столкнуться с понятием соответствующих углов. Если взять две параллельные прямые и нарисовать еще одну прямую, которая пересекает их обе, то будет образовано восемь углов. При этом образуется так соответствующие углы, которые равны между собой. На картинке они показаны красным. При этом сумма односторонних углов равна 180°. То есть, сумма красного и синего угла равна 180°. Отсюда также видно, что углу, которые расположены накрест, также равны. Что касается суммы соответствующих углов, то однозначного ответа нет. Она может быть самой разной в численном выражении. Сумма таких углов — это разница между 180° и односторонним углом, умноженная на два. Galina7v7 6 лет назад Если две прямые пересекающиеся в пределах чертежа) пересечь третьей прямой, называемой — секущей, то образуются множество углов. Но рассмотрим углы соответственные.Так они называются (соответственными) по логике их отношения к чему-то аналогичному.То есть два соответственных угла образованные , допустим, двумя параллельными прямыми и общей секущей, и один из углов будет образован верхней прямой и секущей, и будет находиться сверху от этой прямой, такая же история (соответственно) образован нижней параллельной прямой, и секущей и тоже расположен сверху этой прямой.То есть определение аналогично, но 1-е определение и угол касается 1-й верхней прямой, а второе ко нижней. Также можно повторить для угла под прямой-нижней и верхней. Сколько пар соответственных углов при двух прямых и секущей? Я считаю — 4 пары соответственных углов, а всего их будет 8, но соответственных пар будет 4.И ещё: при параллельных прямых соответственные углы равны между собой. Повторю с чертежом: Соответственные углы : пара 1 с 5 ,2 и 6, 4 и 8 , 3 и 7. Но тут чертёжж не с параллельными прямыми.и соответственые углы не равны. 127771 3 года назад Это определение известно из школьного курса геометрии. Итак, соответственными углами называют такие углы, которые образуются при пересечении двух прямых секущей. При пересечении 2-х прямых секущей образуется четыре пары соответственных углом. Ниже в ответе рисунок, на котором представлены такие углы: Перед нами 4 пары соответственных углов, а именно: углы 2 и 6, углы 1 и 5, углы 3 и 7, углы 4 и 8. Особый интерес представляет, если перед нами параллельные прямые: В этом случае у нас получается, что угол один равен углу пять. Угол два равен углу шесть. Угол четыре равен углу восемь. Угол три равен углу семь. davsenorm 6 лет назад Когда две прямые линии пересекаются одной секущей — получаются соответственные, односторонние и накрест лежащие углы. Если прямые линии параллельны друг другу — соответственные углы будут равны, если же не параллельны — не равны. Чтобы высчитать сумму соответственных углов при параллельных прямых линиях, нужно применить следующую формулу: 360 — с*2 где С — это односторонний угол к любому из соответственных углов. Profilaktika 6 лет назад Соответственные углы — это вид углов, которые образуются при пересечении двух произвольных прямых секущей. При этом образуется 4 пары соответственных углов. Соответственные углы равны между собой, в случае параллельных прямых. Равенство соответствующих углов используется в доказательствах подобия и равенства двух треугольников. Также, если соответственные углы равны, то внутренние накрест лежащие углы тоже равны, и наоборот. Один угол из пары соответственных всегда будет внешним, второй — внутренним. Визуально они как будто находятся на разных ступеньках. Уже из названия видно что «соответственные» углы, значит что они тождественны, либо чему то еще, либо между собой. Так и есть, соответствующие углы образуются при пересечении двух параллельных прямых(!) одной секущей прямой проходящей через их обе. В месте пересечения каждой из параллельных они образуют углы равные между собой. Так перпендикуляр проведенный через две параллельные углы образует четыре соответственных угла. Если секущая идет под углом не равным 90 градусов, то образует два одинаковых острых угла и два одинаковых тупых угла. МариМари28 6 лет назад Соответственные это углы образованные двумя параллельными прямыми и секущей (то есть пересекающей прямой). Соответственные углы равны между собой. Чтобы посчитать чему равна сумма двух соответственных углов, надо из 180 градусов вычесть односторонний угол и умножить на два. TheSun 3 года назад Соответственные углы образуются при пересечении двух прямых линий с секущей. При пересечении эти углы обязательно находятся по одну сторону от секущей линии. Соответственные углы могут быть равными и не равными. Углы равны в том случае, если линии, которые пересекает секущая параллельны. В этом случае, их сумма будет равна 360° минус удвоенный односторонний угол. На рисунке приведённом ниже показаны соответственные углы, которые равны между собой. Знаете ответ? |