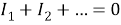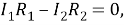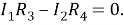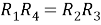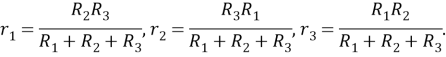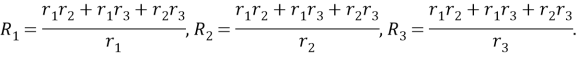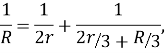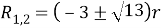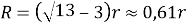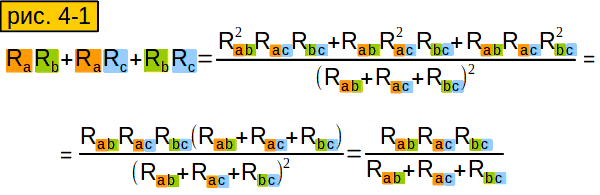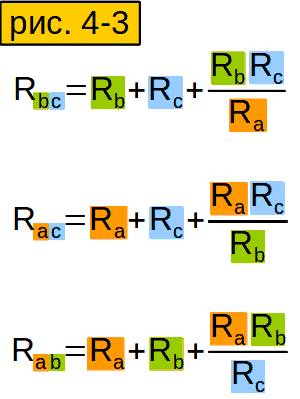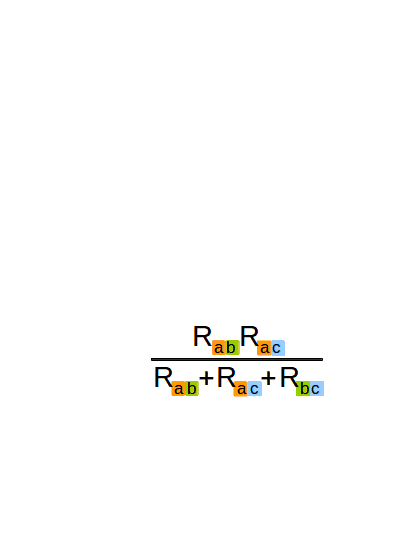Библиографическое описание:
Мусин, А. И. Методы решения задач с разветвленными электрическими цепями / А. И. Мусин, М. Ю. Осипова. — Текст : непосредственный // Школьная педагогика. — 2022. — № 3 (25). — С. 15-28. — URL: https://moluch.ru/th/2/archive/222/7209/ (дата обращения: 29.05.2023).
В учебных и олимпиадных задачах, связанных с расчетом параметров электрических цепей постоянного тока, зачастую требуется рассчитать общее сопротивление цепи. Для решения подобных задач электрические цепи
преобразовывают
, то есть исходную схему заменяют другой с тем же числом выводов. Причём замена должна осуществляться так, чтобы сопротивления между любыми двумя выводами новой схемы были такими же, как у старой. Токи, потребляемые новой схемой от источника, должны оставаться прежними. Общее сопротивление схемы, рассчитанное для подключения к источнику для каждой пары выводов, также не изменяется. Такие преобразования называются
эквивалентными
. Расчёт потребления тока и общего сопротивления при этом обычно упрощается.
Универсального метода преобразования электрических цепей нет. Некоторые методы изложены методических пособиях и задачниках, например [1–4]. Однако изложение не носит систематического характера — обычно суть метода излагается прямо по ходу решения той или иной задачи.
В настоящей статье мы попытались собрать и кратко изложить (в виде конспекта) методы преобразования электрических цепей с сопротивлениями, которые могут быть полезны при решении широкого круга задач. Конспект будет полезен школьникам 8–11 классов, преподавателям физики, тем, кто интересуется проблемами углубленного изучения физики и подготовки школьников к олимпиадам (в частности, к Всероссийской олимпиаде и вузовским олимпиадам).
Метод простейших эквивалентных преобразований.
Простейшие примеры преобразования цепи — это 1) замена двух последовательно соединённых сопротивлений
r
1
и
r
2
одним сопротивлением
r
1
+
r
2
; 2) замена двух параллельно соединённых сопротивлений
r
1
и
r
2
одним сопротивлением
r
1
·
r
2
/(
r
1
+
r
2
). Эти две замены лежат в основе данного метода.
При решении задач в первую очередь необходимо установить, какие проводники соединены между собой последовательно, какие параллельно. Отдельные участки схемы с параллельно или последовательно соединенными резисторами заменяются одним эквивалентным резистором. Постепенным преобразованием участков схему упрощают и приводят к простейшей схеме, состоящей из одного резистора. При этом используются свойства последовательно и параллельно соединенных проводников.
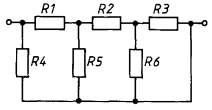
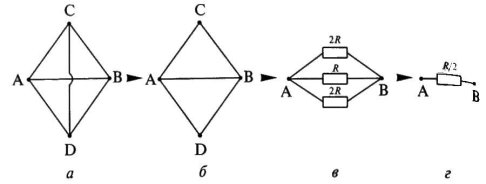
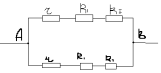
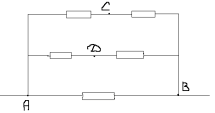
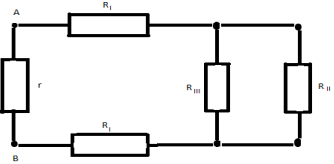
Задача 1.
Найти общее сопротивление цепи.
R
1
=
R
2
= 4 Ом,
R
3
=
R
4
=
R
5
=
R
6
= 8 Ом.
Решение
: В этой задаче часто неправильно определяют, какие сопротивления включены последовательно, а какие параллельно. Эквивалентная схема представлена на рисунке. Расчет по формулам дает ответ 4 Ом.
Ответ
: 4 Ом.
Для отработки метода можно использовать следующие задачи.
– Задачи 6,11–12 с разобранными решениями, а также 10.13–10.14, 10.21–10.28 для самостоятельного решения из главы 10 [1];
– 2.22–2.24 из [2];
– 19.2–19.6 из [3].
Использование правил Кирхгофа.
Правила Кирхгофа позволяют упростить расчеты параметров разветвленных электрических цепей. Этих правил два.
Первое правило Кирхгофа
: алгебраическая сумма токов, сходящихся в узле, равна нулю.
.
Второе правило Кирхгофа
: для любого замкнутого контура разветвленной электрической цепи алгебраическая сумма напряжений на сопротивлениях равна алгебраической сумме ЭДС, действующих в этом контуре.
Первое правило Кирхгофа является следствием закона сохранения заряда, второе — следствием закона Ома для неоднородного участка цепи.
Правила Кирхгофа в каждом конкретном случае позволяют написать полную систему алгебраических уравнений, из которых могут быть найдены неизвестные токи и напряжения. При расчете разветвленной цепи данным методом следует применять следующий порядок:
- произвольно выбрать направления токов во всех участках разветвленной цепи, отметив их стрелками на чертеже;
- при составлении уравнений для узлов токи считать положительными, если они втекают к узлу, и отрицательными, если они вытекают от узла;
- следует помнить, что число независимых уравнений, составленных по первому правилу Кирхгофа, всегда на одно меньше числа узлов, имеющихся в данной цепи;
- выбрать направление обхода контуров цепи;
- написать уравнения, соответствующие второму правилу Кирхгофа, соблюдая правило знаков: токи, совпадающие с направлением обхода, записывать со знаками «+», обратные направлению обхода − со знаками «−». ЭДС считать положительными, если они повышают потенциал в направлении обхода (при обходе по контуру сначала встречается отрицательный полюс источника, затем положительный);
- следует помнить, что число независимых уравнений, составленных по второму правилу Кирхгофа, равно наименьшему числу разрывов, которые следует сделать в цепи, чтобы нарушить все контуры. Если удается изобразить схему на плоскости без пересечений, то это число равно числу областей, ограниченных проводниками (числу «дырок» в графе схемы);
- если в полученном ответе какой-либо ток будет иметь отрицательный знак, то это указывает на ошибочность первоначального выбора направления данного тока.
Для отработки метода можно использовать, например, задачи 4.4.29–4.4.32 из [5].
Важнейшим примером задачи на применение правил Кирхгофа является задача о согласованном мосте Уитстона.
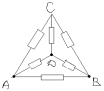
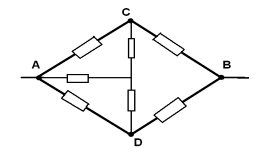
Задача 2.
Определить, при каких условиях в мостовой схеме через перемычку моста не течет ток.
Решение
: Схема моста представлена на рисунке, в качестве перемычки выступает гальванометр G. Если мостик подключить к источнику току, то мы получим разветвленную электрическую цепь, содержащую 4 узла и 3 дырки. Значит, для расчета токов и напряжений можно составить систему 6 независимых уравнений: 3 уравнения для узлов и три уравнения для контуров. Мы ограничимся выводом условия, при котором ток через гальванометр G идти не будет. Такой мостик называется
согласованным
. В этом случае токи через сопротивления
R
1
и
R
3
будут одинаковы. На схеме эти токи обозначены
I
1
. Одинаковыми будут токи и через сопротивления
R
2
и
R
4
. На схеме токи через
R
2
и
R
4
обозначены
I
2
.
Из второго правила Кирхгофа получаем:
Преобразовав систему, получим искомое условие:
. Это соотношение очень полезно для решения задач. Из него, в частности, следует, что мост, собранный из одинаковых сопротивлений, всегда будет согласованным.
Ответ:
.
Если бы вместо гальванометра в схеме было бы сопротивление
R
, то удаление этого сопротивления не привело бы к изменению токов и потенциалов в цепи. Поэтому в тех частях электрических схем, где будут согласованные мосты, перемычку можно будет удалять.
Пример с мостом Уитстона вплотную подвёл нас к следующему методу расчёта сопротивления разветвлённой электрической цепи — к методу удаления сопротивления.
Метод удаления сопротивления.
Идея этого метода состоит в том, чтобы исключить участок цепи, через который не течет ток. Полученная схема будет эквивалентна исходной.
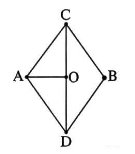
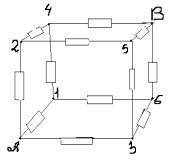
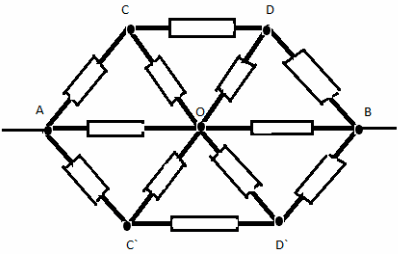
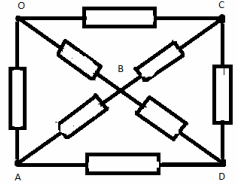
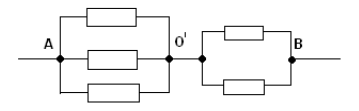
Задача 3.
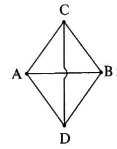
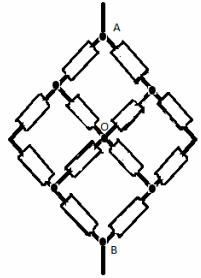
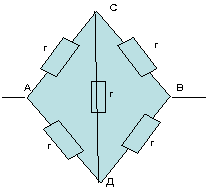
Найти сопротивление участка цепи между точками А и В, изображенного на рисунке.
Решение:
Узлы С и D симметричны относительно прямой АВ. Если повернуть схему на 180° вокруг прямой АВ, то схема на изменяется. Можно представить себе такую ситуацию: независимый наблюдатель следит за ходом измерений для данной схемы. Его попросили выйти из лаборатории. После этого отсоединили источник тока, несколько раз повернули схему вокруг АВ, затем подсоединили источник и пригласили наблюдателя. Из-за симметрии никакими экспериментами он не сможет определить, сколько раз повернули схему и где теперь находится точка С. Значит, между симметричными точками C и D ток течь не может — иначе бы наблюдатель измерил его направление и определил местонахождение точки C. Следовательно, перемычку CD можно удалить.
Удаление сопротивления CD можно обосновать и с использованием моста Уитстона. Заметим, что часть цепи A-C-B-D-A представляет из себя согласованный мост с перемычкой CD, которую, как мы ранее доказали, можно убрать.
После исключения участка CD получим эквивалентную цепь, сопротивление которой равно
R
/2.
Для отработки метода удаления сопротивления можно использовать следующие задачи:
– Каркасный тетраэдр: задача 8 из главы 10 [1], 19.15(3) из [3].
– N-полюсник: 19.18 из [3].
Метод эквипотенциальных узлов
. Эквипотенциальными называются узлы с равными потенциалами. Если в цепи, содержащей сопротивления, имеются эквипотенциальные узлы, то их можно рассматривать как один узел, проводя операцию склейки узлов.Поэтому данный метод еще называют
методом склейки узлов
.
Почему операция сведения в один узел правомочна? В электрических схемах соединительные провода, не имеющие сопротивления (их изображают на схемах тонкой линией), можно удлинять или укорачивать. Общее сопротивление цепи при этом не изменяется. Если узлы соединены накоротко (соединительный провод имеет сопротивление равное нулю), то соединительный провод можно укорачивать до тех пор, пока узлы не «склеятся», образуя один узел. Если узлы имеют одинаковые потенциалы и не соединены проводом, то электрические условия в этих точках не изменяются (а значит и сопротивление всей цепи) при соединении их проводником, не имеющим сопротивления. После чего можно провести операцию склейки.
Но есть ещё один случай, когда эквипотенциальные узлы соединены проводником с не равным нулю сопротивлением. Если при подключении цепи к источнику тока, по этому проводнику не идёт ток, то по закону Ома для однородного участка цепи разность потенциалов на концах этого проводника равна нулю. А, значит, узлы на концах проводника являются эквипотенциальными. В этом случае проводник с сопротивлением можно заменить на соединительный провод без сопротивления, после чего узлы также склеиваются.
Как найти эквипотенциальные точки в разветвленной электрической цепи? Общих правил нет. Нахождению эквипотенциальных точек часто помогает симметрия включения участков цепи. При этом граф схемы должен иметь ось симметрии или плоскость симметрии, проходящую через точки подключения. Можно мысленно повернуть или трансформировать граф таким образом, чтобы «кандидаты» в эквипотенциальные узлы поменялись местами. Если после обмена наименований точек получается исходная схема, значит, выбранные узлы эквипотенциальны.
Операция склейки приводит к уменьшению количества узлов. После этой операции схема обычно упрощается и к ней можно применить метод эквивалентных преобразований.
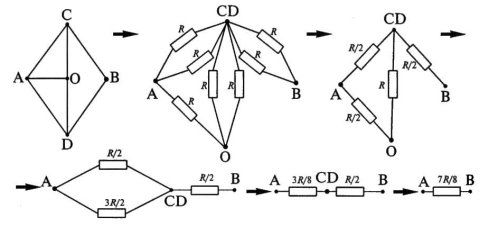
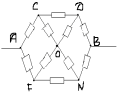
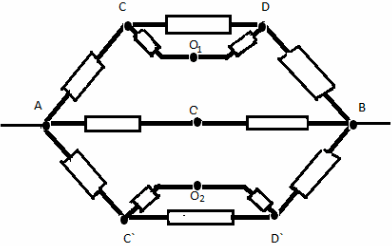
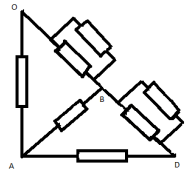
Задача 4.
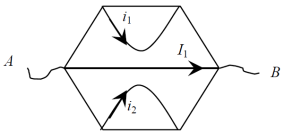
Найти сопротивление участка цепи между точками А и В. Считать сопротивление каждого проводника равным
R.
Решение
:
Докажем, что точки С и D эквипотенциальны. Точки С и D симметричны относительно прямой, проходящей через точки А и В. Если повернуть четырёхугольник вокруг прямой АВ на 180°, точка С перейдёт в точку D и наоборот. Если после поворота на 180° заменить наименование точек С на D, а D на С, мы получим исходную схему. Следовательно, потенциалы ϕ
С
и ϕ
D
равны.
Соединив точки С и D в один узел, получим эквивалентную схему, которую можно разложить на элементы последовательного и параллельного соединений. Сопротивление между точками А и В рассчитываем, используя преобразования схемы.
Ответ
:
R
АВ
=7
R
/8.
Метод эквипотенциальных узлов помогает решать задачи, которые предлагаются на некоторых олимпиадах. К таким задачам, в частности, относятся следующие.
– Каркасный куб: задача 7 и задачи 10.15–10.16 из главы 10 [1], 2.28 из [2], 19.15(5) из [3];
– Каркасный многоугольник: 2.27а из [2];
– Склейка узлов, к которым подсоединен идеальный амперметр: 19.20–19.21 из [3].
Метод разрезания узлов
.Чуть более сложный метод, который заключается в замене одного узла несколькими эквипотенциальными. Главное условие — чтобы при разрезании не нарушилось распределение токов в цепи.
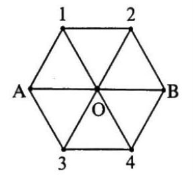
Задача 5.
Определить сопротивление участка цепи между точками А и В. Сопротивления отдельных участков одинаковы и равны
R
.
Решение
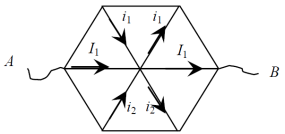
: Здесь нет ни одной пары проводников, соединенных между собой последовательно или параллельно. Поэтому необходимо обратить внимание на возможную симметрию цепи. Для применения метода разрезания узлов сначала надо провести анализ распределения токов в цепи.
Из симметрии схемы относительно прямой АВ следует, что токи в проводниках А-1 и А-3 будут равны между собой. А значит, в узлах 1 и 3 токи делятся в одинаковых пропорциях. Поэтому токи между узлами 1-О и 3-О также будут одинаковыми друг другу. Токи
I
AO
=
I
OB
=
I
1
,
I
1O
=
I
O2
=
i
1
,
I
3O
=
I
O4
=
i
2
.
Следовательно, узел O можно разрезать так, чтобы не нарушалось протекание токов
I
1
,
i
1
и
i
2
. После преобразований получаем окончательный ответ 4
R
/5.
Для отработки метода можно использовать следующие задачи: задачи 9 и 10.17 из главы 10 [1], 2.27в из [2], 19.15(1,2,4) и 19.16 из [3].
Метод замены «треугольника» на «звезду»
. Данный метод позволяет быстро рассчитать сопротивления участков цепи в том случае, когда не удается установить симметричного распределения токов. Метод замечательно изложен в статье А. Р. Зильбермана [6].
В основе этого метода лежит задача 19.13 из [3], разобрать которую мы предлагаем читателям самостоятельно. Выпишем только полученный результат.
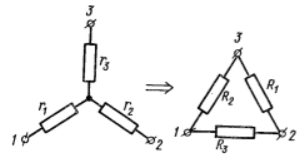
Если в схеме к некоторым узлам подключены сопротивления
R
1
,
R
2
,
R
3
в виде «треугольника», то его можно заменить на элемент «звезда» с сопротивлениями
r
1
,
r
2
,
r
3
, которые рассчитываются по формулам
Результат легко запомнить, если заметить, что в знаменателе всегда стоит сумма сопротивлений «треугольника», в числителе — произведение сопротивлений с дополняющими номерами, причем индексы у
r
1
,
R
2
,
R
3
в первой формуле можно менять по циклу 1–2–3–1 и таким образом получить остальные две формулы.
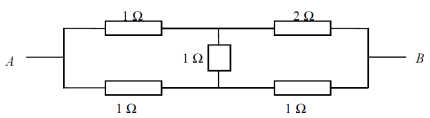
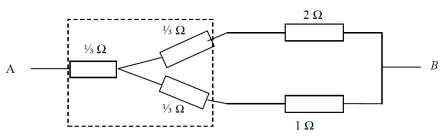
Задача 6.
В схеме, изображенной на рисунке, определить сопротивление между точками A и B.
Решение:
Данный мост не является согласованным, что легко проверить. Симметрия в схеме отсутствует. Однако левую половину моста (с сопротивлениями по 1 Ом) можно рассматривать как «треугольник». После замены на «звезду» получается схема с последовательным и параллельным соединениями, сопротивление которой предлагаем читателям подсчитать самостоятельно.
Ответ:
13/11 Ом.
Замена «треугольника» на «звезду» уменьшает на один количество контуров в схеме и увеличивает на один количество узлов. Если мы, напротив, хотим уменьшить число узлов в схеме, то можно провести обратную замену — «звезды» на «треугольник» по формулам [6]:
При удалении большего числа узлов можно использовать обобщенный метод, изложенный в статье Е. Соколова [7].
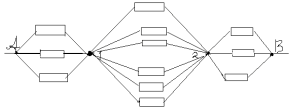
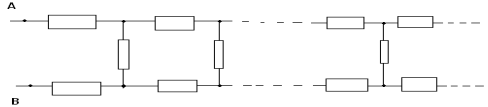
Расчет бесконечных цепей.
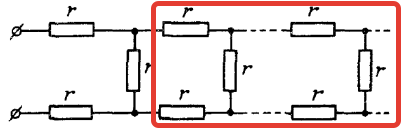
В олимпиадных задачах иногда встречаются электрические цепи, в которых повторяется одно и то же звено цепи до бесконечности. С практической точки зрения это означает, что число повторяющихся звеньев
N
очень велико и добавление очередного звена не приводит к сколько-нибудь значительному изменению общего сопротивления. С математической точки зрения
сопротивлением бесконечной цепиR
называется предельное значение сопротивления при
N
→ ∞.
Идея решения заключается в том, что при удалении первого звена сопротивление оставшейся части также будет равно
R
(ведь число элементов останется бесконечным. Значит, бесконечную цепь (без первого звена) можно заменить эквивалентным сопротивлением
R
, причем общее сопротивление также равно
R
. После этого составляется уравнение и находится его решение относительно
R
. Рисунок иллюстрирует сказанное применительно к задаче 19.19 из [3], которую мы предлагаем сделать читателям самостоятельно, как и задачу 2.26 из [2].
Повторяющиеся звенья цепи могут быть не в точности одинаковы, а быть подобны друг другу (т. е. все сопротивления в звеньях отличается в какое-то фиксированное количество раз). Такая схема, в частности, может быть реализована в виде
фрактала
, как это было в задаче № 6 для 8–11 кл. в Турнире Ломоносова 2015 г.
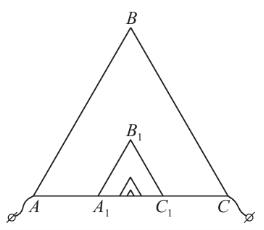
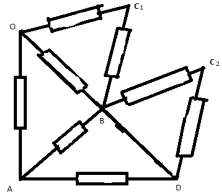
Задача 7.
Из однородной проволоки изготовлен равносторонний треугольник
ABC
, сторона которого равна
a
. К точкам
A
1
и
C
1
, делящим сторону
AC
на три равные части, прикреплены еще два куска проволоки — вместе с отрезком
A
1
и
C
1
они образуют равносторонний треугольник со стороной
a
/3. Внутри этого треугольника сделан еще один (в три раза меньший) и т. д. Найдите сопротивление всей конструкции, если число треугольников очень велико. Сопротивление куска проволоки длины
a
равно
r
.
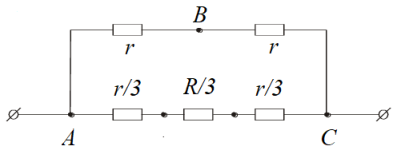
Решение:
Обозначим искомое сопротивление за
R
.
Если разорвать куски проволоки
AA
1
и
C
1
C
, то оставшийся треугольник, как подобный исходному с коэффициентом 1/3, будет иметь сопротивление
R
/3, поскольку все сопротивления в нем (по сравнению с исходным) меньше в 3 раза. Эквивалентная схема показана на рисунке.
Вычисляя ее сопротивление, получим уравнение:
решения которого
. Один из корней отрицателен, другой положителен. Он и является ответом в задаче.
Ответ:
.
Напоследок предлагаем читателям еще одну задачу 3.52 из [4] с бесконечными цепями, содержащими подобные друг другу звенья.
Принцип суперпозиции
. Уравнения закона Ома и правил Кирхгофа линейны относительно токов. Это значит, что если в цепи есть несколько источников тока, то можно рассчитать, какой ток создаст в данном проводнике каждый источник в отдельности. А реальный ток через выбранный проводник будет равен сумме токов, создаваемых каждым источником в отдельности.
Задача 8
(задача 10 из главы 10 [1])
.
В каждое ребро бесконечной сетки с квадратными ячейками включено сопротивление
r =
20 Ом. Чему равно сопротивление сетки при подключении её соседними узлами?
Решение:
К узлам А и В подключается внешний источник тока. Он создаёт ток
I
, входящий через узел А, и такой же ток, выходящий через узел В. Будем измерять напряжение
U
между точками А и В идеальным вольтметром и ток
I
в измерительной цепи, содержащей источник тока и идеальный вольтметр. Во время измерений напряжение и ток в очень далёких от А и В узлах равны нулю. Поэтому, если соединить далёкие точки хорошо проводящим проводом, то ничего не изменится. Назовём этот провод «бесконечность». Его можно представить как провод, идущий по окружности очень большого радиуса.
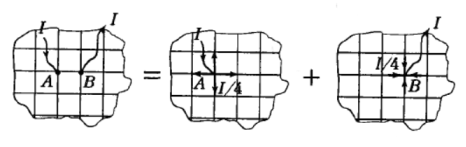
Теперь возьмём два одинаковых источника тока. Первый подключим к точке А и «бесконечности» так, чтобы ток
I
, шёл по сетке от точки А к «бесконечности». При этом распределение тока по разным направлениям (по четырём проводникам, подключённым к узлу А) равномерно. Поэтому по каждому такому проводнику пойдёт ток
I
/4 от узла А.
Второй источник подключим к узлу В и «бесконечности» так, чтобы ток
I
, шёл по сетке от «бесконечности» к точки В (см. рис. 25 в). По каждому проводнику, подключённому к узлу В пойдёт ток
I
/4 в направлении к узлу В. В силу указанной выше линейности уравнений закона Ома на каждом участке бесконечной сетки ток в любом ребре сетки будет суммой токов этих двух источников. Причём, для каждого источника распределение тока симметрично относительно узла, к которому источник подключён.
От первого источника по ребру АВ течёт ток
I
/4 в направлении от А к В. Такой же ток в том же направлении протекает по ребру АВ от второго источника. Значит, по ребру АВ течет ток
I
/2.
Тогда напряжение, измеренное на этом ребре, будет равно
U =
(
I
/2)
r
. Сопротивление сетки
R
=
U/I
=
r
/2.
Ответ:
10 Ом.
Для отработки метода предлагаем сформулировать и решить две аналогичные задачи с бесконечной сеткой из шестиугольников (должен получиться ответ 2
r
/3) и треугольников (
r
/3), а также разобрать еще более сложную задачу 3.53 с треугольной сеткой из [4].
Работа выполнена на базе ГБОУ Школа № 1557 имени Петра Леонидовича Капицы в рамках проекта «Курчатовский проект в московской школе». Авторы благодарят администрацию ГБОУ Школа № 1557 за помощь и поддержку.
Литература:
1. Черноуцан А. И. Физика. Задачи с ответами и решениями: учебное пособие. 9-е изд. М.: КДУ, 2017. 352 с.
2. Сборник задач по физике с решениями и ответами. Часть III. Электричество и оптика / Под ред. А. Н. Долгова. М.: МИФИ, 2001. 188 с.
3. Гольдфарб Н. И. Сборник вопросов и задач по физике. 9-е изд. М.: Дрофа, 2005. 351 с.
4. Варламов С. Д. и др. Задачи Московских городских олимпиад по физике. 1986–2005 / Под ред. М. В. Семенова, А. А. Якуты. 2-е изд., исправл. М.: МЦНМО, 2007. 624 с.
5. Павленко Ю. Г. Физика. Избранные задачи. Кн. I. М.: Экзамен, 2008. 544 c.
6. Зильберман А. Р. Преобразование электрических цепей // Квант, 1971. № 3. С. 10–14.
7. Соколов Е. О простом и сложном // Квант, 2002. № 2. С. 7–12.

4 инструмента крутого Кирхгофщика
Внимание! Чтобы увидеть ответы на вопросы, кликните по ним. Кликать надо по тексту, а не по пустому месту. Чтобы сменить картинку, кликните по кнопке. Если ответ на вопрос вам не ясен, советую хорошо подумать, прежде чем смотреть ответ.
Инструмент 1. Вычисление сопротивления цепи из нескольких последовательно соединённых сопротивлений
Просто, как ….. Сложил все эти сопротивления и получил сопротивление цепи.
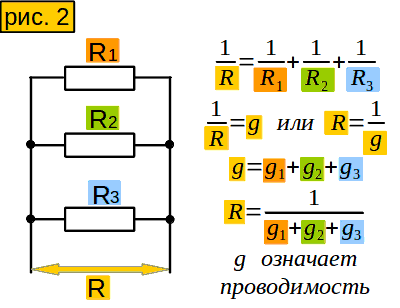
Инструмент 2. Вычисление сопротивления участка из нескольких параллельно соединённых сопротивлений
Рассмотрим участок с двумя параллельными одинаковыми сопротивлениями. Сопротивление его в два раза меньше, чем каждого сопротивления. Если сопротивлений три, сопротивление участка будет в три раза меньше.
Какую тут можно провести аналогию?
Несколько одинаковых дырок. Через них протечёт воды в столько раз больше, чем через одну дырку, сколько дырок имеется.
А как быть, если сопротивления не одинаковые? Есть такое понятие — проводимость. Оно означает величину, обратную сопротивлению. (рисунок 2)
Так если сопротивление больше, то проводимость что?
меньше
Чтобы вычислить проводимость нашего участка, надо сложить проводимости сопротивлений. Потом можно легко найти сопротивление участка.
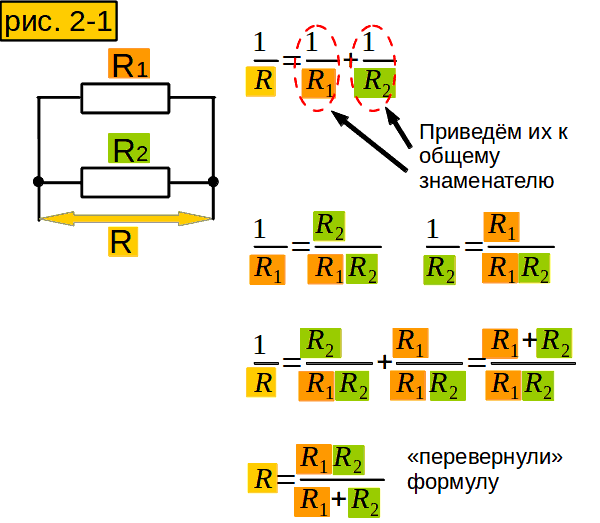
А нельзя ли вычислить сопротивление участка, не преобразуя сопротивления в проводимости, а потом обратно? Можно. Пусть у нас участок из двух параллельно соединённых сопротивлений (рис. 2-1). Проводимость его равна сумме проводимостей сопротивлений (1 строчка). Приведём проводимости сопротивлений к общему знаменателю (2 строчка). Сложим их и получим суммарную проводимость (3 строчка). «Переворачиваем» формулу (4 строчка) и получаем формулу для участка из двух параллельно соединённых сопротивлений. А если сопротивлений не два, а больше?
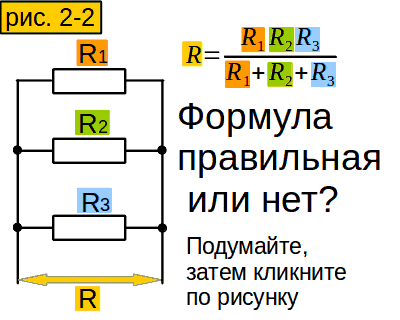

Сформулируйте своими словами формулу сопротивления участка из нескольких параллельных сопротивлений, чтобы лучше её запомнить.
Надо умножить все сопротивления, и разделить на сумму произведений этих сопротивлений, но в каждом этом произведнии одного сопротивления не хватает. Вы, может быть, и получше сформулируете.
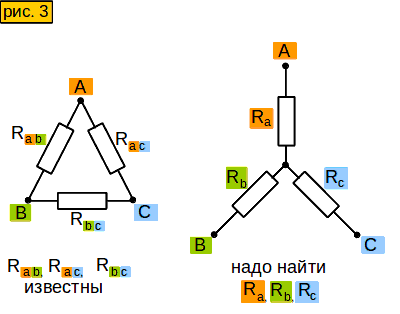
Инструмент 3. Преобразование «треугольника» в «звезду»
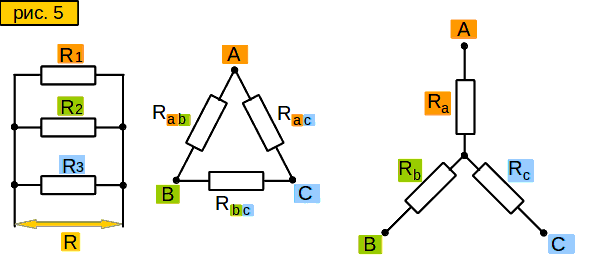
Пусть у нас в схеме есть вот такой участок цепи — «треугольник» (рис. 3, слева). Нам надо заменить его участком вот такого вида — «звездой» (рис. 3, справа), но чтобы сопротивления между сторонами «звезды» были такими же, как между соответствующими лучами «треугольника». Зачем это нужно? Позже узнаете.
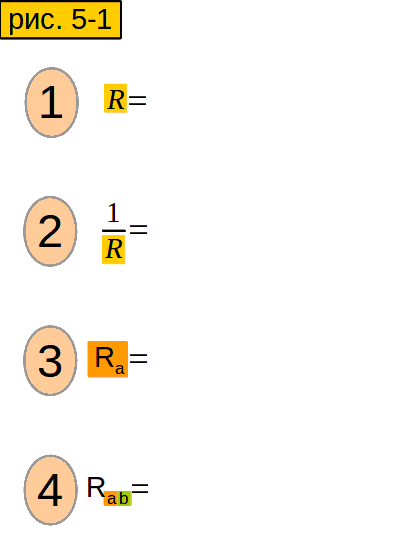
Смотрим на «звезду» на рис. 3. Допустим, мы знаем сопротивления между точками
A и B, то есть (Ra+Rb);
A и C, то есть (Ra+Rc);
B и C, то есть (Rb+Rc).
Чему будут равны сопротивления Ra, Rb, Rc ?
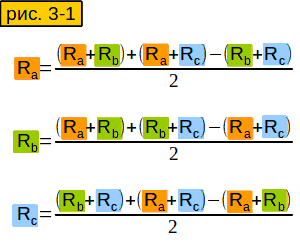
Зная все сопротивления между концами лучей «звезды», мы можем вычислить сопротивление каждого отдельного луча.
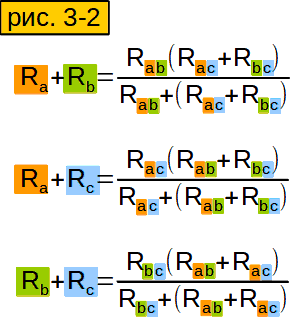
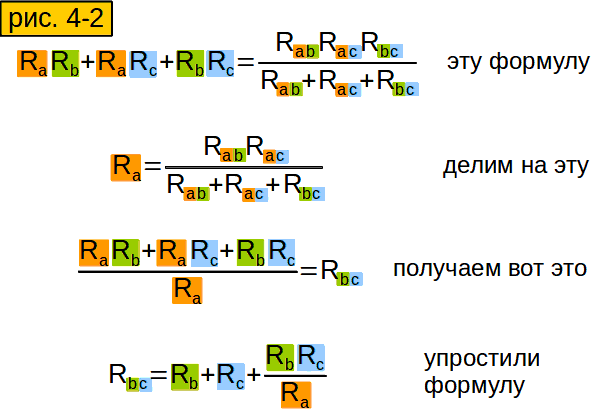
Теперь будем вычислять сопротивления между точками A, B, и C (звезды) через сопротивления треугольника, которые нам известны (рис. 3-2). Для начала вычислим сопротивление между точками A и B звезды (рис. 3-2 верхняя строчка). В нашем треугольнике мы имеем два параллельно включённых сопротивления — Rab и (Rac+Rbc). Вычислять их общее сопротивление мы умеем (ответы на вопросы 3 и 4). Вычисляем сопротивления между точками A и C, B и C (2 и 3 строчки). Обратите внимание, что во всех формулах знаменатель одинаковый.
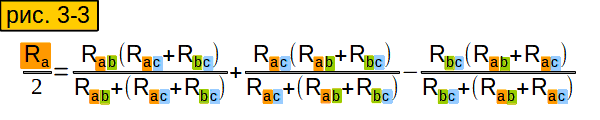
Теперь можно вычислить сопротивление отдельного луча (рис. 3-3). Формула получилась очень громоздкая, но мы её хорошенько подсократим.
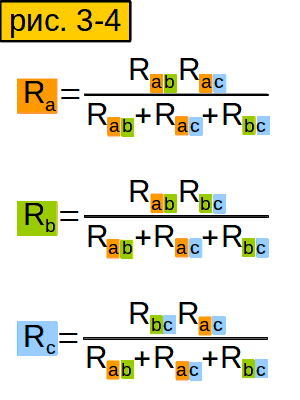
И получим вот такую стройную и изящную формулу (рис. 3-4, верхняя строчка). Аналогично вычисляем сопротивления других лучей звезды.
Сформулируйте своими словами формулу из рисунка 3-4, чтобы лучше её запомнить.
Чтобы найти сопротивление луча «звезды», надо умножить сопротивления сторон «треугольника», которые «прилегают» («имеют ту же букву»), и разделить на сумму сопротивлений всех сторон «треугольника».
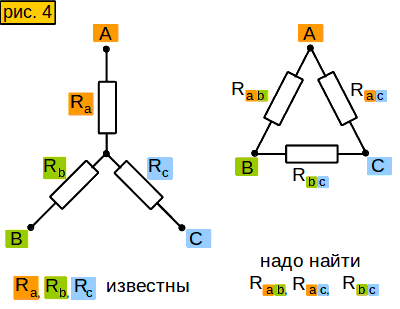
Инструмент 4. Преобразование «звезды» в «треугольник»
Иногда полезно делать обратное преобразование — «звезды» в «треугольник». Нельзя ли вычислить сопротивление стороны «треугольника» через сопротивления эквивалентной «звезды», используя формулы, которые мы уже вывели? Можно. Смотрим рисунок 3-4. Проделаем с формулами этого рисунка следующий трюк: попарно их перемножим и результаты сложим (смотрим рис. 4-1).
Затем результат разделим на верхнюю формулу рисунка 3-4. Получится у нас вот что: рисунок 4-2, третья сверху формула. Маленько её подсократим и получим нижнюю формулу.
Как раз то, что нам надо!
Сопротивления других сторон «треугольника» выводятся аналогично (рисунок 4-3).
Сформулируйте своими словами формулу из рисунка 4-3, чтобы лучше её запомнить.
Чтобы найти сопротивление стороны «треугольника», надо сложить сопротивления соответствующих сторон «звезды» (у которых «те же буквы»), и ещё прибавить произведение тех же сторон «звезды», делёное на оставшуюся сторону.
Зубрилка
об ошибках сообщайте по адресу obuchmat@mail.ru
Продолжение следует
На домашнюю страницу

33
Бондаров Михаил Николаевич
Учитель физики лицея №1501 и ГОУ ЦО «Технологии обучения» г. Москвы.
Расч¸т сопротивления электрической цепи
В статье на примерах решения конкретных задач показано применение различных способов расч¸та сопротивления электриче- ской цепи. Рассмотрены некоторые методы преобразования электрических схем к эквивалентным схемам.
Введение
Задачи на расч¸т сопротивления электрической цепи можно встретить среди экзаменационных и олимпиадных задач, а также в заданиях ЕГЭ. В данной статье мы рас-
смотрим некоторые при¸мы, позволяющие достаточно эффективно определять сопротивления различных цепей. Напомним основные закономерности.
1. Последовательное и параллельное соединения проводников
В электрических цепях, с которыми можно встретиться на практике, проводники соединяются различными способами. Наиболее простые соединения известны как последовательное и параллельное соединения.
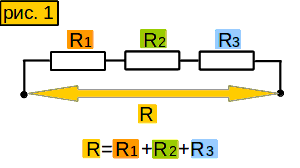
При последовательном соединении один проводник следует за другим так, что конец одного служит началом другого (рис. 1). Обратите внимание, что при этом между проводниками нет разветвлений проводов.
Из курса физики 8 класса известно, что общее сопротивление R последовательно соедин¸нных про-
|
à |
á |
â |
||||||||||||||
|
Ðèñ. 1 |
||||||||||||||||
|
водников сопротивлениями R1 è R2 |
||||||||||||||||
|
определяется по формуле: |
||||||||||||||||
|
R |
R1 R2. |
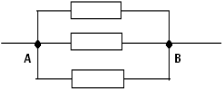
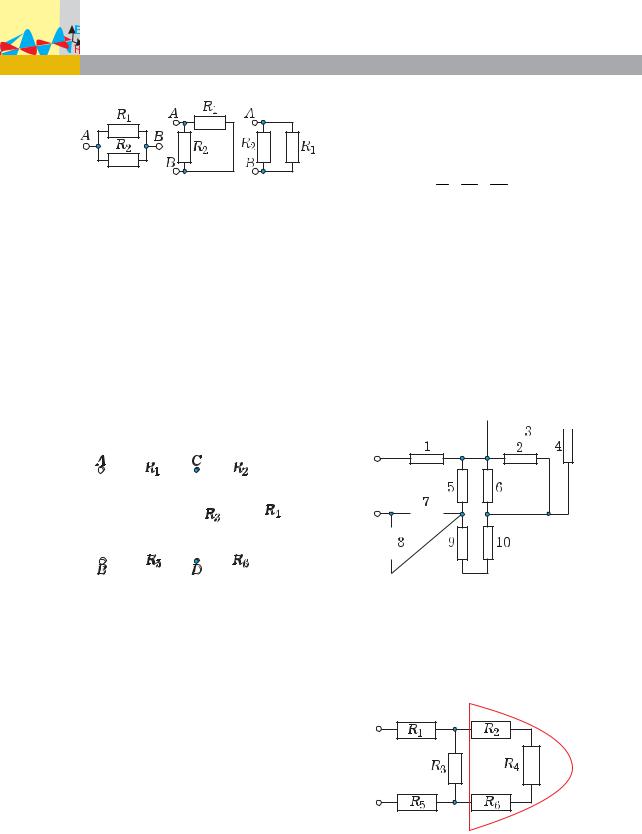
При параллельном соединении проводники подключаются к одной и той же паре точек А и В (рис. 2).
34 Физика
|
Общее сопротивление R парал- |
||||||
|
лельно |
соедин¸нных |
проводников |
||||
|
сопротивлениями R1 è R2 опреде- |
||||||
|
ляется из соотношения: |
||||||
|
à |
á |
â |
1 |
1 |
1 . |
|
|
Ðèñ. 2 |
R |
R1 |
R2 |
|||
2. Распознавание типов соединений
|
Для уверенного |
решения |
задач |
соединены последовательно, не за- |
||||||||||
|
на определение общего сопротивле- |
мечая того, что узлы C и D между |
||||||||||||
|
íèÿ |
электрической |
öåïè |
важно |
ними свидетельствуют о разветвле- |
|||||||||
|
уметь в сложных схемах распозна- |
нии проводов. |
||||||||||||
|
вать проводники, соедин¸нные по- |
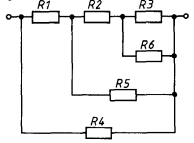
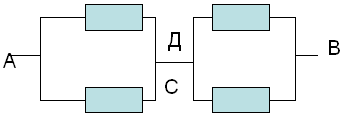
Пример 2. |
Рассмотрим |
åù¸ |
||||||||||
|
следовательно или параллельно. |
одну схему (рис. 4). Попробуйте |
||||||||||||
|
Рассмотрим конкретные примеры. |
найти в ней последовательно и |
||||||||||||
|
Пример 1. В схеме, изображ¸н- |
параллельно |
соедин¸нные |
ïðî- |
||||||||||
|
íîé |
на рис. 3, только проводники |
водники (свой ответ проверьте по |
|||||||||||
|
R2, |
R4 è R6 соединены последо- |
ðèñ. 28). |
|||||||||||
|
вательно. Иногда |
ошибочно |
ñ÷è- |
|||||||||||
|
тают, что все проводники, кроме R3, |
|
Ðèñ. 3 |
Ðèñ. 4 |
3. Смешанное соединение проводников
Приступим теперь к расч¸ту сопротивления при смешанном соединении проводников. Начн¸м с простых цепей.
Задача 1. Определите общее сопротивление цепи, схема которой изображена на рис. 3, если все проводники имеют сопротивление по 4 Ом.
Решение. Учитывая анализ, провед¸нный в примере 1, выделим три последовательно соедин¸нных проводника R2, R4 è R6 (ðèñ. 5).
На эквивалентной схеме (рис. 6) их можно заменить одним проводником сопротивлением
R246 R2 R4 R6 12 Îì.
Теперь ясно видно, что проводник сопротивлением R246 соедин¸н
Ðèñ. 5
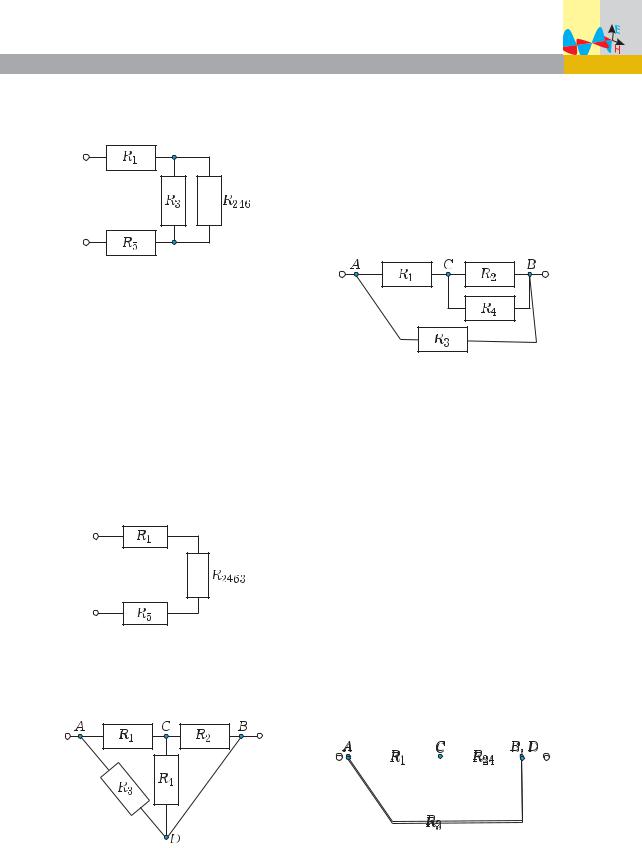
параллельно с проводником сопротивлением R3 .
Ðèñ. 6
Определим их общее сопротивление R2463 :
|
1 |
1 |
1 |
|||||||
|
R2463 |
R3 |
R246 |
|||||||
|
R2463 |
R246 |
R3 |
3 Ом. |
||||||
|
R246 |
R3 |
||||||||
На эквивалентной схеме (рис. 7) видно, что исчезли узлы между
проводниками R1, R2463 è R5 , поэтому эти проводники оказались соедин¸нными последовательно, и их общее сопротивление
R R1 R2463 R5 11 Îì.
Ðèñ. 7
Ответ: 11 Ом.
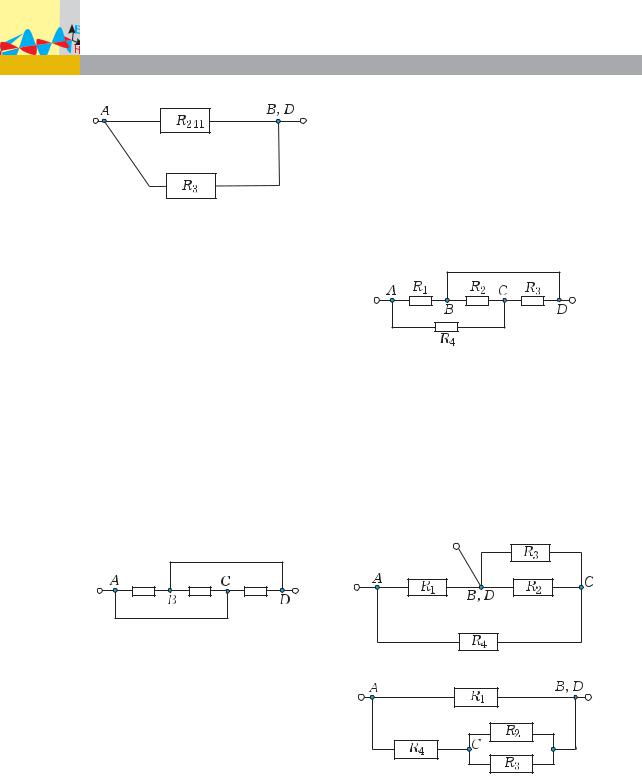
Задача 2. В цепи, схема которой изображена на рис. 8, все проводни-
Физика 35
ки имеют сопротивление по 10 Ом. Чему равно общее сопротивление цепи между точками А и В?
Решение. Обратите внимание, что точки В и D соединены проводом с нулевым сопротивлением, следовательно, их можно объединить в один узел. Тогда эквивалентная схема будет иметь вид, изобра- ж¸нный на рис. 9.
Ðèñ. 9
Теперь общее сопротивление цепи легко находится в три этапа.
1) Сначала вычисляем сопротивление параллельно соедин¸нных проводников R2 è R4 :
|
R24 |
R2 |
R4 |
5 |
Îì. |
|
|
R2 |
R4 |
||||
На преобразованной схеме вместо проводников R2 è R4 рисуем эквивалентный им проводник R24 (ðèñ. 10 a).
2) Затем определяем сопротивление последовательно соедин¸нных проводников R24 è R1:
R241 R24 R1 15 Îì.
На рис. 10 б показана новая эквивалентная схема.
3) Наконец, находим общее сопротивление цепи:
|
R |
R241 |
R3 |
6 |
Îì. |
|||||||
|
R241 |
R3 |
||||||||||
36 Физика
Ðèñ. 10 á
Ответ: 6 Ом.
Заметим, что преобразуя цепь к более простой эквивалентной, можно на схемах изгибать, удлинять или укорачивать провода, перемещать узлы вдоль проводов, поскольку провода, соединяющие элементы схемы, считаются идеальными, т. е. имеющими нулевое сопротивление.
Рассмотрим теперь, как может видоизмениться цепь, состоящая из тр¸х последовательно соедин¸нных проводников, если к ним добавить другие проводники. Сначала добавим два проводника с нулевым сопротивлением, соединив ими точку А с точ- кой С, а В – с D (рис. 11).
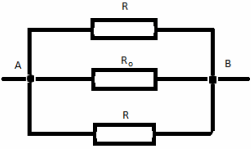
Задача 3. Найдите сопротивление между точками А и D цепи (рис. 11), если каждый проводник имеет сопротивление 3 Ом.
Ðèñ. 11
Решение. Так как точки А и С соединены проводом с нулевым сопротивлением, то их потенциалы равны, а значит, эти точки имеют одинаковый потенциал, и их можно собрать в один общий узел. Аналогично поступим с точками В и D. Таким образом, полу- чилось, что каждый проводник оказался подключенным к одним и тем же точкам, т. е. все три проводника соединены параллельно. Теперь уже легко найти общее сопротивление цепи, учи- тывая, что все проводники имеют одинаковое сопротивление:
|
1 |
1 |
1 |
1 |
3 |
R |
R1 |
1 |
Îì. |
||
|
R |
R1 |
R1 |
R1 |
R1 |
3 |
|||||
Ответ: 1 Ом.
Заменим теперь один из идеальных проводников реальным – с ненулевым сопротивлением.
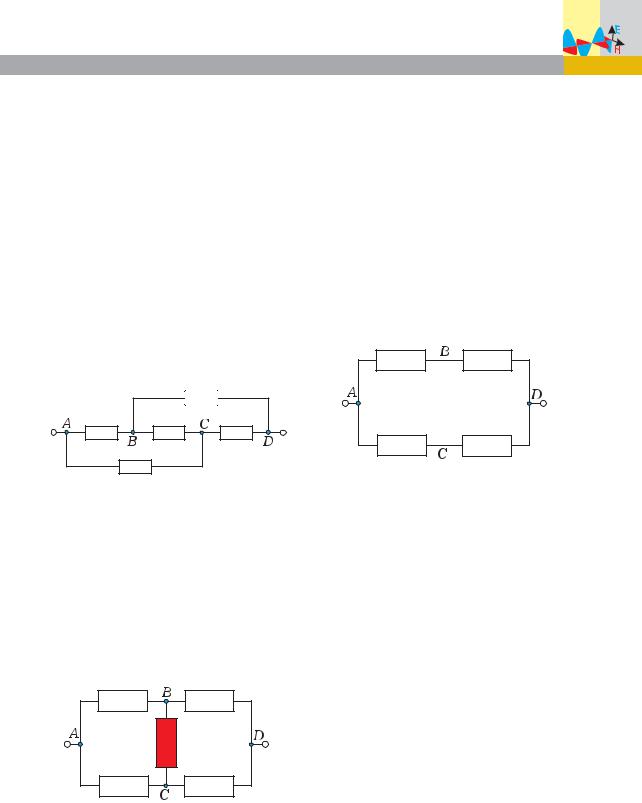
Задача 4. Определите сопротивление между точками А и D цепи (рис. 12), если каждый проводник имеет сопротивление 6 Ом.
Ðèñ. 12
Заметим, что точки В и D попрежнему соединены проводником с нулевым сопротивлением. Следовательно, они имеют одинаковый потенциал. Соединив их в один узел, получим эквивалентную схему (рис. 13 а). Если же затем «распрямить» е¸, то участки с параллельно и последовательно соедин¸н- ными проводниками станут хорошо видны (рис. 13 б).
Ðèñ. 13 à
Ðèñ. 13 á
После этого останется лишь произвести расч¸т сопротивления для эквивалентной схемы в три этапа:
Физика 37
|
1) |
1 |
1 |
1 |
3) |
1 |
1 |
1 |
||||||||||||||||
|
R23 |
|||||||||||||||||||||||
|
R2 |
R3 |
R R1 R234 |
|||||||||||||||||||||
|
R23 |
R2 |
R3 |
3 |
Îì; |
R |
R1 |
R234 |
3,6 |
Îì. |
||||||||||||||
|
R2 |
R3 |
R1 |
R234 |
||||||||||||||||||||
|
2) |
R234 |
R4 |
R23 |
9 Îì; |
Ответ: 3,6 Ом. |
4. Мостиковая схема
Заменив второй идеальный проводник в цепи, схема которой показана на рис. 11, реальным, получим новую цепь, схема которой изображена на рис. 14.
Задача 5. Определите сопротивление между точками А и D цепи, схема которой изображена на рис. 14, если сопротивление каждого проводника равно 2 Ом.
Ðèñ. 14
Решение. На этот раз все попытки обнаружить хотя бы одну пару последовательно или параллельно соедин¸нных проводников оказываются безуспешными. И вс¸ же попробуем немного видоизменить схему так, чтобы можно было увидеть в ней элементы симметрии. Немного потренировавшись, можно получить следующую схему – она носит название «мостиковая схема» (рис. 15).
Ðèñ. 15
Поскольку все проводники имеют одинаковое сопротивление, то по
ветвям ABD и ACD текут одинаковые токи, а через выделенную красным цветом перемычку ВС ток идти не будет. Поэтому перемычку можно безболезненно удалить из цепи, не изменив при этом общее сопротивление цепи (рис. 16).
Ðèñ. 16
Заметим кстати, что ток через перемычку не будет идти при любом е¸ сопротивлении, если для остальных проводников выполняется соотношение:
|
RAB |
RBD |
. |
(*) |
|
|
RAC |
RCD |
Теперь же ясно видно, что цепь состоит из двух параллельно соеди- н¸нных участков, в которых находится по два последовательно соеди- н¸нных проводника. Определим сна- чала сопротивление каждого из этих участков: RABD RAСD (2 2) Ом
4 Ом. Затем находим общее сопротивление цепи:
|
1 |
1 |
1 |
2 |
|||||
|
RABD |
RACD |
|||||||
|
R |
RABD |
|||||||
|
R |
RABD |
2 Ом. |
||||||
|
2 |
||||||||
Ответ: 2 Ом.
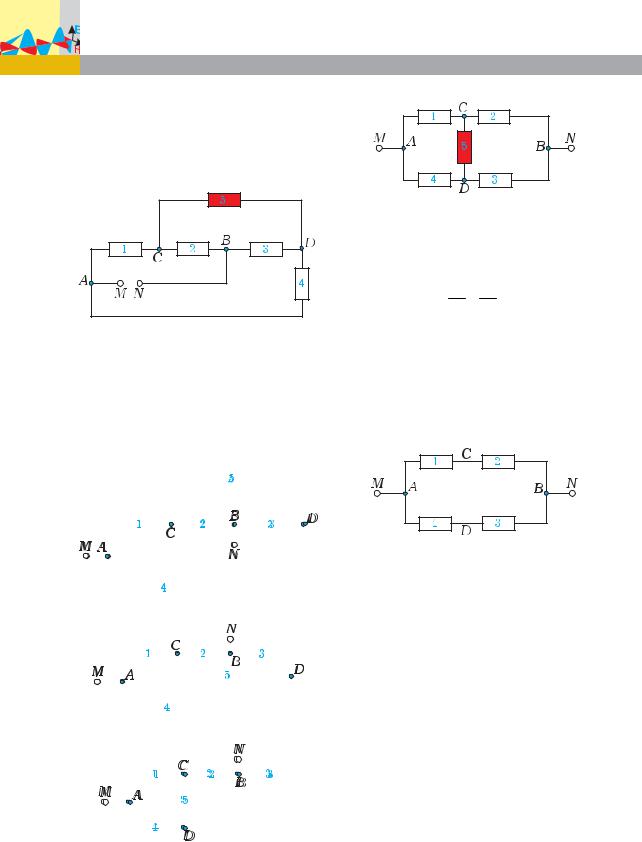
Задача 6. Каково сопротивление
38 Физика
между точками N и M цепи, схема которой показана на рис. 17, если сопротивления проводников
R1 1 Ом, R2 2 Ом, R3 4 Ом, R4 2 Ом, R5 5 Ом?
Решение. В данном случае не очевидно, что ток через выделенный красным цветом проводник 5 идти не будет. И вс¸ же, проделав несколько манипуляций с цепью, можно полу- чить мостиковую схему (этапы преобразований показаны на рис. 18 a–г).
ã
Ðèñ. 18
Обратим внимание, что по условию задачи
R1 R2 ,
R4 R3
то есть выполняется соотношение (*). Следовательно, потенциалы точек С и D одинаковы, через проводник 5 ток не ид¸т, и его можно удалить, не изменяя сопротивление цепи. После этого эквивалентная схема выглядит совсем просто (рис. 18 д).
|
Ðèñ. 18 ä |
||||||||||||||||||||||||||||||||||||||||||
|
Произвед¸м |
ðàñ÷¸ò |
сопротивле- |
||||||||||||||||||||||||||||||||||||||||
|
íèÿ öåïè: |
R2 |
3 |
||||||||||||||||||||||||||||||||||||||||
|
à |
R12 |
R1 |
Îì; |
|||||||||||||||||||||||||||||||||||||||
|
R43 |
R4 |
R3 |
6 Îì; |
|||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
R |
R12 |
R43 |
2 Îì. |
||||||||||||||||||||||||||||||||||||
|
R |
R12 |
R43 |
R12 |
R43 |
||||||||||||||||||||||||||||||||||||||
|
Ответ: 2 Ом. |
||||||||||||||||||||||||||||||||||||||||||
|
Заметим, что если все попытки |
||||||||||||||||||||||||||||||||||||||||||
|
распутать и упростить схему из пя- |
||||||||||||||||||||||||||||||||||||||||||
|
á |
||||||||||||||||||||||||||||||||||||||||||
|
ти проводников не приводят к успе- |
||||||||||||||||||||||||||||||||||||||||||
|
ху, вполне вероятно, что вы натолк- |
||||||||||||||||||||||||||||||||||||||||||
|
нулись на «мостиковую схему» (как, |
||||||||||||||||||||||||||||||||||||||||||
|
например, на рис. 17). |
||||||||||||||||||||||||||||||||||||||||||
|
При определении общего сопро- |
||||||||||||||||||||||||||||||||||||||||||
|
тивления в задачах 5 и 6 мы ис- |
||||||||||||||||||||||||||||||||||||||||||
|
пользовали симметрию схемы. По- |
||||||||||||||||||||||||||||||||||||||||||
|
знакомимся более подробно с при¸- |
||||||||||||||||||||||||||||||||||||||||||
|
â |
мами, позволяющими рассчитывать |
Физика 39
|
сопротивления подобных |
цепей. |
|
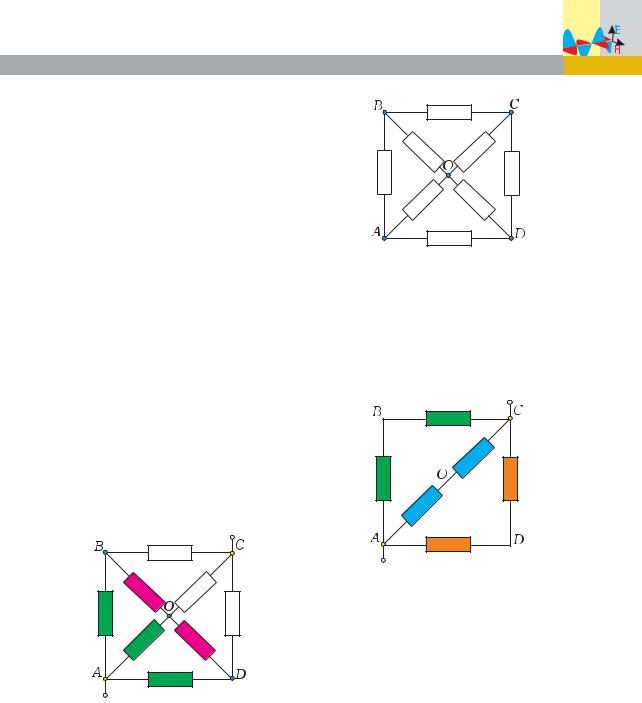
Для этого рассмотрим цепь, со- |
|
|
стоящую из одинаковых проводни- |
|
|
ков, включ¸нных в каждую из сто- |
|
|
рон квадрата. Кроме того, каждая |
|
|
из вершин соединена с центром |
|
|
квадрата такими же проводниками |
|
|
(ðèñ. 19). |
|
|
В зависимости от точек под- |
|
|
ключения цепи в ней проявляются |
|
|
различные виды симметрии. |
Ðèñ. 19 |
5. Метод исключения участков цепи
Задача 7. Определите сопротивление между точками А и С цепи (рис. 19), если каждый проводник имеет сопротивление 3 Ом.
Решение. Из симметрии схемы (рис. 20) следует, что по выделенным зел¸ным цветом проводникам будут идти одинаковые токи, следовательно, потенциалы точек В, О и D будут одинаковы. Тогда по проводникам, выделенным красным цветом, токи идти не будут, и их можно удалить из цепи, не изменив при этом е¸ общее сопротивление.
Ðèñ. 20
В результате схема упростится (рис. 21), выделенные одинаково проводники тр¸х ветвей окажутся соедин¸нными последовательно, а сами ветви соединены между собой параллельно.
Ðèñ. 21
Теперь уже дальнейший расч¸т несложен: сопротивление каждой ветви равно 6 Ом, а общее сопротивление цепи составляет 2 Ом.
Ответ: 2 Ом.
Заметим, что именно этот при¸м был использован при решении задач 5 и 6.
6. Метод разрезания узлов
Рассмотрим другое подключение цепи, схема которой показана на рис. 19.
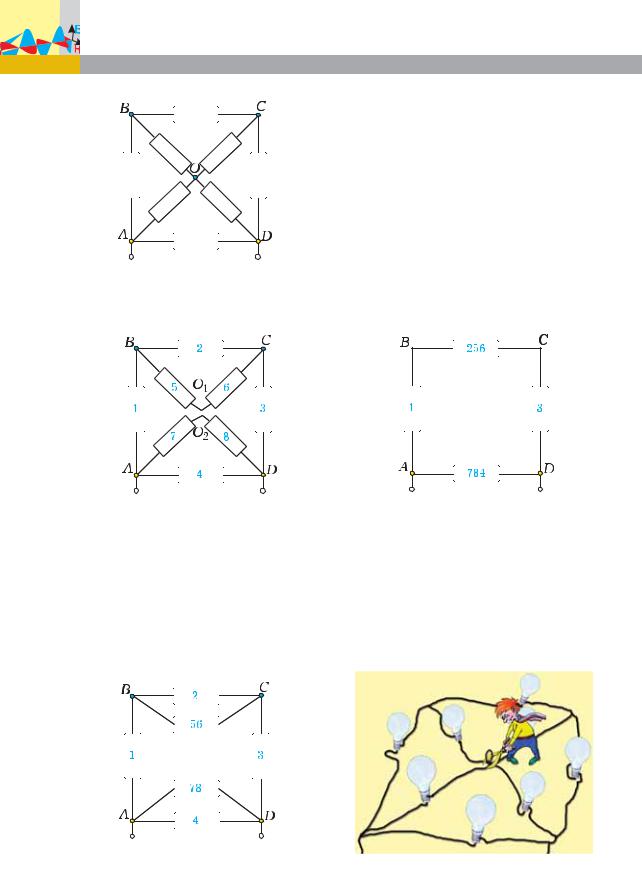
Задача 8. Найдите сопротивление между точками А и D цепи (рис. 22), если каждый проводник имеет сопротивление 6 Ом.
Решение. Используем теперь
метод разрезания узлов. Для этого узел О разделим на два, получив при этом точки O1 è O2 с одинаковыми потенциалами (равными среднему арифметическому между потенциалами узлов А и D). Пронуме-
40 Физика
Ðèñ. 22
руем также проводники для удобства описания (рис. 23).
Ðèñ. 23
После разрезания узла О проводники 5 и 6 оказались соедин¸н- ными последовательно так же, как и проводники 7 и 8. Заменив их проводниками с эквивалентными сопротивлениями
|
R56 |
R5 R6 |
12 Îì è |
|
R78 |
R7 R8 |
12 Îì, |
получим более простую схему (рис. 24).
Ðèñ. 24
Заменим теперь параллельно соедин¸нные проводники 2 и 56 проводником с эквивалентным сопротивлением R256 :
|
1 |
1 |
1 |
||||
|
R256 |
R2 |
R56 |
||||
|
R256 |
R2 R56 |
4 Ом. |
||||
|
R2 R56 |
||||||
Поступим аналогично и с проводниками 78 и 4: эквивалентное сопротивление R784 также равно 4 Ом.
Теперь схема ещ¸ более упрощается (рис. 25).
Ðèñ. 25
Дальнейший расч¸т несложен:
|
R12563 |
R1 R256 R3 16 Îì; |
|||||||
|
1 |
1 |
1 |
||||||
|
R |
R12563 |
R784 |
||||||
|
R |
R12563 R784 |
16 4 |
3,2 Ом. |
|||||
|
R12563 R784 |
16 4 |
|||||||
Ответ: 3,2 Ом.
Физика 41
7. Метод склеивания узлов
Этот метод является обратным по отношению к предыдущему.
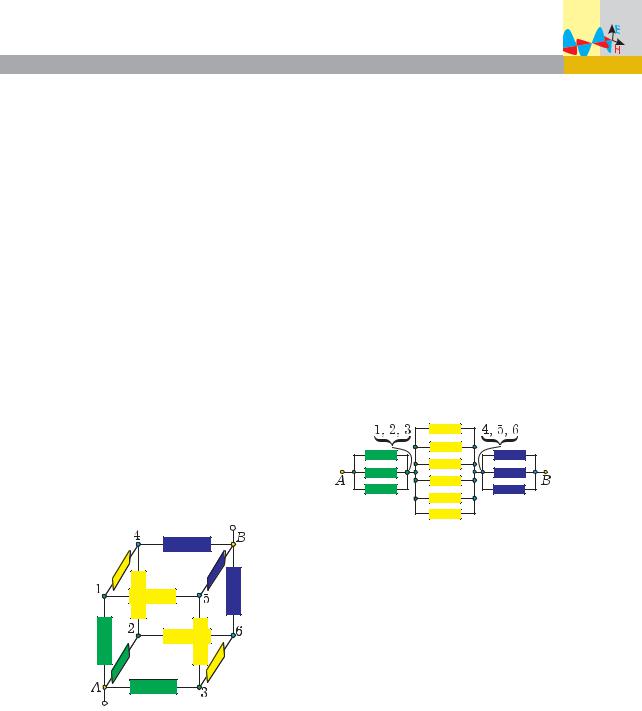
Задача 9. В каждое из р¸бер куба включ¸н проводник сопротивлением 6 Ом. Чему равно сопротивление получившейся конструкции между вершинами А и В, находящимися на концах большой диагонали куба?
Решение. Используем теперь метод склеивания узлов.
Изобразим на чертеже схему включения проводников (рис. 26). Учитывая симметрию схемы, заметим, что токи через проводники, выделенные зел¸ным, одинаковы. Следовательно, потенциалы точек 1, 2 и 3 равны. Тогда, если их соединить идеальными проводниками, то по этим проводникам ток идти не будет, а значит общее сопротивление цепи не изменится. Таким образом, точки 1, 2 и 3 оказались собранными в один узел, а выделенные зел¸ным проводники стали соедин¸нными параллельно.
Ðèñ. 26
Поступив аналогично с проводниками, выделенными синим, полу- чим три других параллельно соеди- н¸нных проводника.
Обратим внимание, что шесть оставшихся проводников (они выделены ж¸лтым цветом) теперь оказываются соедин¸нными параллельно. Действительно, каждый из них одним концом подключ¸н к узлу, выделенному зел¸ным цветом, а другим – к узлу, выделенному синим цветом.
Таким образом, эквивалентная схема состоит из тр¸х последовательно соедин¸нных участков: 1) три параллельно соедин¸нных проводника; 2) затем ещ¸ шесть; 3) и, наконец, снова три (рис. 27).
Ðèñ. 27
Аналогично произвед¸нному в задаче 3 расч¸ту сопротивление тр¸х параллельно соедин¸нных проводников равно 2 Ом, а у шести таких же проводников – вдвое меньше: 1 Ом. Теперь эквивалентная схема состоит из тр¸х последовательно соедин¸нных проводников, и их общее сопротивление
R (2 1 2) Ом 5 Ом.
Ответ: 5 Ом.
Заключение
Итак, подвед¸м краткий итог. При определении общего сопро-
тивления электрической цепи надо попытаться отыскать в ней те проводники, которые соединены друг с другом последовательно либо парал-
лельно. Заменяя их проводниками с эквивалентным сопротивлением, получить более простую схему цепи. Затем продолжить упрощение до тех пор, пока в схеме не оста¸тся лишь один тип соединения – последова-

42 Физика
тельное или параллельное. Попутно нужно находить эквивалентные сопротивления.
Если же не уда¸тся определить ни одной пары проводников, которые были бы соединены последовательно или параллельно, то нужно поискать симметрию в предложенной схеме. Если симметрию удастся найти, то можно использовать один из основных методов преобразования схемы, каждый из которых не изменяет сопротивления цепи.
1. Метод склеивания узлов. Если два или более узлов имеют одинаковый потенциал, то их можно соединить в один узел.
2.Метод исключения участков цепи. Проводник можно удалить, если через него не теч¸т ток (узлы, которые он соединяет, имеют одинаковый потенциал).
3.Метод разрезания узлов. Действие, противоположное склеиванию узлов.
А что делать в том случае, если число проводников в цепи стремится
êбесконечности или не уда¸тся найти не только последовательно или параллельно соедин¸нные проводники, но и симметрию в схеме? Об этом будет рассказано в другой статье.
Ответ на пример 2
Ж¸лтым цветом выделены последовательно соедин¸нные проводники, зел¸ным – параллельно соедин¸нные.
Ðèñ. 28
Задачи для самостоятельного решения
|
1. В цепи, схема которой изо- |
рой показана на рис. 19, если каж- |
|||||||||||||||||||
|
бражена на рисунке 29, все провод- |
дый проводник имеет сопротивление |
|||||||||||||||||||
|
ники имеют сопротивление 8 Ом. |
15 Ом. (Ответ: 7 Ом.) |
|||||||||||||||||||
|
Определите общее сопротивление |
3. В каждое из р¸бер куба вклю- |
|||||||||||||||||||
|
цепи. (Ответ: 13 Ом.) |
чен проводник сопротивлением 8 Ом. |
|||||||||||||||||||
|
Чему равно сопротивление полу- |
||||||||||||||||||||
|
чившейся конструкции между вер- |
||||||||||||||||||||
|
шинами, принадлежащими одной из |
||||||||||||||||||||
|
граней и лежащими на концах е¸ |
||||||||||||||||||||
|
диагонали (на рис. 26 это вершины |
||||||||||||||||||||
|
А и 6)? (Ответ: 6 Ом.) |
||||||||||||||||||||
|
4. Определите сопротивление ме- |
||||||||||||||||||||
|
Ðèñ. 29 |
||||||||||||||||||||
|
жду точками А и В цепи, схема ко- |
||||||||||||||||||||
|
2. Определите сопротивление ме- |
||||||||||||||||||||
|
торой изображена на рис. 30, если |
||||||||||||||||||||
|
жду точкам А и О цепи, схема кото- |
||||||||||||||||||||
Соседние файлы в папке Моделирование
- #
- #
- #
Расчет сопротивлений сеток
Попались мне интересные задачки, близкие друг другу по стилю, что ли. В них нужно либо определить входное сопротивление схемы, либо потенциалы в точках. В каждой будем использовать хитрый метод на основе законов Кирхгофа. Только первые схемы простые, прозрачные, а последняя посложнее.
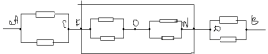
Задача. На рисунках изображены 4 схемы, составленные из проволок. В местах соединений проволоки спаяны. Определить: а) входное сопротивление между точками и
схем 1 и 2, полагая сопротивление каждой проволоки
; б) входное сопротивление между точками
и
,
и
для схемы 3, полагая сопротивление каждой проволоки
; в) потенциалы точек
схемы 4, полагая
В,
В. Считать сопротивление каждой проволоки для этой схемы равным 3 Ом.
Схема 1.
Рисунок 1
Схема имеет ось симметрии. Расставим токи в схеме так, чтобы симметрия сохранялась и чтобы при этом соблюдались первый и второй законы Кирхгофа. Поэтому начинать расставлять нужно от середины.
Рисунок 2
Чтобы соблюдался второй закон, расставим токи «внутри»
Рисунок 3
Теперь проследим за тем, чтобы соблюдался первый закон:
Рисунок 4
Наконец, сосчитаем входной ток:
Рисунок 5
Чтобы определить сопротивление схемы, надо пройти любым путем от точки до точки
, считая по дороге падения напряжений и складывая их:
Рисунок 6
Разделим на входной (он же выходной) ток – и сопротивление схемы нам известно!
Ответ: .
Схема 2.
Рисунок 7
Схема имеет ось симметрии, поэтому действовать будем точно так же. Расставим токи в цепи, начав с середины и придерживаясь симметрии:
Рисунок 8
Чтобы соблюсти 2 закон, в центре токи будут по 1,5I:
Рисунок 9
Теперь опять следим за соблюдением первого закона Кирхгофа:
Рисунок 10
Расставляем последние и , наконец, входной:
Рисунок 11
Теперь выбираем произвольный путь от точки до точки
, и «собираем» по дороге падения напряжений. Я пройду по правым ветвям:
Рисунок 12
Определяем сопротивление схемы, деля общее падение напряжения на общий (входной) ток:
Ответ: .
Схема 3. Действуем тем же манером. Расставляем токи, соблюдая симметрию и законы Кирхгофа. Через помеченные крестом ветви ток не потечет: на их концах точки, потенциалы которых равны.
Рисунок 13
Рисунок 14
Выходной ток — , сумма падений напряжений равна
, сопротивление будет равно
Для определения сопротивления надо расставить токи по новой:
Рисунок 15
Теперь проходим от до
, «собирая» падения напряжений:
.
И, чтобы найти сопротивление, делим на входной ток:
Ответ: ,
.
Схема 4. Здесь придется попотеть. Схема сложная, большая.
Рисунок 16
Начинаем расстановку токов с середины, причем я сделаю эти токи «четными» — просто для того, чтобы не пришлось возиться с дробями:
Рисунок 17
Так как схема, очевидно, симметрична, то точки ,
и другие, оказавшиеся на данной горизонтали – точки равного потенциала (учитывая данные задачи – нулевого). Поэтому в указанных перемычках ток не потечет. Также тока не будет в других помеченных крестами перемычках по тем же соображениям. Так как нужно, кроме симметрии, следить и за соблюдением законов Кирхгофа (и первого, и второго), то расстановку токов я сделала так:
Рисунок 18
Проходим любым путем, «собирая» падения напряжений:
Это напряжение равно 36 В: В.
Определим ток:
Тогда
Определяем потенциалы точек:
Ответ: B,
B,
B,
B.
12 комментариев
Виталий
✉️
27.10.2021 05:30:01
Добрый день, поясните, пожалуйста для какого замкнутого контура рассматривается второй закон Кирхгофа в схеме 2 на этапе «Чтобы соблюсти 2 закон, в центре токи будут по 1,5I».
Анна Валерьевна
✨
27.10.2021 05:43:46
Рыжий и синий токи в сумме — 2I, поэтому на той перемычке, где этот ток протекает (суммарный), будет создано падение напряжения 2IR. Далее рассматриваем второй ряд, квадратик слева. По левой стороне падение напряжения 3IR, значит, и по правой должно быть тоже 3IR. Отсюда ток, равный 1,5I — ведь он протекает через две перемычки сопротивлением R.
Виталий
✉️
30.10.2021 08:19:06
Спасибо за пояснение. Объясните, пожалуйста, как в 4 схеме был получен ток в 1I на горизонтальной перемычке. Если выбрать этот ток равным, например, 2I мы сможем расставить остальные токи в соответствии с двумя законами Кирхгофа, но ток на выходе будет другим, также будет отличаться суммарное падение напряжения при обходе
Анна Валерьевна
✨
30.10.2021 08:44:45
Всегда долго подбираю токи, все проверяю. Если сделать 2I, то в квадратике, диагональю которого является эта перемычка, второй закон не выполнится (в треугольнике под этой перемычкой).
АннА
✉️
09.12.2021 13:41:27
Здравствуйте, подскажите, а если в схеме на рис.2 выводы тока сделать из соседних вершин, этот метод работать не будет?
Анна Валерьевна
✨
09.12.2021 13:42:38
Почему же не будет, будет, конечно!
АннА
✉️
10.12.2021 06:15:24
Еще раз здравствуйте. Простите мою навязчивость,но очень хочется разобраться в теме!!!
У меня получились токи между соседними вершинами квадрата(где вход и выход цепи) 2i — 1i. В центре (перекрестие) 1i- 1i- 1i -1i , а между входом и выходом тока по дальним ребрам 2i-1i-1i-2i-2i-3i. Но если взять обходной ток (по ребру, кратчайшему пути между входом и выходом общее сопротивление получается 3/4, а если беру обходной ток по трем дальним ребрам, сопротивление-11/4).Что я делаю не так??? Помогите пожалуйста
АннА
✨
10.12.2021 06:21:19
Это если выводы тока в соседних вершинах
Анна Валерьевна
✨
11.12.2021 06:39:50
Присылайте полный текст задачи на почту.
Александр
✨
14.02.2022 10:29:49
Здравствуйте, а почему тогда также нельзя сказать про 3 схему 14 рисунок, верхний квадрат?
Александр
✨
14.02.2022 10:44:45
То есть почему мы не можем сказать тоже самое для верхней и нижней стороны, а говорим только для правой и левой
Анна Валерьевна
✨
16.02.2022 06:25:42
Все правильно: при обходе в любую сторону сумма падений напряжений в контуре равна нулю.
Введение
Решение задач — неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.
В ходе решения задач могут быть поставлены и
успешно реализованы следующие дидактические
цели:
- Выдвижение проблемы и создание проблемной
ситуации; - Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников
воспитываются трудолюбие, пытливость ума,
смекалка, самостоятельность в суждениях, интерес
к учению, воля и характер, упорство в достижении
поставленной цели. Для реализации перечисленных
целей особенно удобно использовать
нетрадиционные задачи.
§1. Задачи по расчету электрических
цепей постоянного тока
По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету
электрических цепей постоянного тока можно
отнести задачи, схемы которых:
1) содержат большое число элементов –
резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений
элементов.
В общем случае всякую цепь можно рассчитать,
используя законы Кирхгофа. Однако эти законы не
входят в школьную программу. К тому же, правильно
решить систему из большого числа уравнений со
многими неизвестными под силу не многим учащимся
и этот путь не является лучшим способом тратить
время. Поэтому нужно уметь пользоваться
методами, позволяющими быстро найти
сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при
подаче одинаковых напряжений на исходную и
преобразованную схемы, ток в обеих цепях будет
одинаков на соответствующих участках. В этом
случае все расчеты производятся с
преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи
со сложным смешанным соединением резисторов
можно воспользоваться несколькими приемами. Мы
ограничимся рассмотрением в подробностях лишь
одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.
Таким образом, замена нескольких узлов равных
потенциалов приводит к более простой
эквивалентной схеме. Но иногда бывает
целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что
не нарушает электрических условий в остальной
части.
Рассмотрим примеры решения задач эти методом.
З а д а ч а №1
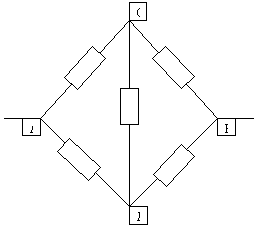
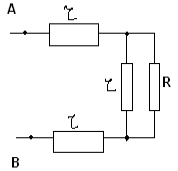
Рассчитать сопротивление между точками А и В
данного участка цепи. Все резисторы одинаковы и
их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д
являются эквипотенциальными. Поэтому резистор
между ними мы можем исключить. Эквипотенциальные
точки С и Д соединяем в один узел. Получаем очень
простую эквивалентную схему:
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
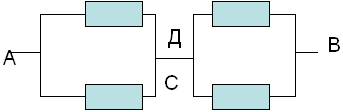
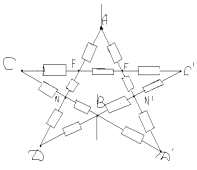
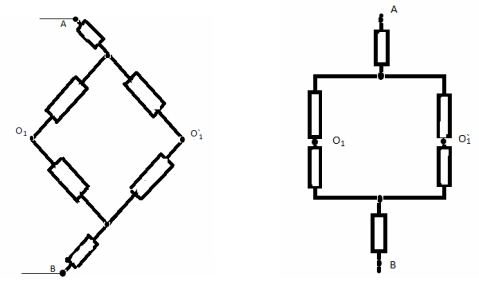
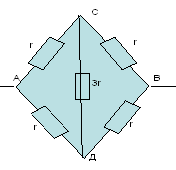
З а д а ч а № 2
Решение:
В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить.
Эквивалентная схема выглядит так:
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны
между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная
схема:
Ее сопротивление и сопротивление исходной цепи
RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
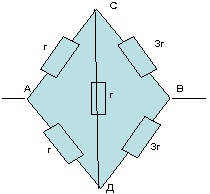
З а д а ч а № 3.
Решение:
Точки С и Д имеют равные потенциалы.
Исключением сопротивление между ними. Получаем
эквивалентную схему:
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
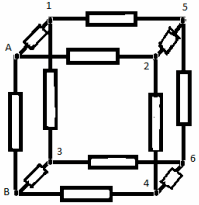
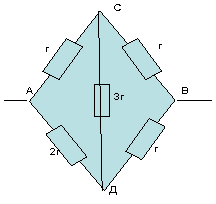
З а д а ч а № 4.
Решение:
Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.
Получим такую эквивалентную схему:
Сопротивление на участке А-1, R 1-равно
сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
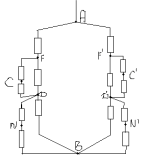
З а д а ч а № 5.
Решение:
Точки C и F-эквивалентные. Соединим их в один
узел. Тогда эквивалентная схема будет иметь
следующий вид:
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN =
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
Искомое общее сопротивление равно:
RAB= r.
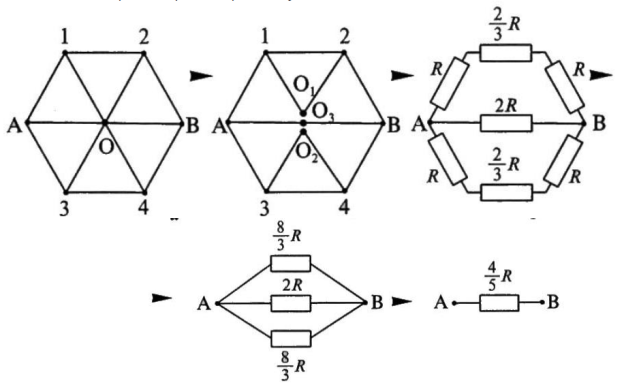
Задача №6
Решение:
Заменим общий узел О тремя узлами с равными
потенциалами О, О1 , О2. Получим
эквивалентную систему:
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
Искомое общее сопротивление цепи RAB
равно:
RAB= (8/10)*r.
Задача №7.
Решение:
“Разделим” узел О на два эквипотенциальных
угла О1 и О2. Теперь схему можно
представить, как параллельные соединение двух
одинаковых цепей. Поэтому достаточно подробно
рассмотреть одну из них:
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
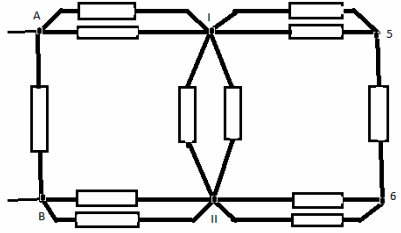
З а д а ч а №8
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
Сопротивление на участке A- I равно
сопротивлению на участке B- II и равно:
RI =
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII =
Получаем окончательную эквивалентную схему:
Искомое общее сопротивление цепи RAB=(7/12)*r.
З а д а ч а №9
В ветви ОС заменим сопротивление на два
параллельно соединенных сопротивления по 2r.
Теперь узел С можно разделить на 2
эквипотенциальных узла С1 и С2.
Эквивалентная схема в этом случае выглядит так:
Сопротивление на участках ОСIB и DCIIB
одинаковы и равны, как легко подсчитать 2r. Опять
чертим соответствующую эквивалентную схему:
Сопротивление на участке AOB равно
сопротивлению на участке ADB и равно (7/4)*r. Таким
образом получаем окончательную эквивалентную
схему из трех параллельно соединенных
сопротивлений:
Ее общее сопротивление равно RAB= (7/15)*r
З а д а ч а № 10
Точки СОD имеют равные потенциалы – соединим их
в один узел ОI .Эквивалентная схема
изображена на рисунке :
Сопротивление на участке А ОI равно . На участке
ОIВ сопротивление равно .Получаем совсем
простую эквивалентную схему:
ЕЕ сопротивление равно искомому общему
сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.
Задача № 11
Решение
Выделим в этой цепи бесконечно повторяющееся
звено, оно состоит в данном случае из трех первых
сопротивлений. Если мы отбросим это звено, то
полное сопротивление бесконечной цепи R не
измениться от этого , так как получится точно
такая же бесконечная цепь. Так же ничего не
измениться, если мы выделенное звено подключим
обратно к бесконечному сопротивлению R, но при
этом следует обратить внимание , что часть звена
и бесконечная цепь сопротивлением R соединены
параллельно. Таким образом получаем
эквивалентную схему :
Получается уравнения
RAB=2ч +
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ).
§3. Обучение решению задач по расчету
электрических цепей способом эквипотенциальных
узлов
Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
В то же время. Теоретические знания можно
считать усвоенными только тогда, когда они
удачно применяются на практике. Задачи по физике
описывают часто встречающиеся в жизни и на
производстве проблемы, которые могут быть решены
с помощью законов физики и, если ученик успешно
решает задачи, то можно сказать, что он хорошо
знает физику.
Для того, чтобы ученики успешно решали задачи,
недостаточно иметь набор методов и способов
решения задач, необходимо еще специально учить
школьников применению этих способов.
Рассмотрим план решения задач по расчету
электрических цепей постоянного тока методом
эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов; - начертить эквивалентную схему;
- найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом участке по законам
последовательного и параллельного соединения; - начертить эквивалентную схему, заменяя участки
соответствующими им расчетными сопротивлениями; - пункты 5 и 6 повторять до тех пор, пока не
останется одно сопротивление, величина которого
и будет решением задачи. - Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее
половина является зеркальным отражением другой.
Причем симметрия должна быть не только
геометрической, но должны быть симметричны и
численные значения сопротивлений или
конденсаторов.
Примеры:
1)
Схема симметричная, так как ветви АСВ и АДВ
симметричны геометрически и отношение
сопротивления на одном участке АС:АД=1:1 такое же,
как и на другом участке СД:ДВ=1:1.
2)
Схема симметричная, так как отношение
сопротивлений на участке АС:АД=1:1 такое же, как и
на другом участке СВ:ДВ=3:3=1:1
3)
Схема не симметрична, так как отношения
сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
Пример:
Из соображений симметрии делаем вывод, что в
симметричных точках потенциалы равны. В данном
случае симметричными точками являются точки С и
Д. Таким образом, точки С и Д – эквипотенциальные
точки.
в) выбрать, что целесообразно сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов.
Мы видим в этом примере, что между точками
равных потенциалов С и Д включено сопротивление,
по которому ток не будет течь. Следовательно, мы
можем отбросить это сопротивление, а точки С и Д
соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем
схему с соединенными в одну точку точками С и Д.
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.
Из полученной эквивалентной схемы видно, что на
участке АС мы имеем два параллельно соединенных
резистора. Их общее сопротивление находится по
закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя
участки соответствующими им расчетными
сопротивлениями.
Чертим эквивалентную схему подставляя в нее
рассчитанные сопротивления участков RAC и RCB:
ж)пункты д) и е) повторять до тех пор, пока
останется одно сопротивление, величина которого
и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два
последовательно соединенных сопротивления. Их
общее сопротивление находим по закону
последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную
схему:
Мы получили схему с одним сопротивлением,
величина которого равна сопротивлению исходной
схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала
можно учащимся предложить задания для
самостоятельной работы, взятые из
дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. —
М: Просвещение,1983. - Лукашик В.И. Физическая олимпиада.- М:
Просвещение, 2007 - Усова А.В., Бобров А.А. Формирование учебных
умений и навыков учащихся на уроках физики.- М:
Просвещение,1988 - Хацет А. Методы расчета эквивалентных схем
//Квант. - Чертов А. Г. Задачник по физике. – М.: Высшая
школа,1983 - Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
рекомендации) г. Бирск,1994г - Марон А.Е., Марон Е.А. Физика. Дидактические
материалы. Москва, “Дрофа”, 2004г