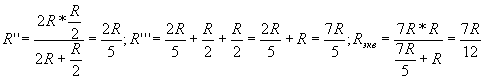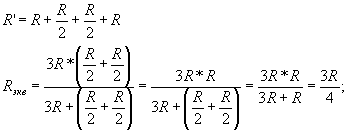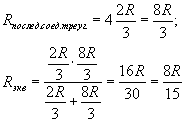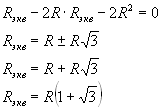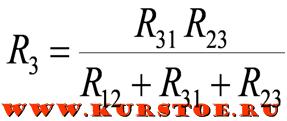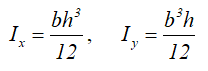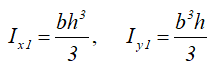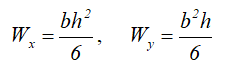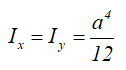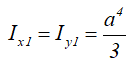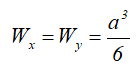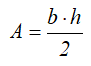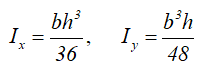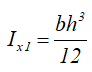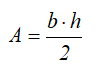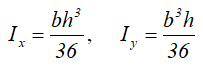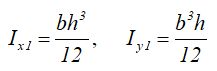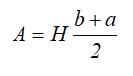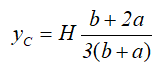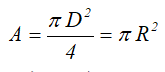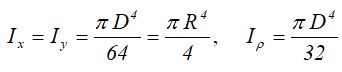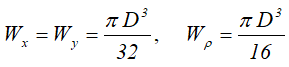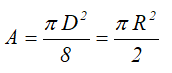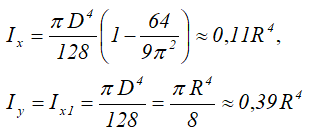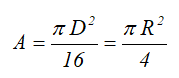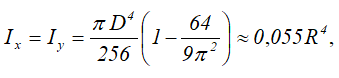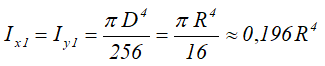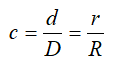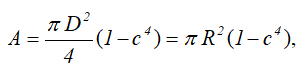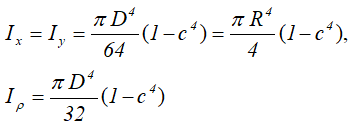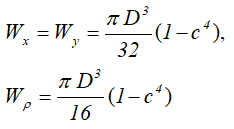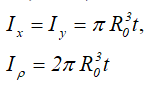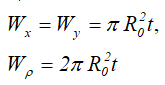Как найти сопротивление фигуры

Цели: обучающая: систематизировать
знания и умения учащихся решать задачи ан расчет
эквивалентных сопротивлений с помощью моделей,
каркасов и т.д.

Развивающая: развитие навыков логического
мышления абстрактного мышления, умений заменять
схемы эквивалентности, упрощать расчет схем.

Воспитательная: воспитание чувства
ответственности, самостоятельности ,
необходимости навыков приобретенных на уроке в
будущем

Оборудование: проволочный каркас куба,
тетраэдера, сетки бесконечной цепочки
сопротивлений.

ХОД УРОКА

Актуализация:

1. Учитель: “Вспомним последовательное
соединение сопротивлений”.

Учащиеся на доске зарисовывают схему.

и записывают

R_эк=n*R

U_об=U₁+U₂

Y_об=Y₁=Y₂

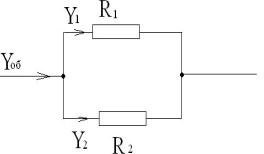
Учитель: вспомним параллельное соединение
сопротивлений.

Учащийся на доске зарисовывает элементарную
схему:

 U_об=U₁+U₂

Y_об=Y₁=Y₂

; для для n равных

Учитель: А теперь будем решать задачи на расчет
эквивалентного сопротивления участок цепи
представлен в виде геометрической фигуры, либо
металлической сетки.

Задача № 1

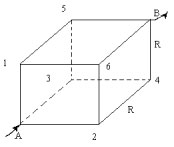
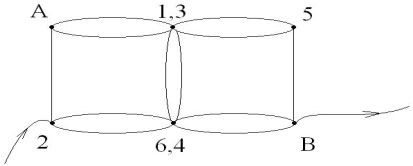
Проволочный каркас в виде куба, рёбра которого
представляют равные сопротивления R. Рассчитать
эквивалентное сопротивление между точками А и В.
Чтобы рассчитать эквивалентное сопротивление
данного каркаса необходимо заменить
эквивалентной схемой. Точки 1, 2, 3 имеют
одинаковый потенциал, их можно соединить в один
узел. А точки (вершины) куба 4, 5, 6 можно соединить в
другой узел по той же причине. Учащиеся имеют на
каждой парте такую модель. После выполнения
описанных действий зарисовывают эквивалентную
схему.

 

На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно
для последовательного соединения сопротивлений
имеем:

Задача № 2

Рассчитать R_ЭКВ. этого же куба, если куб
включён в цепь в точках 2 и 4.

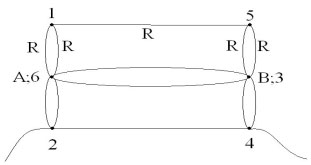
По тому же принципу потенциалы точек А и 6 равны,
В и 3 равны. Учащиеся совмещают эти точки на своей
модели и получают эквивалентную схему:

Расчёт эквивалентного сопротивления такой
цепи прост

Задача № 3

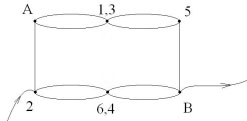
Эта же модель куба, с включением в цепь между
точками 2 и В. Учащиеся соединяют точки с равными
потенциалами 1 и 3; 6 и 4. Тогда схема будет
выглядеть так:

Точки 1,3 и 6,4 имеют равные потенциалы, и ток по
сопротивлениям между этими точками не потечёт и
схема упрощается до вида; эквивалентное
сопротивление которой рассчитывается так:

Задача № 4

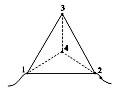
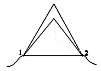
Равносторонняя треугольная пирамида, ребро
которой имеет сопротивление R. Рассчитать
эквивалентное сопротивление при включении в
цепь.

Точки 3 и 4 имеют равный потенциал, поэтому по
ребру 3,4 ток не потечёт. Учащиеся убирают его.

Тогда схема будет выглядеть так:

либо

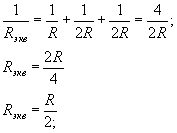
Эквивалентное сопротивление рассчитывается
так:

Задача № 5

Металлическая сетка с сопротивлением звена
равном R. Рассчитать эквивалентное сопротивление
между точками 1 и 2.

В точке 0 можно звенья отделить, тогда схема
будет иметь вид:

—
сопротивление одной половины симметричной по 1-2
точкам. Параллельно ей такая же ветвь, поэтому

Задача № 6

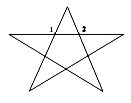
Рассчитать эквивалентное сопротивление
проволочной звезды с сопротивлением каждого
звена R, включённой в цепь между точками 1 и 2.

 Звезда состоит из 5-и равносторонних
треугольников, сопротивление каждого.

Между точками 1 и 2 один треугольник параллелен
четырём, последовательно соединенным между
собой

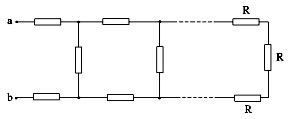
Имея опыт расчёта эквивалентного
сопротивления проволочных каркасов можно
приступить к расчету сопротивлений цепи,
содержащий бесконечное число сопротивлений.
Например:

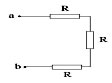
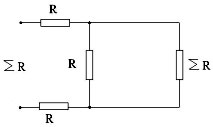
 Если отделить звено

от общей схемы, то схема не изменится, тогда
 можно представить ввиде

или ,

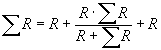
решаем данное уравнение относительно R_экв.

Итог урока: мы научились абстрактно
представлять схемы участков цепи, заменять их
эквивалентными схемами, которые позволяют легко
рассчитать эквивалентное сопротивление.

На дом:

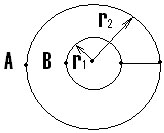
Рассчитать эквивалентное сопротивление
проволочного каркаса из двух окружностей с
радиусами r₁ и r_2, r₂₌2r₁ между
точками А и В. Сопротивление единицы длинны
проволоки?

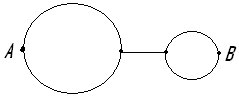
Указание: Эту модель представить в виде:

Расчет сопротивлений сеток

Попались мне  интересные задачки, близкие друг другу по стилю, что ли. В них нужно либо определить входное сопротивление схемы, либо потенциалы в точках. В каждой будем использовать хитрый метод на основе законов Кирхгофа. Только первые схемы простые, прозрачные, а последняя посложнее.

Задача. На рисунках изображены 4 схемы, составленные из проволок. В местах соединений проволоки спаяны. Определить: а) входное сопротивление между точками и схем 1 и 2, полагая сопротивление каждой проволоки ; б) входное сопротивление между точками и , и для схемы 3, полагая сопротивление каждой проволоки ; в) потенциалы точек схемы 4, полагая В, В. Считать сопротивление каждой проволоки для этой схемы равным 3 Ом.

Схема 1.

Схема имеет ось симметрии. Расставим токи в схеме так, чтобы симметрия сохранялась и чтобы при этом соблюдались первый и второй законы Кирхгофа. Поэтому начинать расставлять нужно от середины.

Чтобы соблюдался второй закон, расставим токи «внутри»

Теперь проследим за тем, чтобы соблюдался первый закон:

Наконец, сосчитаем входной ток:

Чтобы определить сопротивление схемы, надо пройти любым путем от точки до точки , считая по дороге падения напряжений и складывая их:

Разделим на входной (он же выходной) ток – и сопротивление схемы нам известно!

Ответ: .

Схема 2.

Схема имеет ось симметрии, поэтому действовать будем точно так же. Расставим токи в цепи, начав с середины и придерживаясь симметрии:

Чтобы соблюсти 2 закон, в центре токи будут по 1,5I:

Теперь опять следим за соблюдением первого закона Кирхгофа:

Расставляем последние и , наконец, входной:

Теперь выбираем произвольный путь от точки до точки , и «собираем» по дороге падения напряжений. Я пройду по правым ветвям:

Определяем сопротивление схемы, деля общее падение напряжения на общий (входной) ток:

Ответ: .

Схема 3. Действуем тем же манером. Расставляем токи, соблюдая симметрию и законы Кирхгофа. Через помеченные крестом ветви ток не потечет: на их концах точки, потенциалы которых равны.

Выходной ток — , сумма падений напряжений равна , сопротивление будет равно

Для определения сопротивления надо расставить токи по новой:

Теперь проходим от до , «собирая» падения напряжений:

.

И, чтобы найти сопротивление, делим на входной ток:

Ответ: , .

Схема 4. Здесь придется попотеть. Схема сложная, большая.

Начинаем расстановку токов с середины, причем я сделаю эти токи «четными» — просто для того, чтобы не пришлось возиться с дробями:

Так  как схема, очевидно, симметрична, то точки , и другие, оказавшиеся на данной горизонтали – точки равного потенциала (учитывая данные задачи – нулевого). Поэтому в указанных перемычках ток не потечет. Также тока не будет в других помеченных крестами перемычках по тем же соображениям. Так как нужно, кроме симметрии, следить и за соблюдением законов Кирхгофа (и первого, и второго), то расстановку токов я сделала так:

Проходим любым путем, «собирая» падения напряжений:

Это напряжение равно 36 В: В.

Определим ток:

Тогда

Определяем потенциалы точек:

Ответ: B, B, B, B.

12 комментариев

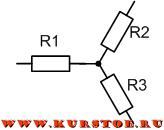
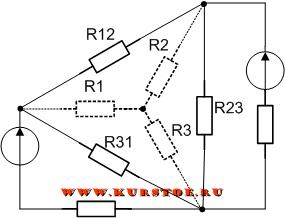
№7 Эквивалентное преобразование треугольника и звезды сопротивлений.

Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.

Рис. 7.1 — Преобразования электрической цепи

Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

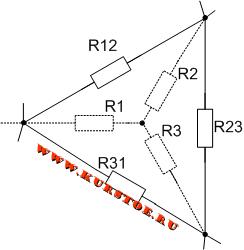
Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.

Рис. 7.2 — Треугольник и звезда сопротивлений

Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

б) при преобразовании звузды в треугольник:

Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.

При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.

Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.

а) Решение преобразованием треугольника в звезду.

Теперь общее сопротивление цепи легко находится:

Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:

Токи в паралельных ветвях:

Возвращаемся к исходной схеме (рис. 7.1, а):

Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.

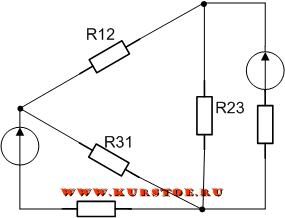
б) Решение преобразованием звезды в треугольник.

Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).

Определяем сопротивления треугольника:

Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:

Затем определяем общее сопротивление и токи:

Возвращаемся к исходной схеме:

Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.

Треугольник в звезду

Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.

Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.

Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур — называется треугольником.

Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.

Определение соединения сопротивлений звездой

Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.

Причина преобразования треугольника в звезду

При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.

Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.

Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.

Формулы для расчета преобразования треугольника в звезду

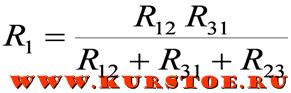
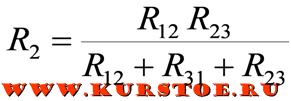
Пример преобразования

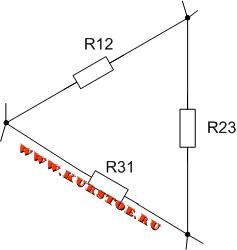
Для электрической цепи необходимо выполнить преобразование треуголькника R12 — R23 — R31 в звезду.

Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.

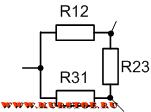
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.

4 инструмента крутого Кирхгофщика

Зачёт кое-как сдал, а всё равно толком не понял?

Я тебе расскажу, как учиться, чтобы понимать.
Как учиться эффективно. Практические советы.

Инструмент 1. Вычисление сопротивления цепи из нескольких последовательно соединённых сопротивлений

Просто, как . Сложил все эти сопротивления и получил сопротивление цепи.

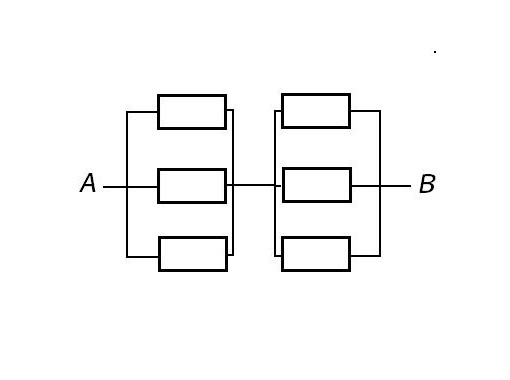
Инструмент 2. Вычисление сопротивления участка из нескольких параллельно соединённых сопротивлений

Рассмотрим участок с двумя параллельными одинаковыми сопротивлениями. Сопротивление его в два раза меньше, чем каждого сопротивления. Если сопротивлений три, сопротивление участка будет в три раза меньше.

Какую тут можно провести аналогию?

Несколько одинаковых дырок. Через них протечёт воды в столько раз больше, чем через одну дырку, сколько дырок имеется.

А как быть, если сопротивления не одинаковые? Есть такое понятие — проводимость. Оно означает величину, обратную сопротивлению. (рисунок 2)

Так если сопротивление больше, то проводимость что?

Чтобы вычислить проводимость нашего участка, надо сложить проводимости сопротивлений. Потом можно легко найти сопротивление участка.

А нельзя ли вычислить сопротивление участка, не преобразуя сопротивления в проводимости, а потом обратно? Можно. Пусть у нас участок из двух параллельно соединённых сопротивлений (рис. 2-1). Проводимость его равна сумме проводимостей сопротивлений (1 строчка). Приведём проводимости сопротивлений к общему знаменателю (2 строчка). Сложим их и получим суммарную проводимость (3 строчка). «Переворачиваем» формулу (4 строчка) и получаем формулу для участка из двух параллельно соединённых сопротивлений. А если сопротивлений не два, а больше?

Сформулируйте своими словами формулу сопротивления участка из нескольких параллельных сопротивлений, чтобы лучше её запомнить.

Надо умножить все сопротивления, и разделить на сумму произведений этих сопротивлений, но в каждом этом произведнии одного сопротивления не хватает. Вы, может быть, и получше сформулируете.

Инструмент 3. Преобразование «треугольника» в «звезду»

Пусть у нас в схеме есть вот такой участок цепи — «треугольник» (рис. 3, слева). Нам надо заменить его участком вот такого вида — «звездой» (рис. 3, справа), но чтобы сопротивления между сторонами «звезды» были такими же, как между соответствующими лучами «треугольника». Зачем это нужно? Позже узнаете.

Смотрим на «звезду» на рис. 3. Допустим, мы знаем сопротивления между точками A и B, то есть (R_a+R_b); A и C, то есть (R_a+R_c); B и C, то есть (R_b+R_c). Чему будут равны сопротивления R_a,   R_b,   R_c ?

Зная все сопротивления между концами лучей «звезды», мы можем вычислить сопротивление каждого отдельного луча.

Теперь будем вычислять сопротивления между точками A, B, и C (звезды) через сопротивления треугольника, которые нам известны (рис. 3-2). Для начала вычислим сопротивление между точками A и B звезды (рис. 3-2 верхняя строчка). В нашем треугольнике мы имеем два параллельно включённых сопротивления — R_ab и (R_ac+R_bc). Вычислять их общее сопротивление мы умеем (ответы на вопросы 3 и 4). Вычисляем сопротивления между точками A и C, B и C (2 и 3 строчки). Обратите внимание, что во всех формулах знаменатель одинаковый.

Теперь можно вычислить сопротивление отдельного луча (рис. 3-3). Формула получилась очень громоздкая, но мы её хорошенько подсократим.

И получим вот такую стройную и изящную формулу (рис. 3-4, верхняя строчка). Аналогично вычисляем сопротивления других лучей звезды.

Сформулируйте своими словами формулу из рисунка 3-4, чтобы лучше её запомнить.

Чтобы найти сопротивление луча «звезды», надо умножить сопротивления сторон «треугольника», которые «прилегают» («имеют ту же букву»), и разделить на сумму сопротивлений всех сторон «треугольника».

Инструмент 4. Преобразование «звезды» в «треугольник»

Иногда полезно делать обратное преобразование — «звезды» в «треугольник». Нельзя ли вычислить сопротивление стороны «треугольника» через сопротивления эквивалентной «звезды», используя формулы, которые мы уже вывели? Можно. Смотрим рисунок 3-4. Проделаем с формулами этого рисунка следующий трюк: попарно их перемножим и результаты сложим (смотрим рис. 4-1).

Затем результат разделим на верхнюю формулу рисунка 3-4. Получится у нас вот что: рисунок 4-2, третья сверху формула. Маленько её подсократим и получим нижнюю формулу. Как раз то, что нам надо!

Сопротивления других сторон «треугольника» выводятся аналогично (рисунок 4-3).

Сформулируйте своими словами формулу из рисунка 4-3, чтобы лучше её запомнить.

Чтобы найти сопротивление стороны «треугольника», надо сложить сопротивления соответствующих сторон «звезды» (у которых «те же буквы»), и ещё прибавить произведение тех же сторон «звезды», делёное на оставшуюся сторону.

Зубрилка

формула 1 формула 2 формула 3 формула 4 скрыть все формулы

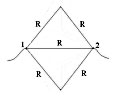
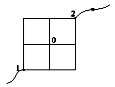
Найти сопротивление фигуры, включенной в цепь точками

#20904
2015-01-25 11:03 GMT

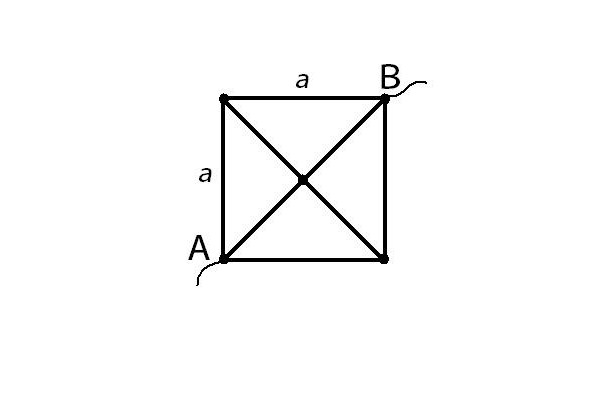
Из проволоки, площадь поперечного сечения которой постоянна, спаяна фигура. Длина стороны квадрата а, а сопротивление единицы длины ρ. Определите сопротивление R фигуры, включенной в церь точками А и В.

#20905
2015-01-25 16:26 GMT

И в чём трудность? Режем или рвём пересечение диагоналей и считаем.

Рвём хоть по вертикали, хоть по горизонтали.

Если ни то, ни другое, ни третье не помогает, прочтите, наконец инструкцию.

#20912
2015-01-25 19:22 GMT

В том-то и дело, что не могу разобраться, как именно эти диагонали разорвать и выгнуть. Туговато это идет мне.

#20913
2015-01-25 19:40 GMT

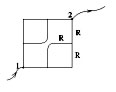
В силу симметрии фигуры относительно диагонали АВ вершины квадрата (которые не обозначены) находятся под одинаковым потенциалом и их можно соединить.

#20914
2015-01-25 20:52 GMT

Такая схема получится в итоге?

#20917
2015-01-26 10:25 GMT

отредактировал(а) iskander: 2015-01-26 12:17 GMT

#20919
2015-01-26 13:12 GMT

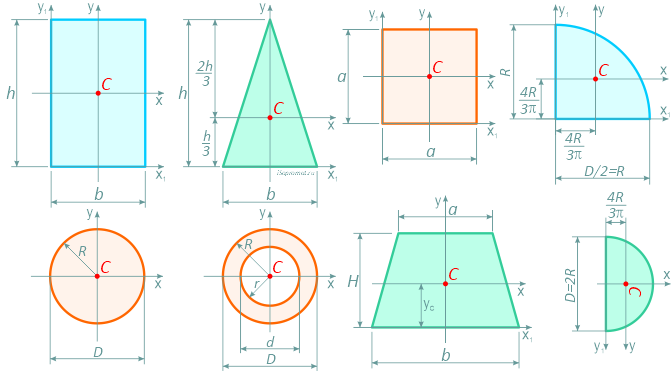
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

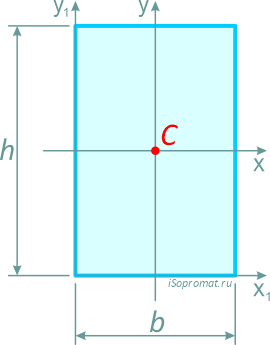
Прямоугольник

Прямоугольник высотой h и шириной b.

Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевые моменты сопротивления прямоугольного сечения

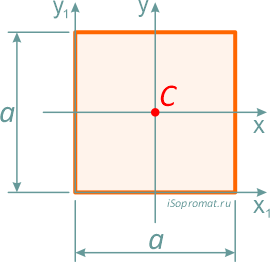
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

Площадь

Центральные осевые моменты инерции квадрата

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевой момент сопротивления квадратного сечения

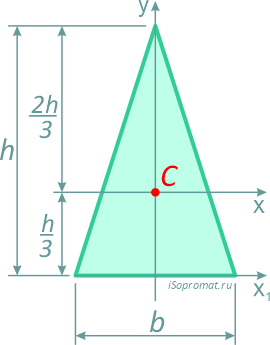
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

Центральные осевые моменты инерции треугольника

Момент инерции относительно смещенной оси x₁, проходящей через его основание

Прямоугольный треугольник

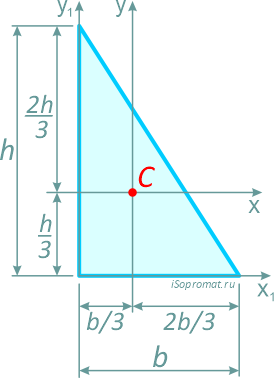
Прямоугольный треугольник высотой h и шириной основания b.

Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

Центральные осевые моменты инерции прямоугольного треугольника

Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

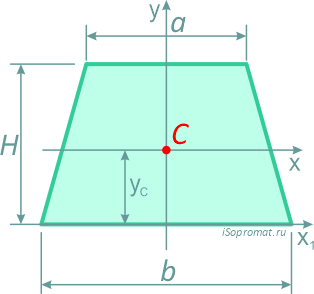
Трапеция

Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

Площадь трапеции

Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

Круг

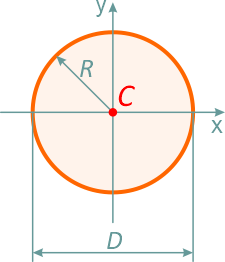
Круг диаметром D (d) или радиусом R (r)

Площадь круга через его диаметр и радиус

Центральные осевые и полярный моменты инерции круга

Осевые и полярный моменты сопротивления

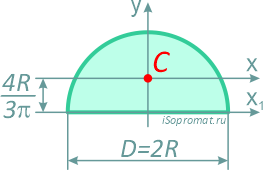
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

Площадь

Осевые моменты инерции полукруга

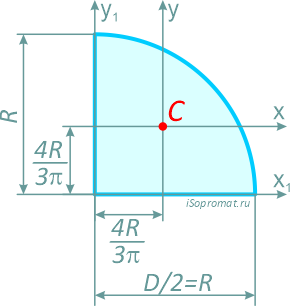
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

Площадь

Центральные осевые моменты инерции четверти круга

Моменты инерции относительно смещенных осей x₁ и y₁

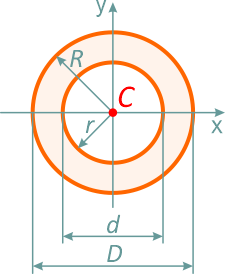
Кольцо

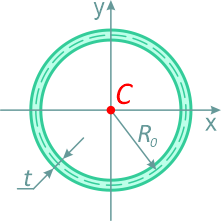
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

Площадь

Центральные осевые и полярный моменты инерции кольца

Осевые и полярный моменты сопротивления

Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

Площадь

Центральные осевые и полярный моменты инерции трубного сечения

Осевые и полярный моменты сопротивления

Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее