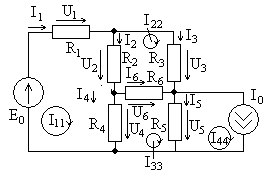
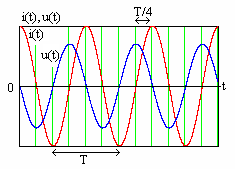
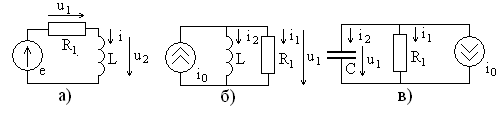
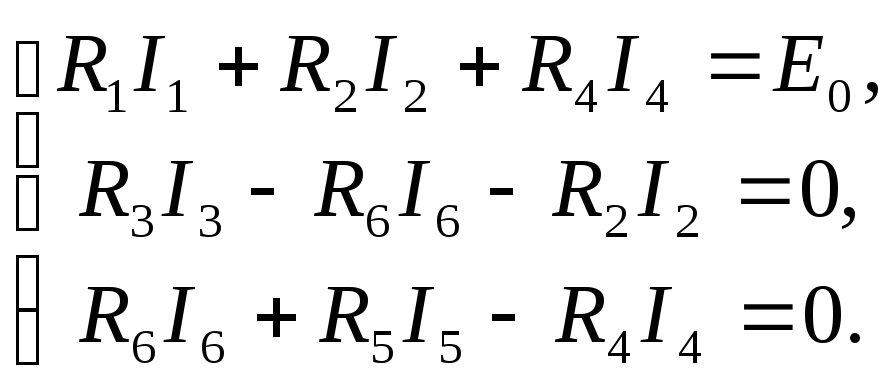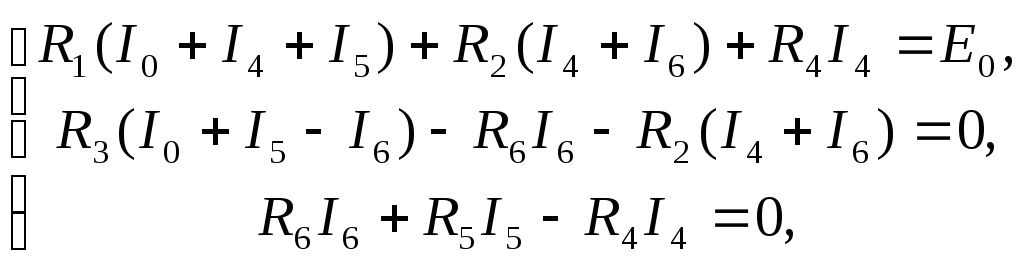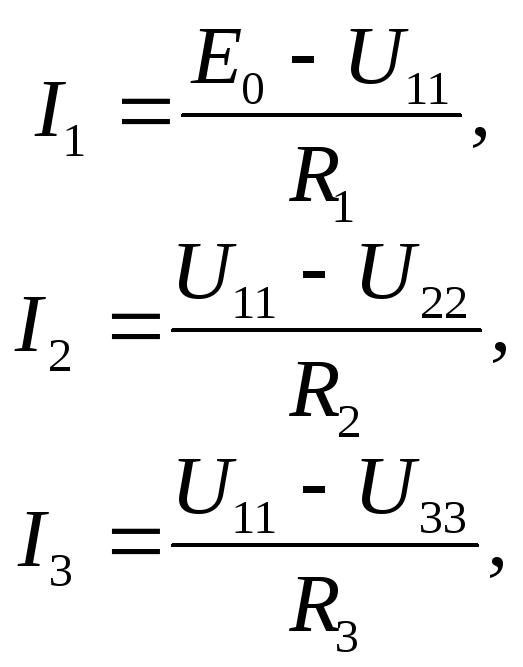Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
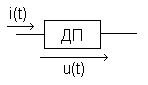
Идеальный источник ЭДС
Имеем источник ЭДС
Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
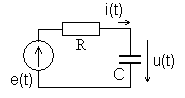
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что
Далее
Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»
где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
[quads id=1]
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r
Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
ЭДС. Закон Ома для полной цепи
-
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
-
Сторонняя сила
-
Закон Ома для полной цепи
-
КПД электрической цепи
-
Закон Ома для неоднородного участка
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила
, направленная против движения заряда (т.е. против направления тока).
к оглавлению ▴
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы
называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом,
— это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду
. Поэтому отношение
уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается
:
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
к оглавлению ▴
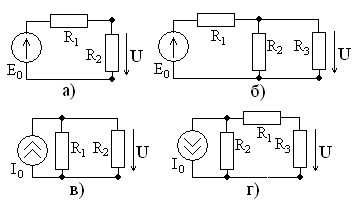
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением
подключён к резистору
(который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение
на резисторе
.
За время по цепи проходит заряд
. Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и
. Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и
(рис. 2). Потенциал точки
равен потенциалу положительной клеммы источника; потенциал точки
равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь
умножается на дробь, меньшую единицы. Но есть два случая, когда
.
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт
.
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина
неотличима от
, и формула (5) снова даёт нам
.
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
к оглавлению ▴
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время
, обозначим
.
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
к оглавлению ▴
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна
, его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно
, можно просто заменить резистор
на резистор
).
Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки
к точке
. Этот ток не обязательно вызван одним лишь источником
. Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток
является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и
равны соответственно
и
. Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время
через участок проходит заряд
, при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло:
.
Подставляем сюда выражения для ,
и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд
от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки
к точке
.
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем
— закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене
на
:
Теперь замкнём наш участок, соединив точки и
. Получим рассмотренную выше полную цепь. При этом окажется, что
и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от
к
, направлен против действия сторонних сил источника.
Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке
. Если направление тока совпадает с направлением сторонних сил, то перед
ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Повторим основные понятия и определения по теме «Закон Ома».
Напомним, что напряжение измеряется в вольтах.
Сила тока измеряется в амперах.
Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.
Основные определения, которые мы используем в решении задач:
Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.
Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.
Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.
По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).
Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.
Сопротивление измеряют в омах (Ом).
Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).
Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:
- Сопротивление проводника тем больше, чем больше его длина.
- Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.
Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:
Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.
Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм2 от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм2/м.
Решение:
Из закона Ома для проводника или участка цепи без источника следует:
По графику: при
Из формулы сопротивления выражаем и находим длину проводника:
Ответ: 10.
Задача 2. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике? Ответ дайте в амперах.
Решение:
По определению силы тока:
Заряд всех электронов: где е — модуль заряда электрона,
Кл.
Тогда
Ответ: 2.
Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)
Решение:
По закону Ома для полной цепи:
Тогда
Ответ: 0,07.
Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.
Решение:
Сила тока короткого замыкания определяется следующим образом:
Отсюда выражаем и находим внутреннее сопротивление источника:
При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:
Отсюда выражаем сопротивление резистора и находим его:
Ответ: 1,9.
Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.
Решение:
Выражаем время в секундах: t = 10 минут = 600 с.
Определяем силу тока по закону Ома для полной цепи:
Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.
По определению силы тока:
Отсюда Кл.
Ответ: 1500.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Загрузить PDF
Загрузить PDF
Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.
-
1
Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
-
2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.[1]
Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
-
3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.[2]
Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи. - Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.[3]
- Сила тока в любых частях последовательной цепи одна и та же.[2]
-
4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: RO = 12 В / 8 А = 1,5 Ом.
Реклама
-
1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
-
2
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления:
, где R1 – сопротивление первой ветви, R2 – сопротивление второй ветви и так далее до последней ветви Rn.
-
3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока. - В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
-
4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
-
5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
Реклама
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
-
1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
-
2
Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи:
.
-
3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
-
4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
Ом.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
-
5
Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.
Реклама
-
1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).[6]
Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
-
2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I2R.
- Обособьте переменную R: R = P / I2.
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
-
3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V2/R.
- Обособьте переменную R: R = V2/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама
Советы
- Мощность измеряется в ваттах (Вт).
- Напряжение измеряется в вольтах (В).
- Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА =
A = 0,001 А.
- В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: PСР = VIcosθ, где cosθ – это коэффициент мощности цепи.[8]
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 408 213 раз.
Была ли эта статья полезной?
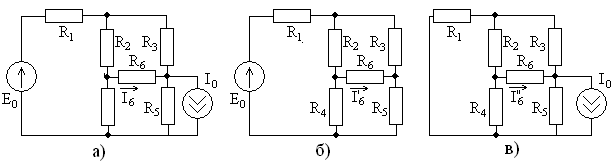
3.1. Модель цепи постоянного тока
Если в электрической цепи действуют
постоянные напряжения и протекают
постоянные токи, то модели реактивных
элементов LиCсущественно упрощаются.
Модель сопротивления
остается прежней и связь между напряжением
и током
определяется законом Ома в виде
.
(3.1)
В идеальной индуктивности мгновенные
значения напряжения и тока связаны
соотношением
.
(3.2)
Аналогично в емкости связь между
мгновенными значениями напряжения и
тока определяется в виде
.
(3.3)
53
Таким образом, в модели цепи постоянного
тока присутствуют только сопротивления
(модели резисторов) и источники сигнала,
а реактивные элементы (индуктивности
и емкости) отсутствуют.
3.2. Расчет цепи на основе закона Ома
Этот метод удобен для расчета сравнительно
простых цепей с одним источником
сигнала. Он предполагает вычисление
сопротивлений участков цепи, для которых
известна величина тока (или напряжения),
с последующим определением неизвестного
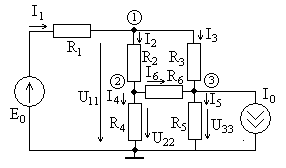
напряжения (или тока). Рассмотрим пример
расчета цепи, схема которой приведена
на рис. 3.1, при токе идеального источникаА
и сопротивленияхОм,
Ом,
Ом.
Необходимо определить токи ветвейи
,
а также напряжения на сопротивлениях,
и
.

ток источника,
тогда можно вычислить сопротивление
цепиотносительно зажимов источника тока
(параллельного соединения сопротивленияи последовательно соединен-
Рис. 3.1. ных
сопротивлений
и
),
.
Тогда напряжение
на источнике тока (на сопротивлении
)
равно
В.
54
Затем можно найти токи ветвей
А,
А.
Полученные результаты можно проверить
с помощью первого закона Кирхгофа в
виде
.
Подставляя вычисленные значения, получимА,
что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти
напряжения на сопротивлениях (величина
уже найдена)
В,
В.
По второму закону Кирхгофа
.
Складывая полученные результаты,
убеждаемся в его выполнении.
3.3. Общий метод расчета цепи на основе
законов Ома
и Кирхгофа
Общий метод расчета токов и напряжений
в электрической цепи на основе законов
Ома и Кирхгофа пригоден для расчета
сложных цепей с несколькими источниками
сигнала.
Расчет начинается с задания обозначений
и положительных направлений токов и
напряжений для каждого элемента
(сопротивления) цепи.
Система уравнений включает в себя
подсистему компонентных уравнений,
связывающих по закону Ома токи и
напряжения в каждом элементе
(сопротивлении) и подсистему
55
топологических уравнений, построенную
на основе первого и второго законов
Кирхгофа.
Рассмотрим расчет простой цепи из
предыдущего примера, показанной на рис.
3.1, при тех же исходных данных.
Подсистема компонентных уравнений
имеет вид
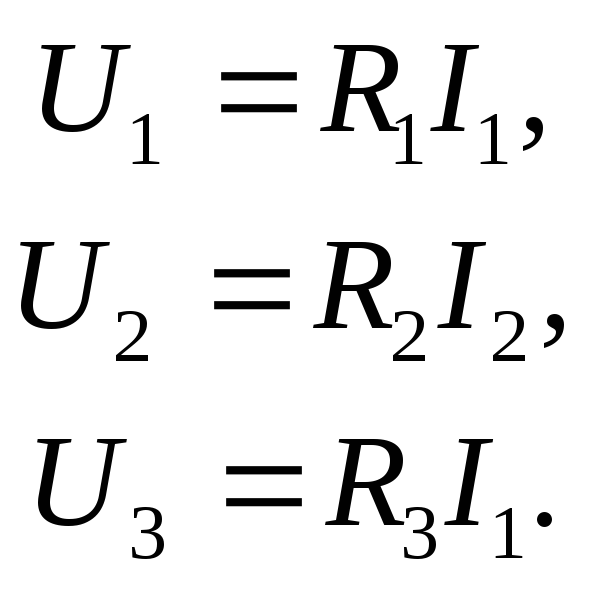
В цепи имеется два узла ()
и две ветви, не содержащие идеальных
источников тока ().
Следовательно, необходимо записать
одно уравнение ()
по первому закону Кирхгофа,
,
(3.5)
и одно уравнение второго закона Кирхгофа
(),
,
(3.6)
которые и образуют подсистему
топологических уравнений.
Уравнения (3.4)-(3.6) являются полной
системой уравнений цепи. Подставляя
(3.4) в (3.6), получим
,
(3.7)
а, объединив (3.5) и (3.7), получим два
уравнения с двумя неизвестными токами
ветвей,
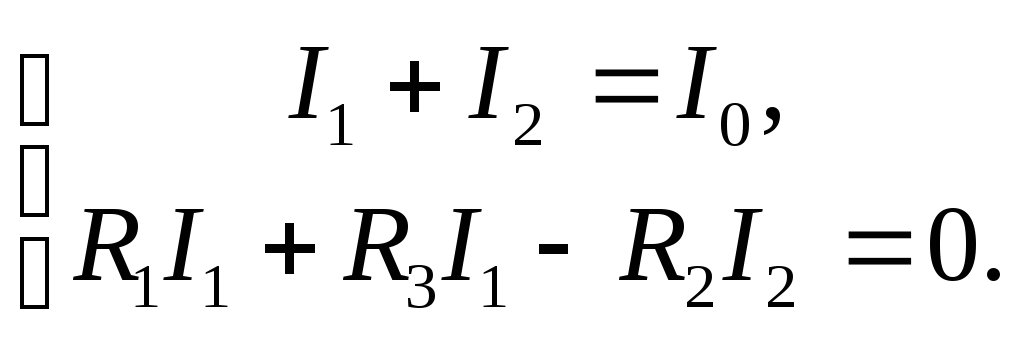
56
Выражая из первого уравнения (3.8) ток
и подставляя его во второе, найдем
значение тока,
А,
(3.9)
а затем найдем
А.
По вычисленным токам ветвей из компонентных
уравнений (3.4) определим напряжения.
Результаты расчета совпадают с полученными
ранее в подразделе 3.2.
Рассмотрим более сложный пример расчета
цепи в схеме, показанной на рис. 3.2, с
параметрами
Ом,
Ом,
Ом,
Ом,
Ом,
Ом,
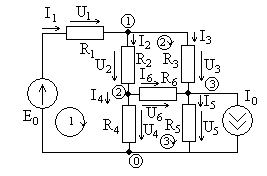
А.
Цепь содержит
узла (их номера указаны в кружках) и
ветвей, не содержащих идеальные источники
тока. Система компонентных уравнений
цепи имеет вид
Рис. 3.2
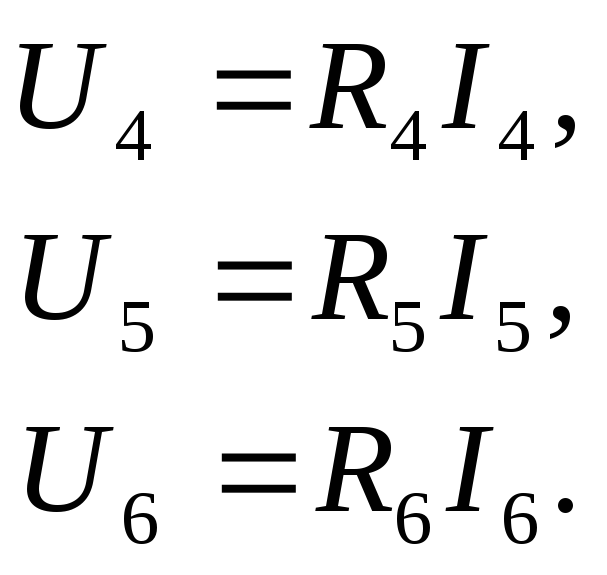
По первому закону Кирхгофа необходимо
записать
уравнения (узел 0 не используется),
57
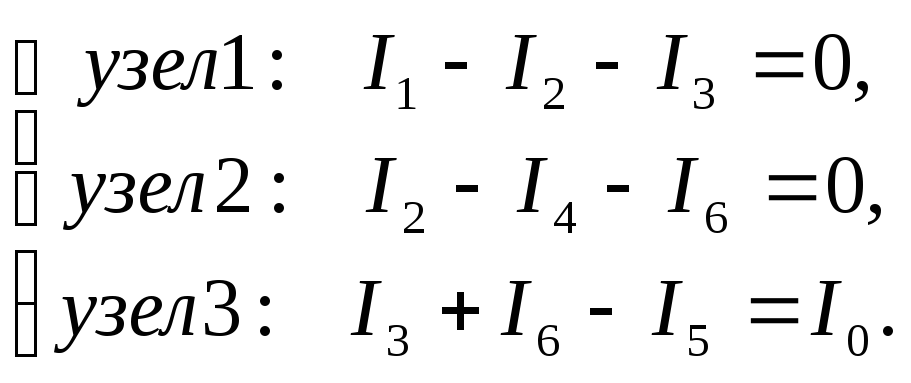
По второму закону Кирхгофа составляется
уравнения для трех независимых контуров,
отмеченных на схеме окружностями со
стрелками (внутри указаны номера
контуров),
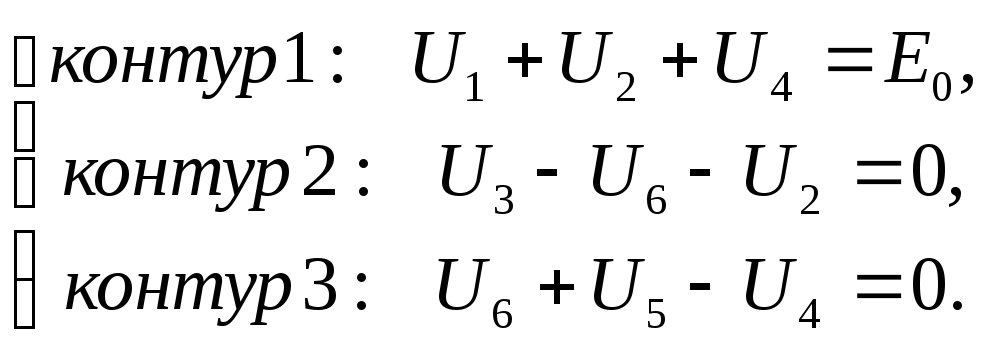
Подставляя (3.11) в (3.13), совместно с (3.12)
получим систему шести
уравнений вида
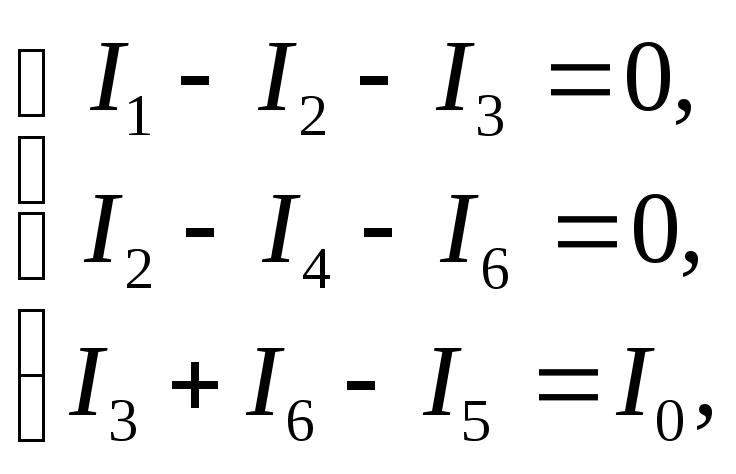
Из второго и третьего уравнений выразим
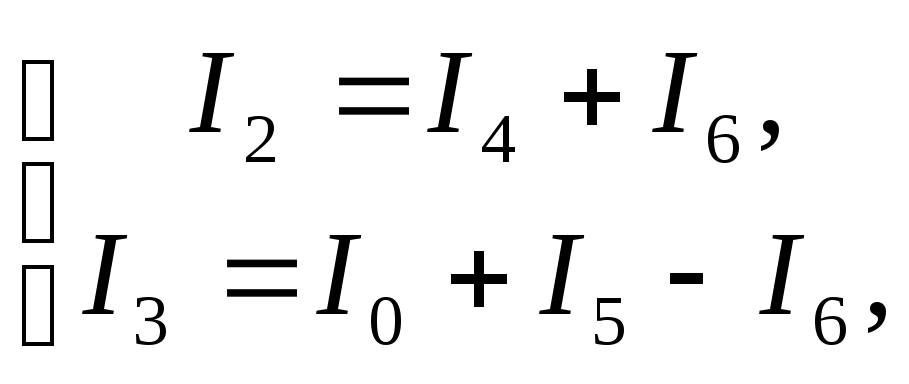
а из первого
,
тогда подставиви
,
получим.
Подставляя токи,
и
в уравнения второго закона Кирхгофа,
запишем систему из трех уравнений
58
которую после приведения подобных
запишем в виде

Обозначим
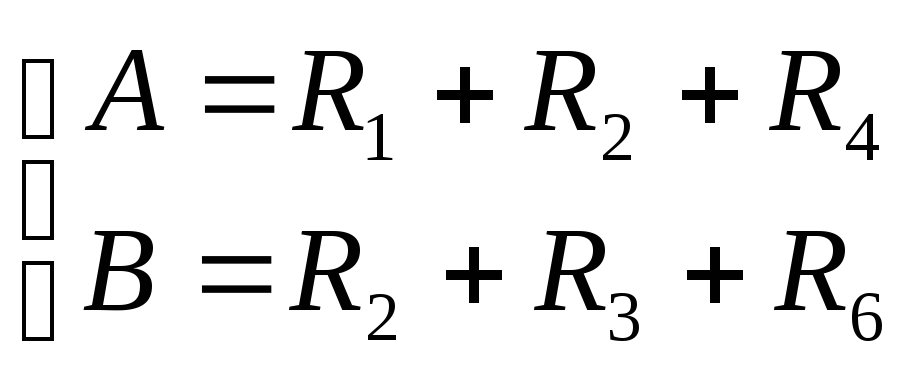
(3.16)
и из третьего уравнения системы (3.15)
запишем
.
(3.17)
Подставляя полученное значение
в первые два уравнения (3.15), получим
систему из двух уравнений вида

Из второго уравнения (3.18) получим
59
,
(3.19)
тогда из первого уравнения найдем ток
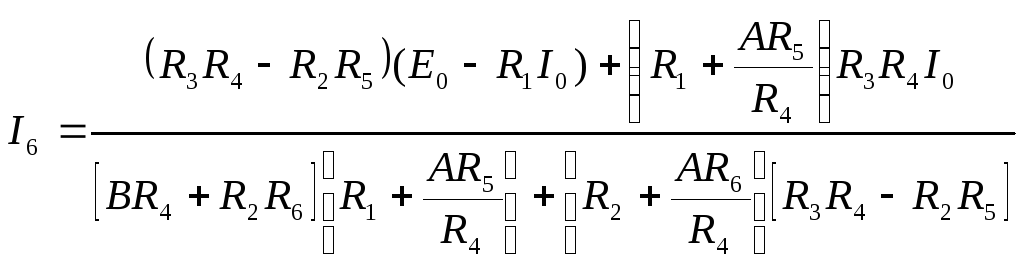
(3.20)
Вычислив
,
из (3.19) найдем,
из (3.17) вычислим,
а затем из уравнений подстановки найдем
токи,
,
.
Как видно, аналитические вычисления
достаточно громоздки, и для численных
расчетов целесообразней использовать
современные программные пакеты, например,
MathCAD2001. Пример программы
показан на рис. 3.3.
Матрица — столбец
содержит значения токов
А,
А,
А.
Остальные
токи вычисляются согласно уравнениям
(3.14) и равны
А,
А,
А.
Вычисленные значения токов совпадают
с полученными по приведенным выше
формулам.
Общий метод расчета цепи по уравнениям
Кирхгофа приводит к необходимости
решения
линейных алгебраических уравнений. При
большом числе ветвейвозникают математические и вычислительные
трудности. Это означает, что целесообразно
искатьметоды расчета, требующие
составления и решения меньшего числа
уравнений.
60
Рис. 3.3
3.4. Метод контурных токов
Метод контурных токов базируется
на уравненияхвторого закона
Кирхгофаи приводит к необходимости
решенияуравнений,
—
число всех ветвей, в том числе и содержащих
идеальные источники тока.
В цепи выбираются
независимых контуров и для каждого
-го
из них вводится кольцевой (замкнутый)
контурный ток(двойная индексация позволяет отличать
кон-
61
турные токи от токов ветвей). Через
контурные токи можно выразить все токи
ветвей и для каждого независимого
контура записать уравнения второго
закона Кирхгофа. Система уравнений
содержит
уравнений, из которых определяются все
контурные токи. По найденным контурным
токам находятся токи или напряжения
ветвей (элементов).
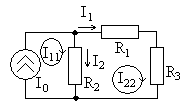
пример цепи на рис. 3.1. На рис 3.4 приведена
схема с указанием обозначений и
положительных направлений двух контурных
токови
(
,
,
).
Рис. 3.4 Через
ветвь
проте-
кает только
контурный ток
и его направление совпадает с
,
поэтому ток ветвиравен
.
(3.21)
В ветви
протекают два контурных тока, ток
совпадает по направлению с
,
а токимеет противоположное направление,
следовательно
.
(3.22)
Для контуров, не содержащих идеальные
источники тока, составляем уравнения
второго закона Кирхгофа с использованием
закона Ома, в данном примере записывается
одно уравнение
.
(3.23)
Если в контур включен идеальный
источник тока, то для него
62
уравнение второго закона Кирхгофа не
составляется, а его контурный ток
равен току источника с учетом их
положительных направлений, в рассматриваемом
случае
.
(3.24)
Тогда система уравнений принимает вид
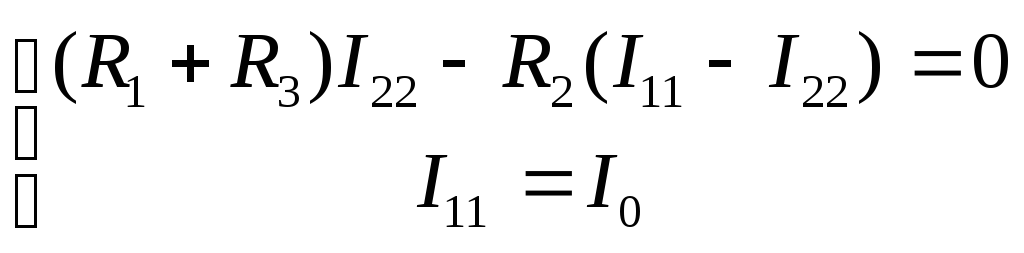
(3.25)
В результате подстановки второго
уравнения в первое получим
,
(3.26)
тогда ток
равен
А,
(3.27)
а ток
А.
Из (3.21)А,
а из (3.22) соответственноА,
что полностью совпадает с полученными
ранее результатами. При необходимости
по найденным значениям токов ветвей по
закону Ома можно вычислить напряжения
на элементах цепи.
Рассмотрим более сложный пример цепи
на рис. 3.2, схема которой с заданными
контурными токами показана на рис. 3.5.
В этом случае число ветвей
,
количество узлов,
тогда число независимых контуров и
уравнений по методу контурных токов
равно.
Для токов ветвей можно записать
63
Рис. 3.5

Первые три контура не содержат идеальных
источников тока, тогда с учетом (3.28) и
использованием закона Ома для них можно
записать уравнения второго закона
Кирхгофа,
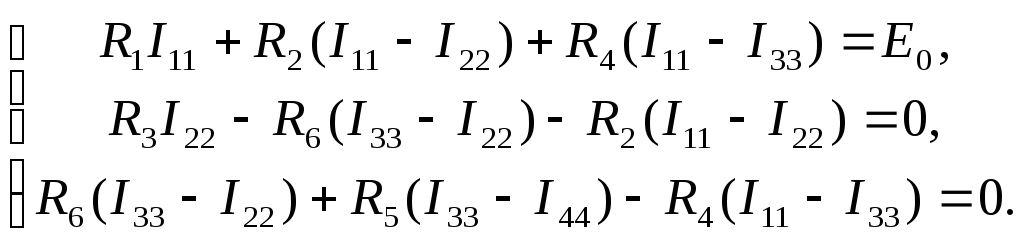
В четвертом контуре присутствует
идеальный источник тока, поэтому для
него уравнение второго закона Кирхгофа
не составляется, а контурный ток равен
току источника (они совпадают по
направлению),
.
(3.30)
Подставляя (3.30) в систему (3.29), после
преобразования получим три уравнения
для контурных токов в виде
64

Систему уравнений (3.31) можно решить
аналитически (например, методом
подстановки – проделайте это),
получив формулы для контурных токов, а
затем из (3.28) определить токи ветвей.
Для численных расчетов удобно использовать
пакет программMathCAD, пример
программы показан на рис. 3.6. Результаты
вычислений совпадают с расчетами,
приведенными на рис. 3.3. Как видно, метод
контурных токов требует составления и
решения меньшего числа уравнений по
сравнению с общим методом расчета по
уравнениям Кирхгофа.
Рис. 3.6
65
3.5. Метод узловых напряжений
Метод узловых напряженийбазируется
на первом законе Кирхгофа, при этом
число уравнений равно.
В цепи выделяются все
узлов и один из них выбирается в качествебазисного, которому присваивается
нулевой потенциал. Потенциалы (напряжения)…
остальных
узлов отсчитываются от базисного, их
положительные направления обычно
выбираются стрелкой в базисный узел.
Через узловые напряжения с использованием
закона Ома и второго закона Кирхгофа
выражаются токи всех ветвей
и для
узлов записываются уравнения первого
закона Кирхгофа.

пример цепи, показанной на рис. 3.1, для
метода узловых напряжений ее схема
показана на рис. 3.7. Нижний узел обозначен
как базисный (для этого используется
символ «земля» — точка нулевого
потенциала), напряжение верхнего узла
относительно базисного обо-
Рис. 3.7 значено как
.
Выразим через
него токи
ветвей
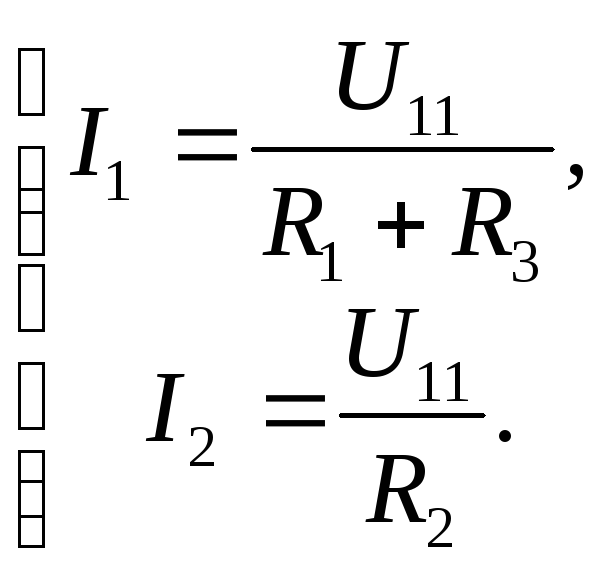
По первому закону Кирхгофа с учетом
(3.32) запишем единственное уравнение
метода узловых напряжений (),
66
.
(3.33)
Решая уравнение, получим
,
(3.34)
а из (3.32) определим токи ветвей
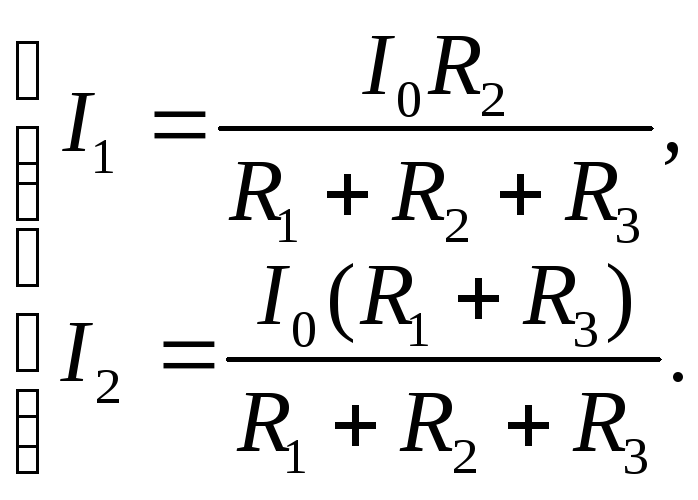
Полученные результаты совпадают с
полученными рассмотренными ранее
методами.
более сложный пример цепи, показанной
на рис. 3.2 при тех же исходных данных, ее
схема показана на рис. 3.8. В цепиузла, нижний выбран базисным, а три
остальные обозначены номерами в кружках.
Введены
положительные на- Рис.
3.8
правления и обозна-
чения узловых напряжений
,
и
.
По Закону Ома с использованием второго
закона Кирхгофа определим токи ветвей,
67
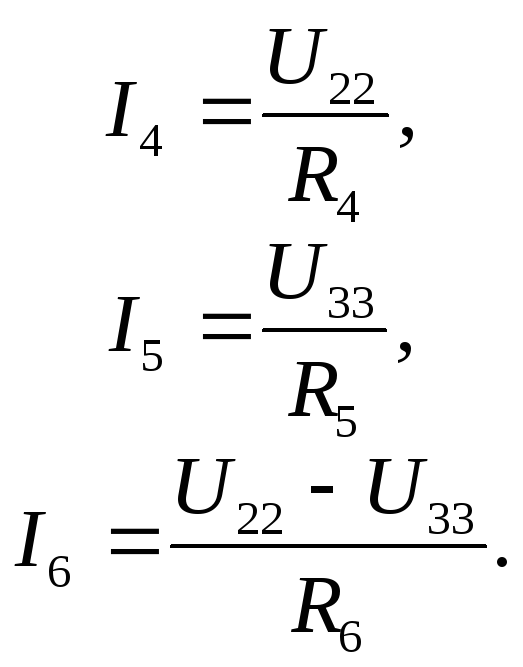
По первому закону Кирхгофа для узлов
с номерами 1, 2 и 3 необходимо составить
три уравнения,
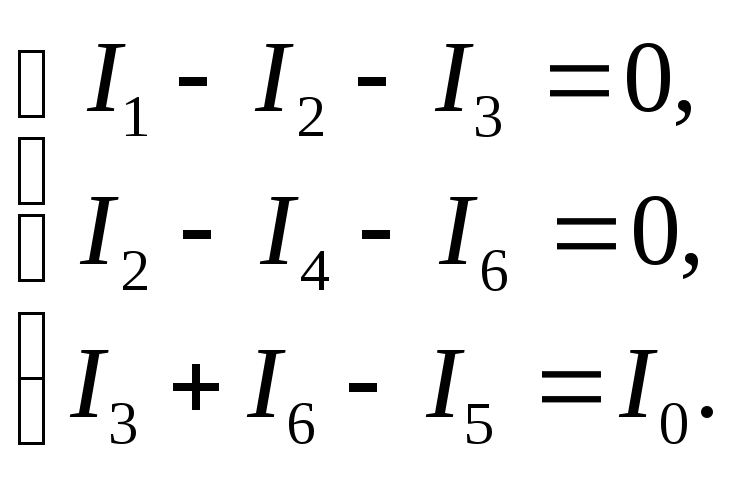
Подставляя (3.36) в (3.37), получим систему
уравнений метода узловых напряжений,

После преобразования и приведения
подобных получим

68
Программа расчета узловых напряжений
и токов ветвей приведена на рис. 3.9. Как
видно, полученные результаты совпадают
с полученными ранее другими методами
расчета.
Проведите аналитический расчет узловых
напряжений, получите формулы для токов
ветвей и вычислите их значения.
Рис. 3.9
69
3.6. Метод наложения
Метод наложениязаключается в
следующем.
Расчет проводится следующим образом.
В цепи, содержащей несколько источников,
поочередно выбирается каждый из них, а
остальные отключаются. При этом образуются
цепи с одним источником, число которых
равно количеству источников в исходной
цепи. В каждой из них проводится расчет
искомого сигнала, а результирующий
сигнал определяется их суммой. В качестве
примера рассмотрим расчет тока
в цепи, показанной на рис. 3.2, ее схема
показана на рис. 3.10а.
Рис. 3.10
70
При выключении идеального источника
тока (его цепь разрывается) получается
цепь, показанная на рис. 3.9б, в которой
любым из рассмотренных методов
определяется ток
.
Затем выключается идеальный источник
напряжения (он заменяется коротким
замыканием) и получается цепь, показанная
на рис. 3.9а, в которой находится ток
.
Искомый токравен
.
Проведите аналитические и численные
расчеты самостоятельно, сравните с
полученными ранее результатами, например,
(3.20).
3.7. Сравнительный анализ методов расчета
Метод расчета, основанный
на законе Ома, пригоден для сравнительно
простых цепей с одним источником. Его
нельзя использовать для анализа цепей
сложной структуры, например, мостового
типа вида рис.3.9.
Общий метод расчета цепи на основе
уравнений законов Ома и Кирхгофа
универсален, но требует составления и
решения системы из
уравнений, которая легко преобразуется
в систему изуравнений. При большом числе ветвей
резко возрастают вычислительные затраты,
особенно при необходимости аналитических
расчетов.
Методы контурных токов и узловых
напряжений более эффективны, так как
приводят к системам с меньшим числом
уравнений, равным соответственно
и
.
При условии
или
(3.40)
метод контурных токов эффективнее, а
иначе целесообразно применять метод
узловых напряжений.
71
Метод наложения удобен, когда при
отключении источников происходит резкое
упрощение цепи.
В системах схемотехнического моделирования
цепей, например, MicroCAPилиOrCADв основном применяют
метод узловых напряжений.
3.8. Задания для самостоятельного решения
Задание 3.1 С помощью
закона Ома определите напряжениев цепях, схемы которых показаны на рис.
3.11 приВ,
мА,
кОм,
кОм,
кОм.
Рис. 3.11
Задание 3.2Общим методом расчета
на основе законов Ома и Кирхгофа
определите токв цепях, схемы которых показаны на рис.
3.11 приВ,
В,
мА,
мА,
кОм,
кОм,
кОм.
Задание 3.3Методами контурных токов,
узловых напряжений и наложения определите
токв цепях, схемы которых показаны на рис.
3.12, параметры цепи возьмите из задания
3.1, сравните полученные результаты.
72
Рис. 3.12
3.4.Методами контурных токов и узловых
напряжений определите токв цепи, схема которой показана на рис.
3.13 приВ,
мА,
мА,
кОм,
кОм,
кОм.
Рис. 3.13
Задание 3.5. Общим методом расчета,
методами контурных токов и узловых
напряжений определите в цепи рис. 3.14
напряжениепри
мА
кОм,
кОм,
кОм,
кОм,
кОм.
Проведите сравнительный анализ
методов расчета.
Рис. 3.14
73
4. ГАРМОНИЧЕСКИЕ ТОКИ И НАПРЯЖЕНИЯ
В ЛИНЕЙНЫХ ЦЕПЯХ
4.1. Гармонические ток и напряжение в
элементах цепи
В элементах цепи R,L,
иCвзаимосвязь произвольных
мгновенных значений тока и напряжения
определяется законом Ома, необходимые
соотношения приведены в табл. 1.1.
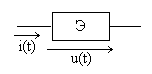
элементе Э (рис. 4.1) в виде
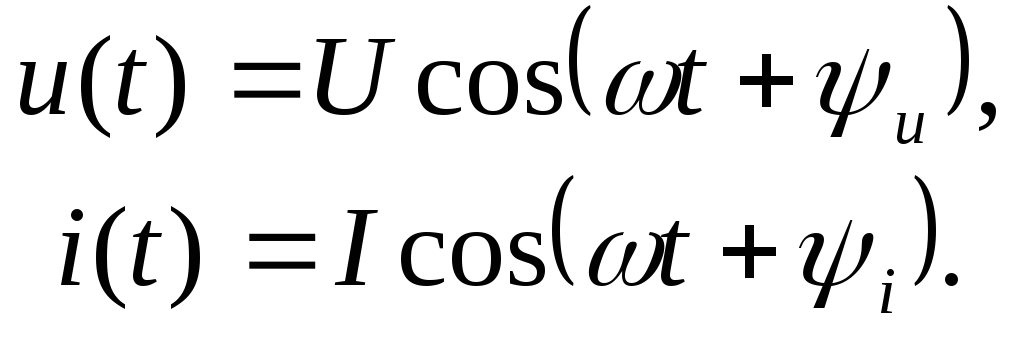
Рис. 4.1
Для сопротивления Rможно записать
.
(4.2)
Сравнивая полученный результат с
выражением для напряжения из (4.1), получим
выражение закона Ома для амплитуд тока
и напряжения.
,
(4.3)
и соотношение для начальных фаз
.
(4.4)
Как видно из (4.3), амплитуды
(и действующие значения) гармонических
тока и напряжения в сопротивлении
связанызаконом Омав классической
формулировке прямой пропорциональности.
74
Начальные фазы тока
и напряжения
в сопротивленииодинаковы, сдвиг
фазмежду напряжением и током равен нулю,
.
(4.5)
Мгновенная мощность (1.6) гармонических
сигналов в сопротивлении равна
,
(4.6)
где
.
Ее зависимость от времени показана на
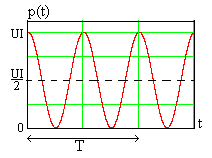
рис. 4.2. Величинавсегда положительна, то есть
сопротивление толькопотребляет
мощностьот источника сигнала. Это
гармоническая функция времени с
периодом по-
вторения в два раза меньше пе-
Рис. 4.2
риода сигнала.
Средняя мощность (1.8) гармонических
сигналов в сопротивлении определяется
выражением
,
(4.7)
где
и
— действующие значения тока и напряжения,
.
(4.8)
75
Это значение показано пунктирной линией
на временной диаграмме рис. 4.2.
В емкости Cмгновенные значения тока и напряжения
связаны соотношением (табл.1.1)
.
(4.9)
После преобразования тригонометрической
функции к канонической форме гармонического
сигнала получим
.
(4.10)
Сравнивая (4.10) с формулой тока из (4.1),
можно записать
,
(4.11)
.
(4.12)
Введем обозначения
,
(4.13)
,
(4.14)
где
—модуль реактивного сопротивления
емкости (Ом), а—реактивная проводимость емкости
(См=1/Ом). Позднее увидим, что реактивное
сопротивление емкостиотрицательно.
Из (4.11) получим уравнения связи амплитуд
(и действующих значений) гармоническихтока и напряжения в емкости
76
,
(4.15)
которые представляют собой выражение
закона Омадля емкости в классической
формулировке прямой пропорциональности.
Из (4.12) следует, что гармонический ток
в емкости опережает по фазе приложенное
к ней напряжение(напряжение отстает
по фазе от тока) на уголрадиан или 900. Сдвиг фаз между
напряжением и током в емкости равен
.
(4.16)
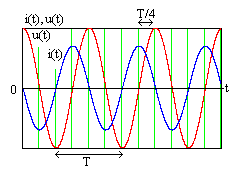
На рис. 4.3 показаны временные диаграммы
тока и напряжения в емкости. Ток
опережает по фазе напряжение на 900,
что отражается навременной
диаграмме смещением
кривой тока влево на чет-
Рис. 4.3
верть периода.
Мгновенная мощность в емкости из (4.1) и
(4.9) равна
,
а после тригонометрических преобразований
получим
.
(4.17)
Временная диаграмма мгновенной мощности
показана на рис. 4.4
77
мощность электрических сигналов в
емкости может быть положительной
(емкость накапливает энергию электрического
поля) и отрицательной (емкость отдает
во внешнюю цепь ранее накопленную
энергию).Средняя мощность гармонических
сигналов в емкости равна нулю, то
Рис. 4.4 есть емкость
не потребляет мощ-
ность
от гармонического источника.
Для индуктивности Lмгновенные значения тока и напряжения
связаны соотношением закона Ома из
табл.1.1, тогда с учетом выражения для
тока из (4.1) получим
,
а после преобразований
.
(4.18)
Сравнивая (4.18) с выражением для напряжения
(4.1), получим уравнения связи для амплитуд
(действующих значений) тока и напряжения
(4.19)
и их начальных фаз
.
(4.20)
Введем обозначения
78
,
(4.21)
,
(4.22)
где
—реактивное сопротивление индуктивности
(Ом), а—модуль реактивной проводимости
индуктивности (См=1/Ом). Позднее увидим,
что реактивная проводимость индуктивностиотрицательна.
Тогда получим выражения закона Омадля амплитуд (действующих значений)
тока и напряжения в индуктивности
.
(4.23)
Согласно (4.20) гармонический ток в
индуктивности отстает по фазе от
напряжения(напряжение опережает по
фазе ток) на уголрадиан или 900. Сдвиг фаз между
напряжением и током в индуктивности
равен
.
(4.24)
Временные диаграммы тока и напряжения
в индуктивности показаны на рис. 4.5. В
отличие от аналогичных графиков для
емкости на рис. 4.3 ток и напряжение
меняются
местами, кривая напряже-
Рис. 4.5
ния смещена вправо отно-
сительно тока на четверть периода, что
соответствует опережению по фазе на
900.
79
Мгновенная мощность гармонических
сигналов в индуктивности равна
,
(4.25)
а после тригонометрических преобразований
получим
.
(4.26)
Временная диаграмма мгновенной мощности
в индуктивности совпадает с показанной
на рис. 4.4 для емкости.
Средняя мощность гармонических
сигналов в индуктивности (как и в емкости)
равна нулю, то есть индуктивность не
потребляет мощность
от гармонического источника.
В табл. 4.1 приведены сводные результаты
для гармонических сигналов в элементах
цепи.
Таблица 4.1
|
Элемент |
Ток |
Напряжение |
Средняя мощность |
|
R |
|
|
|
|
C |
|
|
|
|
L |
|
|
|
4.2. Средняя мощность гармонических
сигналов в
линейном двухполюснике
Рассмотрим двухполюсник
(ДП) на рис. 4.6, через который протекает
гармонический токи к которому приложе-
80
но напряжение
вила (4.1).
мощность равна
(4.27)
а после тригонометрических преобра-
Рис.4.6
зований получим
.
(4.28)
Как видно, мгновенная мощность изменяется
по гармоническому закону с частотой
и содержит постоянную составляющую.
Средняя мощность равна
,
(4.29)
где
— сдвиг фаз между напряжением и током.
Величинуназываюткоэффициентом мощности.
Как видно, потребляемая двухполюсником
мощность определяется амплитудами
(действующими значениями) тока и
напряжения и коэффициентом мощности.
Для максимизации потребляемой мощности
(например, электродвигателем) необходимо
обеспечить условие
,
то есть нулевой сдвиг фаз между напряжением
и током ().
Это означает, что двухполюсник должен
вести себя как сопротивление.
В чисто реактивной цепи, содержащей
только индуктивности и емкости, сдвиг
фаз
,
при этом потребляемая мощность будет
рана нулю при любых амплитудах тока и
81
напряжения.
Полученное выражение (4.29) для средней
мощности полностью согласуется со
значениями
в элементах цепиR,LиC(табл. 4.1), так как в
сопротивлении,
а в индуктивности и емкости.
4.3. Тригонометрический метод расчета
Тригонометрический метод
расчета гармонических токов и напряжений
в линейной цепи базируется на законах
Ома и Кирхгофа для мгновенных значений
сигналов в тригонометрической форме.
качестве примера рассмотрим цепь на
рис. 4.7 при,
В,
рад/с,
,
кОм
инФ.
Обозначим гармонический токв виде
Рис. 4.7
,
(4.30)
тогда с учетом свойств гармонических
напряжений в сопротивлении и емкости
на основе второго закона Кирхгофа
получим
.
(4.31)
82
Левая часть (4.31) может быть преобразована
в тригонометрическую функцию,
,
(4.32)
тогда, уравнивая коэффициенты в правой
и левой частях уравнения, получим
,
(4.33)
.
(4.34)
Из полученных выражений нетрудно
определить амплитуду и начальную фазу
тока в цепи,

.
При найденном токе нетрудно определить
напряжение
на емкости (проведите расчет
самостоятельно).
Как видно, тригонометрический метод
требует суммирования гармонических
функций с неизвестными параметрами,
что приводит к громоздким расчетам,
если число слагаемых функций более
двух. Этот метод применим для расчета
очень простых цепей.
83
4.4. Векторная диаграмма цепи
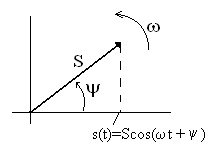
сигналможно представить проекцией на
горизонтальную ось вектора, вращающегося
против часовой стрелки вокруг начала
координат с круговой (угловой) частотой,
как показано на рис. 4.8. Длина (модуль)
вектора равна амплитуде гармонического
сигналаи в момент начала вращения (при
)
угол его наклона к горизонтальной
Рис. 4.8 оси равен
начальной фазе сиг-
нала
(отсчет положительных значений проводится
против часовой стрелки).
Все гармонические токи и напряжения в
цепи с одинаковой частотой, равной
частоте источников сигнала, можно
представить совокупностью синхронно
вращающихся векторов вида рис. 4.8. Так
как все векторы вращаются синхронно и
между ними сохраняются амплитудные и
угловые соотношения, то вращение можно
остановить и рассматривать неподвижную
совокупность векторов. Если вращение
остановлено в момент времени
,
то угол наклона каждого вектора к
горизонтальной оси равен начальной
фазе соответствующего вектору
гармонического сигнала.
84
Для векторного представления гармонических
сигналов выполняются законы Кирхгофав классической формулировке.
В качестве примера рассмотрим векторную
диаграмму цепи, показанной на рис. 4.7.
Результаты ее расчета тригонометрическим
методом приведены в табл. 4.2 (проведите
соответствующие расчеты).
Таблица 4.2
|
Сигнал |
Амплитуда |
Начальная фаза |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
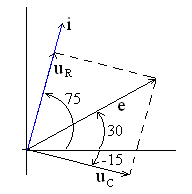
диаграмма цепи приведена на рис. 4.9.
Векторы тока и напряжений построены по
данным табл. 4.2, длина вектора равна
амплитуде сигнала, а угол отклонения
от горизонтальной оси равен начальной
фазе (отсчет положительных значений
угла против часовой стрелки). Вектор
токасовпадает по направлению с вектором
напряженияна сопротивлении, их длины (модули)
не одинаковы, так как масштабы
Рис. 4.9
штабы (например, В/см и мА/см)
токов и напряжений различны (ток и
напряжение не сравнимы между собой).
Напряжение на сопротивлении
опережает по фазе напряжение на емкости
на 900. Это обусловлено тем, что в
85
последовательной цепи рис. 4.7 через
сопротивление и емкость протекает один
и тот же ток, причем напряжение на
сопротивлении совпадает по фазе с током,
а на емкости – отстает по фазе от тока
на 900.
Сумма векторов напряжений на сопротивлении
и емкости в цепи рис. 4.7 по второму закону
Кирхгофа (в векторной форме) равна ЭДС
источника, что и показано на векторной
диаграмме рис. 4.9.
Как видно, векторная диаграмма цепи
может быть построена по результатам
расчета всех гармонических токов и
напряжений. Однако ее можно построить
«качественно» (без знания точных
параметров векторов, но с правильными
соотношениями между ними) и не проводя
численных расчетов.
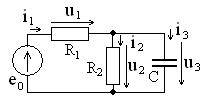
примерRCцепи, показанной
на рис. 4.10, в которой заданы положительные
направления и условные обозначения
всех токов и напряжений.
Прежде всего, необходимо проанализироватьструктуру цепи. В ней присутствует
Рис. 4.10 параллельный
фрагмент (со-
единение
элементов CиR2),
который соединен последовательно с
сопротивлениемR1и источником напряжения.
Тогда построение необходимо начать с
напряжения на параллельном фрагменте,
при этом,
этот вектор проведем произвольно по
модулю и направлению, например,
горизонтально, векторная диаграмма
показана на рис. 4.11.
Ток
совпадает по фазе с напряжениями
,
а токопережает их по фазе на 900.
Соответствующие векторы изображены на
диаграмме рис. 4.11 с произвольной длиной
и указанными угловыми соотношениями
относительно вектора
86
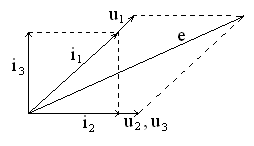
Векторная сумма этих токов по первому
закону Кирхгофа равна току,
то есть этот вектор строится исходя из
векторови
.
Вектор напряженияна сопротивленииR1совпадает по направлению с вектором
токаи имеет произвольную длину, а вектор
ЭДСпо второму закону Кирхгофа Кирхгофа
равен Рис. 4.11
сумме векторов
и
.
На этом построение «качественной»
векторной диаграммы цепи заканчивается.
Если цепь содержит последовательный
фрагмент, входящий в смешанное соединение,
то построение целесообразно начинать
с вектора тока этого фрагмента.
Векторная диаграмма электрической
цепи может использоваться для иллюстрацииамплитудных и фазовых соотношений между
токами и напряжениями, и для формированияаналитических выражений, связывающих
их амплитуды (действующие значения) и
начальные фазы.
Например, для диаграммы рис. 4.11 амплитуды
(действующие значения) токов
,
и
по теореме Пифагора связаны выражением
.
Для других соотношений можно использовать
теорему косинусов (пример приведите
самостоятельно).
Для сложной цепи построение «качественной»
векторной диаграммы требует вдумчивого
подхода при выборе начального вектора
и способов построения остальных векторов.
87
4.5. Особенности расчета цепи с
гармоническими
сигналами
Мгновенные значения токов и напряжений
в электрической цепи связаны между
собой уравнениями законов Ома и Кирхгофа.
Последние предполагают суммирование
гармонических функций времени с
неизвестными амплитудами и начальными
фазами, например, с помощью теоремы
косинусов, а это приводит к громоздким
расчетам даже в относительно простых
цепях.
Существенно упростить расчеты можно,
отказавшись от описания сигналов с
помощью тригонометрических функций
времени и заменив его числами, на
зависящими от времени. На эту возможность
указывает векторная диаграмма цепи,
которая полностью отражает свойства
гармонических сигналов и не зависит от
времени.
Известно, что вектор, выходящий из
начала координат, можно представить
комплексным числом. Таким образом, в
теории электрических цепей при расчете
гармонических процессов возникает
метод комплексных амплитуд.
4.6. Расчет средней (потребляемой) мощности
По результатам расчета гармонических
токов и напряжений можно определить
мощность, потребляемую цепью от источника
сигнала.
В качестве примера используем цепь на
рис. 4.7, результаты расчета приведены в
табл. 4.2. Рассматривая цепь относительно
зажимов источника как двухполюсник,
при амплитуде напряжения
В,
токамА
и сдвиге фаз между ними,
получим
мВт.
88
С другой стороны, в рассматриваемой
цепи емкость не потребляет мощность
гармонического сигнала, и она может
выделяться только в сопротивлении.
Тогда получим
мВт.
Как видно результаты совпадают.
Если в цепи имеется несколько
сопротивлений, то общая потребляемая
цепью мощность будет равна сумме
мощностей, потребляемых каждым
сопротивлением в отдельности.
4.7. Задания для самостоятельного решения
Задание 4.1. Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепей, показанных на рис. 4.12, приВ,
мА,
кОм,
мГн
инФ.
Рис. 4.12
По результатам расчета постройте полные
векторные диаграммы цепей, проверьте
выполнимость законов Кирхгофа.
Задание 4.2.Постройте «качественные»
векторные диаграммы цепей, показанных
на рис. 4.12. Сравните их с расчетными
диаграммами из задания 4.1.
89
Задание 4.3.Определите мощность,
потребляемую от источника сигнала в
цепях, показанных на рис. 4.12. Проведите
расчеты, рассматривая цепь как двухполюсник
или выделив в ней энергопотребляющие
элементы.
Задание 4.4.Постройте «качественные»
полные векторные диаграммы цепей,
показанных на рис. 4.13.
Рис. 4.13
Задание 4.5.Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепи, показанной на рис. 4.10, прикОм,
нФ
иВ.
Постройте полную векторную диаграмму
цепи, сравните ее с приведенной на рис.
4.11. Определите мощность, потребляемую
цепью от источника.
90
Способы нахождения общего сопротивления цепи
Содержание
- 1 Определение сопротивления
- 2 Соединение параллельным и последовательным способом
- 2.1 Сопротивление при подключении проводников последовательно
- 2.2 Напряжение при подключении проводников последовательно
- 2.3 Параллельное подключение потребителей
- 2.4 Сопротивление при подключении проводников параллельно
- 2.5 Напряжение при подключении проводников параллельно
- 2.6 Сила тока при подключении проводников параллельно
- 3 Практическое применение
- 4 Комбинированное соединение
- 5 Видео по теме
Нередко при использовании электрооборудования бывает необходимо найти общее сопротивление цепи. С помощью данной величины определяют противодействие перемещению электричества в цепи или проводнике. В первый раз ее обосновали в законе Ома – трудах физика из Германии, ставившего опыты, связанные электричеством. По его имени и получила название единица сопротивления – Ом.
Определение сопротивления
Есть 2 вида напряжения – переменное и постоянное, а сопротивление электрической цепи может быть активным и реактивным. Дополнительно оно подразделяется на емкостное и индуктивное. Частоты в электросети не влияют на активное сопротивление. Этому параметру совершенно неважно, какой вид электроэнергии перемещается по проводам. А вот реактивная разновидность, наоборот, способна изменяться при перемене частоты. Дополнительно емкостные показатели в конденсаторах, а также индуктивные в трансформаторах проявляют себя по-разному.
Кроме сопротивления электрических приборов, работающих от сети, на ее общее состояние воздействуют промежуточные проводники, также способные сопротивляться электронапряжению. Чтобы правильно определить параметры электроцепи, необходимо понимать, что такое общее сопротивление, и по каким формулам осуществляется его расчет.
Необходимо учитывать, что индуктивный вид сопротивления при увеличении частоты электротока в сети также увеличивается. Его находят по формуле:
Емкостное сопротивление конденсатора с увеличением частоты электротока, наоборот, снижается. По этой причине принимается, что конденсатор при использовании постоянного тока имеет бесконечно большое сопротивление. Чтобы рассчитать емкостное сопротивление участка цепи, следует воспользоваться формулой:
Полное сопротивление включает в себя активную и реактивную составляющие. Графически оно выражается гипотенузой прямоугольного треугольника, катеты которого – активное и реактивное сопротивление.
Чтобы посчитать общее активное сопротивление, достаточно знать значение тока и напряжения в цепи, подключенной к определенному источнику питания. В данной ситуации достаточно воспользоваться законом Ома.
Но значение общего сопротивления в электроцепи зависит не только от используемых радиоэлементов и присутствующего в схеме вида сопротивления. Особое влияние в этом случае оказывает метод сборки электроцепи из отдельных элементов. На практике используется 2 способа подключения потребителей:
- Параллельный;
- Последовательный.
Соединение параллельным и последовательным способом
Эти способы часто используются в электротехнике и электронике, во многих случаях без них невозможна правильная работа оборудования или узла электроники. В первую очередь нужно понять, как функционируют простейшие цепи радиоэлектронных устройств — проводники.
По существу, проводник — особый материал, хорошо передающий электрический ток. Каждый из них обладает собственным сопротивлением. Вычисляют этот параметр для какого-либо проводника по следующей формуле:
По факту каждый проводник – это простейший резистор, имеющий собственное сопротивление.
Сопротивление при подключении проводников последовательно
При таком соединении к одному из проводников подключается следующий и таким образом соединяется цепочка из отдельных элементов. Подобная сборка электроцепи называется последовательной. Допустимо соединять в одну систему необходимое количество резисторов и прочих компонентов.
Узнать общее сопротивление схемы с последовательным подключением элементов совсем несложно. Для этого найдем, чему равна сумма сопротивлений всех использованных проводников. В результате получается формула для определения общего сопротивления цепи с последовательным подключением:
Например, соединяют последовательно в одну цепь 3 проводника. Один из них имеет сопротивление 3 Ома, следующий 4 Ома и последний 2 Ома. Для подсчета общего сопротивления нужно суммировать значение всех установленных элементов:
R цепи = R1 + R2 + R3 = 3 + 4 + 2 = 9 Ом.
Напряжение при подключении проводников последовательно
При соединении элементов цепи последовательно, через каждый из них проходит одинаковая сила тока. Но нужно понять, как определить напряжение и что с ним происходит на каждом участке цепи.
Следует вспомнить закон Ома и станет просто находить, чему равно реальное напряжение на каждом резисторе. Например, есть собранная система элементов с такими характеристиками как на рисунке:
В этой цепи, как выяснили выше, везде присутствует одинаковая сила тока. Но как узнать ее номинальное напряжение? Сперва нужно модифицировать систему, изменив ее как на изображении, представленном ниже. При этом принимаем сумму сопротивлений всех элементов системы, как RАВ:
В результате выходит по расчетам, что:
RАВ = R1 + R2 + R3 = 2 + 3 + 4 = 9 Ом.
По вычисленному RАВ с учетом закона Ома определяется сила тока, имеющаяся в цепи:
I = U/R = 9/9 = 1 Ампер.
После этого нужно найти напряжение на всех установленных резисторах. Точнее говоря, требуется вычислить значения, соответствующие UR1, UR2, UR3. Для их нахождения также следует воспользоваться законом Ома, согласно которому U = IR.
В результате выходит, что:
- UR1 = IR1= 1×2 = 2 В.
- UR2= IR2 = 1×3 = 3 В.
- UR3= IR3 = 1×4 = 4 В.
После этих вычислений если суммировать все найденные напряжения на отдельных участках, то в результате получится характеристика, равная 10 Вольтам. С учетом этого выходит, что U = UR1 + UR2 + UR3. В результате мы получили элементарный делитель напряжения.
Следовательно, при последовательном подключении сумма изменения напряжения на отдельных участках соответствует общему напряжению источника питания.
Параллельное подключение потребителей
Это соединение выполняется по-другому, пример показан на рисунке:
Сопротивление при подключении проводников параллельно
Общее сопротивление считают по формуле:
Если подсоединены параллельно только 2 компонента, то формулу можно сделать проще. Выглядеть она должна таким образом:
Напряжение при подключении проводников параллельно
С этим все просто. Благодаря тому, что все потребители подключаются параллельно, то они имеют равное напряжение. По этой причине выходит, что напряжение, которое можно получить на R1 не станет отличаться от показаний на всех других участках.
Сила тока при подключении проводников параллельно
Если все было просто с напряжением, то появляются сложности с силой тока. При соединении последовательным способом на всех проводниках одинаковая сила тока, а при параллельном все происходит наоборот. На установленные потребители будет поступать разная сила тока. Чтобы ее определить, придется еще раз воспользоваться законом Ома.
Проще разобраться в принципе работы и расчетов, на реальном примере. На изображении, расположенном ниже, 3 резистора соединены параллельно, и запитаны от источника U.
В любом из установленных устройств напряжение отличаться не будет, как выяснили ранее. Но на разных участках цепи будет собственная сила тока. Для каждого потребителя ее определяют по закону Ома, используя для этой цели соотношение I=U/R.
Таким образом получается:
- I1 = U/R1
- I2 = U/R2
- I3 = U/R3
Если в системе присутствуют другие подключенные параллельно приборы, для них используют: In = U/Rn
В результате сила тока всей цепи определяется по формуле:
В электронике способ параллельного подсоединения потребителей называют дополнительно «делителем тока», причина в том, что в схемах резисторы поступающий ток делят между установленными элементами.
Практическое применение
Попробуем решить следующую задачу: найти проходящую через каждый резистор силу тока и определить общую силу тока при известных номиналах резисторов и напряжении питания.
Решение
Расчет проводится с помощью выше приведенных формул:
- I1 = U/R1
- I2 = U/R2
- I3 = U/R3
В результате получается:
- I1 = U/R1 = 10/2=5 Ампер
- I2 = U/R2 = 10/5=2 Ампера
- I3 = U/R3 = 10/10=1 Ампер
После этого используется формула расчета общего сопротивления цепи, позволяющая определить силу тока, проходящую по ней.
Следовательно, Iобщ = 5 + 2 + 1 = 8 Ампер.
В результате получается I=I1 + I2 + I3 = 5+2+1=8 Ампер
Комбинированное соединение
На практике используются довольно сложные электроцепи, состоящие и из последовательно подключенных сопротивлений, и из параллельно. Такую цепь следует разбить на отдельные участки, включающие элементы, соединенные только последовательным способом или только параллельным.
Расчет следует начинать с того участка цепи, который является наиболее удаленным от двух конечных выводов, выступающих в роли контактов общего сопротивления. Схему соединения элементов, называемую «треугольником» можно трансформировать в «звезду» и обратно.
Чтобы не напрягаться с различными расчетами, на практике очень часто используют онлайн-калькуляторы.