Два кольца радиуса R изготовлены из одной и той же проволоки. Сопротивление проволоки, из которой изготовлено каждое кольцо, равно r. Кольца накладывают друг на друга так, что точки их касания опираются на сектор с углом раствора 
В точках контакта колец обеспечен хороший электрический контакт между ними. Кольца включают в электрическую цепь точками, наиболее удаленными от области пересечения (см. рис.). Найти сопротивление колец.
Спрятать решение
Решение.
Поскольку электрическое составленная из колец цепь симметрична относительно прямой, проходящей через точки А и В, поэтому ток между точками С и D (см. рисунок) не потечет, и эти участки можно выбросить из цепи без изменения ее сопротивления. Поэтому данная цепь эквивалентна цепи, показанной на следующем рисунке, причем сопротивления резисторов равны сопротивлениям проводов AC (или CB, или AD, или DB).
Эти сопротивления найдем из следующих соображений. Очевидно, что длины дуг CD равны 
Поэтому длина участка AC (или CB, или AD, или DB ) равна
А поскольку сопротивление проволоки пропорционально ее длине, сопротивление этих участков 
найдем из пропорции
Отсюда находим
Используя далее правила нахождения общих сопротивлений при последовательном и параллельном соединении проводников, получим для сопротивления цепи из колец
Ответ:
Спрятать критерии
Критерии проверки:
Классификатор: Электродинамика. Расчет электрического сопротивления
На этой странице ты можешь найти формулы для расчёта осевых моментов сопротивления простых сечений (фигур).
Формулы для расчёта моментов сопротивления
Моменты сопротивления обозначаются буквой – W.
Моменты сопротивления квадрата
Моменты сопротивления круга
Моменты сопротивления прямоугольника
Моменты сопротивления кольца
На проекте ssopromat.ru, ты также можешь найти другие справочные материалы здесь.
Момент сопротивления трубы или кольца (формула и расчет)
D — наружный диаметр сечения в мм; d — внутренний диаметр сечения в мм; y, z — центральные оси сечения.
Введите наружный диаметр сечения D в мм:
Введите внутренний диаметр сечения d в мм:
В результате моменты сопротивления относительно центральных осей y и z равны Wy = Wz=
0.00мм3
0.00см3
0.00м3
Как найти момент сопротивления трубы или кольца?
Момент сопротивления трубы (кольца) относительно центральной оси z равен моменту сопротивления относительно центральной оси y и рассчитывается по формуле:
Wy = Wz = Π.D3 (1-(d/D)4)/32 ,
где
Wy — момент сопротивления относительно центральной оси y в мм3 ;
Wz — момент сопротивления относительно центральной оси z в мм3 ;
D — наружный диаметр сечения в мм;
d — внутренний диаметр сечения в мм.
Момент инерции трубы или кольца (формула и расчет)
Радиус инерции трубы или кольца (формула и расчет)
|
Гл. 6. Постоянный электрический ток |
191 |
|
ρ(x) = div D =
|
= |
dD |
= ε0ε |
dE |
=ε0ε j |
d |
1 |
= − |
ε02ε jα = −ε0ε |
α2U |
1 |
= |
||||
|
dx |
dx |
ln(λ |
2 |
||||||||||||
|
dx λ(x) |
λ (x) |
2 |
/λ ) λ (x) |
||||||||||||
|
1 |
|
λ |
− λ |
2 |
U |
1 |
|||||||||||||||
|
= −ε0 |
ε |
2 |
1 |
= |
|||||||||||||||
|
d |
ln(λ2 |
/ λ1) λ |
2 |
(x) |
|||||||||||||||
|
= − |
ε |
0 |
ε(λ |
2 |
− λ |
)2 |
U |
||||||||||||
|
1 |
. |
||||||||||||||||||
|
ln(λ2 |
/ λ1) |
(λ d + (λ |
2 |
− λ |
)x)2 |
||||||||||||||
|
1 |
1 |
Полный свободный заряд в объеме конденсатора равен
|
d |
d |
dD |
|||||||||||||||
|
q = ∫ρ(x)dV = S∫ρ(x)dx = S∫ |
dx = |
||||||||||||||||
|
V |
0 |
0 |
dx |
||||||||||||||
|
1 |
1 |
(λ |
2 |
− λ )2 SU |
|||||||||||||
|
= S(D(d) − D(0)) = −q |
− q = ε |
εI |
− |
= −ε |
ε |
1 |
. |
||||||||||
|
λ |
λ |
λ λ |
/λ ) |
||||||||||||||
|
2 |
1 0 |
2 |
0 |
d ln(λ |
2 |
||||||||||||
|
1 |
1 2 |
1 |
Поскольку поле Е внутри неоднородно, в среде появится неоднородная поляризация P(x) = ε0(ε–1)E(x) и связанные поляризаци-
|
онные заряды, плотностью ρ′(x) = −div P = −ε |
(ε −1) |
dE |
. Учитывая, |
||||||||||||||||||||||||||||
|
0 |
dx |
||||||||||||||||||||||||||||||
|
что ρ(x) = ε |
ε |
dE |
, для объемной плотности поляризационных заря- |
||||||||||||||||||||||||||||
|
0 |
dx |
||||||||||||||||||||||||||||||
|
дов получаем |
|||||||||||||||||||||||||||||||
|
ρ′(x) = − |
ε −1 |
ε −1 (λ2 − λ1 )2 |
U |
||||||||||||||||||||||||||||
|
ρ(x) = −ε0 ε |
. |
||||||||||||||||||||||||||||||
|
ε |
ln(λ2 /λ1) |
(λ1d + (λ2 − λ1)x)2 |
|||||||||||||||||||||||||||||
|
Ответ: |
1) |
I = |
λ2 − λ1 |
SU ; |
|||||||||||||||||||||||||||
|
d ln(λ |
2 |
/λ ) |
|||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||
|
(λ2 − λ1)SU |
(λ2 − λ1)SU |
||||||||||||||||||||||||||||||
|
2) q1 = |
, q2 = − |
||||||||||||||||||||||||||||||
|
λ d ln(λ |
2 |
/λ ) |
λ |
2 |
d ln(λ |
2 |
/λ |
) |
|||||||||||||||||||||||
|
1 |
1 |
1 |
|||||||||||||||||||||||||||||
|
3) q = max (|q1|, |q2|); т.е. q = |q1| при λ1 < λ2 и q = |q2| при λ1 > λ2; |
|||||||||||||||||||||||||||||||
|
4) ρ(x) = − |
ε0 ε(λ2 − λ1)2 |
U |
; |
||||||||||||||||||||||||||||
|
ln(λ2 /λ1) |
(λ1d + (λ2 − λ1)x)2 |
||||||||||||||||||||||||||||||
|
5) ρ‘(x) = −ε0 |
ε −1 (λ2 − λ1 )2 |
U |
; |
||||||||||||||||||||||||||||
|
ε |
ln(λ2 / λ1) |
(λ1d + (λ2 − λ1)x)2 |
192 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
(λ − λ )2 SU 6) qсвоб = −ε0ε λ λ2 1λ λ .
1 2d ln( 2 / 1)
Задачи типа 6.2
Нахождение теплоты, выделяющейся в проводнике (среде) при протекании тока
Метод решения. Задачи этого типа решаются с помощью закона Джоуля–Ленца в интегральной или дифференциальной форме (6.8) и (6.9). Особое внимание во многих задачах следует уделить расчету сопротивления цепи.
Задача 6.3.7 (базовая задача). Пространство между обкладками цилиндрического конденсатора длиной L заполнено веществом с удельным сопротивлением ρ и диэлектрической проницаемостью ε = 1. Определить тепловую мощность тока, выделяемую в конденсаторе, если напряжение между его обкладками U0, радиусы обкладок R1 и R2. Краевыми эффектами пренебречь (рис. 6.7).
Рис.6.7. Цилиндрический конденсатор задачи 6.3.7
Решение
Сила тока, текущего в такой цепи, постоянна, однако плотность тока j зависит от расстояния до оси цилиндров.
По закону Джоуля–Ленца в дифференциальной форме (6.8) объёмная плотность тепловой мощности равна
1
PV = j E = ρ E2 .
В слое dr, находящемся на расстоянии r от оси конденсатора, будет выделяться мощность
dP = PV dV = ρ1 E2 2πrLdr .
По теореме Гаусса (см. (1.10), глава 1) напряженность электрического поля на расстоянии r от оси конденсатора равна
(где q – заряд на внутренней обкладке конденсатора). Тогда
|
Гл. 6. Постоянный электрический ток |
193 |
|
|
R2 1 |
2 |
q2 |
R2 dr |
q2 |
R |
|||||||||||||||||||
|
P = ∫ |
E |
2πrLdr = |
∫ |
= |
ln |
2 |
. |
|||||||||||||||||
|
ρ |
ρ 2πε2L |
r |
ρ 2πε2L |
R |
||||||||||||||||||||
|
R1 |
0 |
R1 |
0 |
1 |
||||||||||||||||||||
|
Используя выражение для емкости цилиндрического конденса- |
||||||||||||||||||||||||
|
тора ((3.8) |
главы 3) C = |
2πε0L |
, можно найти его заряд, как |
|||||||||||||||||||||
|
ln(R2 / R1) |
||||||||||||||||||||||||
|
q = CU = |
2πε |
LU |
0 |
P = |
2πLU |
2 |
||||||||||||||||||
|
0 |
. Окончательно получим |
0 |
. |
|||||||||||||||||||||
|
ln(R / R ) |
ρln(R / R ) |
|||||||||||||||||||||||
|
2 |
1 |
2 |
1 |
|||||||||||||||||||||
|
Ответ: P = |
2πLU 2 |
|||||||||||||||||||||||
|
0 |
. |
|||||||||||||||||||||||
|
ρln(R / R ) |
||||||||||||||||||||||||
|
2 |
1 |
Замечание 1. Можно решить данную задачу и другим способом
– найти сопротивление конденсатора (согласно методу, предложенному в п. 6.2.1), а затем воспользоваться законами Ома и Джоуля– Ленца в интегральной форме (6.5) и (6.8).
Замечание 2. Еще проще получить результат, воспользовавшись формулой (6.7) теоретического материала RC = ρε0ε, справедливой для электродов любой формы. Действительно, (учитывая, что ε = 1
и R = ρε0 ) сразу получаем
C
|
U 2 |
CU 2 |
2πLU 2 |
||||||
|
P = |
= |
= |
. |
|||||
|
ρε |
||||||||
|
R |
0 |
ρln(R / R ) |
||||||
|
2 |
1 |
Задача 6.3.8. Сферический конденсатор заполнен однородным веществом с диэлектрической проницаемостью ε и удельным сопротивлением ρ. Первоначально конденсатор не заряжен. Найти количество теплоты, выделившееся в системе, после сообщения внутренней обкладке конденсатора заряда q0. Радиусы обкладок конденсатора равны а и b = 3а.
Решение
После сообщения внутренней обкладке конденсатора заряда между его обкладками возникнет электрический ток, который будет течь до тех пор, пока разность потенциалов между внутренней и внешней обкладками не станет равной нулю. То есть в конечном состоянии весь заряд окажется распределенным по внешней обкладке конденсатора.
194 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Способ 1. Опираясь на решение задачи 6.3.3 можно рассматривать такой конденсатор как проводник сопротивлением R.
Обозначим через q1 = q заряд на внутренней сфере в произвольный момент времени, тогда заряд внешней сферы q2 = q0 – q. Разность потенциалов между ними в процессе перетекания заряда
|
U (q) = ϕ1 |
– ϕ2 |
1 |
q |
+ |
q |
2 |
− |
1 q + q |
2 |
= |
q b − a |
= |
q |
|||
|
= |
1 |
1 |
, |
|||||||||||||
|
4πε0 |
4πε0 |
4πε0 ab |
||||||||||||||
|
a |
b |
b |
C |
ab
где C = 4πεε0 b − a – ёмкость сферического конденсатора (см. (3.9),
глава 3). В соответствии с законом Джоуля–Ленца для тепла dQ, выделившегося в проводнике за время dt, получим:
dQ = I2Rdt = IR Idt = U R Idt = −U dq = − q dq ,
R C
где dq = –Idt – убыль заряда внутренней обкладки за время dt.
Всё тепло, выделившееся в конденсаторе за время перетекания заряда, можно рассчитать как
|
0 |
q |
q |
2 |
q2 |
b − a |
q2 |
|||||||||||||||||||||||||||||||
|
Q = −∫ |
dq = |
0 |
= |
0 |
= |
0 |
. |
||||||||||||||||||||||||||||||
|
8πεε |
|||||||||||||||||||||||||||||||||||||
|
q0 |
C |
2C |
0 |
ab |
12πaεε |
0 |
|||||||||||||||||||||||||||||||
|
Способ 2. |
Согласно замечанию к задаче 6.3.4, заряд на внут- |
||||||||||||||||||||||||||||||||||||
|
ренней обкладке конденсатора |
будет |
убывать |
по закону |
||||||||||||||||||||||||||||||||||
|
t |
|||||||||||||||||||||||||||||||||||||
|
q = q0 exp |
− |
. Тогда |
сила |
тока, |
текущего |
между обкладками |
|||||||||||||||||||||||||||||||
|
RC |
|||||||||||||||||||||||||||||||||||||
|
конденсатора будет зависеть от времени как |
|||||||||||||||||||||||||||||||||||||
|
dq |
q |
t |
|||||||||||||||||||||||||||||||||||
|
I(t) = |
= − |
0 |
exp − |
. |
|||||||||||||||||||||||||||||||||
|
dt |
RC |
RC |
|||||||||||||||||||||||||||||||||||
|
Все тепло, выделившееся в конденсаторе, вычисляется как |
|||||||||||||||||||||||||||||||||||||
|
∞ |
∞ |
q |
2 |
2t |
q2 |
q2 |
b − a |
||||||||||||||||||||||||||||||
|
Q = ∫I 2Rdt = ∫R |
0 |
exp − |
dt |
= |
0 |
= |
0 |
. |
|||||||||||||||||||||||||||||
|
8πεε0 |
|||||||||||||||||||||||||||||||||||||
|
0 |
0 |
RC |
RC |
2C |
ab |
q2
Ответ: Q = 0 . 12πaεε0
Замечание 1. Выделившееся тепло не зависит от сопротивления между обкладками конденсатора. Величина сопротивления влияет только на скорость процесса.
|
Гл. 6. Постоянный электрический ток |
195 |
|
Замечание 2. Выделившееся тепло проще найти из закона сохранения энергии без расчета силы тока. Оно будет равно разности начальной и конечной электростатической энергии системы. Учи-
q2
тывая, что энергия заряженной сферы радиуса r равна 8πε0r , сразу
|
получаем Q = W1 −W2 = |
q2 |
− |
q2 |
= |
q2 |
||||
|
0 |
. |
||||||||
|
8πε |
a |
8πε |
0 |
3a |
12πaεε |
0 |
|||
|
0 |
Задачи типа 6.3
Цепи квазилинейных проводников
Метод решения. Для неразветвленных (последовательных) цепей – применение закона Ома для полной цепи (6.12). Для разветвленных цепей – применение правил Кирхгофа в форме (6.13– 6.14) или (6.15).
Два примера решения задач типа 6.2.3 были рассмотрены выше при анализе формул (6.12–6.14).
Задача 6.3.9 (базовая задача). Найти сопротивление между точками А и В в схеме, представленной на рис. 6.8а.
Решение
|
E |
2r |
r |
F |
||||||||||||||||||||
|
G |
|||||||||||||||||||||||
|
I2 |
r |
I3 |
|||||||||||||||||||||
|
H |
|||||||||||||||||||||||
|
A |
2r |
r |
В |
A |
r |
2r |
В |
||||||||||||||||
|
r |
|||||||||||||||||||||||
|
I1 |
|||||||||||||||||||||||
|
r |
2r |
E |
|||||||||||||||||||||
|
D |
C |
||||||||||||||||||||||
Рис. 6.8 а – схема соединения резисторов в задаче 6.3.9; б – схема цепи и контурные токи
Пусть к точкам А и В, между которыми нужно определить сопротивление, подключен источник с ЭДС E (рис. 6.8б). Применим метод контурных токов. Проводники разбивают данную схему на 3 области. Каждой из них сопоставим соответствующие контурные
196 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
токи I1-3, направление которых произвольно выберем, например, как показано на рис. 6.8б, пунктирными линиями со стрелкой. Запишем 3 независимых уравнений Кирхгофа, совершив обходы трех контуров.
|
Контур ABCD: |
(I1 − I2 )r + (I1 − I3 )2r = E, |
|||||
|
DEFC: |
I2 2r + I3r = E , |
|||||
|
AEGH: |
I2 2r + ( I2 − I3 )r + ( I2 − I1 )r = 0 . |
|||||
|
Решая получившуюся систему уравнений, получаем I |
= |
5E |
, |
|||
|
1 |
7r |
|||||
откуда находим сопротивление цепи RAB = E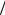
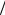
I1 = (7
5)r .
Ответ: RAB = (7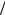
5)r .
Задачи типа 6.4
Разветвленные цепи, сводимые к неразветвленным благодаря элементам симметрии
Методы решения. Задачи этого типа, в принципе, можно решить общим методом с помощью правил Кирхгофа. При этом, однако, решение зачастую получается громоздким или в ряде случаев приводит к бесконечной системе уравнений, анализ которой требует особых методов.
Возможны разные способы сведения к задаче с неразветвленной цепью: соединение точек равного потенциала, удаление проводников с нулевым током, соединяющих точки равного потенциала, добавление дополнительного звена к бесконечной повторяющейся цепочке и др.
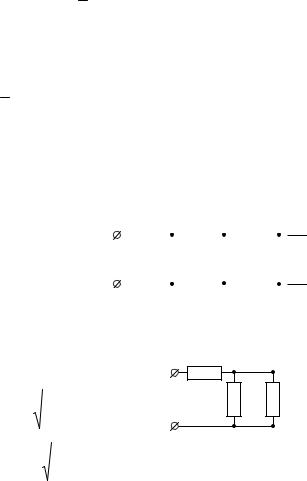
Задача 6.3.10. Найти сопротивление RAB между точками А и В в схеме, представленной на рис. 6.9. Даны величины сопротивлений
R, r, R1.
|
Решение |
||
|
При подключении данной це- |
A |
|
|
пи к источнику ЭДС в силу сим- |
||
|
метрии схемы потенциалы точек С |
||
|
и D будут одинаковы и ток в R1 |
||
|
отсутствует. |
|
С |
|||||||||
|
R |
r |
В |
|||||||
|
R1 |
|||||||||
|
R |
r |
||||||||
|
D |
|||||||||
Рис. 6.9. Схема к задаче 6.3.10
|
Гл. 6. Постоянный электрический ток |
197 |
|
Способ 1. Ввиду равенства потенциалов точек С и D их можно соединить между собой. Схема сводится к последовательному соединению левого и правого участков с сопротивлениями R/2 и r/2
соответственно, что дает RAB = 1 (R + r) . 2
Способ 2. Поскольку тока в участке CD нет, резистор R1 можно убрать. Схема сводится к параллельному соединению двух одинаковых участков с сопротивлением R + r, что дает тот же результат.
1
Ответ: RAB = 2 (R + r) .
Задача 6.3.11 (базовая задача). Бесконечная цепь образована повторением звена R1, R2. Найти сопротивление RАВ между точками
А и В (рис.6.10).
Решение
Пусть вся цепочка эквивалентна сопротивлению RАВ. Ввиду ее бесконечности добавление еще одного звена R1, R2 не изменит ее сопротивления (рис. 6.11), поэтому
|
R |
= R + |
R2RAB |
. |
||
|
AB |
1 |
R + R |
AB |
||
|
2 |
Решая это уравнение, получаем:
|
A |
R1 |
R1 |
R1 |
||||||||||||||
|
R2 |
R2 |
R2 |
|||||||||||||||
|
В |
|||||||||||||||||
|
Рис. 6.10. Бесконечная |
цепь |
(задача |
|||||||||||||||
|
6.3.11) |
AR1
|
R |
1+ 4R |
|||||||||||||
|
R |
= |
1 |
1+ |
2 |
. |
|||||||||
|
AB |
2 |
R1 |
||||||||||||
|
R |
1+ 4R |
|||||||||||||
|
Ответ: R |
= |
1 |
1 |
+ |
2 |
. |
||||||||
|
AB |
2 |
R1 |
||||||||||||
В
Рис. 6.11. Эквивалентная
схема соединения элементов цепи в задаче 6.3.11
Задача 6.3.12. Имеется бесконечная сетка с квадратными ячейками. Сопротивление каждого проводника между узлами ячейки равно R. Найти сопротивление RAB между соседними узлами (рис. 6.12).
198 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Решение
Данная задача не сводится к нераз-
|
ветвленной цепи, но позволяет ввиду |
|||||||||||
|
симметрии эффективно применить прин- |
|||||||||||
|
цип суперпозиции. |
|||||||||||
|
A |
B |
||||||||||
|
На бесконечности потенциал везде |
|||||||||||
|
равен нулю, поэтому бесконечно удален- |
|||||||||||
|
ные узлы можно соединить между собой |
|||||||||||
|
проводником, не меняя картины протека- |
|||||||||||
|
Рис. 6.12. Бесконечная про- |
|||||||||||
|
ния токов. Подсоединим источник ЭДС |
|||||||||||
|
плюсом к точке А, а минусом – к этому |
водящая сетка с квадрат- |
||||||||||
|
ными ячейками (задача |
|||||||||||
|
бесконечно удаленному проводнику. То- |
6.3.12 |
||||||||||
|
гда в силу симметрии ток I, входящий в |
|||||||||||
|
А, разделится на четыре части величиной |
I 4 на каждом из 4 про- |
водников, выходящих из А. Подсоединим теперь такой же источник ЭДС минусом к точке В, а плюсом – к бесконечно удаленному проводнику. Поскольку относительно бесконечности точка В эквивалентна А, то в точку В по каждому из 4 проводников будут сходиться токи величиной − I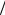
4 , давая в сумме полный ток –I. Пусть будут теперь подключены оба источника ЭДС. Полный ток на бесконечно удаленный проводник обратится в нуль, т.е. ток будет течь только между точками А и В.
|
По проводу АВ потечет ток |
IAB = I 4 + I 4 = I 2 , следователь- |
|
но, напряжение на нем будет |
UAB = (I 2)R . По закону Ома |
RAB = UAB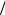 
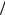
IAB = R
2 . Решение этой задачи по правилам Кирхгофа привело бы к бесконечной системе уравнений.
1
Ответ: RAB = 2 R .
§6.4. Задачи для самостоятельного решения
6.4.1. Два одинаковых металлических шара с радиусами a находятся в однородной среде с удельным сопротивлением ρ. Определить сопротивление R между шарами, считая, что расстояние между шарами много больше их радиуса.
ρ
Ответ: R = 2πa .
|
Гл. 6. Постоянный электрический ток |
199 |
|
6.4.2. Найти сопротивление между внутренней и внешней поверхностями кольца толщиной d. Материал кольца имеет удельное сопротивление ρ. Радиусы внутренней и внешней частей кольца равны a и b (a < b).
Ответ: R = ρ ln b . 2πd a
6.4.3. Плоский конденсатор, заполненный веществом, диэлектрическая проницаемость которого равна ε, за время τ теряет треть сообщенного ему заряда. Считая, что утечка заряда происходит только через диэлектрическую прокладку, найти удельное сопротивление её материала.
τ
Ответ: ρ = ( ) .
εε0 ln 3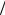
2
6.4.4. Обкладкам конденсатора емкости С сообщили заряды, равные соответственно +q0 и –q0. Затем обкладки замкнули через сопротивление R. Найти заряд, протекший в цепи за время τ.
Ответ: q = q0 (1− e−τ
RC ).
6.4.5. Зазор между обкладками плоского конденсатора толщиной d заполнен последовательно двумя диэлектрическими слоями одинаковой толщины. Удельные сопротивления слоев соответственно равны ρ1 и ρ2, диэлектрическая проницаемость ε = 1. Площадь обкладок S. На конденсатор подано напряжение U. Найти тепловую мощность, выделяемую в каждом слое.
|
Ответ: P1 = |
2U 2 |
ρ |
P2 = |
2U 2 |
ρ |
2 |
||||||||
|
1 |
S , |
S . |
||||||||||||
|
d |
(ρ + ρ |
2 |
)2 |
d |
(ρ + ρ |
2 |
)2 |
|||||||
|
1 |
1 |
6.4.6. Металлический шар радиуса R находится в среде с удельной проводимостью λ. На шар в некоторый момент времени помещен заряд q. Определить количество теплоты, выделившееся во всей среде за время, пока весь заряд стечет с шара.
q2
Ответ: Q= 8πε0R .
200ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
6.4.7.Пространство между обкладками цилиндрического конденсатора длины L заполнено двумя слоями веществ с удельными
проводимостями λ1 и λ2 соответственно. Определить мощность, выделяемую в первом слое, если напряжение между обкладками U. Радиусы цилиндров равны R1, R2, R3.
|
2πU 2L λ λ |
2 ln |
R2 |
|||||||||
|
1 |
2 |
R1 |
|||||||||
|
Ответ: P = |
. |
||||||||||
|
R2 |
R3 |
2 |
|||||||||
|
λ2 ln |
+ λ1 ln |
||||||||||
|
R1 |
R2 |
||||||||||
6.4.8. Пространство между обкладками сферического конденсатора, радиусы обкладок которого равны R1 и R2, заполнено веществом с удельным сопротивлением ρ. Какое количество теплоты будет выделяться в единицу времени в такой системе, если между электродами конденсатора поддерживается постоянная разность потенциалов U?
4πU 2R R
Ответ: P = ( 1 2) .
ρ R2 − R1
6.4.9. В схеме, представленной на рис. 6.13. известны ЭДС и внутренние сопротивления источников E1, E2, E3, r1, r2, r3.
1)Найти напряжение U, показываемое идеальным вольтметром V (рис. 6.13).
E2, r2
V
E1, r1
E3, r3
Рис. 6.13. Электрическая схема задачи 6.4.9
2) Чему равно U, если E1/r1 = E2/r2 = E3/r3?
|
Ответ: 1) U = −r |
E1 + E2 + E3 |
− E ; 2) U = 0. |
||
|
+ r |
+ r |
|||
|
1 r |
1 |
|||
|
1 |
2 |
3 |
6.4.10. Аккумулятор с ЭДС E = 2,6 В, замкнутый на внешнюю цепь, дает ток I = 1 А при напряжении на его клеммах U = 2 В. Найти тепловую мощность Р, выделяемую в аккумуляторе, и мощность Pэл, которую развивают в нем электрические силы.
Ответ: P = I(E – U) = 0,6 Вт, Pэл = –IU = –2 Вт.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Проволока из нихрома изогнута в виде кольца радиусом 1 м. В центре кольца помещен источник тока с ЭДС 2 В и внутренним сопротивлением 1,5 Ом. Элемент соединен с точками C и D кольца по диаметру с помощью такой же нихромовой проволоки сечением 1 мм2. Определить разность потенциалов между точками C и D.
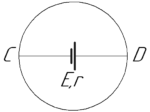
Задача №7.2.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(r_{рад}=1) м, (rm E=2) В, (r=1,5) Ом, (S=1) мм2, (U-?)
Решение задачи:
Изображенную в условии задачи электрическую цепь представим в другом виде, смотрите схему, приведенную справа. Здесь (R_1) – сопротивление проводника из нихрома, длиной (r_{рад}) (т.е. двумя резисторами (R_1) мы показали участки от источника до точек C и D), (R_2) – сопротивление проводника из нихрома, длиной ({pi}r_{рад}) (т.е. двумя резисторами (R_2) мы показали участки в виде дуг окружности от точки C до точки D).
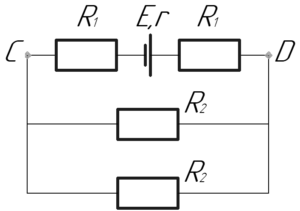
Понятно, что численные значения сопротивлений (R_1) и (R_2) можно найти по таким известным формулам:
[left{ begin{gathered}
{R_1} = rho frac{{{r_{рад}}}}{S} hfill \
{R_2} = rho frac{{pi {r_{рад}}}}{S} hfill \
end{gathered} right.]
В этих формулах (rho) – удельное электрическое сопротивление нихрома, равное 1100 нОм·м.
Учитывая, что два проводника (R_2) соединены параллельно, то разность потенциалов между точками C и D можно определить таким образом:
[U = Ifrac{{{R_2}}}{2};;;;(1)]
Силу тока (I) в электрической цепи найдем, применив закон Ома для полной цепи:
[I = frac{{rm E}}{{R + r}};;;;(2)]
Здесь (R) – полное внешнее сопротивление электрической цепи, которое можно посчитать по такой формуле (поскольку два последовательно соединенных резистора (R_1) соединены последовательно с двумя параллельно соединенными резисторами (R_2)):
[R = 2{R_1} + frac{{{R_2}}}{2}]
[R = frac{{4{R_1} + {R_2}}}{2};;;;(3)]
Подставим (3) в (2):
[I = frac{{rm E}}{{frac{{4{R_1} + {R_2}}}{2} + r}}]
[I = frac{{2{rm E}}}{{4{R_1} + {R_2} + 2r}}]
Это выражение подставим в (1), тогда:
[U = frac{{{rm E}{R_2}}}{{4{R_1} + {R_2} + 2r}}]
Осталось только использовать формулы для нахождения (R_1) и (R_2), приведенные в системе:
[U = frac{{{rm E}rho frac{{pi {r_{рад}}}}{S}}}{{4rho frac{{{r_{рад}}}}{S} + rho frac{{pi {r_{рад}}}}{S} + 2r}}]
Домножим и числитель, и знаменатель на (S):
[U = frac{{{rm E}rho pi {r_{рад}}}}{{4rho {r_{рад}} + rho pi {r_{рад}} + 2rS}}]
[U = frac{{{rm E}rho pi {r_{рад}}}}{{rho {r_{рад}}left( {4 + pi } right) + 2rS}}]
Задача решена в общем виде, теперь посчитаем ответ:
[U = frac{{2 cdot 1100 cdot {{10}^{ – 9}} cdot 3,14 cdot 1}}{{1100 cdot {{10}^{ – 9}} cdot 1 cdot left( {4 + 3,14} right) + 2 cdot 1,5 cdot {{10}^{ – 6}}}} = 0,637;В = 637;мВ]
Ответ: 637 мВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.40 Определите заряд на обкладках конденсатора C=1 мкФ. ЭДС источника 4 В, внутреннее
7.2.42 Указать направление вектора сторонней силы, действующей на положительный заряд q
7.2.43 В конце заряда батареи аккумуляторов током I1 присоединенный к ней вольтметр показывал