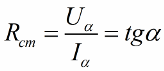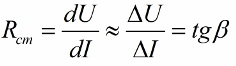Как найти сопротивление по вольт амперной характеристики

Как по вах определить сопротивление цепи

В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями.

В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения.
Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат.
Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
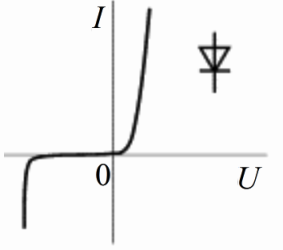
Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.1), а полупроводниковые диоды — несимметричные характеристики (рис. 5.2).

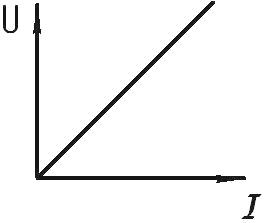
Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3)

.

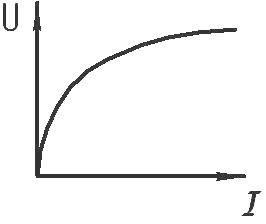
Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока.

Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики (рис. 5.4).

.

При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения.

5.2. Графический метод расчета нелинейных цепей
постоянного тока

Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения. Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6.

К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:

(5.1)

По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).

При параллельном соединении двух нелинейных элементов (рис. 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3.
(аг = ав + аб)

Далее задаваясь произвольным значением напряжения больше и меньше U’, можно построить ВАХ всей цепи (кривая 3). Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I₁ и I₂ в отдельных ветвях с учетом масштаба тока m_I.

В случае смешанного (рис. 5.9) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.

6. Электрические цепи однофазного
переменного тока

Не нашли то, что искали? Воспользуйтесь поиском:

В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями.

В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения.
Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат.
Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.1), а полупроводниковые диоды — несимметричные характеристики (рис. 5.2).

Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3)

.

Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока.

Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики (рис. 5.4).

.

При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения.

5.2. Графический метод расчета нелинейных цепей
постоянного тока

Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения. Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6.

К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:

(5.1)

По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).

При параллельном соединении двух нелинейных элементов (рис. 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3.
(аг = ав + аб)

Далее задаваясь произвольным значением напряжения больше и меньше U’, можно построить ВАХ всей цепи (кривая 3). Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I₁ и I₂ в отдельных ветвях с учетом масштаба тока m_I.

В случае смешанного (рис. 5.9) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.

6. Электрические цепи однофазного
переменного тока

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8832 — | 7545 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.

Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется.

Кроме того речь может идти не только об элементах, обладающих чисто активными сопротивлениями R, но и о линейных индуктивностях L и емкостях C, где постоянными будут зависимость магнитного потока от тока — Ф(I) и зависимость заряда конденсатора от напряжения между его обкладками — q(U).

Яркий пример линейного элемента — проволочный резистор. Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.

Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью.

Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется.

В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.

Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи нелинеен.

Для нелинейных элементов свойственно определенное статическое сопротивление в каждой точке их ВАХ, то есть каждому отношению напряжения к току, в каждой точке на графике, — ставится в соответствие определенное значение сопротивления. Оно может быть посчитано как тангенс угла альфа наклона графика к горизонтальной оси I, как если бы эта точка лежала на линейном графике.

Еще у нелинейных элементов есть так называемое дифференциальное сопротивление, которое выражается как отношение бесконечно малого приращения напряжения — к соответствующему изменению тока. Данное сопротивление можно посчитать как тангенс угла между касательной к ВАХ в данной точке и горизонтальной осью.

Такой подход делает возможным простейший анализ и расчет простых нелинейных цепей.

На рисунке выше показана ВАХ типичного диода. Она располагается в первом и в третьем квадрантах координатной плоскости, это говорит нам о том, что при положительном или отрицательном приложенном к p-n-переходу диода напряжении (в том или ином направлении) будет иметь место прямое либо обратное смещение p-n-перехода диода. С ростом напряжения на диоде в любом из направлений ток сначала слабо увеличивается, а после резко возрастает. По этой причине диод относится к неуправляемым нелинейным двухполюсникам.

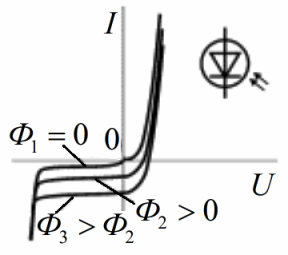
На этом рисунке показано семейство типичных ВАХ фотодиода в разных условиях освещенности. Основной режимом работы фотодиода — режим обратного смещения, когда при постоянном световом потоке Ф ток практически неизменен в довольно широком диапазоне рабочих напряжений. В данных условиях модуляция освещающего фотодиод светового потока, приведет к одновременной модуляции тока через фотодиод. Таким образом, фотодиод — это управляемый нелинейный двухполюсник.

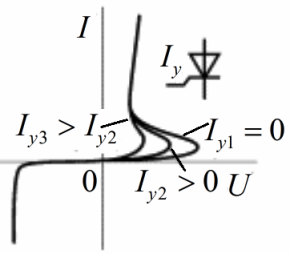
Это ВАХ тиристора, здесь видна ее явная зависимость от величины тока управляющего электрода. В первом квадранте — рабочий участок тиристора. В третьем квадранте начало ВАХ — малый ток и большое приложенное напряжение (в запертом состоянии сопротивление тиристора очень велико). В первом квадранте ток велик, падение напряжения мало — тиристор в данный момент открыт.

Момент перехода из закрытого — в открытое состояние наступает тогда, когда на управляющий электрод подан определенный ток. Переключение из открытого состояния — в закрытое происходит при снижении тока через тиристор. Таким образом, тиристор — это управляемый нелинейный трехполюсник (как и транзистор, у которого ток коллектора зависит от тока базы).