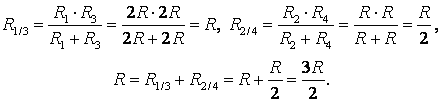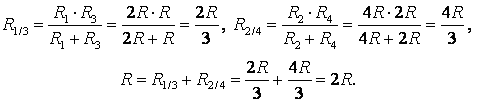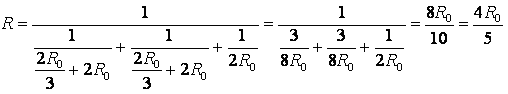Как найти сопротивление проволочного куба

Рассмотрим классическую задачу. Дан куб, рёбра которого представляют собой проводники с каким-то одинаковым сопротивлением. Этот куб включается в электрическую цепь между всевозможными его точками. Вопрос: чему равно сопротивление куба в каждом из этих случаев? В данной статье репетитор по физике и математике рассказывает о том, как решается эта классическая задача. Присутствует также видеоурок, в котором вы найдёте не только подробное объяснение решения задачи, но и реальную физическую демонстрацию, подтверждающую все вычисления.

Итак, куб может быть включен в цепь тремя различными способами.

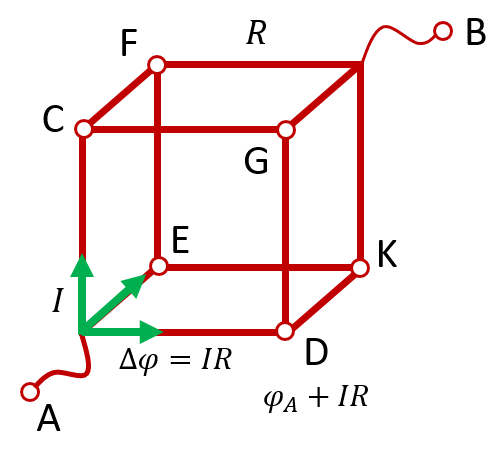
Сопротивление куба между противоположными вершинами

В этом случае ток, дойдя до точки A, распределяется между тремя рёбрами куба. При этом, поскольку все три ребра эквивалентны с точки зрения симметрии, ни одному из рёбер нельзя придать большую или меньшую «значимость». Поэтому ток между этими рёбрами должен распределиться обязательно поровну. То есть сила тока в каждом ребре равна :

В результате получается, что падение напряжения на каждом из этих трёх рёбер одинаково и равно , где — сопротивление каждого ребра. Но падение напряжение между двумя точками равно разности потенциалов между этими точками. То есть потенциалы точек C, D и E одинаковы и равены . Из соображений симметрии потенциалы точек F, G и K также одинаковы.

Точки с одинаковым потенциалом можно соединять проводниками. Это ничего не изменит, потому что по этим проводникам всё равно не потечёт никакой ток:

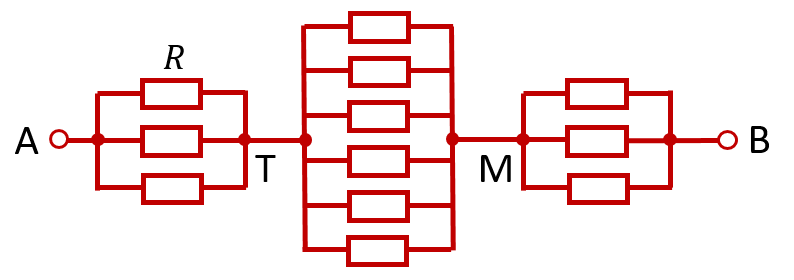
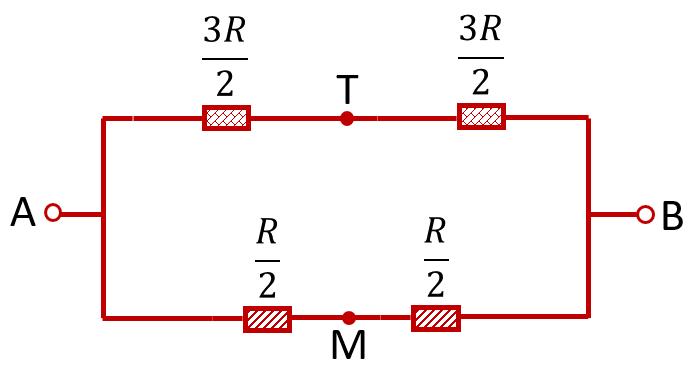
В результате получим, что рёбра AC, AD и AE соединятся в одной точке. Назовём её точкой T. Точно также рёбра FB, GB и KB соединятся в одной точке. Назовём её точкой M. Что касается оставшихся 6 рёбер, то все их «начала» окажутся соединены в точке T, а все концы — в точке M. В результате мы получим следующую эквивалентную схему:

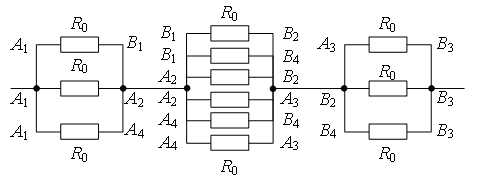
Посчитать сопротивление такой схемы уже не составляет труда:

Сопротивление куба между противолежащими углами одной грани

В данном случае эквивалентными являются рёбра AD и AC. По ним потечёт одинаковый ток . Кроме того, эквивалентными также являются KE и KF. По ним потечёт одинаковый ток . Ещё раз повторим, что ток между эквивалентными рёбрами должен распределиться поровну, в противном случае нарушится симметрия:

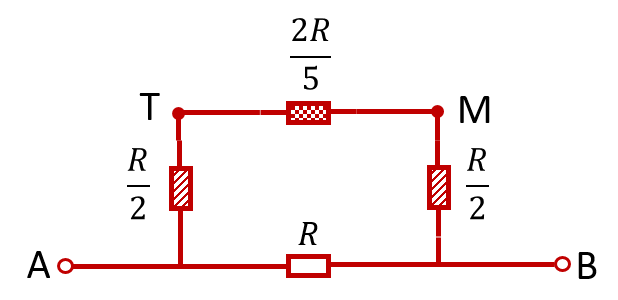
Таким образом, в данном случае одинаковым потенциалом обладают точки C и D, а также точки E и F. Значит эти точки можно объединить. Пусть точки C и D объединятся в точке M, а точки E и F — в точке T. Тогда получится следующая эквивалентная схема:

На вертикальном участке (непосредственно между точками T и M) ток не течёт. Действительно, ситуация аналогична уравновешенному измерительному мосту. Это означает, что данной звено можно исключить из цепи. После этого посчитать общее сопротивление не составит труда:

Сопротивление верхнего звена равно , нижнего — . Тогда общее сопротивление равно:

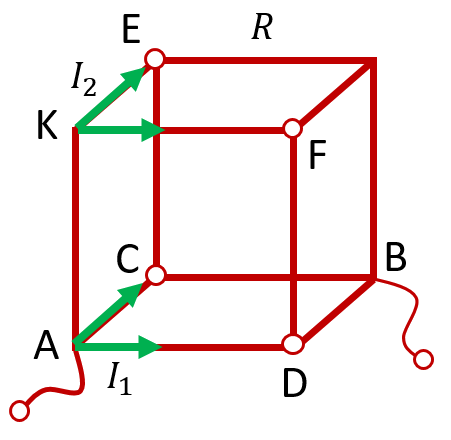
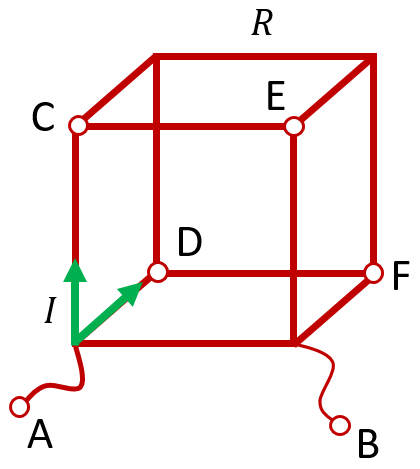
Сопротивление куба между прилежащими вершинами одной грани

Это последний возможный вариант подключения куба в электрическую цепь. В этом случае эквивалентными рёбрами, через которые будет течь одинаковый ток, являются рёбра AC и AD. И, соответственно, одинаковые потенциалы будут иметь точки C и D, а также симметричные им точки E и F:

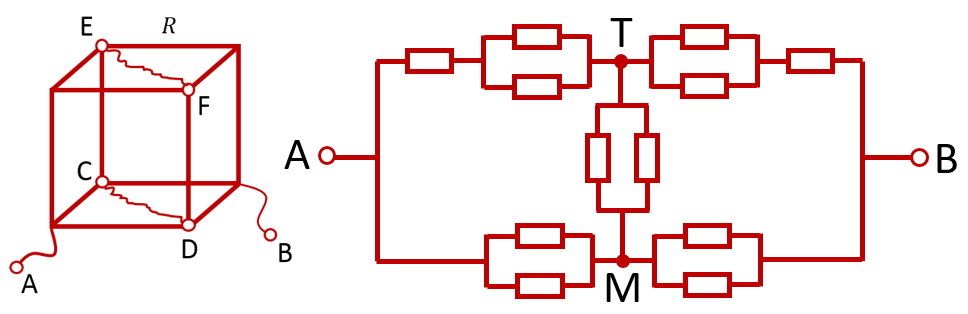
Вновь соединяем попарно точки с одинаковыми потенциалами. Мы можем это сделать, потому что ток между этими точками не потечёт, даже если соединить их проводником. Пусть точки C и D объединятся в точку T, а точки E и F — в точку M. Тогда можно нарисовать следующую эквивалентную схему:

Общее сопротивление полученной схемы рассчитывается стандартными способами. Каждый сегмент из двух параллельно соединённых резисторов заменяем на резистор сопротивлением . Тогда сопротивление «верхнего» сегмента, состоящего из последовательно соединённых резисторов , и , равно .

Этот сегмент соединён со «средним» сегментом, состоящим из одного резистора сопротивлением , параллельно. Сопротивление цепи, состоящей из двух параллельно соединённых резисторов сопротивлением и , равно:

То есть схема упрощается до ещё более простого вида:

Как видно, сопротивление «верхнего» П-образного сегмента равно:

Ну а общее сопротивление двух параллельно соединённых резисторов сопротивлением и равно:

Эксперимент на измерению сопротивления куба

Чтобы показать, что всё это не математический трюк и что за всеми этими вычислениями стоит реальная физика, я решил провести прямой физической эксперимент по измерению сопротивления куба. Вы можете посмотреть этот эксперимент в видео, которые находится в начале статьи. Здесь я размещу фотографии экспериментальной установки.

Специально для этого эксперимента я спаял куб, рёбрами которого являются одинаковые резисторы. Также у меня есть мультиметр, который я включил в режиме измерения сопротивления. Сопротивление одиночного резистора равно 38.3 кОм:

Теперь смотрим сопротивление куба при различных его подключениях:

1) При подключении между диаметрально противоположным граням сопротивление равно 32.3 кОм:

Расчётное значение равно кОм.

2) При подключении между соседним вершинам одной грани измеренное значение сопротивления равно 22.6 кОм:

Расчётное значение составляет кОм.

3) При подключении между противоположным вершинам одной грани сопротивление равно 28.9 кОм:

Расчётное значение равно кОм.

Как видите, мы получили очень хорошее согласование экспериментальных данных с результатам наших расчётов. Ошибка находится на уровне 1%. Погрешность измерений есть всегда. Это нормально. В данном случае эта погрешность связана, скорее всего, с тем, что сопротивление резисторов не строго 38.3 кОм, а может немного варьироваться.

Материал подготовил репетитор по физике и математике, Сергей Валерьевич

Если вам понравилась статья, смотрите также:

• Задачи на тему «Концентрические проводящие сферы»
• Решение задач на тему «Потенциал»
• Потенциал электростатического поля

2017-01-19   

Рассчитайте полное сопротивление проволочного куба, каждое ребро которого имеет сопротивление $r$, если он подключен к источнику

а) по главной диагонали куба;

б) по диагонали грани;

в) вдоль ребра.

Решение:

рис.1



рис.2



рис.3



рис.4

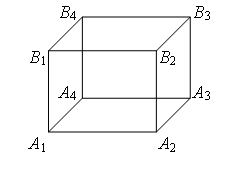
На рис. 1 все вершины куба пронумерованы. Симметрия системы позволяет утверждать, что некоторые вершины будут иметь один и тот же потенциал. Это позволяет в каждом случае свести задачу к расчету эквивалентной схемы, содержащей только последовательно и параллельно соединенные сопротивления.

а) Напряжение приложено к вершинам / и 8. В этом случае одинаковы потенциалы вершин 2, 3, 4, поскольку при повороте куба на угол $120^{ circ}$ вокруг главной диагонали они переходят друг в друга, а сам куб переходит в себя (отвернувшийся на минуту человек не сможет определить, повернули мы куб или нет). Аналогично, одинаковый потенциал имеют вершины 5, 6, 7. Точки с одинаковым потенциалом можно замкнуть накоротко. Эквивалентная схема имеет вид, представленный на рис. 2. Очевидно, что $R = r/3 + r/6 + r/3 = (5/6)r$.

К тому же результату можно прийти иначе, если заметить, что из-за симметрии подключения вершин куба токи в ребрах 1-2, 1-3 и 1-4 одинаковы и составляют 1/3 тока $I$ в неразветвленной части цепи. Точно также одинаковы и равны $I/3$ токи в ребрах 5-8, 6-8, 7-8, а токи в ребрах 2-7 и 2-6 составляют половину тока в ребре 1-2 и, следовательно, равны $I/6$. Запишем теперь напряжение между точками 1 и 8 в виде

$U = phi_{8} phi_{1} = phi_{8} — phi_{7} + phi_{7} — phi_{2} + phi_{2} — phi_{1} = frac{I}{3} r + frac{I}{6} r + frac{I}{3} r = frac{5}{6} Ir$

Теперь для $R$ получаем: $R = U/I = (5/6)r$.

б) Напряжение приложено между точками 1 и 5. Теперь одинаковы потенциалы вершин 3-4 и 6-7. Эквивалентная схема показана на рис. 3. Очевидно, что и сопротивления, соединяющие точки 3-4 и 6-7, могут быть удалены без изменения полного сопротивления, поскольку потенциалы этих точек тоже оказываются одинаковыми. Теперь полное сопротивление легко сосчитать: $R = = (3/4)r$.

в) Напряжение приложено между точками 1 и 2. Снова одинаковы потенциалы вершин 3-4 и 6-7. Эквивалентная схема приведена на рис. 4. Используя формулы для параллельного и последовательного соединения сопротивлений, получаем $R = (7/12)r$.

Ответ: а) $R = (5/6)r$; б) $R = (3/4)r$ в) $R = (7/12)r$.

Содержание книги

Предыдующая страница

§11. Постоянный электрический ток

11.7 Примеры расчета сопротивлений цепи.

Пользуясь полученными правилами расчета последовательного и параллельного соединения, можно рассчитать сопротивление сложной цепи, содержащей резисторы, соединенные различными комбинированными способами. Для этого необходимо последовательно заменять участки цепи (последовательного, параллельного соединения) эквивалентными сопротивлениями.

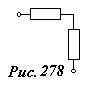
Подчеркнем, что вид соединения определяется порядком протекания электрического тока, а не тем как элементы расположены в том или ином приборе, и тем более не тем, как они изображены на схеме. Так два резистора, показанные на рис. 278 соединены последовательно, а не перпендикулярно!

Рассмотрим несколько примеров расчета сопротивлений разветвленных цепей.

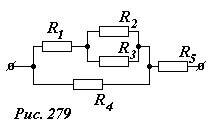
Рассчитаем сопротивление цепи, изображенной на рисунке 279. Для упрощения расчетов и экономии места положим, что сопротивления всех резисторов одинаковы и равны R.

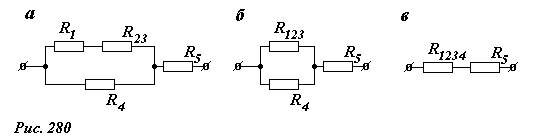
Будем шаг за шагом упрощать схему, заменяя ее части эквивалентными сопротивлениями (Рис 280).

Резисторы R₂ и R₃ соединены параллельно, поэтому их общее сопротивление равно (~R_{23} = frac{1}{2} R) (рис. 280а); резисторы R₁ и R₂₃ соединены последовательно, следовательно, их сопротивление (~R_{123} = R_1 + R_{23} = R + frac{1}{2} R = frac{3}{2} R) (рис. 280б); для расчета параллельно соединенных резисторов R₁₂₃ и R₄ (рис. 280 в) воспользуемся формулой

(~R_{1234} = frac{R_{123} cdot R_4}{R_{123} + R_4} = frac{frac{3}{2} R cdot R}{frac{3}{2} R + R} = frac{3}{5} R) ;

наконец, этот резистор последовательно соединен с резистором R₅, поэтому общее сопротивление исходной цепи равно (~R_{ob} = R_{1234} + R_5 = frac{3}{5} R + R = frac{8}{5} R).

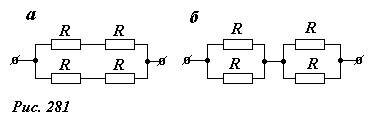
Рассмотрим теперь две схемы, изображенные на рисунке 281. Элементарные расчеты, которые можно провести в уме, приводят к результату: сопротивления обеих цепей равны R.

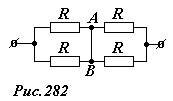
Зададимся вопросом, является ли это совпадение случайным? Схема а, превращается в схему б, если соединить проводником точки А и В (рис. 282). Однако из симметрии схемы следует, что электрический ток по этому проводнику АВ не пойдет. Действительно, в какую сторону ему идти? – оба направления равноправны. Еще одним доказательством отсутствия тока в этом проводнике является равенство потенциалов точек А и В.

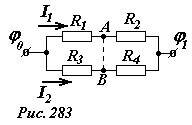
Рассмотрим общую схему такого соединения с произвольными значениями сопротивлений резисторов (рис. 283) и вычислим потенциалы точек А и В. Сила тока через последовательно соединенные резисторы R₁ и R₂ определяется законом Ома

(~I_1 = frac{varphi_0 — varphi_1}{R_1 + R_2}) .

Разность потенциалов на резисторе R₁ равна

(~varphi_0 — varphi_A = I_1 R_1 = frac{varphi_0 — varphi_1}{R_1 + R_2} R_1) ,

поэтому потенциал точки А равен

(~varphi_A = varphi_0 — frac{varphi_0 — varphi_1}{R_1 + R_2} R_1) .

Аналогичные рассуждения для нижней ветви цепи позволяют записать потенциал точки В

(~varphi_B = varphi_0 — frac{varphi_0 — varphi_1}{R_3 + R_4} R_3) .

Итак, условие отсутствия тока между точками А и В при их соединении точек, следующее из равенства потенциалов (varphi_A = varphi_B) , имеет вид

(~frac{R_1}{R_1 + R_2} = frac{R_3}{R_3 + R_4}) , или (~frac{R_1}{R_2} = frac{R_3}{R_4}) . (1)

Рассмотренная схема называется мостиком Уитсона, а условия (1) – условием уравновешенности (или сбалансированности) моста. Подобные схемы широко используются в различных электроизмерительных устройствах.

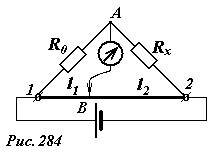
Простейший пример такого использования показа на рис. 284. Кусок однородной проволоки (1-2) с достаточно высоким удельным сопротивлением натянут на измерительную линейку, параллельно ей подключают два резистора, сопротивление одного из них R₀ известно, сопротивление второго R_x измеряется. К образованной таким образом мостовой схеме подключается источник тока. К точке соединения резисторов А, подключен чувствительный гальванометр ^[1], второй вывод которого с помощью скользящего контакта В подключается к проволоке. Передвигая контакт по проволоке, добиваются того, чтобы ток через гальванометр прекратился. В этом случае мот оказывается уравновешенным. Так как сопротивление проволоки пропорционально ее длине, то условие уравновешенности (1) в данном случае имеет вид

(~frac{R_x}{R_0} = frac{l_2}{l_1}) ,

из которого легко определить неизвестное сопротивление, по измерению длин частей проволоки. В данной схеме электрическое сопротивление измеряется, фактически, с помощью линейки. Помимо простоты данной схемы, ее достоинством является отсутствие необходимости измерять значение силы тока, достаточно убедится в его отсутствии, что может быть сделано с высокой точностью. Подобный метод измерения называется «нулевым».

В некоторых случаях точки цепи, имеющие одинаковый потенциал, определяются просто, исходя из симметрии схемы. В таких ситуациях расчет электрического сопротивления значительно упрощается: во-первых, если такими точками включены элементы цепи, то их можно отбросить, так как электрический ток через них не течет; во-вторых, точки равного потенциала можно соединить проводником – это не приведет к изменению сопротивления, так как распределение токов в цепи не изменится.

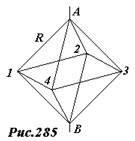
Рассчитаем, например, сопротивление каркасного октаэдра ^[2], изготовленного из проволоки, сопротивление каждого ребра которого равно R (рис. 285). При подключении источника тока к противоположным вершинам А и В, точки 1,2,3,4 равноправны, поэтому имеют одинаковый потенциал. Следовательно, ток не течет по ребрам октаэдра, соединяющим эти вершины, поэтому, их можно отбросить, не нарушая распределения токов по остальным ребрам. Тогда сопротивление каркаса становится эквивалентным сопротивлению четырех параллельно соединенных ветвей, состоящих из двух ребер, общее сопротивление равно (~frac{R}{2}) .

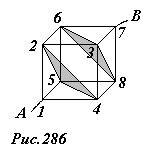
Найдем сопротивление проволочного куба, сопротивление каждого ребра которого равно R, при подключении источника тока к противоположным вершинам А и В (рис. 286). Вершины куба 2,4,5 находятся на расстоянии одного ребра от точки «входа» А, поэтому их потенциалы равны, следовательно, их можно соединить между собой, не нарушая при этом распределения токов по ребрам куба. Аналогично, можно соединить между собой вершины 3,6,8. Таким образом, точка А оказывается соединенной с «объединенной точкой 2,4,5» тремя параллельно соединенными ребрами, от «точки 2,4,5» до «точки 3,6,8» включено параллельно шесть ребер, и далее до выхода, точки В, еще три параллельно соединенных ребра. Таким образом, получаем эквивалентную схему рассматриваемого каркаса (рис. 287), общее сопротивление которой рассчитывается элементарно

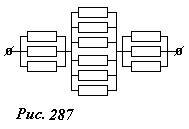
(~R_{ob} = frac{R}{3} + frac{R}{6} + frac{R}{3} = frac{5}{6} R) .

Примечания

1. ↑ Гальванометр – индикаторный прибор, задача которого показывать наличие даже малых токов.
2. ↑ Октаэдр – один из пяти правильных многогранников, образованный восьмью правильными треугольниками.

Следующая страница

В литературе описано несколько методов преобразования электрических цепей [1; 2; 3]. В этих статьях описаны и методы упрощения схем, имеющих точки равного потенциала. Но при решении подобных задач авторы обычно пишут так: «Из симметрии ветвей цепи видно, что точки В и D имеют равные потенциалы» [2], хотя эта видимость не совсем очевидна.

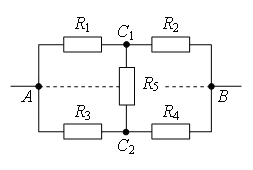
Рассмотрим способы нахождения точек одинакового потенциала более подробно. Пусть нам дана электрическая цепь, состоящая из сопротивлений R₁, R₂, …, R₈ (рис. 1 а). Проведем через точки подключения цепи прямую АВ (рис. 1 б).

1 способ. Если схема содержит проводники с одинаковым сопротивлением, расположенные симметрично относительно определенной оси или плоскости, то концы этих проводников имеют одинаковый потенциал. При этом точки будут симметричными относительно прямой АВ, если равны сопротивления участков цепи между данными точками и любыми точками этой прямой.

Используя этой признак, можно сделать вывод, что точки С₁ и С₂ (рис. 1 б) будут симметричны относительно прямой АВ, если R₁ = R₂ (сопротивления между точкой А и С₁ и между точкой А и С₂ равны) и R₅ = R₆ (сопротивления между точкой В и С₁ и между точкой В и С₂ равны). Аналогично, точки С₃ и С₄ будут симметричны относительно прямой АВ, если R₃ = R₄ и R₇ = R₈.

а.

б.
Рис. 1.

2 способ. Точки имеют одинаковый потенциал, если равны отношения сопротивлений между данными точками и точками подключения.

Например, точки С₁ и С₂ (рис. 1 а) имеют одинаковый потенциал, если . Аналогично, точки С₃ и С₄ имеют одинаковый потенциал, если .

Покажем на примерах, как можно использовать эти способы для преобразования электрических цепей.

Метод объединения равнопотенциальных узлов:точки с одинаковыми потенциалами можно соединять в узлы.

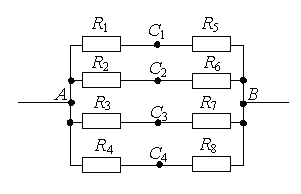
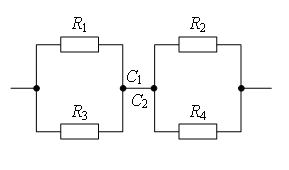
Пример 1. Определите сопротивление электрической цепи (рис. 2), если: а) R₁ = R₃ = 2R, R₂ = R₄ = R, R₅ = 3R; б) R₁ = R₄ = 2R, R₂ = 4R, R₃ = R, R₅ = 5R.

Рис. 2.

а) Если провести через точки подключения прямую АВ (рис. 3 а), то равны сопротивления участков АС₁ и АС₂ (R₁ = R₃), и равны сопротивления участков ВС₁ и ВС₂ (R₂ = R₄). Следовательно, точки С₁ и С₂ симметричны относительно прямой АВ и имеют равные потенциалы.

Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3, б). Резисторы R₁ и R₃ соединены параллельно, и резисторы R₂ и R₄ – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,

б) Если провести прямую АВ (рис. 3 а), то сопротивления участков АС₁ и АС₂ не равны , следовательно, точки С₁ и С₂ не симметричны относительно прямой АВ. НО точки С₁ и С₂имеют равные потенциалы, т.к. .

Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3 б). Резисторы R₁ и R₃ соединены параллельно, и резисторы R₂ и R₄ – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,

а

б
Рис. 3.

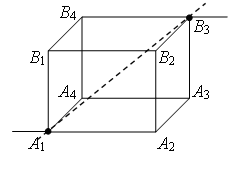
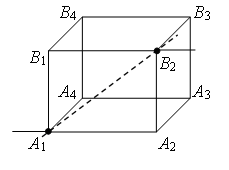
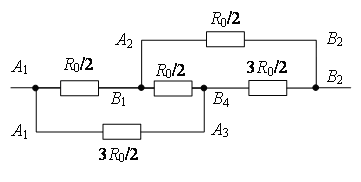
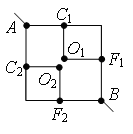
Пример 2. Найдите сопротивление проволочного куба между точками А₁ и В₃ (рис. 4). Сопротивление каждого ребра R₀.

Рис. 4.

Рис. 5.

Проведем через точки подключения прямую А₁В₃ (рис. 5). Равны сопротивления (равны длины – ребра) участков А₁В₁, А₁А₂ и А₁А₄, и равны сопротивления (равны длины – диагонали) участков В₃В₁, В₃А₂ и В₃А₄. Следовательно точки В₁, А₂ и А₄ симметричны относительно прямой А₁В₃ и имеют равные потенциалы. Равны сопротивления участков А₁А₃, А₁В₂ и А₁В₄, и равны сопротивления участков В₃А₃, В₃В₂ и В₃В₄. Следовательно точки А₃, В₂ и В₄ симметричны относительно прямой А₁В₃ и имеют равные потенциалы.

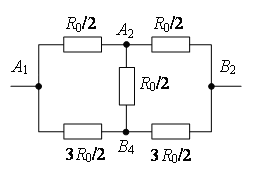
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 6). Три резистора R₀ соединены параллельно между точками А₁ и А₂ (В₁, А₄), шесть резисторов R₀ – параллельно между точками А₂ (В₁, А₄) и А₃ (В₂, В₄), три резистора R₀ – параллельно между точками А₃ (В₂, В₄) и В₃, участки между этими точками соединены последовательно. Следовательно,

.

Рис. 6.

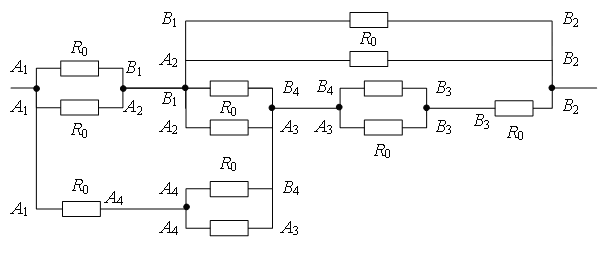
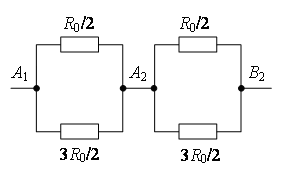
Пример 3. Найдите сопротивление проволочного куба между точками А₁ и В₂ (рис. 4). Сопротивление каждого ребра R₀.

Проведем через точки подключения прямую А₁В₂ (рис. 7 а). Равны сопротивления (равны длины – ребра) участков А₁В₁, А₁А₂, и равны сопротивления (равны длины – ребра) участков В₂В₁, В₂А₂. Следовательно точки В₁ и А₂ симметричны относительно прямой А₁В₂ и имеют равные потенциалы. Равны сопротивления участков А₁А₃ и А₁В₄, и равны сопротивления участков В₂А₃ и В₂В₄. Следовательно, точки А₃ и В₄А₁  симметричны относительно прямой В₂ и имеют равные потенциалы.

Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 б). Используя рекуррентный метод, схему можно упростить (рис. 7 в или г).

Точки А₂ и В₄имеют равные потенциалы, т.к. . Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 д). Резисторы на участке А₁А₂ соединены параллельно, и резисторы на участке А₂В₂ – параллельно, а эти участки соединены последовательно. Следовательно,

а

б

в

г

д
Рис. 7.

Если возможно объединение двух равнопотенциальных узлов, то возможен и обратный переход.

Метод разделения узлов: узел схемы можно разделить на два или несколько узлов, если получившиеся при этом узлы имеют одинаковые потенциалы.

Обязательным условием при этом является проверка получившихся при разделении узлов на равенство потенциалов (симметричность или пропорциональность сопротивлений).

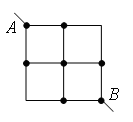
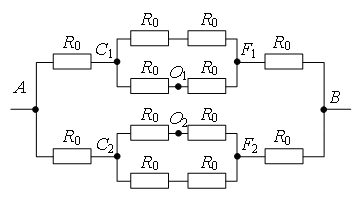
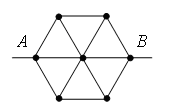
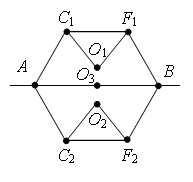
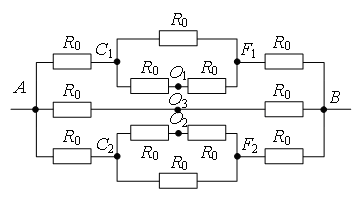
Пример 4. Найдите сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. сопротивлением R₀ каждый.

Рис. 8.

Разделим узел в середине каркаса на два узла О₁ и О₂ так, как показано на рис. 9 а. Это можно сделать, так как точки О₁ и О₂ имеют равные потенциалы: равны сопротивления участков AO₁, AO₂, и равны сопротивления участков BO₁, BO₂. Перерисуем схему в стандартный вид (рис. 9 б). Используя рекуррентный метод, схему можно упростить (рис. 9 в), т.к. сопротивление участка C₁F₁ равно , аналогично . Тогда общее сопротивление цепи равно .

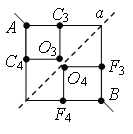
Обратите внимание. С точки зрения геометрии точки О₃ и О₄ симметричны относительно прямой а (рис. 9 г), но потенциалы этих точек не равны, т.к. сопротивления участков АО₃ и АО₄ не равны, а отношения сопротивлений участков АО₃ и АО₄ не равны отношению сопротивлений участков ВО₃ и ВО₄.

а

б

в

г
Рис. 9.

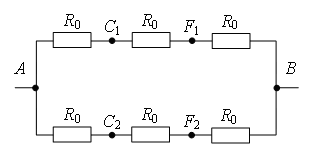
Пример 5. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 10) сопротивлением R₀ каждый.

Разделим узел в середине каркаса на три узла О₁, О₂ и О₃ так, как показано на рис. 11 а. Это можно сделать, так как точки О₁, О₂ и О₃ имеют равные потенциалы: равны сопротивления участков AO₁ и BO₁, участков AO₂ и BO₂, и участков AO₃ и BO₃, следовательно, отношения сопротивления этих участков равны.

Перерисуем схему в стандартный вид (рис. 11, б). Используя рекуррентный метод, схему можно упростить (рис. 11 в), т.к. сопротивление участка C₁F₁ равно , аналогично , сопротивление . Тогда общее сопротивление цепи равно

а

б

в
Рис. 11.

Литература

1. Зильберман А. Расчет электрических цепей // Квант. – 1988. – № 8. – С. 30-34.
2. Петросян В.Г., Долгополова Л.В., Лихицкая И.В. Методы расчета резисторных схем постоянного тока // Физика. – 2002. – № 14, 18, 22.
3. Хацет А. Методы расчета эквивалентных сопротивлений // Квант. – 1972. – № 2. – С. 54-59.

Электрическое сопротивление куба

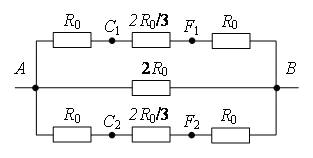
Дан каркас в виде куба, изготовленный из металлической проволоки. Электрическое сопротивление каждого ребра куба равно одному Ому. Чему равно сопротивление куба при прохождении электрического тока от одной вершины к другое, если он подключен к источнику постоянного тока как это показано на рисунке?

Решение задачи про электрическое сопротивление куба

	Рисуем куб резистров.
	Соединяем дополнительными проводниками точки с равными напряжениями, ток через них течь не будет.
	Упрощаем схему

Считаем сопротивление схемы по формулам для параллельного и последовательного подключения сопротивлений, получаем ответ — электрическое сопротивление куба равно 5/6 Ом.

Интересные факты про задачу про сопротивление куба резисторов

1. Решение задачки про сопротивление куба в общем виде можно прочитать на сайте журнала Квант или посмотреть здесь: «В конце сороковых годов в математических кружках Москвы появилась задача об электрическом сопротивлении проволочного куба. Кто ее придумал или нашел в старых учебниках мы не знаем. Задача была очень популярной, и о ней быстро узнали все. Очень скоро ее стали задавать на экзаменах и она стала почти тривиальной…» —  Ф.Недемейер, Я.Смородинский «Сопротивление ребер многомерного куба».

Благодаря тому, что решение задачи про сопротивление куба неоднократно приводилось в сборниках задач, учебниках и т.п., она обычно не вызывает таких споров, как, например, задачка про самолет.

2. Задача может попасться на ЕГЭ. Это тоже является интересным фактом:)

3. Задачу про «сопротивление в кубе» можно решить более сложными способами, например, с помощью правил Кирхгофа. Вот одно из таких решений:

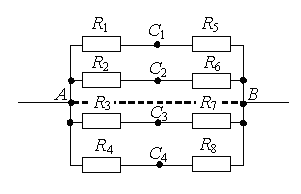
Изображаем куб резистров на плоскости в виде обычной электрической схемы.

Обозначим все сопротивления ребер R. Заменяем 2 сопротивления R на эквивалентное им параллельное подключение сопротивлений по 2R каждое — как это показано выше на рисунке.

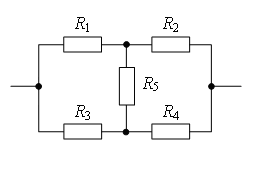
Мысленно сгибаем лист с изображенной на нем схемой пополам — вдоль оси симметрии. Получаем схему для «половины куба», изображенную на рисунке выше. Обозначим ее сопротивление за Rх

Рассуждаем следующим образом: по правой и левой половинам текут одинаковые токи, т.к. они абсолютно симметричны. Значит можно условно изобразить схему для сопротивления куба так как показано на рисунке выше: как два параллельных сопротивления, каждое из которых эквивалентно половине схемы. Общее сопротивление куба будет, таким образом, равно одной второй от сопротивления схемы Rх, изображенной ранее (см. схему для «половины» куба)