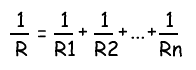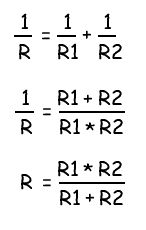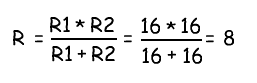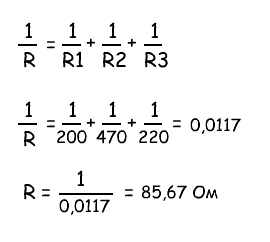Главная » Справочник » Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
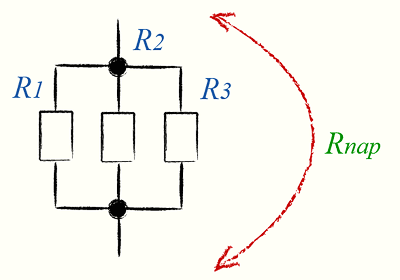
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Закон Ома
- Главная
- /
- Физика
- /
- Закон Ома
Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:
Закон Ома для участка цепи
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U =В
Сопротивление: R =Ом
Сила тока: I =
0
А
Формула
I = U/R
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12/2= 6 А
Найти напряжение
Сила тока: I =A
Сопротивление: R =Ом
Напряжение: U =
0
В
Формула
U = I ⋅ R
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U =В
Сила тока: I =A
Сопротивление: R =
0
Ом
Формула
R = U/I
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12/6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
Сила тока: I =
0
А
Формула
I = ε/R+r
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12/4+2 = 2 А
Найти ЭДС
Сила тока: I =А
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
ЭДС: ε =
0
В
Формула
ε = I ⋅ (R+r)
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I =А
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =
0
Ом
Формула
r = ε/I — R
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I =А
ЭДС: ε =В
Внутреннее сопротивление источника напряжения: r =Ом
Сопротивление всех внешних элементов цепи: R =
0
Ом
Формула
R = ε/I — r
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Сопротивление всех внешних элементов цепи: R = 12/2 — 2 = 4 Ом
См. также
Резистор и сопротивление
Теория
Резистор — искусственное «препятствие» для тока. Сопротивление в чистом виде. Резистор ограничивает силу тока, переводя часть электроэнергии в тепло. Сегодня невозможно изготовить ни одно, сколько-нибудь функциональное, электронное устройство без резисторов. Они используются везде: от компьютеров до систем охраны.
Сопротивление резистора — его основная характеристика. Основной единицей электрического сопротивления является Ом. На практике используются также производные единицы — килоом (кОм), мегаом (МОм), гигаом (ГОм), которые связаны с основной единицей следующими соотношениями:
1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
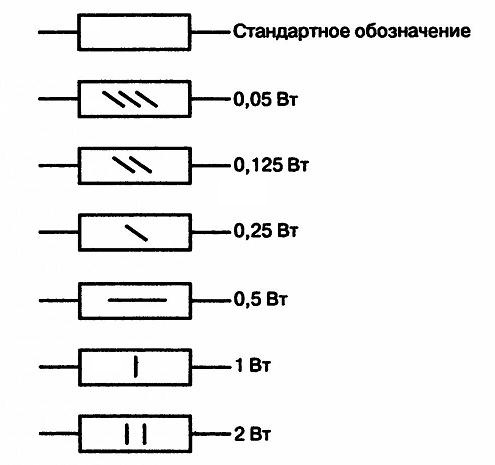
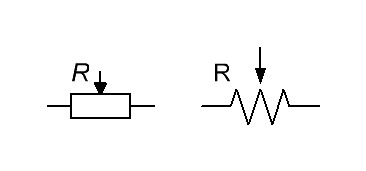
Ниже на рисунке видна маркировка резисторов на схемах:
Наклонные линии обозначают мощность резистора до 1 Вт. Вертикальные линии и знаки V и X (римские цифры), указывают на мощность резистора в несколько Ватт, в соответствии со значением римской цифры.
Для соединения резисторов в схемах используются три разных способа подключения: параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
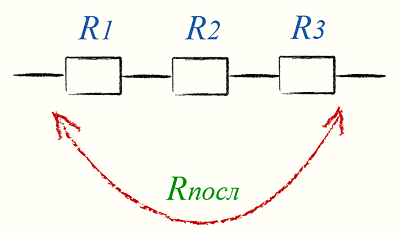
Последовательное соединение резисторов
Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
Rобщ = R1 + R2
Это справедливо и для большего количества соединённых последовательно резисторов:
Rобщ = R1 + R2 + R3 + … + Rn
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Мощность при последовательном соединении
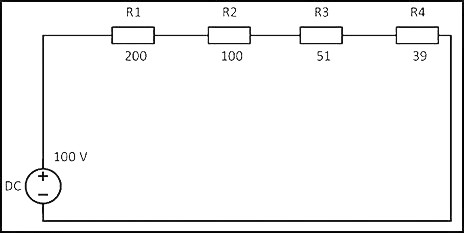
При соединении резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат:
R = 200 + 100 + 51 + 39 = 390 Ом
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 A
На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I2 x R = 0,2562 x 390 = 25,55 Вт
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
Параллельное соединение резисторов
Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Rобщ = (R1 × R2) / (R1 + R2)
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
1 / Rобщ = 1 / R1 + 1 / R2 + … + 1 / Rn
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Мощность при параллельном соединении
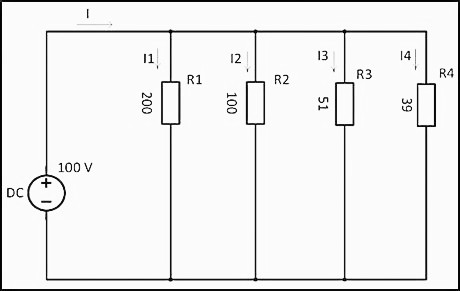
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 A
Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I2 x R = 6,0242 x 16,6 = 602,3 Вт
Расчет силы тока для каждого резистора выполняется по формулам:
I1 = U/R1 = 100/200 = 0,5 A;
I2 = U/R2 = 100/100 = 1 A;
I3 = U/R3 = 100/51 = 1,96 A;
I4 = U/R4 = 100/39 = 2,56 A
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U2/R1 = 1002/200 = 50 Вт;
P2 = U2/R2 = 1002/100 = 100 Вт;
P3 = U22/R3 = 1002/51 = 195,9 Вт;
P4 = U22/R4 = 1002/39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Калькулятор
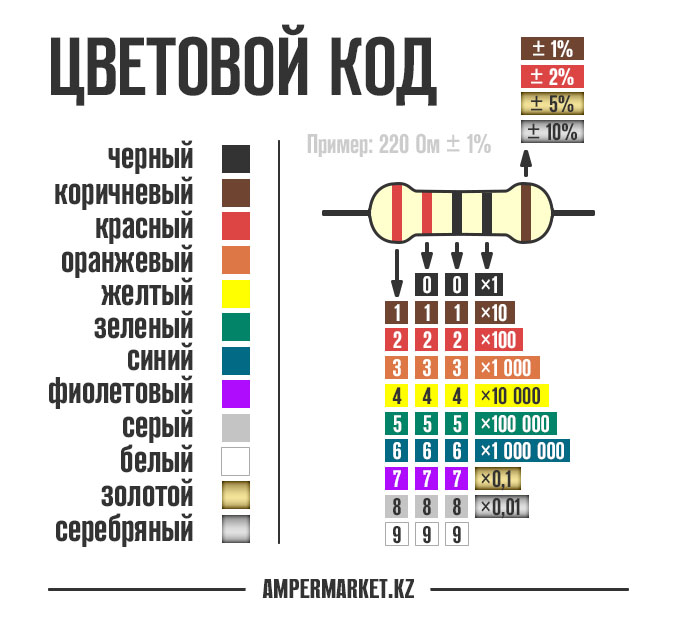
Цветовая маркировка резисторов
Наносить номинал резистора на корпус числами — дорого и непрактично: они получаются очень мелкими. Поэтому номинал и допуск кодируют цветными полосками. Разные серии резисторов содержат разное количество полос, но принцип расшифровки одинаков. Цвет корпуса резистора может быть бежевым, голубым, белым. Это не играет роли. Если не уверены в том, что правильно прочитали полосы, можете проверить себя с помощью мультиметра или калькулятора цветовой маркировки.
Калькулятор цветовой маркировки резисторов
Основные характеристики
| Сопротивление (номинал) | R | Ом |
| Точность (допуск) | ± | % |
| Мощность | P | Ватт |
Переменный резистор
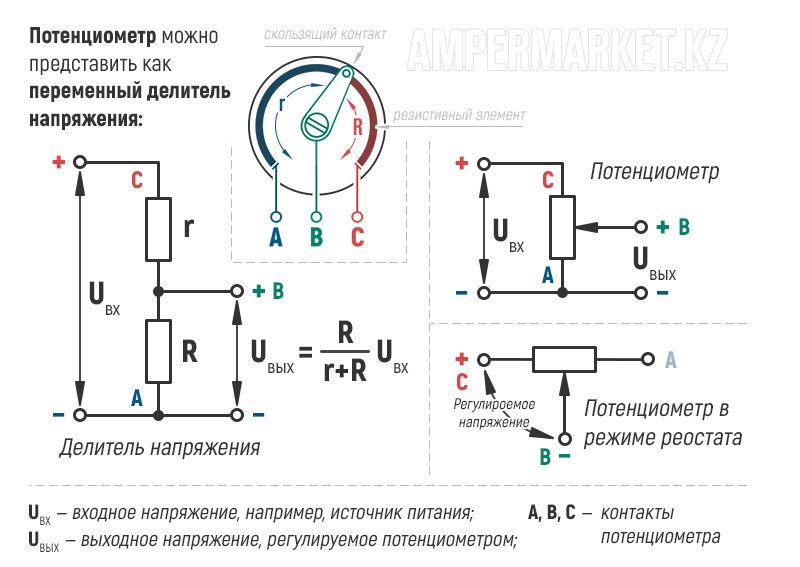
Переменный резистор — это резистор, у которого электрическое сопротивление между подвижным контактом и выводами резистивного элемента можно изменять механическим способом. Переменные резисторы (их также называют реостатами или потенциометрами) предназначены для постепенного регулирования силы тока и напряжения. Разница в том, что реостат регулирует силу тока в электрической цепи, а потенциометр — напряжение. Выглядят переменные резисторы так:
На радиосхемах переменные резисторы обозначаются прямоугольником с пририсованной к их корпусу стрелочкой.
Регулировать величину сопротивления переменных резисторов можно с помощью вращения специальной ручки. Те из резисторов, у которых регулировка сопротивления резистора может осуществляться только с помощью отвертки или специального ключа-шестигранника, называются подстроечными переменными резисторами.
Термисторы, варисторы и фоторезисторы
Кроме реостатов и потенциометров есть и другие виды резисторов: термисторы, варисторы и фоторезисторы. Термисторы, в свою очередь, делятся на термисторы и позисторы. Позистор – это термистор, у которого сопротивление возрастает вместе с ростом температуры окружающей среды. У термисторов, наоборот, чем выше температура вокруг, тем меньше сопротивление. Это свойство обозначают как ТКС – тепловой коэффициент сопротивления.
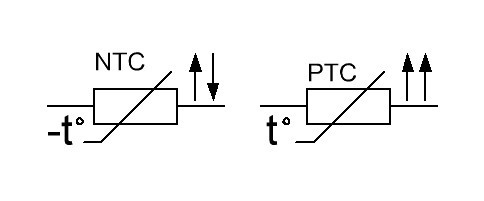
В зависимости от ТКС (отрицательный он или положительный) обозначают на схеме термисторы следующим образом:
Следующий особый класс резисторов – это варисторы. Они изменяют силу сопротивления в зависимости от подаваемого на них напряжения. Зная свойства варистора, можно догадаться, что такой резистор защищает электрическую цепь от перенапряжения.
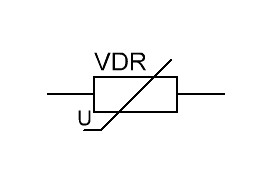
На схемах варисторы обозначаются так:
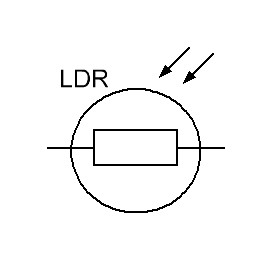
В зависимости от интенсивности освещения изменяет свое сопротивление еще один вид резисторов – фоторезисторы. Причем не важно, каков источник освещения: искусственный или естественный. Их особенность еще и в том, что ток в них протекает как в одном, так и в другом направлении, то есть еще говорят, что фоторезисторы не имеют p-n перехода.
А на схемах изображаются так:
Калькулятор параллельных сопротивлений
Параллельные (как и последовательные) схемы соединения резисторов, часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет и его необходимо подобрать.
Req
Эквивалентное сопротивление Req параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
Эквивалентное сопротивление группы параллельно соединенных резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе ,а добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Расчет сопротивления
Расчет эквивалентного сопротивления
Расчет при известном эквивалентном значении
Для расчета введите данные сопротивления резисторов и добавьте необходимое количество (max 8 шт.).
Для расчета введите данные эквивалентного сопротивления и одного из резисторов.
Поиск резистора на сайте
Для подбора резистора укажите необходимое напряжение
Внимание! Производители объединяют резисторы в серии или ряды: E6, E12, E24…
Для подбора компонента будет использована серия E24.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Онлайн-калькулятор позволяет быстро и удобно произвести расчет общего сопротивления резисторов при последовательном или параллельном соединениях. При расчете можно добавлять до 10 единиц резисторов для подсчета нужного результата, для этого достаточно нажать кнопку “Добавить сопротивление”
Расчет сопротивления при параллельном подключении производится по формуле:
RT = 1 / (1/R1 + 1/R2 + 1/R3 + 1/Rn..)
Расчет сопротивления при последовательном подключении производится по формуле:
RT = R1 + R2 + R3 + Rn..