Смешанное соединение резисторов. Расчет смешанного соединения
26 Ноя 2018г | Раздел: Радио и Электрика начинающим
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов:
Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:
Вычисляем их общее сопротивление используя формулу параллельного соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:
Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!
Поделиться с друзьями:
Соединение резисторов
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
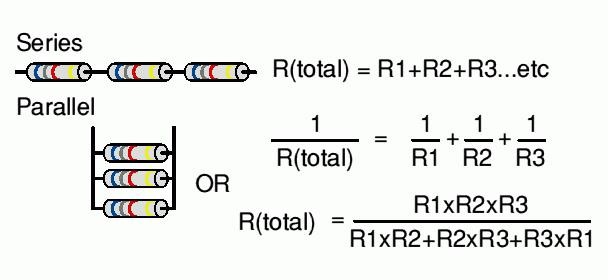
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов.
Последовательное соединение резисторов
Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).
Рисунок 2. Последовательное соединение резисторов.
То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:
Rобщ = R1 + R2 + R3+…+ Rn.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).
Рисунок 3. Параллельное соединение резисторов.
При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:
1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn
Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:
Rобщ= R1*R2/R1+R2
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.
Смешанное соединение резисторов
Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.
Рисунок 4. Смешанное соединение резисторов.
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.
Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.
Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Смешаннымсоединением называют
сочетание последовательного и
параллельного соединений резисторов.
Большое разнообразие этих соединений
не позволяет вывести общую формулу для
определения эквивалентного сопротивления
цепи. Поэтому в каждом конкретном случае,
используя методы расчета при
последовательном и параллельном
соединениях, можно рассчитать
эквивалентное сопротивление при
смешанном соединении. Поясним это на
конкретном примере расчета электрической
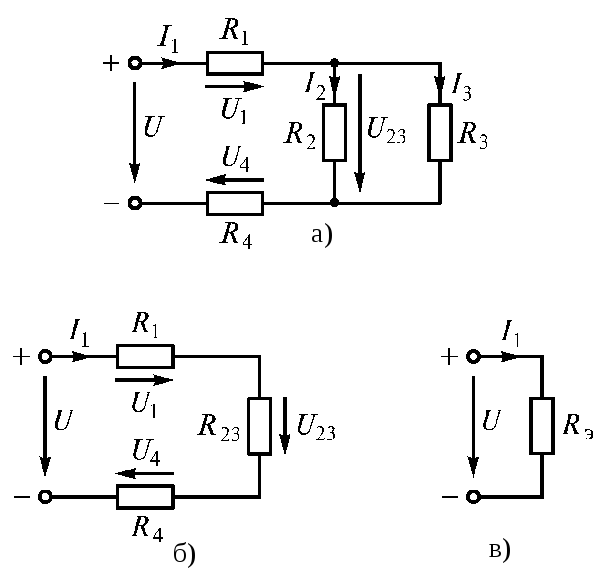
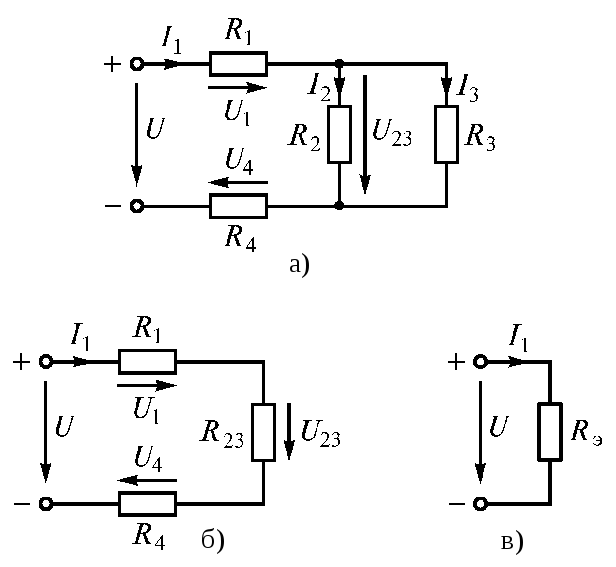
цепи (рис. 1.20 а).
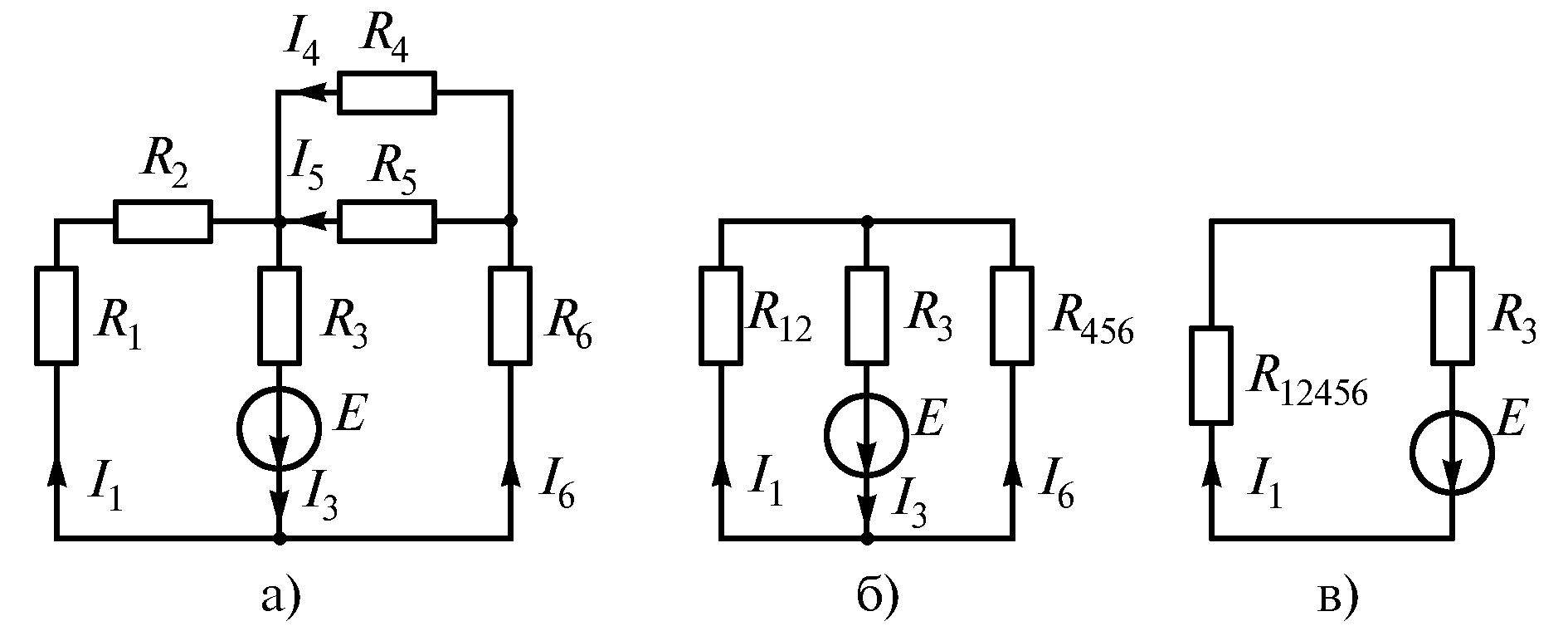
Электрическую цепь постепенно упрощают
и приводят к простейшему виду (рис. 1.20
б, в)
;
;
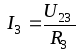
.
Рис. 1.20
Проверка: 1)2)
.
1.8.4. Метод преобразований треугольника резисторов в эквивалентную звезду и наоборот
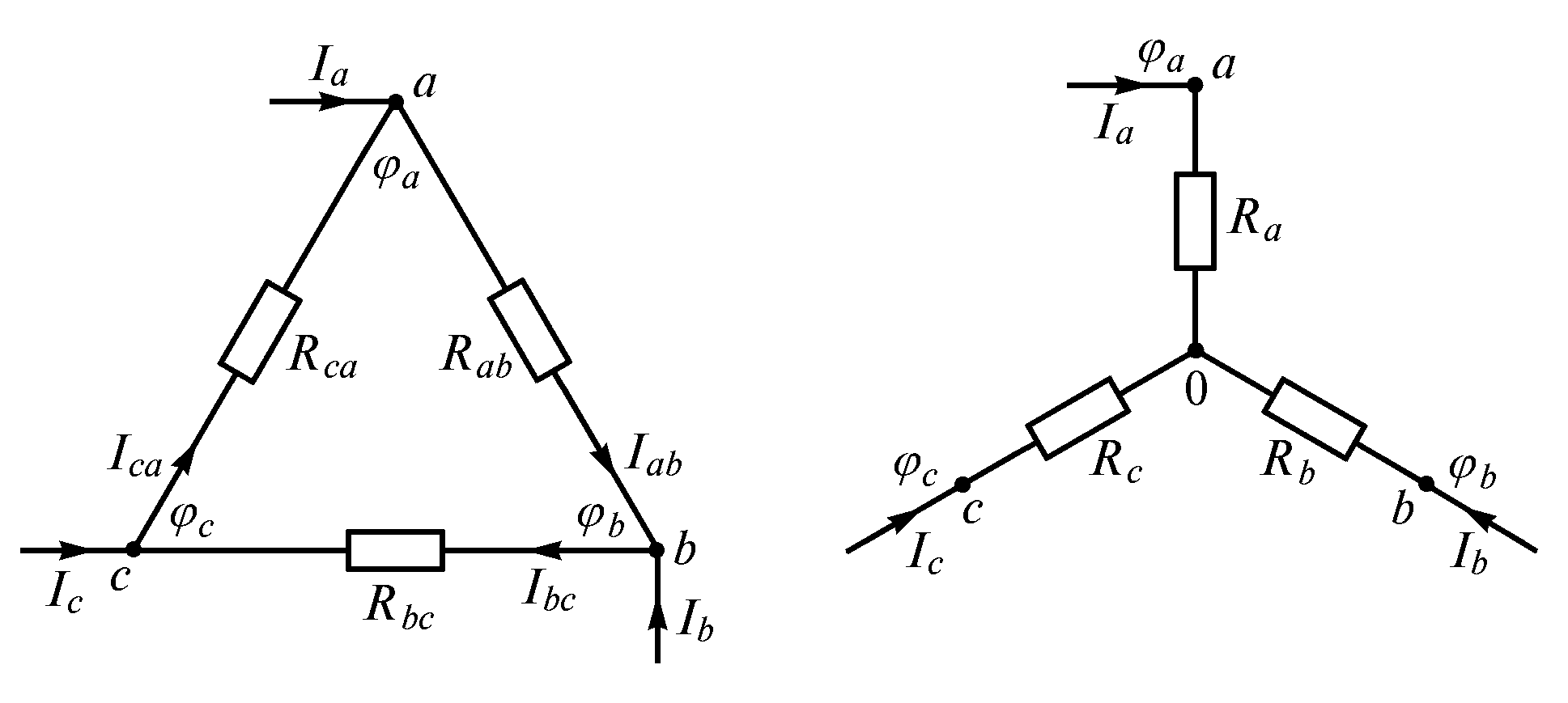
Рассмотрим
две электрические цепи (рис. 1.21). Одна
из них имеет вид треугольника, другая
– трехлучевой звезды. В дальнейшем
такие соединения будем называть
соответственно соединением в треугольник
и соединением звездой.
Рис. 1.21
Соединения такого вида очень распространены
в трехфазных цепях, в которых часто
возникает необходимость перехода от
одного вида соединения к другому
(эквивалентному). Эквивалентность
треугольника и звезды резисторов
заключается в том, что их замена не
изменяет потенциалов узловых точек
(φа,
φb
иφс),
являющихся вершинами треугольника и
эквивалентной звезды. Не изменяются
также токи, напряжения и мощности в
остальной части схемы, не затронутой
преобразованием.
Формулы пересчета без вывода сопротивлений
ветвей треугольника
,
,
в эквивалентную звезду
,
,
имеют вид
(1.39)
При переходе от звезды к треугольнику
можно воспользоваться следующими
формулами
(1.40)
Если сопротивления всех ветвей цепи
по схеме треугольник одинаковы, т.е.
,
сопротивления эквивалентной звезды
будут также одинаковые:,
причем
.
1.8.5. Последовательное соединение источников энергии
В практике последовательное и согласное
включение источников применяют для
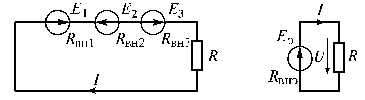
увеличения напряжения. Рассмотрим схему
с двумя согласно и одним встречно
включенными источниками (рис. 1.22).
Рис. 1.22
По второму закону Кирхгофа запишем
.
(1.41)
Отсюда
,
(1.42)
где
.
Напряжения на зажимах источников и
приемника
.
При последовательном соединении
источников с одинаковыми параметрами
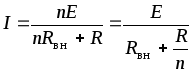
(1.43)
1.8.6. Параллельное соединение источников энергии
В тех случаях, когда номинальное
напряжение приемника равно напряжению
одного источника, а его ток больше
допустимого тока одного источника,
применяют параллельное соединение
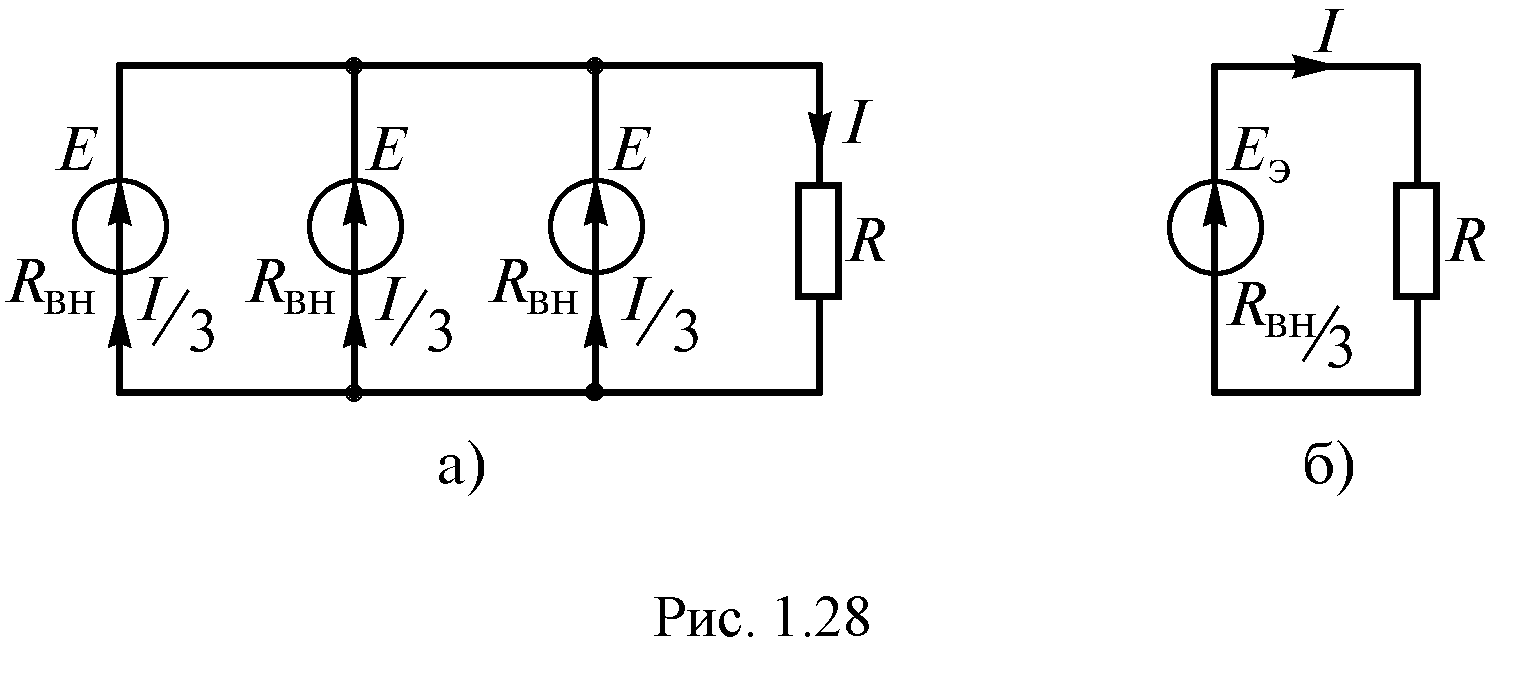
источников (рис. 1.23 а).
При параллельном
соединении источников с одинаковыми
параметрами их общая ЭДС не изменится,
но уменьшатся токи через каждый источник
и внутреннее сопротивление общего
источника. Тогда эквивалентный источник
(рис. 1.23 б) имеет следующие параметры:
.
Рис. 1.23
Приисточниках
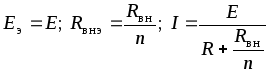
(1.44)
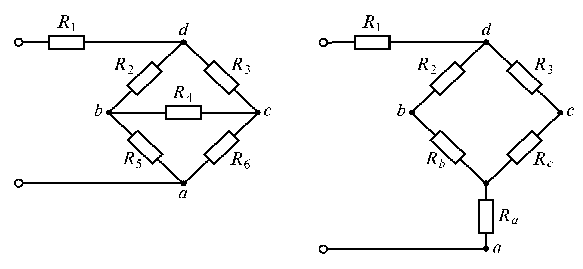
1.1. Определить
эквивалентное сопротивление цепи (рис.
1.24 а),
если
1Ом;
3Ом.
а) б)
в) г)
Рис. 1.24
Решение. Преобразуем
треугольник сопротивлений
в эквивалентную
звезду сопротивлений
(рис. 1.24 б).
Так как
,
то
Ом.
Дальнейшее решение
выполним преобразованием последовательно
или параллельно
соединенных сопротивлений резисторов
их эквивалентными сопротивлениями
«свертыванием» схемы. Резисторы
и
,
а такжеи
соединены последовательно, поэтому их
общие сопротивления
Ом;
Ом.
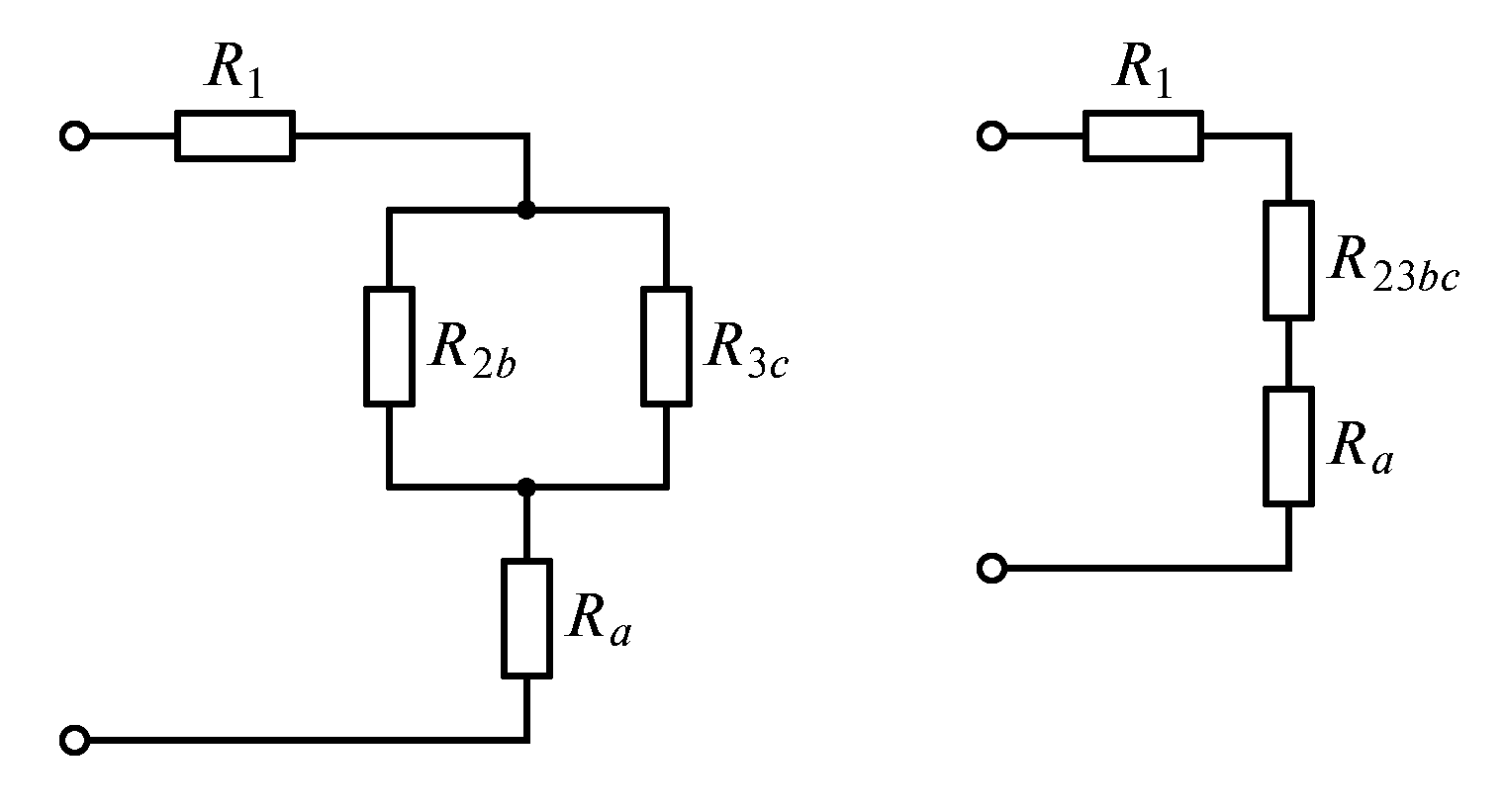
Полученная
схема приведена на рис. 1.24 в.
Резисторы
и
соединены параллельно, поэтому (рис.
1.24 г)
Ом.
Эквивалентное сопротивление всей цепи
Ом.
Пример 1.2.Определить токи в ветвях
цепи (рис. 1.25 а), если задано:Ом;
= 6Ом;
Ом;
= 2Ом;
= 100В.
Решение. Резисторы
и
соединены последовательно и образуют
ветвь с током.
Резисторыи
включены параллельно, а относительно
резистора– последовательно. Вычислим эквивалентные
сопротивления:
Ом;
Ом.
Рис. 1.25
Резисторы
и
соединены параллельно, а по отношению
к– последовательно, поэтому (рис. 1.25
б, в)
Ом.
Эквивалентное сопротивление цепи
Ом.
Ток в ветви с источником
А.
Так как сопротивления резисторов
и
одинаковы, то
А.
Аналогично, при
А.
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
- 1 Что такое резистор и для чего он нужен
- 2 Последовательное соединение сопротивлений
- 2.1 Теоретическая часть
- 2.2 Примеры расчета
- 3 Параллельное соединение резисторов
- 3.1 Теория и законы параллельного соединения
- 3.2 Примеры расчета параллельного соединения сопротивлений
- 4 Смешанное соединение
- 5 Практическое применение параллельного и последовательного соединения резисторов
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.
Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.
Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.
Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.
Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.
Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов.
Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение
встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
топологические понятия, элементы, схема замещения
2.Законы Ома и Кирхгофа для цепей постоянного тока
3.Последовательное, параллельное и смешанное соединение потребителей
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3,
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
4.Расчёт цепи постоянного тока методами контурных токов и узловых потенциалов
Метод контурных токов. В основе лежит 2-й закон Кирхгофа. Суть метода в ведении фиктивных контурных токов и их расчёт.
1.Определение числа уравнений: у=в-ви.т-(n-1).
В-число ветвей, ви.т-с источником тока,n-число узлов.
2.Составляем уравнения для неизвестных контурных токов в общем виде.
3.Определяем неизвестные коэффициенты левой и правой части (Е и R).
4.Подставив коэффициенты, решаем уравнения, находим токи контуров.
5.Определяем через контурные токи токи в ветвях.
Метод узловых потенциалов. В основе лежит 1-й закон Кирхгофа. Определяем потенциалы узлов цепи с последующим определением токов в ветвях, используя закон Ома для участков цепи.
1.Подготовка схемы. Обозначим узлы. Потенциал одного из них принимаем за 0.
2.Составляем уравнения потенциалов в общем виде:
Фи1*g11 + фи2*g12 = I11 – для первого узла
Фи1g21 + фи*g22 = I22 – для второго узла
3.Определяем неизвестные проводимости gmn –сумма проводимостей ветвей, подходящих к узлу n.
4.Подставив, решаем уравнения, находим фи1 и фи2.
5.Произвольно выбираем направления токов и, используя закон Ома для участка цепи определяем эти токи: In = (фиX-фиY+En)/Rn.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания. Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ
. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении
количества элементов в цепи с целью
упрощения схемы
и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов
:
Самым дальним участком схемы оказались резисторы R6
и
R7
, соединенные
параллельно
:
Вычисляем их общее сопротивление используя формулу параллельного
соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6
с суммарным сопротивлением равным
30, 709 кОм
.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5
и
R6
, соединенные
последовательно
:
Вычисляем их общее сопротивление используя формулу последовательного
соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4
и
R5
соединенные
параллельно
:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно
. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного
соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения. Удачи!
Виды соединений потребителей.
Различают последовательное, параллельное и смешанное соединение потребителей.
Припоследовательном соединении потребителей конец первого потребителя присоединяется к началу второго, конец второго – к началу третьего и т.д.
Рисунок 9 – Схема последовательного соединения потребителей
1) Сила тока на всех потребителях одинаковая
2)
Общее сопротивление равно сумме сопротивлений отдельных потребителей
3) Напряжение на зажимах цепи равно сумме падений напряжений на отдельных её участках .
При необходимости уменьшить U и I приемника последовательно ему подключают резистор.
Вывод: при выходе из работы одного элемента вся цепь обесточивается, и при изменении сопротивления одного из них меняется ток во всей цепи и напряжение на каждом элементе.
При параллельном соединении элементов цепи все начала собираются в одну точку, а концы в другую точку и включаются в электрическую цепь, образуя параллельные ветви.
Рисунок 10 – Схема параллельного соединения потребителей
1) Общий ток равен сумме токов параллельных ветвей
2) Напряжение на всех потребителях включенных параллельно одинаковое
3) Общее сопротивление будет меньше наименьшего из включенных параллельно
Из закона Ома для участка цепи
—
для двух потребителей
Если сопротивление потребителей равны, то
Вывод:
При выходе из строя одного потребителя остальные остаются включенные в цепь.
Все приемники находятся под одним напряжением независимо от их мощности (сопротивления).
Смешанным называется такое соединение потребителей, когда в цепи имеются одновременно и параллельное и последовательное их соединение.
Цепь постепенно упрощают, заменяя эквивалентным (равноценным) сопротивлением, используя формулы для последовательного и параллельного соединения потребителей.
Дата добавления: 2017-11-21; ;
Похожие статьи:
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»: