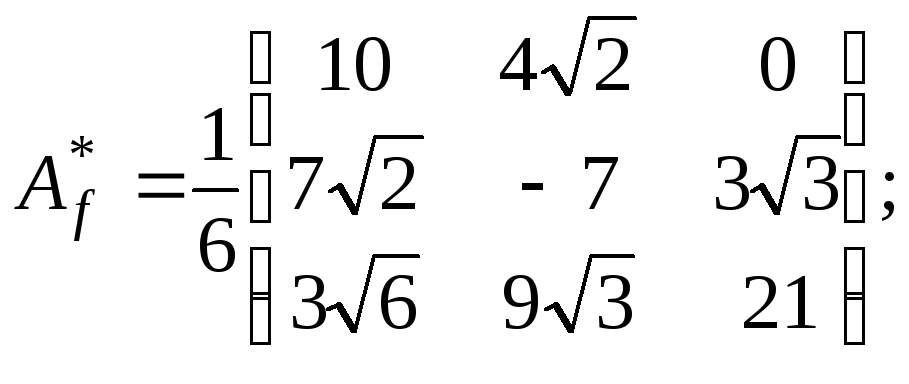Как найти сопрягающую матрицу - Исправление недочетов и поиск решений вместе с Examum.ru

Транспонирование и сопряжение матриц

Транспонирование матриц

Для любой матрицы

$A=begin{pmatrix}a_{11}&a_{12}&cdots&a_{1n}\ a_{21}&a_{22}&cdots&a_{2n}\ vdots&vdots&ddots&vdots\ a_{m1}&a_{m2}&cdots&a_{mn}end{pmatrix}$ транспонированной матрицей называется матрица $A^T=begin{pmatrix}a_{11}&a_{21}&cdots&a_{m1}\ a_{12}&a_{22}&cdots&a_{m2}\ vdots&vdots&ddots&vdots\ a_{1n}&a_{2n}&cdots&a_{mn}end{pmatrix}!,$

получающаяся из матрицы заменой строк столбцами, а столбцов — строками. Чтобы по данной матрице получить матрицу A^T , нужно первую строку матрицы записать как первый столбец матрицы A^T , вторую строку матрица записать как второй столбец матрицы A^T и т.д. Эта операция называется транспонированием матрицы .

Квадратная матрица называется симметрической, если

A^T=A и кососимметрической, если A^T=-A .

У симметрической матрицы элементы, расположенные симметрично относительно главной диагонали, равны между собой. У кососимметрической матрицы элементы, расположенные симметрично относительно главной диагонали, имеют противоположные знаки, а все диагональные элементы равны нулю.

Свойства операции транспонирования матриц

Пусть lambda — любое число, A,,B — произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:

$begin{aligned}&text{1.}quad (lambda A)^T=lambdacdot A^T; \ &text{2.}quad (A+B)^T=A^T+B^T; \ &text{3.}quad (Acdot B)^T=B^Tcdot A^T ;\ &text{4.}quad (A^T)^T=A. end{aligned}$

Пример 1.18. Найти транспонированные матрицы A^T,,B^T,,C^T , если

$A=underbrace{begin{pmatrix}1&2&3\0&1&2end{pmatrix}}_{(2times3)},quad B=begin{pmatrix}0&4&-5\-4&0&6\5&-6&0end{pmatrix}!,quad C=begin{pmatrix}1&4&5\4&2&6\5&6&3end{pmatrix}!.$

Решение. Согласно определению, при транспонировании первая строка матрицы является первым столбцом матрицы A^T , вторая строка — вторым столбцом:

$A^T=underbrace{begin{pmatrix}1&0\2&1\3&2end{pmatrix}}_{(3times2)}.$ Аналогично находим $B^T=begin{pmatrix}0&-4&5\4&0&-6\-5&6&0end{pmatrix}!,quad C^T=begin{pmatrix}1&4&5\4&2&6\5&6&3end{pmatrix}!.$

Так как B^T=-B , то матрица — кососимметрическая. Поскольку C^T=C , то матрица — симметрическая.

Пример 1.19. Продемонстрировать справедливость свойств 1, 2, 3, 4, если $lambda=2,~ A=begin{pmatrix} 1&2\3&4 end{pmatrix}!,~ B=begin{pmatrix} 5&6\7&8end{pmatrix}!.$

Решение. Продемонстрируем свойство 1: (lambda A)^T=lambdacdot A^T . Вычисляя левую и правую части, получаем равные матрицы

$(2cdot A)^T= {begin{pmatrix}2cdot! begin{pmatrix}1&2\3&4end{pmatrix}end{pmatrix}!}^T= {begin{pmatrix}2&4\6&8end{pmatrix}!}^T= begin{pmatrix}2&6\4&8end{pmatrix}!,quad 2cdot A^T=2cdot{begin{pmatrix}1&2\3&4end{pmatrix}!}^T= 2cdot!begin{pmatrix}1&3\2&4end{pmatrix}= begin{pmatrix}2&6\4&8end{pmatrix}!.$

Продемонстрируем свойство 2: (A+B)^T=A^T+B^T . Вычисляя левую и правую части, получаем равные матрицы

$begin{gathered}(A+B)^T= {left[begin{pmatrix}1&2\3&4end{pmatrix}+begin{pmatrix}5&6\7&8end{pmatrix}right]!}^T= {begin{pmatrix}6&8\10&12end{pmatrix}!}^T= begin{pmatrix}6&10\8&12end{pmatrix}!,\[3pt] A^T+B^T= {begin{pmatrix}1&2\3&4end{pmatrix}!}^T+{begin{pmatrix}5&6\7&8end{pmatrix}!}^T= begin{pmatrix}1&3\2&4end{pmatrix}+ begin{pmatrix}5&7\6&8end{pmatrix}= begin{pmatrix}6&10\8&12end{pmatrix}!.end{gathered}$

Продемонстрируем свойство 3: (Acdot B)^T=B^Tcdot A^T . Вычисляя левую и правую части, получаем равные матрицы:

$begin{gathered}(Acdot B)^T= {left[begin{pmatrix}1&2\3&4end{pmatrix}!cdot! begin{pmatrix}5&6\7&8end{pmatrix}right]!}^T= begin{pmatrix}19&22\43&50end{pmatrix}^T= begin{pmatrix}19&43\22&50end{pmatrix}!,\[3pt] B^Tcdot A^T= begin{pmatrix}5&6\7&8end{pmatrix}^Tcdot! begin{pmatrix}1&2\3&4end{pmatrix}^T= begin{pmatrix}5&7\6&8end{pmatrix}!cdot! begin{pmatrix}1&3\2&4end{pmatrix}= begin{pmatrix}19&43\22&50end{pmatrix}!.end{gathered}$

Продемонстрируем свойство 4: (A^T)^T=A . Вычисляя левую часть, получаем правую:

$(A^T)^T= begin{pmatrix} begin{pmatrix} 1&2\3&4 end{pmatrix}^Tend{pmatrix}^T= begin{pmatrix} 1&3\2&4 end{pmatrix}^T= begin{pmatrix}1&2\3&4end{pmatrix}= A.$

Пример 1.20. Пусть — произвольная матрица размеров mtimes n , — любая квадратная n-го порядка. Доказать, что матрицы AA^T,~A^TA,~B+B^T — симметрические, а матрица B-B^T — кососимметрическая.

Решение. По свойствам 3,4 получаем:

$begin{aligned}(Acdot A^T)^T&= (A^T)^Tcdot A^T= Acdot A^T;\[5pt] (A^Tcdot A)^T&= A^Tcdot (A^T)^T= A^Tcdot A.end{aligned}$

По свойствам 2,4 имеем:

$begin{aligned}(B+B^T)^T&= B^T+(B^T)^T= B^T+B=B+B^T;\[5pt] (B-B^T)^T&= B^T-(B^T)^T= B^T-B=-(B-B^T)^T.end{aligned}$

Сопряжение матриц

Пусть — матрица размеров mtimes n , элементы которой являются комплексными числами $a_{kell}=alpha_{kell}+beta_{kell}i$ (комплексная матрица). Сопряженной матрицей $A^{ast}$ называется матрица размеров ntimes m , получаемая из матрицы в результате транспонирования и замены каждого элемента транспонированной матрицы A^T комплексным сопряженным.

Квадратная матрица называется эрмитовой, если ${A}^{ast}=A$ .

Пример 1.21. Даны матрицы A,,B и . Найти сопряженные матрицы ${A}^{ast},,{B}^{ast},,{C}^{ast}$ .

$A=begin{pmatrix} 1&i&1+i\2i&2-3i&0 end{pmatrix}!,quad B=begin{pmatrix} 2i&1+i\ 1-i&2+3iend{pmatrix}!,quad C=begin{pmatrix} 1&3-2i\ 3+2i&2end{pmatrix}!.$

Решение. Найдем транспонированные матрицы:

$A^T=begin{pmatrix}1&2i\i&2-3i\1+i&0end{pmatrix}!,quad B^T=begin{pmatrix}2i&1-i\1+i&2+3iend{pmatrix}!,quad C^T=begin{pmatrix}1&3+2i\3-2i&2end{pmatrix}!.$

Заменим все элементы сопряженными:

$A^{ast}=begin{pmatrix}1&-2i\-i&2+3i\1-i&0end{pmatrix}!,quad B^{ast}=begin{pmatrix}-2i&1+i\1-i&2-3iend{pmatrix}!,quad C^{ast}=begin{pmatrix}1&3-2i\3+2i&2end{pmatrix}!.$

Заметим, что матрица — эрмитова, так как $C^{ast}=C$ .

Свойства операции сопряжения матриц

1. $(lambdacdot A)^{ast}=overline{lambda}cdot A^{ast}$ ;

2. $(A+B)^{ast}= A^{ast}+B^{ast}$ ;

3. $(Acdot B)^{ast}= B^{ast}cdot A^{ast}$ ;

4. $(A^{ast})^{ast}= A$ ,

где A,,B — произвольные матрицы, для которых определены соответствующие операции, lambda=alpha+beta i — любое комплексное число, overline{lambda}=alpha-beta i — сопряженное к lambda число.

Пример 1.22. Продемонстрировать справедливость свойств 1, 2, 3, 4, если

$lambda=1+i,quad A=begin{pmatrix} -i&1+i\1-2i&1end{pmatrix}!,quad B=begin{pmatrix}2i&1+i\1-i&2+3iend{pmatrix}!.$

Решение. 1. Вычисляем и сравниваем левую и правую части равенства 1:

$begin{aligned} (lambdacdot A)^{ast}&= {left[(1+i)! begin{pmatrix}-i&1+i\1-2i&1end{pmatrix}right]!}^{ast}= begin{pmatrix}-(1+i)i&(1+i)^2\(1+i)(1-2i)&1+iend{pmatrix}^{ast}=\ &=begin{pmatrix}-i-i^2&1+2i+i^2\1-i-2i^2&1+iend{pmatrix}^{ast}= begin{pmatrix}1-i&2i\3-i&1+iend{pmatrix}^{ast}= begin{pmatrix}1+i&3+i\-2i&1-iend{pmatrix}!,\[5pt] overline{lambda}cdot A^{ast}&= overline{(1+i)}! begin{pmatrix}-i&1+i\1-2i&1end{pmatrix}^{ast}= (1-i)! begin{pmatrix}i&1+2i\1-i&1end{pmatrix}= begin{pmatrix}(1-i)i& (1-i)(1+2i)\ (1-i)^2&1-iend{pmatrix}=\ &=begin{pmatrix}i-i^2&1+i-2i^2\1-2i+i^2&1-iend{pmatrix}=begin{pmatrix}1+i&3+i\-2i&1-iend{pmatrix}!.end{aligned}$

2. Вычисляем и сравниваем левую и правую части равенства 2:

$begin{aligned}(A+B)^{ast}&= {left[begin{pmatrix}-i&1+i\1-2i&1end{pmatrix}+ begin{pmatrix}2i&1+i\1-i&2+3i\end{pmatrix}right]!}^{ast}= begin{pmatrix}i&2+2i\2-3i&3+3iend{pmatrix}^{ast}=begin{pmatrix}-i&2+3i\2-2i&3-3iend{pmatrix}!,\[5pt] A^{ast}+B^{ast}&= begin{pmatrix}i&1+2i\1-i&1end{pmatrix}+ begin{pmatrix}-2i&1+i\1-i&2-3iend{pmatrix}= begin{pmatrix}-i&2+3i\2-2i&3-3iend{pmatrix}!.end{aligned}$

3. Вычисляем и сравниваем левую и правую части равенства

$begin{aligned}(Acdot B)^{ast}&= {left[begin{pmatrix}-i&1+i\ 1-2i&1end{pmatrix}!! begin{pmatrix}2i&1+i\1-i&2+3iend{pmatrix}right]!}^{ast}= begin{pmatrix}-icdot2i+(1+i)(1-i)&-i(1+i)+(1+i)(2+3i)\(1-2i)cdot2i+1cdot(1-i)&(1-2i)(1+i)+1cdot(2+3i)end{pmatrix}^{ast}=\ &=begin{pmatrix}4&4i\5+i&5+2iend{pmatrix}^{ast}= begin{pmatrix}4&5-i\-4i&5-2iend{pmatrix}!,\[5pt] B^{ast}cdot A^{ast}&= begin{pmatrix}-2i&1+i\1-i&2-3iend{pmatrix}!! begin{pmatrix}i&1+2i\1-i&1end{pmatrix}= begin{pmatrix}-2icdot i+(1+i)(1-i)&-2icdot(1+2i)+(1+i)cdot1\ (1-i) i+(2-3i)(1-i)&(1-i)(1+2i)+(2-3i)cdot1end{pmatrix}=\ &=begin{pmatrix}4&5-i\-4i&5-2iend{pmatrix}!. end{aligned}$

4. Вычисляем левую часть равенства 4 и сравниваем ее с правой частью:

$(A^{ast})^{ast}= {left[begin{pmatrix}-i&1+i\1-2i&1end{pmatrix}^{ast}right]!}^{ast}= begin{pmatrix}i&1+2i\1-i&1end{pmatrix}^{ast}= begin{pmatrix} -i&1+i\1-2i&1end{pmatrix}=A.$

Замечания 1.4.

1. Если все элементы матрицы действительные числа (действительная матрица), то сопряженная матрица совпадает с транспонированной, т.е. $A^{ast}=A^T$ .

2. Всякую комплексную матрицу (с элементами $c_{kell}=a_{kell}+b_{kell}i$ ) можно представить в виде C=A+Bi , где A=operatorname{Re}C и B=operatorname{Im}C — действительная и мнимая части матрицы (с элементами $a_{kell}=operatorname{Re}c_{kell}$ и $b_{kell}= operatorname{Im}c_{kell}$ соответственно). При этом сопряженную матрицу можно представить в виде $C^{ast}=A^T-B^Ti$ .

3. Всякую эрмитову матрицу можно представить в виде C=A+Bi , где A=operatorname{Re}C — действительная симметрическая матрица (A^T=A) , а B=operatorname{Im}C — действительная кососимметрическая матрица (B^T=-B) . В самом деле, из равенства ${C}^{ast}=C$ , учитывая пункт 2, следует, что A^T-B^Ti=A+Bi . Равенство действительных частей дает A^T=A , а равенство мнимых частей влечет B^T=-B .

Пример 1.23. Пусть — комплексная матрица размеров mtimes n . Доказать, что матрицы $AA^{ast},,A^{ast}A$ — эрмитовы m-го и n-го порядков соответственно.

Решение. Используя свойства 3, 4, получаем:

$(Acdot A^{ast})^{ast}=(A^{ast})^{ast}cdot A^{ast}= Acdot A^{ast};qquad (A^{ast}cdot A)^{ast}=A^{ast}cdot (A^{ast})^{ast}=A^{ast}cdot A,$

что и требовалось доказать.

Замечания 1.5

1. Эрмитова матрица с действительными элементами является симметрической.

2. Элементы эрмитовой матрицы, стоящие на главной диагонали, действительны (например, матрица в примере 1.21).

След матрицы

Следом квадратной матрицы называется сумма ее элементов, стоящих на главной диагонали. След квадратной матрицы n-го порядка обозначается

$operatorname{tr}A=sum_{i=1}^{n}a_{ii}.$

Для любых квадратных матриц A,,B,,C n-го порядка и столбцов x,,y размеров ntimes1 справедливы следующие свойства:

1. operatorname{tr}(A+B)= operatorname{tr}A+operatorname{tr}B ;

2. $operatorname{tr}A=operatorname{tr}A^T$ ;

3. $operatorname{tr}(A^T B)= operatorname{tr}(B^T A)= operatorname{tr}(AB^T)= operatorname{tr}(BA^T)$ ;

4. $operatorname{tr}(xcdot y^T)=x^Tcdot y$ ;

5. $operatorname{tr}(Acdot xcdot x^T)= x^Tcdot Acdot x$ ;

6. operatorname{tr}(ABC)= operatorname{tr}(BCA)= operatorname{tr}(CAB) ;

7. $textstyle{sumlimits_{i=1}^{n}sumlimits_{j=1}^{n}a_{ij}b_{ij}=operatorname{tr}(AB^T)}$ .

Замечание 1.6. След матрицы также обозначается operatorname{sp}A .

Пример 1.24. Даны квадратные матрицы $A=begin{pmatrix}1&2\3&4end{pmatrix}!,~B=begin{pmatrix}5&6\7&8end{pmatrix}$ и столбцы $x=begin{pmatrix} 1\2 end{pmatrix}!,~ y=begin{pmatrix}3\4end{pmatrix}$ . Продемонстрировать справедливость свойств 1, 2, 3, 4, 5, 7.

Решение.

1. $operatorname{tr}A= 1+4=5,~~ operatorname{tr}B=5+8=13,~~ operatorname{tr}A+operatorname{tr}B=18,~~ operatorname{tr}(A+B)= operatorname{tr}!begin{pmatrix}6&8\10&12end{pmatrix}=18$ ;

2. $operatorname{tr}A=5,~~ operatorname{tr}A^T=operatorname{tr}! begin{pmatrix}1&3\2&4end{pmatrix}=5;$ ;

$begin{aligned}text{3.}~~operatorname{tr}(A^T B)&= operatorname{tr}!left[begin{pmatrix}1&3\2&4end{pmatrix}!! begin{pmatrix}5&6\7&8end{pmatrix}right]= operatorname{tr}!begin{pmatrix}26&30\38&44end{pmatrix}=26+44=70,\[2pt] operatorname{tr}(B^TA)&= operatorname{tr}!left[begin{pmatrix}5&7\6&8end{pmatrix}!! begin{pmatrix}1&2\3&4end{pmatrix}right]= operatorname{tr}begin{pmatrix}26&38\30&44end{pmatrix}=26+44=70,\[2pt] operatorname{tr}(AB^T)&= operatorname{tr}!left[begin{pmatrix}1&2\3&4end{pmatrix}!! begin{pmatrix}5&7\6&8end{pmatrix}right]= operatorname{tr}begin{pmatrix}17&23\39&53end{pmatrix}=17+53=70,\[2pt] operatorname{tr}(BA^T)&= operatorname{tr}!left[begin{pmatrix}5&6\7&8end{pmatrix}!! begin{pmatrix}1&3\2&4end{pmatrix}right]= operatorname{tr}begin{pmatrix}17&39\23&53end{pmatrix}=17+53=70.end{aligned}$

4. $operatorname{tr}(xy^T)= operatorname{tr}!left[begin{pmatrix}1\2end{pmatrix}!! begin{pmatrix}3&4end{pmatrix}right]= operatorname{tr}! begin{pmatrix}3&4\6&8end{pmatrix}=3+8=11.,quad x^Ty=begin{pmatrix}1&2end{pmatrix}!! begin{pmatrix}3\4end{pmatrix}=1cdot3+2cdot4=11;$

5. $operatorname{tr}(Axx^T)= operatorname{tr}!left[begin{pmatrix}1&2\3&4end{pmatrix}!! begin{pmatrix}1\2end{pmatrix}!! begin{pmatrix}1&2end{pmatrix}right]= operatorname{tr}!left[begin{pmatrix}1&2\3&4end{pmatrix}!! begin{pmatrix}1&2\2&4end{pmatrix}right]= operatorname{tr}! begin{pmatrix}5&10\11&22end{pmatrix}=27;$

6. $x^Tax= begin{pmatrix}1&2end{pmatrix}!! begin{pmatrix}1&2\3&4end{pmatrix}!! begin{pmatrix}1\2end{pmatrix}= begin{pmatrix}1&2end{pmatrix}!! begin{pmatrix}5\11end{pmatrix}=27.$

7. $sum_{i=1}^{2}sum_{j=1}^{2}a_{ij}b_{ij}= 1cdot5+2cdot6+3cdot7+4cdot8=70= operatorname{tr}(AB^T).$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Инструкции:

Используйте этот калькулятор, чтобы найти сопряженную матрицу, которую вы предоставляете, показывая все шаги. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы.

Затем щелкните первую ячейку и введите значение и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы определить ВСЕ значения матрицы.

Подробнее об этом калькуляторе сопряженных матриц.

Так же, как и кофакторы, присоединенная матрица тесно связана с обратной матрицей. Действительно, обратная матрица и присоединенная матрица очень похожи.

Справедливости ради стоит отметить, что понятие сопряжения матрицы играет очень важную роль в высшей математике (где вместо матриц мы имеем дело с линейными операторами). Но в математике в колледже единственный раз, когда вы, вероятно, наткнетесь на сопряженное, это когда вы

вычислить обратную матрицу

используя формулу сопряжения.

Как найти сопряжение матрицы?

Во-первых, с точки зрения того, как вычисляется сопряженная матрица, давайте вспомним

матрица миноров

который вычисляется путем вычисления определителя подматриц, образованных удалением i-й строки и j-го столбца данной матрицы (A).

Итак, несовершеннолетние были определены как:

[ M_{ij} = det A^{i,j}]

Как добраться до матрицы кофакторов?

матрица кофакторов

, (C) получается из миноров добавлением определенных «признаков» и определяется как:

[ C_{ij} = (-1)^{i+j} M_{ij}]

Наконец, как добраться до присоединенной матрицы? Что такое формула сопряжения?

Простой! Как только у вас есть

рассчитанная матрица кофакторов

уже, вам нужно

транспонировать матрицу

чтобы получить сопряженное. Конкретно:

[ adj(A) = C^T ]

Итак, чтобы облегчить запоминание, мы разбили формулу сопряжения на 3 этапа: сначала вы вычисляете матрицу миноров, затем вычисляете кофакторы, а затем переставляете кофакторы, чтобы получить сопряженное.

Сопряженное и транспонированное одно и то же?

Хотя сопряженная включает в себя транспонирование матрицы, в общем случае сопряженная и транспонированная матрицы отличаются друг от друга.

Как найти сопряженную матрицу 4×4 или больше?

Процесс нахождения сопряженного может быть численно обширным, учитывая, что вам нужно вычислить субдетерминанты (n^2), которые могут быстро расти с (n ge 4).

Пример расчета сопряженной матрицы

Вопрос:

Рассмотрим следующую матрицу

[ begin{bmatrix}
displaystyle 2&displaystyle 3&displaystyle 1\[0.6em]displaystyle 2&displaystyle 4&displaystyle 1\[0.6em]displaystyle 1&displaystyle 1&displaystyle 1
end{bmatrix}]

Вычислите соответствующую сопряженную матрицу (adj A).

Решение:

Нам нужно вычислить сопряженную матрицу предоставленной матрицы (3 times 3):

Шаг 1: вычислить матрицу кофакторов

Сначала мы вычисляем матрицу миноров. Имеем, что по определению матрица миноров (M) определяется формулой

[ M_{ij} = det A^{i,j}]

где в данном случае ( A^{i,j}) — это матрица (A) после удаления строки (i) и столбца (j).

Следовательно, и на основе матрицы (A) при условии, что мы получаем следующие коэффициенты матрицы миноров:

Для (A^{ 1, 1}):

[M_{ 1 1} = det A^{ 1 1} = begin{vmatrix}
displaystyle 4&displaystyle 1\[0.6em]displaystyle 1&displaystyle 1
end{vmatrix}
= 4 cdot left( 1 right) — 1 cdot left(1 right) = 3]

Для (A^{ 1, 2}):

[M_{ 1 2} = det A^{ 1 2} = begin{vmatrix}
displaystyle 2&displaystyle 1\[0.6em]displaystyle 1&displaystyle 1
end{vmatrix}
= 2 cdot left( 1 right) — 1 cdot left(1 right) = 1]

Для (A^{ 1, 3}):

[M_{ 1 3} = det A^{ 1 3} = begin{vmatrix}
displaystyle 2&displaystyle 4\[0.6em]displaystyle 1&displaystyle 1
end{vmatrix}
= 2 cdot left( 1 right) — 1 cdot left(4 right) = -2]

Для (A^{ 2, 1}):

[M_{ 2 1} = det A^{ 2 1} = begin{vmatrix}
displaystyle 3&displaystyle 1\[0.6em]displaystyle 1&displaystyle 1
end{vmatrix}
= 3 cdot left( 1 right) — 1 cdot left(1 right) = 2]

Для (A^{ 2, 2}):

[M_{ 2 2} = det A^{ 2 2} = begin{vmatrix}
displaystyle 2&displaystyle 1\[0.6em]displaystyle 1&displaystyle 1
end{vmatrix}
= 2 cdot left( 1 right) — 1 cdot left(1 right) = 1]

Для (A^{ 2, 3}):

[M_{ 2 3} = det A^{ 2 3} = begin{vmatrix}
displaystyle 2&displaystyle 3\[0.6em]displaystyle 1&displaystyle 1
end{vmatrix}
= 2 cdot left( 1 right) — 1 cdot left(3 right) = -1]

Для (A^{ 3, 1}):

[M_{ 3 1} = det A^{ 3 1} = begin{vmatrix}
displaystyle 3&displaystyle 1\[0.6em]displaystyle 4&displaystyle 1
end{vmatrix}
= 3 cdot left( 1 right) — 4 cdot left(1 right) = -1]

Для (A^{ 3, 2}):

[M_{ 3 2} = det A^{ 3 2} = begin{vmatrix}
displaystyle 2&displaystyle 1\[0.6em]displaystyle 2&displaystyle 1
end{vmatrix}
= 2 cdot left( 1 right) — 2 cdot left(1 right) = 0]

Для (A^{ 3, 3}):

[M_{ 3 3} = det A^{ 3 3} = begin{vmatrix}
displaystyle 2&displaystyle 3\[0.6em]displaystyle 2&displaystyle 4
end{vmatrix}
= 2 cdot left( 4 right) — 2 cdot left(3 right) = 2]

Подводя итог, матрица несовершеннолетних выглядит следующим образом:

[M = begin{bmatrix}
displaystyle 3&displaystyle 1&displaystyle -2\[0.6em]displaystyle 2&displaystyle 1&displaystyle -1\[0.6em]displaystyle -1&displaystyle 0&displaystyle 2
end{bmatrix}
]

Теперь мы можем вычислить элементы матрицы кофакторов (C), используя формулу

[ C_{ij} = (-1)^{i+j}M_{ij}]

Приведенную выше формулу можно использовать напрямую, поскольку миноры уже известны. Мы получаем

[ C_{ 1 1} = (-1)^{ 1+1} cdot 3 = (-1)^{ 2} cdot 3 = 3]
[C_{ 1 2} = (-1)^{ 1+2} cdot 1 = (-1)^{ 3} cdot 1 = -1]
[C_{ 1 3} = (-1)^{ 1+3} left(-2right)= (-1)^{ 4} left(-2right) = -2]
[C_{ 2 1} = (-1)^{ 2+1} cdot 2 = (-1)^{ 3} cdot 2 = -2]
[C_{ 2 2} = (-1)^{ 2+2} cdot 1 = (-1)^{ 4} cdot 1 = -1]
[C_{ 2 3} = (-1)^{ 2+3} left(-1right)= (-1)^{ 5} left(-1right) = 1]
[C_{ 3 1} = (-1)^{ 3+1} left(-1right)= (-1)^{ 4} left(-1right) = 1]
[C_{ 3 2} = (-1)^{ 3+2} cdot 0 = (-1)^{ 5} cdot 0 = 0]
[C_{ 3 3} = (-1)^{ 3+3} cdot 2 = (-1)^{ 6} cdot 2 = -2]

Подводя итог, матрица кофакторов:

[C = begin{bmatrix}
displaystyle 3&displaystyle -1&displaystyle -2\[0.6em]displaystyle -2&displaystyle -1&displaystyle 1\[0.6em]displaystyle 1&displaystyle 0&displaystyle -2
end{bmatrix}
]

Шаг 2: вычислить сопряженную матрицу из матрицы кофакторов

Теперь нам нужно просто транспонировать матрицу кофакторов, которую мы нашли, чтобы вычислить сопряженную матрицу. Мы получаем:

[adj(A) = C^T = begin{bmatrix}
displaystyle 3&displaystyle -1&displaystyle -2\[0.6em]displaystyle -2&displaystyle -1&displaystyle 1\[0.6em]displaystyle 1&displaystyle 0&displaystyle -2
end{bmatrix}
^T = begin{bmatrix}
displaystyle 3&displaystyle -2&displaystyle 1\[0.6em]displaystyle -1&displaystyle -1&displaystyle 0\[0.6em]displaystyle -2&displaystyle 1&displaystyle -2
end{bmatrix}
]

что завершает вычисление сопряженной матрицы.

Источник

Сопряженная матрица

Пусть ||aij|| (i=1,2,…,m; j=1,2…,n) и пусть элементы матрицы A комплексные числа. Сопряженной по отношению к A называется матрица ||aij|| (p=1,2,…,n; q=1,2…,m), где b_pq=a_qp ( a_qp сопряженное значение числа a_qp).

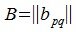
Для обозначения сопряженного к A матрицу используют запись A^*.

Для построения сопряженной матрицы достаточно взять в качестве столбцов − соответствующие строки исходной матрицы (т.е. транспонирование исходной матрицы), с последующей заменой каждого элемента полученной матрицы на соответствующий комплексно-сопряженный элемент. Например:

Свойства сопряженных матриц

(A^*)^*=A.
Если матрицы A и B одинакового размера, то (A+B)^*=A^*+B^*.
Если определено произведение AB (т.е. количество строк A равен количеству столбцов B ), то (AB)^*=B^*A^*.
(βA)^*=βA*, где β — произвольное комплексное число, а β число, комплексно сопряженное к β.
Если A квадратная матрица, то (A^-1)^*=(A^*)^-1, где A^-1 обратная к A матрица .

Если A− вещественная матрица, т.е. все элементы матрицы A вещественны, то A^*=A^T.

Для операций с матрицами пользуйтесь матричным онлайн калькулятором.

Источник

You can calculate the adjoint matrix, by taking the transpose of the calculated cofactor matrix. Adjoint matrix is also referred as Adjunct matrix or Adjugate or classical adjoint matrix. ‘Adjoint’ of a matrix refers to the corresponding adjoint operator, which is its conjugate transpose. The adjugate matrix is also used in Jacobi’s formula for the derivative of the determinant. Use our online adjoint matrix calculator to find the adjugate matrix of the square matrix.

Adjugate Matrix Calculator

Code to add this calci to your website

The adjugate matrix can be calculated by adjoint matrix calculator and is denoted by the symbol adj A. Adjugate matrix is found by the cofactor matrix and transpose of it.

Related Calculators:

Determinant Calculator
Product Of Determinants Calculator
Sum Of Determinants Calculator
Square Matrix Calculator
Eigen Value Eigen Vector Calculator
Mutual Inductance Calculator
Distance On A Coordinate Plane Calculator

Источник

Линейный
оператор ,
действующий в
— мерном унитарном (евклидовом) пространстве
,
называется сопряженным
к линейному оператору
,
если для любых векторов
и
из
выполняется равенство

(7.6.1)

В
унитарном (евклидовом) пространстве
каждому линейному оператору отвечает
сопряженный оператор и притом только
один.

Пусть

— комплексная квадратная матрица порядка
.
Квадратная матрица
порядка
называется сопряженной
к матрице
,
если для всех
и

(7.6.2)

В
ортонормированном базисе

унитарного пространства

матрица

сопряженного оператора

получается из матрицы

оператора

переходом к транспонированной и
комплексно сопряженной матрице:

(7.6.3)

В
ортонормированном базисе унитарного
пространства сопряженному оператору
соответствует сопряженная матрица, и
обратно. В случае евклидова пространства
таким же образом устанавливается
соответствие между сопряженными
операторами и транспонированными
матрицами.

Линейный
оператор ,
действующий в унитарном пространстве
,
называется самосопряженным
или эрмитовым,
если он совпадает со своим сопряженным
оператором, т.е. если ,
или, что то же самое, для любых векторов

и
из

(7.6.4)

Матрицей
самосопряженного оператора в
ортонормированном базисе является
эрмитова
матрица
,
для которой .
Все собственные значения самосопряженного
оператора являются действительными
числами. Собственные векторы
самосопряженного оператора, отвечающие
различным собственным значениям,
ортогональны.

Основным
свойством самосопряженного оператора
является то, что в унитарном пространстве
существует ортонормированный базис,
состоящий из собственных векторов этого
оператора. Это означает, что самосопряженный
оператор является оператором простой
структуры, а среди матриц
,
приводящих эрмитову матрицу

к действительной диагональной матрице

,
имеется унитарная матрица, для которой

.
Таким образом, эрмитова матрица

обладает каноническим разложением

с унитарной трансформирующей матрицей

.

Эрмитов
оператор
называется неотрицательным
(положительно
определенным),
если для любого ненулевого вектора
выполняется неравенство .
Неотрицательный и положительно
определенный операторы обозначаются
соответственно через
и .
Аналогично определяются и обозначаются
неотрицательные
и положительно
определенные матрицы.

Линейный
оператор ,
действующий в унитарно пространстве
,
называется унитарным,
если .
Другими словами, для унитарного оператора
.

Унитарный
оператор сохраняет скалярное произведение
и длины векторов, т.е.

;

(7.6.5)

(7.6.6)

Унитарный
оператор любую ортонормированную
систему векторов переводит в
ортонормированную систему векторов,
ортонормированный базис — в ортонормированный
базис. Собственные значения унитарного
оператора по модулю равны единице. В
ортонормированном базисе пространства
матрицей унитарного оператора является
унитарная матрица, и обратно, если в
ортонормированном базисе оператор
имеет унитарную матрицу, то этот оператор
унитарный. Столбцы (строки) унитарной
матрицы, рассматриваемые как векторы
унитарного арифметического пространства,
образуют ортонормированную систему.

Основным
свойством унитарного оператора является
то, что в унитарном пространстве, в
котором он действует, существует
ортонормированный базис, состоящий из
собственных векторов этого оператора.
Это означает, что унитарный оператор
является оператором простой структуры,
а среди матриц
,
приводящих унитарную матрицу

к диагональной матрице

с диагональными элементами, равными по
модулю единице, имеется унитарная
матрица. Таким образом, унитарная матрица

обладает каноническим разложением

с унитарной трансформирующей матрицей

и диагональной матрицей

с диагональными элементами, равными по
модулю единице.

Линейный
оператор ,
действующий в унитарном (евклидовом)
пространстве ,
называется нормальным,
если он перестановочен со своим
сопряженным оператором, т.е. если .

В
ортонормированном базисе матрицей
нормального оператора является матрица
,
перестановочная со своей сопряжённой
матрицей, т.е. удовлетворяющая условию
.
Такие матрицы называются нормальными.

Основным
свойством нормального оператора,
действующего в унитарном пространстве,
является то, что в этом пространстве
существует ортонормированный базис,
состоящий из собственных векторов этого
оператора. Верно и обратное утверждение,
т.е. если в унитарном пространстве
существует базис, состоящий из собственных
векторов оператора, то этот оператор
нормальный.

Если
оператор —
нормальный, то собственные значения
операторов
и ,
соответствующие общему собственному
вектору, комплексно сопряжены.

Примерами
нормальных операторов являются эрмитовы
и унитарные операторы.

Нормальный
оператор является оператором простой
структуры. На матричном языке это
означает, что нормальная матрица
приводится к диагональному виду.
Нормальная матрица обладает каноническим
разложением с унитарной трансформирующей
матрицей.

У
всякого линейного оператора

в действительном линейном пространстве

существует одномерное или двумерное
инвариантное подпространство.

Линейный
оператор ,
действующий в евклидовом пространстве
,
называется симметричным
или самосопряженным,
если для любых векторов
и
из
выполняется равенство (7.6.4).

Матрицей
симметричного оператора в ортонормированном
базисе является симметричная
матрица
,
для которой .
Все собственные значения симметричного
оператора являются действительными
числами. Собственные векторы симметричного
оператора, отвечающие различным
собственным значениям, ортогональны.

Основным
свойством симметричного оператора
является то, что в евклидовом пространстве
существует ортонормированный базис,
состоящий из собственных векторов этого
оператора. Это означает, что симметричный
оператор является оператором простой
структуры, а среди матриц ,
приводящих симметричную матрицу
к диагональной матрице ,
имеется ортогональная
матрица,
для которой .
Таким образом, симметричная матрица
обладает каноническим разложением
с ортогональной трансформирующей
матрицей .
Правило построения этой ортогональной
матрицы
отличается от рассмотренного в §
7.5 лишь тем, что здесь необходимо
ортонормировать найденный базис из
собственных векторов матрицы .

Симметричный
оператор
называется неотрицательным
( положительно
определенным),
если для любого ненулевого вектора
выполняется неравенство .
Так же определяются одноименные классы
действительных матриц.

Линейный
оператор ,
действующий в евклидовом пространстве
,
называется ортогональным,
если он сохраняет скалярное произведение
любых векторов
и
из ,
т.е. если выполняется равенство

(7.6.7)

Ортогональный
оператор сохраняет длины векторов и
углы между векторами. Ортогональный
оператор любую ортонормированную
систему векторов переводит в
ортонормированную систему векторов, а
ортонормированный базис — в ортонормированный
базис. Ортогональный оператор в любом
ортонормированном базисе евклидова
пространства
имеет ортогональную матрицу. Определитель
матрицы ортогонального оператора равен
.

Для
любого ортогонального оператора ,
действующего в
— мерном евклидовом пространстве ,
существует в
ортонормированный базис ,
в котором матрица
оператора
имеет следующий вид

,
(7.6.8)

где
все невыписанные элементы равны нулю.

Пример
1.
Линейный оператор
в базисе ,
,

имеет матрицу .
Найдите матрицу
сопряженного оператора

в этом же базисе, если векторы
заданы координатами в ортонормированном
базисе .

Решение.
Матрица
сопряженного оператора
в базисе
связана с матрицей
этого же оператора в базисе
соотношением ,
где
— матрица перехода от базиса
к базису .
Поскольку для евклидова пространства
в ортонормированном базисе матрицей
сопряженного оператора
является транспонированная матрица к
матрице оператора ,
.
Матрицу
оператора
в базисе
найдем через матрицу
этого же оператора в базисе по
формуле ,
где
— матрица перехода от базиса
к базису .
Очевидно, что .
В силу того, что ,
а ,
получаем:

Пример
2.
В базисе

скалярное произведение задано формулой

,
(7.6.9)

а
линейный оператор
— матрицей .
Найдите матрицу
сопряженного оператора
в том же базисе .

Решение.
Начнем с построения ортонормированного
базиса .
Зная ,
можно по формуле
вычислить матрицу
оператора
в этом базисе (здесь
— матрица перехода от базиса
к базису )
и найти матрицу
сопряженного оператора
в базисе .
Матрицу
сопряженного оператора
в базисе
найдем при помощи соотношения ,
где
— матрица перехода от базиса
к базису .
В силу того, что .

Построение
ортонормированного базиса осуществим,
применяя процесс ортогонализации Грама
— Шмидта и нормирование векторов

Векторы

ортогональны в смысле скалярного
произведения (7.6.9). Учитывая, что
,
получаем:

Таким
образом, матрица перехода от базиса
к ортонормированному базису

а
обратная к ней матрица

Отсюда
следует, что

Пример
3.
Для симметричной матрицы
постройте каноническое разложение с
ортогональной трансформирующей матрицей
и, пользуясь им, найдите .

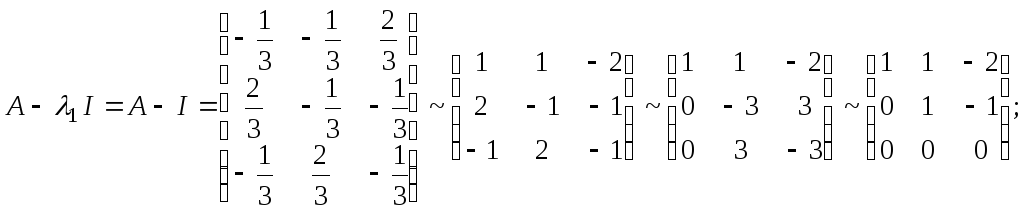
Решение.
Характеристический многочлен

имеет
корни .
Поэтому матрицей
в каноническом разложении является .

Перейдем
к построению ортогональной матрицы
в каноническом разложении. Найдем
собственные векторы ,
отвечающие собственным значениям .

Общим
решением
однородной
системы
является вектор .
Выбирая ,
получаем .

Общим
решением
однородной
системы
является вектор .
Выбирая ,
получаем .
Подчеркнем, что
и
сразу ортогональны как собственные
векторы симметричного оператора,
отвечающие различным собственным
значениям. Поскольку
,
получаем ортонормированную систему
собственных векторов
матрицы ,
являющуюся столбцами искомой
транформирующей матрицы, т.е. .

Проверим
правильность построения канонического
разложения .
Учитывая, что ,
имеем:

Полученное
каноническое разложение позволяет
вычислить
по формуле ,
где .

Пример
4.
Линейный оператор
пространства
в базисе ,
,

задан матрицей .
Является ли
ортогональным оператором?

Решение.
Найдем матрицу
оператора
в ортонормированном базисе ,
,

и проверим, будет ли полученная матрица
ортогональной.

где

— матрица перехода от базиса
к базису .
Поскольку ,
,
,
матрица перехода от базиса
к базису

.
Следовательно, ,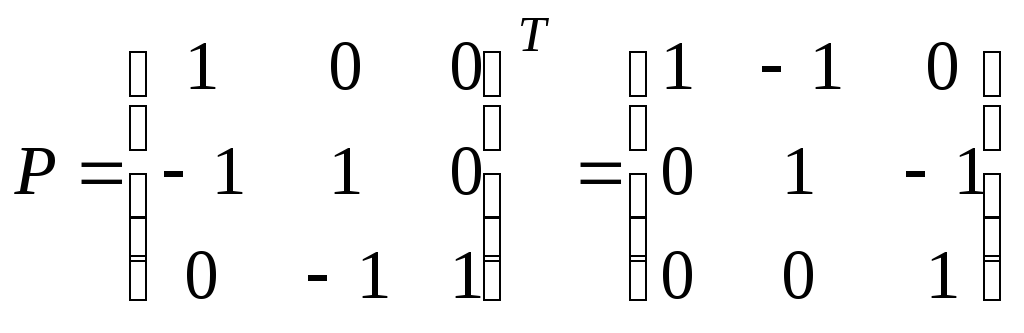
и

В
силу того, что

отсюда
заключаем, что
является ортогональным оператором.

Пример
5.
Ортогональный оператор
в ортонормированном базисе
имеет ортогональную матрицу .
Постройте базис ,
в котором оператор
имеет матрицу
канонического вида (7.6.8) и найдите матрицу
.

Решение.
Характеристический многочлен

оператора

имеет корни .

В
силу того, что

однородная
система
имеет общее решение ,
а однородная система
имеет общее решение .
Выбирая
и ,
получаем векторы
и
.
Заметим, что векторы
ортогональны (см. задачи 7.6.40 и 7.6.46).
Нормируя их, придем к искомому базису

в
котором оператор
имеет каноническую матрицу

Проверим
правильность вычислений:

где

7.6.1.
Из определения сопряженного оператора
выведите следующие свойства:

а)

б)

в)

г)

д)

е)

ж)
если оператор
невырожден, то

з)

для всякого целого неотрицательного
;

и)
если оператор
невырожден, то свойство з)
имеет место для любого целого числа ;

к)
если
— произвольный многочлен, то
,
где .

7.6.2.
Докажите, что свойства, перечисленные
в предыдущей задаче, выполняются и для
сопряженных матриц.

7.6.3.
Покажите, что если операторы
и
перестановочны, то перестановочны и
сопряженные и операторы
и
(операторы
и
из
называются перестановочными,
если ).

7.6.4.
Пусть
— ортогональный (но не ортонормированный!)
базис пространства .
Найдите связь между матрицами в этом
базисе оператора из

и сопряженного оператора .

7.6.5.
Пусть оператор
действует в одномерном унитарном
(евклидовом) пространстве. В чем состоит
преобразование ,
сопряженное по отношению к ?

7.6.6.
Пусть
— ортонормированный базис евклидова
пространства,
— матрица линейного оператора
в базисе
.
Найдите матрицу оператора
в базисе .

7.6.7. Линейный
оператор
евклидова пространства в базисе ,
,

задан матрицей .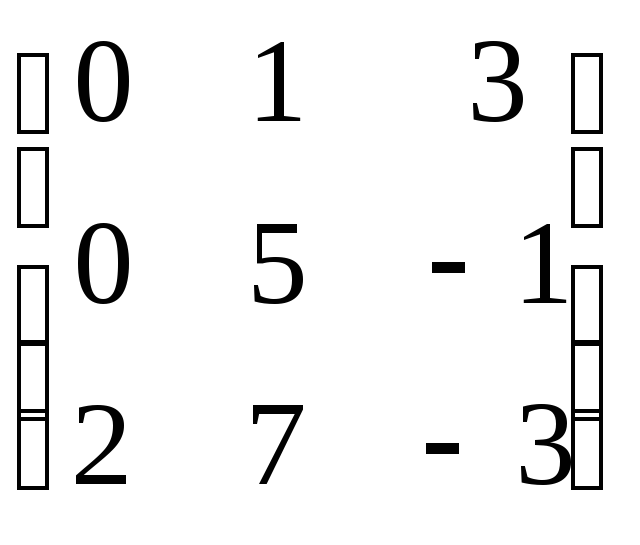
Найдите матрицу оператора
в том же базисе, считая, что координаты
векторов базиса даны в некотором
ортонормированном базисе.

7.6.8.
Найдите матрицу линейного оператора
в ортонормированном базисе ,
если
переводит векторы ,
,

в векторы ,
,

соответственно, считая, что координаты
всех векторов даны в базисе .

Пусть
в некотором базисе скалярное произведение
задано билинейной формой ,
а линейный оператор — матрицей .
Найдите матрицу
сопряженного оператора в том же базисе:

7.6.9.

Соседние файлы в папке Задачник-2

Источник