Сопряжения
В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
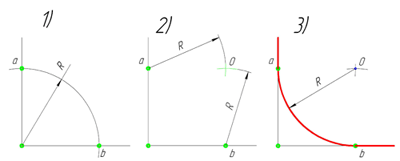
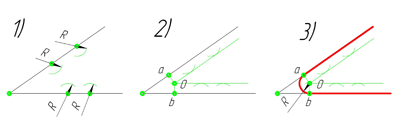
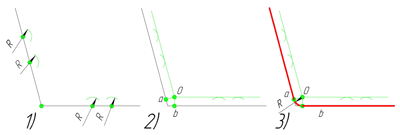
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Сопряжение параллельных прямых линий
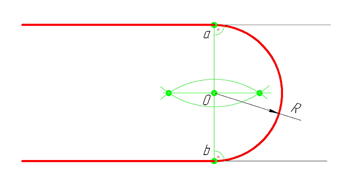
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Сопряжение окружностей (дуг)
Внешнее сопряжение дуг окружностей
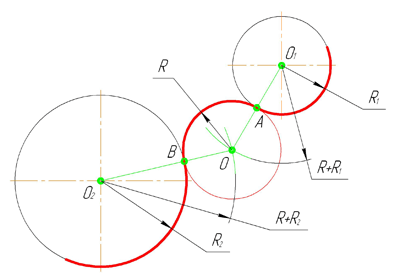
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Внутреннее сопряжение дуг окружностей
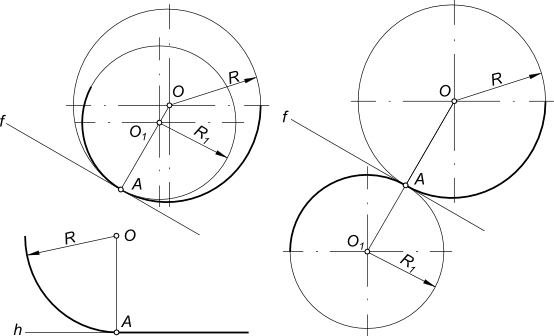
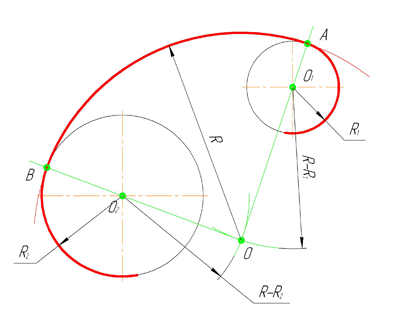
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
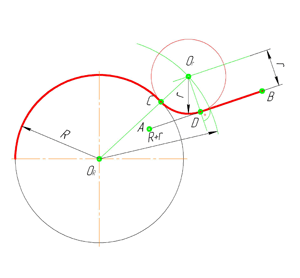
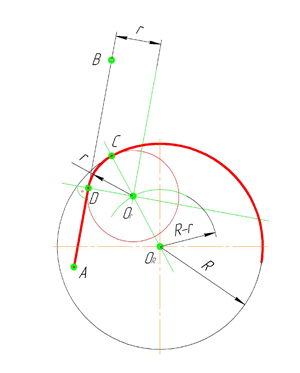
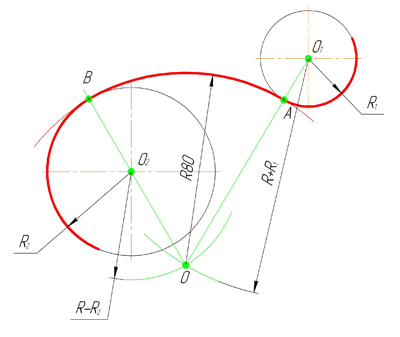
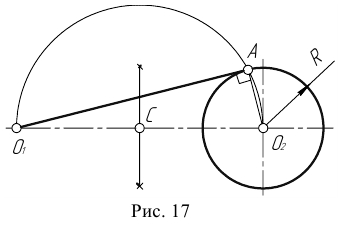
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Преподаватель который помогает студентам и школьникам в учёбе.
Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
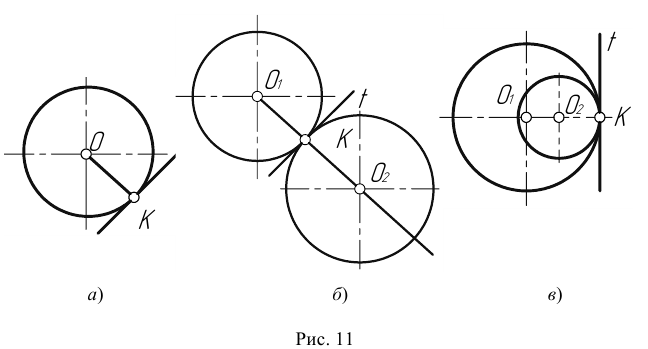
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 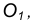
- Заказать чертежи
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
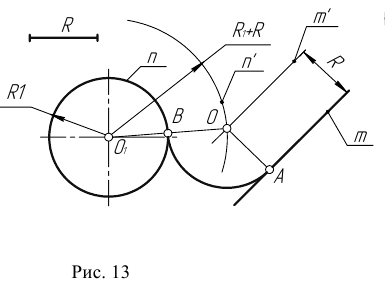
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 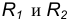
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 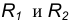
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Построение касательных
Пример 1. Дана окружность с центром в точке 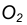
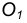
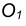
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 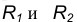
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
Сопряжение
Сопряжение — это плавный переход от одной прямой или кривой линии к другой кривой линии. Сопряжение
Дуги окружностей, при помощи которых выполняется сопряжение, называют дугами сопряжения. На рисунке это дуги радиусов R и R1. Сопряжение
На рисунке это точки O, O1 и O2. Сопряжение
Геометрическим местом точек, равноудаленных от окружности, является концентричная окружность. Радиус этой окружности определяется в зависимости от вида сопряжения. + |


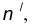 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.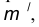 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.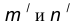 найдем центр сопряжения О.
найдем центр сопряжения О.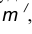 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.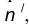 проведенная радиусом
проведенная радиусом 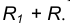
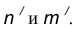
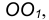 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.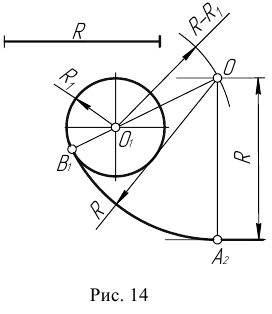
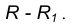
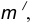 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 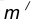 равен
равен 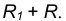
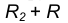 проведем окружность
проведем окружность 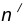 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.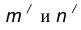 .
.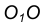 с дугой m.
с дугой m. с дугой n .
с дугой n .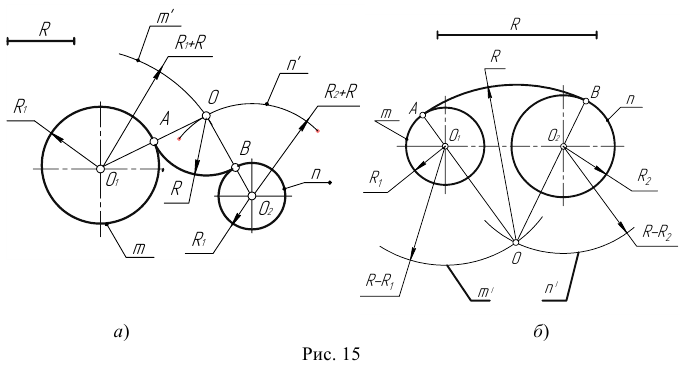
 на расстоянии
на расстоянии 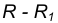 от данной окружности m.
от данной окружности m.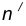 на расстоянии
на расстоянии 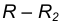 от данной окружности n.
от данной окружности n.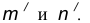
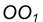 с заданной окружностью m.
с заданной окружностью m.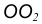 c заданной окружностью n.
c заданной окружностью n.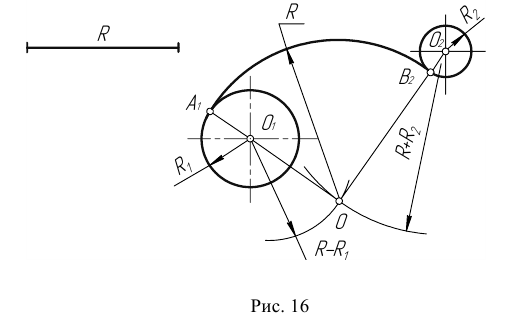
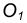 с центром окружности
с центром окружности 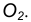
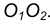
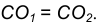
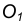 с точкой А.
с точкой А. 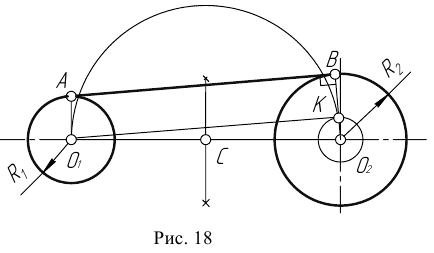
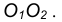
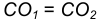 проведем вспомогательную окружность.
проведем вспомогательную окружность.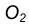 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 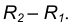
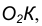 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем