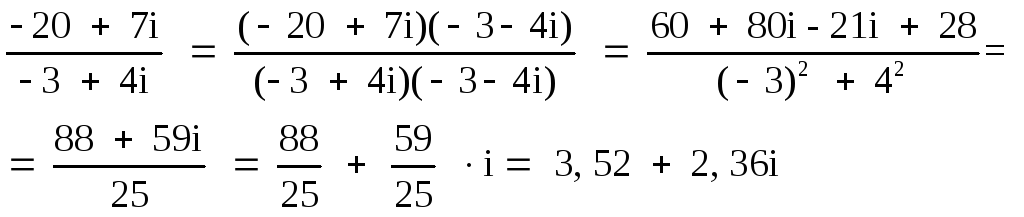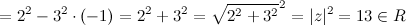Как найти сопряженное значение комплексного числа - Исправление недочетов и поиск решений вместе с Examum.ru

Комплексно сопряженные числа

ОПРЕДЕЛЕНИЕ

Сопряженное (или комплексно сопряженное) число с комплексным числом (
z=x+i y
) является числом (
overline{z}=x-i y
)

ПРИМЕР

Задачей

поиска для комплексного числа (
z=-34-i
) является его сопряженное число.

Решение.

Комплексное сопряженное число является числом вида (
overline{z}=x-i y
) . Вещественной частью комплексного числа (
z=-34-i
) является число (
x=operatorname{Re}
), (
z=-34
), мнимая часть равна (
y=operatorname{lm}
), (
z=-1
).

Следовательно, сопряженное число имеет вид: (
overline{z}=-34+i
)

Ответ

(
overline{z}=-34+i
)

На комплексной плоскости сопряженные числа зеркалируются относительно оси действительных чисел.

Свойства комплексно-сопряженных чисел

1. (
|z|=|z|
), т. е. модули сопряженных чисел равны.

Например.

Модуль комплексного числа (
z=-4+i
) равен (
r=sqrt{(-4)^{2}+1^{2}}=sqrt{17}
). Присоединенным к комплексному числу является число (
z=-4-i
), модуль (
r=sqrt{(-4)^{2}+(-1)^{2}}=sqrt{17}
) которого равен модулю исходного числа.

2. (
arg z=-arg overline{z}
) т. е. Аргументы сопряженных чисел различаются по знаку.

3. (
overline{overline{z}}=z
) т. е. Комплексное сопряженное сопряженное число является исходным комплексным числом.

4. (
z cdot overline{z}=|z|^{2}
) т. е. В результате произведения сопряженных чисел получается вещественное число.

5.(
z+overline{z}=2 operatorname{Re} z
) т. е. Сумма сопряженных чисел также является вещественным числом.

6.(
overline{z_{1} cdot z_{2}}=overline{z_{1}} cdot overline{z_{2}}
) т. е. Сопряженное произведение двух комплексных чисел является произведением их сопряженных чисел.

7.(
overline{z_{1} div z_{2}}=overline{z_{1}} div overline{z_{2}}
) т. е. Сопряженное к ним частное число есть фактор сопряженного.

Примеры решения проблем

ПРИМЕР 1

Задача

Чтобы умножить комплексное число (
z=4-7 i
) на его сопряженное.

Решение.

Сопряженное с номером (
z=4-7 i
) — это число (
z=4+7 i
). Найдите произведение двух чисел:

(
z cdot overline{z}=(4-7 i) cdot(4+7 i)=4 cdot 4+(-7) cdot 7 cdot i^{2}+i(4 cdot 7-7 cdot 4)=65
)

Ответ

(
z cdot overline{z}=65
)

ПРИМЕР 2

Задача

Чтобы найти сопряженное к частному два комплексных числа: (
z 1=1-3 i
), (
z 2=2+5 i
).

Решение

Фактор комплексных чисел определяется путем умножения числителя и знаменателя на сопряженное число:

(
z_{1} div z_{2}=frac{1-3 i}{2+5 i}=frac{(1-3 i)(2-5 i)}{(2+5 i)(2-5 i)}=frac{1 cdot 2-3 cdot 5}{2^{2}+5^{2}}+i frac{-5 cdot 1-3 cdot 2}{2^{2}+5^{2}}=-frac{13}{29}-i frac{11}{29}
)

Сопряженным числом для конкретного будет число (
-frac{13}{29}+i frac{11}{29}
)

Мы получим тот же результат, если найдем фактор сопряженных чисел (
z rceil=1-3 i
), (
z 2=2+5 i
):

(
overline{z_{1}} div overline{z_{2}}=frac{1+3 i}{2-5 i}=frac{(1+3 i)(2+5 i)}{(2-5 i)(2+5 i)}=frac{1 cdot 2-3 cdot 5}{2^{2}+5^{2}}+i frac{5 cdot 1+3 cdot 2}{2^{2}+5^{2}}=-frac{13}{29}+i frac{11}{29}
)

Ответ

(
overline{z_{1} div z_{2}}=-frac{13}{29}+i frac{11}{29}
)

Источник

Операция
деления

Операция
комплексного сопряжения– это
изменение знака перед мнимой частью.
Еслиz=x+iy, то числоx–iyназывается сопряженным
числуzи обозначается
:

=
= х –iy.

Пример
4.1 Найти
числа, сопряженные

а)
z₁
= i;
б) z₂
= 5; в) z₃
= 1 – 2i;
г) z₄
= 7i
+ 1.

Решение.

а)
z₁
= 0 + 1i , то

₁
= –i;

б)
z₂=5
+ 0 · i , то

₂
= 5 – 0 · i = 5;

в)

₃=
1 + 2i;

г)

₄₌–_{7 i +

1.}

_{Свойства

комплексно-сопряженных чисел:}

1)
z +

= x + iy + x – iy = 2x = 2Re z;

2)
z —

= x + iy – (x – iy) = 2iy = 2i lm z;

3)
z ·

= (x + iy) (x – iy) = x²
+ y².

Таким
образом, сумма и произведение комплексно
сопряженных чисел являются действительными
числами, а
их разность – число мнимое.

=

=

= x + iy = z
С;

5)
z =


lm z = 0 

;

=
;

;

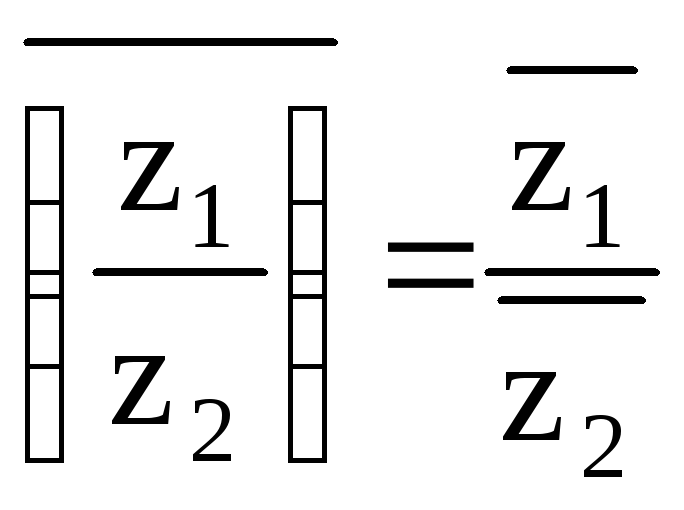
Операция
деления
определяется как действие, обратное
умножению. Частное

двух комплексных чисел z₁
и z₂

0 – это такое комплексное число z,
которое удовлетворяет условию z₂
· z = z₁.

Частное
получается путем умножения числителя
и знаменателя на число
,
сопряженное знаменателю.

Пример
4.2 Найти
,
если z₁
= 2 – 5i
, z₂
= –3 – 2i
.

Решение.

Пример
4.3 Записать
в алгебраической форме число

Решение.

Выполняем
последовательно все операции:

Re(1
+ 2i)²
= Re(–3
+ 4i) = –3;

(3
– 2i)(5
+ i) = 15 + 3i – 10i + 2 = 17 – 7i;

–3
– (17 – 7i) = –3
– 17 + 7i = –20
+ 7i;

;

1
+ 5i – (4 + i) = 1 + 5i – 4 – i = –3
+ 4i;

;

35,2
+ 2,36i – (– i) = 3,52 + 2,36i + i = 3,52 + 3,36i.

Упражнения

1 Вычислить:

а)
i⁴;
i⁸¹;
б)

в)
i²³¹;
i²⁰²⁴.

2
Найти
число, сопряженное данному:

а)
2i ; –3i; б)
(1 + i)(2 + 3i); (2 – i)(3 + i);

в)

г) (1 + i)²;
(2 – i)².

3
Представить
число в алгебраической форме:

а)

б)

в)

;
г)
;

д)

;
е)
;

ж)

;
з)

4 Выполнить действия:

а)

;
б)

;

в)
(1 – i)(4 + 3i)(2 + i)(3 + i) ; г)

;

д)

;
е)
;

ж)

5
Найти
значение выражения:

а)

z²
+ 3z + 1 + 3i при
z = 2 + 3i;

б)
(z – z²
+ 2z³)(2
– z + z²)
при
z =.

6
Найти
решение уравнений, где x
и y
– действительные числа:

а)
(1 + i)
∙ x
+ (2 + i)
∙ y
= 5 + 3i;

б)
2x
+ (1 + i)(x
+ y)
= 7 + i;

в)
(3 – y
+ x)(1
+ i)
+ (x
– y)(2
+ i)
= 6 – 3i;

г)
(i
– z)(1
+ 2i)
+ (1 – iz)(3
– 4i)
= 1 + 7i.

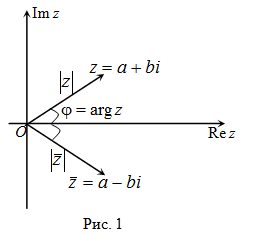
§5 Геометрическая интерпретация комплексных чисел

Определение
комплексного числа как упорядоченной
пары чисел (х; у) позволяет установить
взаимно однозначное соответст- вие
между комплексным числом

z
= x
+ iy
и точкой М(х; у) в декартовой системе
координат ОХУ (рисунок 1). Числовую
плоскость в этом случае называют
комплекс—

Рисунок
1 ной
плоскостью.

Ось
абсцисс называют действительной
осью, а ось ординат – мнимой
осью. С другой стороны, комплексное
число z
= x
+ iy
можно взаимно однозначно поставить в
соответствие вектору с координатами х
и у и началом в точке О (радиус-вектор).
Поэтому понятия «комплексное число»,
«точка z»
и «вектор z»
употребляются как синонимы.

Пример
5.1 Изобразить
на комплексной плоскости числа

а)
z
и
;
б) z
= 1 + 2i.

Решение:
а) – рисунок
2; б) – рисунок 3.

Рисунок 2
Рисунок 3

Соседние файлы в папке КЧ

Источник

Содержание:

Определение
Свойства комплексно-сопряженных чисел

Определение

Если $z=a+b i$, то число
$overline{z}=a-b i$ называется
комплексным сопряженным к числу $z$ .

То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.

Например. Комплексно сопряженным к числу
$z=2-i$ есть число
$overline{z}=2+i$ .

На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.

Свойства комплексно сопряженных чисел

1) Если $z=overline{z}$, то можно сделать вывод,
что рассматриваемое число $z$ является действительным.

Например. $z=2 in R Rightarrow overline{z}=2$ и
$z=overline{z}$

2) Для любого комплексного числа
$z$ сумма
$z+overline{z}=2 operatorname{Re} z$ —
действительное число.

Например. Пусть
$z=2-3 i$, тогда
$overline{z}=2+3 i$, а тогда

$z+overline{z}=2-3 i+(2+3 i)=2-3 i+2+3 i=2+2=4 in R$

3) Для произвольного комплексного числа
$z=a+b i$ произведение
$z cdot overline{z}=|z|^{2} in R$ .

Например. Пусть
$z=2-3 i$, комплексно сопряженное к нему число
$overline{z}=2+3 i$, тогда произведение

$z cdot overline{z}=(2-3 i)(2+3 i)=2^{2}-(3 i)^{2}=2^{2}-3^{2} cdot i^{2}=$

4) Модули комплексно сопряженных чисел равны:
$|z|=|overline{z}|$, а аргументы отличаются знаком (рис. 1).

5) $overline{z_{1} pm z_{2}}=overline{z}_{1} pm overline{z}_{2}$

6) $overline{z_{1} cdot z_{2}}=overline{z_{1}} cdot overline{z}_{2}$

7) $frac{overline{z_{1}}}{z_{2}}=frac{overline{z}_{1}}{overline{z}_{2}}$

$overline{(overline{z})}=z$

9) Если $z=a+b i$ и
$overline{z}=a-b i$ — комплексно сопряженные числа, то

$a=operatorname{Re} z=frac{z+overline{z}}{2}, b=operatorname{Im} z=frac{z-overline{z}}{2 i}$

Читать дальше: формы записи комплексного числа.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

В данной публикации мы рассмотрим, что такое комплексно сопряженные числа, а также перечислим их основные свойства. Представленная теоретическая информация сопровождается практическими примерами для лучшего понимания.

Определение комплексно сопряженных чисел
Свойства комплексно сопряженных чисел

Определение комплексно сопряженных чисел

Дано комплексное число z = a + bi. Комплексно сопряженным к нему является число z = a – bi (для обозначения используется черточка сверху).

Таким образом, у комплексно сопряженных чисел действительные части одинаковые, а мнимые отличаются по знаку.

Пример:
Для числа z = 3 + 2i комплексно сопряженным является z = 3 – 2i.

Геометрическая интерпретация

Если перенести комплексно сопряженные числа на комплексную плоскость, то они будут зеркальным отражением друг друга относительно действительной оси (RE).

Свойства комплексно сопряженных чисел

1. Если z = z, значит число z является действительным.

Пример:
z = 2, значит z ∈ R, следовательно z = 2, т.е. z = z.

2. Модули комплексно сопряженных чисел равны, т.е. |z| = |z|. А так как такие числа на комплексной плоскости зеркальны, то их аргументы отличаются по знаку.

3. Сумма комплексно сопряженных чисел – это действительное число: z + z = 2 RE z.

Пример:
z = 5 + 2i
z = 5 – 2i
z + z = 5 + 2i + 5 – 2i = 5 + 5 = 10, а 10 ∈ R.

4. Произведение комплексно сопряженных чисел равняется квадрату их модуля и является действительным числом: z ⋅ z = |z|² ∈ R.

Пример:
z = 6 – 4i
z = 6 + 4i
z ⋅ z = (6 – 4i)(6 + 4i) = 36 + 24i – 24i – 16i² = 36 – 16 ⋅ (-1) = 52, а 52 ∈ R.

Модуль считается так:

5. Для z = a + bi и z = a – bi справедливо:

6. Для произвольных комплексных чисел z₁ и z₂:

Источник

Комплексные числа в алгебраической форме

Определение комплексного числа

Комплексным числом называется выражение вида x+iy , где x,,y — действительные числа (x,yinmathbb{R}) ; — число, квадрат которого равен минус единице (i^2=-1) ; число обозначается z=x+iy .

Числа и при этом называются соответственно действительной и мнимой частью комплексного числа и обозначаются x=operatorname{Re}z,, y=operatorname{Im}z ; — мнимая единица.

Выражение z=x+iy называется алгебраической формой записи комплексного числа; знаки между составляющими числа — обычные знаки операций сложения и умножения, которые обладают теми же свойствами, что и в действительной области.

Множество комплексных чисел обозначается mathbb{C} , а zin mathbb{C} — элемент данного множества.

Из определения следует, что действительные числа можно рассматривать как частный случай комплексных, т.е. mathbb{R}subsetmathbb{C} , а именно при y=0 получаем z=x — действительное число.

Число z=iy называется чисто мнимым.

Пример 1.1. Записать действительную и мнимую части чисел: z_1=3-2i,~ z_2=5,~ z_3=-3i,~ z_4=1+i, .

Решение. $operatorname{Re}z_1=3,~ operatorname{Im}z_1=-2;~~ operatorname{Re}z_2=5,~ operatorname{Im}z_2=0;~~ operatorname{Re}z_3=0,~ operatorname{Im}z_3=-3,~~ operatorname{Re}z_4=1,~ operatorname{Im}z_4=1$ .

Равенство комплексных чисел

Комплексные числа z_1=x_1+iy_1 и z_2=x_2+iy_2 называются равными, если у них соответственно равны действительные и мнимые части:

$z_1=z_2quad Leftrightarrowquad begin{cases}operatorname{Re}z_1= operatorname{Re}z_2,\ operatorname{Im}z_1= operatorname{Im}z_2;end{cases} Leftrightarrowquad begin{cases}x_1=x_2,\ y_1=y_2.end{cases}$

(1.1)

Сопряженные комплексные числа

Комплексные числа называются сопряженными, если у них равны действительные чисти, и мнимые противоположны по знаку. Число, сопряженное числу z=x+iy , обозначается overline{z}=x-iy . Определение сопряженных чисел можно записать и виде равенств:

operatorname{Re}overline{z}= operatorname{Re}z,qquad operatorname{Im}overline{z}= -operatorname{Im}z.

(1.2)

Из определения, в частности, следует, что число, сопряженное действительному числу, совпадает с ним: overline{x}=x,~ xin mathbb{R} .

Пример 1.2. Записать числа, сопряженные комплексным числам из примера 1.1.

Решение. Используя равенства (1.2), получаем:

$z_1=3-2i~ Rightarrow~ overline{z}_1=3+2i;quad z_2=5~ Rightarrow~ overline{z}_2=5;quad z_3=-3i~ Rightarrow~ overline{z}_3=3i;quad z_4=-1+i~ Rightarrow~ overline{z}_4=-1-i.$

Комплексная плоскость

Из определения комплексного числа как упорядоченной пары действительных чисел (см. введение) получаем, что задание комплексного числа можно рассматривать как задание точки на плоскости, абсциссой которой является x=operatorname{Re}z , ординатой y=operatorname{Im}z , т.е. числу z=x+iy соответствует точка M(x,y) . Между множеством точек плоскости Oxy и множеством комплексных чисел (множество mathbb{C} ) устанавливается взаимно однозначное соответствие: каждой точке M(x,y) соответствует единственное число z=x+iy , каждому числу z=x+iy соответствует единственная точка с координатами (x,y) ; плоскость Oxy при этом называется комплексной плоскостью (плоскость (z) ). На рис. 1.1 отмечены точки, соответствующие комплексным числам из примера 1.2.

Точки на комплексной плоскости

Используя геометрическую интерпретацию комплексных чисел как точек плоскости, убеждаемся в справедливости утверждения, что комплексные числа не сравниваются, т.е. на множестве mathbb{C} не определены операции сравнения (не имени места знаки <,,leqslant,,>,,geqslant ). Это следует из того, что множество точек плоскости не упорядочено.

Понятие бесконечности на множестве комплексных чисел

Как и в действительной области, на множестве комплексных чисел вводится понятие бесконечности, бесконечно удаленной точки. Это можно сделать по аналогии с множеством mathbb{R} действительных чисел из геометрических соображений.

Рассмотрим числовую прямую и окружность , которая касается прямой в точке ; точку, диаметрально противоположную точке , обозначим (рис. 1.2,б).

Будем соединять прямыми различные точки оси с точкой ; точки пересечения прямых с окружностью будем обозначать . Очевидно, каждой точке xin mathbb{R} соответствует точка Xin S . Обратное справедливо для всех точек окружности, за исключением точки . Но по мере удаления по прямой от точки (с увеличением расстояния, равного |x| ), ее образ на окружности приближается к точке . Для последовательности такого вида в анализе принято название бесконечно большая последовательность (величина). Ее предел обозначается $lim_{ntoinfty}x_n=infty$ и называется бесконечностью или бесконечно удаленной точкой. Поэтому точку можно рассматривать как образ бесконечно удаленной точки на окружности, а бесконечность — как «точку» оси , образом которой на окружности является точка .

Сфера Римана и стереографическая проекция

По аналогии рассмотрим плоскость (плоскость Oxy ) и сферу , касающуюся ее в начале координат, т.е. в точке (рис. 1.2,а). Лучи, соединяющие точки zinmathbb{C} с точкой пересекают сферу в точках Zin S . При этом любой точке соответствует единственная точка Zin S , и наоборот, любой точке Zin Ssetminus N соответствует единственная точка zin mathbb{C} . Очевидно, чем дальше расположена точка от начала координат ( $lim_{ntoinfty} rho_n=infty,~ rho_n=sqrt{x_n^2+y_n^2}$ — длина радиуса-вектора точки z=x+iy ), тем ближе ее образ Zin S к точке . Чтобы соответствие было полным, вводится «несобственный» элемент (символ infty ) , бесконечно удаленная точка как точка плоскости, образом которой на является точка .

Плоскость mathbb{C} , дополненная элементом infty , называется расширенной комплексной плоскостью и обозначается overline{mathbb{C}}= mathbb{C}cup{infty} .

Построенное взаимно однозначное соответствие точек сферы и множества mathbb{C} называется стереографической проекцией, а сфера — сферой Римана.

Сложение комплексных чисел

Суммой двух комплексных чисел z_1=x_1+iy_1 и z_2=x_2+iy_2 называется число z=x+iy такое, что справедливы равенства

x=x_1+x_2,quad y=y_1+y_2 , то есть z=z_1+z_2= (x_1+x_2)+ i(y_1+y_2)= x+iy .

Обозначение: z=z_1+z_2 .

Правило сложения: при сложении комплексных чисел складываются действительные и мнимые части соответственно.

Пример 1.3. Найти сумму чисел z_1 и z_2 , z_2 и z_3 , где z_1=3-2i,~ z_2=5+2i,~ z_3=1-i .

Решение.

$begin{gathered}z_1+z_2= (3-2i)+(5+2i)= (3+5)+i(-2+2)=8;\[2pt] z_2+z_3= (5+2i)+(1-i)= 6+i.end{gathered}$

Вычитание комплексных чисел

Разностью чисел z_1 и z_2 называется число такое, что z_1=z+z_2 . Обозначение: z=z_1-z_2 . Используя правило сложения, получаем для нахождения разности z=z_1-z_2,~ z=x+iy равенства x=x_1-x_2,~ y=y_1-y_2 .

Правило вычитания. При нахождении разности z_1-z_2 из действительной и мнимой частей уменьшаемого z_1 вычитаются соответственно действительная и мнимая части вычитаемого:

z=(x_1-x_2)+ (y_1-y_2)i,.

Пример 1.4. Найти разность z_1-z_2,~ z_2-z_3 для чисел из примера 1.3.

Решение.

$begin{gathered}z_1-z_2= (3-2i)-(5+2i)= (3-5)+ (-2i-2i)= -2-4i,\[2pt] z_2-z_3= (5+2i)- (1-i)= 4+3i. end{gathered}$

Умножение комплексных чисел

Произведением чисел z_1=x_1+iy_1 и z_2=x_2+iy_2 называется число z=x+iy такое, что выполняются равенства x=x_1x_2-y_1y_2, y=x_1y_2+x_2y_1 . Обозначение: z=z_1cdot z_2 .

Нетрудно убедиться, что эти равенства имеют место, если произвести формальное перемножение выражений (x_1+iy_1) и (x_2+iy_2) , как двучленов:

(x_1+iy_1)(x_2+iy_2)= x_1x_2+ i,x_1y_2+ i,y_1x_2+ i^2y_1y_2= (x_1x_2-y_1y_2)+ i(x_1y_2+ y_1x_2).

Правило умножения. Комплексные числа перемножаются, как двучлены, при этом учитывается, что i^2=-1 .

Пример 1.5. Найти произведение комплексных чисел z_1=1-2i и z_2=3+4i .

Решение.

z_1cdot z_2= (1-2i)(3+4i)= 1cdot3+ 1cdot4i- 3cdot2i+ 4icdot(-2i)= 3-2i-8i^2= 11-2i,.

Пример 1.6. Найти сумму и произведение пары комплексных сопряженных чисел

Решение. Для чисел z=x+iy,~ overline{z}= x-iy получаем

$begin{gathered} z+overline{z}= (x+iy)+ (x-iy)=2xquad Leftrightarrowquad z+overline{z}= 2 operatorname{Re}z,;\[2pt] zcdot overline{z}= (x+iy)(x-iy)= x^2+ i,xy- i,xy- i^2y^2= x^2+y^2. end{gathered}$

Результат решения примера можно сформулировать как свойство: сумма и произведение сопряженных комплексных чисел — числа действительные.

Деление комплексных чисел

Частным от деления числа z_1 на z_2, (z_2ne0) называется число , такое, что справедливо равенство zcdot z_2=z_1 . Обозначение: $z=frac{z_1}{z_2}$ . Задача нахождения частного сводится к определению operatorname{Re}z и operatorname{Im}z из системы

$begin{cases}operatorname{Re}(zcdot z_2)= operatorname{Re}z_1,\ operatorname{Im}(zcdot z_2)= operatorname{Im}z_1.end{cases}$

При нахождении частного удобно использовать свойство произведения сопряженных чисел.

Правило деления. Чтобы разделить число z_1 на z_1, (z_2ne0) следует числитель и знаменатель дроби $frac{z_1}{z_2}$ умножить на число $overline{z}_2$ , сопряженное знаменателю.

Пример 1.7. Найти частное от деления комплексного числа z_1=3+2i на z_2=2-i .

Решение.

$frac{z_1}{z_2}= frac{3+2i}{2-i}= frac{(3+2i)(2+i)}{(2-i)(2+i)}= frac{(6-2)+i(3+4)}{4+1}= frac{4}{5}+ frac{7}{5},i,.$

Возведение комплексного числа в степень

Возведение комплексного числа в степень — это нахождение произведения сомножителей, каждый из которых равен , т.е. $z^n= underbrace{zcdot zcdotldotscdot z}_{n}$ .

Правило возведения в степень. При возведении в степень числа (нахождении $operatorname{Re}z^n$ и $operatorname{Im}z^n$ ) используется правило возведения в степень двучлена (x+iy) , в общем случае применяется формула бинома Ньютона:

$(x+iy)^n= sum_{k=0}^{n}C_n^k x^{n-k}(iy)^k$ , где $C_n^k= frac{n!}{k!(n-k)!}$ .

Пример 1.8. Найти различные степени числа , то есть i^n .

Решение. Имеем i^2=-1,~ i^3=i^2cdot i=-i,~ i^4=(i^2)^2= (-1)^2=1 . Замечая закономерность, получаем для n=4k,~ n=4k+1, n=4k+2,~ n=4k+3 следующие значения:

$i^{4k}= (i^4)^k=1;quad i^{4k+1}= i^{4k}cdot i=i;quad i^{4k+2}= i^{4k}cdot i^2= -1;quad i^{4k+3}= i^{4k}cdot i^3= -i,.$

Пример 1.9. Найти мнимую и вещественную части комплексных чисел: $operatorname{Im}(1-i)^4,~ operatorname{Re}(2-i)^3$ .

Решение.

$begin{gathered}(1-i)^4= bigl((1-i)^2bigr)^2= (1-2i-1)^2= (-2i)^2=-4quad Rightarrowquad operatorname{Im}(1-i)^4=0;\[5pt] (2-i)^3= 2^3+ 3cdot 2^2cdot (-i)+ 3cdot 2cdot (-i)^2+ (-i)^3= 8-12i-6+i= 2-11iquad Rightarrowquad operatorname{Re}(2-i)^3=2,. end{gathered}$

Пример 1.10. Возвести комплексное число (2+i) в пятую степень.

Решение. Используем формулу бинома Ньютона при n=5:

$begin{aligned}(2+i)^5&= 2^5+5cdot 2^4cdot i+ frac{5cdot 4}{2!}cdot 2^3cdot i^2+ frac{5cdot 4cdot 3}{3!}cdot 2^2cdot i^3+ frac{5cdot 4cdot 3cdot 2}{4!}cdot 2cdot i^4+ i^5=\ &=32+80i- 80-40i+10+i= -38+41i,.end{aligned}$

Извлечение корня из комплексного числа

Корнем n-й степени из комплексного числа называется число , такое, что w^n=z . Обозначение: w=sqrt[LARGE{n}]{z} .

Правило извлечения корня. Для извлечения корня sqrt[LARGE{n}]{z} (нахождения x=operatorname{Re}sqrt[LARGE{n}]{z} и y=operatorname{Im}sqrt[LARGE{n}]{z} ) следует, используя определение корня и правило возведения в степень, составить и решить систему уравнений относительно искомых и :

$sqrt[LARGE{n}]{z}=x+iyquad Rightarrowquad z=(x+iy)^nquad Rightarrowquad begin{cases}operatorname{Re}z= operatorname{Re}(x+iy)^n,\ operatorname{Im}z= operatorname{Im}(x+iy)^n,.end{cases}$

Пример 1.11. Извлечь корень sqrt{3-4i} .

Решение. Обозначим sqrt{3-4i}= x+iy , тогда (x+iy)^2= 3-4i , или x^2-y^2+i2xy=3-4i . Используя условие равенства комплексных чисел, записываем систему

$begin{cases}x^2-y^2=3,\ 2xy=-4.end{cases}$ Решая ее, находим $left[begin{aligned} &begin{cases}x_1=2,\ y_1=-1;end{cases}\ &begin{cases}x_2=-2,\ y_2=1.end{cases} end{aligned}right.$

В результате получаем два значения квадратного корня: sqrt{3-4i}=2-i и sqrt{3-4i}=-2+i .

Свойства операции комплексного сопряжения

Используя определение сопряженных чисел и правила нахождения суммы, произведения, частного комплексных чисел, можно установить справедливость следующих свойств операции комплексного сопряжения:

$begin{array}{lll}bold{1)}~ overline{z_1pm z_2}= overline{z}_1pm overline{z}_2,;quad & bold{2)}~ overline{z_1cdot z_2}= overline{z}_1cdot overline{z}_2,;quad & bold{3)}~ overline{left(dfrac{z_1}{z_2}right)}= dfrac{overline{z}_1}{overline{z}_2},;\[10pt] bold{4)}~ overline{P}_n(z)= P_n(overline{z});quad & bold{5)}~overline{left(dfrac{P_n(z)}{Q_m(z)}right)}= dfrac{P_n (overline{z})}{Q_m (overline{z})},.quad & end{array}$

В двух последних равенствах P_n(z) и Q_m(z) — многочлены с действительными коэффициентами степени и соответственно.

Пример 1.12. Вычислить $P(overline{z}_0)+ P(z_0)$ , если P(z)= 2z^2+3z+1 и $z_0=frac{1+2i}{1-i}$ .

Решение. Используя свойство 4 из пункта 7, находим

$P(overline{z}_0)+ P(z_0)= overline{P(z_0)}+ P(z_0)= 2 operatorname{Re} P(z_0).$

Далее, производя деление, записываем число z_0 в алгебраической форме:

$z_0=frac{1+2i}{1-i}= frac{(1+2i)(1+i)}{2}= frac{-1+3i}{2}$

и подставляем в выражение для P(z) . Получаем

$P(z_0)= 2cdot frac{(3i-1)^2}{4}+ frac{3(3i-1)}{2}+1= frac{-9-6i+1+9i-3+2}{2}= -frac{9}{2}+ i,frac{3}{2},,$

поэтому $operatorname{Re}P(z_0)=-frac{9}{2}$ . Окончательно имеем: $P(overline{z}_0)+ P(z_0)= 2 operatorname{Re}P(z_0)=-9$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник