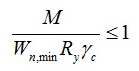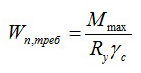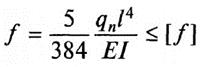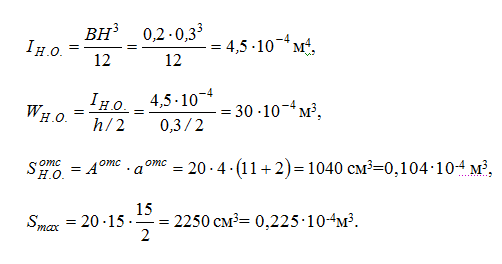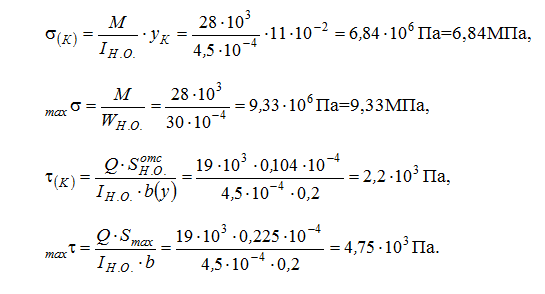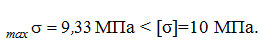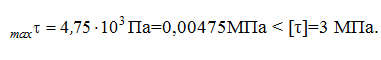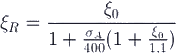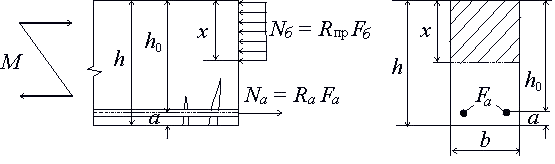Как найти сосредоточенную нагрузку на балку

Информация

Балка занимает роль основополагающего элемента в несущей конструкции. Её функция приравнивается к стержню всей конструкции, который прочно закрепили. При строительстве какого-либо сооружения очень важно осуществить грамотный расчет балки на прогиб и исключить допущение ошибки в расчетах. Прежде всего расчет требуется для определения того, на сколько балка деформируется в процессе эксплуатации сооружения. Если при расчете показатель деформации находится в пределах нормы, то можно определить нужные показатели будущей балки (сечение, материал, размер и так далее).

Делая расчет балки на прочность, необходимо четко знать виды материала, из которого изготавливаются балки (сталь, дерево, бетон, алюминий, стекло и медь). Далее нужно обратить внимание на то, что типы нагрузок, как и их схемы также различаются. Так, например, распределенная нагрузка означает, что давление оказывается не на одну точку, а распределено по всей площади балки. Сосредоточенный тип нагрузки характеризует направленность давления на один небольшой участок (точку) балки.

Вместе с типами, существуют четыре схемы нагрузок:

• Шарнир-Шарнир
• Заделка-Шарнир
• Заделка-Заделка»
• Свободный конец

Наш онлайн калькулятор позволяет сделать расчет, комбинируя все виды балок, типы и схемы нагрузок, при этом абсолютно исключив вероятность допущения ошибки в процессе расчета. Обычно рассчитывают деревянные балки, а также металлические. В процессе вычисления показателя определяется сумма сил, воздействующих на балку, которые направлены перпендикулярно конструкции. Расчет деревянной балки на прогиб осуществляется с учетом материала, т.е. учитывают вид древесины, её гибкость и многие другие параметры, также важно учесть форму сечения балки и нагрузка какого вида оказывается на балку. Сравнивая с расчетом балки из древесины, расчет металлической балки на прогиб существенно отличается, поскольку важное внимание уделяют виду соединения: электросварка, заклепки, болты и другие виды соединений.

Все перечисленные выше нюансы позволяют понять, что расчет балки на прогиб — крайне ответственный этап в процессе стройки какого-либо объекта. От него зависит надежность, долговечность и целостность всей конструкции. Наш калькулятор позволит Вам быстро и безошибочно провести предельно точный расчет.

Какие преимущества даёт наш калькулятор?

• экономия времени;
• исключение допущения ошибки;
• предельная точность в расчете;
• приятный и понятный интерфейс;
• дополнительный справочный материал.

Таким образом, созданный нами онлайн калькулятор является незаменимым инструментом в процессе работы специалиста, которому необходимо осуществить расчет балки или любого другого важного показателя.

Содержание:

1. Сосредоточенные силы и распределенные нагрузки
2. Плоская система параллельных сил
3. Равновесие системы тел
4. Статически обозначенные и статически неопределенные задачи
5. Методика решения задач на равновесие системы тел

Такие силы называются сосредоточенными. Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Сосредоточенные силы и распределенные нагрузки

Мы рассматривали силы, которые были представлены в виде вектора, приложенного к точке. Однако в природе существует большое количество взаимодействий тел, осуществляются не в точке и которые нельзя представить в виде вектора, приложенного к точке.

Такими силовыми факторами являются силы давления жидкости или газа в поверхность твердых тел, силы тяжести, как массовые силы, электромагнитные силы тому подобное. Поэтому в теоретической механике вводится понятие о распределенных силах, которые делятся на поверхностные и объемные.

Поверхностные силы действуют на некоторую поверхность тела. Объемные силы действуют на каждый элемент объема тела, рассматривается. Примером последних сил является сила притяжения.

В теоретической механике рассматривается воздействие на тело только сосредоточенных сил, приложенных к абсолютно твердым телам. А потому
распределенную нагрузку необходимо заменить его равнодействующей, то есть
сосредоточенной силой. Введем несколько общих положений.

Распределенная нагрузка характеризуется его интенсивностью , то есть величиной силы, приходящейся на единицу объема тела (в случае объемных сил), на единицу площади (в случае поверхностных сил) и на единицу длины (если поверхность, на которую действует нагрузка, можно считать линией, то есть шириной поверхности можно пренебречь). В последнем случае распределенная нагрузка называется плоской, на
силовых схемах оно изображается в виде эпюры элементарных сил, то есть графика интенсивности нагрузки, приложенная к линейному элементу тела.

В общем случае распределенная нагрузка изображается в виде определенной кривой, отражающей данный закон изменения интенсивности нагрузки на участке тела (рис. 1.20). Направление действия нагрузки показывается стрелками.

Сначала рассмотрим равномерно распределенную нагрузку и нагрузку, распределенную по линейному закону. Заменяем распределенную нагрузку сосредоточенной силой.

Рассмотрим эти два случая:

— равномерно распределенная нагрузка (или нагрузка, распределенная по закону прямоугольника) изображается на схемах в виде прямоугольника, размеры которого таковы: высота — это интенсивность нагрузки , длина — это длина l участка тела, на которой действует нагрузка. Стрелки показывают направление действия нагрузки (рис. 1.21). Для того, чтобы заменить эту нагрузку равнодействующей силой , надо определить ее. В данном случае

Q = q · l,

где q — интенсивность нагрузки, Н/м; l — длина участка тела, на которой приложенная нагрузка, м.

Точка C приложения равнодействующей силы  размещается посередине участка тела, на которой действует нагрузка. То есть , а направление совпадает с направлением распределенной нагрузки.

— нагрузка распределена по линейному закону (то есть по закону треугольника). В этом случае (рис. 1.22) интенсивность распределенной нагрузки на участке l меняется от 0 до максимального значения q_max. Равнодействующая сила  от этой нагрузки по величине равна

Точка C приложения равнодействующей  расположена на расстоянии  или , а направление совпадает с направлением нагрузки.

Плоская система параллельных сил

Когда линии действия всех сил параллельны, то всегда в плоскости можно так
расположить оси координат, одна из них будет обязательно параллельной заданным силам, а вторая — перпендикулярной. А потому, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо приравнять к нулю алгебраическую сумму проекций всех сил на параллельную ось и алгебраическую сумму моментов всех сил относительно произвольной точки. В данном случае система условий равновесия (1.54) упрощается и будет иметь такой вид

Для равновесия тела, находящегося под действием системы параллельных сил
на плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил
на ось, параллельная силам, и алгебраическая сумма моментов всех сил относительно произвольной точки А плоскости равны нулю.

Для системы параллельных сил на плоскости можно использовать и такие условия равновесия

Для равновесия тела, находящегося под действием системы параллельных сил на плоскости, необходимо и достаточно, чтобы алгебраические суммы моментов всех
сил относительно любых двух точек плоскости равны нулю.

Однако для этих условиях существует ограничение: линия АВ, которой можно соединить
центры моментов, не должна быть параллельной силам.

Данные условия наиболее пригодны при расчетах двухопорных балок. Используя эти условия, составляют алгебраические суммы моментов всех сил относительно точек A и B, в которых установлены опоры балки.

Рассмотрим примеры задач на равновесие тела под действием плоской системы произвольных сил.

Пример:

Однородная балка АВ прямоугольного сечения весом 400 Н имеет один конец А, который закреплен шарнирно, и опирается на точечную опору O (рис. 1.23). Ко второму концу балки В подвешен груз весом 200 Н. Длина балки 4 м, точечная опора расположена на расстоянии ¾ длины балки от шарнирной опоры. Угол наклона балки к горизонту составляет α = 30º.

Определить реакции опор балки.

Краткое условие задачи:

G = 400 H ;

Q = 200 H ;

AB = 4 м;

AO = 3/4 AB = 3 м ;

α = 30º.

R_A = ?

R_о = ?

Решение.

Составляем расчетно–силовую схему задачи. Приложим к оси балки заданные активные силы: силу тяжести  самой балки и силу притяжения  груза. Сила притяжения балки приложена посередине балки в точке C (поскольку балка однородна) и направлена ​​вертикально вниз. Сила притяжения груза приложена к концу балки В и направлена ​​вертикально вниз.

Далее условно освобождаем балку от связей и заменяем их соответствующими реакциями связей. В точке A размещена неподвижная шарнирная опора, она имеет
две составляющие реакции _A и _A, которые расположены вдоль соответствующих осей
координат. В точке O — точечная опора, которая имеет одну реакцию _o, что направлена ​​перпендикулярно к балке.

Таким образом, балка находится в равновесии под действием плоской системы произвольных сил. Для решения этой задачи используем условия равновесия (1.54),

Поскольку оси координат x и y заданные по условию задачи, то составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получим

С третьего уравнения вычислим реакцию R_o:

R_o =   = 461,86 Н,

и подставим ее значение в первые два уравнения. Будем иметь

Х_А =   = R_o = 230,93 Н;

Y_А = 400 + 200 – 0,866 · 461,86 = 160,04 Н.

Поскольку определены две составляющие реакции, приложенные в точке A, — Х_А  и Y_А, то геометрическим добавлением можно вычислить модуль полной реакции R_A. А именно:

Таким образом определении все искомые реакции.

Ответ: R_A = 280,97 Н;

R_о = 461,86 Н.

Пример.

Определить реакции опоры однородной балки АВ прямоугольного сечения, один конец которого A жестко закреплен в стене и находящийся под действием сосредоточенной силы P = 4,0 kH, пары сил с моментом m = 2,0 kH · м и равномерно распределенной нагрузки интенсивностью q = 1,5 .  Длина балки АВ — 5 м, равномерно распределенная
нагрузка действует на участке 3 м от точки A. Угол наклона сосредоточенной силы к горизонту составляет α = 30º, оси x и y показаны на рис. 1.24.

Краткое условие задачи:

P = 4,0 kH;

m = 2,0 kH · м;

q = 1,5 ;

АВ = 5 м;

AС = 3 м;

α = 30º

R_A = ?

М_A = ?

Решение.

Составляем расчетно-силовую схему. Покажем все силы, приложенные к балке АВ. Прежде всего, это заданные активные силы — сила , приложена к концу балки В и направлена под углом α к горизонту. Равномерно распределенную нагрузка заменяем сосредоточенной силой , которая равна

= q · AC =1,5 · 3 = 4,5 kH .

Сила приложена посредине участка AC и направлена ​​в ту же сторону, что и сама нагрузка, то есть вертикально вниз. Покажем на силовой схеме пару сил, которая определяется моментом m.

Далее условно освобождаем балку от вязи и заменяем ее соответствующими реакциями вязи. В точке A — жесткое закрепление балки в стене, а потому оно имеет две составляющие реакции: _A, _A, которые расположены вдоль соответствующих осей
координат, и реактивный момент M_A. Направление этого неизвестного момента
показываем на силовой схеме произвольно, например, — против направления стрелки
часов. Если же при окончательном определении момента M_A получим отрицательный знак, то получим, что действительное направление момента — противоположно. Покажем на силовой схеме линейные и угловые размеры. Оси координат показаны на схеме.

Как видно из построенной расчетно–силовой схемы, балка находится под действием плоской системы произвольных сил. Используем условия равновесия (1.54). А именно            = 0.

Составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получаем

Из первого уравнения вычислим X_A:

X_A = 4,0 =  = 3,46 kH.

Из второго уравнения вычислим Y_A:

Y_A = 4,5 + 4,0 ·  = 6,50 kH.

С третьего уравнения вычислим M_A:

M_A = 2,0 + 4,5  + 4,0  · 5 = 2,0 + 6,75 + 10,0 = 18,75 kH.

Поскольку составляющие реакций X_A и Y_A, приложенных в точке A, вычислены, то можно найти модуль R_A полной реакции в точке A. Будем иметь

Таким образом, определены все искомые реакции.

Ответ: R_A = 4,30 kH; M_A = 18,75 kH.

Равновесие системы тел

Системой тел называется совокупность нескольких тел, или которые опираются друг на друга, или соединены шарнирами, которые дают возможность относительного движения тел.

При решении задач на систему тел различают силы внешние и внутренние.

Внешние силы — это силы взаимодействия тел данной системы с другими телами, которые не входят в состав системы.

Внутренние силы — это силы взаимодействия между отдельными телами, которые входят в состав данной системы. Внутренние силы существуют попарно, как действие и
противодействие.

Статически обозначенные и статически неопределенные задачи

Задача является статически обозначенной, если для нее можно составить такое
количество уравнений равновесия материальной системы, не меньше, чем число
неизвестных.

Задача, является статически неопределенной, если число уравнений равновесия
системы меньше, чем число неизвестных.

В теоретической механике рассматриваются только статически обозначенные
материальные системы.

Методика решения задач на равновесие системы тел

Равновесие системы тел можно рассматривать в целом под действием только
внешних сил. Но может так случиться, что количество уравнений равновесия будет
меньше, чем количество неизвестных. Тогда необходимо рассматривать равновесие
отдельных тел системы, условно разделяя ее обязательно по внутренним связям. Причем необходимо учитывать, что внутренние силы реакций входят попарно, как действие и противодействие.

Рассмотрим пример решения задач на равновесие системы тел.

Пример.

На трех-шарнирную арку А В С (рис. 1.25) действует вертикальная сила Р = 10 kH. Вес каждой части балки Q₁ = Q₂ = 6 kH. Определить реакции шарниров А, В, С арки, размеры которой данные на рисунке.

Решение.

Как видно из схемы, заданная система тел состоит из двух пиварок I и II, которые соединены шарниром в точке С. Составим расчетно–силовую схему, где покажем заданные активные силы Q₁, Q₂, и реакции связей: в точках A и B (неподвижные шарнирные опоры) — _A ,A и _В , В и в точке C (шарнирное соединение) — _C , ´_C и _{C ,} ´_С. Эти неизвестные реакции в точке С являются внутренними силами системы тел, а потому _C = ´_C  и _C = ´_С.

Покажем оси прямоугольной декартовой системы координат Axy.

Условно разделяем систему тел на два отдельных тела по шарниру С. Действие отброшенной части заменяем двумя реакциями _C и _C, которые равны

Теперь рассмотрим отдельно равновесие каждого тела, для чего составим две системы уравнений равновесия. Используем условия равновесия.

Для первого тела (левая половина арки):

 = 0; Х_А — Х_С = 0,

    = 0; Y_A + Y_C — Q₁ — P = 0,

  = 0; Х_С · 4 + Y_C · 5 — Q₁ · 1 — P · 4 = 0.

Для второго тела (правая половина арки):

 = 0; Х_B — Х´_С = 0,

    = 0; Y_B + Y´_C — Q₂ — P = 0,

 = 0; Q₂ · 1 — Х´_С · 4 + Y´_C · 5 = 0.

Как видно из полученных шести уравнений равновесия, в них содержатся шесть неизвестных: Х_А, Х_B, Х_С, Y_A, Y_B, Y_{C .}

Определим эти неизвестные величины. С третьего уравнения второй системы определим Y´_{C .} Перепишем это уравнение следующим образом:

5Y´_C = 4Х´_С — Q₂,

откуда находим реакцию Y´_C :

Поскольку численно Y´_C = Y_C , а Х_С = Х´_С, то подставив значения этих реакций в третье уравнение первой системы, получаем

или

8Х_С = Q₁ + Q₂ + 4P,

откуда

Теперь есть возможность определить неизвестную реакцию Y´_C . Подставив значение X_C в третье уравнение второй системы, будем иметь

Из первого уравнения первой системы имеем X_A = X_C = 6,5 kH. А с первого уравнения второй системы должны X_B = – X´_C = – 6,5 kH. Направление этой реакции противоположно показанному на силовой схеме. Из второго уравнения первой системы получаем

Y_A = Q₁ + P – Y_C = 6,0 + 10,0 – 4,0 = 12,0 kH.

Из второго уравнения второй системы вычислим последнюю неизвестную реакцию Y_B. Она будет равняться Y_B = Y´_C + Q₂ = 4,0 + 6,0 = 10,0 kH.

Таким образом вычислено все искомые величины.

Ответ:

X_A = 6,5 kH; Y_A = 12,0 kH; X_B = — 6,5 kH; Y_B = 10,0 kH; X_C = 6,5 kH; Y_C = 4,0 kH.

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации. 

Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению. 

Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.

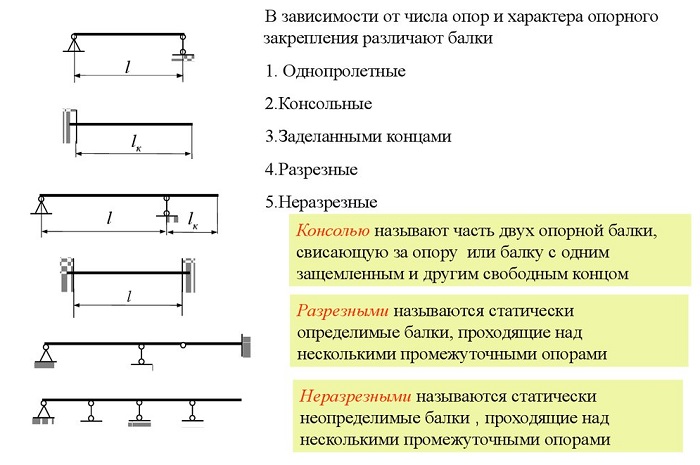
Виды балок

При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.

Виды балок:

1. Деревянные — их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.

2. Металлические — такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.

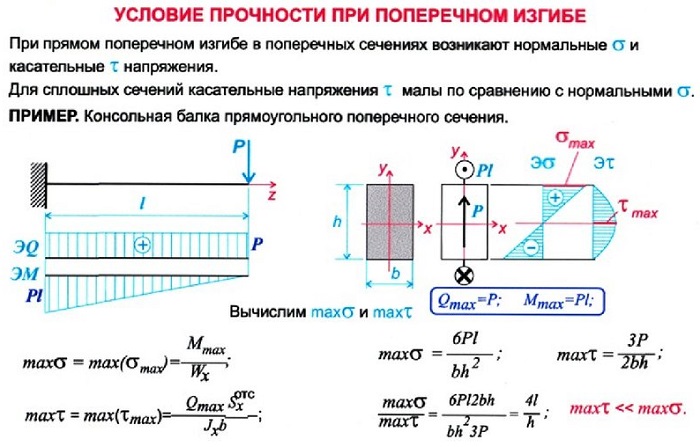
Прочность и жесткость балки

При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.

На эти параметры влияют следующие факторы:

• величина наружных нагрузок, их положение;

• параметры, характер, нахождение поперечного сечения;

• продольные величины;

• материал;

• число опор, метод их закрепления.

Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты. 

Построение эпюр балки

Эпюра распределения величины нагрузки на объект:

Расчет на жесткость

Алгоритм исчисления:

В формуле обозначены:

• M – max момент, возникающий в брусе;

• W_n,min – момент сопротивления сечения (табличный показатель);

• R_y – сопротивление на изгиб (расчётный показатель);

• γ_c – показатель условий труда (табличный показатель).

Такой расчет не трудоемок, но для более верного значения требуется следующее:

• рабочий план объекта;

• определение характеристик балки, характер сечения;

• определение max нагрузки, воздействующей на брус;

• оценка точки max прогиба;

• проверка прочности max изгибающего момента.

Расчет моментов инерции и сопротивления сечения

Алгоритм исчисления:

Где:

• J – момент инерции сечения;

• W – момент сопротивления.

Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.

Нахождение максимальной нагрузки и прогиба

Формула для вычисления:

Здесь обозначены:

• q – нагрузка равномерно-распределенная;

• E – гибкость (табличный показатель);

• l – длина;

• I – момент инерции сечения.

Нагрузки учитываются статические и периодические.

Расчет на прогиб и его особенности

Он необходим для всех перекрытий при высоких эксплуатационных нагрузках. 

При применении соответствующих коэффициентов, придерживаются следующего:

• балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;

• балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;

• нагрузка консольного типа;

• воздействие комплексной нагрузки.

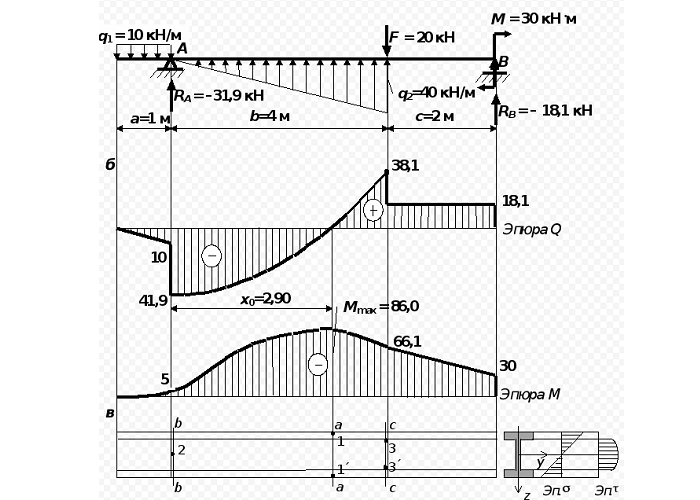
Пример расчет балки на прогиб

Рассмотрим задачу из курса сопромата.

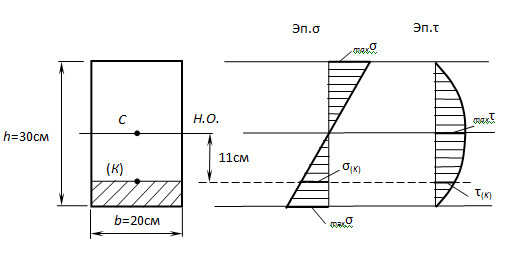
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм. 

Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.

Решение.

Чтобы узнать σ_(К), τ_(К), σ_max, τ_max
определяем значение осевого момента инерции общего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсеченного ряда и статического момента середины сечения S_max:

Из этого следует:

Определение прочности по нормальному напряжению:

Определение прочности по касательному напряжению:

Задача решена.

При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки. 

Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.

Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.

В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

 В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (R_A), горизонтальная (H_A) и момент (M_A).

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

• если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;

• если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как H_A, R_A и R_B:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — H_A. Так как H_A направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда H_A будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила R_B поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30^°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что M_A, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции R_A:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!