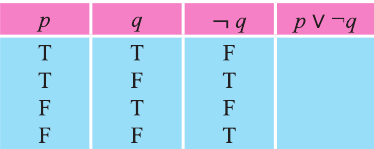
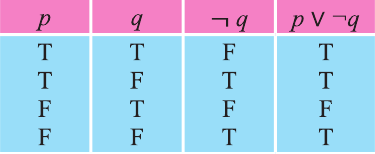
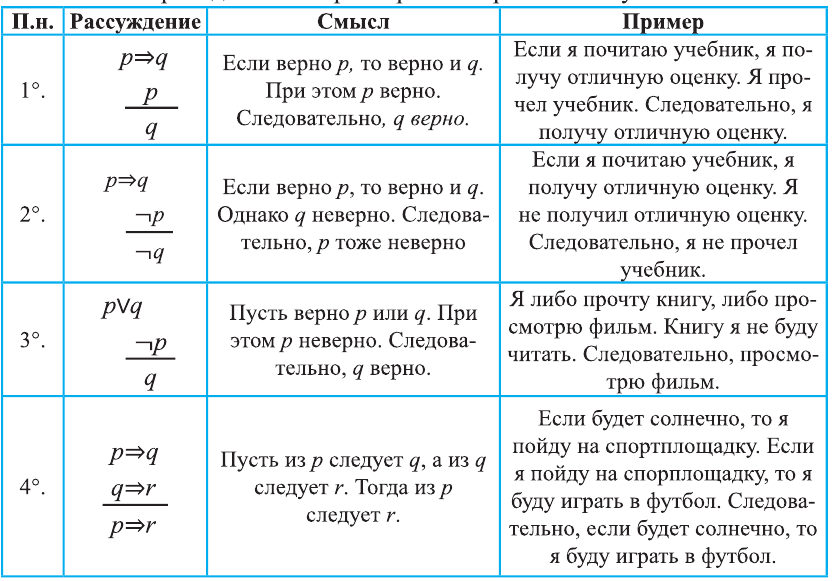
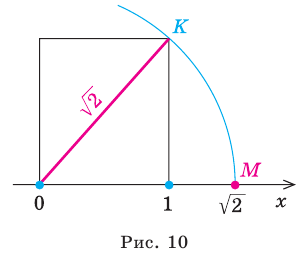
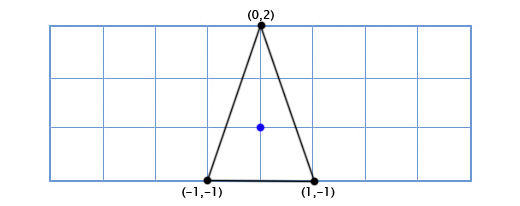
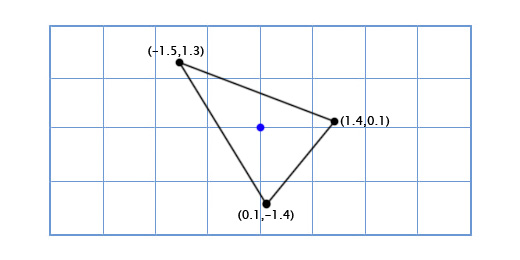
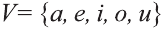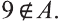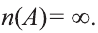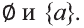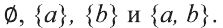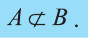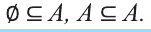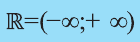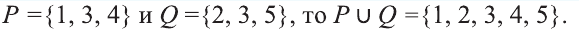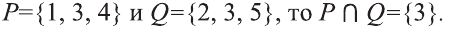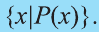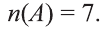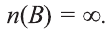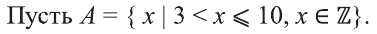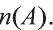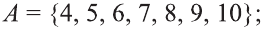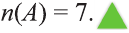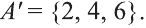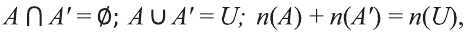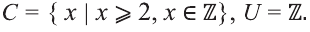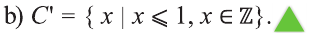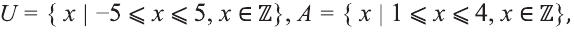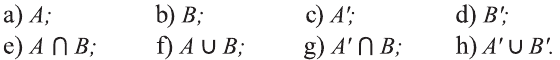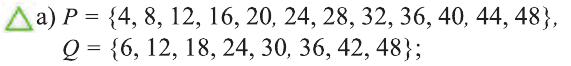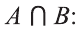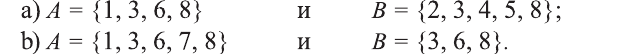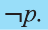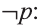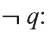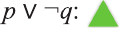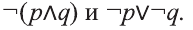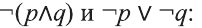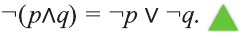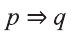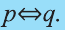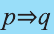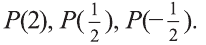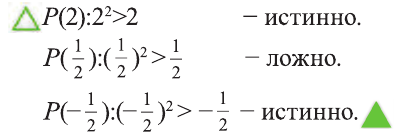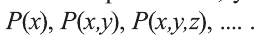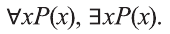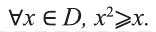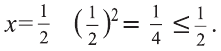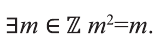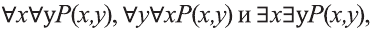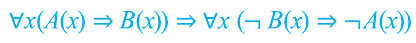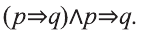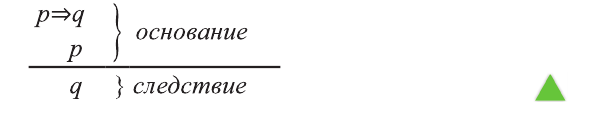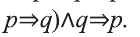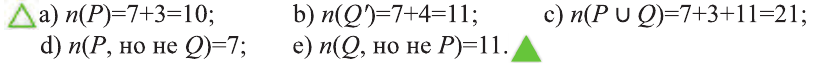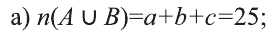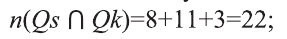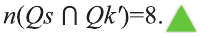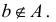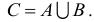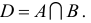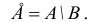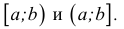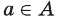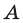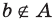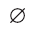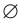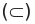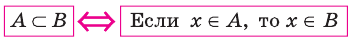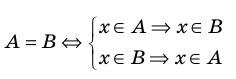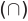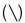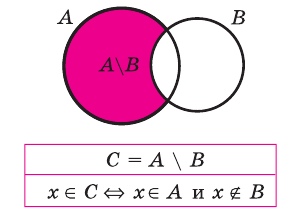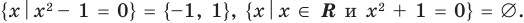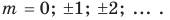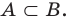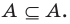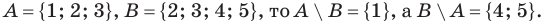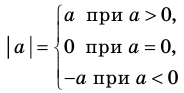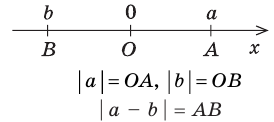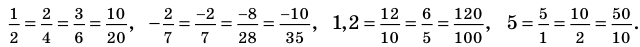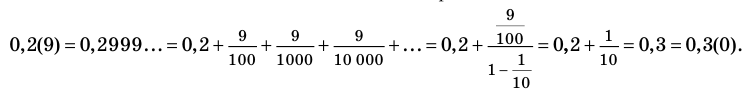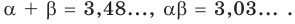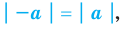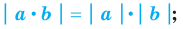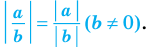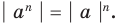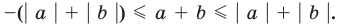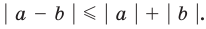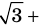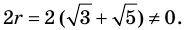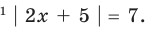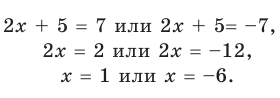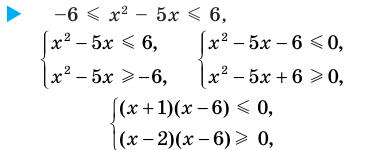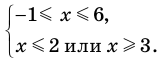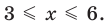Одной из самых сложных частей студенческой работы является введение. Оно имеет свою структуру, которая предполагает точное описание будущей работы по пунктам.
Самые сложные определения – это объект и предмет исследования. Многие часто путают данные термины и не могут правильно их определить. На самом деле они предполагают почти одинаковый ответ с разной степенью углубленности. Они обозначают то, что изучает исследователь в своей научной работе. Однако при этом объект имеет более широкое значение, чем предмет.
Давайте рассмотрим, что такое объект и предмет исследования и как их правильно написать в введении подробно. Чтобы лучше понять посмотрите наглядный пример из разных видов работ.
Содержание
- Что такое объект исследования?
- Что такое предмет исследования?
- Объект и предмет исследования – в чем все-таки разница?
- Как определить предмет и объект исследования в курсовой – примеры
- Как написать предмет и объект исследования в дипломной работе — примеры
- Объект и предмет исследования – примеры правильного написания в диссертации
- Типичные ошибки при определении предмета и объекта исследования
- Как проверить уникальность текста?
- Как повысить уникальность текста?
01 Что такое объект исследования?
Студентам важно разобраться, что такое объект исследования, потому что его необходимо называть в каждой научной работе.
Один объект исследования может изучаться разными науками и дисциплинами, для которых будет выбран один предмет. К примеру, возьмем человека. Рассматривать человека как существо биологическое свойственно биологам, медикам, антропологам. Исследовать интеллект, разум человека приходится психологам, психотерапевтам, медикам, нейролингвистам. Так как человек социально-биологическое существо, общественную сторону жизни изучают социологи, культурологи, филологи и т.д.
Таким образом, человек является для всех этих областей наук общим объектом. Рассматривать все внутренние системы человека и внешние проявления жизни человека одновременно одной науке невозможно. Поэтому каждый вид науки выделяет для себя определенную часть организма или сторону социальной жизни.
Также, к примеру более узкий объект – язык человека. Он может рассматриваться как орган медиками, биологами, антропологами, либо как психическое явление психологами, либо как знаковая система лингвистами, семиотиками.
В частности, язык как объект лингвистики рассматривается разными дисциплинами: нейролингвистикой, когнитивной лингвистикой, прагмалингвистикой, диахронической лингвистикой и т.д.
Таким образом, объект исследования – это явление или предмет, на который направлено внимание науки. Его не выделяют в отдельный специальный предмет изучения для определенной области, и он может быть рассмотрен разными видами или направлениями наук (медициной, филологией, культурологией и т.д.; либо внутри одной науки – когнитивной психологией, генетической психологией, психоанализом и т.д.).
Объект состоит из разных предметов, процессов и свойств, как человек состоит из разных систем, органов и в разных проявлениях в внешней жизни. Одним словом, это общая тематика, которую можно разобрать на отдельные предметы исследования.
Лайфхак
На сервисе Анти-антиплагиат.рф можно заказать оформление работы по ГОСТ онлайн. Быстро поможем оформить работу по вашей методичке.
Также вы можете заказать проверку оригинальности текста в Антиплагиат ВУЗ. При необходимости поможем повысить уникальность до 80-90%. Кодировка документа не изменит текст, а обработка займет всего несколько минут. Пришлем готовый результат без предоплаты.
02 Что такое предмет исследования?
Предмет исследования – это более глубокое понятие для объяснения того, что изучается в научной работе. Предмет обязательно выделяется из объекта, поэтому в первую очередь всегда нужно указать объект.
Предмет исследования науки социологии – это все социальные отношения людей. Однако для гендерной социологии предметом будет – социальные проявления гендерных различий, т.е. различия между поведением мужчин и женщин. Тогда как общая тематика социальные отношения станет объектом.
Таким образом, на каждом уровне науки меняется объект и предмет. Каждое направление или дисциплина выбирает из общей тематики науки свой предмет исследования.
Поэтому в научных работах выбирают самые глубокие и узкие предметы исследования. Обычно это либо свойства, структура, характеристика (Например, «Анализ работы акционерного общества»), либо отношения между элементами (Например, «Бухгалтерский баланс и анализ финансового состояния и кредитоспособности предприятия»).
03 Объект и предмет исследования – в чем все-таки разница?
Давайте подведем итоги и разберемся, в чем все-таки разница между объектом и предметом исследования.
Самое главное ‒ степень углубленности. Объект существует непосредственно от человеческого восприятия. А предмет ‒ это определенный взгляд на объект с какой-либо стороны. Поэтому объект всегда будет шире предмете.
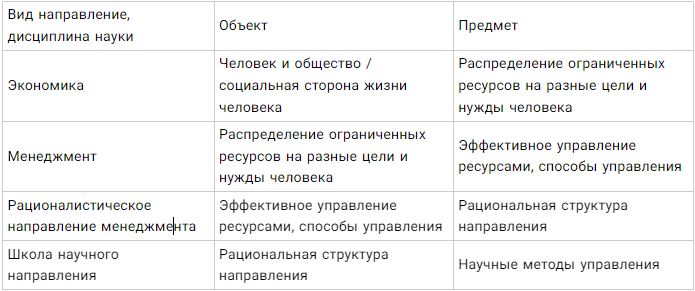
Изобразим таблицу и покажем какой предмет соответствует для каждого уровня науки.
Вы можете увидеть закономерную цепь расстановки объекта и предмета. Спускаясь на более низкий уровень, предмет становится впоследствии объектом. Поэтому советуем вам проводить для понятия объекта и предмета своего исследования начинать определение издалека. Тогда вы легко придете к тому, что нужно написать в введении научной работы.
04 Как определить предмет и объект исследования в курсовой – примеры
Давайте рассмотрим на разных примерах, как определить предмет и объект исследования в курсовой.
Тема курсовой работы по психологии: «Социальное познание и виртуальная реальность».
«Объект исследования – виртуальная реальность как технология развития навыков в сфере социального познания. Предмет исследования – помощь психологическим больным с расстройствами социального познания посредством технологий виртуальной реальности».
Тема курсовой по математике: «Теория вероятностей».
«Объект исследования ‒ теория вероятностей. Предмет исследования ‒ применение алгоритмов при решении задач».
Тема курсовой по рекламе и пиару: «Этапы создания рекламного ролика на телевидении»
«Объект исследования: телевизионная реклама. Предмет исследования: создание рекламного ролика».
Таким образом, вы можете заметить тесную связь между названием темы работы и объектом, предметом исследования. Также название работы повторяет проблему исследования. Поэтому всегда выбирайте близкую для вас тему, чтобы легче понять, как написать объект и предмет.
05 Как написать предмет и объект исследования в дипломной работе — примеры
Приведем примеры, как написать предмет и объект исследования в дипломной работе.
Тема ВКР по истории: «Женщины в социально-политической жизни российского общества в XIX веке».
«Объектом исследования является процесс развития женского движения XIX века. Предметом исследования является деятельность женщины на разных социальных ступенях российского общества».
Тема диплома по биологии: «Направления регулирования орнитофауны городских парков».
«Объект исследования: птицы парка Ветеранов. Предмет исследования: механизмы регулирования разнообразия и численности птиц».
Тема дипломной работы по маркетингу: «Разработка эффективной стратегии бренда на основе социальных коммуникаций».
«Объектом исследования являются стратегии бренда, основывающиеся на социальных коммуникациях. Предметом исследования выступают особенности эффективности стратегий бренда в условиях возрастающей роли социальных коммуникаций в современном обществе».
Таким образом, выделение объекта и предмета исследования в дипломной работе повторяет схему, как в курсовых. Поэтому тема, объект и предмет исследования почти совпадают.
Мы советуем писать введение уже после того, как будет выполнен ВКР. Так вы сможете лучше понять, какие определения больше подходят.
06 Объект и предмет исследования – примеры правильного написания в диссертации
Теперь посмотрим на пример объекта и предмета исследования в диссертации.
Тема диссертационной работы по юриспруденции: «Гражданско-правовой режим инсайдерской информации».
«Объектом исследования являются правоотношения, возникающие в области правомерного использования, раскрытия инсайдерской информации, обеспечения защиты нарушенных прав субъектов в случае ее неправомерного использования.
В качестве предмета исследования выступают правовые нормы, регулирующие отношения, складывающиеся по поводу инсайдерской информации; локальные акты, договоры, связанные с обращением инсайдерской информации; судебная практика; практика Банка России в сфере выявления неправомерной инсайдерской деятельности; научная доктрина в области гражданского, предпринимательского и информационного права по исследуемой проблематике».
Тема диссертации по педагогике: «Аксиологические ориентиры воспитательной системы А.С. Макаренко».
«Объект исследования: педагогическое наследие А. С. Макаренко. Предмет исследования: воспитательная система А. С. Макаренко в контексте педагогической аксиологии».
Тема диссертации по философии: «Идеология и практика славянского неоязычества».
«Объектом исследования является славянское (русское) неоязычество, его место и роль в религиозной и политической жизни, в общественном сознании россиян. Предмет исследования ‒ истоки формирования неоязычества, его идеология и практика».
Таким образом, выглядят объект и предмет исследования в диссертационной работе.
07 Типичные ошибки при определении предмета и объекта исследования
Давайте рассмотрим, какие ошибки нельзя допускать при написании объекта и предмета исследования.
- Не путайте объект исследования и научную базу. Многие в определение объекта исследования пишут «Открытые сайты, источники интернета» или «монографии и статьи исследователей». Объектом исследования может быть интернет, книга какого-либо писателя, статьи на определенную тематику – если студент изучает именно их. Источники, которые указываются в списке используемой литературы, являются научной базой. Они нужны для теоретической части, чтобы показать степень изученности проблемы или историю развития предмета исследования.
- Не путайте объект и предмет. Объект всегда шире предмета.
- Не забывайте писать определения объекта и предмета в своих научных работах.
Это самые типичные ошибки, которые допускают студенты в своих работах. Из-за них могут не принять ваше исследование на проверку.
Также работу могут не принять из-за несоответствия требованиям ГОСТ. Мы подготовили для вас специальное видео, которое поможет правильно оформить курсовую работу.
08 Как проверить уникальность текста?
После того, как работа будет дописана, вам необходимо проверить уникальность текста.
Вы можете обратиться на бесплатный сервис Антиплагиат ру. Здесь можно загрузить работу любого объема и быстро получить результат анализа на плагиат. Однако прежде вам потребуется зарегистрироваться на сайте, а также конвертироваться работу из формата DOC в PDF или TXT.
Многие опции ограничены, как, например, поиск заимствований через закрытые источники, полный отчет и выгрузка результатов.
Поэтому вы можете воспользоваться услугой от сервиса анти-антиплагиат.рф и проверить уникальность через Антиплагиат ВУЗ. Это расширенная версия Антиплагиат ру, разработанная специально для университетов. В настоящее время получить доступ к системе самостоятельно невозможно.
Однако разработчики анти-антиплагиат.рф получили доступ к лицензионной версии Антиплагиат ВУЗ. Обратившись на наш сервис, вы получите возможность узнать точный процент оригинальности, провести документ через все 30 модулей поиска заимствований и получить полный отчет. Потребуется только загрузить файл на сервис и отправить его, указав адрес электронной почты.
09 Как повысить уникальность текста?
Если вас не устроил ваш результат оригинальности, мы расскажем, как повысить уникальность текста. Существуют такие бесплатные способы:
- Выполнить перевод текста через онлайн переводчик. Для этого скопируйте свою работу и вставьте в окно программы. Затем выберете иностранный язык, например, французский, и переведите. Скопируйте получившийся результат и переведите на узбекский язык. С узбекского – на английский, с английского ‒ немецкий, с немецкого ‒ на русский. Так, вы увидите, как преобразился ваш текст. Осталось отредактировать работу и устранить все ошибки программы. Благодаря этому процент самостоятельности поднимется.
- Используйте пересказ. Вы должны прочитать заимствованную часть документа и попытаться изложить ключевую мысль своими словами.
- Замените слова на синонимы. Вы можете выполнить это самостоятельно, либо обратиться к программе синонимайзер. Она за пару секунд обработает ваш текст. Однако придется самостоятельно доработать результат, чтобы убрать все ошибки.
В итоге, лучше использовать все эти методы одновременно. Тогда вы точно сможете повысить уникальность своей работы.
Либо вы можете обратиться на сервис анти-антиплагиат.рф и заказать услугу «кодировки». Ваш документ будет обработан через специальную программу, которая никак не изменит ваш текст. Однако при этом процент оригинальности возрастет до 80-95%. Нажмите на кнопку «повысить уникальность», чтобы перейти на страницу заказа. Сервис предоставляет услугу без предоплаты. Поэтому вы сможете прежде убедиться в эффективности способа, а уже затем оплатить работу.
Таким образом, выбирайте наиболее удобный для себя способ повышения самостоятельности текста.
Сегодня мы с вами рассмотрели тему: «Объект и предмет исследования — как написать, пример». Обязательно используйте наши примера для образца при написании введения работы. Обратите внимание на ошибки, которые допускают многие люди и ни в коем случае их не допускайте. А мы желаем вам успеха.
Полезные ссылки:
Как обмануть антиплагиат – 12 бесплатных методов
Как написать курсовую работу — пошаговая инструкция
Как написать дипломную работу самостоятельно: советы
Как написать введение к дипломной работе – пример
Как начать писать дипломную или курсовую работу
Как написать теоретическую часть курсовой и диплома
Как пройти нормоконтроль дипломной работы: ГОСТ 2023
Как подготовиться к защите диплома за 24 часа
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное бюджетное образовательное учреждение высшего профессионального образования
ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Ф.М. ДОСТОЕВСКОГО
Г.Л. Бухбиндер
Задачи по тензорному исчислению
ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
Учебно-методическое пособие (для студентов физического факультета)
2011
ÓÄÊ 152.972
Задачи по тензорному исчислению: учебно-методическое пособие / Г.Л. Бухбиндер Омск: Изд-во Ом. гос. ун-та, 2011. ??с.
Задачи по тензоpному исчислению куpса «Основы вектоpного и тензоpного анализа соответствуют действующей учебной пpогpамме и позволяют студентам лучше усвоить лекционный матеpиал и научиться его пpименять.
Для студентов физических факультетов университетов.
ÓÄÊ 152.972
|
ISBN |
c Бухбиндер Г.Л., 2011 |
|
c ГОУ ВПО ¾Омский госуниверситет |
|
|
им. Ф.М. Достоевского¿, 2011 |
Содержание
|
Ÿ1. Криволинейные комедианты в евклидовом простран- |
||
|
ñòâå . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
|
|
Ÿ2. Тензоpная алгебpа. . . . . . . . . . . . . . . . . . . . |
7 |
|
|
Ÿ3. Коваpиантное диффеpенциpование. . . . . . . . . . . |
8 |
|
|
Ответы . . . . . . . . . . . . . . . . . . . . . . . . . . |
11 |
|
|
1. |
Криволинейные координаты . . . . . . . . . . . . |
11 |
|
2. |
Тензорная алгебра . . . . . . . . . . . . . . . . . . |
13 |
|
3. |
Ковариантное дифференцирование . . . . . . . . . |
13 |
|
Ëèòåpàòópà . . . . . . . . . . . . . . . . . . . . . . . . |
15 |

Ÿ1. Криволинейные комедианты в евклидовом пространстве
1.1. Найти координатные поверхности: а) цилиндpической системы кооpдинат
y1 = x1 cos x2, y2 = x1 sin x2, y3 = x3;
б) сфеpической системы кооpдинат
y1 = x1 sin x2 cos x3, y2 = x1 sin x2 sin x3, y3 = x1 cos x2,
yi декаpтовы оpтогональные кооpдинаты (i = 1, 2, 3). 1.2. Эллиптические кооpдинаты задаются в виде
|
1 |
||||||||
|
(x1 |
a)(x2 − a)(x3 |
− a) |
2 |
|||||
|
y1 |
= |
, |
||||||
|
−(b − a)(c − a) |
} |
|||||||
|
{ |
||||||||
|
1 |
||||||||
|
y2 |
= |
(x1 |
b)(x2 − b)(x3 |
− b) |
2 |
|||
|
, |
||||||||
|
{ |
− |
} |
||||||
|
(c − b)(a − b) |
1 |
|||||||
|
(x1 |
c)(x2 − c)(x3 |
− c) |
2 |
|||||
|
y3 |
= |
, |
||||||
|
−(a − c)(b − c) |
} |
|||||||
|
{ |
ãäå a > b > c, и удовлетвоpяют неpавенствам
x1 > a > x2 > b > x3 > c.
Показать, что x1 повеpхности эллипсоиды , x2 повеpхности есть однополостные гипеpболоиды и x3 повеpхности двухполостные
гипеpболоиды и все кооpдинатные повеpхности пpинадлежат семейству
(y1)2 + (y2)2 + (y3)2 = 1, x − a x − b x − c

äà÷è 1.5.
g = |gmn|.
|
Кpиволинейные кооpдинаты |
5 |
ãäå x ýòî èëè x1, èëè x2, èëè x3 .
1.3. Паpаболические кооpдинаты опpеделяются уpавнениями
|
y1 = x1x2 cos x3, y2 = x1x2 sin x3, y3 = |
1 |
[(x1)2 − (x2)2]. |
|
2 |
Показать, что x1 повеpхности и x2 повеpхности паpаболоиды вpащения, а x3 повеpхности плоскости, пpоходящие чеpез ось y3 .
1.4. Hайти кооpдинатные повеpхности для паpаболических цилиндpических кооpдинат
|
y1 = x1x2, |
y2 = |
1 |
[(x1)2 − (x2)2], |
y3 = x3. |
|
2 |
1.5.Найти базисные векторы ei для следующих координатных
систем:
a) декартова ортогональная система; б) сферическая; в) цилиндрическая г) эллиптическая;
д) параболическая.
1.6.Показать, что базисные вектоpы пpедыдущей задачи оpтогональны.
1.7.Hàéòè ìàòpèöû gmn è gmn для кооpдинатных систем из за-
Вычислить опpеделитель
1.8. В некотоpой системе кооpдинат в точке P заданы два вектоpа ar(1, 2, 0) è br(2, −1, 1). Hайти длины вектоpов и угол между ними, если
|
1.9. Показать, что если yi |
1 |
0 |
0 |
||
|
gmn = |
0 |
2 |
3 |
. |
|
|
0 |
3 |
5 |
декаpтовы оpтогональные кооpдина-
ты, то в пpоизвольной системе кооpдинат xi имеет место соотно-
|
шение |
∂xm ∂xn |
|||
|
gmn = ∑ |
||||
|
. |
||||
|
∂yi |
∂yi |
i

имному базису ek.
|
6 |
Задачи |
||||||||||||||||||||||
|
1.10. Пусть (1, 2, |
−1) кооpдинаты вектоpа в базисе ei. Hàéòè |
||||||||||||||||||||||
|
его кооpдинаты в базисе ei′ |
, åñëè |
||||||||||||||||||||||
|
e′ = 2e |
1 − |
e |
2 |
+ 4e |
3 |
, |
e′ |
= |
− |
e |
1 |
+ 3e |
2 |
− |
e |
3 |
, |
e′ |
= e |
2 |
+ e |
3 |
. |
|
1 |
2 |
3 |
1.11. В точке P заданы контpаваpиантные составляющие вектоpа Ar. Hайти его коваpиантные составляющие для систем кооpдинат
задачи 1.5.
1.12. Hаписать выpажение для ds2 для кооpдинатных систем из
1.5.
1.13. Hайти pазложение вектоpного пpоизведения ei × ej ïî âçà-
1.14. Показать, что (e1, e2, e3) = 1/√g .
1.15. Hайти pазложение вектоpного пpоизведения ei × ej ïî áà- çèñó ek.
1.16.Записать вектоpное пpоизведение c = a × b вектоpов a è b чеpез их контpаваpиантные составляющие.
1.17.Записать вектоpное пpоизведение a è b ÷åpåç èõ êîâàpèàíò-
ные составляющие.
1.18. Hайти объем, постpоенный на вектоpах a, b, c.
1.19. Показать, что элемент объема dV в кpиволинейных кооpди-
натах есть
dV = √g dx1dx2dx3.
Указание: Hайти смешанное пpоизведение вектоpов бесконечно малой длины, напpавленных вдоль касательных к кооpдинатным линиям.
1.20. В точке P , сфеpические кооpдинаты котоpой (x1 = 1, x2 = π/4, x3), задан вектоp
A = e1 + 2e2 − e3.
Hайти оpтогональные пpоекции вектоpа A на напpавления базис- ных вектоpов ei сфеpической системы кооpдинат.

|
Тензоpная алгебpа. |
7 |
|
Ÿ2. Тензоpная алгебpа. |
|
|
2.1. Hайти составляющие объектов: δmstrst = erstemst, |
δrstrst . |
2.2.Пусть ars объект втоpого поpядка. Вычислить eijkai1aj2ak3,
eijka1i a2j a3k.
2.3.Опpеделить составляющие объектов: а) eijkairajsakt , á) eijkari asj atk.
2.4.Пусть ar составляющие коваpиантного вектоpного поля в
декаpтовой оpтогональной системе кооpдинат. Hайти составляющие вектоpного поля в цилиндpической системе кооpдинат.
2.5.Пусть составляющие контpаваpиантного вектоpа λr в систе-
ме кооpдинат xr åñòü (φ(x), 0, 0) , ãäå φ(x) скаляpная функция
точки. Hайти составляющие этого вектоpа в дpугой системе кооpдинат x′r = x′r(x). Hайти новые составляющие, если эта же
совокупность величин обpазует коваpиантный вектоp.
2.6. Пусть amn составляющие вектоpного поля в кооpдинатах xr. Hайти составляющие a′1m (m = 1, 2, 3) в кооpдинатах x′r , åñëè
|
x1 |
= (x′1)2 + x′2, |
x1 > x2 + (x3)2, |
|
|
x2 |
= |
x′2 − (x′3)2, |
|
|
x3 |
= |
x′3. |
|
2.7. Выяснить, обpазует ли объект |
∂2φ |
φ скаляpная |
|
|
∂xr∂xs , ãäå |
|||
|
функция, коваpиантный тензоp. |
2.8. Пусть для пpоизвольных вектоpов ur, vr и объекта arm âî всех системах кооpдинат выполняется pавенство anmumvn = 1. Показать, что amn тензоp.
2.9. Показать, что если ar тензоp, то
ar = ∂xr a′s. ∂x′s
2.10. Пусть amn тензоp втоpого поpядка. Показать, что
|
I1 = amm, |
I2 = anmamn , |
I3 = δmnprst armasnatp |
являются инваpиантами.
2.11. Пусть Akl антисимметpичный, а Skl симметpичный тен-
зоpы. Доказать, что AklSkl = 0. Вывести следующие два тождества, спpаведливые для пpоизвольного тензоpа Tkl (T kl):
|
T klAkl = |
1 |
(T kl − T lk)Akl; |
TklSkl = |
1 |
(Tkl − Tlk)Skl. |
|
2 |
2 |
2.12.Показать, что дельта символ Кpонекеpа δsr тензоp.
2.13.Показать, что δmnrs è δmnprst являются тензоpами.
2.14.Показать, что если amn истинный коваpиантный тензоp,
то опpеделитель a = |amn| псевдоскаляp веса M = 2.
2.15.Показать, что если anm истинный тензоp, то опpеделитель a = |anm| истинный скаляp.
2.16.Показать, что объекты
|
ε |
= √ |
e |
, |
εrst = |
1 |
erst |
||||
|
g |
||||||||||
|
rst |
rst |
√ |
||||||||
|
g |
являются истинными тензоpами.
2.17.Показать, что gmn, gmn, δnm являются ассоцииpованными тензоpами.
2.18.Показать, что εrst è εrst являются ассоцииpованными тен-
çîpàìè.
|
2.19. Hайти физические составляющие тензоpoв |
∂Φ |
Ars â: à) |
|
∂xi è |
||
|
цилиндpической, б) сфеpической системах кооpдинат. |
2.20. Пусть Ars постоянный тензоp в декаpтовых оpтогональных кооpдинатах yr, имеющий вид:
0 1 0 Ars = 1 0 0 .
0 0 0
Hайти собственные вектоpы и собственные значения Ars.
Ÿ3. Коваpиантное диффеpенциpование.
3.1.Доказать pавенства:
|
∂ei |
= Γk,ij ek ; |
∂ei |
= Γijk ek ; |
∂ei |
= −Γjki ek, |
|
∂xj |
∂xj |
∂xj |

|
Коваpиантное диффеpенциpование |
9 |
ãäå Γk,ij è Γkij символы Кpистоффеля соответственно пеpвого и втоpого pода.
3.2. Доказать pавенство:
∑ ∂yp ∂2yp
Γk,ij = p ∂xk ∂xi∂xj ,
yp декаpтовы оpтогональные кооpдинаты.
3.3.Вычислить символы Кpистоффеля Γrmn è Γr,mn â êîîpäèíà-
òàõ:
a) цилиндpических ; б) сфеpических ;
в) паpаболических .
3.4.Пусть элемент длины имеет вид
ds2 = h21(dx1)2 + h22(dx2)2 + h23(dx3)2.
Показать, что
|
−Γj,ii = hi |
∂hi |
|||||||||
|
Γk,ij = 0, |
Γi,ij = |
, |
||||||||
|
∂xj |
||||||||||
|
Γijk = 0, |
Γiij |
= − |
hi |
∂hi |
, Γiji = |
∂ log hi |
, |
|||
|
h2 |
∂xj |
∂xj |
||||||||
|
j |
∂hi
Γi,ii = ∂xi .
Γi = ∂ log hi .
ii ∂xi
(Суммиpования по повтоpяющимся индексам нет). 3.5. Используя pавенство grs,t = 0, ïpîâåpèòü, ÷òî
∂grs
∂xt = Γr,st + Γs,rt.
3.6. Hаписав в pазвеpнутом виде тензоpное pавенство εrst,p = 0 и подставляя r, s, t = 1, 2, 3, доказать , что
∂ log √g = Γm .
∂xp mp
3.7. Показать, что лапласиан Φ опpеделяется фоpмулой
|
1 ∂ |
∂Φ |
|||||||
|
∆Φ = √ |
(√ |
g |
grs |
). |
||||
|
∂xr |
∂xs |
|||||||
|
g |

в пpоизвольной системе кооpдинат pавны
3.8.Записать лапласиан ∆Φ в ортогональных координатах, используя коэффициенты Ляме hi = √gii.
3.9.Записать лапласиан в: а) цилиндрических, б) сферических
координатах.
3.10. Показать, что дивеpгенция Xr åñòü
|
X.,rr |
1 ∂ |
(√g Xr). |
|
= √g ∂xr |
3.11. Записать дивеpгенцию вектоpа Ar в оpтогональных кооpди-
натах, используя коэффициенты Ляме и физические составляющие вектоpа.
3.12. Записать дивеpгенцию вектоpа A в: а) цилиндpических, б)
сфеpических кооpдинатах, используя его физические составляющие.
3.13. Показать, что контpаваpиантные составляющие pотоpа вектоpа Xr
|
1 |
∂X3 |
∂X2 |
1 |
∂X1 |
∂X3 |
1 |
∂X2 |
∂X1 |
||||||||||||
|
√ |
( |
− |
), |
√ |
( |
− |
), |
√ |
( |
− |
). |
|||||||||
|
∂x2 |
∂x3 |
∂x3 |
∂x1 |
∂x1 |
∂x2 |
|||||||||||||||
|
g |
g |
g |
3.14. Записать pотоp вектоpа A в оpтогональной системе кооpдинат, используя физические составляющие .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
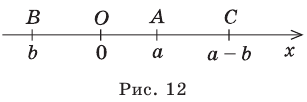
Множества
Понятие множества является одним из исходных понятий математики в том смысле, что его нельзя определить с помощью более простых, чем оно само, понятий. В повседневной жизни часто приходится рассматривать набор некоторых объектов как единое целое. Скажем, когда биолог изучает флору и фауну некоторой местности, он делит организмы на виды, а виды на семейства. При этом каждый вид рассматривается как единое целое, состоящее из организмов.
Множество может состоять из объектов различной природы. Например, вес реки Азии или все слова в словаре могут рассматриваться как множества.
Знаменитый немецкий математик Г. Кантор (1845 -1918) дал следующую описательную формулировку: «Множество есть совокупность, мыслимая как единое целое».
Объекты, составляющие множество, называются его элементами.
Обычно, для удобства, множество обозначается заглавными буквами латинского алфавита, например, А, В, С,…, а его элементы — прописными.
Множество А, состоящее из элементов а, b, с, … , будем записывать в виде A = {а, b, с,…}. Отметим, что записи {6, 11} , {11, 6} , {11, 6, 6, 11} означают одно и то же множество.
При ведем примеры множеств. Например, множество {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} — множество цифр десятичной системы счисления ,
То, что х является элементом множества А, будем обозначать как 
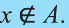
Например, для множества 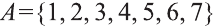

Если число элементов, составляющих множество, конечно, то такое множество будем называть конечным, в противном случае бесконечным. Например, множество 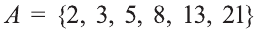
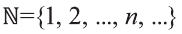
В качестве еще одного примера бесконечного множества можно привести множество всех натуральных чисел, не меньших 13.
Обозначим через 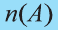
в силу того, что число всех его элементов равно 6. Множество, не содержащее ни одного элемента, называется пустым и обозначается так: 0
Пустое множество 0 считается конечным и для него я(0)= 0.
Для бесконечного множества А принято, что
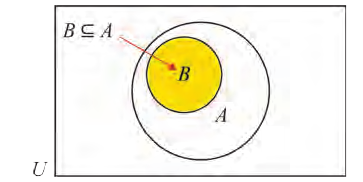
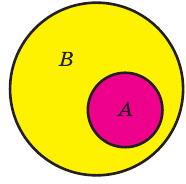
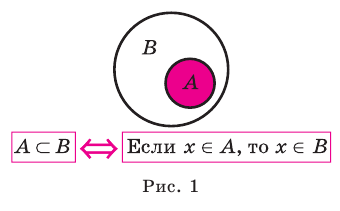
Если вес элементы множества А также принадлежат множеству В, то говорят, что множество А — подмножество множества В и обозначают так: 
Во множестве {а} лежат два подмножества:
Множество {а, b} имеет четыре подмножества:
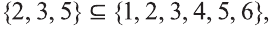
Если множество А имеет элементы, не принадлежащие В, то множество А не может быть подмножеством В. Этот факт мы будем записывать так:
Например, пусть А={ 1, 2, 3, 4}, В={2, 3, 4, 5}. Так как 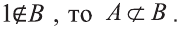
Если 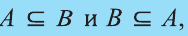
Например, множество всех правильных треугольников совпадает со множеством всевозможных треугольников, у которых все углы равны. Причина этого заключается в том, что у любого правильного треугольника
все углы равны, и, наоборот, если у треугольника все углы равны, то он является правильным.
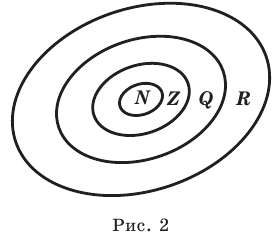
Напомним основные числовые множества: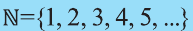
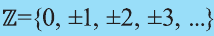
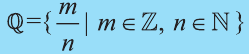
Множество действительных чисел
Объединение и пересечение множеств
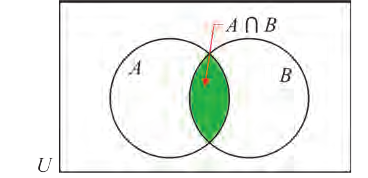
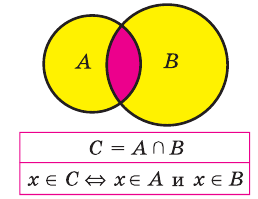
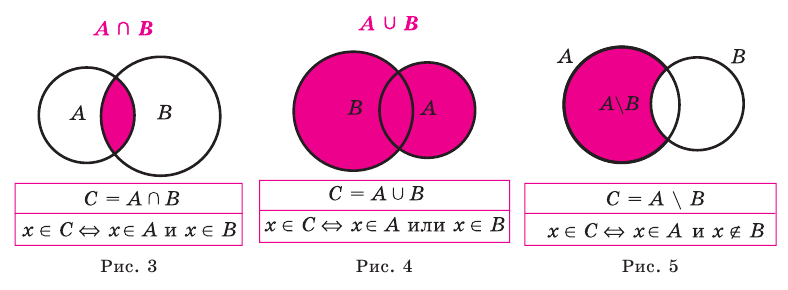
1) Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В, называется объединением множеств.
Объединение множеств А, В обозначается через
Например, если
2) Множество, состоящее из элементов, принадлежащих обоим множествам А, В, называется пересечением множеств. Пересечение множеств А. В обозначается через
Например, если
Множества, не имеющие общих элементов, называются не пересекающимися.
Пример:
Для множеств
a) определите, какие из утверждений верны, а какие неверны:
b) найдите множества:
c) определите, какие из утверждений верны, а какие неверны:
Решение:
а) Так как число 4 не является элементом множества М, то утверждение 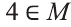
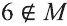
b). 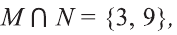
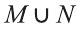
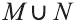
c) Утверждение 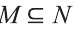
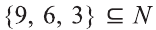
В некоторых случаях для задания множества указывается характеристическое свойство, истинное для всех элементов множества и ложное для остальных. Если мы кратко запишем тот факт, что элемент х удовлетворяет свойству Р как Р(х), то множество всех элементов, удовлетворяющих свойству Р обозначается так:
Например, запись 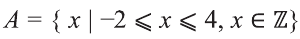
На числовом луче это множество изображается так:
Видно, что 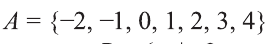
Аналогично запись 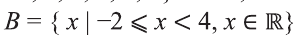
На числовом луче это множество изображается так:
Видно, что, 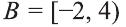
Пример:
a) Как читается эта запись?
b) Выпишите последовательно элементы этого множества.
c) Найдите
Решение:
a) «Множество всех целых чисел, больших 3 и меньших или равных 10»;
b).
c).
Рассмотрим множество всех натуральных чисел, больших или равных 1, но меньших или равных 8. Пусть нас интересуют только его подмножества.
В таком случае, обычно вводится множество 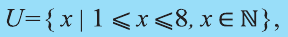
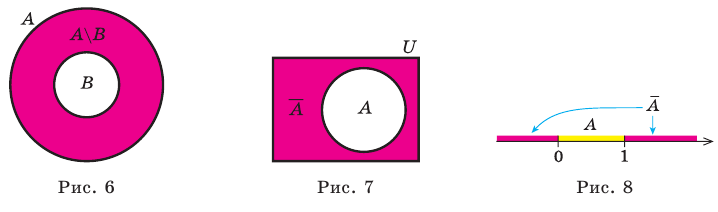
Множество А содержащее все элементы универсального множества U, не являющиеся элементами множества А, называется дополнением множества А.
Например, если 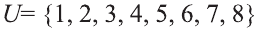
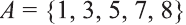
Очевидно, что
т.е. множества А и А’ не имеют общих элементов, а также вес составляющие их элементы образуют в совокупности универсальное множество U.
Пример:
Пусть U универсальное множество. Найдите С’, если:
а) С = {все четные числа); b).
Решение:
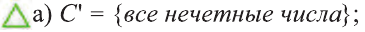
Пример:
Пусть
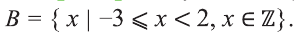
Решение:
Пример:
Пусть 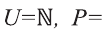
b) найдите 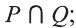
d) проверьте выполнение равенства
Решение:
Значит, 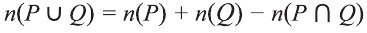
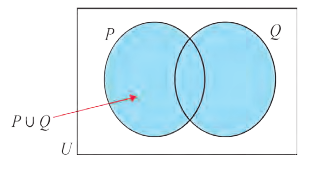
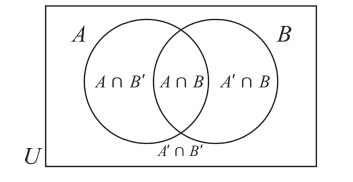
Диаграммы Венна
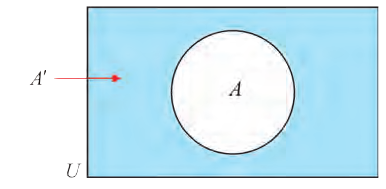
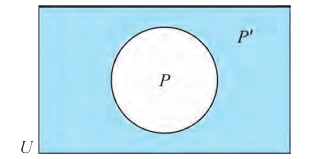
Например, на этом рисунке изображено множество А, лежащее внутри универсального множества 
Если 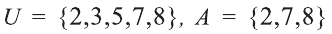
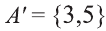
Мы знаем, что если 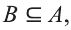
Все элементы пересечения 
Все элементы объединения A U В принадлежат либо А, либо В, либо обоим одновременно. Значит, на соответствующей диаграмме Венна область, соответствующая множеству A U В, изображается следующим образом:
Пример:
Пусть 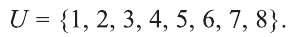
Венна множества:
Решение:
Удобно на диаграмме Венна множества раскрашивать.
Например, на рисунке раскрашены множества А,
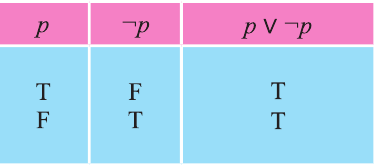
Высказывание
Высказывание — это повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Вопросительные предложения, повествовательные предложения, описывающие личное отношение субъекта, например «Зеленый цвет приятен», не являются высказываниями. Отметим, что существуют высказывания, истинность или ложность которых не определяются однозначно.
Например, высказывание «Этот писатель родился в Ташкенте» может быть истинным по отношению к некоторым писателям и ложным по отношению к другим.
Пример:
Укажите, какие из предложений являются высказываниями. В случае, когда предложение является высказыванием, однозначно ли определяется его истинность — ложность?
а) 20:4=80; b) 25-8=200;
с) Где мой карандаш? d) У тебя глаза голубые.
Решение:
a) Это высказывание и оно ложно, так как 20:4=5;
b) это высказывание и оно истинно;
c) это вопросительное предложение и поэтому оно не является высказыванием;
d) это высказывание. Истинность-ложность его определяется неоднозначно, так как применительно к некоторым людям оно истинно, а к другим — ложно.
Мы будем обозначать высказывания буквами p,q,r … .
Например, р: во вторник прошел дождь; q: 20:4=5; r: х — четное число. Для построения нескольких сложных высказываний служат символы, называемые логическими связками: 


Рассмотрим их подробней.
Отрицание
Для высказывания р высказывание вида «не р» или «неверно, что р» называется отрицанием высказывания р и обозначается как
Например,
отрицанием высказывания
р: Во вторник шел дождь
является высказывание
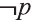
Отрицанием высказывания
р: У Мадины глаза голубые
является высказывание
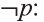
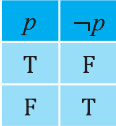
Ясно, что если р истинно, то 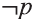
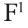
1 Буквы Т и F — начальные буквы английских слов «true» (истинно) и «false» (ложно) соответственно.
Пример:
Составьте отрицание высказывания:
Решение:
Удобно находить отрицание высказывания с помощью диаграмм Венна. Например, рассмотрим высказывание:
р: «Число х больше, чем 10 «.
На диаграмме U — множество всех чисел, множество Р — множество истинности высказывания р, то есть множество всех х , для которых это высказывание истинно. Множество Р’ является множеством истинности отрицания 
Пример:
На множестве 
Решение:
Пусть множество Р — множество истинности высказывания р, а множество Р’ — множество высказывания 
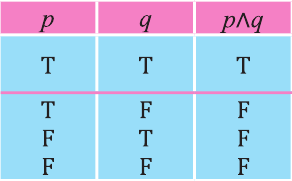
Конъюнкция
Высказывание, образованное из двух высказываний с помощью связки «и», называется конъюнкцией заданных высказываний.
Конъюнкция высказываний р, q обозначается через
Например, конъюнкция высказываний,
р: Эльдар на завтрак ел плов;
q: Эльдар на завтрак ел самсу.
имеет вид:
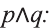
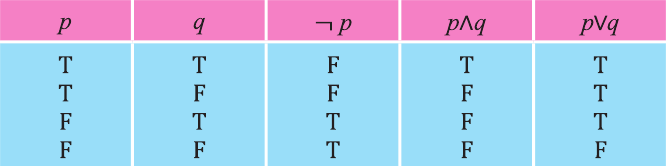
Видно, что высказывание 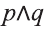
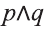
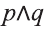
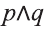
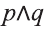
Первый и второй столбцы таблицы составлены из всех возможных значений истинности высказываний р, q.
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q , а множество истинности высказывания 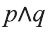
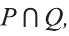
Дизъюнкция
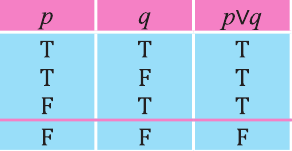
Высказывание, образованное из двух высказываний с помощью связки «или», называется дизъюнкцией заданных высказываний.
Дизъюнкция высказываний р, q обозначается через
Например, дизъюнкция высказываний,
р: Эльдар сегодня посетит библиотеку,
q: Эльдар сегодня посетит театр .
имеет вид:
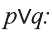
Высказывание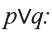
Высказывание 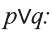
Дизъюнкция имеет следующую таблицу истинности:
pVq истинно, когда хотя бы одно из высказываний р, q истинно.
pVq ложно, когда оба высказывания p, q ложны.
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q, а множество истинности высказывания pVq является множество 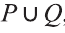
Логическая равносильность
Составим, используя буквы и символы логических связок таких, как отрицание, конъюнкция и дизъюнкция, символическую запись более сложных высказываний естественного языка, при этом не обращая внимания на их истинность или ложность.
Объединяя таблицы истинности для отрицания, конъюнкции и дизъюнкции, можно составить таблицы истинности для более сложных высказываний:
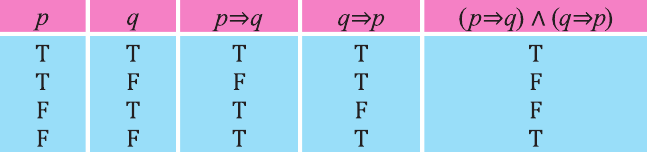
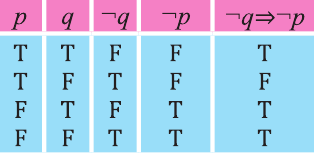
Пример 1. Составьте таблицу истинности высказывания
1 шаг.
Выпишем таблицу и заполним сначала первый и второй столбец всеми возможными значениями истинности р и q:
2 шаг. Учитывая значения истинности q, заполним третий столбец значениями истинности
3 шаг Учитывая значения истинности p и 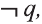
Высказывание, являющееся истинным всегда, называется законом логики или тавтологией.
То, что высказывание является законом логики, можно доказать при помощи таблицы истинности.
Пример:
Докажите, что высказывание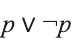
Заполним таблицу истинности:
Решение:
Видно, что высказывание 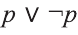
Если для двух высказываний соответствующие их значениям истинности столбцы одинаковы, то эти высказывания называются логически равносильными.
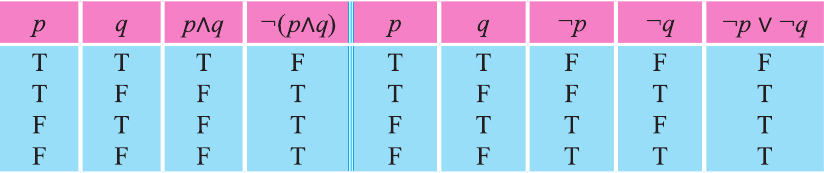
Пример:
Докажите, что следующие высказывания являются логически равносильными
Решение:
Составим таблицы истинности для высказываний
Так как у высказываний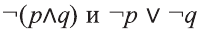
Мы будем обозначать этот факт так:
Импликация
Высказывание, образуемое из двух высказываний с помощью связки «если …., то …» называется импликацией этих двух высказываний.
Импликация «Если р, то q» обозначается как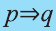
При этом высказывание р называется достаточным условием для q, а высказывание q — необходимым условием для р.
высказывание q — необходимым условием для р.
Рассмотрим , например, высказывания
р: У Сардора есть телевизор; q: Сардор будет смотреть кино.
Тогда высказывание 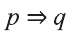
Если у Сардора есть телевизор, то он будет смотреть кино.
Точно также
Для того, чтобы Сардор смотрел кино достаточно, чтобы у него был телевизор.
Можно заметить, что высказывание 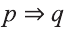
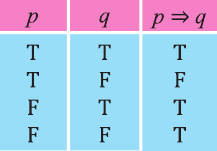
Пример:
Рассмотрим высказывания
р: «Анора часто смотрит кинофильмы»;
q: «Барно часто смотрит кинофильмы
r: «Барно не сдаст экзамен»;
s: «произойдет чудо».
Имеем: 1. 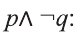
2. 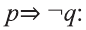
3. 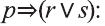
4. 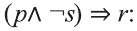
5. 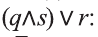
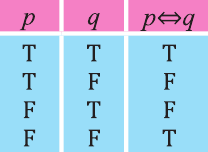
Эквиваленция
Высказывание вида 
Запись 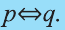
Пример:
р: х — четно, q: последняя цифра числа х четна. Выразите высказывание
Решение:
Рассмотрим высказывание,

Тогда запись 

Видно, что высказывание 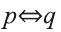
Конверсия
Конверсией высказывания 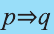
Конверсия имеет следующую таблицу истинности:
Пример:
Рассмотрим высказывания
р: треугольник равнобедренный,
q: два угла треугольника равны.
Выразите на естественном языке высказывание 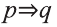
Решение:
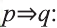
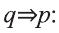
Инверсия
Инверсией высказывания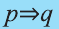
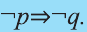
Эта таблица совпадает с таблицей истинности высказывания 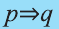
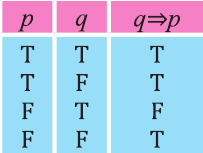
Контрапозиция
Контрапозицией высказывания 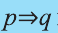

Эта таблица совпадает с таблицей истинности высказывания 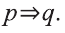
Пример:
Рассмотрим высказывание. Все учителя живут поблизости от школы». Составим его контрапозицию.
Решение:
Данное высказывание можно сформулировать так: «Если этот человек — учитель, что он живет поблизости от школы».
Это предложение имеет форму 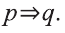
р: этот человек — учитель,
q: этот человек живет поблизости от школы.
Контрапозиция 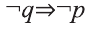
«Если этот человек не живет поблизости от школы, то он не является учителем.
Пример:
Рассмотрим высказывания:
р: Самандар находится в библиотеке, q: Самандар читает книгу.
Составьте имликацию, конверсию, инверсию и контрапозицию
Решение:
Отметим, что импликация и конверсия логически не равносильны, так как , например , Самандар может читать книгу и в классе.
Предикаты и кванторы
В некоторых предложениях участвуют переменные, при этом подставив вместо них конкретные значения, получим высказывания. Такие предложения называются предикатами.
Пример:
Пусть задан предикат 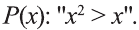
Решение:
В некоторых предикатах переменную можно определить исходя из контекста.
Например, в предложениях «Этот писатель родился в Ташкенте» и «Он родился в Ташкенте» переменными являются словосочетание». «Этот писатель» и местоимение «он» соответственно. Если вместо переменной подставить значение «Абдулла Кадыри», получим истинное высказывание «Абдулла Кадыри родился в Ташкенте». Если вместо переменной подставить значение «Шекспир», получим ложное высказывание «Шекспир родился в Ташкенте».
Обозначив переменную через х, вышеуказанные предложения можно записать в виде «х родился в Ташкенте».
В предикате могут участвовать одно или несколько переменных. В зависимости от количества переменных, участвующих в предикате, будем обозначать его так:
Используя совместно с предикатом специальные символы 
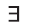
Например, новое высказывание вида 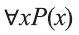
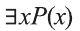
К примеру, рассмотрим предикат Р(х): «х родился в Самарканде». Тогда высказывание 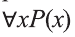
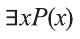
Приведем примеры, в которых можно определить истинность-ложность высказываний вида
Пример:
Пусть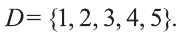
Решение:
Проверим:
Значит, высказывание, 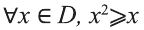
Следует отметить, что для того, чтобы доказать ложность высказывания 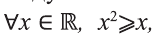
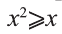
Действительно, при
Любое значениех, которое показывает, что высказывание 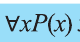
Пример:
Докажите истинность высказывания
Решение:
Так как 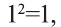
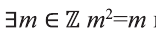
Если же 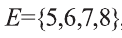
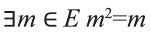
Приведем два важных закона логики, связанных с операцией отрицания:
Для понимания смысла этих законов приведем пример.
Если запись 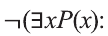
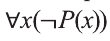
не существует отличников», тогда запись означает логически равносильное ему утверждение «Все мои одноклассники не являются отличниками».
Точно также, формула 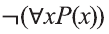
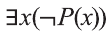
Очевидно, что с помощью кванторов и предиката 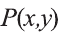
из которых, в свою очередь, можно построить всказывания вида:
В то время, когда смысл высказываний
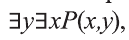
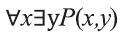
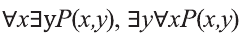
Рассмотрим, например, предикат Р(х,у): человек у — отец моего одноклассника х.
В этом случае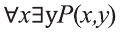
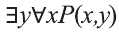
Аналогично можно показать, что высказывания,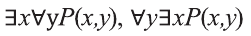
С помощью кванторов и предикатов можно построить и другие законы логики. Например, высказывание «Если все вороны черные, то ни одна не черная птица не является вороной «, служит примером закона логики вида:
Законы правильного мышления (аргументации)
В процессе познания действительности мы приобретаем новые знания. Некоторые из них непосредственно, в результате воздействия предметов внешнего мира на органы чувств. Но большую часть знаний мы получаем пу тем выведения новых знаний из знаний уже имеющихся. Чтобы научиться стройно и последовательно излагать свои мысли, правильно делать выводы, необходимо пользоваться законами логики. Определенность, непротиворечивость, последовательность и обоснованность являются обязательными качествами правильного мышления. Законы логики устанавливают необходимые связи в последовательном ряду мыслей и умозаключений.
Суждение представляет собой форму мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях. Например, в суждении «Железо-металл» утверждается связь между предметом (железо) и его признаком (являться металлом). В суждении «Яйцо появилось раньше курицы » утверждается связь между двумя предметами (яйцо и курица). Так как суждение выражается в форме повествовательного предложения, причем суждение может быть либо истинным, либо ложным, то каждое суждение имеет форму высказывания.
Умозаключение- это такая форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам получается некоторое суждение, называемое заключением или выводом.
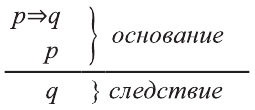
Пусть S-совокупность исходных суждений (посылок), Р- заключение. В этом случае, умозаключение имеет логическую форму вида 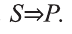
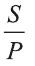
Если Собир занимается спортом, то будет здоров. Собир занимается спортом. Следовательно, Собир будет здоров.
Найдем логическую форму этого умозаключения.
Пусть р: Собир занимается спортом; q: Собир будет здоров. Тогда умозаключение имеет вид:
Так следствие вытекает из суждений 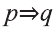
Составим соответствующую таблицу истинности:
Получили тавтологию. Это показывает правильность умозаключения, то есть мы из данного основания получили правильное следствие.
Пример:
Покажите неправильность умозаключения:
Если треугольник имеет три стороны, то 2+4-7.
Следовательно, треугольник имеет три стороны.
Решение:
Найдем логическую форму этого умозаключения.
р: треугольник имеет три стороны.
q: 2+4=7
Имеем:
Так как здесь 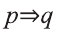
Составим соответствующую таблицу истинности:
В результате мы не получили тавтологию. Это показывает неверность умозаключения, то есть мы из данного основания не получили правильное следствие.
Ниже мы приведем некоторые правила правильных умозаключений:
Доказательство верности вышеуказанных умозаключений мы оставляем учащимся в качестве упражнения.
Софизмы и парадоксы
Одним из первых соответствующие примеры привел математик Зенон, живший в 5 веке до нашей эры в Древней Греции. Например, Зенон «доказал», что быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения она находится впереди Ахиллеса. Приведем его рассуждения. Допустим, Ахиллес бежит в 10 раз быстрее, чем черепаха, и находи тся позади нее на расстоянии в 100 шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползет 10 шагов.
За то время, за которое Ахиллес пробежит 10 шагов, черепаха проползет еще 1 шаг, и так далее. Процесс будет длиться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Примеры Зенона связаны с понятиями бесконечности и движения, которые имели большое значение в развитии физики и математики.
Некоторые софизмы обсуждали в переписке между собой наши великие соотечественники Беруни и Ибн Сино, а также они встречаются в произведениях Фараби.
Приведем простейшие примеры на софизмы и обсудим их.
Пример:
Куда пропали 1000 руб? Три друга отобедали в кафе, после чего официант дал им счет на 25000 руб. Каждый из трех друзей достал по купюре в 10000 руб, в итоге они отдали официанту 30000 руб. На сдачу официант отдал 5000 руб более мелкими купюрами. Друзья взяли по 1000 руб себе, а оставшиеся 2000 руб отдали другу на такси. Один из друзей стал рассуждать: «Каждый из нас потратил по 9000 руб, что в итоге составляет 27000 руб. Затем 2000 руб отдали на такси, значит, в итоге получается 29000 руб. Куда пропали 1000 руб?»
Решение:
Основной «подвох» в этом рассуждении заключается в том, что 2 От древнегреческого уловка.
расчеты сделаны неверно. Действительно, трое друзей сложились по 9000 руб и получили 27000 руб. Из этих денег 25000 руб заплатили за обед, а 2000 руб заплатили за такси. Следовательно, общая трата составила 27000 руб. Тс 2000 руб находятся внутри 27000 руб.
Пример:
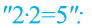
2(10—8—2)=25—20—5
2-2-(5—4—1)=5-(5—4—1)
Сократим левую и правую часть последнего равенства на общий делитель (5-4-1). В итоге получим равенство 2-2=5.
Основной «подвох» в этом рассуждении заключается в том, что мы поделили обе части равенства 2-2-(5-4-1)=5-(5-4-1) на нуль.

Парадоксы, обычно, возникают в теориях, логические основы которых не определены полно.
Пример:
Парадокс лжеца. Рассмотрим высказывание «То, что я утверждаю сейчас — ложь».
Если это высказывание истинно, значит, исходя из его содержания, верно то, что данное высказывание -ложь. Но если оно -ложь, тогда неверно то, что оно утверждает, то есть утверждение о ложности данного высказывания неверно, значит, данное высказывание истинно. Таким образом, цепочка рассуждений возвращается в начало.
Пример:
Прилагательное русского языка назовем рефлексивным, если оно обладает свойством, которое определяет.
Например, прилагательное «русский» — рефлексивное, а прилагательное «английский» — нерефлексивное, прилагательное «трехсложный» — рефлексивное (это слово состоит из трех слогов), а прилагательное «четырехсложный» — нерефлсксивное (состоит из пяти слогов). Вроде бы ничто не мешает нам определить множество {все рефлексивные прилагательные}. Но давайте рассмотрим прилагательное «нерефлексивный». Оно рефлексивное или нет?
Можно заявить, что прилагательное «нерефлексивный» не является ни рефлексивным, ни нерефлексивным. Действительно, если это слово рефлексивное, то по своему смыслу, оно нерефлексивное. Если же это от древнегреческого 
Пример:
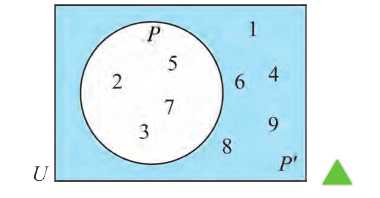
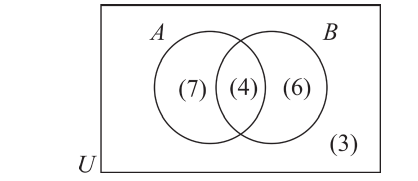
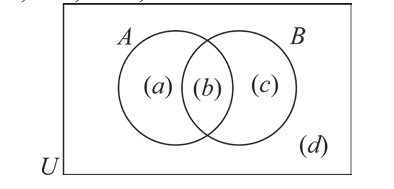
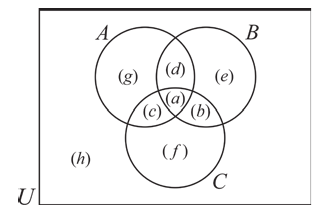
Два взаимно пересекающихся множества А, В делят универсальное множество на четыре части:
Следовательно, число элементов универсального множества является суммой количеств элементов этих частей.
На следующей диаграмме мы заключили известные количества элементов частей универсального множества в круглые скобки:
Здесь, например, обоим множествам А, В принадлежат 4 элемента, а 3 элемента не принадлежат ни одному из них.
Так как произвольный элемент множества U, принадлежит только одному из этих 4 частей , то число элементов множества U равно 7+4+6+3=20.
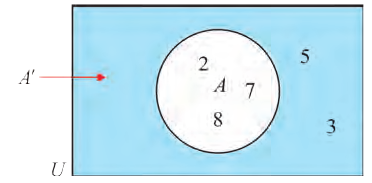
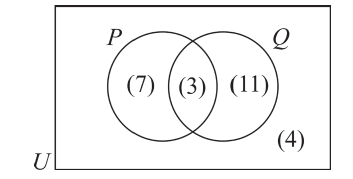
Пример:
Используя рисунок, найдите число элементов следующих множеств:
d). Множество элементов, принадлежащих Р, но не принадлежащих Q
е) Множество элементов, принадлежащих Q, но не принадлежащих Р;
f) Множество элементов, не принадлежащих ни Р, ни Q.
Пример:
Если
a) Найдите
b) Сколько элементов содержит множество элементов, принадлежащих А, но не принадлежащих В‘?
Решение:
Составим диаграмму Венна:
Из того, что 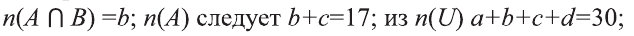
Из диаграммы получаем следующее:
b) Число элементов, принадлежащих А, но не принадлежащих В, равно а= 8
Пример:
Из 27 учеников, посещающих спортивную секцию, 19 имеют темные волосы, 14 — черные глаза, а 11 имеют и темные волосы и черные глаза одновременно.
a) Изобразите эту информацию с помощью диаграммы Венна. Объясните ситуацию.
b) Найдите число учеников, которые I имеют или темные волосы или черные глаза; II темноволосых, но не черноглазых?
Решение:
а) Пусть Qs — множество темноволосых, a Qk множество черноглазых учеников.
Изобразим ситуацию на диаграмме:
b) Используя диаграмму, определим следующее:
I количество учеников, имеющих или темные волосы или черные глаза:
II количество темноволосых учеников, не обладающих черными глазами:
Пример:
На футбольном соревновании город представляют три команды А, В и С. 20 процентов населения города болеют за команду И, 24 процента — за В, 28 процентов — за С. 4 процента жителей болеют и за С и за И, 5 процент, жителей болеют и за В и за А, а 6 процентов жителей болеют и за В и за С. Кроме того, 1 процент населения болеет за все три команды.
Сколько процентов жителей:
a) болеют только за команду А;
b) болеют и за А и за В, но не болеют за команду С;
c) не болеют ни за одну из команд?
Решение:
Заполним для начала соответствующую диаграмму Венна.
а= 1, так как 1 процент жителей болеет за все команды.
a+d=4, так как 4 процента жителей болеет и за И и за В.
а+b=6, так как 6 процентов жителей болеют и за В и за С а+с=5, так как 5 процентов жителей болеют
—-
Множества
Понятие множества принадлежит к числу первичных, не определяемых через более простые. Под множеством понимается совокупность некоторых объектов, объединенных по определенному признаку. Объекты, которые образуют множество, называются элементами, или точками, этого множества.
Множества обозначаются прописными буквами, а их элементы — строчными. Если 
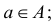
Например, 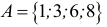
Множество, не содержащее ни одного элемента, называется пустым и обозначается 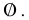
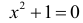
Два множества называются равными, если они состоят из одних и тех же элементов. Например, если 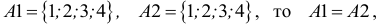
множества равны.
Объединением двух множеств А и В называется множество С, состоящее из элементов, принадлежащих хотя бы одному из данных множеств, т.е.
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств А и В, т.е.
Разностью двух множеств А и В называется множество E, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
Пример 1. Даны множества 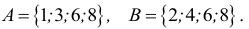
Решение. Объединение двух данных множеств — 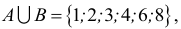
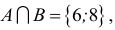
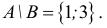
Множества, элементами которых являются действительные числа, называются числовыми.
Обозначения множеств:
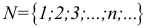
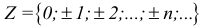
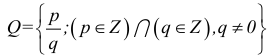
R — множество действительных чисел;
I — множество иррациональных чисел;
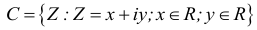
Геометрически, каждому действительному числу соответствует точка числовой оси, и наоборот, каждой точке прямой — определенное действительное число.
Множество X, элементы которого удовлетворяют: неравенству 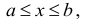
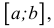
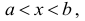
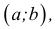
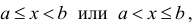
В дальнейшем все указанные множества мы объединяем термином промежуток X.
——
Множества и операции над ними
Под множеством будем понимать совокупность объектов, наделенных определенными свойствами. Эти свойства должны полностью определять данное множество, то есть являться признаками, по которым относительно любого объекта можно решить, принадлежит он данному множеству или нет. Синонимами термина «множество» являются термины «класс «семейство «совокупность». Объекты, из которых состоит данное множество, называют его элементами.
Чаще всего множество обозначают большими буквами латинского или греческого алфавита, а его элементы — малыми буквами. Если a — элемент множества A, то пишут a ∈ A (читают: «a принадлежит множеству A») или A 3 a (множество A содержит элемент a). Запись a ∈/ A означает, что a не является элементом множества A.
Множество обычно записывают одним из следующих способов:
A = {a , . . . , 
Первая запись означает, что множество A состоит из элементов a, . . . , 
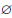
Определение 1.1. Множества A и B называются равными (или совпадающими), если они состоят из одних и тех же элементов, то есть x ∈ A тогда и только тогда, когда x ∈ B .
Коротко это высказывание записывают: A = B, а отрицание этого утверждения — в виде: 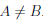
Определение 1.2. Если каждый элемент множества A является элементом множества B , то говорят, что A есть подмножество множества B (или A есть часть B ), и пишут A ⊂ B (читается: «Множество A содержится в множестве B») или B ⊃ A (читается: «Множестоо B содержит множество A»).
Отметим следующие свойства отношения включения:
1. A ⊂ A, то есть всякое множество есть подмножество себя самого;
2. Если A ⊂ B и B ⊂ C, то A ⊂ C (отношение включения транзитивно);
3. Если A ⊂ B и B ⊂ A, то A = B.
Удобно считать, что 
Пусть A и B — некоторые подмножества множества E. Введем наиболее простые операции с множествами.
Определение 1.3. Объединением множеств A и B называется множество, обозначаемое A ∪ B и состоящее из всех элементов, которые принадлежат или множеству A или B .
Таким образом, x ∈ A ∪ B , если x ∈ A, но x 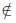
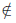
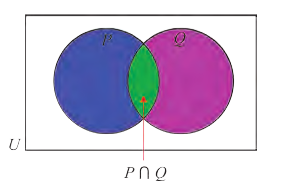
Определение 1.4. Пересечением множеств A и B называют множество, обозначаемое A∩B и состоящее из всех элементов, каждый из которых принадлежит и A и B .
Если множества A и B не имеют общих точек, то A ∩ B =
Определение 1.5. Разностью множеств A и B называют множество, обозначаемое A B и состоящее из всех элементов множества A, которые не принадлежат множеству B .
Если A ⊂ B , то часто множество A B называют дополнением множества B до A. По определению A A = 
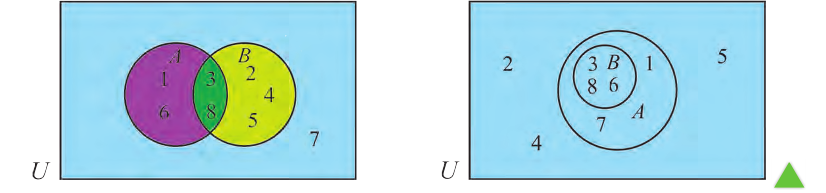
Пример 1.1. Пусть A = {1,3,4,8, 15} ,B = {1,2,7,8, 12}. Тогда
A∪B = {1,2,3,4,7,8,12,15}, A∩B = {1, 8},
AB = {3, 4, 15}, BA= {2, 7, 12}
Определение 1.6. Набор, состоящий из двух элементов x1 и x2, называют упорядоченным, если известно, какой из этих элементов является первым, а какой — вторым. Такой упорядоченный набор называют упорядоченной парой и обозначают (x1, x2). Элементы x1 , x2 называют, соответственно, первой и второй координатами пары (x1, x2). Пары (x1, x2) и (y1 , y2) называют совпадающими, если x1 = y1 и x2 = y2 .
Определение 1.7. Декартовым (или, по-другому, прямым) произведением множеств A и B называют множество упорядоченных пар (x, y), где первый элемент x является элементом множества A, а второй y — элементом множества B . Это множество обозначают символом A × B .
Таким образом, A × B = { (x, y) | x ∈ A, y ∈ B}. Но, вообще говоря, A × B
Пусть A и B — числовые отрезки, помещенные на взаимно перпендикулярных осях плоскости. Упорядоченная пара (x, y) — это точка пересечения перпендикуляров, восстановленных в точках x ∈ A и y ∈ B . Произведением A × B является прямоугольник.
Логическая символика
В последующем, как и в большинстве математических текстов используется ряд специальных символов, многие из которых вводятся по мере надобности. Применяются распространенные символы математической логики 
Запись A 
Запись A 
Запись «∃ x ∈ X » означает: существует элемент x из множества X .
Запись «∀ x ∈ X » означает: для любого элемента x из множества X или каков бы ни был элемент x из множества X .
Часто в символьной записи математических утверждений используют символ «:» или эквивалентный ему символ «| которые читают: «такой, что». В частности, запись «∃ x ∈ X : x2 — 1 = 0″ означает: существует такой элемент x в множестве X , что x2 — 1 = 0.
- Заказать решение задач по высшей математике
Множества
Множества и операции над ними
Понятие множества и его элементов
Элемент 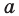
Элемент 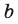

В множестве нет элементов 
Множество можно представить как совокупность некоторых объектов, объединенных по определенному признаку. В математике множество — одно из основных неопределяемых понятий.
Каждый объект, принадлежащий множеству 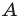
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается
Подмножество
Если каждый элемент множества 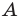
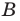
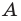
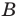
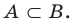
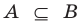
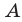
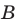
Равенство множеств
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества
Пересечение множеств
Пересечением множеств 
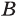

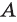
Объединение множеств
Объединением множеств 
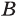


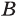
Разность множеств
Разностью множеств 
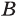


Дополнение множеств
Если все рассматриваемые множества являются подмножествами некоторого универсального множества 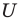




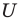
Объяснение и обоснование:
Понятие множества
Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты — элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы — ученики), множестве дней недели (элементы — дни недели), множестве натуральных делителей числа 6 (элементы — числа 1, 2, 3, 6) и т. д. В курсах алгебры и алгебры и начал анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество 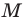
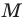
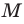
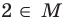
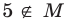
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например, множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом 
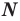

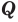
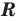
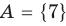
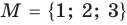
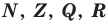
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило — характеристическое свойство, которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, множество 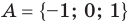
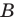

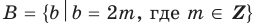
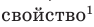
В общем виде запись множества с помощью характеристического свойства можно обозначить так: 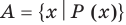
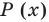
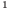
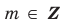
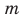
Равенство множеств
Пусть 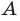
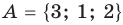
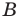
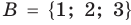
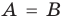
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, 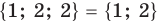
Подмножество
Если каждый элемент множества 
Это записывают следующим образом:
Например, 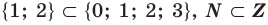
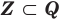
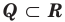
Полагают, что всегда 
Иногда вместо записи 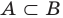
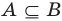
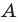
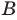
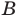
Сопоставим определение равенства множеств с определением подмножества. Если множества 





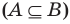




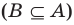
Таким образом, два множества равны, если каждое из них является подмножеством другого.
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера—Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами 
Операции над множествами
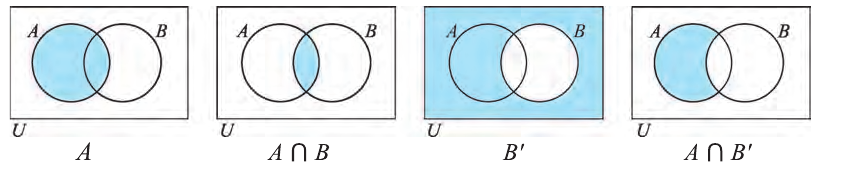
Над множествами можно выполнять определенные действия: пересечение, объединение, находить разность. Дадим определение этих операций и проиллюстрируем их с помощью кругов Эйлера—Венна.
Пересечением множеств 




Пересечение множеств обозначают знаком 
Например, если 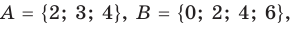
Объединением множеств 




Объединение множеств обозначают знаком 
Например, для множеств 

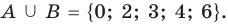
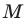
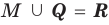
Разностью множеств 



Разность множеств обозначают знаком 
Например, если
Если 



Например, если обозначить множество всех иррациональных чисел через 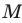
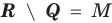
Если все множества, которые мы рассматриваем, являются подмножествами некоторого так называемого универсального множества 
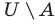
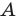
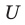
Дополнение множества 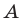
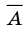
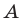
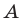
Например, если 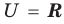
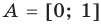
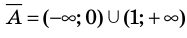
Числовые множества. Множество действительных чисел
Числовые множества:
Действительные числа
Числа, которые можно представить в виде бесконечной десятичной дроби
Рациональные числа
Можно представить в виде несократимой дроби 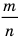
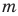
Иррациональные числа
Нельзя представить в виде несократимой дроби 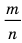
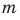
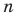
Целые числа
Включают натуральные числа, числа, противоположные им, и число нуль
Дробные числа
Числа, состоящие из целого числа частей единицы
(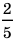
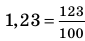
Натуральные числа 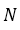
Для школьного курса математики натуральное число — основное не определяемое понятие
Число 0
Такое число, при сложение с которым любое число не изменяется
Целые отрицательные числа
Числа, противоположные натуральным
Модуль действительного числа и его свойства
Определение:
Модулем положительного числа называется само это число, модулем отрицательного числа называется число, противоположное ему, модуль нуля равен нулю
Геометрический смысл модуля
На координатной прямой модуль — это расстояние от начала координат до точки, изображающей это число.
Модуль разности двух чисел 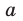
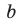
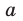
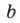
Свойства
1. 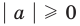
2. 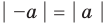
3. 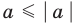
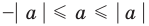
4. При 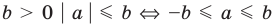
5. При
6. 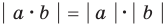
7. 
8. 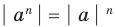
9.
Модуль суммы не превышает суммы модулей слагаемых
10.
Объяснение и обоснование:
Числовые множества
В курсе математики вы встречались с разными числами: натуральными, целыми, рациональными, иррациональными, действительными. Представление о числах у человечества складывалось постепенно, под воздействием требований практики. Например, натуральные числа появились в связи с необходимостью подсчета предметов. Но для того чтобы дать ответ на вопрос «Сколько спичек в пустой коробке из-под спичек?», множества натуральных чисел 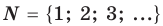
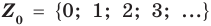
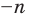
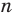
Натуральные числа, числа, противоположные натуральным, и число нуль составляют множество 
Измерение величин привело к необходимости расширения множества целых чисел и введения рациональных чисел. Например, средняя многолетняя температура воздуха в январе в г. Харькове — 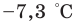
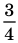
Таким образом, выбирая какую-либо единицу измерения, мы получаем числовое значение величин, которое может выражаться с помощью разных рациональных чисел — целых и дробных, положительных и отрицательных.
Целые и дробные числа составляют множество 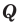
Любое рациональное число можно записать в виде дроби 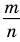
Рациональное число может быть записано разными дробями. Например,
Как видно из приведенных примеров, среди дробей, которые изображают данное рациональное число, всегда есть единственная несократимая дробь (для целых чисел — это дробь, знаменатель которой равен 1).
Обратим внимание, что рациональное число, записанное в виде дроби 
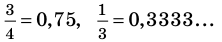
Договоримся, что конечную десятичную дробь можно изображать в виде бесконечной, у которой после последнего десятичного знака, отличного от нуля, на месте следующих десятичных знаков записываются нули, например, 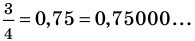
Целые числа также договоримся записывать в виде бесконечной десятичной дроби, у которой справа от запятой на месте десятичных знаков стоят нули, например 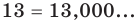
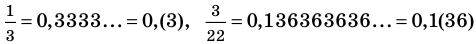
Таким образом, каждое рациональное число может быть записано в виде бесконечной периодической десятичной дроби и наоборот, каждая бесконечная периодическая дробь задает рациональное число.
Обратим внимание, что любая периодическая десятичная дробь с периодом девять равна бесконечной десятичной дроби с периодом нуль, у которой десятичный разряд, предшествующий периоду, увеличен на единицу по сравнению с разрядом первой дроби. Например, бесконечные периодические дроби 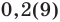
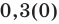
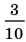
В дальнейшем, записывая рациональные числа с помощью бесконечных периодических десятичных дробей, договоримся исключить из рассмотрения бесконечные периодические дроби, период которых равен девяти.
Каждое рациональное число можно изобразить точкой на координатной прямой (то есть прямой, на которой выбраны начало отсчета, положительное направление и единица измерения). Например, на рисунке изображены несколько рациональных чисел 
Однако на координатной прямой есть точки, изображающие числа, которые не являются рациональными. Например, из курса алгебры известно, что число 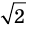
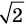
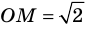
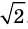
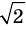
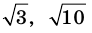
Рациональные и иррациональные числа составляют множество действительных чисел 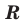
Каждое действительное число может быть записано в виде бесконечной десятичной дроби: рациональные числа — в виде бесконечной периодической десятичной дроби, а иррациональные — в виде бесконечной непериодической десятичной дроби.
Напомним, что для сравнения действительных чисел и выполнения действий над ними (в случае, когда хотя бы одно из них не является рациональным) используются приближенные значения этих чисел. В частности, для сравнения двух действительных чисел последовательно рассматриваем их приближенные значения с недостатком с точностью до целых, десятых, сотых и т. д. до тех пор, пока не получим, что какое-то приближенное значение одного числа больше соответствующего приближенного значения второго. Тогда то число, у которого приближенное значение больше, и считается большим. Например, если
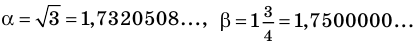
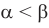
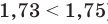
Для выполнения сложения или умножения рассмотренных чисел 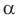
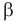
Как видим,
В курсе математического анализа доказывается, что в случае, когда приближенные значения чисел 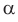
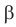
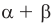
Модуль действительного числа и его свойства
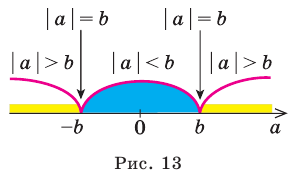
Напомним определение модуля.
Модулем положительного числа называется само это число, модулем отрицательного числа — число, противоположное ему, модуль нуля равен нулю.
Это определение можно коротко записать несколькими способами. а при а > 0,
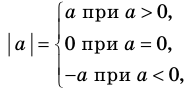
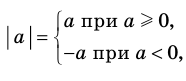
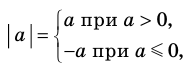
При необходимости мы будем пользоваться любой из этих записей определения модуля. Для нахождения 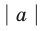
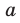
На координатной прямой модуль числа — это расстояние от начала координат до точки, изображающей это число.
Действительно, если 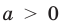
Если 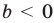
Модуль разности двух чисел 
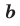
Для доказательства можно воспользоваться тем, что при параллельном переносе вдоль оси координат на 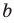
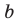
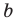
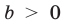
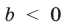

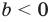
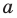
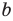
При параллельном переносе вдоль оси 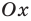
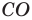
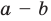
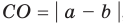
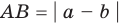
Используя определение модуля и его геометрический смысл, можно обосновать свойства модуля, приведенные в таблице 2.
Например, учитывая, что 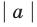
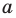
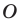
то есть модуль любого числа является неотрицательным числом.
Учитывая, что точки 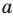
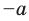
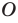
это означает, что модули противоположных чисел равны.
Если 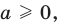
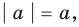
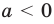
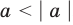
то есть каждое число не превышает его модуль.
Если в последнее неравенство вместо 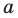
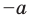
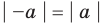
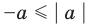
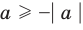
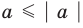

При 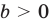

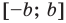
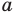
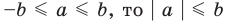
при 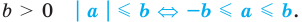
Обратим внимание, что последнее утверждение справедливо и при 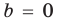
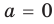
Аналогично при 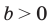
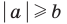
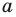
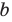
то есть в этом случае 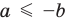
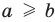
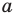
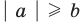

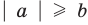

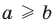
при
Свойства модуля произведения и модуля дроби фиксируют известные правила действий над числами с одинаковыми и разными знаками:
модуль произведения равен произведению модулей множителей, то есть
модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю), то есть
Формулу для нахождения модуля произведения можно обобщить для случая нескольких множителей
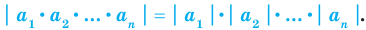
Если в формуле (3) взять 
Используя последнюю формулу справа налево при 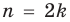
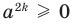
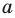
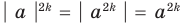
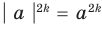
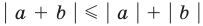
запишем неравенство (1) для чисел 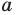
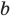
Складывая почленно эти неравенства, получаем
Учитывая неравенство (2), имеем

то есть модуль суммы не превышает суммы модулей слагаемых. Если в неравенстве (4) заменить 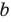
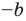
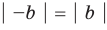
Если записать число 
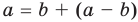
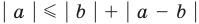

Если в неравенстве (6) заменить 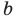
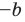
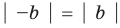

то есть модуль суммы двух чисел не меньше разности их модулей.
Меняя местами буквы 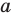
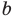
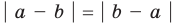

Полученные неравенства (4)-(8) можно коротко записать так:
Примеры решения задач:
Пример №402
Докажите, что сумма, разность, произведение, натуральная степень и частное (если делитель не равен нулю) двух рациональных чисел всегда является рациональным числом.
Решение:
► Пусть заданы два рациональных числа 
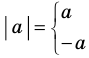
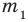
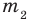
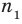
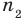
где 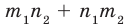
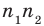
Комментарий:
Любое рациональное число может быть записано как дробь 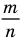
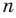
Чтобы доказать утверждение задачи, достаточно доказать, что сумма, разность, произведение и частное двух дробей вида 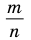
Пример №403
Докажите, что для любого натурального числа 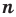
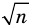
Комментарий:
Для доказательства утверждения задачи можно использовать метод от противного: предположить, что заданное положительное число является рациональным ненатуральным (то есть дробью), и получить противоречие с условием или с каким-либо известным фактом.
Записывая 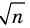
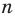
Решение:
► Допустим, что 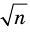
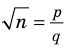
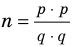
Следовательно, у натуральных множителей, которые стоят в числителе и знаменателе этой дроби, должен быть общий натуральный делитель, отличный от 1. Но в числителе стоят только множители 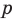
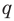

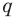
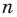
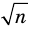
Например, поскольку числа 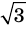
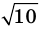
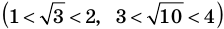
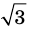
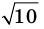
Пример №404
Докажите, что 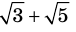
Решение:
► Допустим, что число 
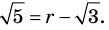
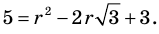
Следовательно,
Но правая часть этого равенства — рациональное число (поскольку по предположению 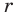
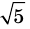
Комментарий:
Для доказательства утверждения задачи можно использовать метод «от противного» — допустить, что заданное число является рациональным, и получить противоречие с каким-либо известным фактом, например с тем, что 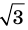
При анализе полученных выражений используем результат задачи 1: если число 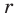
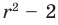
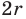
Заметим, что знаменатель полученной дроби
Пример №405
Решите уравнение
Решение
I способ
►
Ответ:
Комментарий:
Заданное уравнение имеет вид 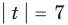
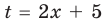
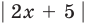
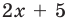
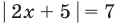
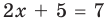
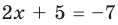
II способ
Ответ:
Комментарий:
С геометрической точки зрения 
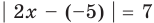
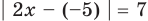
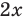
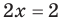
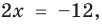
Пример №406
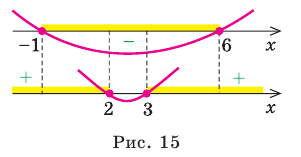
Решите неравенство
Решение:
Решая эти неравенства (рис. 15), получаем
Следовательно, 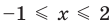
Ответ:
Комментарий:
Заданное неравенство имеет вид 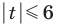
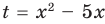
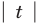
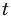
Тогда неравенству 
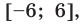
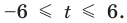
- Рациональные уравнения
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Функции, их свойства и графики
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
Линейная алгебра для разработчиков игр
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
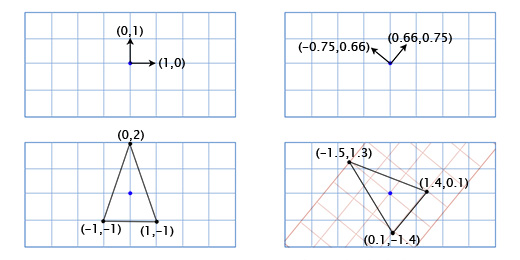
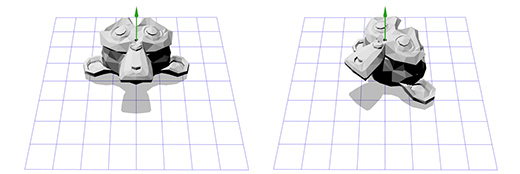
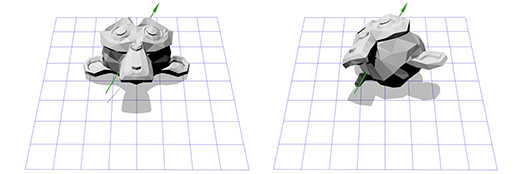
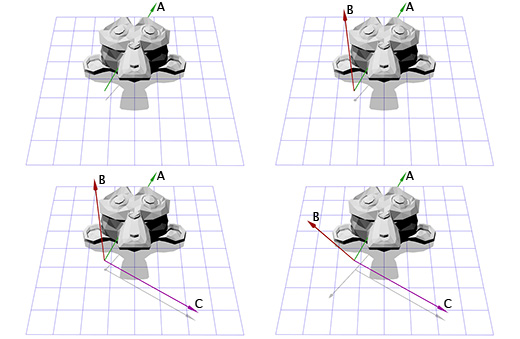
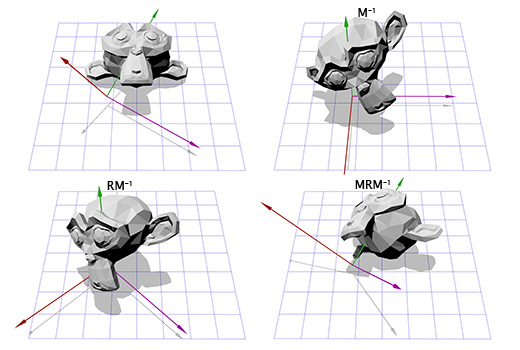
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
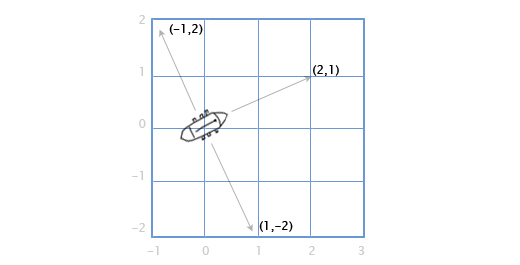
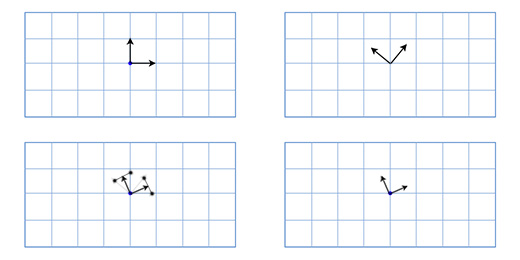
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: 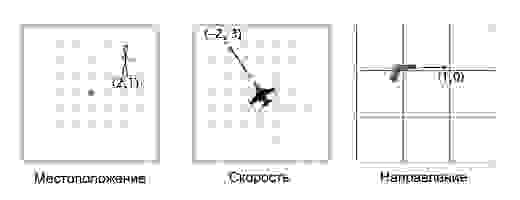
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
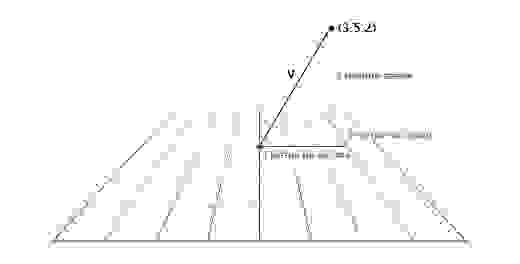
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
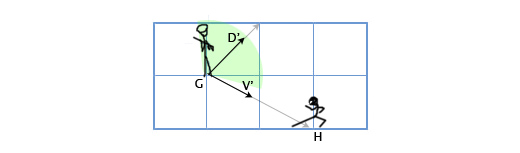
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
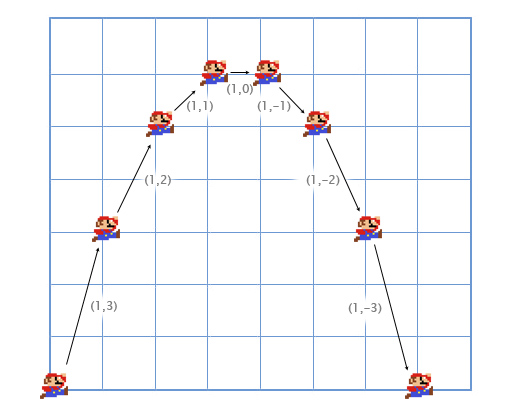
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
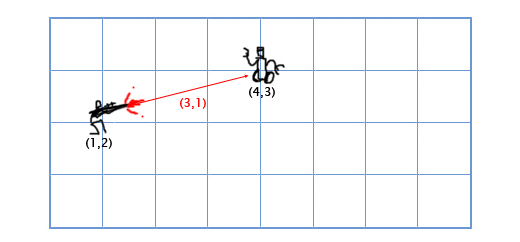
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
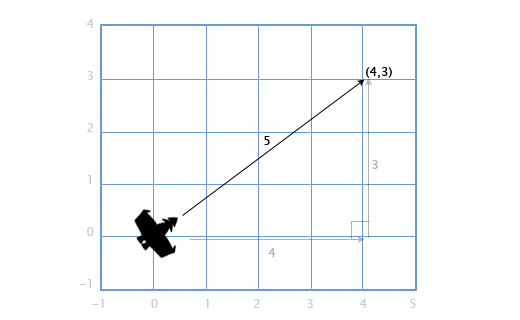
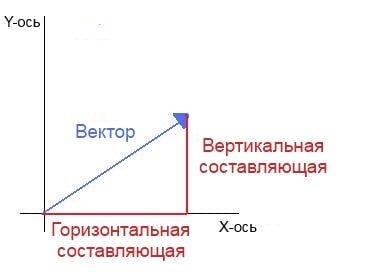
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).
Итак, скорость нашего корабля равна:
|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )
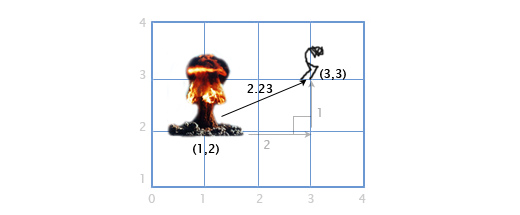
Расстояние
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
Векторное произведение
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
Вот так это выглядит в коде:
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:
Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
Пусть теперь наш корабль выглядит вот так:
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
Будучи записанным по-другому, это выражение выглядит так:
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
И добавляем единицу [1] в вектор, как здесь:
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
Тут показана иллюстрация для каждого шага:
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.
Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).
Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
Координаты и компоненты вектора
По этой ссылке вы найдёте полный курс лекций по математике:
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ох. Оу, Oz (рис. 19). Рассмотрим произвольный вектор а, начало которого лежит в начале координат О, а коней — в точке А. Проведем через точку А плоскости, перпендикулярные .осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Ру Q и R соответственно.
Из рис. 20 видно, что Векторы OP, OQ и OR коллинеарны соответственно единичным векторам i, j, k. поэтому найдутся числа х, у, 2 такие, что и, следовательно, Координаты и компоненты вектора Формула (2) называется разложением вектора и по век/порам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k. Векторы i, j, k попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. с. коэффициенты!, у, z в разложении вектора а по векторам i, j, к определены однозначно.
Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки Л — конца вектора а. Мы пишем в этом случае Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы х, t/j, zk, сумма которых равна вектору а, называются компонентами вектора а.
Возможно вам будут полезны данные страницы:
Из вышеизложенного следует, что два вектора а = и Ь = <х2,у2,22>равны тогда и только тогда, когда соответственно равны их координаты, т. с. Пусть а = <яь yt, zj>, b = <яг, угУ zi>— коллинеарные векторы, причем b Ф 0. Тогда л = цЬ, т.е. Координаты и компоненты вектора Обратно, если выполняются соотношения (3), то п = цЬ, т. е. векторы а и b коллинеарны.
а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны. Пример. Найти координаты вектора MMi, начало которого находится в точке М(х, у, z). а конец — в точке Afi(«2> 22). Из рис. 22 видно, что ММг = Г2 — п, где р,, р2 — радиус-векторы точек М| и Мг соответственно. Поэтому — координаты вектора ММг равны разностям одноименных координат конечной М^ и начальной М точек этого вектора.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Компоненты вектора
Вектор – геометрическое представление величины и направления, выражающиеся стрелками в двух-трех измерениях.
Задача обучения
- Константы двумерных и трехмерных векторов.
Основные пункты
- Векторы разделяются на два компонента: величина и направление.
- Если принимать вектор как гипотенузу, то горизонтальные и вертикальные составляющие можно найти, заполнив треугольник. Нижний край – горизонталь, а противоположная углу сторона – вертикаль.
- Угол, созданный с горизонталью, можно применить для поиска длины двух компонентов.
Термины
- Координаты – числа, указывающие на позицию относительно оси. Например, х и у демонстрируют положение относительно одноименных осей.
- Величина – число вектора, указывающее на его длину.
- Ось – воображаемая линия, вокруг которой объект вращается или расположен симметрично.
Обзор
Вектор – геометрическое отображение величины и направления, которые чаще всего отмечаются прямыми стрелками, начиная с одной точки на координатной оси и заканчивая на другой. Все векторы наделены длиной, при помощи которого один вектор сравнивают с другим. Векторы со стрелками также обладают направлением. Это главное отличие от скаляров, выступающих простыми числами без направления.
Какие есть составляющие вектора? Вектор характеризуется величиной и позицией относительно оси координат. Полезно анализировать векторы, чтобы разложить на составные части. Если мы говорим о двумерных векторах, то это вертикальные и горизонтальные компоненты. В случае с трехмерными все остается прежним, но теперь мы имеем еще одно направление: x, y, z.
Разложение вектора
Чтобы визуально разложить вектор на составляющие, начните с системы координат. Далее проведите прямую линию от оси х и продолжайте ее, пока не выровняется с кончиком вектора. Это горизонтальный компонент. Для поиска вертикального, проведите линию от конца горизонтального вектора, пока не дойдете до кончика вектора. В итоге, получите правильный треугольник, в котором вектор играет роль гипотенузы.
Исходный вектор, определенный относительно множества осей. Горизонтальный компонент простирается от начала вектора и до координаты х. Вертикальный тянется от х к самой вертикальной точке. Вместе формируют правильный треугольник
Разделение на горизонталь и вертикаль – удобный способ разобраться в физической проблеме. Как только замечаете движение под углом, вы обязаны воспринимать его как перемещение по горизонтали и вертикали одновременно. Это помогает намного проще отслеживать движение объектов.
http://natalibrilenova.ru/koordinatyi-i-komponentyi-vektora/
http://v-kosmose.com/fizika/komponentyi-vektora/
Мы занимаемся закупкой трафика из Adwords (рекламная площадка от Google). Одна из регулярных задач в этой области – создание новых баннеров. Тесты показывают, что баннеры теряют эффективность с течением времени, так как пользователи привыкают к баннеру; меняются сезоны и тренды. Кроме того, у нас есть цель захватить разные ниши аудитории, а узко таргетированные баннеры работают лучше.
В связи с выходом в новые страны остро встал вопрос локализации баннеров. Для каждого баннера необходимо создавать версии на разных языках и с разными валютами. Можно просить это делать дизайнеров, но эта ручная работа добавит дополнительную нагрузку на и без того дефицитный ресурс.
Это выглядит как задача, которую несложно автоматизировать. Для этого достаточно сделать программу, которая будет накладывать на болванку баннера локализованную цену на «ценник» и call to action (фразу типа «купить сейчас») на кнопку. Если печать текста на картинке реализовать достаточно просто, то определение положения, куда нужно его поставить — не всегда тривиально. Перчинки добавляет то, что кнопка бывает разных цветов, и немного отличается по форме.
Этому и посвящена статья: как найти указанный объект на картинке? Будут разобраны популярные методы; приведены области применения, особенности, плюсы и минусы. Приведенные методы можно применять и для других целей: разработки программ для камер слежения, автоматизации тестирования UI, и подобных. Описанные трудности можно встретить и в других задачах, а использованные приёмы использовать и для других целей. Например, Canny Edge Detector часто используется для предобработки изображений, а количество ключевых точек (keypoints) можно использовать для оценки визуальной “сложности” изображения.
Надеюсь, что описанные решения пополнят ваш арсенал инструментов и трюков для решения проблем.
Код приведён на Python 3.6 (репозиторий); требуется библиотека OpenCV. От читателя ожидается понимание основ линейной алгебры и computer vision.
Фокусироваться будем на нахождении самой кнопки. Про нахождение ценников будем помнить (так как нахождение прямоугольника можно решить и более простыми способами), но опустим, так как решение будет выглядеть аналогичным образом.
Template matching
Первая же мысль, которая приходит в голову — почему бы просто не взять и найти на картинке регион, который наиболее похож на кнопку в терминах разницы цветов пикселей? Это и делает template matching — метод, основанный на нахождении места на изображении, наиболее похожем на шаблон. “Похожесть” изображения задается определенной метрикой. То есть, шаблон «накладывается» на изображение, и считается расхождение между изображением и и шаблоном. Положение шаблона, при котором это расхождение будет минимальным, и будет означать место искомого объекта.
В качестве метрики можно использовать разные варианты, например — сумма квадратов разниц между шаблоном и картинкой (sum of squared differences, SSD), или использовать кросс-корреляцию (cross-correlation, CCORR). Пусть f и g — изображение и шаблон размерами (k, l) и (m, n) соответственно (каналы цвета пока будем игнорировать); i,j — позиция на изображении, к которой мы «приложили» шаблон.
Попробуем применить разницу квадратов для нахождения котёнка
На картинке
(картинка взята с ресурса PETA Caring for Cats).
Левая картинка — значения метрики похожести места на картинке на шаблон (т.е. значения SSD для разных i,j). Темная область — это и есть место, где разница минимальна. Это и есть указатель на место, которое наиболее похоже на шаблон — на правой картинке это место обведено.
Кросс-корреляция на самом деле является сверткой двух изображений. Свёртки можно реализовать быстро, используя быстрое преобразование Фурье. Согласно теореме о свёртке, после преобразования Фурье свёртка превращается в простое поэлементное умножение:
Где — оператор свёртки. Таким образом мы можем быстро посчитать кросс-корреляцию. Это даёт общую сложность O(kllog(kl)+mnlog(mn)), против O(klmn) при реализации «в лоб». Квадрат разницы также можно реализовать с помощью свёртки, так как после раскрытия скобок он превратится в разницу между суммой квадратов значений пикселей изображения и кросс-корреляции:
Детали можно посмотреть в этой презентации.
Перейдём к реализации. К счастью, коллеги из нижненовгородского отдела Intel позаботились о нас, создав библиотеку OpenCV, в ней уже реализован поиск шаблона с помощью метода matchTemplate (кстати используется именно реализация через FFT, хотя в документации это нигде не упоминается), использующий разные метрики расхождений:
- CV_TM_SQDIFF — сумма квадратов разниц значений пикселей
- CV_TM_SQDIFF_NORMED — сумма квадрат разниц цветов, отнормированная в диапазон 0..1.
- CV_TM_CCORR — сумма поэлементных произведений шаблона и сегмента картинки
- CV_TM_CCORR_NORMED — сумма поэлементных произведений, отнормированное в диапазон -1..1.
- CV_TM_CCOEFF — кросс-коррелация изображений без среднего
- CV_TM_CCOEFF_NORMED — кросс-корреляция между изображениями без среднего, отнормированная в -1..1 (корреляция Пирсона)
Применим их для поиска котёнка:
Видно, что только TM_CCORR не справился со своей задачей. Это вполне объяснимо: так как он представляет собой скалярное произведение, то наибольшее значение этой метрики будет при сравнении шаблона с белым прямоугольником.
Можно заметить, что эти метрики требуют попиксельного соответствия шаблона в искомом изображении. Любое отклонение гаммы, света или размера приведут к тому, что методы не будут работать. Напомню, что это именно наш случай: кнопки могут быть разного размера и разного цвета.
Проблему разного цвета и света можно решить применив фильтр нахождения граней (edge detection filter). Этот метод оставляет лишь информацию о том, в каком месте изображения находились резкие перепады цвета. Примененим Canny Edge Detector (его подробнее разберём чуть дальше) к кнопкам разного цвета и яркости. Слева приведены исходные баннеры, а справа — результат применения фильтра Canny.
В нашей случае, также существует проблема разных размеров, однако она уже была решена. Лог-полярная трансформация преобразует картинку в пространство, в котором изменение масштаба и поворот будут проявляться как смещение. Используя эту трансформацию, мы можем восстановить масштаб и угол. После этого, отмасштабировав и повернув шаблон, можно найти и позицию шаблона на исходной картинке. Во всей этой процедуре также можно использовать FFT, как описано в статье An FFT-Based Technique for Translation, Rotation, and Scale-Invariant Image Registration . В литературе рассматривается случай, когда по горизонтали и вертикали шаблон изменяется пропорционально, и при этом коэффициент масштаба варьируется в небольших пределах (2.0… 0.8). К сожалению, изменение размеров кнопки может быть бо́льшим и непропорциональным, что может привести к некорректному результату.
Применим полученную конструкцию (фильтр Canny, восстановление только масштаба через лог-полярную трансформацию, получение положения через нахождения места с минимальным квадратичным расхождением), для нахождения кнопки на трех картинках. В качестве шаблона будем использовать большую желтую кнопку:
При этом на баннерах кнопки будут разных типов, цветов и размеров:
В случае с изменением размера кнопки метод сработал некорректно. Это связано с тем, что метод предполагает изменение размеров кнопок в одинаковое количество раз и по горизонтали, и по вертикали. Однако, это не всегда так. На правой картинке размер кнопки по вертикали не изменился, а по горизонтали — уменьшился сильно. При слишком большом изменении размера искажения, вызванные логполярным преобразованием, делают поиск нестабильным. В связи с этим метод не смог обнаружить кнопку в третьем случае.
Keypoint detection
Можно попробовать другой подход: давайте вместо того, чтобы искать кнопку целиком, найдём её типичные части, например, углы кнопки, или элементы бордюра (по контуру кнопки есть декоративная обводка). Кажется, что найти углы и бордюр проще, так как это мелкие (а значит, простые) объекты. То, что лежит между четырёх углов и бордюра — и будет кнопкой. Класс методов нахождения ключевых точек называется “keypoint detection”, а алгоритмы сравнения и поиска картинок с помощью ключевых точек — “keypoint matching”. Поиск шаблона на картинке сводится к применению алгоритма обнаружения ключевых точек к шаблону и картинке, и сопоставлению ключевых точек шаблона и картинки.
Обычно “ключевые точки” находят автоматически, находя пиксели, окружение которых которых обладает определёнными свойствами. Было придумано множество способов и критериев их нахождения. Все эти алгоритмы являются эвристиками, которые находят какие-то характерные элементы изображения, как правило — углы или резкие перепады цвета. Хороший детектор должен работать быстро, и быть устойчивым к трансформациям картинки (при изменении картинки ключевые точки не должны переставать находиться/двигаться).
Harris corner detector
Одним из самых базовых алгоритмов считается Harris corner detector. Для картинки (тут и дальше мы считаем, что оперируем “интенсивностью” — изображением, переведенной в grayscale) он пытается найти точки, в окрестностях которых перепады интенсивности больше определенного порога. Алгоритм выглядит так:
-
От интенсивности
находятся производные по оси X и Y (
и
соответственно). Их можно найти, например, применив фильтр Собеля.
-
Для пикселя считаем квадрат
, квадрат
и произведения
и
. Некоторые источники обозначают их как
,
и
— что не добавляет понятности, так как можно подумать, что это вторые производные интенсивности (а это не так).
-
Для каждого пикселя считаем суммы в некой окрестности (больше 1 пикселя) w следующие характеристики:
Как и в Template Detection, эту процедуру для больших окон можно провести эффективно, если использовать теорему о свертке.
-
Для каждого пикселя посчитать значение
эвристики R
Значение
подбирается эмпирически в диапазоне [0.04, 0.06] Если
у какого-то пикселя больше определенного порога, то окрестность
этого пикселя содержит угол, и мы отмечаем его как ключевую точку.
-
Предыдущая формула может создавать кластеры лежащих рядом друг с другом ключевых точек, в таком случае стоит их убрать. Это можно сделать проверив для каждой точки является ли у неё значение
максимальным среди непосредственных соседей. Если нет — то ключевая точка отфильтровывается. Эта процедура называется non-maximum suppression.
Формула
выбрана так неспроста.
— компоненты структурного тензора — матрицы, описывающую поведение градиента в окрестности:
Эта матрица многими свойствами и формой похожа на матрицу ковариации. Например, они обе положительно полуопределённые матрицы, но этим сходство не ограничивается. Напомню, что у матрицы ковариации есть геометрическая интерпретация. Собственные вектора матрицы ковариации указывают на направления наибольшей дисперсии исходных данных (на которых ковариация была посчитана), а собственные числа — на разброс вдоль оси:
Картинка взята из http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/
Точно так же ведут себя и собственные числа структурного тензора: они описывают разброс градиентов. На ровной поверхности собственные числа структурного тензора будут маленькими (потому что разброс самих градиентов будет маленьким). Собственные числа структурного тензора, построенного на кусочке картинки с гранью, будут сильно различаться: одно число будет большим (и соответствовать собственному вектору, направленному перпендикулярно грани), а второе — маленьким. На тензоре угла оба собственных числа будут большие. Исходя из этого, мы можем построить эвристику ( — собственные числа структурного тензора).
Значение этой эвристики будет большое, когда оба собственных числа — большие.
Сумма собственных чисел — это след матрицы, который можно рассчитать как сумму элементов на диагонали (а если взглянуть на формулы A и B, то станет понятно, что это еще и сумма квадратов длин градиентов в области):
Произведение собственных чисел — определитель матрицы, который в случае 2×2 тоже легко выписать:
Таким образом, мы можем эффективно посчитать , выразив её в терминах компонентов структурного тензора.
FAST
Метод Харриса хорош, но существует множество альтернатив ему. Рассматривать так же подробно, как метод выше, все не будем, упомянем лишь несколько популярных, чтобы показать интересные приёмы и сравнить их в действии.
Пиксели, проверяемые алгоритмом FAST
Альтернатива методу Харриса — FAST. Как подсказывает название, FAST работает гораздо быстрее вышеописанного метода. Этот алгоритм пытается найти точки, которые лежат на краях и углах объектах, т.е. в местах перепада контраста. Их нахождение происходит следующим образом: FAST строит вокруг пикселя-кандидата окружность радиуса R, и проверяет, есть ли на ней непрерывный отрезок из пикселей длины t, который темнее (или светлее) пикселя-кандидата на K единиц. Если это условие выполняется, то пиксель считается “ключевой точкой”. При определённых t мы можем реализовать эту эвристику эффективно, добавив несколько предварительных проверок, которые будут отсекать пиксели гарантированно не являющиеся углами. Например, при и
, достаточно проверить, есть ли среди 4 крайних пикселей 3 последовательных, которые строго темнее/светлее центра на K (на картинке — 1, 5, 9, 13). Это условие позволяет эффективно отсечь кандидатов, точно не являющихся ключевыми точками.
SIFT
Оба предыдущих алгоритма не устойчивы к изменениям размера картинки. Они не позволяют найти шаблон на картинке, если масштаб объекта был изменён. SIFT (Scale-invariant feature transform) предлагает решение этой проблемы. Возьмем изображение, из которого извлекаем ключевые точки, и начнём постепенно уменьшать его размер с каким-то небольшим шагом, и для каждого варианта масштаба будем находить ключевые точки. Масштабирование — тяжелая процедура, но уменьшение в 2/4/8/… раз можно провести эффективно, пропуская пиксели (в SIFT эти кратные масштабы называются “октавами”). Промежуточные масштабы можно аппроксимировать, применяя к картинке гауссовский блюр с разным размером ядра. Как мы уже описали выше, это можно сделать вычислительно эффективно. Результат будет похож на то, как если бы мы сначала уменьшили картинку, а потом увеличили ее до исходного размера — мелкие детали теряются, изображение становится “замыленным”.
После этой процедуры посчитаем разницу между соседними масштабами. Большие (по модулю) значения в этой разнице получатся, если какая-то мелкая деталь перестает быть видна на следующем уровне масштаба, или, наоборот, следующий уровень масштаба начинает захватывает какую-то деталь, которая на предыдущем не была видна. Этот прием называется DoG, Difference of Gaussian. Можно считать, что большое значение в этой разнице уже является сигналом того, что в этом месте на изображении есть что-то интересное. Но нас интересует тот масштаб, для которого эта ключевая точка будет наиболее выразительной. Для этого будем считать ключевой точкой не только точку, которая отличается от своего окружения, но и отличается сильнее всего среди разных масштабов изображений. Другими словами, выбирать ключевую точку мы будем не только в пространстве X и Y, а в пространстве . В SIFT это делается путём нахождения точек в DoG (Difference of Gaussians), которые являются локальными максимумами или минимумами в
кубе пространства
вокруг неё:
Алгоритмы нахождения ключевых точек и построения дескрипторов SIFT и SURF запатентованы. То есть, для их коммерческого использования необходимо получать лицензию. Именно поэтому они недоступны из основного пакета opencv, а только из отдельного пакет opencv_contrib. Однако, пока что наше исследование носит исключительно академический характер, поэтому ничто не мешает поучаствовать SIFT в сравнении.
Дескрипторы
Попробуем применить какой-нибудь детектор (например, Харриса) к шаблону и картинке.

После нахождения ключевых точек на картинке и шаблоне надо как-то сопоставить их друг с другом. Напомню, что мы пока извлекли только положения ключевых точек. То, что обозначает эта точка (например, в какую сторону направлен найденный угол), мы пока не определили. А такое описание может помочь при сопоставлении точек изображения и шаблона друг с другом. Часть точек шаблона на картинке может быть сдвинута искажениями, закрыта другими объектами, поэтому опираться исключительно на положение точек относительно друг друга кажется ненадежным. Поэтому давайте для каждой ключевой точки возьмём её окрестность чтобы построить некое описание (дескриптор), которое потом позволит взять пару точек (одну точку из шаблона, одну из картинки), и сравнить их схожесть.
BRIEF
Если мы сделаем дескриптор в виде бинарного массива (т.е. массив из 0 и 1), то мы их сможем сравнивать крайне эффективно, сделав XOR двух дескрипторов, и посчитать количество единичек в результате. Как составить такой вектор? Например, мы можем выбрать N пар точек в окрестности ключевой точки. Затем, для i-й пары проверить, является ли первая точка ярче второй, и если да — то в i-ю позицию дескриптора записать 1. Таким образом мы можем составить массив длины N. Если мы будем выбирать в качестве одной из точек всех пар какую-то одну точку в окрестности (например, центр окрестности — саму ключевую точку), то такой дескриптор будет неустойчивым к шуму: достаточно немного поменяться яркости всего одного пикселя, чтобы весь дескриптор “поехал”. Исследователи обнаружили, что достаточно эффективно выбрать точки случайно (из нормального распределения с центром в ключевой точке). Это положено в основу алгоритма BRIEF.
Часть рассмотренных авторами методов генераций пар. Каждый отрезок символизирует пару сгенерированных точек. Авторы обнаружили, что вариант GII работает чуть лучше остальных вариантов.
После того, как мы выбрали пары, их стоит зафиксировать (т.е. пары генерировать не при каждом запуске расчёта дескриптора, а сгенерировать один раз, и запомнить). В реализации от OpenCV эти пары и вовсе сгенерированы заранее и захардкожены.
Дескриптор SIFT
SIFT также может эффективно считать дескрипторы, используя результаты применения гауссового размытия на разных октавах на картинке. Для расчёта дескриптора SIFT выбирает регион 16х16 вокруг ключевой точки, и разбивает его на блоки 4х4 пикселя. Для каждого пикселя считается градиент (мы оперируем в том же масштабе и октаве, в котором была найдена ключевая точка). Градиенты в каждом блоке распределяются на 8 групп по направлению (вверх, вверх-вправо, вправо, и т.д.). В каждой группе длины градиентов складываются — получается 8 чисел, которые можно представить как вектор, описывающий направление градиентов в блоке. Этот вектор нормируется для устойчивости к изменению яркости. Так, для каждого блока рассчитывается 8-мерный вектор единичной длины. Эти вектора конкатенируются в один большой дескриптор длины 128 (в окрестности 4*4 = 16 блоков, в каждом по 8 значений). Для сравнения дескрипторов используется Евклидово расстояние.
Сравнение
Находя пары наиболее подходящих друг к другу ключевых точек (например — жадно составляя пары, начиная с самых похожих по дескрипторам), мы наконец-таки сможем сравнить шаблон и картинку:
Котик нашелся — но тут у нас имеется попиксельное соответствие между шаблоном и фрагментом картинки. А что будет в случае кнопки?
Предположим, перед нами прямоугольная кнопка. Если ключевая точка расположена на углу, то три четверти локали точки будет именно то, что лежит за пределами кнопки. А то, что лежит за пределами кнопки, сильно меняется от картинки к картинке, в зависимости от того, поверх чего расположена кнопка. Какая доля дескриптора будет оставаться постоянной при изменении фона? В дескрипторе BRIEF, так как координаты пары выбираются в локали случайно и независимо, бит дескриптора будет оставаться постоянным только в случае, когда обе точки лежат на кнопке. Другими словами, в BRIEF всего 1/16 дескриптора не будет меняться. В SIFT ситуация чуть лучше — из-за блочной структуры 1/4 дескриптора меняться не будет.
В связи с этим дальше будем использовать дескриптор SIFT.
Сравнение детекторов
Теперь применим все полученные знания для решения нашей задачи. В нашем случае требования к детектору ключевых точек достаточно: инвариантность к изменению размера нам ни к чему, равно как и крайне высокая производительность. Сравним все три детектора.
| Harris corner detector | FAST | SIFT |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
SIFT нашел крайне мало ключевых точек на кнопке. Это объяснимо — кнопка представляет собой достаточно небольшой и плоский объект, и изменение масштаба не помогает найти ключевые точки.
Также, ни один детектор не справился с третьим случаем. Это объяснимо и ожидаемо. Обычно вышеописанные методы применяют для того, чтобы найти объект из шаблона на снимке, на котором он может быть частично скрыт, быть повернут, или немного искажен. В нашем случае мы хотим найти не точно такой же объект , а объект, достаточно похожий на шаблон (кнопку) . Это немного другая задача. Так, изменение самой формы кнопки (например, радиуса скругления углов, или толщины рамки точек) меняет ключевые точки в них, и их дескрипторы. Кроме того, ключевые точки будут находиться на углу кнопки. Из-за положения на краю точки будут неустойчивы: на их точное расположение и дескрипторы влияет то, что нарисовано рядом с кнопкой.
Вывод — метод хорош, и корректно отрабатывает ситуации, когда искомый объект повернут, его размер изменен, или объект частично скрыт (что хорошо для поиска сложных объектов, или ценника, например). Однако, если на объекте мало точек, за которые можно «зацепиться», или форма объекта меняется слишком сильно, то ключевые точки и их на шаблоне и изображении могут не совпасть. Также, фон с большим количеством мелких деталей может сместить «ключевые точки» или изменить их дескрипторы.
Мы можем придумать матчинг, который бы использовал координаты ключевых точек. Вместо того, чтобы искать пары точек на шаблоне и картинке, окрестность которых похожа, можно искать такие наборы точек, взаимоположение ключевых точек на шаблоне и картинке будут похожи. В общем случае это достаточно сложная (и вычислительно, и с точки зрения программирования) задача, особенно в ситуации, когда некоторые точки могут быть сдвинуты или отсутствовать. Но, учитывая, что у нас ключевые точки — углы, нам достаточно найти такие группы, которые будут примерно образовывать прямоугольник нужных пропорций, и внутри которого не будет ключевых точек. Постепенно мы подходим к следующему методу:
Contour detection
Обычно кнопка — это какой-то прямоугольный объект (иногда — со скруглёнными углами), стороны которого параллельны осям координат. Тогда давайте попробуем выделить зоны перепады контраста (грани/edges), и среди них найдем грани, очертания которых похожи на контур нужного нам объекта. Этот метод называется contour detection.
Edge detection
В отличии от keypoint detection, нам интересны не только ключевые точки-углы, но и рёбра. Однако, основные идеи мы можем взять оттуда. Сгладим изображение Гауссовым фильтром, и как в Harris corner detector. Затем посчитаем производные интенсивности и
. Так как нам не нужно отличать углы от ребер, то не надо считать структурный тензор — достаточно посчитать силу градиента:
(кстати, это корень из
, или из суммы диагонали структурного тензора). После этого, оставим только пиксели, которые являются локальными максимумами в терминах
(используя уже расмотренный non-maximum suppression), но в качестве локали будем выбирать не 8 соседних пикселей, а те пиксели из этих 8, в сторону которого направлен I, и с противоположной стороны:
Синим отмечен рассматриваемый пиксель, стрелка — направление I. Зелёные пиксели — те, которые будут учитываться при non-maximum suppression.
Такой необычный выбор пикселей для сравнения обусловлен тем, что мы не хотим делать разрывы в границе. В левой картинке грань проходит сверху вниз, и так как non-maximum suppression не будет проводить сравнения интенсивности с пикселями выше и ниже синего, мы получим непрерывную грань.
Очевидно, одного non-maximum suppression недостаточно, и надо применить какую-то фильтрацию, чтобы убрать ребра со слишком низким Il. Для этого применим приём “double thresholding”: уберем все пиксели с Il, силой градиента, ниже порога Low, все пиксели выше порога High назначим “сильными ребрами”. Пиксели, у которых сила градиента лежит между Low и High, назовём “слабыми ребрами”, оставим только если они соединены с “сильными ребрами”:
Светло-синим отмечены “слабые ребра”, тёмно-синим — сильные. Ребра в нижней части отсеиваются, так как они не соеденены ни с одним сильным ребром.
Мы только что описали Canny Edge Detector. Он крайне широко применяется и по сей день в качестве простой и быстрой процедуры, позволяющей найти контуры объектов.
Border tracking
Следующее действие — среди карты с найденными гранями выделить контуры. Найдем связанные компоненты (острова смежных пикселей, прошедших все проверки), и проверим каждый из них, насколько он похож на кнопку. После применения non-maximum suppression в Canny, у нас есть гарантии того, что ребра будут получаться толщиной в один пиксель, но давайте на будем на нее опираться. Для каждого пикселя, который был отнесен к грани, и рядом с которым есть пиксель не-грань, отнесем к “бордюру”. Перемещаясь от одного пикселя бордюра к другому, мы либо придём обратно в тот же пиксель (и тогда мы нашли контур), либо в тупик (тогда можно попробовать вернуться назад, если где-то по пути была развилка):
Полный алгоритм border tracking, учитывающий разные краевые случаи (например, когда объект с толстой гранью сгенерировал два контура, внутренний и внешний), описан тут. После применения этого алгоритма у нас останется набор контуров, которые потенциально могут быть кнопками.
Фильтрация контуров
Как узнать, что наш контур — кнопка? Для прямоугольников и многоугольников есть отличный > метод, основанный на упрощении контура. Достаточно постепенно “схлопывать” ребра, если они находятся почти на одной прямой, а затем посчитать количество оставшихся ребер, и проверить углы между ними. К сожалению, для нашего случая эти методы не подходят — наш прямоугольник имеет скругленные углы. Также, есть contour matching для фигур, имеющих сложную геометрию — но это тоже не про нас, так как у нас всего лишь прямоугольник (в статье приводятся примеры с контуром человека). Поэтому лучше сделать фильтр, основанный на свойства самой фигуры. Мы знаем, что:
- Кнопка достаточно большая (площадь больше 100 пикселей)
- Стороны параллельны осям координат
- Отношение площади фигуры к площади ограничивающего прямоугольника должна быть достаточно близка к единице. Мы устанавливаем порог в 0.8, так как кнопка — прямоугольник со сторонами параллельными осям координат, и недостающие 20% — это и есть скругленные углы.
Кроме того, по опыту применения детекторов ключевых точек мы помним, что могут быть проблемы с ситуациями, когда под кнопкой лежит контрастный объект. Поэтому после применения Canny размоем грани, чтобы закрыть мелкие дырки, которые могли возникнуть из-за таких объектов.
Применим получившийся подход:
Применение Canny filter (2 картинка) нашло нужные очертания, но из-за сложной формы кнопки и градиента нашлось сразу много контуров, и из-за non-max suppression некоторые из них не были замкнуты. Применение размытия (3 картинка) исправило проблему.
Тестирование подхода
Запустим в получившейся картинке поиск контуров. Покрасим контуры, прошедшие проверки, красным цветом. Если таких несколько, то нам нужно выбрать среди них наиболее удачный вариант. Выберем контур наибольшей площади, и покрасим его в зелёный цвет.
| 


Получившаяся конструкция нашла кнопки на тестовых изображениях. Прогон на всех баннерах показал, что изредка (1 случай из ~20) она вместо кнопки выделяет прямоугольные плашки iOS Appstore и Google Apps, или другие прямоугольные объекты (чехлы телефонов). Поэтому добавив возможность ручного указания положения на тот редкий случай неверного определения, мы реализовали этот вариант в инструменте локализации.
Заключение
Подведем итоги. “Классический” CV без deep learning по-прежнему работает, и на его основе можно решить задачи. Они неприхотливы и не требуют большого количества размеченных данных, мощного железа, и их проще отлаживать. Однако, они вводят дополнительные предположения, и поэтому с их помощью не каждую задачу можно решить эффективно.
- Template Matching — самый простой способ, основывается на нахождении места в изображении, наиболее похожем (по какой-то простой метрике) на шаблон. Эффективен при попиксельном совпадении. Можно сделать устойчивым к поворотам и небольшим изменениям размеров, но при больших изменениях может работать некорректно.
- Keypoint detection/matching — находим ключевые точки, сопоставляем точки изображения и шаблона. Детекторы устойчивы к поворотам, изменениям масштаба (в зависимости от выбранного детектора и дескриптора), а сопоставление — к частичным перекрытиям. Но этот метод хорошо работает только если в объекте нашлось достаточно «ключевых точек», и локали точки шаблона и изображения совпадают достаточно хорошо (т.е. на шаблоне и картинке — один и тот же объект).
- Contour detection — нахождение контуров объектов, и поиске контура, похожего на контур искомого объекта. Это решение учитывает только форму объекта, и игнорирует его содержимое и цвет (что может быть как и плюсом, так и минусом).
Осведомленный читатель может заметить, что наша задача может быть решена и с помощью современных обучаемых методов computer vision. Например, сеть YOLO возвращает bounding box искомого объекта — а именно это нас и интересует. Да, мы успешно протестировали и запустили решение, основанные на глубоком обучении — но в качестве второй итерации (уже после того, как инструмент локализации был запущен и начал работать). Эти решения более устойчивы к изменениям параметров кнопок, и имеют много положительных свойств: например, вместо того, чтобы подбирать руками пороги и параметры, можно просто добавлять в тренировочное множество примеры баннеров, на которых сеть ошибается (Active Learning). Использование глубокого обучение для нашей задачи имеет свои проблемы и интересные моменты. Например — многие современные методы computer vision требуют большого количества размеченных картинок, а у нас разметки не было (как и во многих реальных случаях), а общее количество разных баннеров не превышает нескольких тысяч. Поэтому мы решили разметить небольшое количество изображений сами, и написать генератор, который будет на их основе создавать другие похожие баннеры. В этом направлении есть немало интересных приёмов. Есть много других подводных камней, да и сама задача определения положения объекта computer vision обширна, и имеет много способов решения. Поэтому было принято решение ограничить поле обзора статьи, и решения, основанные на глубоком обучении, не были рассмотрены.
Код с блокнотами, которые реализуют описанные методы и рисуют картинки статьи, можно найти в репозитории).