Обновлено: 26.05.2023
В процессе общей характеристики физики как основной отрасли естествознания часто употреблялся термин “состояние физической системы”. Рассмотрим его более подробно.
Категория состояния сложилась в античной философии. В науке она впервые нашла широкое применение в ньютоновской механике. Здесь состояние рассматривалось как количественная характеристика механического движения. Значение механики Ньютона для физики далеко не в последнюю очередь определяется именно тем, что Ньютон первым понял: состояние систем материальных точек в любой заданный момент времениt полностью определяется значением их координат и импульсов (а не ускорениями, взаимодействиями и т.д.). Зная эти величины в момент t, можно определить эволюцию системы под влиянием известных сил во все последующие моменты времени, решив систему уравнений Ньютона:
Представим себе тело, которое с точки зрения физики можно назвать макроскопическим. Это может быть газ в сосуде, песчинка, кусочек железа и т.д. Другими словами — это любое тело, состоящее из очень большого числа частиц.
На протяжении более 200 лет считалось, что механика Ньютона описывает перемещение тел любых размеров, т.е. любых размеров масс друг относительно друга. Но с этими телами происходят и другие изменения, не связанные с их макроскопическими перемещениями. В первую очередь, это тепловые процессы. Тела могут нагреваться и остывать. При этом их температура меняется.
Температура — очень важная характеристика состояния тел. Ее изменения могут вызывать изменения тел гораздо более существенные, чем простые перемещения из одной области пространства в другую. Так, газ может превратиться в жидкость, жидкость — в твердое тело (или наоборот), и т.д.
Подобного рода процессы описываются термодинамикой. Эта наука возникла вслед за классической механикой. Термодинамика изучает тепловые свойства макроскопических систем, не обращаясь к их микроскопическому состоянию.
Состояние тел может меняться не только с изменением температуры. Так, макроскопические свойства куска железа изменяются, если его намагнитить. Соответственно вводится величина, характеризующая магнитное состояние образца – вектор намагничивания.
Электрическое поле также изменяет состояние макроскопического тела (оно поляризуется).
Итак, классическая физика считала, что состояние физической системы всегда задается физическими параметрами. Это, например, координата, импульс, температура, вектор намагничивания и т.д. Состояние системы — это значение таких параметров системы в определенный момент времени, которые позволяют решать определенные классы задач по отношению к данной системе. Бессмысленно задавать состояние физической системы безотносительно к классу поставленных по отношению к системе задач. Какие именно параметры характеризуют конкретное состояние системы определяется законами, на основании которых и решаются поставленные задачи.
Любая система может быть описана лишь с какой-то степенью приближения. Это касается и набора параметров, задающих состояние системы, и значения параметров, которые всегда, конечно, приближенны. Другими словами, всегда существует разница между истинным состоянием системы и описанием этого состояния.
Всевозможные состояния, в которых может находиться то или иное вещество, прежде всего, разбиваются на так называемые агрегатные состояния: твердое, жидкое и газообразное. Эти состояния выделяются по основным физическим свойствам вещества.
Следует учесть, что у некоторых веществ нет резкой границы между различными агрегатными состояниями. Например, при нагревании стекла происходит постепенное его размягчение, и невозможно установить, когда оно переходит из твердого состояния в жидкое. При очень большом внешнем давления твердые металлы начинают “течь”, т.е. подобно жидкости, принимают форму сосуда, в котором они находятся.
Различные состояния одного и того же вещества можно отличать друг от друга также и по значениям физических величин, которые характеризуют эти состояния, например, по значениям объема, температуры и давления. Поэтому каждому агрегатному состоянию вещества соответствует бесконечное множество различных состояний, которые отличаются друг от друга различными значениями объема, давления, температуры и других физических величин. При изменении этих величин вещество переходит из одного состояния в другое, оставаясь твердым, жидким или газообразным.
Физические величины, характеризующие то или иное состояние вещества, иногда называют параметрами состояния. Основные параметры: объем V, внешнее давление Р и температура Т. Если между параметрами состояния существует какое-нибудь определенное однозначное соотношение, которое сохраняется при переходе из одного состояния в другое, то это соотношение называется уравнением состояния. Например, для разряженных газов соблюдается уравнение:
Это соотношение связывает между собой значения объема, давления и температуры для множества отличающихся друг от друга состояний данной массы газообразного вещества. Для других агрегатных состояний — твердого и жидкого — такие простые соотношения между параметрами не найдены.
В физике широко используется понятие стационарного состояния. Состояние физической системы, при котором некоторые существенные для характеристики системы величины не меняются со временем называется стационарным. Например, состояние потока жидкости стационарно, если скорость движения (и другие характеристики) остаются в каждой точке пространства неизменными.
В квантовой механике стационарным состоянием называется состояние, в котором энергия имеет определенное значение.
Состояния микрообъектов методами классической физики описать нельзя. Это очевидно хотя бы из соотношения неопределенностей. Принцип неопределенности, установленный В. Гейзенбергом в 1927 г., записывается так:
где выступает как неточность (неопределенность) значения координаты х частицы;
– как неопределенность компоненты Px ее импульса .
Принцип неопределенностей подчеркивает различие в описании состояния систем в классической и в квантовой теории. Мы уже неоднократно подчеркивали, что состояние классической материальной точки описывается с помощью координат и импульса. Квантовая же частица в состоянии с определенными координатами не обладает определенным импульсом. Иными словами, для квантовой частицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точное значение. Поэтому в квантовой теории состояние микрообъектов, как уже подчеркивалось, описывается принципиально по-новому – с помощью волновой функции.
В процессе общей характеристики физики как основной отрасли естествознания часто употреблялся термин “состояние физической системы”. Рассмотрим его более подробно.
Категория состояния сложилась в античной философии. В науке она впервые нашла широкое применение в ньютоновской механике. Здесь состояние рассматривалось как количественная характеристика механического движения. Значение механики Ньютона для физики далеко не в последнюю очередь определяется именно тем, что Ньютон первым понял: состояние систем материальных точек в любой заданный момент времениt полностью определяется значением их координат и импульсов (а не ускорениями, взаимодействиями и т.д.). Зная эти величины в момент t, можно определить эволюцию системы под влиянием известных сил во все последующие моменты времени, решив систему уравнений Ньютона:
Представим себе тело, которое с точки зрения физики можно назвать макроскопическим. Это может быть газ в сосуде, песчинка, кусочек железа и т.д. Другими словами — это любое тело, состоящее из очень большого числа частиц.
На протяжении более 200 лет считалось, что механика Ньютона описывает перемещение тел любых размеров, т.е. любых размеров масс друг относительно друга. Но с этими телами происходят и другие изменения, не связанные с их макроскопическими перемещениями. В первую очередь, это тепловые процессы. Тела могут нагреваться и остывать. При этом их температура меняется.
Температура — очень важная характеристика состояния тел. Ее изменения могут вызывать изменения тел гораздо более существенные, чем простые перемещения из одной области пространства в другую. Так, газ может превратиться в жидкость, жидкость — в твердое тело (или наоборот), и т.д.
Подобного рода процессы описываются термодинамикой. Эта наука возникла вслед за классической механикой. Термодинамика изучает тепловые свойства макроскопических систем, не обращаясь к их микроскопическому состоянию.
Состояние тел может меняться не только с изменением температуры. Так, макроскопические свойства куска железа изменяются, если его намагнитить. Соответственно вводится величина, характеризующая магнитное состояние образца – вектор намагничивания.
Электрическое поле также изменяет состояние макроскопического тела (оно поляризуется).
Итак, классическая физика считала, что состояние физической системы всегда задается физическими параметрами. Это, например, координата, импульс, температура, вектор намагничивания и т.д. Состояние системы — это значение таких параметров системы в определенный момент времени, которые позволяют решать определенные классы задач по отношению к данной системе. Бессмысленно задавать состояние физической системы безотносительно к классу поставленных по отношению к системе задач. Какие именно параметры характеризуют конкретное состояние системы определяется законами, на основании которых и решаются поставленные задачи.
Любая система может быть описана лишь с какой-то степенью приближения. Это касается и набора параметров, задающих состояние системы, и значения параметров, которые всегда, конечно, приближенны. Другими словами, всегда существует разница между истинным состоянием системы и описанием этого состояния.
Всевозможные состояния, в которых может находиться то или иное вещество, прежде всего, разбиваются на так называемые агрегатные состояния: твердое, жидкое и газообразное. Эти состояния выделяются по основным физическим свойствам вещества.
Следует учесть, что у некоторых веществ нет резкой границы между различными агрегатными состояниями. Например, при нагревании стекла происходит постепенное его размягчение, и невозможно установить, когда оно переходит из твердого состояния в жидкое. При очень большом внешнем давления твердые металлы начинают “течь”, т.е. подобно жидкости, принимают форму сосуда, в котором они находятся.
Различные состояния одного и того же вещества можно отличать друг от друга также и по значениям физических величин, которые характеризуют эти состояния, например, по значениям объема, температуры и давления. Поэтому каждому агрегатному состоянию вещества соответствует бесконечное множество различных состояний, которые отличаются друг от друга различными значениями объема, давления, температуры и других физических величин. При изменении этих величин вещество переходит из одного состояния в другое, оставаясь твердым, жидким или газообразным.
Физические величины, характеризующие то или иное состояние вещества, иногда называют параметрами состояния. Основные параметры: объем V, внешнее давление Р и температура Т. Если между параметрами состояния существует какое-нибудь определенное однозначное соотношение, которое сохраняется при переходе из одного состояния в другое, то это соотношение называется уравнением состояния. Например, для разряженных газов соблюдается уравнение:
Это соотношение связывает между собой значения объема, давления и температуры для множества отличающихся друг от друга состояний данной массы газообразного вещества. Для других агрегатных состояний — твердого и жидкого — такие простые соотношения между параметрами не найдены.
В физике широко используется понятие стационарного состояния. Состояние физической системы, при котором некоторые существенные для характеристики системы величины не меняются со временем называется стационарным. Например, состояние потока жидкости стационарно, если скорость движения (и другие характеристики) остаются в каждой точке пространства неизменными.
В квантовой механике стационарным состоянием называется состояние, в котором энергия имеет определенное значение.
Состояния микрообъектов методами классической физики описать нельзя. Это очевидно хотя бы из соотношения неопределенностей. Принцип неопределенности, установленный В. Гейзенбергом в 1927 г., записывается так:
где выступает как неточность (неопределенность) значения координаты х частицы;
– как неопределенность компоненты Px ее импульса .
Принцип неопределенностей подчеркивает различие в описании состояния систем в классической и в квантовой теории. Мы уже неоднократно подчеркивали, что состояние классической материальной точки описывается с помощью координат и импульса. Квантовая же частица в состоянии с определенными координатами не обладает определенным импульсом. Иными словами, для квантовой частицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точное значение. Поэтому в квантовой теории состояние микрообъектов, как уже подчеркивалось, описывается принципиально по-новому – с помощью волновой функции.
Кратко о 1 законе Ньютона: формула, определение и формулировка
Помни.
- В основе динамики материальной точки лежат три закона Ньютона.
- Первый закон Ньютона — закон инерции
- Под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.
1. Формулировка
2. Определение
Первый закон Ньютона — всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.
Первый закон Ньютона — закон инерции (Галилей вывел закон инерции)
Закон инерции: Если на тело нет внешних воздействий, то данное тело сохраняет состояние покоя или равномерного прямолинейного движения относительно Земли.
Инерциальная система отсчёта (ИСО) – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Т.е. система отсчета, в которой выполняется 1-й закон Ньютона.
- Масса тела – количественная мера его инертности. В СИ она измеряется в килограммах.
- Сила – количественная мера взаимодействия тел. Сила – векторная величина и измеряется в ньютонах (Н). Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.
3. Формула
Формулы нет. Формула первого закона Ньютона не существует.
- Состояние покоя, или гипобиоз, — состояние пониженной функциональной активности живых организмов, обусловлен факторами среды (низкой и высокой температурой, отсутствием влаги и т. д.), при сохранении их высокой жизнеспособности.
После восстановления нормальных условий для существования организмов возобновляется активная деятельность всех его функциональных систем. Эти адаптационные приспособления к условиям окружающей среды растений и животных, заложены в анатомо-физиологической, молекулярно-генетической и биохимической особенностях строения.
Понятие гипобиоз применяют как обобщающий термин для таких явлений, как гипотермия, спячка, диапауза и т. д. Глубокий гипобиоз может перейти в анабиоз. Различают естественный гипобиоз — состояние, наблюдаемое при определённых условиях у различных животных и искусственный — применяют в экспериментальной биологии и различных областях хирургии.
Связанные понятия
Экологи́ческие фа́кторы — свойства среды обитания, оказывающие какое-либо воздействие на организм. Например, наличие минеральных веществ, доступ кислорода, влажность почвы, температура почвы, рыхлость почвы. Индифферентные элементы среды, например инертные газы, экологическими факторами не являются.
Биоиндикация — оценка качества природной среды по состоянию её биоты. Биоиндикация основана на наблюдении за составом и численностью видов-индикаторов.
Реактивность организма — свойство организма как целого отвечать изменениями жизнедеятельности на воздействия окружающей среды, представляющее собой такое же важное свойство всего живого, как обмен веществ, рост, размножение и др.
Упоминания в литературе
Главное воздействие двигательная активность оказывает на кардио-респираторную систему человеческого организма. Сердце нетренированного человека, за одно сокращение в состоянии покоя выталкивает в аорту до 70 мл крови, то есть за минуту 3,5–5 литров. Систематические тренировки способствуют увеличению этого показателя до 110 мл, а при тяжелых физических нагрузках цифра возрастает до 200 мл и более. Это развивает резервную мощь сердца. Наблюдается увеличение просвета сосудов и плотности капилляров вместе со снижением реактивности миокарда на действие стрессоров. Все описанные изменения служат проявлением биохимической адаптации организма к новой, более интенсивной или более длительной мышечной работе. Результат такой адаптации организма, происходящей в организме – повышение его работоспособности.
Мышечная деятельность вызывает целый ряд морфологических, физиологических, функциональных биохимических изменений в организме. Это обеспечивает наиболее рациональный способ функционирования микроциркуляторной системы в организме тренированных лиц при физических нагрузках. Под влиянием систематической тренировки происходит экономизация мышечного кровотока, выражающаяся в том, что его интенсивность в состоянии покоя снижается: это создает возможность усиления кровотока в мышце под влиянием физической нагрузки и соответствующего повышения доставки кислорода, а также изменением обмена мышечной ткани.
В состоянии покоя у человека при адаптации кусловиям Севера обнаружена существенная утилизация свободных жирных кислот, особенно после дозированной скелетномышечной нагрузки. В этой связи и происходит сдвиг липопротеидного спектра в сторону липопротеидов высокой плотности. Наряду с увеличением липидного обмена, при адаптации кусловиям Севера, наблюдается торможение углеводного обмена (ингибирование гексокиназы). При этом возникает дефицит водорастворимых витаминов В1 и В2, что, однако, не сопровождается развитием типичной клинической картины гиповитаминоза.
Косвенные показатели работоспособности делятся на показатели текущего функционального состояния организма и его резервных возможностей. Первые можно регистрировать объективно в состоянии покоя или в процессе деятельности путем физиологических, психологических, биохимических и других измерений, а также субъективно – путем беседы, заполнения анкет, опросников и т. п. Показатели резервных возможностей организма определяются при проведении функциональных нагрузочных проб, которые характеризуют, в первую очередь, степень напряжения и уровень компенсаторных возможностей различных систем организма при выполнении дополнительных задач на фоне основной деятельности, введении отказов техники в ходе выполнения задания на тренажере и т. п.
Связанные понятия (продолжение)
Жизнедеятельность — совокупность процессов, протекающих в живом организме, служащих поддержанию в нём жизни и являющихся проявлениями жизни.
Гомотоксикология — вид альтернативной медицины, основоположником которого является Ганс-Генрих Рекевег; разновидность гомеопатии, в которой применение гомеопатических средств основывается на теории о гомотоксинах как о причине развития и прогрессирования заболеваний.
Метод краниоцеребральной гипотермии (КЦГ) предполагает понижение температуры мозга теплокровных животных и человека из-за преобладания теплоотдачи над теплопродукцией, то есть искусственное охлаждение головного мозга через наружные покровы головы при помощи специального аппарата. Название происходит от гипо. и греч. therme — тепло (охлаждение).
Акклиматиза́ция (от лат. ac (ad) — к, для и др.-греч. κλίμα — климат) — приспособление организмов к новым условиям существования после территориального, искусственного или естественного перемещения с образованием стабильных воспроизводящихся групп организмов (популяций); частным случаем акклиматизации является реакклиматизация — приспособление организмов к местности, из которой они по каким-либо причинам исчезли. Естественная акклиматизация, как правило, обусловлена случайными причинами (заносы семян.
Тератогенное действие (от греч. τέρατος, род. п. от греч. τέρας — чудовище, урод; и др.-греч. γεννάω — рождаю) — нарушение эмбрионального развития под воздействием тератогенных факторов — некоторых физических, химических (в том числе лекарственных препаратов) и биологических агентов (например, вирусов) с возникновением морфологических аномалий и пороков развития.
Биологическая адаптация (от лат. adaptatio — приспособление) — приспособление организма к внешним условиям в процессе эволюции, включая морфофизиологическую и поведенческую составляющие. Адаптация может обеспечивать выживаемость в условиях конкретного местообитания, устойчивость к воздействию факторов абиотического и биологического характера, а также успех в конкуренции с другими видами, популяциями, особями. Каждый вид имеет собственную способность к адаптации, ограниченную физиологией (индивидуальная.
‘Физи́ческое разви́тие — динамический процесс роста (увеличение длины и массы тела, развитие органов и систем организма и так далее) и биологического созревания ребёнка в определённом периоде детства. Процесс развития совокупности морфологических и функциональных свойств организма (скорость роста, прирост массы тела, определённая последовательность увеличения различных частей организма и их пропорций, а также созревание различных органов и систем на определённом этапе развития), в основном запрограммированных.
Криоконсерва́ция (от греч. κρύος — холод и лат. conservo — сохраняю) — низкотемпературное хранение живых биологических объектов с возможностью восстановления их биологических функций после размораживания.
Биоритмы подразделяются на физиологические и экологические. Физиологические ритмы, как правило, имеют периоды от долей секунды до нескольких минут. Это, например, ритмы давления, биения сердца и артериального давления. Экологические ритмы по длительности совпадают с каким-либо естественным ритмом окружающей среды.
Модулированная электрогипертермия или Онкотермия (oncothermia) — метод лечения солидных злокачественных опухолей путём локального воздействия высокочастотного электромагнитного поля (13.56 МГц), модулированного фрактальными гармоническими колебаниями в диапазоне частот 0-5 кГц, посредством импедансно-сопряженных, функционально асимметричных электродов.
Преде́льно допусти́мая концентра́ция (ПДК) — утверждённый в законодательном порядке санитарно-гигиенический норматив. Под ПДК понимается такая максимальная концентрация химических элементов и их соединений в окружающей среде, которая при повседневном влиянии в течение длительного времени на организм человека не вызывает патологических изменений или заболеваний, устанавливаемых современными методами исследований, в любые сроки жизни настоящего и последующего поколений.
Физиоло́гия челове́ка и живо́тных (от греч. φύσις — природа, греч. λόγος — учение) — это наука о функциональной активности животных организмов, в том числе и человека, использующая для её изучения и объяснения методы и понятия биологии, физики, химии, математики и кибернетики.
Физиоло́гия (от др.-греч. φύσις — природа и λόγος — слово) — наука о сущности живого, жизни в норме и при патологиях, то есть о закономерностях функционирования и регуляции биологических систем разного уровня организации, о пределах нормы жизненных процессов и болезненных отклонений от неё (см. патофизиология).
Терморегуля́ция — способность живых организмов поддерживать температуру тела в определённых границах, даже если температура внешней среды значительно отличается.
Старение — в биологии процесс постепенного нарушения и потери важных функций организма или его частей, в частности способности к размножению и регенерации. Вследствие старения организм становится менее приспособленным к условиям окружающей среды, уменьшает и теряет свою способность бороться с хищниками и противостоять болезням и травмам.
Фено́мика — функциональное направление генетики, посвящённое изучению фенома, представляющего набор фенотипических черт индивида в виде норм реакций систем его организма. Феном описывается структурой органов и систем живых организмов учитывающей направленность их взаимодействия между собой на уровне функциональной активности в процессе адаптации к воздействиям внешней среды.
Синтетический морфогенез (англ. synthetic morphogenesis) — контролируемое развитие органов, систем и частей тела организмов посредством активации специфических молекулярных механизмов, включая создание программируемых тканей и органов, синтетических биоматериалов и программируемого живого вещества, а также de novo инженерии сложных морфогенных систем.
Электрическая активность кожи (ЭАК), ранее именовалась как кожно-гальваническая реакция (КГР) — биоэлектрическая реакция, которая регистрируется с поверхности кожи, показатель активности вегетативной нервной системы, широко применяемый в психофизиологии.
Биотехноло́гия — дисциплина, изучающая возможности использования живых организмов, их систем или продуктов их жизнедеятельности для решения технологических задач, а также возможности создания живых организмов с необходимыми свойствами методом генной инженерии.
Закон оптимума (в экологии) — любой экологический фактор имеет определённые пределы положительного влияния на живые организмы.
Экосисте́ма, или экологи́ческая систе́ма (от др.-греч. οἶκος — жилище, местопребывание и σύστημα — система) — биологическая система (биогеоценоз), состоящая из сообщества живых организмов (биоценоз), среды их обитания (биотоп), системы связей, осуществляющей обмен веществом и энергией между ними. Одно из основных понятий экологии.
Гелиобиоло́гия — раздел биофизики, изучающий влияние изменений активности Солнца на земные организмы.
Уровни организации жизни — иерархически соподчинённые уровни организации биосистем, отражающие уровни их усложнения. Чаще всего выделяют семь основных структурных уровней жизни.
Терапевтический ангиогенез (называемый также биологическим шунтированием) — тактика стимуляции образования новых кровеносных сосудов для лечения или профилактики патологических состояний, характеризующихся снижением этой функции.
Радиобиологические эффекты — функциональные и морфологические изменения, развивающиеся в организме в результате воздействия на него излучения. Биологические эффекты ионизирующих излучений различны, и зависят от вида и интенсивности облучения. Биологические эффекты различных излучений изучаются радиобиологией.
Генетика развития растений (биология развития растений) — частная отрасль генетики, изучающая особенности развития растений, гены, экспрессирующиеся и обеспечивающие нормальное формирование и функционирование тканей и органов растений.
Биологическая обратная связь (англ. biofeedback) — технология, включающая в себя комплекс исследовательских, немедицинских, физиологических, профилактических и лечебных процедур, в ходе которых человеку посредством внешней цепи обратной связи, организованной преимущественно с помощью микропроцессорной или компьютерной техники, предъявляется информация о состоянии и изменении тех или иных собственных физиологических процессов.
Питательная среда для эмбрионов (культуральная среда для эмбрионов) – водный раствор сложного состава для содержания ранних (преимплантационных) эмбрионов млекопитающих (в том числе человека) в культуре in vitro.
Микрополяризация (англ. Transcranial direct current stimulation) — лечебный метод, позволяющий изменять функциональное состояние различных звеньев ЦНС под действием малого постоянного тока (до 1 мА).ТКМП (транскраниальная микрополяризация) и ТВМП (трансвертебральная микрополяризация) сочетают неинвазивность традиционных физиотерапевтических процедур с некоторой степенью избирательности воздействия, характерной в высокой степени для стимуляции через интрацеребральные электроды.Культивируется в основном.
Тяжесть труда — характеристика трудовой деятельности, определяемая степенью совокупного воздействия всех элементов условий труда на функциональное состояние человека — его работоспособность, состояние здоровья и процесс воспроизводства рабочей силы. Все многообразие работ по степени Т. т. ученые сводят в три основных класса: нормальный, пограничный (переходнй между нормальным и патологическим) и патологический. Внутри этой классификации все работы по их тяжести делятся на шесть более детальных групп.
Госсипо́л — природный полифенол, жёлтый пигмент, получаемый из хлопчатника (лат. Gossypium), ингибитор ряда ферментов-дегидрогеназ.
ТЭС-терапия — метод лечения с помощью неинвазивной тра́нскраниальной (trans, лат. — через; cranium, лат. — череп) электрической стимуляции. Является физиотерапевтическим методом. На рынок готовятся выйти модуляторы настроения, основанные на принципах электростимуляции.
Ветеринарная психоневрология — новая, развивающаяся с начала 2000-х гг. отрасль ветеринарной медицины, изучающая деятельность нервной системы как единого целого (в отличие от неврологии), её управляющую и регулирующую роль в организме, а также взаимосвязи между процессами в нервной системе и других системах организма. Дисциплина возникла на стыке зоопсихологии и неврологии, откуда и получила своё название.
Биома́ркер — характеристика (биологический признак), которая используется в качестве индикатора состояния всего организма.
Боле́знь (лат. morbus) — это состояние организма, выраженное в нарушении его нормальной жизнедеятельности, продолжительности жизни, и его способности поддерживать свой гомеостаз. Является следствием ограниченных энергетических и функциональных возможностей живой системы в ее противостоянии патогенным факторам.
Упоминания в литературе (продолжение)
Обмен веществ непостоянен, он меняется в зависимости от условий среды обитания. Когда требуется больше энергии, например при тяжелых нагрузках или на холоде, его интенсивность возрастает, а в состоянии покоя , наоборот, падает. У детей уровень обмена веществ выше, чем у взрослых, что обусловлено потребностями роста и развития. В пожилом возрасте скорость метаболизма несколько снижается.
Несколько сложнее проблема верификации представляется в отношении ИБС. Скрининговым методом диагностики и оценки коронарной недостаточности пока остается электрокардиография (ЭКГ), хотя известно, что в состоянии покоя этот метод далеко не всегда позволяет выявить ишемию миокарда и другие признаки патологии сердца. У лиц, без клинических проявлений коронарной недостаточности, ЭКГ имеет малую чувствительность1. Другими словами, нормальные результаты исследования в покое не исключают ИБС, а у половины больных заболевание протекает без выраженных клинических симптомов. Между тем в старших возрастных группах распространенность стенокардии достигает 20 % популяции1,2. С учетом того, что только у части больных заболевание проявляется клиническими признаками, достаточными для обращения к врачу, эту цифру можно смело увеличить вдвое. Еще меньше информации врачи получают о количестве больных с цереброваскулярной недостаточностью. Если стенокардия, как правило, проявляется яркими клиническими признаками, то недостаточность мозгового кровообращения часто остается незамеченной, вплоть до развития острого нарушения мозгового кровообращения или признаков грубых диффузных повреждений.
Успокаивающее влияние бега на организм усиливается действием гормонов гипофиза (эндорфинов), которые выделяются в кровь в процессе упражнений на выносливость. При интенсивной тренировке их содержание в крови возрастает в 5 раз по сравнению с уровнем состояния покоя и удерживается в повышенной концентрации в течение нескольких часов. Эндорфины вызывают состояние своеобразной эйфории, ощущение радости, физического и психического благополучия, подавляют чувство голода и боли, в результате чего резко улучшается настроение. Психиатры широко используют циклические упражнения при лечении депрессивных состояний – независимо от их причины. Согласно данным К. Купера (1989), полученным в Далласском центре аэробики, большинство людей, пробегающих за время тренировки 5 км, испытывают состояние эйфории во время и после ФН, что является ведущей мотивацией для занятий оздоровительным бегом.
Вибрация – механические колебания материальных точек или тел. Под вибрацией понимается движение точки или механической системы, при которой происходят поочередные возрастание и убывание во времени значений по крайней мере одной координаты. Самый простой вид вибрации – это колебание, или повторяющееся движение объекта около положения равновесия. Этот тип вибрации называется общей вибрацией, потому что тело перемещается как единое целое, все его части имеют одинаковую по величине и направлению скорость. Положением равновесия называют такое положение, в котором тело находится в состоянии покоя , или положение, которое оно займет, если сумма действующих на него сил равна нулю. Колебательное движение твердого тела может быть полностью описано в виде комбинации шести простейших типов движения: поступательного в трех взаимно перпендикулярных направлениях (x, у, z в декартовых координатах) и вращательного относительно трех взаимно перпендикулярных осей (OX, OY, OZ). Любое сложное перемещение тела можно разложить на эти шесть составляющих.
Вот беда: велосипедист наезжает на камень и падает с велосипеда. Или наездник слетает с лошади, если та резко остановилась. Почему так происходит, помогает понять такое явление, как инерция.
О чем эта статья:
Понятие инерция в формулировках Галилея и Ньютона
Галилео Галилей и Исаак Ньютон внесли свой вклад в развитие такого раздела физики, как механика. Неудивительно, что каждый из них предложил свою формулировку.
Галилео Галилей
Исаак Ньютон
Формулировка закона инерции
Когда тело движется по горизонтальной поверхности, не встречая никакого сопротивления движению, то его движение — равномерно, и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца.
Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние.
Инерция — это физическое явление, при котором тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела.
Инерция – это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано.
Варианты формулировки не противоречат друг другу и говорят по сути об одном и том же, просто разными словами — выбирайте ту, что вам нравится больше.
Сила: первый закон Ньютона
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — сила.
Сила — это физическая векторная величина, которая описывает взаимодействие тел. Она измеряется в ньютонах (в честь Исаака Ньютона, разумеется).
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Теперь зная, что такое сила, мы можем вернуться к ньютоновской формулировке закона инерции — он же, Его Величество, первый закон Ньютона:
Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость постоянной, в том числе равной нулю, если действие на него других сил отсутствует или скомпенсировано.
Первый закон Ньютона
R — результирующая сила, сумма всех сил, действующих на тело [Н]
const — постоянная величина
Системы отсчета: инерциальные и неинерциальные
Чтобы описать движение нам нужны три штуки:
- тело отсчета, относительно которого определяем местоположение других тел;
- система координат: в школьном курсе мы используем прямоугольную декартову систему координат;
- часы, чтобы измерять время.
В совокупности эти три опции образуют систему отсчета:
Инерциальная система отсчета — система отсчета, в которой все тела движутся прямолинейно и равномерно, либо покоятся.
Неинерциальная система отсчета — система отсчета, в которой тела движутся с ускорением.
Рассмотрим разницу между этими системами отсчета на примере задачи.
Аэростат — летательный аппарат на картиночке ниже — движется равномерно и прямолинейно параллельно горизонтальной дороге, по которой равноускоренно движется автомобиль.
Выберите правильное утверждение:
- Система отсчёта, связанная с аэростатом, является инерциальной, а система отсчёта, связанная с автомобилем, инерциальной не является.
- Система отсчёта, связанная с автомобилем, является инерциальной, а система отсчёта, связанная с аэростатом, инерциальной не является.
- Система отсчёта, связанная с любым из этих тел, является инерциальной.
- Система отсчёта, связанная с любым из этих тел, не является инерциальной.
Решение:
Система отсчёта, связанная с землёй, инерциальна. Да, планета движется и вращается, но для всех процессов вблизи планеты этим можно пренебречь. Во всех задачах систему отсчета, связанную с землей можно считать инерциальной.
Поскольку система отсчёта, связанная с землёй инерциальна, любая другая система, которая движется относительно земли равномерно и прямолинейно или покоится — по первому закону Ньютона тоже инерциальна.
Движение аэростата удовлетворяет этому условию, так как оно равномерное и прямолинейное, а равноускоренное движение автомобиля — нет. Аэростат — инерциальная система отсчёта, а автомобиль — неинерциальная.
Ответ: 1.
Инерция покоя
На столе лежит лист бумаги. На него поставили стакан и резко выдернули лист бумаги из-под него. Стакан почти не двинулся.
Так, например, если выбивать пыль из ковра, то в ковер-самолет ваш любимый предмет интерьера не превратится — вместе с пылью не улетит.
Инерция движения
В случае с движением мы берем ту часть первого закона Ньютона, в которой скорость постоянна, но не равна нулю. Здесь мы откроем способность тела к движению, которое было вызвано силой, прекратившей своё действие на тело.
Вернемся к самому началу:
Велосипедист наезжает на камень и падает с велосипеда. Благодаря инерции скорость велосипедиста сохраняется, несмотря на то, что сам велосипед не едет дальше.
Наездник слетает с лошади, если та остановилась. Это тоже происходит из-за инерции — скорость наездника остается постоянной, при этом сама лошадь останавливается.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Мир не идеален
К сожалению, а может быть и к счастью, мы не живем в мире, в котором все тела движутся прямолинейно и равномерно. Из-за этого инерция в реальной жизни невозможна, потому что всегда есть трение, сопротивление воздуха и прочие, препятствующие движению, факторы.
Пуля, вылетевшая из ружья, продолжала бы двигаться, сохраняя свою скорость, если бы на неё не действовало другое тело — воздух. Поэтому скорость пули уменьшается.
Велосипедист, перестав работать педалями, смог бы сохранить скорость своего движения, если бы на велосипед не действовало трение. Поэтому, если педали не крутить — скорость велосипедиста уменьшается, и он останавливается.
Читайте также:
- 430 школа ломоносов проектная деятельность
- Как формируется цик рф кратко
- В чем на ваш взгляд заключается сила общественного мнения кратко
- Какие два основных приема улучшения пород животных используется в племенной работе кратко
- Почему общество рассматривается как сложная система 10 класс кратко
Содержание:
Законы ньютона:
Ежедневно мы наблюдаем самые разнообразные механические движения: идут люди и едут машины, летят самолеты и птицы, вращаются колеса велосипедов, автомобилей и карусель в парке.
Почему движется, например, автомобиль? Каждый из вас сразу скажет: потому что работает двигатель автомобиля. Но давайте представим, что колеса автомобиля не соприкасаются с поверхностью Земли (рис. 24), а двигатель работает… Колеса вращаются, а привычное движение автомобиля не происходит. Почему?
Почему для движения автомобиля со скоростью, например, 90
Чтобы ответить на эти вопросы, нужно знать причины, вызывающие механическое движение или изменение состояния движения тел.
Наши жизненные наблюдения, многочисленные опыты показывают, что изменение скорости тела всегда вызывается воздействием на данное тело каких-либо других тел.
Для описания взаимодействий тел друг с другом в физике вводится понятие «сила» (греч. dynamis). Отсюда и название данного раздела — динамика.
Динамика — раздел механики, изучающий различные виды механического движения с учетом взаимодействий между телами.
В динамике решаются две основные задачи:
- устанавливаются законы взаимодействия тел друг с другом;
- определяется влияние этих взаимодействий на механическое движение тел.
Первый закон механики
Некоторое время в физике никто не подвергал сомнению мысль Аристотеля, высказанную им в работе «Механика»: «Движущееся тело останавливается, если сила, толкающая его, прекращает свое действие».
Это ошибочное утверждение, опирающееся на обыденное восприятие явлений природы, впервые опроверг Галилей, сделавший важнейший для науки вывод о вечности, неуничтожаемости движения.
Анализируя движение шарика по наклонной плоскости (рис. 2.1), он писал: «…скорость, которую однажды сообщили телу, будет строго сохранятся, поскольку устранены внешние причины ускорения и замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно, ибо, если скорость будет постоянной, движение не может быть уменьшено или ослаблено, а тем более уничтожено».
Этот фундаментальный вывод Г. Галилея использовал И. Ньютон в своем знаменитом труде «Математические начала натуральной философии» (1687 г.) при формулировании первого закона динамики (закона инерции):
Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, поскольку оно не принуждается приложенными силами изменить это состояние.
А. Эйнштейн и Л. Инфельд в работе «Эволюция физики» проще сформулировали этот закон: «Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, если только оно не вынуждено изменить его под влиянием действующих сил».
Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.
Движение шарика по наклонной плоскости рассматривали относительно поверхности Земли, которая считалась неподвижной. Итак, первый закон динамики установлен для систем отсчета, считающихся неподвижными или движущихся относительно последних прямолинейно, равномерно и поступательно. Такие системы называются инерциальными. Инертность тел проявляется в сохранении ими своего состояния покоя или прямолинейного равномерного движения до того времени, пока какая-нибудь внешняя причина не выведет их из этого состояния.
Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.
Сущность инертности, которая свойственна всем телам, заключается в том, что для изменения скорости тела необходимо взаимодействие с другим телом. Из двух взаимодействующих тел более инертно то, которое медленнее изменяет свою скорость.
Теоретически инерциальных систем отсчета может быть много, поскольку всегда можно представить тела, которые пребывают в состоянии покоя или движутся равномерно и прямолинейно (без ускорения), и связать с ними соответствующее количество систем координат и устройств для отсчета времени (часов).
Понятие инерциальной системы отсчета является научной абстракцией. В реальной жизни таких систем нет, поскольку в природе не существует абсолютно неподвижных тел (например, тело, которое неподвижно относительно Земли, вращается вместе с ней вокруг земной оси, вокруг Солнца и т. д.).
При решении задач динамики систему отсчета связывают с реальным телом, например Землей или Солнцем.
Поэтому при решении задач динамики систему отсчета связывают с реальным телом. Тогда она может рассматриваться как инерциальная с той или иной степенью приближения.
Так, например, при решении задач в небесной механике и космонавтике с высокой степенью точности инерциальной можно считать гелиоцентрическую систему с началом отсчета на Солнце и осями, направленными на некоторые звезды. Для решения большинства технических задач в качестве инерциальной берут систему отсчета, жестко связанную с Землей.
Первый закон Ньютона
Из личного опыта каждый из нас знает, что скорость тела по величине и направлению может изменяться только под действием других тел. Например, футбольный мяч покоится на ровной поверхности, если по нему не ударить ногой (рис. 25).
Рис. 25
При изучении физики в 7-м классе вы познакомились с утверждением древнегреческого философа Аристотеля, считавшего, что покой — естественное состояние тела, а движение — насильственное состояние, которое необходимо все время поддерживать.
Рассмотрим, какие причины определяют покой и равномерное прямолинейное движение тела.
Подвесим шарик на резиновом шнуре (рис. 26, а). Он висит неподвижно, взаимодействуя со шнуром и Землей. Если перерезать шнур, то шарик начнет падать вертикально вниз под действием притяжения Земли, а деформация шнура без воздействия на него шарика станет равной нулю (рис. 26, б).
Рис. 26
Значит, шарик находился в покое потому, что действие резинового шнура компенсировало (уравновешивало) притяжение Земли.
Какие бы тела мы не рассматривали, состояние покоя любого тела сохраняется, если действие на него одних тел компенсируется действием других тел.
Не столь очевидны причины, по которым тело движется с постоянной скоростью, и, возможно, многие из вас будут согласны с мнением Аристотеля о том, что равномерное движение нужно все время поддерживать. Это согласуется с нашим практическим опытом: например, велосипед движется с постоянной скоростью по ровной горизонтальной дороге, если человек крутит педали. Вероятно, поэтому представления Аристотеля господствовали в науке почти 2000 лет.
В XVIl в. движение тел начал изучать итальянский ученый Галилео Галилей. В одном из опытов Галилей исследовал движение шара по двум наклонным плоскостям (рис. 27). Он наблюдал, что вниз шар движется ускоренно, а вверх — замедленно, причем в обоих случаях: чем меньше угол наклона плоскости, тем меньше ускорение шара.
Рис. 27
Галилей предположил, что если шар будет двигаться по горизонтальной плоскости, то его ускорение будет равно нулю и, следовательно, движение шара с постоянной скоростью будет продолжаться как угодно долго.
Но на практике шар всегда останавливался (так как двигался замедленно), хотя, чем более гладкой была плоскость, тем дольше продолжалось движение. Галилей установил, что движение шара замедляется из-за сопротивления воздуха и трения о поверхность плоскости.
Таким образом Галилей пришел к выводу:
- тело будет двигаться как угодно долго с постоянной скоростью по идеально гладкой горизонтальной плоскости в безвоздушном пространстве, так как в этом случае воздействия на тело Земли и плоскости компенсируют друг друга, а сопротивление движению отсутствует.
То же самое наблюдалось бы при отсутствии любых взаимодействий тела с другими телами (нет притяжения Земли, нет плоскости, среды и т. п.), хотя этот идеальный вариант трудно представить.
Скорость, с которой при этом движется данное тело, является результатом его предшествующих взаимодействий с другими телами, а ее численное значение и направление зависят от выбранной системы отсчета.
Инерцией (лат. iners — неподвижный, бездеятельный) называется явление сохранения скорости движения тела неизменной (как по модулю, так и по направлению) при отсутствии внешних воздействий на тело.
Поэтому вывод Галилея позднее стали называть законом инерции.
Впоследствии Исаак Ньютон, обобщая результаты работ Галилея и других ученых, а также своих исследований, сформулировал общие законы движения. На первое место среди этих законов он поставил закон инерции, который и стали называть первым законом Ньютона. Простая и близкая к первоначальной формулировка этого закона следующая:
тело движется равномерно и прямолинейно (или покоится), если на него не действуют другие тела (или действие других тел скомпенсировано).
Можно ли проверить выполнение этого закона в земных условиях? Всегда ли он выполняется?
В окружающем нас мире на любое тело действует хотя бы притяжение Земли, т. е. полное отсутствие воздействий невозможно.
Но множество тел вокруг нас покоится потому, что действие на них одних тел скомпенсировано действием других. В некоторых случаях можно наблюдать и равномерное прямолинейное движение тел, т. е. закон инерции выполняется при определенных условиях.
В то же время можно вспомнить и такие случаи, когда и при компенсации воздействий на данное тело других тел этот закон не выполняется.
Рассмотрим пример с шаром, который покоится на гладкой неподвижной горизонтальной доске, так как притяжение Земли компенсируется воздействием доски (рис. 28, а). Если потянуть доску в горизонтальном направлении, то можно наблюдать движение шара относительно нее (рис. 28, б). Скорость шара изменяется, хотя воздействия Земли и доски по-прежнему скомпенсированы. В чем дело?
Рис. 28
Дело в том, что любое механическое движение невозможно описать без указания системы отсчета. Шар покоился в неподвижной системе отсчета, связанной с доской, а при воздействии на доску эта система отсчета стала двигаться с ускорением. Множество подобных опытных фактов указывает на то, что первый закон Ньютона выполняется только в определенных системах отсчета.
Поэтому в настоящее время в физике принята следующая формулировка первого закона Ньютона:
- существуют такие системы отсчета (называемые инерциальными), относительно которых поступательно движущееся тело сохраняет свою скорость постоянной (или покоится), если на него не действуют другие тела (или действие других тел скомпенсировано).
Важно понимать, что инерциальная система отсчета — это модель, используемая в физике. Почему это так?
В 7-м классе вы узнали, что точность измерения любой физической величины зависит, прежде всего, от цены деления измерительного прибора. Это относится и к определению значения скорости тела. Кроме того, на практике скорость движения тел практически всегда непостоянна, и различными приборами определяется только ее среднее значение за некоторый промежуток времени.
Например, водитель контролирует скорость движения автомобиля по спидометру с ценой деления, равной 10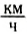
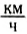
Значит, говоря о постоянном значении скорости тела, нужно понимать, что скорость измерена реальным прибором с определенной точностью.
Инерциальная система отсчета является моделью реальной системы отсчета, движущейся со скоростью, значение которой определяется как постоянное при данной точности измерений.
Таким образом, первый закон Ньютона является постулатом, т. е. утверждением о существовании моделей — инерциальных систем отсчета, и не может быть полностью проверен экспериментально.
Роль первого закона Ньютона в механике в том, что он определяет условия, при которых реальные системы отсчета можно считать инерциальными.
Почему это очень важно? Потому, что практически все физические законы выполняются при определенных условиях. В следующих параграфах вы будете изучать и учиться применять второй и третий законы Ньютона, которые выполняются только в инерциальных системах отсчета.
Главные выводы:
- Инерция — явление сохранения скорости тела постоянной в отсутствии внешних воздействий на него.
- Система отсчета называется инерциальной, если при отсутствии воздействий на данное тело (или их компенсации) скорость тела относительно этой системы отсчета не изменяется.
- Первый закон Ньютона позволяет определить, можно ли считать выбранную систему отсчета инерциальной.
Второй закон механики
Второй закон механики Ньютона устанавливает взаимосвязь между кинематическими и динамическими величинами. Чаще всего он формулируется так: ускорение, которое приобретает тело под действием силы, прямо пропорционально силе, обратно пропорционально массе тела и имеет то же направление, что и сила:
где 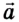
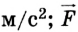
Если по этой формуле определить силу 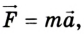
Второй закон механики Ньютона:
И. Ньютон сформулировал второй закон механики несколько иначе, воспользовавшись понятием количества движения (импульса тела).
Импульс или количество движения (от лат. impulsus — удар, толчок) — произведение массы тела на его скорость — одна из мер механического движения: 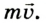
Поскольку ускорение 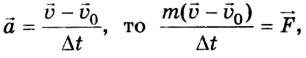
Изменение количества движения тела пропорционально действующей силе и происходит в направлении той прямой, вдоль которой эта сила действует.
По Ньютону второй закон механики звучит так: изменение количества движения тела пропорционально приложенной движущей силе и происходит в направлении той прямой, по которой эта сила действует.
Действие силы не порождает само движение, а лишь изменяет его; сила вызывает изменение скорости (ускорение), а не саму скорость.
Второй закон механики Ньютона обобщил исключительно важный факт: действие силы не порождает само движение, а лишь изменяет его; сила вызывает изменение скорости (ускорение), а не саму скорость.
- Заказать решение задач по физике
Второй закон Ньютона
Как вы уже знаете, изменение скорости тела происходит под действием силы, а быстроту изменения скорости определяет ускорение. Необходимо выяснить, как зависит ускорение тела от действующей на него силы.
Проведем опыт на неподвижном горизонтальном столе, т. е. в инерциальной системе отсчета. Установим легкую тележку на длинные горизонтальные рельсы, по которым она может двигаться почти без трения. Прикрепим к тележке динамометр, к концу которого присоединим перекинутую через блок нить с грузом (рис. 44, а).
Рис. 44
В вертикальном направлении сила тяжести тележки с динамометром уравновешивается силой реакции рельс. Пренебрегая трением и сопротивлением воздуха, можно считать, что тележка движется вдоль стола с ускорением только под действием горизонтальной силы натяжения нити. Модуль этой силы определяется по показаниям динамометра.
Опыт показывает, что направление вектора ускорения 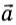
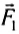
Если увеличить подвешенный к нити груз, то динамометр показывает большее значение действующей на тележку силы 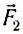
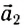
Таким образом, приобретаемое тележкой ускорение по модулю прямо пропорционально действующей, силе и совпадает с ней по направлению.
Изменим условия опыта. Поместим на первую тележку вторую (одинаковой с ней массы) и подберем массу груза так, чтобы показание динамометра вновь стало F1 (рис. 44, в). Масса движущейся тележки с динамометром в первом опыте ml =M + m, а сейчас m3 = 2М + m. При этих условиях тележка с общей массой m3 проходит тот же путь за большее время t3, т. е. ее ускорение m3 меньше . Из расчетов следует, что модуль ускорения 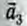
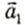
Следовательно, при той же действующей силе модуль ускорения тележки уменьшается во столько же раз, во сколько раз возрастает ее масса.
Многочисленные опыты с различными телами и в других условиях показывают, что, чем больше масса любого тела, тем труднее изменить его скорость на определенную величину, действуя постоянной силой.
Поэтому массу называют основной динамической характеристикой тела — количественной мерой его инертности, т. е. способности тела приобретать ускорение под действием данной силы.
Таким образом, ускорение тела прямо пропорционально действующей силе и обратно пропорционально массе:
Исаак Ньютон, исследуя изменение скорости тела в зависимости от действующей силы, впервые установил подобную закономерность больше 300 лет назад.
В окружающем мире на тело обычно действует несколько сил, и многочисленные эксперименты в различных условиях (с учетом сил трения и сопротивления; тело на горизонтальной опоре и т. д.) позволили установить, что ускорение тела определяется равнодействующей (результирующей) всех действующих на него сил.
Поэтому принята следующая формулировка второго закона Ньютона:
ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально его массе:
Для упрощения длинной последовательности n однотипных слагаемых в математике используется специальный знак суммы:
где 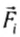
Второй закон Ньютона выполняется только в инерциальных системах отсчета. Следовательно, используя первый закон Ньютона, сначала необходимо выбрать инерциальную систему отсчета, а затем можно в ней применять для расчета ускорения тела второй закон Ньютона.
Часто удобнее использовать второй закон Ньютона в виде
записав в правой части все действующие на тело силы. Поскольку при расчетах целесообразно проводить математические операции со скалярными величинами, то при решении задач записывают второй закон Ньютона для проекций на оси выбранной инерциальной системы отсчета:
- max = Flx+ F2x +F3x+… + Fnx;
- may = Fly+ F2y+F3y+… + Fny.
Второй закон Ньютона позволяет рассчитать ускорение тела в инерциальной системе отсчета при самых разнообразных движениях: при разбеге человека по дорожке (рис. 45) и его катании на карусели, при движении транспорта и выполнении самолетом фигур высшего пилотажа, при вращении деталей станка и старте космического корабля.
Если скорость и координаты тела в начальный момент времени известны, а по второму закону Ньютона определяется его ускорение, можно решить основную задачу механики — определить скорость и координаты тела в любой момент времени.
Главные выводы:
- Модуль ускорения тела прямо пропорционален модулю равнодействующей всех сил и обратно пропорционален массе тела.
- Направление ускорения тела совпадает с направлением равнодействующей всех сил, действующих на него.
- Второй закон Ньютона выполняется только в инерциальных системах отсчета.
Третий закон механики
Согласно утверждению Ньютона сила является следствием взаимодействия двух или большего количества тел. Если одно тело действует на другое, то обязательно и второе тело действует на первое, т. е. если есть действие, то есть и противодействие. Понятия действия и противодействия условны, поскольку каждое из них может быть и тем и другим. Возьмем две одинаковые по мае-
се тележки и к одной из них прикрепим плоскую пружину, сжатую прочной нитью. Другую тележку поставим так, чтобы она касалась этой пружины (рис. 2.7, а).
Если нитку, которой сжата пружина, отпустить или поджечь, то пружина распрямится и обе тележки придут в движение. Это означает, что они приобрели ускорение:
Поскольку масса тележек одинакова, то одинаковы их ускорения и расстояния, которые они проходят за определенное время.
Если на одну из тележек положить некоторый груз (увеличить ее массу) и повторить опыт (рис. 2.7, б), то тележка, которая имеет большую массу, пройдет меньшее расстояние.
Таким образом, при взаимодействии двух тел соотношение модулей их ускорений равно обратному соотношению их масс:
Ускорения взаимодействующих тел имеют противоположные направления, поэтому в векторной форме можно записать
Произведение массы тела на его ускорение равно приложенной к телу силе. 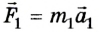
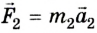
Это равенство и является математическим выражением третьего закона механики. Ньютон его сформулировал так:
- действию всегда есть равное и противоположное противодействие; действия двух тел друг на друга равны между собой и направлены в противоположные стороны.
Существует и такая формулировка: любое действие одного тела на другое имеет характер взаимодействия; силы, с которыми взаимодействуют тела, всегда одинаковы и противоположно направлены.
Опыты подтверждают, что силы любой природы во время взаимодействия тел возникают попарно, имеют противоположные направления и одинаковы по модулю. На рисунке 2.8 показаны электрическое (а) и магнитное (б) взаимодействия, а на рисунке 2.9 — взаимодействия в случае возникновения в телах силы упругости (имеют электромагнитную природу).
В третьем законе механики речь идет о силах, приложенных к разным телам. Поэтому, нельзя считать, что сумма сил, приложенных к каждому из взаимодействующих тел, равна нулю. Равнодействующую сил можно находить лишь в том случае, когда силы приложены к одному телу.
Третий закон Ньютона
По второму закону Ньютона можно рассчитать ускорение движущегося тела и при известных начальных условиях найти его скорость и координаты в любой момент времени.
Но на практике недостаточно знать закон движения, например, автомобиля. Важно знать также силу, с которой он действует на опору, чтобы рассчитать, например, конструкцию моста, по которому автомобиль движется. Следовательно, необходимо установить, как соотносятся между собой силы, с которыми действуют друг на друга тела при взаимодействии.
Проведем некоторые опыты и исследуем этот вопрос.
Закрепим в двух штативах динамометры, соединенные крючками (рис. 47, а). Если потянуть в горизонтальном направлении поочередно за один динамометр, за другой или за оба вместе, то в каждом опыте показания приборов равны. Значит, силы, с которыми динамометры действуют друг на друга, равны по модулю и по условиям опыта направлены в противоположные стороны.
Присоединим к одному динамометру кусок железа, а к другому — магнит. При взаимодействии железа и магнита на динамометрах также установятся одинаковые показания (рис. 47, б).
Рис. 47
Рассмотрим другой опыт. Пусть на гладких горизонтальных рельсах, закрепленных на неподвижном столе, расположены две тележки одинаковой массы. Закрепим на одной из них моторчик, на ось которого при его работе будет наматываться нить, привязанная к другой тележке. На тележку без моторчика поставим дополнительную гирю, масса которой равна массе моторчика, чтобы общие массы тележек были равны.
При работающем моторчике обе тележки устремляются навстречу друг другу с одинаковыми ускорениями. Их можно рассчитать, измерив пройденный путь и время его прохождения (рис. 48, а).
Если массу одной из тележек изменить, то обратно пропорционально массе изменится ее ускорение (рис. 48, б). А для модулей ускорений двух тележек, если их массы различны, выполняется следующее соотношение:
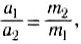
Если учесть, что по второму закону Ньютона m1a1=F1 и m2a2 = F2, а ускорения тележек направлены в противоположные стороны, то можно записать:
Какие бы примеры взаимодействия тел не рассматривались, всегда выполняется установленный Ньютоном третий закон:
силы, с которыми два тела действуют друг на друга, одной природы, равны по модулю, противоположны по направлению и направлены вдоль одной прямой.
Рис. 48
Из третьего закона Ньютона следует, что силы всегда возникают парами и при взаимодействии тел равноправны.
Значит, например, с какой силой каждого человека притягивает наша огромная планета Земля, с такой же силой и человек притягивает Землю.
Третий закон Ньютона выполняется для любых взаимодействий, в том числе и для столкновений тел.
Почему, например, в районах больших аэропортов принимаются специальные меры для удаления из воздушного пространства любых птиц? Столкновение даже небольшой птицы с обшивкой самолета, стеклом иллюминатора или частью двигателя может вызвать их разрушение.
Ускорение и деформация тел при взаимодействии зависят от их массы и от того, с какими другими телами есть еще взаимодействие в данный момент.
Рассмотрим, например, взаимодействие одинаковых бильярдных шаров при различных условиях (рис. 49). Шар, лежащий посередине стола, взаимодействует с опорой и притягивается Землей. Причем силы тяжести и упругости перпендикулярны плоскости стола и равны по модулю. Можно показать, что при центральном ударе по одному шару такого же второго шара бильярдные шары практически обмениваются скоростями (рис. 50).
Если шар лежит у бортика стола, взаимодействуя добавочно и с ним (см. рис. 50), то результат удара совершенно другой. Хотя при этом массы тел не изменились, и скорость движущегося шара перед взаимодействием такая же.
Экспериментально установлено: в каких бы разнообразных взаимодействиях тело не участвовало, третий закон Ньютона выполняется для каждой пары взаимодействующих тел.
Таким образом, третий закон Ньютона утверждает, что силы возникают всегда парами. Любое взаимодействие необходимо характеризовать двумя силами, которые хотя и равны по модулю, но противоположны по направлению и действуют на разные тела.
Главные выводы
- Силы взаимодействия двух тел равны по величине, противоположно направлены и приложены к разным телам.
- Третий закон Ньютона выполняется в инерциальных системах отсчета.
- Результат взаимодействия двух тел зависит от того, в каких еще взаимодействиях каждое из них участвует.
Значение законов Ньютона и принцип относительности в механике
Иногда в разговоре с не очень компетентными людьми можно услышать, что для современного человека важнее последние достижения физической науки, чем законы классической физики, сформулированные Ньютоном больше 300 лет назад.
Такие рассуждения не корректны. Законы Ньютона используются в физике для описания движения различных объектов не только в механике, но и в других разделах физики, в которых изучаются тепловые процессы, электрические и магнитные явления, колебательные системы и т. д.
Законы Ньютона называют основными законами механики, потому что они лежат в основе динамики, в которой устанавливаются количественные зависимости между характером движения тел и действующими на них силами.
Эти законы определяют общие существенные закономерности, свойственные любым механическим движениям. Но механическое движение всегда относительно, а следовательно, для его описания необходимо выбрать систему отсчета.
Первый закон Ньютона позволяет выбрать инерциальную систему отсчета, в которой движение тел однозначно определяется вторым и третьим законами Ньютона.
На основании второго закона Ньютона можно рассчитать ускорение тела при действии на него заданных сил.
Согласно третьему закону Ньютона силы возникают парами при взаимодействии тел, причем модули этих сил равны, независимо от причины, вызвавшей взаимодействие тел.
Законы Ньютона выполняются лишь при определенных условиях. Они хорошо описывают движение макроскопических тел со скоростями, много меньшими скорости света. Поэтому области применения законов Ньютона в окружающем человека мире очень обширны.
Их используют для расчетов результатов самых разнообразных взаимодействий и явлений на Земле и в космосе.
Законы Ньютона применяются при разработках новых двигателей для автомобильного, водного и воздушного транспорта. Без этих законов нельзя рассчитать длину взлетной или посадочной полосы (рис. 51) для различных типов самолетов, параметры (наклон к горизонту и кривизну) скоростных автомобильных дорог.
Рис. 51
Старт космического корабля, его вывод на орбиту вокруг Земли или на определенную траекторию для полета к Луне, другим небесным телам невозможны без предварительных расчетов, в которых используются законы Ньютона.
Кроме этого, законы Ньютона необходимы для расчетов: при строительстве зданий, мостов и других сооружений; при разработке спортивной одежды, обуви, тренажеров; в машиностроении и т. п.
Применив эти законы для описания движения Луны и планет Солнечной системы, Ньютон открыл закон всемирного тяготения, который мы будем изучать в дальнейшем.
Как мы уже обсуждали, чтобы использовать второй и третий законы Ньютона, нужно выбрать с помощью первого закона Ньютона инерциальную систему отсчета. В большинстве задач систему отсчета, связанную с поверхностью Земли, можно считать инерциальной.
Тогда система отсчета, связанная с любым телом, движущимся относительно Земли с постоянной скоростью, также является инерциальной (в пределах той же точности измерений). Таким образом, в любом равномерно движущемся транспорте, на эскалаторе, в лифте и т. п. должны также выполняться второй и третий законы Ньютона.
На этот факт впервые обратил внимание Галилей. Он предположил, что опыты, проведенные в неподвижной системе отсчета, связанной с поверхностью Земли, и «в большой каюте под палубой какого-либо крупного корабля» не должны отличаться друг от друга.
«Если только движение будет равномерным, а не колеблющимся туда и сюда», то капли воды будут падать вертикально вниз, как в неподвижной системе отсчета. Мяч, брошенный вертикально вверх, вернется в точку бросания.
«Ни по одному из этих явлений, ни по чему-либо, что станет происходить с вами самими, вы не сможете удостовериться, движется корабль или стоит неподвижно», — утверждал Галилей.
Таким образом, Галилей выдвинул гипотезу, что относительно всех инерциальных систем отсчета тело получает одинаковое ускорение при одинаковых действиях на него других тел.
Действительно, каждый человек из личного опыта знает, что в вагоне, движущемся с постоянной скоростью по прямолинейной дороге, можно легко вставать, ходить, не теряя равновесия, можно даже играть в теннис (рис. 52).
Рис. 52
В настоящее время положение, высказанное Галилеем, называется принципом относительности Галилея или принципом относительности в механике:
в любых инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях.
Почему важны одинаковые начальные условия? Потому, что координата и скорость тела в начальный момент времени относительны, зависят от выбранной системы отсчета. Относительно равномерно движущегося вагона тело будет падать вниз по вертикали так же, как и в случае, когда вагон неподвижен (рис. 53). но относительно наблюдателя, находящегося на Земле, тело, падающее отвесно в вагоне, движется по параболе (см. рис. 53).
Рис. 53
Следовательно, не существует какой-то одной, избранной, инерциальной системы отсчета, все инерциальные системы отсчета равноправны, и при решении задач для упрощения расчетов можно выбирать любую из них.
Например, взвешивание тела и расчет результатов этого действия в любом равномерно движущемся транспорте (или в лифте и т. п.) можно проводить, не учитывая этого движения.
В системах отсчета, движущихся с ускорением (неинерциальных), в сформулированном нами виде законы Ньютона не выполняются. Но эти законы оказались так удобны для расчетов, что в неинерциальных системах отсчета специально вводят особые силы инерции, чтобы учесть ускоренное движение системы отсчета и использовать законы Ньютона.
Главные выводы:
- Законы Ньютона определяют общие существенные закономерности, свойственные любым механическим движениям.
- Принцип относительности Галилея устанавливает равноправие всех инерциальных систем отсчета, так как механические явления и процессы протекают в них одинаково при одинаковых начальных условиях.
- В соответствии с принципом относительности при решении задач можно использовать любую наиболее удобную инерциальную систему отсчета.
Движение по инерции и первый закон НЬЮТОНА
Возможно, во время летних каникул вы наблюдали или сами пережили описанные ниже явления:
- a) велосипедист равномерно движется по прямой дороге;
- b) велосипедист пытается удержать велосипед в состоянии покоя, не касаясь ногами земли;
- c) из-за невнимательности велосипедист не не замечает, как колесо велосипеда сталкивается с камнем, и перелетает через внезапно остановившийся велосипед (а).
Основу динамики составляют три закона Ньютона. Эти законы—результат обобщения моногочисленых наблюдений и экспериментов. Первое обобщение опытов провел Г.Галилей, живший в XVII веке. В результате экспериментов, аналогичных проведенному вами исследованию, он сформулировал принцип инерции:
Если на какое-либо тело действуют другие тела с силами, компенсирующими друг друга, то это тело либо находится в покое, либо движется равномерно и прямолинейно.
Ссылаясь на принцип инерции Галилея, Ньютон сформулировал I закон динамики, называемый также I законом Ньютона:
Существуют такие системы отсчета, относительно которых тела сохраняют свое состояние покоя или равномерного прямолинейного движения при отсутствии всякого внешнего воздействия на них, или если оказываемые на тело действия компенсируют друг друга.
Система отсчета, относительно которой выполняется I закон Ньютона, называется инерциальной системой отсчета (ИСО). С достаточно большой точностью системы тел, находящихся в состоянии покоя или равномерного прямолинейного движения относительно Земли, можно считать инерциальны-ми системами отсчета. Например, систему отсчета, связанную с равномерно и прямолинейно движущимся локомотивом, можно принять за инерциальную систему отсчета.
Отметим, что понятие «инерциальная система отсчета» является научной абстракцией. В реальной жизни такой системы не существует, потому что в природе тел в состоянии абсолютного покоя нет.
Основной закон динамика и второй закон Ньютона
Из исследования было выяснено, что ускорение тела данной массы прямо-пропорционально результирующей силе, действующей на тело:
С другой стороны, тела с разными массами под действием одной и той же результирующей силы получают разные ускорения — ускорения тел обратно-пропорциональны их массам
Ньютон исследовал эту зависимость, и обобщил ее в виде закона. Этот закон, называемый II законом Ньютона, выражается следующим образом:
В инерциальной системе отсчета ускорение, получаемое телом, прямо пропорционально равнодействующей силе и обратно пропорционально массе этого тела:
или
Этот закон можно выразить и так: равнодействующая сил, действующих на тело, равна произведению массы тела на его ускорение:
Из II закона Ньютона определяется единица силы в СИ — ньютон:
1 ньютон — это сила, под действием которой тело массой 1 кг получает ускорение
Сила является причиной изменения скорости движения! Как известно из кинематики, ускорение тела — это быстрота изменения его скорости:
Приняв во внимание это выражение во II законе Ньютона, получим:
Выполнив преобразования, получим:
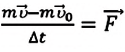
Величина 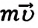
Импульс — векторная физическая величина (иначе называемая количеством механического движения), равная произведению массы тела на его скорость. Обозначается буквой
Единица измерения импульса в СИ:
II закон Ньютона также можно выразить и через импульс:
Изменение импульса (количества движения) тела происходит в направлении равнодействующей силы и пропорционально этой силе:
Произведение силы на время ее действия 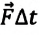
Направление импульса силы, также являющейся векторной величиной, совпадает с направлением вектора силы. Единицей импульса силы в СИ является:
Таким образом, II закон Ньютона обобщил важный факт динамики:
Действие силы приводит к изменению скорости тела, т.е. к возникновению ускорения.
Действие и противодействие и третий закон Ньютона
На рисунке изображены две одинаковые лодки, причаливающие к берегу: это достигается с помощью натягивания каната. Так, лодочник в первой лодке тянет за один конец каната, другой конец которого прикреплен к столбику на берегу. Лодочник во второй лодке тянет за конец каната, а за другой конец которого тянет человек на берегу (а). Каждый из них прикладывает к концу каната одинаковую силу. Какая из лодок быстрее причалит к берегу?
Выполнив исследование, вы установили, что при действии динамометров друг на друга силы взаимодействия по модулю равны, а по направлению противоположны (стрелки отклоняются в противоположные направления):
Это равенство выражает III закон Ньютона:
В инерцианальной системе отсчета силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны.
Этот закон Ньютона показывает, что при взаимодействии тел друг с другом силы всегда возникают попарно. Это означает, что если на произвольное (первое) тело будет действовать с определенной силой другое (второе) тело, то и первое будет действовать на второе тело с той же по модулю силой, только направленной противоположно. Согласно II закону Ньютона, эти силы сообщают телам ускорения в противоположных направлениях:
Где 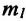
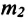
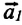
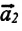
• Силы взаимодействия возникают одновременно и имеют одинаковую природу. Например, силы взаимодействия, возникающие при упругом столкновении тел, оба имеют электромагнитную природу.
Силы, возникающие при взаимодействии тел, прикладываются к разным телам и поэтому не могут уравновешивать друг друга, то есть никогда не компенсируют друг друга. Компенсировать действия друг друга могут только силы, приложенные к одному телу.
Инерциальные системы отсчета
Что является естественным для тела — движение или покой? Древнегреческий философ Аристотель утверждал, что покой, ведь для того, чтобы тело двигалось, нужно действовать на него определенным образом, а если действие прекратится, тело остановится. Кажется, что об этом свидетельствует и наш повседневный опыт. Но действительно ли это так?
Почему остановятся тела (рис. 9.1), если прекратить их толкать, тянуть и т. п.? Остановятся ли тела, если исчезнет сопротивление их движению?
Надеемся, вы правильно ответили на вопрос и пришли к выводу, к которому в свое время пришел Г. Галилей: «Сообщенная движущемуся телу скорость будет сохраняться, если устранены внешние причины ускорения или замедления движения». Итак, «естественным» для тела является не только состояние покоя, но и прямолинейное равномерное движение.
Закон инерции Галилея: тело движется равномерно прямолинейно или находится в состоянии покоя, если на него не действуют другие тела или действия других тел скомпенсированы.
Тело, на которое не действуют другие тела и поля, называют изолированным (свободным), а движение изолированного тела — движением по инерции. В реальности практически невозможно создать условия, когда на тело ничто не действует, поэтому движением по инерции называют равномерное прямолинейное движение при отсутствии или скомпенсированности действия на тело других тел и полей (рис. 9.2).
Справочный материал по первому закону Ньютона
Явление сохранения телом состояния покоя или равномерного прямолинейного движения при условии, что на него не действуют другие тела и поля или их действия скомпенсированы, называют явлением инерции.
Вместе с тем состояние движения и состояние покоя зависят от выбора системы отсчета (СО). А в каждой ли СО наблюдается явление инерции? Из курса физики 9 класса вы хорошо знаете, что не в каждой.
Систему отсчета, относительно которой наблюдается явление инерции, называют инерциальной системой отсчета.
Представьте, что вы сидите в купе поезда, который время от времени увеличивает скорость, тормозит, осуществляет поворот и т. п. Понятно, что СО, связанная с поездом, будет инерциальной только тогда, когда поезд движется равномерно прямолинейно; во всех остальных случаях она будет неинерциальной, ведь относительно нее явление инерции наблюдаться не будет (рис. 9.3).
На каком рисунке (см. рис. 9.3, а–в) показано, что поезд набирает скорость? тормозит? движется равномерно прямолинейно?
Чаще всего в качестве инерциальной выбирают СО, жестко связанную с точкой на поверхности Земли. Но эту систему можно считать инерциальной только условно, поскольку Земля вращается вокруг своей оси. Для более точных измерений используют инерциальную СО, связанную с Солнцем и далекими звездами.
Если мы знаем хотя бы одну инерциальную СО (например, СО, связанную с домом, на рис. 9.4), то можем найти много других (см. рис. 9.4).
Закон инерции Г. Галилея стал первым шагом в установлении основных законов классической механики. Формулируя основные законы движения тел, И. Ньютон назвал этот закон первым законом движения. В современной физике первый закон механики Ньютона формулируют так:
Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют никакие силы или если эти силы скомпенсированы.
В такой формулировке первый закон Ньютона:
- постулирует существование инерциальных СО (утверждает, что они существуют);
- дает возможность из всех имеющихся СО выделить инерциальные СО;
- содержит закон инерции (условия равномерного прямолинейного движения тела).
Справочный материал по второму закону Ньютона
Поставим на твердую горизонтальную поверхность легкоподвижную тележку и станем тянуть ее с помощью груза. Массу груза для каждого опыта будем подбирать так, чтобы растяжение пружин при движении тележки было одинаковым. Измеряя время t, в течение которого тележка проходит, например, расстояние s = 2 м, будем определять ускорение движения тележки 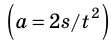
Учитывая, что единицу силы выбирают так, что коэффициент пропорциональности в выражении 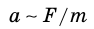
Ускорение, которое приобретает тело в результате действия силы, прямо пропорционально этой силе и обратно пропорционально массе тела:
- Второй закон Ньютона, записанный в виде
, выполняется только в инерциальных системах отсчета.
- Обычно на тело действуют несколько сил. Если тело можно считать материальной точкой, все эти силы можно заменить одной — равнодействующей. Равнодействующая равна геометрической сумме сил, действующих на тело:
(рис. 10.2), поэтому второй закон Ньютона записывают так:
- Направление ускорения движения всегда совпадает с направлением равнодействующей сил, действующих на тело:
.
- Если силы, действующие на тело, скомпенсированы, то есть равнодействующая равна нулю (
), тело не будет изменять скорость своего движения ни по значению, ни по направлению:
= 0 (рис. 10.3), а следовательно, будет двигаться равномерно прямолинейно или находиться в состоянии покоя.
- Тело движется равноускоренно прямолинейно, если равнодействующая сил, приложенных к телу, не изменяется со временем.
Рис. 10.2. Сила 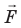
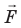
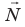
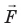
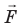
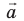
Рис. 10.3. Если равнодействующая сил, приложенных к телу, равна нулю, тело находится в состоянии покоя (а) или движется с постоянной скоростью (б)
Справочный материал по третьему закону Ньютона
«Действию всегда есть равное и противоположное противодействие, иначе: действия двух тел друг на друга между собой равны и направлены в противоположные стороны» — так И. Ньютон сформулировал свою третью и последнюю «аксиому движения».
Силы всегда возникают парами: если тело А действует на тело Б с силой 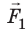
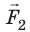
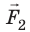
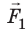
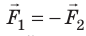
Подчеркнем: «действие» и «противодействие» — это всегда силы одинаковой природы, они всегда направлены вдоль одной прямой (рис. 10.4) — и сформулируем третий закон Ньютона в современном виде:
Тела взаимодействуют с силами, которые имеют одинаковую природу, направлены вдоль одной прямой, равны по модулю и противоположны по направлению:
Рис. 10.4. Силы, возникающие при взаимодействии, имеют одинаковую природу, направлены вдоль одной прямой, равны по модулю и противоположны по направлению
Выводы:
- Сила
— векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются. Единица силы в СИ — ньютон (Н). Если на материальную точку одновременно действуют несколько сил, их можно заменить равнодействующей
- Основной закон динамики — второй закон Ньютона: ускорение, которое приобретает тело в результате действия силы, прямо пропорционально этой силе и обратно пропорционально массе тела:
. Этот закон выполняется только в инерциальных СО.
- Третий закон Ньютона — закон взаимодействия: тела взаимодействуют с силами, которые имеют одинаковую природу, направлены вдоль одной прямой, равны по модулю и противоположны по направлению:
. Пара сил, возникающих при взаимодействии двух тел, не уравновешивают друг друга, поскольку приложены к разным телам.
- Гравитационные силы в физике
- Центр тяжести в физике (центр масс)
- Импульс тела в физике
- Замкнутая система в физике
- Кинематика в физике
- Законы сохранения в физике
- Международная система единиц СИ
- Математика — язык физики
Хочу отметить, что лично я иначе понимаю состояние покоя.
Принято считать, что состояние покоя характеризуется тем, что скорость тела равна нулю. Ввиду относительности движения такое определение покоя является очень условным. Поэтому, с моей точки зрения, состояние покоя характеризуется тем, что не скорость равна нулю, а ускорение равно нулю. То есть покоем является состояние, когда на тело не действуют никакие силы, изменяющие параметры его состояния. В этом смысле равномерно движущееся тело находится в состоянии покоя. Я полагаю, что такое понимание покоя является более продуктивным для физики. Отмечу, что эта трактовка находится в полном соответствии с первым законом Ньютона.
Привлечение математических подходов не позволит нам отличить движение от покоя. Мне представляется, что в математике вообще нет понятия времени. Математика – это наука о числах. Свойства чисел не меняются с течением времени. Поэтому математика – это статичная наука. Она не знает динамики. И при этом пытается описывать динамичную природу. Каким образом?
Для описания динамики можно объявить время аналогом пространственной координаты и добавить координатную ось времени дополнительно к пространственным осям, как это сделано в Общей теории относительности. Но такой математический трюк не вписывается в физическую картину мира.
Логичнее ввести время в математику как внешнюю физическую сущность, интуитивно понимаемую человеком. Так это делается в классической физике. Но и здесь математика, как абстрактная наука, проявляет свои особенности при рассмотрении движения.
В математике принято рассматривать движение тел как перемещение материальных точек в пространстве. Можно ли описать движение материальной точки в абсолютно пустом пространстве? Конечно нет. Для описания положения и перемещения материальной точки необходимо построение системы координат. Но при наличии одной точки никакую систему координат построить невозможно. Следовательно, положение и перемещение этой точки в пространстве описать нельзя.
Движение двух точек также невозможно описать. Рассмотрим условие задачи: в пространстве имеются две материальные точки, двигающиеся навстречу друг другу с некоторой скоростью. Даже такая постановка задачи некорректна. Имея в пространстве только две точки невозможно построить трехмерную систему координат. А одномерную? Тоже невозможно. Координатную ось можно провести через две точки. Но невозможно отложить на этой оси никакую шкалу. Потому что имеется только две точки. Поэтому невозможно определить, изменилось ли с течением времени расстояние между точками. В пространстве нет никакого эталона длины, с которым можно было бы сравнивать расстояние между точками. А сами точки имеют нулевой размер. Поэтому с математической точки зрения расстояние между двумя точками не может ни увеличиться, ни уменьшиться.
Когда в математике рассматривают движение тел, то обычно предполагают заданную систему отсчета, которая должна быть к чему-то привязана, зачастую предполагается внешний наблюдатель, который рассматривает эту картину. Но в абсолютно пустом пространстве в математике нет координатных осей, нет внешнего наблюдателя. Поэтому нет и движения.
Может показаться, что такая ситуация возникает только для случая одиночных точек. Однако, аналогичная картина возможна и для случая бесконечно большого количества точек.
Если какое-либо тело, например куб или шар, равномерно расширяется в пространстве, то это движение также невозможно определить. Можно сказать, что невозможно определить движение, если оно является результатом конформного отображения.
Конформное отображение— непрерывное отображение, сохраняющее углы между кривыми, а значит и форму бесконечно малых фигур.
Рассмотрим два шара, которые находятся в абсолютно пустом пространстве и движутся навстречу друг другу с некоторой скоростью. При этом диаметры шаров уменьшаются пропорционально расстоянию между шарами. Когда шары столкнутся?
Как обозначается в физики состояние покоя.
Вы зашли на страницу вопроса Как обозначается в физики состояние покоя?, который относится к
категории Физика. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
Физика, 11 класс
Урок №21. Релятивистские эффекты
На уроке рассматриваются понятия: энергия покоя, полная энергия частиц; связь массы и энергии в специальной теории относительности; релятивистский импульс частицы, релятивистская кинетическая энергия; принцип соответствия.
Глоссарий урока:
Релятивистская механика — раздел физики, где описывается движение частиц со скоростями близкими к скорости света.
Закон взаимосвязи энергии и массы — тело обладает энергией и при нулевой скорости, такую энергию называют энергией покоя.
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии.
Безмассовыми называют частицы массы, которых в состоянии покоя равны нулю, они существуют только в движении, при этом во всех инерциальных системах отсчёта их импульс и энергия не равны нулю.
Массовыми называют частицы, для которых масса является важной характеристикой, мерой инертности тела.
Принцип соответствия – это подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматриваются как частный случай релятивистских законов при скоростях намного меньших скорость света.
Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай.
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 239 – 241.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 149
Дополнительная литература:
- Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 253-260.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 311-315.
- Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.144-157
Основное содержание темы
«Основы физики претерпели неожиданные и радикальные изменения благодаря смелости молодого и революционно мыслящего гения.»
Вернер Гейзенберг
Эти слова и множество других восхищённых эпитетов будут высказаны в адрес гениального учёного Альберта Эйнштейна. Эйнштейн не боялся опровергать общепринятые утверждения. Он разрушил представление об абсолютном времени и незыблемости пространства. Его теория утверждала, что есть движущиеся системы координат со своим относительным временем. А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости — опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.
Альберт (Einstein) Эйнштейн
14 марта 1879 г. – 18 апреля 1955 г.
Физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист.
По законам классической физики: масса – это мера инертности тела. Но Эйнштейн утверждает другое: масса – это мера энергии, содержащейся в теле.
Любое тело обладает энергией уже в силу своего существования. Альбертом Эйнштейном была установлена пропорциональность между энергией и массой:
На первый взгляд, простая формула, является фундаментальным законом природы, законом взаимосвязи энергии и массы.
Согласно этой формуле тело обладает энергией даже при нулевой скорости, в таком случае энергию называют E энергией покоя. А массу, которая входит в формулу Эйнштейна назовём m0 массой покоя.
Как же будет выглядеть закон взаимосвязи массы и энергии для движущегося тела? К нему добавляем радикал 
Такую формулу называют релятивистской энергией или полной энергией движущегося тела.
Релятивистская механика — раздел физики, где описываются движения тел и частиц со скоростями близкими к скорости света, где используются преобразования Лоренца, перехода из одной инерциальной системы в другую, когда одна система движется относительно другой со скоростью вдоль оси ОХ.
Любые изменения физических величин, связанные с сокращением размеров:
эффект замедления времени:
изменение массы тела при изменении энергии:
закон сложения скоростей:
в специальной теории относительности называют релятивистскими изменениями.
По законам классической физики полная энергия равна сумме кинетической и потенциальной энергий тела или частицы
Отсюда выразим кинетическую энергию тела
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии
В классической физике кинетическая энергия вычисляется по формуле
Получим ещё одно выражение
Выразим кинетическую энергию из формулы релятивистской энергии:
Поставим релятивистский радикал
Или другой способ выражения кинетической энергии, если использовать классическую кинетическую энергию, то получим
— выражение для определения релятивистской кинетической энергии.
Путём не сложных математических вычислений можно доказать, что формула определения кинетической энергии в классической физике
Давайте проверим работают ли главные законы механики — законы Ньютона в релятивистской физике.
Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.
Первый постулат СТО Эйнштейна: все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.
Внимание! Они не противоречат друг другу!
Третий закон Ньютона: силы с которыми тела действуют друг на друга равны по модулю и направлены вдоль одной прямой в противоположные стороны. Этот закон тоже работает в релятивистской физике (смотрите первый постулат СТО).
А что же со вторым законом классической механики? Второй закон Ньютона: ускорение тела прямо пропорционально силе и обратно пропорционально его массе.
Рассмотрим предельный случай: если на тело долгое время t
Отсюда 

Но давайте рассмотрим другую формулировку второго закона Ньютона, когда сила прямо пропорциональна изменению импульсов тела ко времени этого изменения:
В классической механике импульс равен произведению массы тела или частицы на его скорость: 
В релятивистской механике выражение импульса можно записать, используя преобразования Лоренца:
При скоростях намного меньших, чем скорость света 𝟅
Эти проявления — подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматривают как частный случай релятивистских законов при скоростях намного меньших скорости света и называют принципом соответствия. Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.
В природе существуют такие частицы (фотоны, мюоны, нейтрино), скорость которых равна или близка к скорости света. Массы таких частиц в состоянии покоя равны нулю, эти частицы называют безмассовыми. Они существуют только в движении, но во всех инерциальных системах отсчёта их импульс и энергия не равны нулю. Тогда подтверждается утверждение Эйнштейна, что масса – это мера энергии тела. Частицы, для которых масса является важной характеристикой — мерой инертности, называют массовыми.
Найдём соотношение между энергией и импульсом:
Взаимно уничтожаются подкоренные выражения, сокращается произведение массы на скорость света, и мы получим простое соотношение энергии и импульса, где нет зависимости от массы.
Энергия и импульс связаны соотношением
Поэтому во всех инерциальных системах отсчёта импульс и энергия не равны нулю. При превращениях элементарных частиц, обладающих массой покоя 

Во всех инерциальных системах отсчёта импульс частицы и её энергия связаны соотношением:
или
— эта формула является фундаментальным соотношением энергии и импульса для массовых частиц релятивистской механики. Эти соотношения экспериментально подтверждены.
Следовательно, для безмассовых частиц, где 

Основное выражение энергии через её импульс записывают так:
Отсюда, масса, движущейся частицы, будет равна
Если частица покоится, то её значение можно определить из основной формулы Эйнштейна взаимосвязи массы и энергии:
В обычных условиях, при нагревании тела или его охлаждении, при химической реакции, эти приращения массы происходят, их можно вычислить, но изменения массы не так заметны. Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.
Рассмотрим задачи тренировочного блока урока:
1. Чтобы выработать количество энергии, которой обладает тело массой 1 кг, Красноярской ГЭС потребуется времени _________ суток (1,5·107; 173,6; 182,3). Мощность Красноярской ГЭС 6000МВт.
Дано:
m = 1 кг
P = 6000 МВт = 6·109 Вт
t — ? (сутки)
Воспользуемся выражением, описывающим зависимость энергии тела от массы:
И зависимостью мощности от работы и времени:
Выразим секунды в часах, а затем в сутках:
Ответ: 173,6 суток.
2. Чему равен импульс протона, летящего со скоростью 8,3·107 м/с? На сколько будет допущена ошибка, если пользоваться формулами классической физики? Данные поученных вычислений занесите в таблицу:
|
Физические величины |
Показатели |
|
Масса покоя протона, m |
1,67·10-27 кг |
|
Скорость света, с |
3·108 м/с |
|
Скорость движения протона, 𝟅 |
8,3·107 м/с |
|
Импульс протона по классическим законам, рк |
? |
|
Импульс протона по релятивистским законам, рр |
? |
|
Разница в вычислениях импульса протона, |
? |
Воспользуемся формулами для определения импульса релятивистским и классическим способами:
Вычислим разницу показаний:
|
Физические величины |
Показатели |
|
Масса покоя протона, m |
1,67·10-27кг |
|
Скорость света, с |
3·108 м/с |
|
Скорость движения протона, 𝟅 |
8,3·107 м/с |
|
Импульс протона по классическим законам, рк |
1,38·10-19кг·м/с |
|
Импульс протона по релятивистским законам, рр |
5,2·10-19 кг·м/с |
|
Разница в вычислениях импульса протона, |
в 3,8 раза |






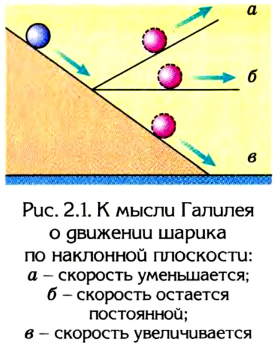

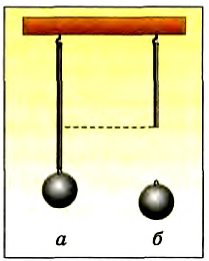
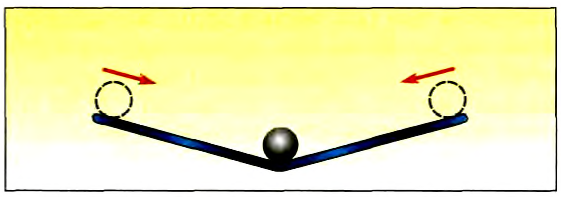
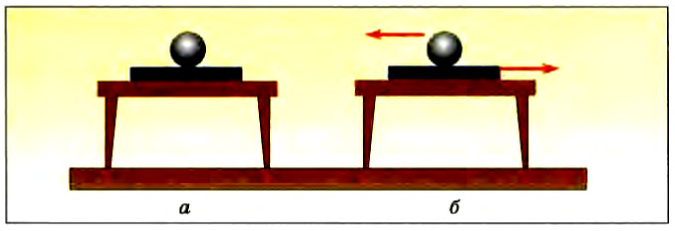
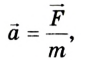
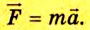
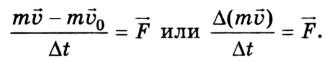
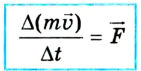
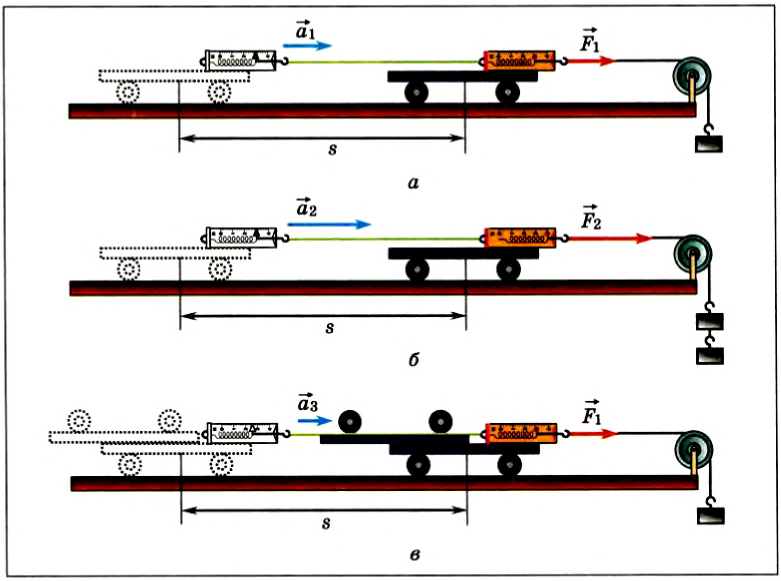
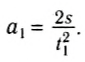
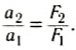
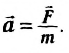
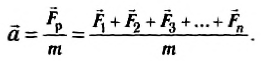
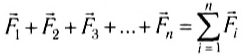
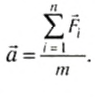
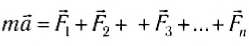
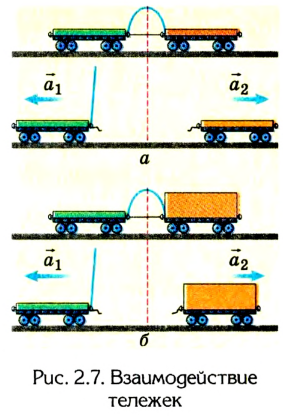
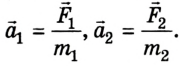
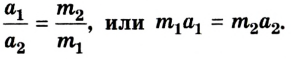
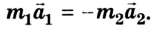
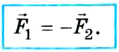
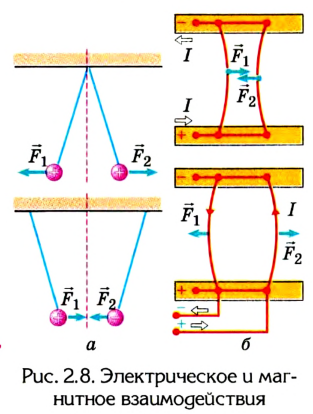
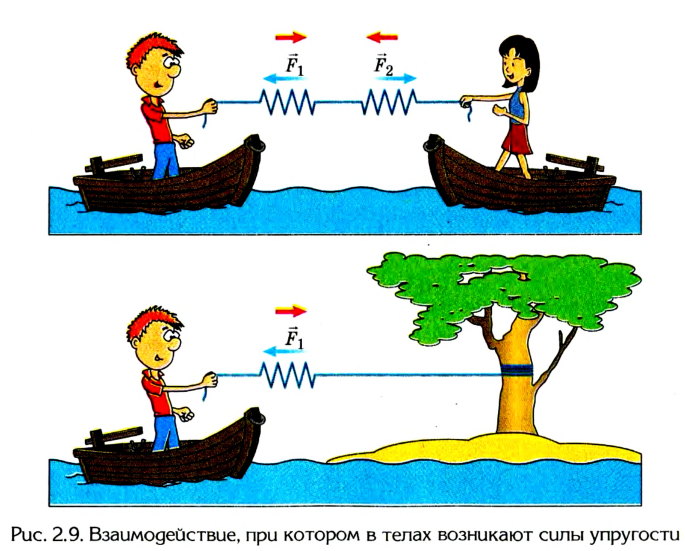
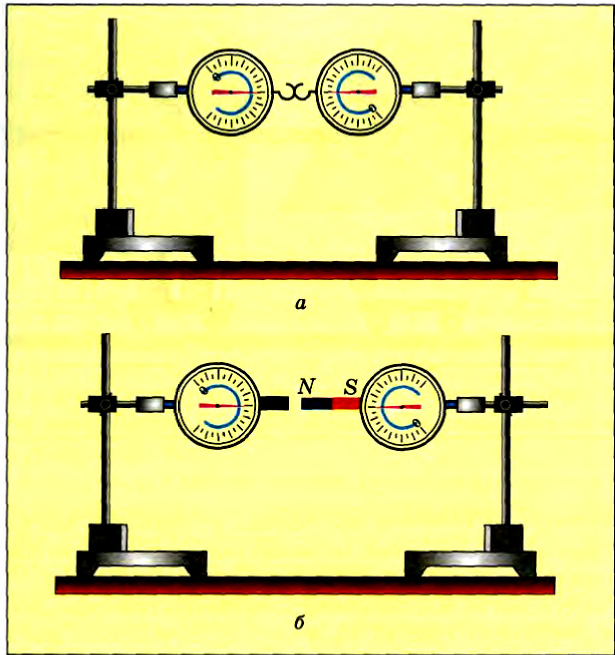
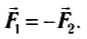
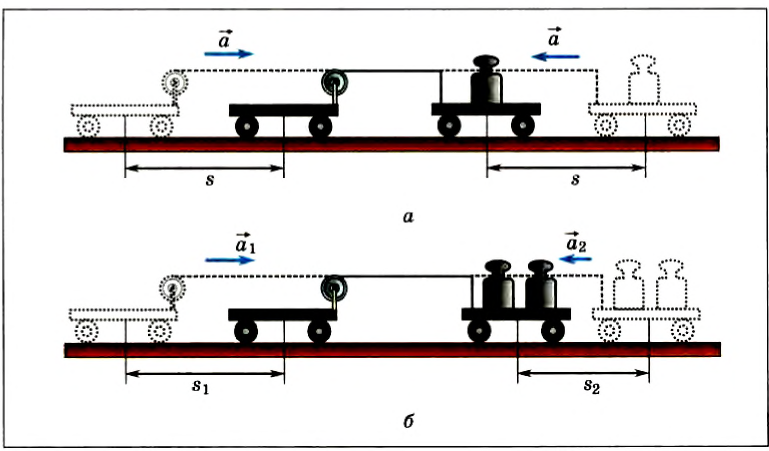

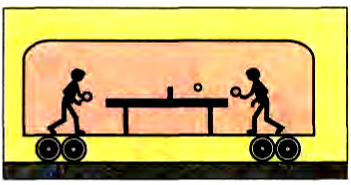
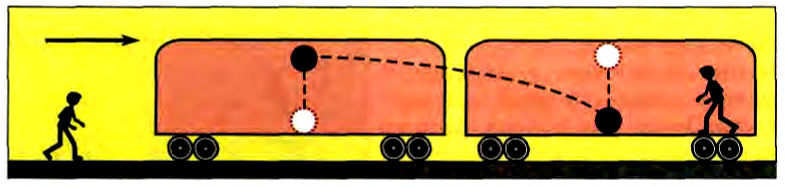

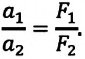
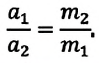


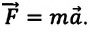
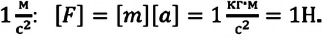
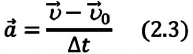
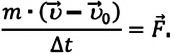
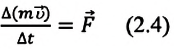
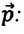
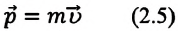
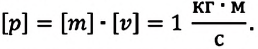
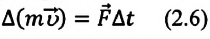
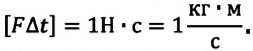

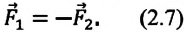
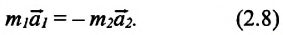
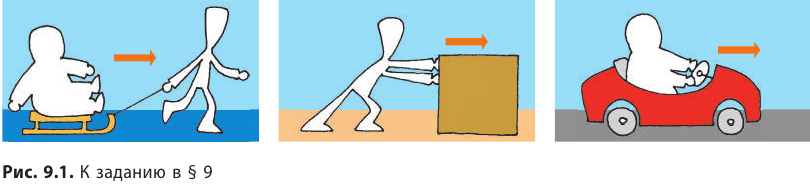
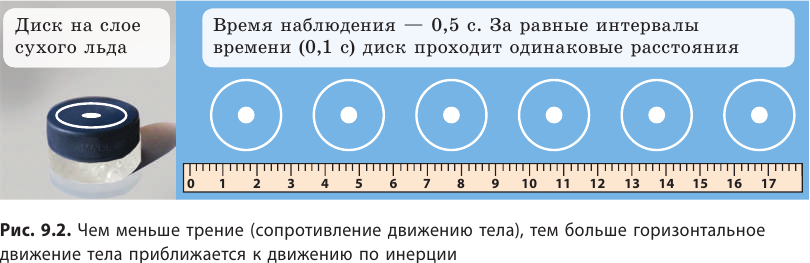
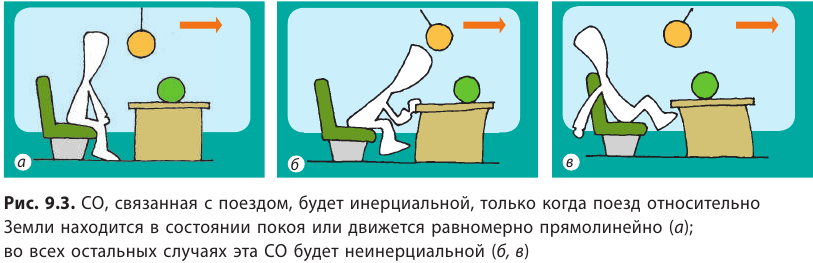
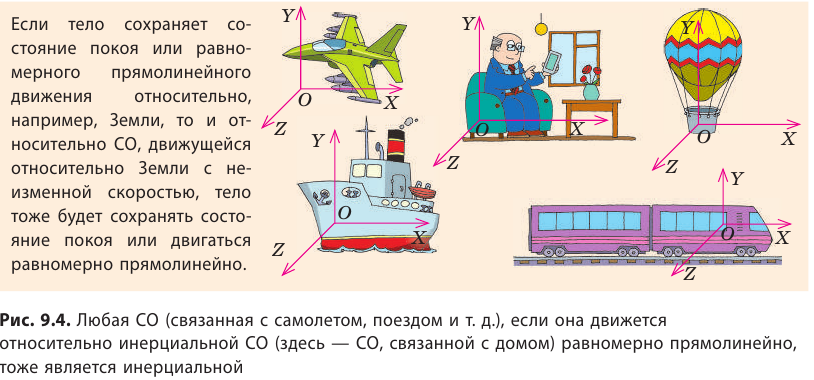
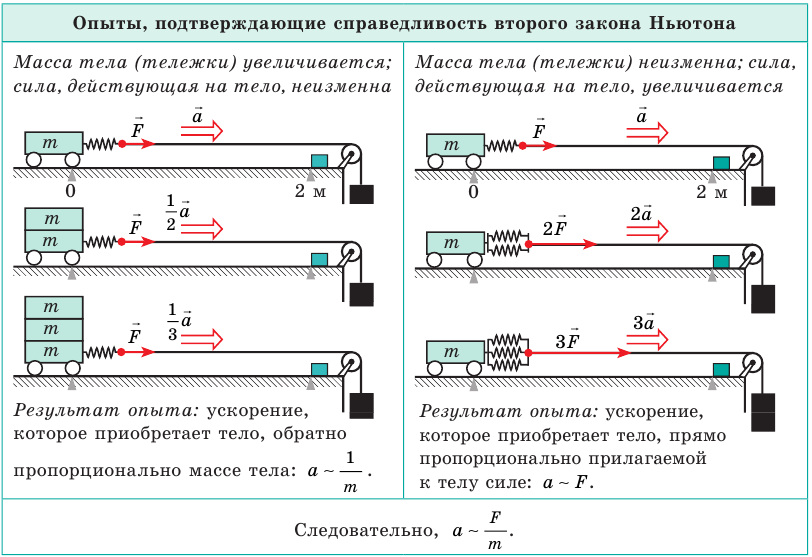
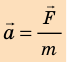
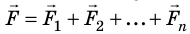 (рис. 10.2), поэтому второй закон Ньютона записывают так:
(рис. 10.2), поэтому второй закон Ньютона записывают так: 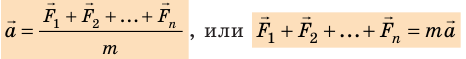
 .
.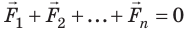 ), тело не будет изменять скорость своего движения ни по значению, ни по направлению:
), тело не будет изменять скорость своего движения ни по значению, ни по направлению: 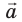 = 0 (рис. 10.3), а следовательно, будет двигаться равномерно прямолинейно или находиться в состоянии покоя.
= 0 (рис. 10.3), а следовательно, будет двигаться равномерно прямолинейно или находиться в состоянии покоя.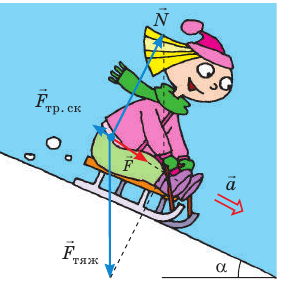
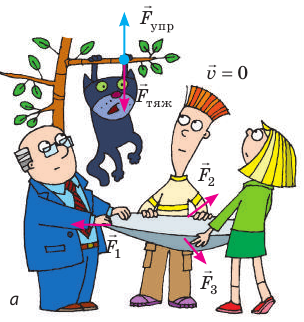
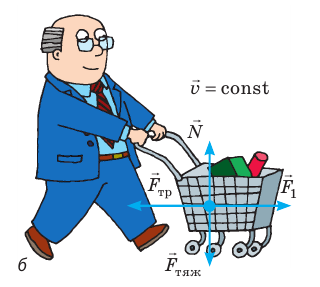
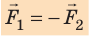

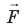 — векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются. Единица силы в СИ — ньютон (Н). Если на материальную точку одновременно действуют несколько сил, их можно заменить равнодействующей
— векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются. Единица силы в СИ — ньютон (Н). Если на материальную точку одновременно действуют несколько сил, их можно заменить равнодействующей 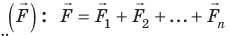
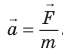 . Этот закон выполняется только в инерциальных СО.
. Этот закон выполняется только в инерциальных СО.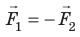 . Пара сил, возникающих при взаимодействии двух тел, не уравновешивают друг друга, поскольку приложены к разным телам.
. Пара сил, возникающих при взаимодействии двух тел, не уравновешивают друг друга, поскольку приложены к разным телам.














































