Как найти состояние равновесия системы дифференциальных уравнений - Исправление недочетов и поиск решений вместе с Examum.ru

Главная
Моделирование
Точки равновесия для динамических систем

08 Декабрь 2011 24898

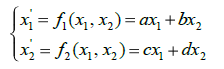
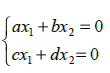
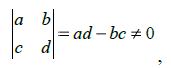
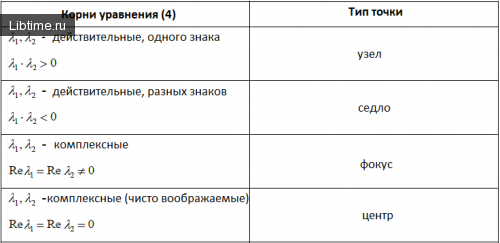
Пусть имеем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами: (1) Точки равновесия системы находят из решения системы: (2) Если определитель системы этой не равен нулю (3) то система имеет единственное решение. Тип положения равновесия определяется собственными числами матрицы системы, которые находят из характеристического уравнения: (4) где: — след матрици, — детерминант. Классификация точек равновесия в случае, когда Δ ≠ 0, представленная в таблице:

Классификация точек равновесия

Характер устойчивости положений равновесия

Собственные значения матрицы системы (1) однозначно определяют характер стойкости положений равновесия:

Устойчивый узел — если действительные части всех корней уравнения (4) отрицательны, то точка равновесия системы (1)асимптотически устойчива.
Седло, неустойчивый узел, неустойчивый фокус — если действительная часть хотя бы одного корня уравнения (4) положительна, то точка равновесия системы (1)неустойчивая.
Центр — если уравнение (4) имеет чисто воображаемые корни, то точка равновесия системы (1) устойчива, но не асимптотически

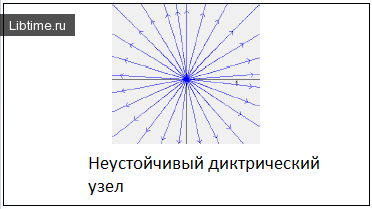
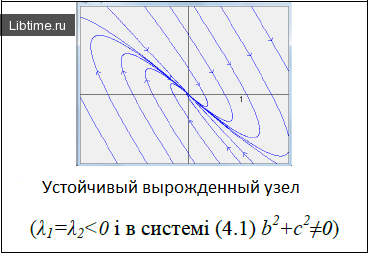
Ниже изображены фазовые портреты динамических систем для каждого типа точек равновесия. Направление стрелок на фазовой кривой указывает направление движения фазовой точки при возрастании t. 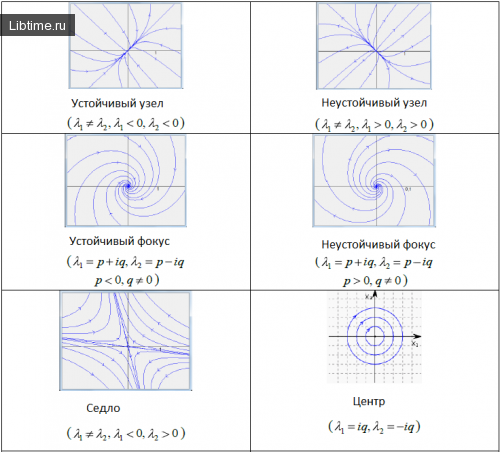Неустойчивый диктрический узел: Устойчивый вырожденный узел: Неустойчивый вырожденный узел: Бифуркационная диаграмма позволяет определить тип точки равновесия.

Рейтинг: 4,4/5 — 7
голосов

Источник

ПРИМЕР. Исследовать
на устойчивость нулевое решение системы дифференциальных уравнений .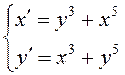

Рассмотрим функцию . Убедимся, что она
удовлетворяет условиям 1) – 3) теоремы Четаева.

3. Производная
в силу данной системы

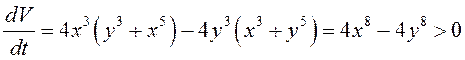
, если , то
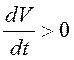
есть во всех внутренних точках . Поэтому нулевое решение системы неустойчиво.

ЗАМЕЧАНИЕ.
Если в некоторой окрестности начала координат функция и ее производная в силу системы положительно определены, то все
условия теоремы Четаева выполнены, следовательно, точка покоя неустойчива.

ЗАМЕЧАНИЕ. Метод
функций Ляпунова универсален и эффективен, но, недостаток метода в том, что не существует
конструктивного алгоритма построения функции Ляпунова для произвольной системы
дифференциальных уравнений. В простейших случаях можно искать функцию
Ляпунова в виде и т.д.. Для системы дифференциальных
уравнений вида

функция
является функцией Ляпунова. Точка покоя такой системы асимптотически устойчива.

ЗАМЕЧАНИЕ.
При исследовании устойчивости произвольного решения системы дифференциальных
уравнений следует сделать замену переменной , преобразовав исходную систему к системе дифференциальных
уравнений, имеющей нулевое решение.

ПРИМЕР.
Найти все положения равновесия системы 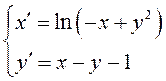и
исследовать их на устойчивость.

Чтобы найти все положения равновесия данной системы,
надо найти точки, в которых правые части обоих дифференциальных уравнений
одновременно обращаются в нуль:

– положения равновесия, или точки покоя.

1)
Исследуем на устойчивость точку .

Пусть , то есть . Подставив в систему
дифференциальных уравнений, получим: .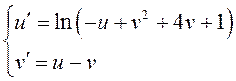

Легко убедиться, что эта система имеет тривиальное
решение Чтобы исследовать его на устойчивость,
составим систему первого приближения в соответствии с (12.11): 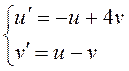. Характеристическое уравнение этой
системы: 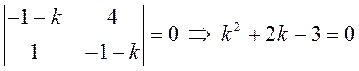. Так как , то
нулевое решение неустойчиво, а, значит, точка –
неустойчивое положение равновесия.

2)
Исследуем на устойчивость точку .

Аналогично,
сделав замену переменных , получим систему дифференциальных
уравнений: 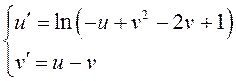, для которой система первого приближения
имеет вид: 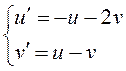. Характеристическое уравнение этой
системы: 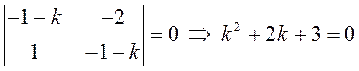. Все коэффициенты квадратного уравнения
положительны, значит и точка –
положение устойчивого равновесия.

Библиографический список

1.
Пискунов, Н.С. Дифференциальное и
интегральное исчисления / Н.С. Пискунов.– М.: Интеграл–пресс, 2005.– Т.1,
2.

2.
Араманович
И. Г .,
Лунц
Г . Л .,
Эльсгольц
Л . Э .
Функции
комплексного
переменного .
Операционное
исчисление .
Теория
устойчивости .
М.: Наука, 1970.– 415 c.

3.
Краснов М. Л .,
Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление .
Теория устойчивости . М.: Наука, 1981.– 304 c.

4.
Филиппов, А.Ф. Сборник задач по
дифференциальным уравнениям. – Ижевск: Регулярная и хаотическая динамика,
2000.–176 с.

Редактор

Компьютерная верстка, дизайн обложки

ИД № 06039 от 12.10.2001 г.

Сводный темплан 2011 г.

Подписано в печать . . . Формат 60×84 ¹/₁₆.
Бумага офсетная.

Отпечатано на дупликаторе. Усл. печ. л. .
Уч.-изд. л. .

Тираж . Заказ .

______________________________________________________

Издательство ОмГТУ. 644050, г. Омск, пр-т Мира, 11

Типография ОмГТУ

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

Чтобы найти положения равновесия, приравниваем производные к нулю. Получается $%y_2=y_1^2$% и $%y_1^2-y_1-2=0$%; корни $%2$% и $%-1$%. Положений равновесия получается два: $%(2;4)$% и $%(-1;1)$%. Исследуем их на устойчивость.

1) Делая замену $%z_1=y_1-2$% и $%z_2=y_2-4$%, линеаризуем систему вблизи нуля: $%z_1’=-(z_1+2)^2+(z_2+4)approx-4z_1+z_2$% и $%z_2’=lnfrac3{1-(z_1+2)+(z_1+2)^2)}=lnfrac3{3+3z_1+z_1^2}approx-z_1$% с точностью до бесконечно малых второго порядка. Матрица линеаризованной системы имеет вид $$begin{pmatrix}
-4 & 1 \
-1 & 0
end{pmatrix}.$$ Характеристическое уравнение имеет вид $%lambda^2+4lambda+1=0$%. Корни $%lambda=-2pmsqrt3$% вещественны и отрицательны. Это устойчивый узел.

2) Здесь $%z_1=y_1+1$%, $%z_2=y_2-1$%; после выделения линейных членов получается $%z_1’approx2z_1+z_2$%; $%z_2’approx z_1$%. Матрица равна $$begin{pmatrix}
2 & 1 \
1 & 0
end{pmatrix}.$$ Характеристическое уравнение имеет вид $%lambda^2-2lambda-1=0$%. Корни $%lambda=1pmsqrt2$% вещественны и имеют разные знаки. Это седло; положение равновесия неустойчивое.

Источник