Как найти совместную производительность труда

Математика

5 класс

Урок № 69

Задачи на совместную работу

Перечень рассматриваемых вопросов:

— введение понятий производительность, общая производительность, время работы;

— алгоритм решения задач на совместную работу арифметическим способом;

— отработка применения алгоритма при решении задач.

Тезаурус

Производительность (Р) – объём работы, выполняемый за единицу времени.

Время работы (Т) – время выполнения всей работы.

Общая производительность – объём работы, выполняемый совместно всеми работниками за единицу времени.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5-6 классы. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

На предыдущих уроках мы научились выполнять арифметические действия с обыкновенными дробями. Сегодня мы рассмотрим, как с помощью обыкновенных дробей решать задачи на совместное выполнение некоторой работы.

Под совместной работой можно понимать абсолютно любое действие: и одновременный поток воды из двух труб при наполнении бассейна, и изготовление деталей двумя рабочими, и вспашку поля несколькими тракторами, и набор текста на компьютере.

Всю работу мы будем принимать за единицу. А объём выполненной работы выражать как часть этой единицы.

Если какая-то работа выполняется за шесть часов, то за час выполняется одна шестая часть этой работы.

Объём работы, выполненный за единицу времени, называется производительностью. Она обозначается как Р.

Рассмотрим задачу.

Первый столяр может выполнить заказ за 36 часов, а второй – за 18 часов. За сколько часов этот заказ выполнят оба столяра, работая вместе?

Вся работа – 1

1-й столяр – 36 ч

2-й столяр – 18 ч

1-й и 2-й столяр – ? ч

(первый столяр за один час, или производительность Р₁ первого столяра)

(второй столяр за один час, или производительность Р₂ второго столяра)

(оба столяра за один час, или общая производительность Р)

(время выполнения всей работы совместно)

Ответ: за 12 ч.

Рассмотрим следующую задачу.

Одна труба заполняет бассейн за 60 минут, а вторая – за 20 минут. За сколько минут заполнится бассейн при включении обеих труб?

Вся работа – 1

1-я труба – 60 минут

2-я труба – 20 минут

Обе трубы – ?

часть бассейна (наполняет первая труба за одну минуту, или производительность Р₁)

часть бассейна (наполняет вторая труба за одну минуту, или производительность Р₂)

часть бассейна (заполняют обе трубы, работая вместе, или общая производительность Р)

минут (время заполнения бассейна двумя трубами)

Ответ: за 15 минут.

Рассмотрим задачу, в которой, зная время выполнения работы совместно, надо найти время работы одного из участников.

Работая вместе, два мастера Гжели выполняют заказ за шесть дней. Первый мастер, работая один, может выполнить этот заказ за 10 дней. За сколько дней этот заказ может выполнить второй мастер?

Вся работа – 1

1-й и 2-й мастер – 6 дней

1-й мастер – 10 дней

2-й мастер – ? дней

часть заказа (первый и второй мастера за один день, или общая производительность Р)

часть заказа (первый мастер за один день, или производительность Р₁)

часть заказа (выполнит второй мастер за один день, или производительность Р₂)

дней – время выполнения заказа вторым мастером

Ответ: за 15 дней.

Алгоритм решения задач на совместную работу

Т₁ – время, за которое первый объект самостоятельно выполнит всю работу;

Т₂ – время, за которое второй объект самостоятельно выполнит всю работу.

1. Всю выполненную работа принимаем за единицу.
2. Находим часть работы, выполненную первым объектом за единицу времени (производительность Р₁ = 1 ꞉ Т₁).
3. Находим часть работы, выполненную вторым объектом за единицу времени (производительность Р₂ = 1 ꞉ Т₂).
4. Находим часть работы, выполненную двумя (или более) объектами за единицу времени (общая производительность Р = Р₁ + Р₂).
5. Находим время, затраченное на выполнение всей работы всеми объектами (Т = 1 ꞉ Р).

Тренировочные задания

№ 1. Путешественник планирует пройти маршрут за семь дней. Какую часть маршрута он пройдёт за один день? За три дня? За пять дней? Какая часть маршрута останется не пройденной за эти же промежутки времени? Используйте следующие значения ; ; ; ; .

За 1 день

Пройденная часть маршрута – ?

Осталось пройти – ?

За 3 дня

Пройденная часть маршрута – ?

Осталось пройти – ?

За 5 дней

Пройденная часть маршрута – ?

Осталось пройти – ?

Пройденная часть маршрута за день – это производительность путешественника. И находится она так же, как и другая производительность. Найдём часть маршрута, пройденную за один день:

Очевидно, что за три дня путешественник пройдет в три раза больше, чем за день. Рассчитаем эту часть пути:

Чтобы найти оставшуюся часть маршрута, надо из всего маршрута, то есть единицы, вычесть пройденную часть. Найдём, например, какую часть маршрута осталось пройти через три дня: .

Аналогично действуем и в остальных случаях.

Правильный ответ:

За 1 день

Пройденная часть маршрута –

Осталось пройти –

За 3 дня

Пройденная часть маршрута –

Осталось пройти –

За 5 дней

Пройденная часть маршрута –

Осталось пройти –

№ 2. Подберите к каждому действию правильное пояснение.

Два тракториста вспахали поле за 6 ч совместной работы. Первый тракторист мог бы один выполнить ту же работу за 10 ч. За сколько часов второй тракторист может вспахать поле?

Пояснения к действиям:

• Время выполнения всей работы вторым трактористом;
• Общая производительность обоих трактористов;
• Часть всей работы, выполняемая вторым трактористом за один час.

Действия:

Рассмотрим первое действие. Единица делится на шесть, где единица – это вся работа, а шесть – время совместной работы. Значит, этим действием мы находим общую производительность обоих тракторов.

Во втором действии из общей производительности вычитаем . Так как первый тракторист выполняет работу за 10 часов, то – это производительность первого тракториста. Значит, мы находим производительность второго тракториста, то есть объём работы, который он выполнил за один час.

В третьем действии единица (вся работа) делится на производительность второго тракториста: таким образом, мы находим время выполнения всей работы вторым трактористом.

Правильный ответ:

– это общая производительность обоих трактористов.

– это часть всей работы, выполняемая вторым трактористом за 1 ч.

ч – это время выполнения всей работы вторым трактористом.

Суть задач на производительность следующая: некоторую работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Они могут выполнять эту работу либо по отдельности, либо совместно друг с другом. Алгоритм решения здесь такой же, как и алгоритм решения задач на движение:

1. Анализ данных.
2. Составление таблицы.
3. Составление уравнения.
4. Решение уравнения.

Основные особенности решения задач на производительность:

• Задачи на производительность схожи с задачами на движение. Основная формула при решении: V = v·t. Сравните её с формулой для решения задач на движение S = v·t. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.
• Объем работы может быть не дан по условию и его не нужно находить при решении задачи (нам просто напросто не важно, какой объем работы выполняется). В таком случае его можно обозначить какой-нибудь буквой, например, V или A. В процессе решения эта переменная, которой мы обозначили объем, сократится и её значение не придется находить.
• Также, если объем работы не дан по условию, удобно принять его просто за 1; тогда время t, требующееся для выполнения всей работы, иv – производительность труда, связаны формулой:

$ t=frac{1}{upsilon}. $

• В отличие от задач на движение, в задачах на производительность скорости выполнения работы не могут вычитаться, а могут только складываться друг с другом. Если два человека или механизма по отдельности работают с производительностями v₁ и v₂, то вместе они будут работать быстрее (никак не медленнее), с суммарной производительностью v₁ + v₂, а время совместной работы будет равно:

$ t=frac{1}{upsilon_{1}+upsilon_{2}} $

Пример:

Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

Решение:

В задаче требуется найти производительность второго рабочего. Примем его скорость за x. Заполним таблицу.

	v, дет/ч	t, ч	V, дет
Первый рабочий	x + 5	$ frac{200}{x+5} $	200
Второй рабочий	x	$ frac{200}{x} $	200

В условии задачи сказано, что первый рабочий выполняет заказ на 2 часа быстрее, чем второй. На основании этого составим уравнение:

$ {frac{200}{x+5}+2=frac{200}{x} frac{200+2x+10}{x+5}=frac{200}{x}.} $

2x² + 210x = 200x + 1000;

x² + 5x – 500 = 0.

Получаем два корня, x₁= 20 и x₂= –25. Второй корень не подходит, так как производительность не может быть отрицательной.

Ответ: 20 дет/ч.

Виды задач на производительность:

1. Задачи на совместную работу:

Задачи на совместную работу — это тип задач, в которых объектами, выполняющими работу, являются люди или группы людей: рабочие, ученики, операторы, бригады рабочих и т п. Объекты могут выполнять работу по отдельности, а могут — вместе.

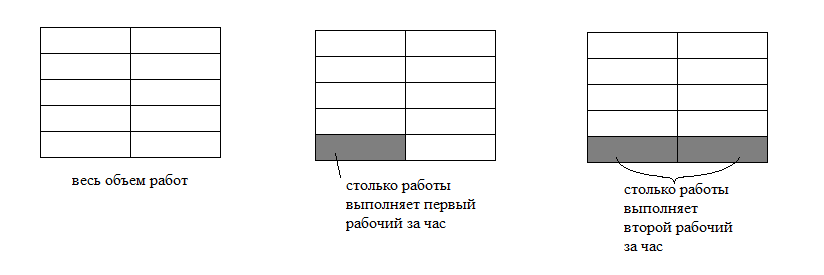
Разберем простой пример. Двум рабочим требуется выполнить работу. Допустим, первый рабочий выполняет всю работу за 10 часов, а второй — за 5. Давайте найдем, за сколько часов рабочие справятся с работой, выполняя её вместе.

Получается, что если принять весь объем работ за 1, то первый рабочий выполняет $ frac{1}{10} $ всей работы за час, а второй $ frac{1}{10} $ то есть $ frac{1}{10} $ всей работы за час. На рисунке весь объем работ — это 10 «кирпичиков», первый выполняет 1 «кирпичик» за час, а второй — 2. Тогда вместе они будут выполнять $ frac{1}{10}+ frac{1}{5}= frac{3}{10} $  всей работы за час, или 3 «кирпичика»:

Чтобы найти совместную производительность рабочих, мы сложили друг с другом их собственные производительности. Теперь, чтобы найти время, за которое оба рабочих справятся с работой, выполняя её вместе, разделим полный объем работ на совместную производительность:

$ 1/frac{3}{10}=frac{10}{3}=3frac{1}{3} $

То есть вместе рабочие справятся с работой за 3 $ frac{1}{3} $ часа, или за 3 часа 20 минут.

2. Задачи на бассейны и трубы:

Отдельно можно выделить группу задач на производительность — задачи на заполнение бассейна несколькими трубами. В таких задачах рабочим будут соответствовать насосы (или трубы) разной производительности, а объему работы — объем бассейна или иного резервуара.

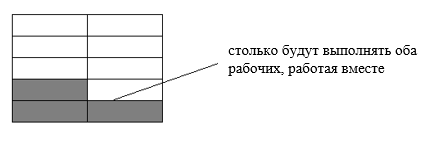
Рассмотрим пример. Две трубы наполняют бассейн за 6 часов, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?

Получается, что за 1 час две трубы наполняют $ frac{1}{6} $ часть бассейна, а одна первая труба наполняет $ frac{1}{9} $ часть бассейна: Так как вместе трубы наполняют бассейн водой со скоростью, равной сумме скоростей отдельно каждой из труб, то вторая труба наполняет бассейн со скоростью $ frac{1}{6}- frac{1}{9}= frac{1}{18} $.

Таким образом, вторая труба заполнит бассейн за $ 1/frac{1}{18}=18 $ часов.

2-й способ решения — без таблицы

Как обойтись без составления таблицы?

Сразу составить уравнение.

Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.

Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.

Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.

А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.

Во-первых, сравним формулы:

Движение	Работа
( displaystyle v=frac{S}{t})	( displaystyle P=frac{A}{t})
Скорость движения	Скорость выполнения работы, т.е. производительность
Пройденный путь	Выполненная работа
Потраченное на движение время	Потраченное на работу время

Теперь рассмотрим задачу:

Пример №1

Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.

Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?

Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).

Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:

( displaystyle frac{112}{x}=frac{112}{x+1}+2).

То же самое уравнение! Вот и получается, что работа и движение – одно и то же.

Как решать задачи на совместную работу

Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).

Пример №2

Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).

За какое время они заполнят бассейн, работая вместе?

Решение

Во-первых, давай придумаем аналогию с движением.

Придумал?

Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).

А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.

Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!

Тогда что нас просят найти? Время, через которое они встретятся.

Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.

Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).

Итак,

( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).

Тогда время, за которое с такой производительностью будет выполнена работа ( A):

( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)

Итак, правило:

При совместной работе производительности складываются

А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.

Пример 8

На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?

Решение:

Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).

Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).

Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).

( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.

То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).

Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:

                        
 Задачи на совместную работу и производительность

Задачи этого типа
содержат обычно сведения о выполнении несколь­кими субъектами (рабочими,
механизмами, насосами и т.п.) некоторой работы, объём которой не указывается и
не является искомым (например, перепечатка рукописи, изготовление деталей,
рытьё тран­шей, заполнение через трубы водоёма и т.д.). Предполагается, что
выполняемая работа проводится равномерно, т.е. с постоянной для каждо­го
субъекта производительностью. Так как величина выполняемой работы (или объём
заполняемого бассейна, например) нас не интересуют, то объём всей работы. или
бассейна принимается за единицу. Время t, требующееся для выполнения всей работы, и Р — производительность
труда, то есть величина работы, сделанной за единицу времени, связаны

соотношением P=1/t .Полезно знать стандартную схему решения типовых
задач.

Пусть один рабочий
выполняет некоторую работу за х часов, а другой — за у часов. Тогда за один час
они выполнят соответственно 1/x и 1/y  часть работы. Вместе за один час они выполнят 1/x +1/y  часть работы.
Следовательно, если они будут работать вместе, то вся работа будет выполнена
за   1/ (1/x+ 1/y)

Решение задач на совместную работу вызывает у
учащихся трудности, поэтому при подготовке к экзамену  можно начать с решения
самых простых задач. Рассмотрим тип задач, при решении которых достаточно
ввести только одну переменную.

Задача 1. Один штукатур может
выполнить задание на 5 часов быстрее другого. Оба вместе они выполнят это
задание за 6 часов. За сколько часов каждый из них выполнит задание?

Решение. Пусть  первый
штукатур выполняет задание за x часов, тогда второй  штукатур выполнит это задание за
x +5 часов. За 1 час
совместной работы они выполнят  1/x + 1/(x+5) задания. Составим уравнение

6×(1/x+ 1/(x+5))= 1 или x² —7x -30 = 0. Решив данное уравнение ,получим x= 10 и   x= -3. По условию
задачи x – величина
положительная. Следовательно, первый штукатур может  выполнить работу за 10
часов , а второй — за 15 часов.

Задача 2. Двое рабочих
выполнили работу за 12 дней. За сколько дней может выполнить работу каждый
рабочий, если одному из них на выполнение всей работы потребовалось на 10 дней
больше, чем другому?

Решение. Пусть первый рабочий
тратит на всю работу x дней, тогда второй- (x-10) дней. За 1 день
совместной работы они выполняют 1/x+ 1/(x-10) задания. Составим  уравнение

12×(1/x+ 1/(x-10)= 1 или  x²- 34x +120=0.  Решив данное
уравнение, получим x=30 и x= 4. Условию задачи удовлетворяет только x=30 .Поэтому  первый
рабочий может выполнить работу за 30 дней, а второй – за 20 дней.

Задача 3. За
4 дня совместной работы двумя тракторами было вспахано 2/3 поля. За сколько
дней можно было бы вспахать все поле каждым трактором , если первым его можно
вспахать на 5 дней быстрее ,чем вторым?

Решение. Пусть 
первый трактор тратит на выполнение задания x
дней, тогда второй – x+ 5
дней.  За 4 дня совместной работы оба трактора вспахали 4×(1/x +
1/(x+5)) задания, то есть 2/3 поля.
Составим уравнение  4×(1/x+
1/ (x+5)) = 2/3  или x² -7x -30 = 0. . Решив
данное уравнение, получим x= 10 и   x= -3. По условию задачи x – величина
положительная. Следовательно, первый трактор может  вспахать поле за 10 часов ,
а второй — за 15 часов.

Задача 4 . Маша может напечатать
10 страниц за 1 ч. Таня – 4 страницы за 0,5 , а Оля- 3 страницы за 20 минут.
Как девочкам распределить 54 страницы текста между собой , .чтобы каждая
работала в течение одного и того же времени?

Решение. По условию Таня
печатает 4 страницы за 0,5ч, т.е. 8 страниц за 1ч., а Оля – 9 страниц за 1ч.
Обозначив за Х часов- время, в течение которого девочки работали, получим
уравнение

                               10Х +8Х+9Х =54,
откуда Х= 2.

Значит, Таня должна напечатать  20 страниц,
Таня-16 страниц, а Оля 18 страниц. 

Задача 5. На двух множительных
аппаратах, работающих  одновременно, можно сделать копию рукописи за 20 мин. За
какое время можно выполнить эту работу на каждом аппарате в отдельности, если
известно, что при работе на первом для этого потребуется на 30 мин меньше, чем
при работе на втором?

Решение. Пусть Х мин — время,
которое требуется на выполнение копии на первом аппарате, тогда  Х+30 мин-
время работы на втором аппарате. Тогда 1/Х  копии выполняет первый аппарат за 1
мин, а 1/(Х+30) копии- второй аппарат.

Составим уравнение: 20× (1/Х + 1/(Х+30)) = 1,
получим X²-10X-600= 0. Откуда Х =30
и Х = — 20. Условию задачи удовлетворяет  Х= 30. Получили : 30 мин — время , за
которое первый аппарат сделает копию, 60 мин- второй.

Задача 6.Фирма А может
выполнить некоторый заказ на производство игрушек на 4 дня быстрее, чем фирма
В. За какое время может выполнить этот заказ каждая фирма, если известно , что
при совместной работе за 24 дня они выполняют заказ в 5 раз больший?

Решение. Обозначив за Х дней-
время , необходимое фирме А на выполнение заказа, тогда Х + 4 дней  — время для
фирмы В. При составлении уравнения необходимо учесть , что за 24 дня  совместной
работы будет выполнено не 1 заказ, а 5 заказов. Получим , 24× (1/X + 1/(X+4)) = 5.Откуда 
следует 5 Х²- 28Х-96 = 0. Решив  квадратное уравнение получаем,  Х = 8 и Х = —
12/5.  Первая фирма может выполнить заказ за 8 дней , фирма  В – за 12 дней.

При решении следующих задач необходимо вводить
более одной переменной и решать уже системы уравнений.

Задача 7. Двое рабочих выполняют
некоторую работу. После 45 мин совместной работы первый рабочий был переведен
на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 ч 15
мин. За какое время мог бы выполнить всю работу каждый рабочий в отдельности,
если известно, что второму для этого понадобится на 1 ч больше, чем первому?

Решение. Пусть первый рабочий выполняет всю работу за х
часов, а второй — за у часов. Из условия задачи имеем х = у -1. За 1 ч первый

рабочий выполнит 1/x  часть работы, а второй
– 1/y  часть работы. Т.к. они работали
вместе ¾ ч, то за это время они выполнили   ¾ ( 1/x + 1/y)

часть работы. За 2и
1/4ч работы второй выполнил  9/4× (1/y) часть работы. Т.к. вся работа
выполнена, то составляем уравнение————————— ¾ ( 1/x+1/y)+9/4×1/y=1 или

 ¾ ×1/x + 3 ×1/y =1

Подставив значение  x в это уравнение,
получаем ¾× 1/ (y-1)+ 3×1/y = 1. Сводим это уравнение
к квадратному  4у² -19у + 12 = 0,
которое имеет

решения у₁
=  ч и у₂
= 4 ч. Первое решение не подходит (оба рабочие только вместе
работали ¾ ч!). Тогда у = 4 , а х = 3.

Ответ. 3 часа, 4 часа.

 Задача 8. Бассейн может
наполниться водой из двух кранов. Если первый кран открыть на 10 мин, а второй
— на 20 мин, то бассейн будет наполнен.

 Если первый кран
открыть на 5 мин, а второй — на 15 мин, то заполнится 3/5 бассейна.

За какое время из
каждого крана в отдельно­сти может заполниться весь бассейн?

Решение. Пусть из первого крана
можно заполнить бассейн за х мин, а из второго — за у 1 мин. Первый кран
заполняет  часть бассейна, а второй . За 10 мин из первого крана заполнится  часть бассейна, а за 20 мин из второго крана — . Т.к. бассейн будет заполнен, то получаем первое уравнение:
. Аналогично составляем второе уравнение   (заполняется на весь бассейн, а только его объема). Для упрощения решения задачи введём новые
переменные:  Тогда имеем линейную систему уравнений:

5u + 15v = 3/5

10u + 20v =1,

,

решение
которой будет u=v=. Отсюда получаем
ответ: x= мин, y=50 мин.

Задача 9. Двое выполняют
работу. Сначала первый работал  времени, за которое второй выполняет всю работу. Затем
второй рабо­тал  времени, за  которое первый закончил бы оставшуюся
работу. Оба они выполнили только  всей работы. Сколько времени требуется каждому для
выполнения этой работы, если известно, что при совместной работе они сделают её
за 3
ч 36 мин?

Решение. Обозначим через х
часов и у часов время, за которое вы­полняют всю работу первый и второй
соответственно. Тогда  и

 — те части работы, которые они выполняют за 1ч. Работая (по усло­вию)  времени, первый
выполнит  часть работы. Останется невыполненной  часть работы, на которую первый затра­тил бы  часов. По условию второй работает 1/3 этого времени. Тогда
он выполнит  часть работы. Вдвоём они выполнили только  всей работы. Следовательно, получаем уравнение. Работая совместно, за 1 час оба сделают + часть работы. Так как по условию задачи они сделают
эту работу за 3 ч 36 мин (то есть зa 3 часа), то за 1 час они сделают  всей работы. Отсюда  1/x + 1/y = 5/18. Обозначив в первом
уравнении , получим квадратное уравнение

6t² — 13t + 6 = 0, корни которого равны
t₁ =2/3 , t₂  =3/2. Так как неизвестно,
кто работает быстрее, то рассматриваем оба случая.

а) t  =  =>  у =   х. Подставляем  у  во второе уравнение:  Очевидно, что это не является решением

задачи, так как вместе они делают работу
больше чем за З ч.

б) t=3/2
=> y=3/2x. Из второго уравнения
имеем 1/x +2/3× 1/x =5/18.Отсюда х=6, у =9.

 Задача10. В резервуар поступает
вода из двух труб различных диа­метров. В первый день обе трубы, работая
одновременно, подали 14 m³
воды. Во второй день была включена лишь малая труба. Она
подала 14 м³ воды, проработав на 5 ч дольше, чем в первый день. В
третий день работа продолжалась столько же времени, сколько во второй, но снача­ла
работали обе трубы, подав 21 м³ воды. А затем работала лишь боль­шая
труба, подавшая еще 20 м³ воды. Найти производительность каждой
трубы.

Решение. В данной задаче нет
абстрактного понятия «объем водо­ема», а указываются конкретные
объемы воды, которые поступают по трубам. Однако методика решения задачи
фактически остается прежней.

Пусть меньшая и
большая трубы перекачивают за 1 час  х  и у м³ во­ды. Работая
вместе, обе трубы подают  х + у м³ воды.

Следовательно, в
первый день трубы работали 14/(x+y) часов. Во второй день малая труба работала на 5
часов больше, т. е. 5+14/(x+y). За это

время она подала 14
м³ воды. Отсюда получаем первое уравнение 14 или 5+14/(x+y)=14/x. В третий день обе трубы вместе работали21/(x+y) часов, а затем
большая труба работала 20/x часов. Суммарное время труб совпадает со временем
работы первой трубы во второй день, т. е.

5+14/(x+y) =21/(x+y)+ 20/x. Так как левые части
уравнения равны, то имеем . Освободившись от знаменателей, получаем однородное
уравнение 20x²+27xy-14y²=0. Разделив уравнение на y² и обозначив x/y=t, имеем 20t²+27t-14=0. Из двух корней
этого квадратного уравнения (t₁=, t₂=) по смыслу задачи подходит только t=. Следовательно, x=y. Подставив x в первое уравнение, находим y=5. Тогда x=2.

Задача 11. Две бригады, работая
совместно, вырыли траншею за два дня. После этого они начали рыть траншею той
же глубины и ширины, но длиннее первой в 5 раз. Сначала работала только первая
бригада, а затем только вторая бригада, выполнив в полтора раза меньший объем
работы, чем первая бригада. Рытье второй траншеи было закончено за 21 день. За
сколько дней вторая бригада смогла бы вырыть первую траншею, если известно, что
объем работы, выполняемый первой брига­дой за один день, больше объема работы,
выполняемого за один день второй бригадой?

Решение. Эту задачу удобнее
решать, если привести выполняемую работу к одному масштабу. Если обе бригады
вырыли, работая вместе, первую траншею за 2 дня, то, очевидно, вторую траншею
(в пять раз длиннее) они вырыли бы за 10 дней. Пусть первая бригада вырыла бы
эту траншею за х дней, а вторая — за у, т.е. за 1 день первая вырыла бы  часть траншеи, вторая — за 1/y , а вместе -1/x+1/y часть траншеи.

Тогда имеем. Бригады при рытье
второй траншеи работали раздельно. Если вторая бригада выполнила объем работы m, то (по условию
задачи) — первая бригада . Так как m + m = m равно объему всей
работы, принимаемому за единицу, то m=. Следовательно, вторая бригада выкопала  траншеи и затратила на
это у дней. Первая бригада выкопала  траншеи и затратила х дней. Отсюда имеем  или х =35-. Подставляя х в первое уравнение, приходим к
квадратному уравнению 2у²
— 95у +1050 = 0, корнями которого будут у ₁ =  и у₂ = 30. Тогда соответственно х₁ = и х₂ =15. Из условия задачи выбираем нужное: у = 30. Так как найденное значение
относится ко второй траншее, то первую траншею (в пять раз короче) вторая
бригада вырыла бы за 6 дней.

Задача 12. Три экскаватора
участвовали в рытье котлована объемом 340
м³. За час первый экскаватор вынимает 40
м³ фунта, второй — на с м³ меньше первого, а третий — на
2с больше первого. Сначала работали одновременно первый и второй экскаваторы, и
выкопали 140 м³ грунта. Затем оставшуюся часть котлована выкопали,
работая одновременно, первый и третий экскаваторы. Определить значения с (0<с<15), при котором котлован был
выкопан за 4 ч, если работа велась без перерыва.

Решение. Так как первый
экскаватор вынимает 40 м³ грунта в час, то второй — (40-с) м³,
а третий — (40+2с) м³ фунта в час. Пусть пер­вый и второй экскаваторы
вместе работали х часов. Тогда из условия задачи следует (40+40-с)х = 140 или
(80-с)х = 140. Если первый и тре­тий экскаваторы работали вместе у часов, то
имеем (40+40+2с)у = 340-140 или (80+2с)у — 200. Так как общее время работы
равно 4 часам, то получаем для определения с следующее уравнение х + у = 4 или

Это уравнение
равносильно квадратному уравнению с²
-30с+ 200 = 0, решениями которого
будут с₁ = 10 м³ и с₂ = 20м³. По
условию задачи подходит только

с = 10
м³.

Задача 10. Каждому из двух
рабочих поручили обработать одинако­вое количество деталей. Первый начал работу
сразу и выполнил ее за 8 ч. Второй же потратил сначала больше 2 ч на наладку
приспособления, а затем с его помощью закончил работу на 3 ч раньше первого.
Извест­но, что второй рабочий через час после начала своей работы обработал
столько же деталей, сколько к этому моменту обработал первый. Во сколько раз
приспособление увеличивает производительность станка (т.е. количество обрабатываемых
деталей за час работы)?

Решение. Это пример задачи, в
которой не все неизвестные надо находить.

Обозначим время
наладки станка вторым рабочим через х (по условию х>2). Пусть необходимо
было обработать каждому по n деталей.

Тогда первый рабочий в
час обрабатывает   деталей, а второй  деталей. Оба рабочих одинаковое число деталей
обработали через час после начала работы второго. Это означает, что  Отсюда получаем уравнение для определения х : х² -4х +
3-0 корнями которого будут х₁
= 1 и х₂ = 3. Т. к.

х > 2 , то
необходимое значение — это х = 3. Следовательно, второй рабочий обра­батывает в
час  деталей. Т. к. первый рабочий в час обрабатывает

деталей, то отсюда находим, что приспособление
увеличивает производительность труда в  = 4 раза.

Задача 13. Трое рабочих должны изготовить некоторое
количество деталей. Сначала к работе приступил только один рабочий, а через
некоторое время к нему присоединился второй. Когда 1/6 часть всех деталей была
изготовлена, к работе приступил и третий рабочий. Работу они закончили
одновременно, причем каждый изготовил одинаковое коли­чество деталей. Сколько
времени работал третий рабочий, если извест­но, что он работал на два часа
меньше второго и что первый и второй, работая вместе, могли бы изготовить все
требуемое количество деталей на 9 часов раньше, чем это бы сделал бы третий,
работая отдельно?

Решение. Пусть первый рабочий
работал х часов, а третий — у часов. Тогда второй рабочий работал на 2 часа
больше, т. е. у+2 часа. Каждый из них изготовил равное количество деталей, т.
е. по 1/3 всех деталей. Следовательно, все детали первый изготовил бы за 3х
часов, второй за 3(у+2) часов, а третий — за 3у часов. Поэтому первый
изготовляет в час  часть всех деталей, второй —  и третий —  .

Так как все трое за время совместной работы
изготовили  всех дета­лей, то получаем первое уравнение (все трое
вместе работали у часов)

.                           (1)

Первый и второй,
работая вместе, изготовили бы вместе все детали на 9 часов раньше, чем это
сделал бы третий рабочий, работая один. Отсюда получаем второе уравнение

.                                    
(2)

Эти два уравнения
легко приводятся к равносильной системе

Выражая из второго
уравнения х и подставляя в первое уравнение, по­лучаем у³ -5у² — 32у — 36 = 0. Это
уравнение разлагается на множители (y — 9)(у + 2)² = 0.

Т. к. у > 0, то
уравнение имеет только один нужный корень у = 9. Ответ: у = 9.

Задача 14. В котлован равномерно
поступает вода, 10 одинаковых насосов, действуя одновременно, могут откачать
воду из заполненного котлована за 12 часов, а 15 таких насосов — за 6 ч. За сколько времени могут откачать воду
из заполненного котлована 25 таких насосов при совместной работе?

Решение. Пусть объем котлована
Vm³, а производительность
ка­ждого насоса — х м³ в час. Вода в котлован поступает непрерывно. Т. к. неизвестно количество
ее поступления, то обозначим через у м³ в час — объем поступления
воды в котлован. Десять насосов за 12 часов отка­чают х = 120х воды. Это
количество воды равно полному объему котлована и объему той воды, которая поступит
в котлован за 12 часов. Весь этот объем равен V+12y. Приравнивая эти
объемы, составляем первое уравнение 120х = V + 12y .

Аналогично
составляется уравнение для 15 таких насосов: 15-6x = V + 6y или 90x = V + 6y. Из первого уравнения
имеем V = 120х — 12у. Подставляя V во второе уравнение, получаем у = 5х.

Время, в течение
которого будут действовать 25 таких насосов, неиз­вестно. Обозначим его через t . Тогда, учитывая
условия задачи, по аналогии составляем последнее уравнение. Имеем 25tx = V + ty . Под­ставляя в это
уравнение у и V находим 25tx = 120х -12  5х +t  5х или 20tx = 60х . Отсюда получаем t = 3 часа. Ответ: за 3 часа.

Задача 15. Две бригады работали
вместе 15 дней, а затем к ним присоединилась третья бригада, и через 5 дней
после этого вся работа была закончена. Известно, что вторая бригада вырабатывает
за день на 20% больше первой. Вторая и третья бригады вместе могли бы выпол­нить
всю работу за  того времени, которое требуется для выполнения всей
работы первой и третьей бригадами при их совместной работе. За какое время
могли бы выполнить всю работу все три бригады, работая совместно?

Решение. Пусть всю работу,
работая отдельно, первая, вторая и третья бригады выполняют соответственно за
х, у и z дней. Тогда в день
они выполняют  часть работы. Преобразуя первое
условие задачи в уравнение, считая, что весь объём работы равен единице,
получаем

15 или

20.

Так как вторая бригада
вырабатывает 120% того, что делает первая (на 20% больше), то имеем  или .         (2)

Вторая и третья
бригады выполнили бы всю работу за 1/ дней, а первая и третья – за 1/ дней. По условию первая величина равна

Второй, то есть 1/. Отсюда получаем третье уравнение .

В задаче требуется
определить время выполнения всей работы тремя бригадами, работающими вместе, то есть величину 1/.

Очевидно, что решать
систему уравнений (1)-(3) удобнее, если вве­сти новые переменные: , Требуется найти величину

 l/(u + v+w).Тогда имеем
равносильную систему

Решая эту линейную
систему, легко находим  u= Тогда искомая величина равна 1/ Таким образом, работая вместе все три бригады
выполнят всю работу за 16 дней.

Ответ: за 16 дней.

Задача 16. Две фабрики должны
совместно переработать некоторое количество сырья. Если бы производительность
второй фабрики повысилась вдвое, то время, необходимое фабрикам для выполнения
работы, уменьшилось бы на  времени, необходимого для выполне­ния работы одной
первой фабрикой. На какой фабрике производительность выше и во сколько раз,
если известно, что каждая фабрика пере­работала не менее  всего объёма сырья?

Решение. Пусть первая фабрика
сможет выполнить всю работу за некоторое время х, а вторая — за у . Тогда
производительность фабрик равна  и . Работая совместно, фабрики смогут выполнить всю
работу за время t₁ = 1/. Если бы
производительность второй фабрики увеличилась в 2 раза, то она равнялась бы . Следовательно, фабрикам при совместной работе
необходимо бы было затратить на всю работу времени t₂ = 1/Так как это время меньше на  времени х, то составляем следующее уравнение t₁ —х= t₂ или  .

Это уравнение легко
приводится к виду 2у² -9ху +
4у² = 0 . В задаче
требуется найти отношение производительностей фабрик. Производительность первой
фабрики относится к производительности второй фабрики как : или как..Следовательно,
необходимо найти величину  .  Разделив последнее
уравнение на х² и
обозначив , имеем 2u²-9u + 4 = 0.

Уравнение имеет корни u₁= и u₂ = 4 . Для выбора необходимо­го значения
используем последнее условие задачи: каждая фабрика переработала не менее  всего объема сырья. Это означает, что при u=4 первая фабрика за
время переработки  сырья второй фабрикой успела бы переработать даже
большее, чем имеется, количество сырья (не менее). Поэтому необходимо взять u =.

Ответ: производительность
первой фабрики в 2 раза меньше про­изводительности второй фабрики.

Мы рассмотрели
практически все типы встречаю­щихся задач на производительность.

Задачи

1.Двое рабочих вместе
могут выполнить некоторую работу за 10 дней. После 7 дней совместной работы
один из них заболел, и другой окончил работу, проработав еще 9 дней. Во сколько
дней каждый рабо­чий отдельно может выполнить всю работу?

2. Некоторое число
рабочих выполнили работу за несколько дней. Ес­ли число рабочих увеличится на
3, то работа будет сделана на 2 дня скорее, а если число рабочих увеличится на
12, то на 5 дней скорее. Определить число рабочих и время, необходимое для
выполнения этой работы.

3. Два насоса различной
мощности, работая вместе, наполняют бас­сейн за 4 ч. Для заполнения половины
бассейна первому насосу требуется времени на 4 ч больше, чем второму для
заполнения трех четвертей бассейна. За какое время может наполнить бассейн
каждый насос в отдельности?

4. Двое рабочих выполнили
вместе некоторую работу за 2 ч. Если бы сначала первый рабочий сделал половину
этой работы, а затем другой -остальную часть, то вся работа была бы выполнена
за 25 ч. За какое время мог бы выполнить эту работу каждый рабочий в
отдельности?

5. Рабочие А и В работали
одинаковое число дней. Если бы А работал на один день меньше, а В — на 7 дней
меньше, то А заработал бы 72 доллара, а В — 64,8 доллара. Если бы, наоборот, бы
А работал на 7 дней меньше, а В — на один день меньше, то В заработал бы на
32,4 доллара больше А. Сколько заработал каждый в действительности?

6.Два токаря должны были
изготовить определенное число деталей. После трехчасовой совместной работы
продолжал работать только второй токарь, который проработал еще 4 ч. После
этого задание оказалось перевыполненным на 12,5%. За какое время мог бы
выполнить задание каждый токарь, если известно, что второму на это понадобится
на 4 ч меньше, чем первому?

7.В бассейн проведены 2
трубы. Если вода будет течь через одну вторую трубу, то бассейн наполнится на 3
часа быстрее, чем если бы вода текла только через одну первую трубу. Вода
втекала в течение 5 часа через первую трубу, затем открыли вторую трубу,
и через 10 часов бассейн наполнился. За сколько часов наполняет бассейн каждая
труба в отдельности?

8.Для разгрузки баржи
выделены бригады грузчиков. Если ко вре­мени, за которое первая бригада может
разгрузить баржу, прибавить время, за которое вторая бригада может разгрузить
баржу, то получится 12 ч. За сколько часов каждая бригада может разгрузить
баржу, если разность этих часов составляет 45% всего времени, за которое обе
бри­гады могут разгрузить баржу, работая совместно?

9.Для прокладки траншеи
выделены два экскаватора разных типов. Время, необходимое первому экскаватору
для прокладки траншеи, на 3 ч меньше времени, необходимого второму экскаватору
для прокладки этой траншеи. Сколько часов требуется каждому экскаватору для
прокладки траншеи, если сумма этих часов в  раза больше времени, необходимого для прокладки
траншеи при совместной работе?

10. Теплоход загружается
подъемными кранами. Сначала в течение 2 ч работали четыре крана одинаковой
мощности, затем к ним присоединились еще два крана, но меньшей мощности, и
через 3 ч после этого погрузка была закончена. Если бы все краны начали
работать одновременно, то погрузка была бы закончена за 4,5 ч. За сколько
времени вы­полнят погрузку один кран большей и один кран меньшей мощности при
совместной работе?

11.За n часов трактор
вспахивает на p гектаров больше, чем ло­шадь. По сколько гектаров вспашут за n часов лошадь и
трактор, если трактор вспахивает 1 га на t часов быстрее?

12.Три автоматические
линии выпускают одинаковую продукцию, но имеют разную производительность.
Производительность всех трех одновременно действующих линий в 1,5 раза выше производительности первой и второй
линий, работающих одновременно. Сменное задание для первой линии вторая и
третья линии, работая одновременно, могут выполнить на 4 ч 48 мин быстрее, чем
его выполняет первая линия; это же задание вторая линия выполняет на 2 ч
быстрее по сравнению с пер­вой линией. Найдите время выполнения сменного
задания первой линией.

13.Три экскаватора заняты
на рытье котлована. Разность производи­тельности первого и третьего
экскаваторов в 3 раза больше разности произ­водительности третьего и второго
экскаваторов. Первый экскаватор выполняет  всей работы за некоторое время. Такое же время
потребуется, если сначала второй экскаватор выполнит  всей работы, а затем третий экскаватор —   оставшейся работы. Во сколько раз
производительность первого экскаватора больше производительности второго?

14. Одну и ту же работу
могут выполнить три бригады. Первая бригада выполняет  всей работы за некоторое время. Такое же время
потребуется, если сначала третья бригада выполнит  всей работы, а затем вторая бригада выполнит  оставшейся работы. Производительность третьей бригады
равна полусумме производительностей первой и второй бригад. Во сколько раз
производительность второй бригады больше производительности третьей бригады?

15. Две бригады
штукатуров, работая совместно, оштукатурили жилой дом за 6 дней. В другой раз
они оштукатурили клуб и выполнили втрое больший объем работы, чем на штукатурке
жилого дома. В клубе сначала работала первая бригада, а затем ее сменила вторая
бригада и довела работу до конца, причем первая бригада выполнила объем работы
вдвое больший, чем вторая. Клуб они оштукатурили за 35 дней. За сколько дней
первая бригада смогла бы оштукатурить жилой дом, если известно, что вторая
бригада потратила бы на это более 14 дней?

16.Две бригады начали
работу в 8 ч. Сделав вместе 72 детали, они стали работать раздельно. В 15 ч
выяснилось, что за время раздельной работы первая бригада сделала на 8 деталей
больше, чем вторая. На другой день первая бригада делала за 1 ч на одну деталь
больше, а вторая бригада за 1 ч на одну деталь меньше, чем в первый день.
Работу брига­ды начали вместе в 8 ч и, сделав 72 детали, снова стали работать
раздельно. Теперь за время раздельной работы первая бригада сделала на 8 деталей
больше, чем вторая, уже к 13 ч. Сколько деталей в час делала каждая бригада?

17.Трое рабочих должны
сделать 80 одинаковых деталей. Известно, что все трое вместе делают за час 20
деталей. К работе приступил сначала первый рабочий. Он сделал 20 деталей,
затратив на их изготовление более 3 ч. Оставшуюся часть работы выполняли вместе
второй и третий рабочие. На всю работу ушло 8 ч. Сколько часов потребовалось бы
первому рабочему на изготовление всех 80 деталей?

18.Бассейн заполняется
водой через первую трубу на 5 ч быстрее, чем через вторую трубу, и на 30 ч
быстрее, чем через третью трубу. Известно, что пропускная способность третьей
трубы в 2,5 раза меньше пропускной способности первой трубы и на 24 м³/ч
меньше пропускной способности второй трубы. Найдите пропускную способность
первой и третьей труб.

19.Два экскаватора, из
которых первый имеет меньшую производи­тельность, вырыли при совместной работе
котлован объемом 240 м³. Потом первый стал рыть второй котлован, а
второй продолжал рыть первый. Через 7 ч после начала их работы объем первого
котлована ока­зался на 480 м³ больше объема второго котлована. На
другой день вто­рой экскаватор увеличил свою производительность на 10 м³/ч,
а первый уменьшил на 10 м³/ч. Сначала они вместе вырыли котлован в 240
м³, после чего первый стал рыть другой котлован, а второй продолжал
рыть первый. Теперь объем первого котлована стал на 480
м³ больше объема второго котлована уже через 5 ч после начала
работы экскаваторов. Сколько грунта в час вынимали экскаваторы в первый день
работы?

20.  Три автомашины
перевозят зерно, загружаясь в каждом рейсе полностью. За один рейс первая и
вторая машины перевозят вместе 6 т зерна, а первая и третья вместе за 2 рейса
перевозят столько же зерна, сколько вторая за 3 рейса. Какое количество зерна
перевозит за один рейс вторая автомашина, если известно, что некоторое
количество зерна вторая и третья перевозят вместе, совершая в 3 раза меньше
рейсов, чем потребовалось бы третьей автомашине для перевозки того же
количества зерна?

21. Бассейн может
наполняться водой с помощью двух насосов раз­ной производительности. Если
половину бассейна наполнить, включив лишь первый насос, а затем, выключив его,
продолжать наполнение с помощью второго насоса, то весь бассейн наполнится за 2
ч 30 мин. При одновременной работе обоих насосов бассейн наполняется за 1412
мин. Какую часть бассейна наполняет за 20 мин работы насос меньшей
производительности?

22. Двое рабочих выполнили
вместе некоторую работу за 12 дней. Если бы сначала первый сделал половину
работы, а затем другой остальную часть, то вся работа была бы выполнена за 25
дней. За какое время мог выполнить эту работу каждый в отдельности?

23. Бассейн наполняется
водой через две трубы за 6 ч. Одна первая труба заполняет его на 5 ч скорее, чем
одна вторая. За сколько времени каждая труба, действуя отдельно, может
заполнить бассейн?

24. Три каменщика (разной
квалификации) выложили кирпичную стену, причем первый каменщик проработал 6 ч, второй — 4 ч и
третий —7 ч. Если бы первый каменщик работал 4 ч, второй — 2 ч и третий -5 ч, то было бы выполнено лишь  всей работы. За сколько часов каменщики закончили бы
кладку, если бы они работали все вместе одно и то же время?

25. Экскаватор роет
котлован. После того как было вынуто 20
м³ грунта, производительность экскаватора снизилась на 5 м³/ч.
Найдите первоначальную производительность экскаватора, если через 8 ч после
работы было вынуто 50 м³ грунта.

26. Две артели с разным
числом мастеров одинаковой квалификации начали изготавливать шапки, причем
каждый мастер делал по 2 шапки за рабочий день. Сперва работала только первая
артель, выпустившая 32 шапки. Затем ее сменила вторая, выпустившая еще 48
шапок. Вся эта работа заняла 4 дня. После этого артели стали работать вместе и
за сле­дующие 6 дней изготовили еще 240 шапок. Сколько мастеров в
каждой артели?

27. Два экскаватора разных
марок (один экскаватор марки А, а дру­гой марки В), работая одновременно,
выкапывают котлован вместимо­стью 20000
м³ за 10 суток. Если бы работал только экскаватор марки В, то он
выкопал бы этот котлован на 8 суток скорее, чем тот же котло­ван выкопал бы один
экскаватор марки А. Сколько кубических метров в сутки выкапывает каждый из
экскаваторов?

28.Два экскаватора разной
конструкции должны проложить две траншеи одинакового поперечного сечения длиной
в 960 ми 180
м. Вся работа продолжалась 22 дня, в течение которых первый экскаватор
прокладывал большую траншею. Второй же экскаватор начал работать на 6 дней
позже первого, отрыл меньшую траншею, 3 дня ремонтировался и затем помогал
первому. Если бы не нужно было тратить времени на ре­монт, то работа была бы
кончена за 21 день. Сколько метров траншеи может отрыть в день каждый
экскаватор?

29.Три бригады вспахали
два поля общей площадью 120 га. Первое поле было вспахано за 3 дня, причем все
три бригады работали вместе. Второе поле было вспахано за 6 дней первой и
второй бригадами. Если бы все три бригады проработали на втором поле 1 день, то
оставшуюся часть второго поля первая бригада могла бы вспахать за 8 дней.
Сколько гектаров в день вспахивала вторая бригада?

30.К двум бассейнам
подведены две трубы равного диаметра (к
ка­ждому бассейну своя труба). Через первую трубу налили в первый бассейн
определенный объем воды и сразу после этого во второй бассейн через вторую
трубу налили такой же объем воды, причем на все это уш­ло 16 ч. Если бы через
первую трубу вода текла столько времени, сколько через вторую, а через вторую —
столько времени, сколько через пер­вую, то через первую трубу налили бы воды на
320 м³ меньше, чем че­рез вторую. Если бы через первую проходило бы
на 10 м³ меньше, а через вторую — на 10
м³ больше воды, то, чтобы налить в бассейн (сначала в первый, а
потом во второй) первоначальные объемы воды, ушло бы 20 ч. Сколько времени
лилась вода через каждую из труб?

31.Две автоколонны,
состоящие из одинакового числа машин, перевозят груз. В каждой из автоколонн
машины имеют одинаковую грузоподъемность и во время рейсов загружаются
полностью. Грузоподъемность машин в разных колоннах различна, и за 1 рейс
первая автоколон­на перевозит на 40 т груза больше, чем вторая автоколонна.
Если уменьшить число машин в первой автоколонне на 2, а во второй автоко­лонне
— на 10, то первая автоколонна перевезет 90 т груза за 1 рейс, а вторая автоколонна
перевезет 90 т груза за 3 рейса. Какова грузоподъ­емность машин второй
автоколонны?

32.  Один рабочий может
изготовить партию деталей за 12 ч. Работу начал один рабочий, через час к нему
присоединился еще один, еще через час — третий и т. д., пока работа не была
выполнена. Сколько времени проработал первый рабочий? (Производительность труда
всех рабочих одинакова.)

33.Бригада рабочих
одинаковой квалификации должна была изготовить партию деталей. Сначала к работе
приступил один рабочий, через час к нему присоединился второй, еще через час —
третий и т. д., до тех пор, пока к работе не приступила вся бригада. Если бы с
самого начала работали все члены бригады, то работа была бы выполнена на 2 ч
быстрее. Сколько рабочих в бригаде?

34.Трое рабочих копали
канаву. Сначала первый рабочий проработал половину времени, необходимого двум
другим, для того чтобы вы­рыть всю канаву, затем второй рабочий проработал половину
времени, необходимого двум другим, чтобы вырыть всю канаву, и, наконец, третий
рабочий проработал половину времени, необходимого двум другим, чтобы вырыть всю
канаву. В результате канава была вырыта. Во сколько раз быстрее была бы вырыта
канава, если бы с самого начала работали все трое рабочих одновременно?

Типичные задачи на совместную работу в 6 классе

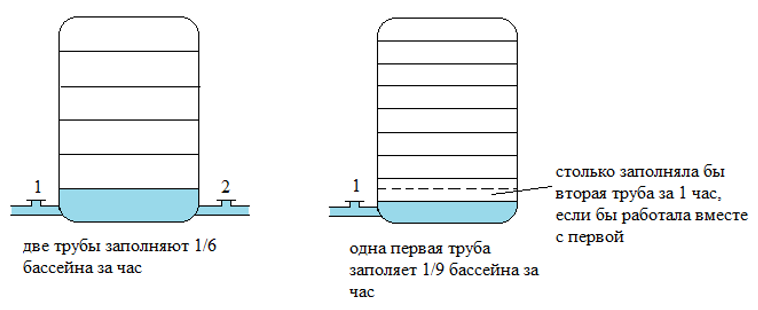
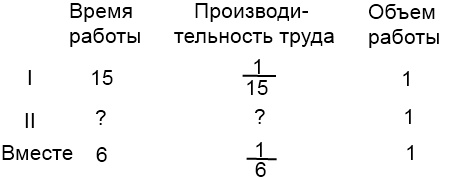
1) Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. За сколько часов может выполнить эту работу другой рабочий?

В отличие от всех других типов задач, задачи на совместную работу начинаются с того, что всю работу (все задание, весь бассейн, все поле — то, о чем идет речь в задаче) принимаем за единицу. То есть объем работы в этом случае равен единице. Чтобы найти объем работы, надо производительность труда умножить на время работы. Соответственно, чтобы найти производительность труда (часть работы, выполненную за определенную единицу времени), надо объем работы разделить на время работы: 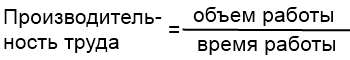Решение задач на совместную работу упрощается, если условие  оформить в виде таблицы.

Перейдем с решению нашей задачи.

Решение.

Примем всю работу за 1.

Чтобы найти производительность труда второго рабочего, из производительности труда совместной работы вычтем производительность труда первого рабочего:

   

Такую часть работы в 1 час выполняет второй рабочий.

Зная производительность труда второго рабочего и объем работы, можем найти время, за которое он может выполнить работу самостоятельно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

   

Значит, второй рабочий, работая отдельно, может выполнить работу за 10 часов.

Ответ: за 10 часов.

2) Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

Решение.

Примем весь бассейн за 1.

Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:

   

Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

   

Таким образом, за 56 часов совместной работы обеих труб бассейн будет наполнен.

Ответ: за 56 часов.