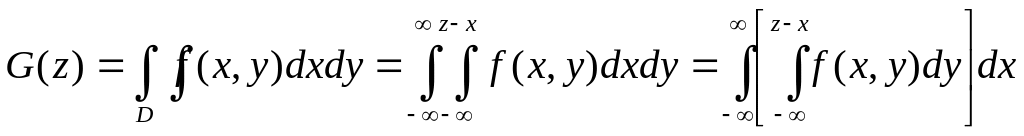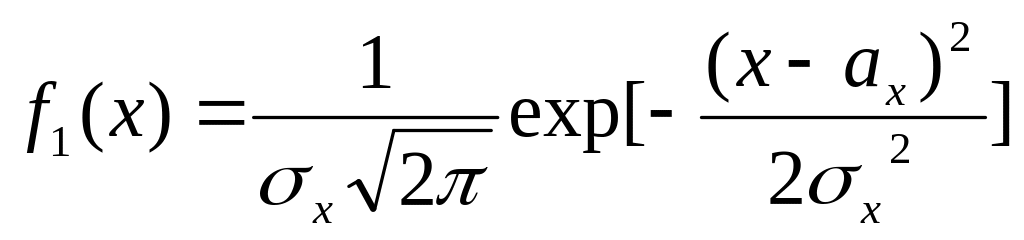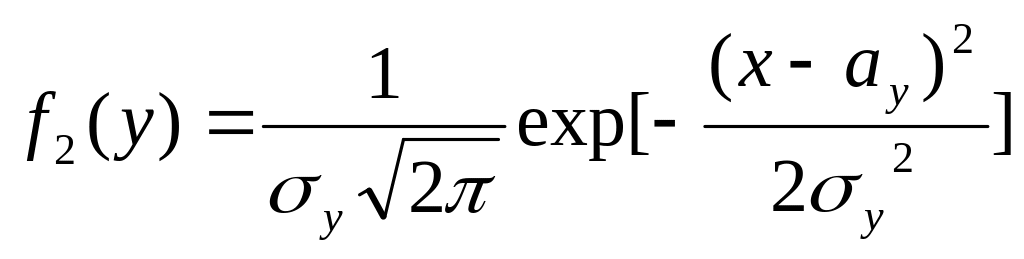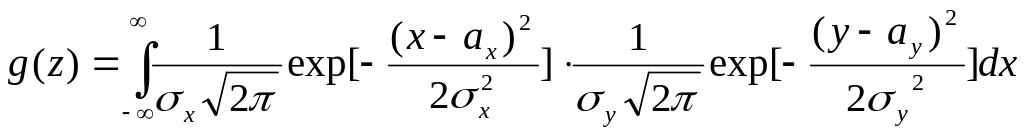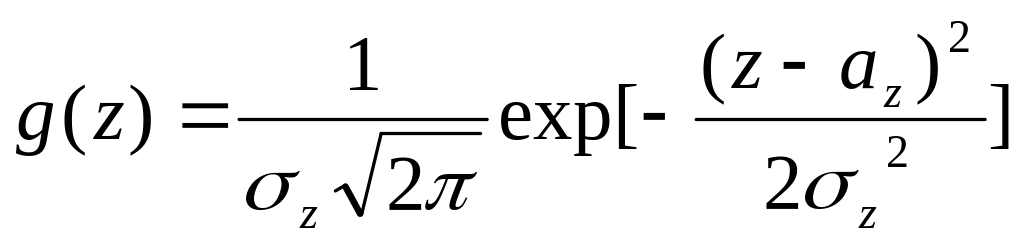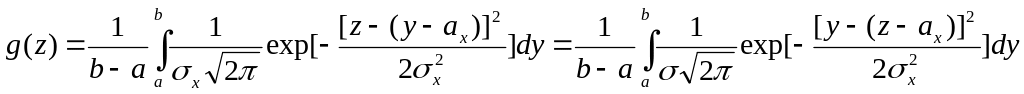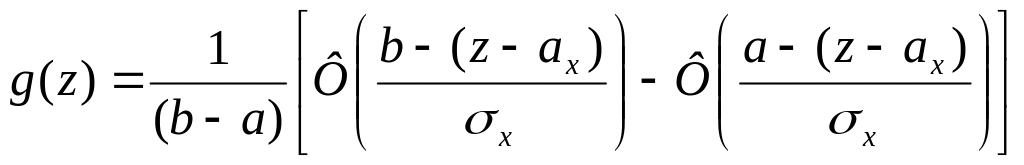Как найти совместный закон распределения

При изучении тех
или иных явлений приходится сталкиваться
со случайными величинами, которые
являются результатом суммирования
некоторого числа случайных величин.
Задача нахождения закона распределения
суммы двух и более случайных величин
может быть решена следующим образом.

Постановка задачи.

Пусть имеется
система случайных величин (X,Y)
с известной совместной плотностью
распределения f(x,y).
Требуется
определить закон распределения случайной
величины

.

Для решения задачи
обозначим функцию распределения
случайной величины Z,
как

и построим на плоскости x0y
прямую x+
y=z,
которая делит плоскость на две области
(рис.4.1).

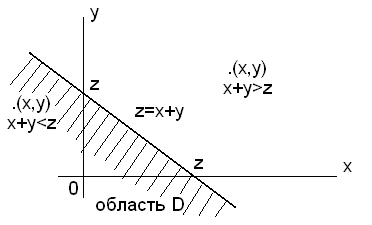
Рисунок 4.1 — График
случайной величины

Заштрихованная
область на рисунке является областью
D.

Вероятность
попадания случайной точки z
в область D
есть функция распределения случайной
величины Z,
которая по определению равна

.

Дифференцируя это
выражение по переменной z,
получим формулу плотности g(z)
суммы двух случайных величин X
и Y.

.

(4.12)

Аналогично можно
получить и формулу плотности g(z),
равную

,

(4.13)

которая равносильна
формуле (4.12) и может применяться вместо
нее.

Если случайные
величины X
и Y
независимы, то закон распределения
суммы X+Y
называется композицией
законов распределения.
В этом случае функции в формулах (4.12),
(4.13) могут быть представлены в виде:

;

.

Тогда плотность
распределения g(z)
будет окончательно равна:

;

.
(4.14)

Композиция
распределений дискретных случайных
величин

Пусть имеется
система ДСВ (X,Y)
с вероятностью совместного распределения

.
Требуется определить закон распределения
случайной величины

,
т.е. найти вероятности

.

(4.15)

Таблица 4.1
иллюстрирует требуемый закон распределения.

Таблица 4.1

zi	z1	z2	z3	…	zn
P(zi)	P(z1)	P(z2)	P(z3)	…	P(zn)

Пример. Дана система
дискретных случайных величин (X,Y),
закон распределения которой задан
таблицей 4.2.

Таблица 4.2

xiyj	4	3
2	0,3	0,1
3	0,4	0,2

Пользуясь выражением
(4.14), находим:

;

;

.

На основе полученных
вероятностей закон распределения
случайной величины

можно
представить таблицей 4.3.

Таблица 4.3

z	5	6	7
P(Z)	0.1	0.5	0.4

Композиция
нормальных распределений

Найти плотность
распределения композиции

нормально
распределенных случайных величин X
и Y
с параметрами

,
если

и

.

Так как по определению
плотность распределения композиции

равна

,
то

.
Откуда

,
где

,

.
(4.16)

Следовательно, в
результате композиции двух нормальных
распределений суммарный закон получается
также нормальным.

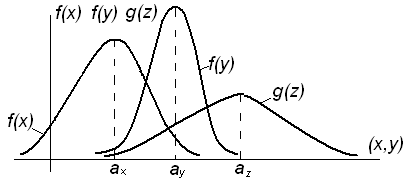
Рисунок 4.2 –
Композиция двух нормальных распределений

При композиции
произвольного числа нормальных
распределений суммарный закон также
является нормальным с параметрами:

;

.

Это свойство часто
называют устойчивостью нормального
закона.

Композиция
нормального и равномерного распределений

Пусть случайная
величина X
подчинена нормальному закону с плотностью
распределения

,
а случайная величина Y
распределена равномерно в интервале
[a,
b]:

.
Требуется найти плотность распределения
композиции случайных величин X
и Y.

Решение.

Применяя формулу
(4.14), получим

.

Подынтегральная
функция есть плотность нормально
распределенной случайной величины Y,
а интеграл представляет собой вероятность
попадания случайной величины в промежуток
[a,
b].

Следовательно,

.
(4.17)

Если выполняется
неравенство

,
то выражение (4.17) можно отнести к
нормальному распределению:

,
где

,

.

Понятие о
центральной предельной теореме Ляпунова

Если случайные
величины

взаимно
независимы и имеют один и тот же закон
распределения с математическим ожиданием

и дисперсией

,
то при неограниченном увеличении n
закон распределения суммы

неограниченно приближается к нормальному
закону:

с параметрами


и

.

Теорема Ляпунова
верна и для суммы случайных величин с
неодинаковыми законами распределения,

у которых
дисперсии примерно одного порядка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

 и

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

 на плоскости

 либо как случайный вектор

.

Дискретной называют двумерную величину, составляющие которой дискретны.

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Закон
распределения дискретной двумерной случайной величины может быть задан:

а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;

б) аналитически, например в виде функции распределения.

Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность

, надо просуммировать
вероятности столбца

. Аналогично сложив
вероятности строки

 получим вероятность

.

Пусть
составляющие

 и

 дискретны и имеют соответственно следующие
возможные значения:

; 

.

Условным распределением составляющей

 при

 (j сохраняет одно и то же
значение при всех возможных значениях

) называют совокупность
условных вероятностей:

Аналогично
определяется условное распределение

.

Условные
вероятности составляющих

 и

 вычисляют соответственно по формулам:

Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.

Ковариация (корреляционный момент)

Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки

.

Ковариацию
(корреляционный момент) можно найти по формуле:

Свойства ковариации

Свойство 1.

Ковариация двух независимых случайных величин равна нулю.

Свойство 2.

Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.

Свойство 3.

Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.

Коэффициент корреляции

Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.

Формула коэффициента корреляции:

Две
случайные величины

 и

 называют коррелированными, если их коэффициент
корреляции отличен от нуля.

 и

 называют некоррелированными величинами, если
их коэффициент корреляции равен нулю

Свойства коэффициента корреляции

Свойство 1.

Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.

Свойство 2.

Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.

Свойство 3.

Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.

Линейная регрессия

Рассмотрим
двумерную случайную величину

, где

 и

 – зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины

 в виде линейной функции величины

:

где

 и

 – параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.

Линейная
средняя квадратическая регрессия

 на

 имеет вид:

Коэффициент

называют
коэффициентом регрессии

 на

, а прямую

называют
прямой среднеквадратической регрессии

 на

.

Аналогично
можно получить прямую среднеквадратической регрессии

 на

:

Смежные темы решебника:

• Двумерная непрерывная случайная величина
• Линейный выборочный коэффициент корреляции
• Парная линейная регрессия и метод наименьших квадратов

Задача 1

Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.

Требуется:

—
определить одномерные законы распределения случайных величин X и Y;

— найти
условные плотности распределения вероятностей величин;

—
вычислить математические ожидания m_x и m_y;

—
вычислить дисперсии σ_x и σ_y;

—
вычислить ковариацию μ_xy;

—
вычислить коэффициент корреляции r_xy.

xy	3	5	8	10	12
-1	0.04	0.04	0.03	0.03	0.01
1	0.04	0.07	0.06	0.05	0.03
3	0.05	0.08	0.09	0.08	0.05
6	0.03	0.04	0.04	0.06	0.08

---

Задача 2

Задана
дискретная двумерная случайная величина (X,Y).

а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X;  в) построить регрессию случайной величины X на Y;  г) найти коэффициент ковариации; д) найти
коэффициент корреляции.

Y	X
1	2	3	4	5
30	0.05	0.03	0.02	0.01	0.01
40	0.03	0.02	0.02	0.04	0.01
50	0.05	0.03	0.02	0.02	0.01
70	0.1	0.03	0.04	0.03	0.01
90	0.1	0.04	0.01	0.07	0.2

---

Задача 3

Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.

x y	1	2	3
1.5	0.03	0.02	0.02
2.9	0.06	0.13	0.03
4.1	0.4	0.07	0.02
5.6	0.15	0.06	0.01

---

Задача 4

Двумерная
случайная величина (X,Y) распределена по закону

XY	1	2
-3	0,1	0,2
0	0,2	0,3
-3	0	0,2

Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.

---

Задача 5

Случайные
величины ξ и η имеют следующий совместный закон распределения:

P(ξ=1,η=1)=0.14

P(ξ=1,η=2)=0.18

P(ξ=1,η=3)=0.16

P(ξ=2,η=1)=0.11

P(ξ=2,η=2)=0.2

P(ξ=2,η=3)=0.21

1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.

2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).

3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}

4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.

---

Задача 6

Дан закон
распределения двумерной случайной величины (ξ,η):

	ξ=-1	ξ=0	ξ=2
η=1	0,1	0,1	0,1
η=2	0,1	0,2	0,1
η=3	0,1	0,1	0,1

1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания M_ξ,
M_η и дисперсии D_ξ, D_η

2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).

3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?

4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти M_γ  и D_γ.

---

Задача 7

Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.

XY	1	2	4
-2	0,25	0	0,25
1	0	0,25	0
3	0	0,25	0

---

Задача 8

Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.

YX	-1	1
-1	0,4	0,1
1	0,2	0,3

---

Задача 9

Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:

	X=-3	X=0	X=1
Y=-2	0,3	?	0,1
Y=1	0,1	0,1	0,2

---

Задача 10

Совместный
закон распределения пары

 задан таблицей:

xh	-1	0	1
-1	1/12	1/4	1/6
1	1/4	1/12	1/6

Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.

---

Задача 11

Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции r_xy?

X	20	25	30	35
P	0.1	0.1	0.4	0.4

и

---

Задача 12

Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):

XY	0	1	2
-1	?	0,1	0,2
1	0,1	0,2	0,3

---

Задача 13

Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:

ξη	-1	1	2
0	1/7	2/7	1/7
1	1/7	1/7	1/7

Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?

---

Задача 14

Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.

XY	2,3	2,9	3,1	3,4
0,2	0,15	0,15	0	0
2,8	0	0,25	0,05	0,01
3,3	0	0,09	0,2	0,1

---

Задача 15

Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.

xy	1	4
-10	0,1	0,2
0	0,3	0,1
20	0,2	0,1

---

Задача 16

Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:

а) законы
распределения ее компонент и их числовые характеристики;

b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.

с)
ковариацию и коэффициент корреляции случайных величин X и Y;

d) составить матрицу ковариаций и матрицу корреляций;

e) вероятность попадания в область, ограниченную линиями y=16-x² и y=0.

f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.

XY	-1	0	1	2
-1	0	1/6	0	1/12
0	1/18	1/9	1/12	1/9
2	1/6	0	1/9	1/9

---

Задача 17

Совместный
закон распределения случайных величин X и Y задан таблицей:

XY	0	1	3
0	0,15	0,05	0,3
-1	0	0,15	0,1
-2	0,15	0	0,1

Найдите:

а) закон
распределения случайной величины X и закон распределения
случайной величины Y;

б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.

---

Задача 18

Известен
закон распределения двумерной случайной величины (X,Y).

а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);

б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;

в)
построить поле распределения и линию регрессии Y по X и X по Y;

г)
вычислить корреляционный момент (коэффициент ковариации) μ_xy и
коэффициент корреляции r_xy.

	5	20	35
100	—	—	0.05
115	—	0.2	0.15
130	0.15	0.35	—
145	0.1	—	—-

From Wikipedia, the free encyclopedia

Given two random variables that are defined on the same probability space,^[1] the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered for any given number of random variables. The joint distribution encodes the marginal distributions, i.e. the distributions of each of the individual random variables. It also encodes the conditional probability distributions, which deal with how the outputs of one random variable are distributed when given information on the outputs of the other random variable(s).

In the formal mathematical setup of measure theory, the joint distribution is given by the pushforward measure, by the map obtained by pairing together the given random variables, of the sample space’s probability measure.

In the case of real-valued random variables, the joint distribution, as a particular multivariate distribution, may be expressed by a multivariate cumulative distribution function, or by a multivariate probability density function together with a multivariate probability mass function. In the special case of continuous random variables, it is sufficient to consider probability density functions, and in the case of discrete random variables, it is sufficient to consider probability mass functions.

Examples[edit]

Draws from an urn[edit]

Each of two urns contains twice as many red balls as blue balls, and no others, and one ball is randomly selected from each urn, with the two draws independent of each other. Let and be discrete random variables associated with the outcomes of the draw from the first urn and second urn respectively. The probability of drawing a red ball from either of the urns is 2/3, and the probability of drawing a blue ball is 1/3. The joint probability distribution is presented in the following table:

	A=Red	A=Blue	P(B)
B=Red	(2/3)(2/3)=4/9	(1/3)(2/3)=2/9	4/9+2/9=2/3
B=Blue	(2/3)(1/3)=2/9	(1/3)(1/3)=1/9	2/9+1/9=1/3
P(A)	4/9+2/9=2/3	2/9+1/9=1/3

Each of the four inner cells shows the probability of a particular combination of results from the two draws; these probabilities are the joint distribution. In any one cell the probability of a particular combination occurring is (since the draws are independent) the product of the probability of the specified result for A and the probability of the specified result for B. The probabilities in these four cells sum to 1, as with all probability distributions.

Moreover, the final row and the final column give the marginal probability distribution for A and the marginal probability distribution for B respectively. For example, for A the first of these cells gives the sum of the probabilities for A being red, regardless of which possibility for B in the column above the cell occurs, as 2/3. Thus the marginal probability distribution for gives ‘s probabilities unconditional on , in a margin of the table.

Coin flips[edit]

Consider the flip of two fair coins; let and be discrete random variables associated with the outcomes of the first and second coin flips respectively. Each coin flip is a Bernoulli trial and has a Bernoulli distribution. If a coin displays «heads» then the associated random variable takes the value 1, and it takes the value 0 otherwise. The probability of each of these outcomes is 1/2, so the marginal (unconditional) density functions are

The joint probability mass function of and defines probabilities for each pair of outcomes. All possible outcomes are

Since each outcome is equally likely the joint probability mass function becomes

Since the coin flips are independent, the joint probability mass function is the product
of the marginals:

Rolling a die[edit]

Consider the roll of a fair die and let if the number is even (i.e. 2, 4, or 6) and otherwise. Furthermore, let if the number is prime (i.e. 2, 3, or 5) and otherwise.

	1	2	3	4	5	6
A	0	1	0	1	0	1
B	0	1	1	0	1	0

Then, the joint distribution of and , expressed as a probability mass function, is

These probabilities necessarily sum to 1, since the probability of some combination of and occurring is 1.

Marginal probability distribution[edit]

If more than one random variable is defined in a random experiment, it is important to distinguish between the joint probability distribution of X and Y and the probability distribution of each variable individually. The individual probability distribution of a random variable is referred to as its marginal probability distribution. In general, the marginal probability distribution of X can be determined from the joint probability distribution of X and other random variables.

If the joint probability density function of random variable X and Y is , the marginal probability density function of X and Y, which defines the marginal distribution, is given by:

where the first integral is over all points in the range of (X,Y) for which X=x and the second integral is over all points in the range of (X,Y) for which Y=y.^[2]

Joint cumulative distribution function[edit]

For a pair of random variables , the joint cumulative distribution function (CDF) is given by^{[3]: p. 89}

where the right-hand side represents the probability that the random variable takes on a value less than or equal to and that takes on a value less than or equal to .

For random variables , the joint CDF is given by

Interpreting the random variables as a random vector yields a shorter notation:

Joint density function or mass function[edit]

Discrete case[edit]

The joint probability mass function of two discrete random variables is:

or written in terms of conditional distributions

where is the probability of given that .

The generalization of the preceding two-variable case is the joint probability distribution of discrete random variables which is:

or equivalently

.

This identity is known as the chain rule of probability.

Since these are probabilities, in the two-variable case

which generalizes for discrete random variables to

Continuous case[edit]

The joint probability density function for two continuous random variables is defined as the derivative of the joint cumulative distribution function (see Eq.1):

This is equal to:

where and are the conditional distributions of given and of given respectively, and and are the marginal distributions for and respectively.

The definition extends naturally to more than two random variables:

Again, since these are probability distributions, one has

respectively

Mixed case[edit]

The «mixed joint density» may be defined where one or more random variables are continuous and the other random variables are discrete. With one variable of each type

One example of a situation in which one may wish to find the cumulative distribution of one random variable which is continuous and another random variable which is discrete arises when one wishes to use a logistic regression in predicting the probability of a binary outcome Y conditional on the value of a continuously distributed outcome . One must use the «mixed» joint density when finding the cumulative distribution of this binary outcome because the input variables were initially defined in such a way that one could not collectively assign it either a probability density function or a probability mass function. Formally, is the probability density function of with respect to the product measure on the respective supports of and . Either of these two decompositions can then be used to recover the joint cumulative distribution function:

The definition generalizes to a mixture of arbitrary numbers of discrete and continuous random variables.

Additional properties[edit]

Joint distribution for independent variables[edit]

In general two random variables and are independent if and only if the joint cumulative distribution function satisfies

Two discrete random variables and are independent if and only if the joint probability mass function satisfies

for all and .

While the number of independent random events grows, the related joint probability value decreases rapidly to zero, according to a negative exponential law.

Similarly, two absolutely continuous random variables are independent if and only if

for all and . This means that acquiring any information about the value of one or more of the random variables leads to a conditional distribution of any other variable that is identical to its unconditional (marginal) distribution; thus no variable provides any information about any other variable.

Joint distribution for conditionally dependent variables[edit]

If a subset of the variables is conditionally dependent given another subset of these variables, then the probability mass function of the joint distribution is . is equal to . Therefore, it can be efficiently represented by the lower-dimensional probability distributions and . Such conditional independence relations can be represented with a Bayesian network or copula functions.

Covariance[edit]

When two or more random variables are defined on a probability space, it is useful to describe how they vary together; that is, it is useful to measure the relationship between the variables. A common measure of the relationship between two random variables is the covariance. Covariance is a measure of linear relationship between the random variables. If the relationship between the random variables is nonlinear, the covariance might not be sensitive to the relationship, which means, it does not relate the correlation between two variables.

The covariance between the random variable X and Y, denoted as cov(X,Y), is :

^[4]

Correlation[edit]

There is another measure of the relationship between two random variables that is often easier to interpret than the covariance.

The correlation just scales the covariance by the product of the standard deviation of each variable. Consequently, the correlation is a dimensionless quantity that can be used to compare the linear relationships between pairs of variables in different units. If the points in the joint probability distribution of X and Y that receive positive probability tend to fall along a line of positive (or negative) slope, ρ_XY is near +1 (or −1). If ρ_XY equals +1 or −1, it can be shown that the points in the joint probability distribution that receive positive probability fall exactly along a straight line. Two random variables with nonzero correlation are said to be correlated. Similar to covariance, the correlation is a measure of the linear relationship between random variables.

The correlation between random variable X and Y, denoted as

Important named distributions[edit]

Named joint distributions that arise frequently in statistics include the multivariate normal distribution, the multivariate stable distribution, the multinomial distribution, the negative multinomial distribution, the multivariate hypergeometric distribution, and the elliptical distribution.

See also[edit]

• Bayesian programming
• Chow–Liu tree
• Conditional probability
• Copula (probability theory)
• Disintegration theorem
• Multivariate statistics
• Statistical interference
• Pairwise independent distribution

References[edit]

External links[edit]

• «Joint distribution», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• «Multi-dimensional distribution», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
• «Joint continuous density function». PlanetMath.
• Mathworld: Joint Distribution Function