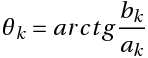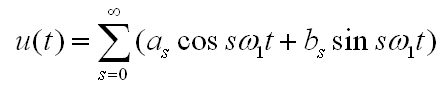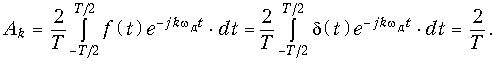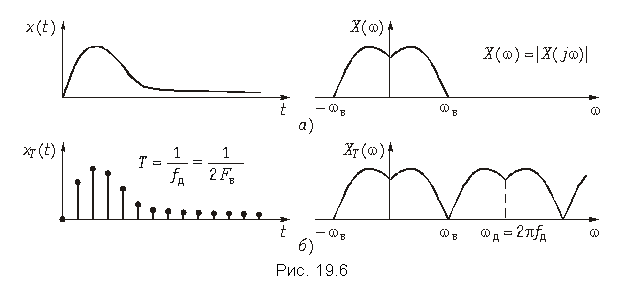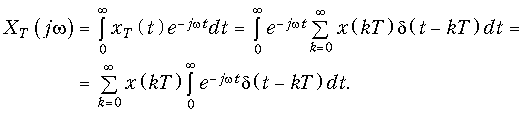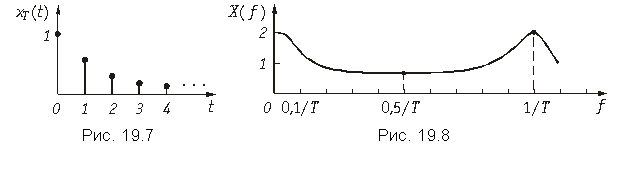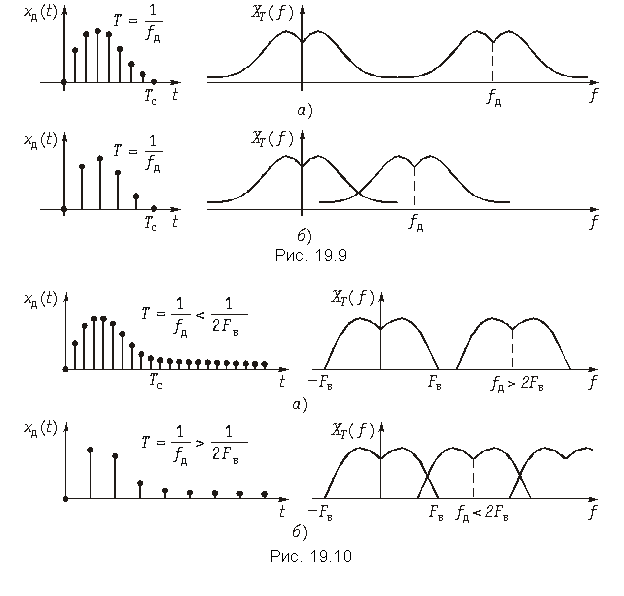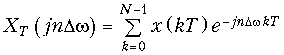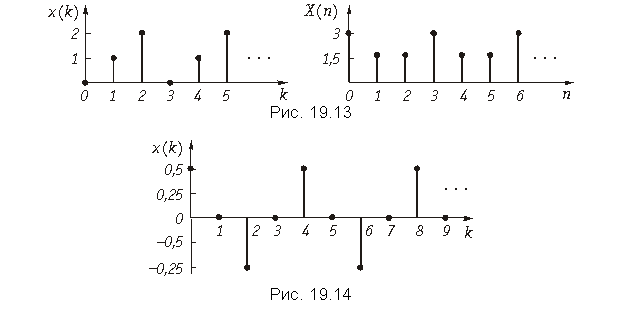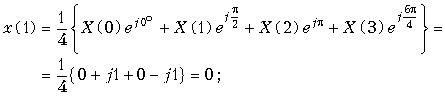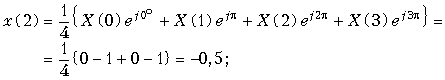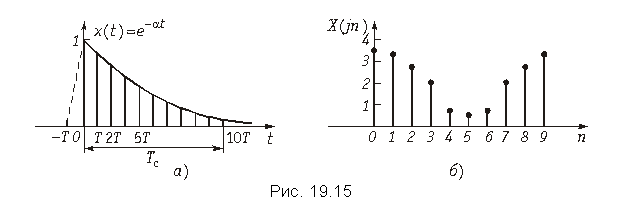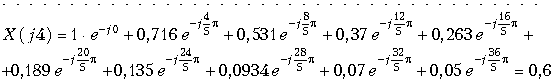Как найти спектр функции

Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих

1. Преобразование Фурье и спектр сигнала

Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).

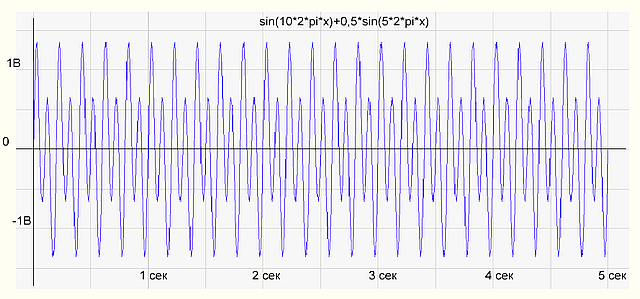
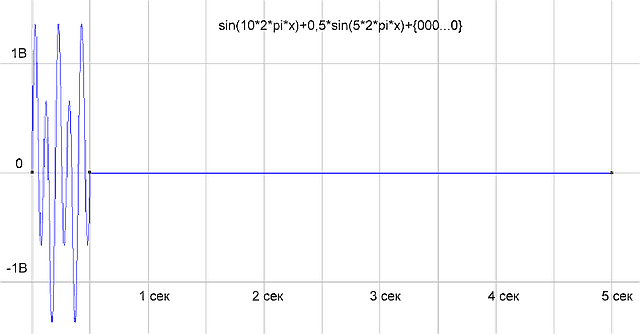
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:

рис.1 График временной функции сигнала

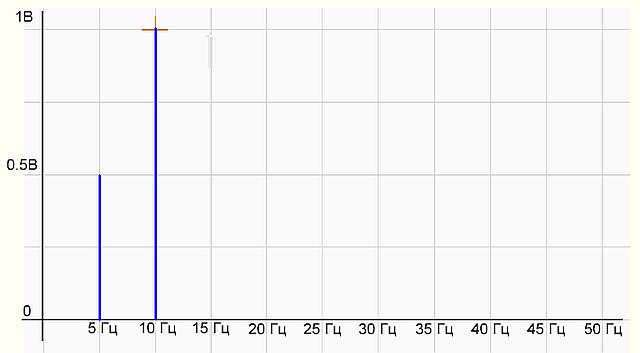
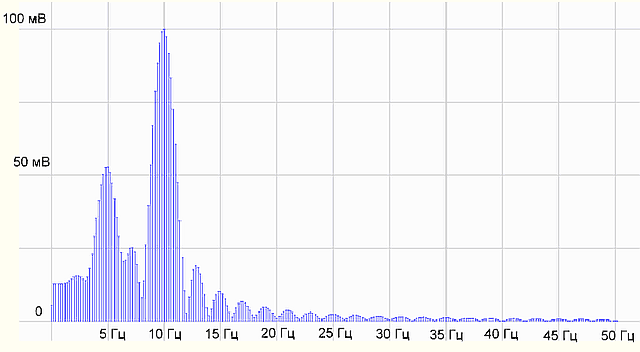
рис.2 График спектра сигнала

На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.

Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.

Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.

С математической точки зрения — сколько ошибок в этой фразе?

Теперь

начальство решило

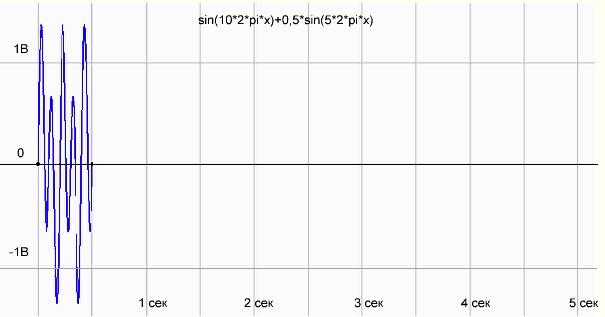
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.

рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек

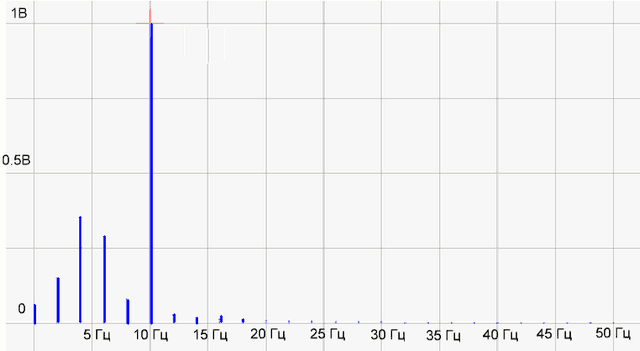
рис.4 Спектр функции

Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…

Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.

рис.5 Добили нулей до 5 сек

рис.6 Получили спектр

Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.

2. Непрерывная функция и представление её рядом Фурье

Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:

(1), где:

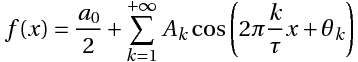
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей

Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.

(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)

Этот ряд может быть также записан в виде:

(2),
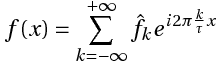
где 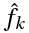, k-я комплексная амплитуда.

или

(3)

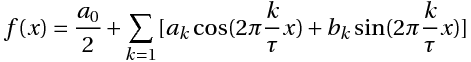
Связь между коэффициентами (1) и (3) выражается следующими формулами:

и

Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»

Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.

Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид иили косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.

Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.

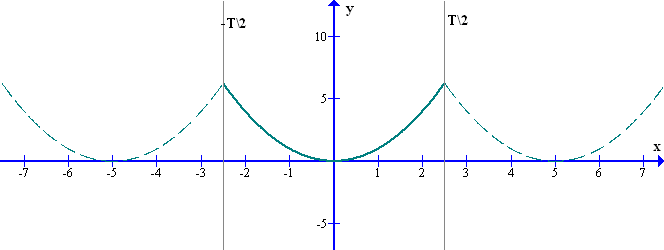
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.

Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.

рис.7 Представление непериодической исходной функции рядом Фурье

Таким образом:

Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.

Далее.

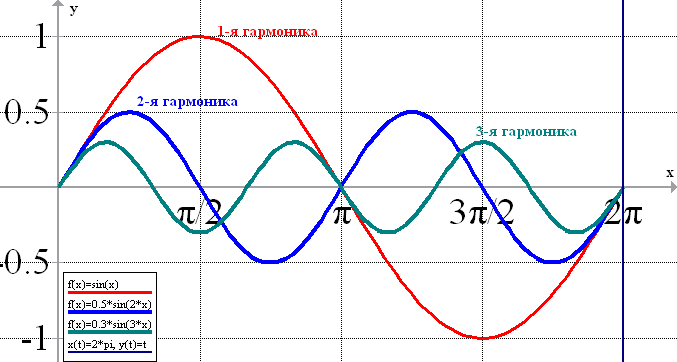
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).

рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)

Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).

Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.

Шаг между гармониками в этом случае равен 1 Гц.

Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.

Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.

3. Дискретные сигналы и дискретное преобразование Фурье

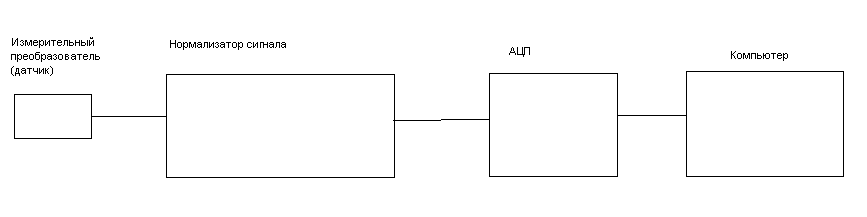
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).

Обычная схема измерения и оцифровки сигнала выглядит следующим образом.

рис.9 Схема измерительного канала

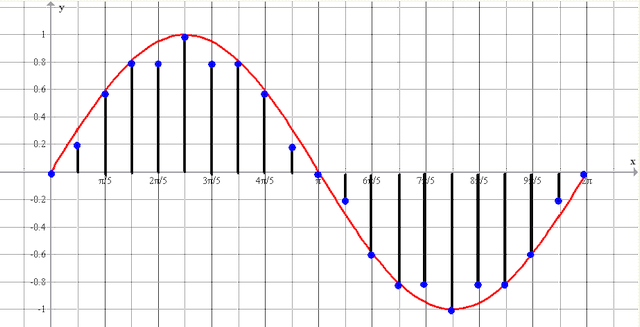
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.

рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т

Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).

Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))

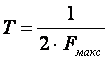
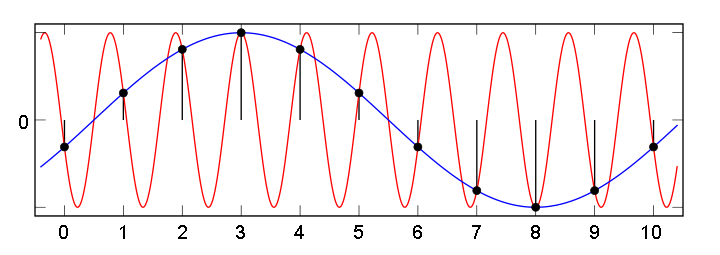
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени , т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.

А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?

В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.

Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации

Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.

Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.

Рассмотрим теперь дискретное преобразование Фурье (ДПФ).

Сравнивая с рядом Фурье

видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.

Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»

Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).

рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0

Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.

Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.

В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.

Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.

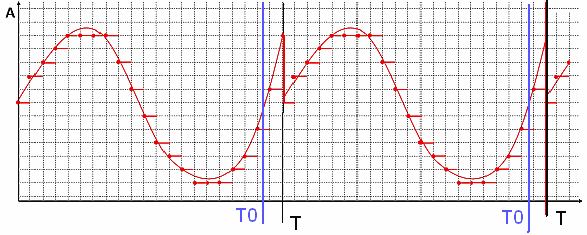
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора

При меньшей длительности картина будет выглядеть «хуже»:

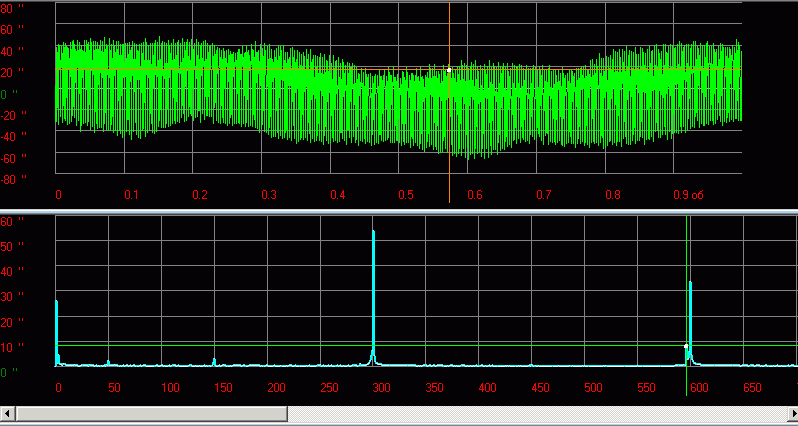
Рис.14 Пример функции и спектра сигнала вибрации ротора

На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.

Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.

Некоторые итоги

1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).

2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».

3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.

Использованные материалы и другие полезные материалы.

FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)

Любой физически
реализуемый сигнал ограничен во времени
и обладает конечной энергией. Функции,
отобра­жающие реальные сигналы,
удовлетворяют условиям Ди­рихле и
абсолютно интегрируемы, т. е.

(98)

где
М
— конечная
величина.

Модели
таких сигналов также могут быть
представлены совокупностью гармонических
составляющих. Конкретный вид спектрального
преобразования для непериодического
сигнала получим, проследив изменения,
происходящие в спектре периоди­ческой
последовательности импульсов u₁(t)
при увеличении периода их повторения.

Абсолютные
значения амплитуд спектральных
составляющих в
(97) при
увели­чении периода уменьшаются. Так
как частоты составляю­щих спектра
кратны основной частоте, то при ее
уменьше­нии линии на спектральной
диаграмме сближаются.

Спектральное
представление для одиночного импульса
u(t)
получим как следствие увеличения периода
сигнала u₁(t)
до бесконечности.

Пару
преобразований Фурье для периодической
функ­ции u₁(t)
запишем в форме:

При
T → ∞ u₁(t)
переходит в u(t),
частота ω₁
уменьшает­ся до dω,
а kω₁
превращается
в текущую частоту ω.
Заме­няя суммирование интегрированием,
находим

.
(99)

Обозначив
интеграл в квадратных скобках S(jω),
полу­чим формулы для прямого и обратного
интегрального преобразования Фурье:

(100)

Величину
S(jω)
называют комплексной спектральной
плотностью или спектральной характеристикой.
Она имеет размерность [амплитуда/частота].
На каждой конкретной частоте амплитуда
соответствующей составляющей равна
нулю. Бесконечно малому интервалу
частоты dω
соответствует составляю­щая с
бесконечно малой комплексной амплитудой
dА(jω):

(101)

Сравнение
выражения
(99) для
спектральной харак­теристики функции
u(t),
заданной на интервале времени t₁
≤ t
≤ t₂,
с формулой

для
огибающей комплексного спектра такой
же функции, периодически продолжающей­ся
во времени, показывает, что они различаются
только множителем

(102)

Поэтому по известной
спектральной характеристике одиночного
импульса легко построить линейчатый
спектр их периодической последовательности.
Как комплексная величина спектральная
характерис­тика может быть записана
в виде

(103)

где
S(ω)
= |S(jω)|
называется спектральной
плотностью амплитуд или спектром
непериодического сигнала.

Так как составляющие
расположены на всех частотах, то спектр
непериодического сигнала является
непрерыв­ным или сплошным. Представим
спектральную характе­ристику состоящей
из действительной и мнимой частей:

где

(105,
106)

Модуль
спектральной характеристики S(ω)
определяет­ся выражением

(107)

и представляет
собой четную функцию частоты.

Для
фазы спектральной характеристики S(jω)
соответ­ственно получаем

.
(108)

Так
как А(ω)
— четная
функция частоты, а В(ω)
—
нечетная, то функция φ(ω) от­носительно
частоты нечетна.

Комплексная форма
интегрального преобразования Фурье
легко приводится к тригонометрической:

Второй
член в связи с нечетностью подынтегрального
выражения равен нулю. Окончательно
имеем

(109)

Преимущество
тригонометрической формы записи
Фурье-преобразования заключается в
возможности неко­торого физического
толкования с использованием идеали­заций,
не очень далеких от реальности.

Пример.
Найти спектр одиночного прямоугольного
импульса, описываемого функцией времени
(рис.
4.5):

Выражение
для спектральной характеристики амплитуд
находим в соответствии с
()

Рис.4.5.Импульс
Рис. 4.6. Спектр

Искомый
спектр представляет собой модуль этого
выражения:

(110)

Спектр
одиночного прямоугольного импульса
(рис.
4.6),
есте­ственно,
имеет ту же форму, что и огибающая
периодической последовательности таких
импульсов (см. рис.
4.7).

Рис.4.7.
Периодическая последовательность
импульсов

Пример.
Определить спектр дельта-функции [см.
рис.
4.3].

Запишем
выражение для спектральной характеристики
S_(j,)
дельта-функции,
сосредоточенной в точке ₁:

В
соответствии с (4.7) имеем

откуда
модуль спектральной характеристики

(111)

Рис.4.8. Спектр дельта-функции

Следовательно,
дельта-функции соответствует сплошной
равномер­ный спектр, включающий в
себя составляющие бесконечно больших
частот (рис.
4.8). При ξ₁=
0 начальные
фазы всех составляющих равны нулю.

Распределение
энергии в спектре.
Рассмотрим неперио­дический сигнал
u(t),
физическим представлением которого
будем считать электрическое на­пряжение
на резисторе с сопротив­лением в
1 Ом.

Тогда
энергия, выделяемая на этом резисторе,

(112)

В
предположении, что интеграл
(112) сходится,
выразим энергию через модуль спектральной
характерис­тики S(ω) сигнала и(t).
Квадрат этого модуля запишем в виде

(113)

где

—
функция, комплексно-сопряжённая
спектральной характеристикеS(jω)
сигна­ла u(t).

Тогда.

После
изменения последовательности
интегрирования и использования обратного
преобразования Фурье
получим

Окончательно имеем

(114)

Соотношение
(114) известно
как равенство
Парсеваля. Оказывается,
что энергию, выделяемую непериодическим
сигналом за время его существования,
можно определить, интегрируя квадрат
модуля его спектральной характерис­тики
в интервале частот.

Каждое
из бесконечно малых слагаемых
(1 /π)|S(ω)|²dω,
соответствующих
бесконечно малым участкам спектра,
характеризует энергию, приходящуюся
на спектральные составляющие сигнала,
сосредоточенные в полосе частот от ω
до ω+dω.

Соседние файлы в папке конспект ТИ

• #

  23.02.20151.26 Mб524.doc

• #
• #
• #

Преобразование Фурье для дискретного сигнала. Определим связь между спектром X(jw) аналогового сигнала x(t) и спектром X_Т(jw) дискретного сигнала x_Т(t), определенного моделью (19.2). Учитывая, что x_Т(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала

(19.4)

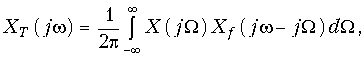
где X_f(jw) – спектральная плотность дискретизирующей последовательности (19.1).

Для нахождения X_f(jw) разложим f(t) в комплексный ряд Фурье (5.6):

(19.5)

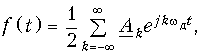
где w_д = 2p/Т – частота дискретизации,

Отсюда согласно (9.42) получаем

(19.6)

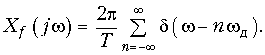
Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства d-функции окончательно получим

(19.7)

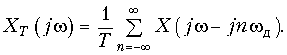
Из (19.7) следует важный вывод: спектр дискретного сигнала x_T(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных на оси частот через одинаковые интервалы.

Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2). Если же использовать вместо дискретизирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр X_Т(jw), энергия которого убывает с ростом w («копии» X(jw) с ростом w уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах.

Спектр дискретного сигнала X_Т(jw) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t Õ 0).

Отсюда с учетом фильтрующего свойства d-функции получим прямое преобразование Фурье для дискретных сигналов.

(19.8)

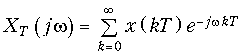
и обратное преобразование Фурье:

(19.8)

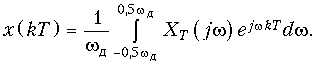
На практике в формулах (19.8), (19.9) часто вместо зависимости X_Т(jw) рассматривают зависимости X_Т(jf), которые легко можно получить путем замены w = 2pf.

Пример. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета x_Т(t) = [a; 0; 0; 0; …].

Воспользуемся формулой (19.8), в которую подставим значения x_t(t) заданного сигнала

.

Пример. Рассчитаем спектр экспоненциальной дискретной функции x_Т(t) = 0,5^k, k 0.

График дискретной функции x_Т(t) приведен на рис. 19.7, а ее отсчеты можно записать в виде последовательности x{k} = {1; 0,5; 0,25; 0,125; 0,0625; …}.

Спектр дискретной экспоненты рассчитаем по формуле (19.8)

где для суммирования ряда использована формула

.

Используя формулу Эйлера , получим выражение для расчета спектра амплитуд X(f).

.

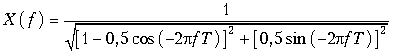
Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать X(f).

График спектра амплитуд X(f) экспоненциальной дискретной функции x_T(t) = 0,5^k приведен на рисунке 19.8.

Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом f_д = 1/Т.

Следует отметить, что если не выполняется условие теоремы Котельникова: f_д 2f_в, то спектры в (19.7) частично перекрываются. На рис. 19.9, рис. 19.10 показан характер изменения спектра дискретного сигнала X_T(f) при изменении частоты дискретизации сигнала x_T(t), ограниченного во времени интервалом T_с (рис. 19.9) и неограниченного во времени (рис. 19.10).

Как следует из представленных графиков увеличение периода дискретизации T > 1/2F_в; F_д < 2F_в приводит к наложению смежных спектров в (19.7), что приводит к наложению спектра Х_T(f). Эти искажения называются ошибками наложения. Чтобы их устранить необходимо частоту дискретизации увеличить до F_д 2F_в.

Пример. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.

Из условия задачи следует, что граничная частота спектра F^в равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации

.

Минимально допустимая частота дискретизации f_д = 2F^в = 2×100 = 200 кГц.

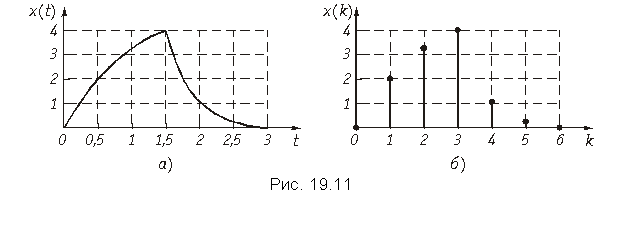
Пример. Определим дискретные отсчеты сигнала длительностью t_и = 3 мс, приведенного на рис. 19.11, а, если в качестве граничной частоты спектра F^в принять значение 3/t_и, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.

Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих F^в, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.

Граничная частота спектра F^в = 3/t_и = 3/(3×10³) = 1 кГц.

Интервал дискретизации T = 1/(2F^в) = 1/(2×1×10³) = 0,5 мс.

Берем отсчеты сигнала, приведенного на рис. 19.11, а, через интервал времени T = 0,5 мс и получаем последовательность x{k} = {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 19.11, б.

Отметим, что аналоговый сигнал x(t) можно полностью восстановить по его дискретным отсчетам x(kT) с помощью ФНЧ, частота среза которого w_с = 0,5w_д = w_в. Этот вывод хорошо иллюстрирует рис. 19.10, а из которого видно, что спектр сигнала на выходе ФНЧ совпадает со спектром аналогового сигнала x(t).

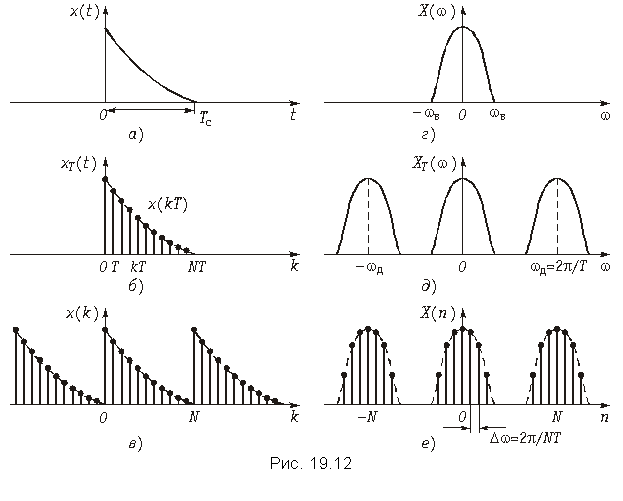
Дискретное преобразования Фурье. Как следует из формулы (19.7) X_T(jw) имеет периодическую структуру с w_д = 2p/T. Причем, как и спектр аналогового сигнала X(jw) спектр дискретного сигнала X_T(jw) является сплошным (см. рис. 19.6, б). Вместе с тем при цифровой обработке сигналов используется не только дискретизация во времени, но и дискретизация в частотной области.

Для сигнала x(t) ограниченного во времени интервалом T_с (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем заменыt ->w; w_в->T_с/2; Т-> Dw:

(19.10)

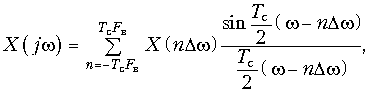
где Dw = 2p/T_с; T_с – длительность сигнала;X(nDw) – отсчеты спектра сигнала в частотной области.

Переходя к дискретному сигналу x_T(t) (рис. 19.12, б) отметим, что общее количество отсчетов сигнала будет равно

где T = 2p/w_д = p/w_в.

Дискретный спектр (рис. 19.12, е) может быть получен путем периодического повторения последовательности {x(kT)} с периодом T_с = NT (рис. 19.12, в). При этом частотный интервал между дискретными отсчетами спектра (рис. 19.12, е) составляет

(19.11)

С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать замену w = nDw. Тогда получим

или с учетом (19.11)

(19.12)

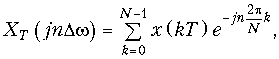
где n = 0; ±1; ±2; ± … N/2.

Для упрощения записи аргумент nDw и kT обычно заменяют индексом n и k соответственно и опускают индекс T, при этом (19.12) примет вид

(19.13)

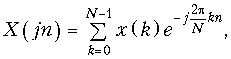
которое определяет прямое ДПФ.

С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k).

Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:

(19.14)

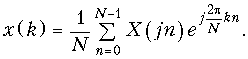
При k < 0 обратное преобразование Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в).

Для ДПФ по аналогии с непрерывными преобразованиями Фурье справедливы основные теоремы и свойства.

В частности, свойство линейности

(19.15)

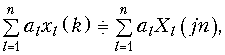
сдвиг дискретного сигнала:

(19.16)

т. е. сдвиг последовательности отсчетов сигнала на m интервалов приводит лишь к изменению фазового спектра дискретного сигнала.

Теорема свертки:

(19.17)

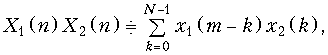
где N = N₁ + N₂; N₁, N₂ – число отсчетов х₁ и х₂ соответственно.

Аналогично можно записать и другие теоремы для ДПФ. Заметим, что ДПФ можно использовать для определения не только спектра дискретных сигналов, но и спектра аналоговых сигналов, для чего его необходимо дискретизировать согласно теоремы Котельникова (19.3).

Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами x{k} = {0; 1; 2}.

Для расчета воспользуемся формулой ДПФ (19.13).

Поскольку

, ,

то ,

.

Графики заданного дискретного периодического сигнала x(k) и рассчитанного дискретного периодического спектра амплитуд X(n) приведены на рис. 19.13.

Пример. Рассчитаем значения дискретного сигнала x(k), ДПФ которого имеет вид X[n] = {0; 1; 0; 1}.
Значения дискретного сигнала x(k) будем рассчитывать по формуле (19.14)

;

График последовательности x{k} = {0,5; 0; –0,5; 0} приведен на рис. 19.14. Сигнал x(k) дискретный и периодический.

Пример. Определить с помощью ДПФ спектр аналогового сигнала, изображенного на рис. 19.15, а.

Ограничим длительность сигнала T_c, где (рис. 9.15, а). Например, при T_c = 3/a, . Выберем число отсчетов N = 10, определим частоту дискретизации

Согласно (19.13) находим отсчеты спектра сигнала

и т.д.

В таблице приведены результаты расчета спектра,

а на рис. 19.15, б спектр сигнала X(jn). Следует отметить, что с увеличением T (уменьшение числа отсчетов N) погрешность аппроксимации x(t) увеличивается (см. рис. 19.5, а).

Как следует из вышеприведенных примеров и формул (19.13), (19.14), для вычисления ДПФ содержащих N отсчетов необходимо осуществить в общем случае N² операций с комплексными числами. Если длина обрабатываемых массивов достаточно велика, то вычисление ДПФ даже на современных быстродействующих ЭВМ занимает достаточно много времени. Для сокращения вычислений используют обычно алгоритм быстрого преобразования Фурье (БПФ). Существует много разновидностей БПФ. Здесь мы рассмотрим один алгоритм, основанный на прореживании по времени.

Быстрое преобразование Фурье. Положим, что число отсчетов N = 2^q, где q – целое число. Разобьем дискретную последовательность отсчетов {x(k)} не две части:

четную {x(k)}_чт = {x(2k)}

и нечетную {x(k)}_нч = {x(2k + 1)}, где k = 0, 1, 2, … N/2 – 1.

Представим спектр (19.13) в виде

(19.18)

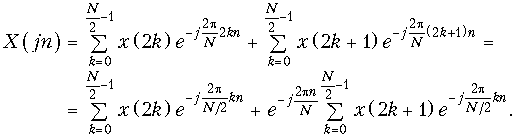
Из (19.18) следует, что

(19.19)

где n = 0, 1, 2, …, ((N/2) – 1).

Из (19.19) следует, что первая половина X(jn) (n = 0, 1, 2, …, (N/2) – 1) выражается через ДПФ двух частных последовательностей: X_чт(jn) и X_нч(jn). Вторую половину (n N/2) X(jn) можно найти, если учесть периодичность его четной и нечетной части с периодом N/2:

и соотношение (при n N/2):

при этом получим

(19.20)

Формула (19.19) и (19.20) лежит в основе БПФ. Как следует из этих формул для вычисления X_чт(jn) и X_нч(jn) требуется (N/2)² операций и для выполнения операции умножения на exp{×} – N операций:

(19.21)

Для ДПФ (19.13) требуется операций, что существенно выше, чем N_БПФ. Например, при N = 10³, получаем N_ДПФ = 10⁶, а N_БПФ ~ 250×10³, т. е. для БПФ требуется в четыре раза меньше операций, чем при ДПФ.

В общем случае число операций, необходимое в БПФ равно

(19.22)

и выигрыш по сравнению с ДПФ равно

(19.23)

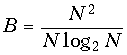
и может достигать сотен и тысяч раз при достаточно больших входных массивах N.

В заключении отметим, что сам процесс вычисления по формулам (19.18), (19.19) производят по итерационному принципу: последовательность отсчетов с четными и нечетными номерами снова разбивают на две части и т. д. Процесс разбиения продолжается до тех пор, пока не получится последовательность, состоящая из одного элемента (исходного ДПФ). Более подробно с алгоритмами БПФ можно ознакомиться в специальной литературе (см. например, Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. М. «Радио и связь. 1990).