Содержание
Характеристический полином, собственные числа, собственные векторы матрицы
§
В настоящем разделе $ n_{} $ означает порядок квадратной матрицы $ A_{} $.
Характеристический полином
определяется для произвольной квадратной матрицы $ A_{} $ как1)
$ det (A_{}-lambda E) $, где $ E_{} $ – единичная матрица одинакового с $ A_{} $ порядка.
П
Пример. Для $ n=2_{} $:
$$ det (A-lambda E)=
begin{vmatrix}
a_{11}-lambda & a_{12}\
a_{21}& a_{22}-lambda
end{vmatrix}=
$$
$$
=lambda^2-(a_{11}+a_{22})lambda + (a_{11}a_{22}-a_{12}a_{21}) ;
$$
для $ n=3_{} $:
$$
det (A-lambda E)=
begin{vmatrix}
a_{11}-lambda & a_{12} & a_{13}\
a_{21}& a_{22}-lambda & a_{23} \
a_{31}& a_{32} & a_{33}-lambda
end{vmatrix}=
$$
$$
=-lambda^3+(a_{11}+a_{22}+a_{33})lambda^2 —
$$
$$
-left {
begin{vmatrix}
a_{11}& a_{12}\
a_{21}& a_{22}
end{vmatrix}
+begin{vmatrix}
a_{22}& a_{23}\
a_{32}& a_{33}
end{vmatrix}+
begin{vmatrix}
a_{11}& a_{13}\
a_{31}& a_{33}
end{vmatrix}
right }lambda+
det A .
$$
Т
Теорема 1.
$$ det (A-lambda E)=
(-1)^nBigg(
lambda^n — lambda^{n-1}sum_{1le jle n} a_{jj}
+ lambda^{n-2}sum_{1le j_1< j_2 le n} left|begin{array}{ll}
a_{j_1j_1}& a_{j_1j_2}\
a_{j_2j_1}& a_{j_2j_2}
end{array}right| — dots +
$$
$$
+(-1)^k lambda^{n-k}
sum_{1le j_1< j_2 < dots < j_kle n} left|begin{array}{llll}
a_{j_1j_1}& a_{j_1j_2} & dots & a_{j_1j_k}\
a_{j_2j_1}& a_{j_2j_2} & dots & a_{j_2j_k}\
vdots & & & vdots \
a_{j_kj_1}& a_{j_kj_2} & dots & a_{j_kj_k}
end{array}right|+ dots + (-1)^n det A
Bigg) .
$$
Образно говоря, коэффициент при $ (-1)^{k}lambda^{n-k} $ получается
суммированием всех миноров $ k_{} $-го порядка матрицы $ A_{} $, построенных на
элементах, стоящих в строках и столбцах с одинаковыми номерами..
Такой минор матрицы
$$
left|begin{array}{cccc}
a_{j_1j_1} & a_{j_1j_2} & dots & a_{j_1j_k} \
a_{j_2j_1} & a_{j_2j_2} & dots & a_{j_2j_k} \
vdots & & ddots & vdots \
a_{j_kj_1} & a_{j_kj_2} & dots & a_{j_kj_k}
end{array}
right|
, quad 1le j_1<j_2< dots < j_k le n
$$
в настоящем ресурсе называется ведущим минором ($k$-го порядка). См. замечание о терминологии
☞
ЗДЕСЬ.
Результат теоремы имеет исключительно теоретическое значение: практическое вычисление характеристического полинома матрицы большого порядка по этой теореме обычно крайне неэффективно. Методы практического вычисления характеристического полинома разбираются
☟
НИЖЕ.
П
Пример. Характеристический полином матрицы Фробениуса
$$
mathfrak F=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n}
$$
равен $ (-1)^n(lambda^n-a_1lambda^{n-1}-dots-a_{n}) $.
Характеристический полином линейного оператора
определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее
☞
ЗДЕСЬ.
Характеристический полином линейного однородного разностного уравнения
$ n_{} $-го порядка
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K, quad a_n ne 0,
$$
определяется как
$$ lambda^n — a_1 lambda^{n-1} — dots — a_n . $$
Подробнее
☞
ЗДЕСЬ.
Свойства
Т
Теорема 2. Характеристический полином матрицы не меняется
1.
при ее транспонировании:
$$ det (A-lambda E) = det (A^{top}-lambda E_{}) , ;$$
2.
при переходе к подобной матрице: если $ B=C^{-1}AC^{} $ при произвольной неособенной матрице $ C_{} $, то
$$ det (A-lambda E) equiv det (B-lambda E_{}) , . $$
Т
Теорема 3. Пусть матрица $ A_{} $ имеет порядок $ mtimes n_{} $, а $ B_{} $ — порядок $ ntimes m_{} $. Тогда эти матрицы допускают умножение в любом порядке, т.е. определены $ AB_{} $ и $ BA_{} $ и оба произведения будут квадратными матрицами — порядков $ m_{} $ и $ n_{} $ соответственно. Тогда характеристические полиномы этих произведений различаются лишь на степень $ lambda_{} $:
$$
lambda^n det (AB — lambda E_{m times m})equiv lambda^m det (BA — lambda E_{n times n}) .
$$
=>
Если матрицы $ A_{} $ и $ B_{} $ — квадратные одинакового порядка, то характеристические полиномы матриц $ AB_{} $ и $ BA_{} $ тождественны.
Т
Теорема 4. Если характеристический полином матрицы $ A_{} $ равен
$$ f(lambda)=(-1)^n lambda^n+a_1lambda^{n-1}+dots+a_{n-1}lambda+a_n $$
и $ a_{n} ne 0 $, то характеристический полином матрицы $ A^{-1}_{} $ равен
$$ f^{ast}(lambda)=frac{(-lambda)^n}{a_n} f(1/lambda) = frac{(-1)^n}{a_n} left[ (-1)^n+a_1 lambda + dots+
a_{n-1}lambda^{n-1}+a_nlambda^{n} right] . $$
Теорема Гамильтона-Кэли
Т
Теорема 5. Результатом подстановки в характеристический полином $ det (A_{}-lambda E) $ самой матрицы $ A_{} $ будет нулевая матрица:
$$
det (A-lambda E)= (-1)^n lambda^n +a_1 lambda^{n-1}+dots+a_{n-1}lambda+ a_n Rightarrow
$$
$$
Rightarrow
(-1)^n A^n +a_1 A^{n-1}+dots+a_{n-1}A+ a_n E = {mathbb O}_{ntimes n} .
$$
В литературе эта теорема обычно приводится в иной формулировке:
матрица является корнем своего характеристического полинома.
Доказательство
☞
ЗДЕСЬ.
П
Пример. Для $ n_{}=2 $:
$$
left(begin{array}{ll} a_{11} & a_{12} \ a_{21} & a_{22}
end{array} right)^2 — (a_{11}+a_{22})left(begin{array}{ll} a_{11} & a_{12} \ a_{21} & a_{22}
end{array} right) +
(a_{11}a_{22}-a_{12}a_{21})
left(begin{array}{ll} 1 & 0 \ 0 & 1
end{array} right) = left(begin{array}{ll} 0 & 0 \ 0 & 0
end{array} right) .
$$
Собственное число
Собственное (или характеристическое) число2) определяется для квадратной матрицы $ A_{} $ как произвольный корень ее характеристического полинома $ det (A_{}-lambda E) $. Уравнение
$$
det(A-lambda E)=0
$$
называется характеристическим уравнением матрицы $ A $.
И
Понятие характеристического уравнения было введено Коши в 1840 г. В литературе XIX века известно также как вековое уравнение.
Набор всех собственных чисел матрицы $ A_{} $ (с учетом их кратностей) называется спектром матрицы3) (таким образом спектр матрицы $ A_{} $ порядка $ n_{} $ всегда состоит из $ n_{} $ чисел, часть из которых могут быть одинаковыми). Максимальный из модулей собственных чисел матрицы $ A_{} $ называется ее спектральным радиусом4), он иногда обозначается $ rho(A) $.
П
Пример. Найти спектр матрицы
$$
A=
left(begin{array}{rrrr}
0&1&2&3\
-1&0&4&7\
-2&-4&0&2\
-3&-7&-2&0
end{array}right).
$$
Решение. Характеристический полином
$$ det (A-lambda E)=left|begin{array}{rrrr}
-lambda&1&2&3\
-1&-lambda&4&7\
-2&-4&-lambda&2\
-3&-7&-2&-lambda
end{array}right|=lambda^4+
83lambda^2
$$
имеет корни $ lambda_1=0, lambda_2 = {mathbf i}sqrt{83}, lambda_3 = — {mathbf i} sqrt{83} $, причем $ lambda_{1} $ — второй кратности.
Ответ. Спектр матрицы $ A_{} $:
$ {0,0, {mathbf i} sqrt{83},- {mathbf i} sqrt {83} } $. Спектральный радиус матрицы $ A_{} $: $ rho(A)= sqrt {83} $.
Т
Теорема 6. Если $ {lambda_{1},lambda_{2},dots,lambda_{n} } $ — спектр матрицы $ A_{} $, то
$$ lambda_1+lambda_{2}+dots+lambda_n = operatorname{Sp}(A)=a_{11}+a_{22}+dots+a_{nn}, $$
$$ lambda_1cdotlambda_{2}times dots times lambda_n = (-1)^ndet (A) . $$
Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета.
♦
Можно, разумеется, привести еще $ n-2 $ зависимостей между собственными числами матрицы и ее минорами, но они редко нужны — а вот равенства из теоремы полезно запомнить.
=>
Для того, чтобы матрица $ A_{} $ была неособенной необходимо и достаточно, чтобы среди ее собственных чисел не было нулевого.
Т
Теорема 7. Пусть $ g(x)=b_{0}x^m+dots+b_m in {mathbb C}[x] $ — произвольный полином. Вычислим полином от матрицы $ A_{} $:
$$ g(A)=b_{0}A^m+dots+b_m E , . $$
Тогда если $ {lambda_{1},dots,lambda_{n} } $ — спектр матрицы $ A_{} $, то $ {g(lambda_{1}),dots,g(lambda_n) } $ — спектр матрицы $ g(A_{}) $.
=>
Результат теоремы обобщается и на более широкий класс функций $ g_{}(x) $ — фактически на любую функцию, которая, вместе со своими производными, может быть определена на спектре матрицы $ A_{} $. В частности, если $ det A_{} ne 0 $, то спектр матрицы $ A^{-1}_{} $ совпадает с $ {1/lambda_j}_{j=1}^n $.
=>
Имеет место следующее равенство, связывающее степени матрицы $ A_{} $ с суммами Ньютона ее характеристического полинома:
$$ operatorname{Sp}(A^k)=lambda_1^k+dots+lambda_n^k . $$
Здесь $ operatorname{Sp}_{} $ обозначает след матрицы (т.е. сумму ее диагональных элементов). Утверждение остается справедливым и для отрицательных показателей $ k_{} $ при условии, что $ det A_{} ne 0 $.
=>
Имеет место следующее равенство:
$$ det g(A) = (-1)^{mn} {mathcal R}(f,g_{}) , $$
где $ {mathcal R}(f,g_{}) $ означает результант полиномов $ f(x) =det (A-x_{} E) $ и $ g_{}(x) $.
Т
Теорема 8. Собственные числа вещественной симметричной матрицы $ A_{} $ все вещественны.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 9. Собственные числа вещественной кососимметричной матрицы $ A_{} $ все мнимы, за исключением, возможно, $ lambda_{} = 0 $.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 10. Собственные числа вещественной ортогональной матрицы все равны $ 1_{} $ по абсолютной величине (модулю). Характеристический полином ортогональной матрицы является возвратным если $ +1 $ не является его корнем или является корнем четной кратности. Хотя бы одно собственное число ортогональной матрицы нечетного порядка равно $ +1 $ или $ (-1) $.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 11. Спектр циклической матрицы
$$
left(begin{array}{lllll}
a_1 & a_2 & a_3 & dots & a_n \
a_n & a_1 & a_2 & dots & a_{n-1} \
a_{n-1} & a_n & a_1 & dots & a_{n-2} \
vdots & & & & vdots \
a_2 & a_3 & a_4 & dots & a_1
end{array}
right) .
$$
совпадает с набором чисел
$$ {f(1),f(varepsilon_1), dots, f(varepsilon_{n-1}) } ,$$
при
$$ f(x)=a_{1}+a_2x+a_3x^2+dots+a_nx^{n-1} $$
и
$$
varepsilon_k=cos frac{2,pi k}{n} + {mathbf i} sin frac{2,pi k}{n}
$$
— корне n-й степени из единицы.
Доказательство
☞
ЗДЕСЬ.
Локализация собственных чисел
Т
Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть
$$A=left[a_{jk} right]_{j,k=1}^n quad , quad B=left[b_{jk} right]_{j,k=1}^n
.
$$
Обозначим
$$M= max_{j,kin{1,dots,n}} left{|a_{jk} |, |b_{jk} | right} quad ,
quad delta = frac{1}{nM}sum_{j,k=1}^n |a_{jk} — b_{jk} | . $$
Тогда любому собственному числу $ lambda_{ast}^{} $ матрицы $ A_{} $ можно поставить
в соответствие такое собственное число $ mu_{ast}^{} $ матрицы $ B_{} $, что
$$ |lambda_{ast}-mu_{ast} | le (n+2) M sqrt[n]{delta} . $$
Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы
☞
ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы.
Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.
Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.
П
Пример [Уилкинсон] [2]. Найти собственные числа матрицы
$$
A=
left(
begin{array}{cccccc}
20 & 20 & & & & \
& 19 & 20 & & & \
& & 18 & 20 & & \
& & & ddots & ddots & \
& & & & 2 & 20 \
{color{Red} varepsilon } & & & & & 1 \
end{array}
right)_{20times 20}
$$
при $ {color{Red} varepsilon }=10^{-10} $
(все неуказанные элементы матрицы считаются равными нулю).
Решение. Характеристический полином
$$
det(A-lambda E) = prod_{j=1}^{20} (j-lambda) — 20^{19} {color{Red} varepsilon } =
$$
$$
=lambda^{20}-{scriptstyle 210},lambda^{19}+{scriptstyle 20615},lambda^{18}-{scriptstyle 1256850}, lambda^{17}
+{scriptstyle 53327946}, lambda^{16}-{scriptstyle 1672280820}, lambda^{15}+
{scriptstyle 40171771630}, lambda^{14}-{scriptstyle 756111184500}, lambda^{13}+
$$
$$
+{scriptstyle 11310276995381}, lambda^{12} —
{scriptstyle 135585182899530}, lambda^{11}
+{scriptstyle 1307535010540395}, lambda^{10}-{scriptstyle 10142299865511450}, lambda^9 +
$$
$$
+{scriptstyle 63030812099294896}, lambda^8 —
{scriptstyle 311333643161390640}, lambda^7+{scriptstyle 1206647803780373360}, lambda^6 -{scriptstyle 3599979517947607200}, lambda^5
+{scriptstyle 8037811822645051776}, lambda^4-
$$
$$
-{scriptstyle 12870931245150988800}, lambda^3
+{scriptstyle 13803759753640704000}, lambda^2
-{scriptstyle 8752948036761600000},lambda +{scriptstyle 2432377720176640000}
$$
очень похож на полином из другого
☞
ПРИМЕРА Уилкинсона. Он имеет корни
$$
lambda_1=0.995754, lambda_2=2.109241, lambda_3=2.574881,
$$
$$
lambda_{4,5}=3.965331pm 1.087735, mathbf i, lambda_{6,7}=5.893977pm 1.948530 , mathbf i,
$$
$$
lambda_{8,9}=8.118073 pm
2.529182 , mathbf i,
lambda_{10,11}=10.5pm 2.733397 , mathbf i,
$$
$$
lambda_{12,13}=12.881926pm 2.529182 , mathbf i, lambda_{14,15}=15.106022 pm 1.948530
, mathbf i, $$
$$
lambda_{16,17}=17.034669pm 1.087735 , mathbf i,
$$
$$
lambda_{18}=18.425118, lambda_{19}=18.890758, lambda_{20}=20.004245 .
$$
Итак, нановозмущение5) в одном-единственном элементе матрицы приводит к существенному изменению спектра: из $ 20 $ вещественных собственных чисел «остаются в живых» только $ 6_{} $; кроме того, у образовавшихся мнимых корней оказываются достаточно большими мнимые части. В данном примере допустимые возмущения для $ {color{Red} varepsilon } $, т.е. такие, при
которых сохранится
свойство вещественности всех корней характеристического полинома, находятся в пределах6)
$$ -8.636174times 10^{-14} < {color{Red} varepsilon } le frac{685872258640569}{8796093022208000000000000000} approx +7.797464 times 10^{-14} .$$
♦
Т
Теорема 13 [Гершгорин].7) Обозначим $ mathbb D_{j} $ круг на комплексной
плоскости $ mathbb C_{} $ с центром в точке $ a_{jj}^{} $ и радиуса
$$ r_j=sum_{ell=1 atop ellne j}^n left|a_{j ell}right| .$$
Тогда спектр матрицы $ A_{} $ лежит внутри объединения этих кругов:
$$ {lambda_1,dots, lambda_n } subset bigcup_{j=1}^n mathbb D_j . $$
Иными словами: любое собственное число матрицы должно удовлетворять хотя бы одному из
неравенств
$$ |z- a_{jj} | < r_j . $$
Доказательство
☞
ЗДЕСЬ
П
Пример. Построить круги Гершгорина для матрицы
$$ A=left(
begin{array}{crr}
-1+3,{mathbf i} & 2- {mathbf i} & 3+2, {mathbf i} \
-1+{mathbf i} & 4+ {mathbf i} & 3, {mathbf i} \
-1& 2-2,{mathbf i}& -2-3, {mathbf i}
end{array}
right) . $$
Решение.
$$|lambda + 1 — 3,{mathbf i} |le | 2-{mathbf i} |+| 3+2,{mathbf i} |=sqrt{5}+sqrt{13}, $$
$$|lambda — 4 — {mathbf i} |le 3+sqrt{2}, $$
$$ |lambda + 2+ 3, {mathbf i} |le 1 + 2sqrt{2} . $$
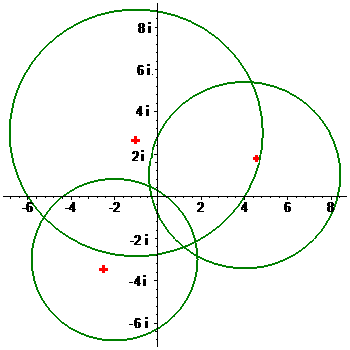
Проверка. Собственные числа матрицы $ A_{} $ (на рисунке обозначены красными крестиками):
$$ { -2.509081750-3.442241533,{mathbf i} , -1.041999986+2.655757676,{mathbf i} , 4.551081736+1.786483857, {mathbf i} } .$$
Локализация вещественных собственных чисел
Симметричная матрица
Т
Теорема 14 [Коши].
Для вещественной симметричной матрицы $ A_{} $ число ее собственных чисел, лежащих на интервале $ ]a,b_{}[ $, определяется по формуле:
$$operatorname{nrr} { det (A-lambda E) =0 | a< lambda<b }= $$
$$= {mathcal P}(1, H_1(a), H_2(a),dots, H_n(a))-
{mathcal P}(1, H_1(b), H_2(b),dots, H_n(b)) . $$
Здесь $ H_1(lambda), H_2(lambda),dots, H_n(lambda) $ —
главные миноры матрицы $ A-lambda, E $, а $ {mathcal P}_{} $ — число знакопостоянств.
Доказательство
☞
ЗДЕСЬ.
Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы
полиномов Штурма для характеристического полинома симметричной матрицы $ A_{} $.
=>
Если все главные миноры $ A_1,A_2,dots,A_{n} $ симметричной матрицы $ A_{} $ отличны от нуля, то
число положительных собственных чисел матрицы $ A_{} $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:
$$ operatorname{nrr} { det (A-lambda E) =0 | lambda>0 } = {mathcal P}(1,A_1,dots,A_n),
$$
$$
operatorname{nrr} { det (A-lambda E) =0 | lambda<0 }={mathcal V}(1,A_1,dots,A_n) .
$$
П
Пример. Локализовать собственные числа матрицы
$$
left(
begin{array}{rrr}
11 & 2 & -8 \
2 & 2 & 10 \
-8 & 10 & 5
end{array}
right)
$$
Решение.
$$ H_1(lambda)=11- lambda, H_2(lambda)=lambda^2-13, lambda+18,
$$
$$
f(lambda)= H_3(lambda)=-lambda^3+18, lambda^2 +81, lambda -1458
.
$$
| $ lambda $ | $ 1_{} $ | $ H_1(lambda) $ | $ H_2(lambda) $ | $ H_3(lambda) $ | $ {mathcal P} $ | Комментарии |
|---|---|---|---|---|---|---|
| $ 0_{} $ | $ + $ | $ + $ | $ + $ | $ — $ | 2 | число положительных =2 |
| $ -10 $ | $ + $ | $ + $ | $ + $ | $ + $ | 3 | собственное число |
| $ -5 $ | $ + $ | $ + $ | $ + $ | $ — $ | 2 | лежит на $ ]-10,-5[ $ |
| $ 5 $ | $ + $ | $ + $ | $ — $ | $ — $ | 2 | собственное число |
| $ 10 $ | $ + $ | $ + $ | $ — $ | $ + $ | 1 | лежит на $ ]5,10[ $ |
| $ 15 $ | $ + $ | $ — $ | $ — $ | $ + $ | 1 | собственное число |
| $ 20 $ | $ + $ | $ — $ | $ + $ | $ — $ | 0 | лежит на $ ]15,20[ $ |
Проверка. Спектр матрицы: $ {-9,9,18 } $.
П
Пример. Локализовать собственные числа матрицы
$$
left(
begin{array}{rrr}
1 & -2 & 2 \
-2 & -2 & 4 \
2 & 4 & -2
end{array}
right) .
$$
Решение.
$$H_1(lambda)=1- lambda, H_2(lambda)=lambda^2+, lambda-6,
f(lambda)=H_3(lambda)=-lambda^3-3, lambda^2 +24, lambda -28
.
$$
| $ lambda_{} $ | $ 1_{} $ | $ H_1(lambda) $ | $ H_2(lambda) $ | $ H_3(lambda) $ | $ {mathcal P} $ | Комментарии |
|---|---|---|---|---|---|---|
| $ 0_{} $ | $ + $ | $ + $ | $ — $ | $ — $ | 2 | число положительных =2 |
| $ -8 $ | $ + $ | $ + $ | $ + $ | $ + $ | 3 | собственное число |
| $ -6 $ | $ + $ | $ + $ | $ + $ | $ — $ | 2 | лежит на $ ]-8,-6[ $ |
| $ 1.5 $ | $ + $ | $ — $ | $ — $ | $ — $ | 2 | два собственных числа |
| $ 3_{} $ | $ + $ | $ — $ | $ + $ | $ — $ | 0 | лежат на $ ]1.5,3[ $ |
Никаким дроблением интервала $ ]1.5, , , 3[ $ не удается отделить
два вещественных собственных числа. Вывод: имеется кратное собственное
число.
Проверка. Спектр матрицы: $ {-7,2,2 } $.
Произвольная матрица
Собственный вектор
Собственный вектор матрицы 
$$
X_{ast}= left(
begin{array}{c} x_{1}^{ast} \ vdots \ x_{n}^{ast}
end{array} right)
in mathbb{C}^n
$$
такой, что
$$ AX_{ast}=lambda_{ast} X_{ast} quad iff quad (A -lambda_{ast}E) X_{ast} = mathbb O_{ntimes 1} . $$
По определению собственного числа, $ det (A^{} -lambda_{ast}E) = 0 $ и, следовательно,
система однородных уравнений $ (A -lambda_{ast}E) X^{} = mathbb O $ всегда имеет нетривиальное решение; более того, этих решений бесконечно много. Таким образом, одному и тому же собственному числу матрицы принадлежит бесконечное множество собственных векторов. Эту бесконечность можно описать с помощью фундаментальной системы решений (ФСР).
Строго говоря, только что введено определение правого собственного вектора матрицы $ A $. Потому как для
этой же матрицы определяется и левый собственный вектор — как строка $ Y_{ast}=(y_1^{ast},dots, y_n^{ast}) ne mathbb O $, такая, что
$$ Y_{ast} A= mu_{ast} A quad mbox{ при некотором } mu_{ast} in mathbb C , . $$
Очевидно, что $ Y_{ast} $ является левым собственным вектором $ A $ тогда и только тогда, когда столбец $ Y_{ast}^{top} $ является правым собственным вектором матрицы $ A^{^{top}} $. Кроме того, поскольку спектры матриц $ A $ и $ A^{^{top}} $ совпадают, то все результаты, полученные для правых собственных векторов, автоматически переносятся и на левые. Традиционно принято рассматривать правые собственные векторы; в этом случае слово «правый» опускают.
П
Пример. Найти собственные векторы матрицы
$$
A=
left(begin{array}{rrrr}
0&1&2&3\
-1&0&4&7\
-2&-4&0&2\
-3&-7&-2&0
end{array}right).
$$
Решение. Спектр матрицы найден выше.
$$(A-0 cdot E)X=mathbb O quad Longrightarrow mbox{ ФСР}=
left{
{mathfrak X}_1=left(begin{array}{r}
4 \ -2 \ 1 \ 0 end{array}right),
{mathfrak X}_2=left(begin{array}{r}
7 \ -3 \ 0 \ 1 end{array} right) right}.$$
Любой вектор вида $ alpha_{1} {mathfrak X}_1 + alpha_2 {mathfrak X}_2 $ будет собственным,
принадлежащим $ lambda_{}=0 $.
$$ begin{array}{c}
(A- mathbf i, sqrt {83} E)X=mathbb O \ \ Downarrow \ \ {mathfrak X}_3=
left(begin{array}{c}
1- mathbf i , sqrt {83} \ 8-2, mathbf i , sqrt {83} \ 12 \ 17+mathbf i , sqrt {83}
end{array}right)
end{array}
qquad
begin{array}{c}
(A+mathbf i sqrt {83} E)X=mathbb O \ \ Downarrow \ \ {mathfrak X}_4=
left(begin{array}{c}
1+mathbf i , sqrt {83} \ 8+2mathbf i , sqrt {83} \ 12 \ 17- mathbf i ,sqrt {83}
end{array}right)
end{array} .
$$
♦
Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.
Т
Теорема 15. Пусть $ lambda_{ast}^{} $ — собственное число матрицы $ A_{} $. Обозначим частное от деления характеристического полинома на линейный множитель $ lambda_{} — lambda_{ast} $ через $ f_{ast}(lambda)^{} $:
$$ f_{ast}(lambda) equiv f(lambda) / (lambda-lambda_{ast}) . $$
Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ является собственным вектором, принадлежащим $ lambda_{ast}^{} $.
Доказательство следует из равенства
$$(A-lambda_{ast} E)f_{ast}(A)=mathbb O_{ntimes n} . $$
На основании определения любой ненулевой столбец $ f_{ast}(A)^{} $ должен быть
собственным вектором матрицы $ A_{} $.
♦
П
Пример. Найти собственные векторы матрицы
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right) .
$$
Решение.
$$ det (A-lambda E)=-lambda^3+ 7, lambda + 6 equiv -(lambda_{}-3) (lambda+2)(lambda+1) , .$$
Пренебрегая знаком – , имеем:
$$
begin{matrix}
f_1(lambda)=lambda^2+3lambda+2 & u & f_1(A)=
left( begin{array}{rrr}
40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20
end{array}
right) , \
f_2(lambda)=lambda^2-2lambda-3 & u & f_2(A)=
left( begin{array}{rrr}
-10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0
end{array}
right) , \
f_3(lambda)=lambda^2-lambda-6 & u & f_3(A)=
left( begin{array}{rrr}
-4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8
end{array}
right) .
end{matrix}
$$
Ответ. $ {mathfrak X}_{1}=[1,0,1]^{^{top}} $ принадлежит $ lambda_{1}^{}=3 $,
$ {mathfrak X}_{2}=[-2,1,0]^{^{top}} $ принадлежит $ lambda_{2}^{}=-2 $,
$ {mathfrak X}_{3}=[-1,1,2]^{^{top}} $ принадлежит $ lambda_{3}^{}=-1 $.
=>
Если $ lambda_{ast}^{} $ является простым корнем характеристического полинома9), то ненулевые столбцы $ f_{ast}(A)^{} $ будут пропорциональными. Или, что то же, $ operatorname{rank} f_{ast}(A)^{} = 1 $.
Тогда очевидно, что и строки матрицы $ f_{ast}(A)^{} $ тоже должны быть пропорциональны!
На практике вычисление полинома $ f_{ast}(lambda)^{} $ может быть осуществлено с помощью схемы Хорнера.
П
Пример. Вычислить собственный вектор матрицы
$$
A=left( begin{array}{rrr}
23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87
end{array}
right) ,
$$
принадлежащий ее вещественному собственному числу.
Решение. Характеристический полином
$$ f(lambda)= -lambda^3+184,lambda^2-14751,lambda+611404 $$
имеет единственное вещественное собственное число $ lambda_{ast} approx 96.8817 $. Составляем схему Хорнера
$$
begin{array}{c|cccc}
& -1 & 184 & -14751 & 611404 \
hline
96.8817 & -1 & 87.1183 & -6310.8310 & -0.0352
end{array}
$$
За счет ошибок округления мы получили ненулевое значение для $ f(lambda_{ast}) $. В качестве частного от деления $ f(lambda) $ на $ lambda-lambda_{ast} $ берем
$$
f_{ast}(lambda)= -lambda^2 + 87.1183, lambda — 6310.8310 .
$$
Подставляем в него матрицу $ A_{} $ и вычисляем первый столбец матрицы
$$ -A^2+87.1183,A -6310, E =
left( begin{array}{rrr}
-1882.1101 & * & * \ -2723.2902 & * & * \ -708.6229 & * & *
end{array}
right) .$$
Проверяем:
$$
left( begin{array}{rrr}
23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87
end{array}
right)
left( begin{array}{r}
-1882.1101 \ -2723.2902 \ -708.6229
end{array}
right) — 96.8817 left( begin{array}{r}
-1882.1101 \ -2723.2902 \ -708.6229
end{array}
right)= left( begin{array}{r}
0.0356 \ 0 \ -0.0002
end{array}
right) .
$$
♦
Можно развить последний метод далее: найти универсальную формулу для собственного вектора как функции ее собственного числа. Действительно, найдем частное от деления характеристического полинома
$$ f(lambda) =a_0lambda^n+a_0lambda^{n-1}+dots+ a_n, quad a_0=(-1)^n $$
на линейный полином $ lambda- lambda_{ast} $, где $ lambda_{ast} $ — произвольное число из $ mathbb C $. С помощью той же схемы Хорнера, получаем
$$ q(lambda)= $$
$$
=a_0lambda^{n-1}+(a_0lambda_{ast}+a_1)lambda^{n-2}+(a_0lambda_{ast}^2+a_1lambda_{ast}+a_2)lambda^{n-3}+dots+ (a_0lambda_{ast}^{n-1}+a_1lambda_{ast}^{n-2}+dots+a_{n-1}) , .
$$
Если $ lambda_{ast} $ является собственным числом матрицы $ A_{} $, то любой ненулевой столбец матрицы
$$ q(A)= $$
$$
=a_0A^{n-1}+(a_0lambda_{ast}+a_1)A^{n-2}+(a_0lambda_{ast}^2+a_1lambda_{ast}+a_2)A^{n-3}+dots+ (a_0lambda_{ast}^{n-1}+a_1lambda_{ast}^{n-2}+dots+a_{n-1})E
$$
будет собственным вектором, принадлежащим $ lambda_{ast} $.
П
Пример. Найти представление всех собственных векторов матрицы
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right)
$$
в виде функции ее собственных чисел.
Решение. Характеристический полином матрицы был вычислен выше: $ f(lambda)=-lambda^3+ 7, lambda + 6 $. Имеем,
$$
q(lambda)=-lambda^2-lambda_{ast}lambda+(7-lambda_{ast}^2)
$$
и
$$
q(A)=-A^2-lambda_{ast}A+(7-lambda_{ast}^2)E=
left(begin{array}{ccc} -lambda_{ast}^2-9lambda_{ast}-4 & -22lambda_{ast}-14 & 6lambda_{ast}+2 \
lambda_{ast}-3 & -lambda_{ast}^2+4lambda_{ast}-3 & -lambda_{ast}+3 \
-8lambda_{ast}-16 & -16lambda_{ast}-32 & -lambda_{ast}^2+5lambda_{ast}+14
end{array} right) , .
$$
Берем произвольный столбец этой матрицы, например, первый:
$$
X_{ast}(lambda_{ast})=
left(begin{array}{c}
-lambda_{ast}^2-9lambda_{ast}-4 \
lambda_{ast}-3 \ -8lambda_{ast}-16
end{array} right) , .
$$
Утверждается, что $ X_{ast} (lambda_{ast}) $ — универсальное представление всех собственных векторов матрицы. Действительно,
$$
X_{ast}(-1)
=
left(begin{array}{r}
4 \
-4 \
-8
end{array} right),
X_{ast}(-2)
=
left(begin{array}{r}
10 \
-5 \ 0
end{array} right),
X_{ast}(3)
=
left(begin{array}{r}
-40 \
0 \
-40
end{array} right) , .
$$
♦
Матрица $ q(A) $, которую мы построили для нахождения универсального представления собственного вектора, может быть получена другим способом. В самом деле, поскольку
$$ f(lambda)equiv q(lambda)(lambda-lambda_{ast})+ f(lambda_{ast}), $$
то имеем справедливость матричного равенства:
$$ f(A)equiv q(A)(A-lambda_{ast}E)+ f(lambda_{ast})E , . $$
Откуда, на основании теоремы Гамильтона-Кэли, получаем равенство
$$ q(A)(A-lambda_{ast}E) = — E det (A-lambda_{ast}E) , . $$
Это равенство означает, что матрица $ (- q(A)) $ является взаимной матрице $ A-lambda_{ast}E $:
$$ — q(A)=operatorname{adj}(A-lambda_{ast}E) , . $$
Следовательно, ее выражение (а нам, собственно, нужно только выражение для какого-то ее столбца)
может быть получено с помощью алгебраических дополнений элементов матрицы $ A-lambda_{ast}E $. Именно такой способ вычисления взаимной матрицы использовался при доказательстве теоремы Гамильтона-Кэли.
Т
Теорема 16. Пусть $ g(x)=b_0x^m+dots+b_{m} in {mathbb C}[x] $ – произвольный полином. Если $ X_{ast}in mathbb C^{n} $ — собственный вектор матрицы $ A_{} $,
соответствующий собственному числу $ lambda_{ast}^{} $, то он же будет собственным и для матрицы $ g(A)^{} $, принадлежащим собственному числу $ g(lambda_{ast})^{} $.
Доказательство. Домножим равенство $ A{mathfrak X}_{ast}=lambda_{ast}^{}{mathfrak X}_{ast} $ слева
на матрицу $ A_{} $:
$$ A^2{mathfrak X}_{ast}=lambda_{ast}A{mathfrak X}_{ast}=lambda_{ast}^2{mathfrak X}_{ast} .$$
По индукции доказывается и общее равенство:
$$ A^k{mathfrak X}_{ast}=lambda_{ast}^k{mathfrak X}_{ast} .$$
Домножим его на $ b_{m-k}^{} $ и просуммируем по $ k_{} $ от $ 0_{} $ до $ m_{} $:
$$ g(A){mathfrak X}_{ast}=g(lambda_{ast}){mathfrak X}_{ast} ,$$
что и доказывает утверждение теоремы.
♦
=>
Если матрица $ A $ невырождена, то теорема остается справедливой и для произвольного полинома от $ A^{-1} $. В частности, собственные векторы $ A^{-1} $ совпадают с собственными векторами матрицы $ A $.
Т
Теорема 17. Собственные векторы, принадлежащие различным собственным числам матрицы $ A_{} $, линейно независимы.
Т
Теорема 18. Собственные векторы, принадлежащие различным собственным числам вещественной симметричной матрицы $ A_{} $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_{1} $, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_{2} $ и $ lambda_1 ne lambda_2 $, то
$$ langle mathfrak X_1, mathfrak X_2 rangle =0 , $$
где $ langle , rangle $ означает скалярное произведение, определяемое стандартным образом: $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.
Доказательство
☞
ЗДЕСЬ.
Теорема Перрона-Фробениуса
Т
Теорема 19 [Перрон, Фробениус]. Для положительной матрицы $ A_{} $ существует положительное собственное число $ lambda_{+} $ такое, что все остальные собственные числа этой матрицы меньше $ lambda_{+} $ по абсолютной величине (модулю). Соответствующий этому собственному числу собственный вектор может быть выбран положительным:
$$ exists mathfrak X_{+} > mathbb O: quad A mathfrak X_{+} = lambda_{+} mathfrak X_{+} . $$
Число $ lambda_{+} $ из теоремы называется собственным числом Перрона или собственным числом Перрона-Фробениуса матрицы $ A_{} $, а соответствующий ему произвольный положительный собственный вектор —
собственным вектором Перрона-Фробениуса матрицы $ A_{} $.
=>
Спектральный радиус положительной матрицы $ A_{} $ совпадает с ее собственным числом Перрона-Фробениуса:
$$ rho(A)=lambda_{+} . $$
П
Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы
$$
A=
left(begin{array}{rrrr}
2 & 7 & 18 & 28 \
1 & 8 & 2 & 8 \
3 & 1 & 4 & 1 \
5 & 9 & 26 & 5
end{array}
right) , .
$$
Решение. Характеристический полином матрицы $ A_{} $
$$
det(A-lambda E)=lambda^4-19, lambda^3-175, lambda^2-285, lambda+10390
$$
имеет корнями
$$
lambda_{1,2} approx -6.260463 pm 5.452465 mathbf i, lambda_3 approx 5.878976, lambda_4 approx 25.641950 .
$$
Числом Перрона-Фробениуса является $ lambda_4 $, а соответствующий ему собственный вектор Перрона-Фробениуса можно взять равным
$$
left(
begin{array}{c}
1 \
0.365240 \ 0.184802 \ 0.634244
end{array}
right) quad mbox{ или } quad
left(
begin{array}{c}
2.737922 \ 1 \ 0.505974 \ 1.736510
end{array}
right) quad mbox{ или }
left(
begin{array}{c}
5.411185 \ 1.976383 \ 1 \ 3.432010
end{array}
right) quad mbox{ или } quad
left(
begin{array}{c}
1.576681 \ 0.575868 \ 0.291374 \ 1
end{array}
right) quad mbox{ или } quad
left(
begin{array}{r}
0.798133 \
0.291510 \
0.147496\
0.506210
end{array}
right) quad mbox{ или } dots
$$
(напоминаю: собственный вектор определяется с точностью до ненулевого сомножителя!). Последний вектор имеет длину равную $ 1_{} $.
♦
Свойства.
1.
Собственное число Перрона-Фробениуса всегда простое для характеристического полинома матрицы $ A_{} $. Отсюда следует, что собственный вектор Перрона-Фробениуса определяется единственным образом — с точностью до домножения на положительный скаляр.
2.
Любой собственный вектор положительной матрицы $ A_{} $, не соответствующий собственному числу Перрона-Фробениуса, не может состоять исключительно только из положительных элементов. Иными словами, хотя бы одна компонента такого вектора должна быть либо отрицательной либо мнимой.
3.
Для собственного числа Перрона-Фробениуса справедливо неравенство
$$ min_{jin{1,dots,n}} sum_{k=1}^n a_{jk} le lambda_{+} le max_{jin{1,dots,n}} sum_{k=1}^n a_{jk} . $$
4.
Собственное число Перрона-Фробениуса матрицы $ A_{} $ совпадает с собственным числом Перрона-Фробениуса матрицы $ A^{top} $.
Какие из перечисленных свойств можно распространить на случай неотрицательных матриц ? Каждую такую матрицу можно рассматривать как предел последовательности (строго)
положительных матриц.
Воспользовавшись теоремой о непрерывной зависимости собственных чисел матрицы от ее элементов, можем сделать вывод, о том, что для неотрицательной матрицы $ A_{} $ всегда найдется вещественное неотрицательное собственное число, которое будет являться максимальным по модулю среди всех собственных чисел матрицы. Другое дело, что в данном случае — в отличие от случая положительных матриц — такое мажорирующее собственное число может оказаться не единственным.
П
Пример. Спектр неотрицательной матрицы
$$ A=left( begin{array}{cc} 0 & 1 \ 1 & 0 end{array} right) $$
состоит из чисел $ lambda_1=+1 $ и $ lambda_1=-1 $ одинакового модуля.
♦
Однако, по-прежнему, хотя бы одно неотрицательное вещественное число $ lambda_{+} $ со свойством $ rho(A) = lambda_{+} $ существовать будет; более того, ему будет соответствовать неотрицательный собственный вектор $ mathfrak X ge mathbb O $. Это число (вектор) по-прежнему называются числом (вектором) Перрона-Фробениуса10) матрицы $ A_{} $.
Частным случаем неотрицательных матриц являются стохастические матрицы, т.е. неотрицательные матрицы, в которых сумма элементов
каждой строки равна $ 1_{} $:
$$
mathfrak P=left[p_{jk}right]_{j,k=1}^n, {p_{jk}ge 0 }_{j,k=1}^n, sum_{k=1}^n p_{jk} = 1 npu quad j in {1,2,dots,n} .
$$
Т
Теорема 20. Собственное число Перрона-Фробениуса стохастической матрицы равно $ 1_{} $. Этому собственному числу соответствует собственный вектор $ X=[1,1,dots,1]^{top} $.
Доказательство существования собственного числа равного $ 1_{} $ и соответствующего ему собственного вектора $ X=[1,1,dots,1]^{top} $ следует из равенства
$$mathfrak P left(
begin{array}{c}
1 \
1 \ vdots \ 1
end{array}
right) =
left(
begin{array}{c}
1 \ 1 \ vdots \ 1
end{array}right) .
$$
Далее, из теоремы Гершгорина следует, что любое собственное
число $ lambda_{}in mathbb C $ стохастической матрицы должно удовлетворять неравенству
$$|lambda — p_{jj}|le sum_{kne j} |p_{jk}|=1-p_{jj} $$
хотя бы при одном $ j_{} $. Воспользовавшись следствием к неравенству треугольника получаем:
$$|lambda| — |p_{jj}|le |lambda — p_{jj}| le 1-p_{jj} Rightarrow
|lambda| le 1 . $$
♦
Численное нахождение собственного числа и собственного вектора Перрона-Фробениуса возможно по методу, разобранному в пункте
☞
ЧАСТИЧНАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ.
Методы вычисления характеристического полинома
Вычисление коэффициентов характеристического полинома матрицы $ A_{} $
непосредственным разложением определителя $ det (A-lambda_{} E) $ на $ n!_{} $ слагаемых — крайне неэффективно. Элементами этого разложения являются выражения, полиномиально зависящие от параметра $ lambda_{} $. На каждом этапе вычислений мы получаем проблему символьных вычислений: хранения таких полиномов и действий над ними.
Основной метод вычисления числовых определителей — метод Гаусса — также неэффективен в приложении к вычислению определителя, элементы которого зависят от параметра.
Источником вычислительных проблем является неудобное расположение переменной $ lambda_{} $ — на главной диагонали матрицы. Первый же шаг метода Гаусса приводит к делению на элемент $ a_{11} — lambda $, и, в дальнейшем, элементы преобразованной матрицы будут уже не полиномами, а рациональными функциями относительно $ lambda_{} $. Следующие шаги метода приводят к возрастанию степеней знаменателей. Необходимость в организации хранения рациональных функций и программировании действий с ними кажется тем более неоправданной, если вспомнить, что окончательный ответ — выражение для $ det (A-lambda_{} E) $ — должно быть полиномом по $ lambda_{} $; т.е. знаменатели дробей в конечном ответе сократятся.
А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.
Какой выход предлагается? — Предварительно преобразовать определитель $ det (A-lambda_{} E) $ к виду, когда переменная $ lambda_{} $ оказывается «выметенной» с диагонали на крайний ряд (в столбец или в строку). При этом допускается увеличение размеров (порядка) определителя. Такое представление дает возможность разложения определителя по этому исключительному ряду, и, тем самым, позволяет свести задачу к вычислению числовых
определителей — а уж для этой задачи применение метода Гаусса вполне эффективно.
Метод Леверье
Метод основан на формуле (см. следствие к теореме $ 7 $
☞
ЗДЕСЬ ):
$$ operatorname{Sp} (A^k)=lambda_1^k+dots+lambda_n^k=s_k , $$
т.е. след $ k_{} $-й степени матрицы $ A_{} $ равен $ k_{} $-й сумме Ньютона ее характеристического полинома $ f(lambda)=det (A-lambda E ) $.
Вычисляем последовательные степени матрицы $ A_{} $:
$$s_1=operatorname{Sp} (A), s_2=operatorname{Sp} (A^2), dots, s_n=operatorname{Sp} (A^n) .$$
Неизвестные коэффициенты $ f(lambda)=(-1)^n(lambda^n+a_1lambda^{n-1}+
dots+a_n) $ находим по рекурсивным формулам Ньютона:
$$
a_1=-s_1, a_2=-(s_2+a_1s_1)/2,
$$
$$
a_k=-(s_{k}+a_1s_{k-1}+a_2s_{k-2}+dots+a_{k-1}s_1)/k npu k le n.
$$
Очевидно, что не имеет смысла вычислять все элементы матрицы $ A^{n} $ — достаточно обойтись лишь элементами ее главной диагонали.
П
Пример [Леверье]. Найти характеристический полином матрицы
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение.
$$
A^2=left(begin{array}{rrrr}
30.91795128&-30.56848188&2.878480155&0.0031325713\
-4.705449283&164.6764010&-141.3504639&-0.4143169528\
0.3341843103&-106.6094396&193.1869924& -6.756396001\
0.0022236138&-1.904168948&-41.16923134& 309.9628536
end{array}
right),
$$
$$
A^3=left(begin{array}{rrrr}
-179.0125092&431.2849919&-198.8601505& -0.9173897610\
66.38829278&-2562.954533& 2771.458834& -15.49709921\
-23.08728044&2090.291485&-3124.010318& 156.9329019\
-0.649145142&-71.21907809&956.2502143& -5463.723497
end{array}
right),
$$
$$
A^4=left(begin{array}{cccc}
1100.720103& ast& ast& ast \
ast& 42332.23816& ast& ast \
ast& ast& 52669.62534& ast \
ast& ast& ast& 96355.91518
end{array}
right) .
$$
Вычисляем следы матриц:
$$s_1=-47.888430, s_2=698.7441983, s_3=-11329.70086, s_4= 192458.4988 ,$$
и по формулам Ньютона получаем:
$$a_1= 47.888430, a_2 = 797.278764_{displaystyle 8}
, a_3 = 5349.45551_{displaystyle 3},
a_4 = 12296.550_{displaystyle 68} . $$
♦
После нахождения коэффициентов характеристического полинома можно найти его корни каким-либо11) методом. Если $ lambda_{ast}^{} $ — одно
из собственных чисел, то для нахождения соответствующего собственного
вектора воспользуемся алгоритмом из
☞
ПУНКТА. Предположив дополнительно, что это собственное число простое12), обозначим
$$
f_{ast}(lambda)= f(lambda)/(lambda-lambda_{ast})=(-1)^n(lambda^{n-1}
+p_1lambda^{n-2}+dots+p_{n-2}lambda+p_{n-1})
$$
т.е. частное от деления $ f(lambda_{}) $ на $ lambda-lambda_{ast} $. Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ будет собственным вектором, принадлежащим $ lambda_{ast}^{} $. Как правило, собственным вектором можно взять комбинацию
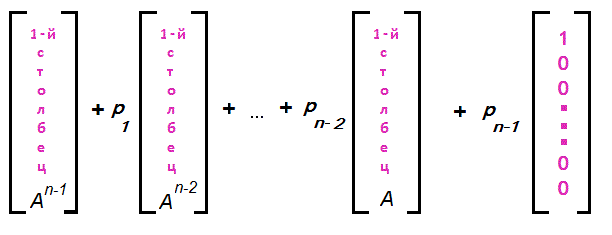
Степени матрицы $ A_{} $ уже нами посчитаны при вычислении коэффициентов характеристического полинома.
П
Пример. Для приведенного выше примера находим собственные числа:
$$
lambda_1=-17.86326,
lambda_2=-17.15242, lambda_3=-7.57404,
lambda_4= -5.29869 .
$$
Коэффициенты $ f_1(lambda) $ можно определить по схеме Хорнера:
$$
begin{array}{r|r|r|r|r|r}
&1 & 47.888430 & 797.2787648 & 5349.455513 & 12296.55068 \ hline
-17.86326 & 1 & underbrace{30.025170}_{p_{_1}}&
underbrace{260.9313465}_{p_{_2}} &underbrace{688.371028}_{p_{_3}}&
approx 0 \
end{array}
$$
Собственным вектором, принадлежащим $ lambda_{1} $, будет
$$left[ -0.0256_{displaystyle 67},
0.21938_{displaystyle 0},
-0.24187_{displaystyle 1},
1.044526 right]^{^{top}} .$$
♦
Т
Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:
$$
f(lambda)=frac{1}{n!}left|
begin{array}{llllll}
s_1 &1 & & & &\
s_2&s_1& 2 & &mathbb O & \
s_3&s_2&s_1&3& & \
vdots& & & ddots &ddots & \
s_n&s_{n-1}& s_{n-2} & dots &s_1&n \
lambda^n&lambda^{n-1}&lambda^{n-2}& dots &lambda&1
end{array}
right|_{(n+1)times (n+1)} .
$$
Этот определитель имеет порядок больший, чем исходный $ det (A_{}-lambda E) $, однако в нем все включения переменной $ lambda_{} $ локализованы в одной строке — именно такое размещение трактовалось как «хорошее» в смысле вычисления определителя
☝
ВЫШЕ.
И
Биографические заметки о Леверье
☞
ЗДЕСЬ.
Существует модификация метода Леверье, позволяющая организовать одновременное вычисление как самого характеристического полинома матрицы $ A_{} $, так и матрицы взаимной к матрице $ A_{}-lambda E $ (что делает возможным получение универсальной формулы для всех собственных векторов матрицы $ A_{} $); этот метод известен как метод Леверье-Фаддеева.
Метод Крылова
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_{1}^{[0]},dots,y_{n}^{[0]} right]^{^{top}} in mathbb C^n $. Cоставим итерационную векторную
последовательность
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{n}=Acdot Y_{n-1} .
$$
Т
Теорема 22. Определитель
$$
det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&Y_{n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]_{(n+1)times (n+1)}
$$
совпадает — с точностью до постоянного множителя — с характеристическим полиномом матрицы $ A_{} $. Здесь $ |_{} $ означает конкатенацию.
Доказательство. Легко видеть, что
$$ Y_K=A^KY_0 quad npu quad K in {1,dots,n} . $$
Если
$$ f(lambda)=det(A-lambda E) =(-1)^n lambda^n+a_1 lambda^{n-1}+a_2 lambda^{n-2}+dots+a_n , $$
то по теореме Гамильтона-Кэли:
$$
(-1)^n A^n+a_1A^{n-1}+dots+a_nE=mathbb O_{n times n} .
$$
Это равенство останется справедливым и после умножения его на произвольный вектор, в том числе на $ Y_{0} $:
$$
(-1)^n A^ncdot Y_0+a_1A^{n-1} cdot Y_0 +dots+a_ncdot Y_0=mathbb O_{n times 1} iff
$$
$$
iff quad (-1)^n Y_n+a_1Y_{n-1} +dots+a_nY_0=mathbb O .
$$
Последнее равенство представляет линейную систему относительно неизвестных коэффициентов характеристического полинома. Можно решать ее по формулам Крамера, но мы пойдем другим путем. Дополним эту систему тождеством $ f(lambda)=(-1)^n lambda^n+a_1 lambda^{n-1}+a_2 lambda^{n-2}+dots+a_n $. Рассмотрим получившуюся систему как линейную однородную относительно столбца $ left[ a_n,a_{n-1},dots,a_1,1right]^{top} $. Поскольку эта система имеет нетривиальное решение, то ее определитель должен равняться нулю:
$$
0=det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&(-1)^nY_{n}\
1& lambda&dots&lambda^{n-1}&(-1)^nlambda^n-f(lambda)
end{array}
right]=
$$
(представляем последний столбец в виде суммы двух столбцов и используем свойство
5
определителя)
$$
=det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&(-1)^nY_{n}\
1& lambda&dots&lambda^{n-1}&(-1)^nlambda^n
end{array}
right]-f(lambda)
det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right] .
$$
Таким образом,
$$ f(lambda)=(-1)^n frac{det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&Y_{n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]}{det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right]} ,
$$
если только знаменатель в этой дроби не обратится в нуль.
♦
П
Пример. Найти характеристический полином матрицы примера Леверье
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение. Возьмем $ Y_0=left[ 1,0,0,0 right]^{top} $. Имеем
$$
begin{array}{cccc}
Y_1=A Y_0= & Y_2=AY_1= & Y_3=AY_2= & Y_4=AY_3= \
left(begin{array}{r}
-5.509882\
0.287865 \
0.049099 \
0.006235
end{array}
right), &
left(begin{array}{r}
30.917951\
-4.705449 \
0.334184 \
0.002223
end{array}
right), &
left(begin{array}{r}
-179.012509\
66.388293 \
-23.087280\
-0.649145
end{array}
right), &
left(begin{array}{r}
1100.720101\
-967.597333\
576.522644\
-4.040153
end{array}
right) .
end{array}
$$
$$
det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&Y_2& Y_{3}& Y_{4}\
1& lambda&lambda^2 &lambda^{3}&lambda^4
end{array}
right]=
left| begin{array}{rrrrr}
1 & -5.509882 & 30.917951 & -179.012509 & 1100.720101 \
0 & 0.287865 & -4.705449 & 66.388293 & -967.597333\
0 & 0.049099 & 0.334184 & -23.087280 & 576.522644\
0 & 0.006235 & 0.002223 & -0.649145 & -4.040153 \
1 & lambda & lambda^2 & lambda^3 & lambda^4
end{array}
right|=
$$
$$
=0.348621 lambda^4+16.694915lambda^3+277.948166lambda^2+1864.932835lambda+4286.836454 =
$$
$$
=0.348621 left(lambda^4+47.888430lambda^3+797.27876_{displaystyle 3}lambda^2+5349.4555_{displaystyle 0}lambda+12296.550_{displaystyle 5} right) .
$$
♦
После нахождения характеристического полинома можно найти его корни каким-либо13) методом. Пусть $ lambda_{ast}^{} $ — одно из собственных чисел, и оно —
простое; тогда для нахождения соответствующего собственного вектора можно воспользоваться тем же приемом, что был задействован в предыдущем ПУНКТЕ. Вычислим14) частное от деления $ f(lambda_{}) $ на $ lambda-lambda_{ast} $
$$
f_{ast}(lambda)= f(lambda)/(lambda-lambda_{ast})=(-1)^n(lambda^{n-1}
+p_1lambda^{n-2}+dots+p_{n-2}lambda+p_{n-1}) .
$$
Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ будет собственным вектором, принадлежащим $ lambda_{ast}^{} $. Но тогда и произвольная комбинация столбцов этой матрицы тоже будет собственным вектором (если только не обратится в нулевой вектор). В частности, это относится и к комбинации, записываемой в матричном виде
$$ (-1)^n f_{ast}(A) Y_0 = A^{n-1}Y_0 +p_1A^{n-2}Y_0+dots+p_{n-1}Y_0=Y_{n-1}+p_1Y_{n-2}+dots+p_{n-1}Y_0 . $$
А комбинируемые векторы уже посчитаны.
Теперь обсудим исключительные случаи. При неудачном выборе $ Y_{0} $ определитель
$$
det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right]
$$
может обратиться в нуль. Эта неприятность обязательно произойдет если, например, наш выбор пал на вектор $ Y_0 $, совпадающий с собственным вектором матрицы $ A_{} $. Вероятность такого события — нулевая. В общем же случае, трудно ожидать, чтобы $ n_{} $ почти произвольных столбцов
$ Y_0,Y_{1},dots,Y_{n-1} $ оказались линейно зависимыми — если только сама матрица $ A_{} $ не обладает «скрытым дефектом» — типа рассмотренного в следующем примере.
П
Пример. Найти характеристический полином матрицы
$$A=left( begin{array}{ccc}
2&1&1 \
1&2&1 \
1&1&2
end{array}
right) .
$$
Решение. При любом выборе $ Y_0 $ векторы $ {Y_0,Y_1,Y_2 } $ оказываются линейно зависимыми:
$$
Y_0=
left(begin{array}{r}
1\
0\
0
end{array}
right),
Y_1=
left(begin{array}{r}
2\
1\
1
end{array}
right),
Y_2=
left(begin{array}{r}
6\
5\
5
end{array}
right),dots ;
Y_0=
left(begin{array}{r}
1\
1\
1
end{array}
right),
Y_1=
left(begin{array}{r}
4\
4\
4
end{array}
right),dots
$$
Объяснение этого феномена состоит в том, что для матрицы $ A_{} $ ее аннулирующий полином имеет степень меньшую ее порядка:
$$ A^2-5 A+4 E = mathbb O . $$
Домножение этого равенства на произвольный столбец $ Y_0 $ и доказывает линейную зависимость системы $ {Y_0,Y_1,Y_2} $.
♦
Такая ситуация возможна только в случае, когда характеристический полином матрицы $ A_{} $ имеет кратные корни (в рассмотренном выше примере $ lambda_{}=1 $ являлся двойным корнем $ det (A-lambda_{} E) $); она исключительно редко встречается на практике.
Поиск всех собственных чисел
Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.
QR-алгоритм
Этот алгоритм основан на QR-разложении матрицы $ A $.
Т
Теорема 23. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^{top} A P $ при произвольной ортогональной матрице $ P $.
Доказательство.
$$ det (P^{top} A P-lambda E)=det (P^{top} A P- lambda P^{top} E P)=det P^{top} (A -lambda E ) P =
det (A -lambda E ) P P^{top} = det (A -lambda E ) , .
$$
♦
Пусть QR-разложение матрицы $ A $ имеет вид
$$ A=Q_1R_1 , , $$
где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица
$$ A_2=R_1Q_1 $$
имеет тот же спектр, что и матрица $ A $. Действительно, поскольку
$$ A_2=Q_1^{top} A Q_1 , $$
то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $
$$ A_2=Q_2R_2 $$
и переставим местами матрицы этого произведения:
$$ A_3=R_2Q_2 , . $$
Матрица
$$ A_3= Q_2^{top} A_2 Q_2=Q_2^{top} Q_1^{top} A Q_1 Q_2 $$
продолжаем иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц
$$ {A_j=R_{j-1}Q_{j-1}}_{j=1}^{infty} $$
как правило, сходится к матрице $ A_{infty} $, которая будет верхнетреугольной.
Т
Теорема 24 [4]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_{infty} $ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.
П
Пример. Найти все собственные числа матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & 4
end{array}
right) , .
$$
Решение.
$$
A_1=Aapprox
underbrace{left(begin{array}{rrr}
0.272165 & 0.759752 & 0.590511 \
0.952579 & -0.299517 & -0.053683 \
-0.136083& -0.577119 & 0.805242
end{array}
right)}_{Q_1}
underbrace{left(begin{array}{rrr}
7.348469 & 3.946400 & 2.041241\
0 & 2.534941 & -3.966781 \
0 & 0 & 2.469409
end{array}
right)}_{R_1}
$$
Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы:
$$
quad Rightarrow quad A_2 = R_1Q_1approx
left(begin{array}{rrr}
5.481481 & 3.222957 & 5.771191 \
2.954542 & 1.530046 & -3.3303021 \
-0.336044 & -1.425143 & 1.988472
end{array}
right)approx
$$
$$
approxunderbrace{left(begin{array}{rrr}
-0.878992 & 0.022595 & 0.476300\
0.473781 & -0.154267 & -0.867026 \
0.053886 & -0.987771 & 0.146304
end{array}
right)}_{Q_2}
underbrace{left(begin{array}{rrr}
-6.236096& -3.634658 & -3.387848\
0 & 1.244502 & -1.319999\
0 & 0 & 5.927198
end{array}
right)}_{R_2}
$$
Продолжим процесс:
$$
quad Rightarrow quad A_3 = R_2Q_2approx
left(begin{array}{rrr}
7.020952& 3.766220 & -0.314568\
-0.660752 & 1.111870 & -1.272137\
0.319398 & -5.854713 & 0.867177
end{array}
right) approx
$$
$$
approx
underbrace{left(begin{array}{rrr}
-0.994581 & -0.065879 & 0.080426 \
0.093601 & -0.230749 & 0.968501 \
-0.045246 & 0.970780 & 0.235665
end{array}
right)}_{Q_3}
underbrace{left(begin{array}{rrr}
-7.059205 & -3.376839 & 0.154554 \
0 & -6.188319 & 1.156106 \
0 & 0 & -1.053002
end{array}
right)}_{R_3}
$$
Замечаем тенденцию убывания элементов матриц $ {A_j} $, стоящих под главной диагональю.
$$
Rightarrow dots Rightarrow A_{10} approx
left(begin{array}{rrr}
mathbf{6.}_{246022} & 2.758769 & -2.160057\
-0.0467437 & mathbf{4.4}_{09292} & -5.341014\
0.000018 &-0.005924 & mathbf{-1.6}_{55314}
end{array}
right) approx
$$
$$
underbrace{left(begin{array}{rrr}
-0.999972 & -0.007483 & 0.000007 \
0.007483 & -0.999971 & 0.001339 \
-0.000003 & 0.001339 & 0.999999
end{array}
right)}_{Q_{10}}
underbrace{left(begin{array}{rrr}
-6.246197 & -2.725694 & 2.120031\
0 & -4.429817 & 5.354807 \
0 & 0 & -1.662479
end{array}
right)}_{R_{10}} , .
$$
Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна.
$$
Rightarrow dots Rightarrow A_{20} approx
left(begin{array}{rrr}
mathbf{6.17}_{5608} & 2.805821 & -2.020513 \
-0.001776 & mathbf{4.48}_{4917} & -5.388407\
0 & 0 & -mathbf{1.660525}
end{array}
right) approx
$$
Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел.
$$
Rightarrow dots Rightarrow A_{30} approx
left(begin{array}{rrr}
mathbf{6.172}_{778} & 2.807524 & -2.015076\
-0.000073 & mathbf{4.487}_{747} & -5.390442\
0 & 0 & -mathbf{1.660525}
end{array}
right) , .
$$
♦
К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю.
§
Как это обстоятельство сказывается на структуре матрицы $ A_{infty} $ и дальнейшее развитие метода
☞
ЗДЕСЬ
Частичная проблема собственных чисел
Задача. Найти максимальное по модулю собственное число матрицы $ A_{} $.
Предположение
. Будем считать сначала, что максимальное по модулю собственное число матрицы единственно.
Излагаемый ниже метод поиска этого собственного числа называется методом степенны́х итераций15).
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_{1}^{[0]},dots,y_{n}^{[0]} right]^{^{top}} in mathbb C^n $. Cоставим такую же итерационную векторную
последовательность, как и в методе Крылова
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{K}=Acdot Y_{K-1},dots ,
$$
(только теперь, в отличие от метода Крылова, считаем ее неограниченно продолжающейся) и выделим последовательность первых элементов этих векторов:
$$y_{1}^{[1]},y_{1}^{[2]},dots,y_{1}^{[K]},dots $$
Т
Теорема 25. Как правило, предел
$$
lim_{Kto +infty}frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}
$$
существует и он равен максимальному по модулю собственному числу матрицы $ A_{} $.
Доказательство. Перенумеруем собственные числа $ lambda_{1},dots,lambda_n $ матрицы $ A_{} $ так, чтобы $ lambda_{1} $ обозначило максимальное по модулю:
$$|lambda_1|= max_{jin {1,dots,n}} |lambda_j| , quad |lambda_1|>|lambda_j| quad npu quad jin {2,dots,n} . $$
Очевидно,
$$
Y_{K}=A^Kcdot Y_0 ;
$$
отсюда следует, что любой элемент столбца $ Y_{K} $ может быть линейно выражен через $ lambda_{1}^K,dots,lambda_n^K $.
В частности, это справедливо и для первого элемента:
$$
y_{1}^{[K]}=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K .
$$
В этом представлении $ {C_j}_{j=1}^n $ — будут константами из $ mathbb C_{} $ в случае если все собственные числа являются простыми, и полиномами из $ mathbb C[K] $ в случае, если имеются кратные собственные числа. Действительно, в первом случае существует базис пространства $ mathbb C^n $, состоящий из собственных векторов матрицы $ A_{} $:
$$ A{mathfrak X}_j=lambda_j{mathfrak X}_j quad npu quad jin {1,dots,n} . $$
Вектор $ Y_0 $ можно разложить по этому базису:
$$Y_0=alpha_1{mathfrak X}_1+dots+alpha_n{mathfrak X}_n .$$
Тогда последовательным домножением на матрицу $ A_{} $ получаем :
$$begin{matrix}
Y_1=AY_0&=& alpha_1 lambda_1{mathfrak X}_1+dots+alpha_nlambda_n{mathfrak X}_n, \
dots & & dots \
Y_K=A^KY_0&=& alpha_1 lambda_1^K{mathfrak X}_1+dots+alpha_nlambda_n^K{mathfrak X}_n
end{matrix}
$$
откуда и следует доказываемое равенство.
Во втором случае — когда имеются кратные собственные числа матрицы $ A_{} $ — придется применять «тяжелую артиллерию» в виде жордановой нормальной формы; см. теорему $ 5 $
☞
ЗДЕСЬ. Для простоты рассуждений, будем в оставшейся части доказательства считать все собственные числа матрицы различными. Имеем тогда
$$
lim_{K to +infty} frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}=
lim_{K to +infty} frac{lambda_1^{K+1} left[C_1+
C_2(lambda_2/lambda_1)^{K+1}+dots+
C_n(lambda_n/lambda_1)^{K+1} right]}
{lambda_1^{K} left[C_1+C_2(lambda_2/lambda_1)^{K}+dots+
C_n(lambda_n/lambda_1)^{K} right]}
=lambda_1
$$
поскольку
$$
lim_{K to +infty} left| frac{lambda_j}{lambda_1} right|^K = 0 quad
npu quad jin {2,dots,n} .
$$
Исключительным случаем является ситуация $ C_1=0 $, в этом случае утверждение теоремы может оказаться несправедливым16).
♦
=>
Как правило, вектор
$$
left[1, lim_{Kto +infty}frac{y_{2}^{[K]}}{y_{1}^{[K]}},dots,
lim_{Kto +infty}frac{y_{n}^{[K]}}{y_{1}^{[K]}}right]^{^{top}}
$$
будет собственным, принадлежащим максимальному по модулю собственному числу матрицы $ A_{} $.
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & -4
end{array}
right)
$$
найти максимальное по модулю собственное число и принадлежащий ему собственный вектор.
Решение. Возьмем в качестве стартового столбца $ Y_0=[1,0,0]^{^{top}} $. Имеем:
$$
Y_1=AY_0=left( begin{array}{r} 2 \ 7 \ -1 end{array} right),
Y_2=AY_1=left( begin{array}{r} 26 \ 32 \ -12 end{array} right),
Y_3=AY_2=left( begin{array}{r} 160 \ 242 \ -42 end{array} right),dots,
$$
$$
Y_{19}=left( begin{array}{r}
{scriptstyle 4259667747238636} \ {scriptstyle 6435097324667832} \ {scriptstyle -1571397155909260}
end{array} right), Y_{20}=AY_{19}=left( begin{array}{r}
{scriptstyle 29396024624390028} \ {scriptstyle 44408774736946168} \ {scriptstyle -10844273772937260}
end{array} right)
$$
Смотрим на отношения первых элементов векторов:
$$
begin{array}{c|c|c|c|c|c|c|c|c|c}
K & 1 & 2 & 3 & 4 & 5 & dots & 15 & dots & 19 \
hline
y_{1}^{[K+1]}/y_{1}^{[K]} & 2 & 13 & 6.153846 & 6.8 & 7.180147 & dots & 6.900726 & dots & mathbf{6.90101}_{displaystyle 3}
end{array}
$$
Далее, в соответствии со следствием, собственный вектор, принадлежащий найденному числу
$$
approx left[1, frac{y_{2}^{[20]}}{y_{1}^{[20]}},frac{y_{3}^{[20]}}{y_{1}^{[20]}}right]^{^{top}} approx left[1, 1.51070_{displaystyle 6}, -0.368902 right]^{^{top}}
$$
♦
Результат теоремы представляет собой обобщение метода Бернулли поиска максимального по модулю корня полинома. Если в качестве матрицы $ A_{} $ взять матрицу Фробениуса
$$
mathfrak F=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n} ,
$$
то равенство
$$ X_K=mathfrak F X_{K-1} npu Kin {1,2,dots } $$
определяет — при задании (произвольным образом) чисел $ x_0,x_1,dots,x_{n-1} $ — линейную рекуррентную последовательность порядка $ n_{} $:
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K .
$$
Здесь столбцы $ X_K $ определяются формулами
$$
X_0=left( begin{array}{l}
x_0 \ x_1 \ vdots \ x_{n-1}
end{array}
right), X_1=left( begin{array}{l}
x_1 \ x_2 \ vdots \ x_{n}
end{array}
right), X_2=left( begin{array}{l}
x_2 \ x_3 \ vdots \ x_{n+1}
end{array}
right), dots,
X_K=left( begin{array}{l}
x_K \ x_{K+1} \ vdots \ x_{K+n-1}
end{array}
right),dots ;
$$
Характеристический полином последовательности совпадает с характеристическим полиномом матрицы $ mathfrak F $, т.е. с $ lambda^n-a_1 lambda^{n-1} -a_2 lambda^{n-2} -dots — a_n $.
Метод степенных итераций используется в поисковике Google для вычисления PageRank.
Теперь обсудим исключительные случаи алгоритма.
1.
Нарушение сходимости итерационного процесса за счет неудачного выбора стартового вектора. Если в качестве $ Y_{0} $ оказался случайно взят собственный вектор $ mathfrak X_{ast} $ матрицы $ A_{} $, принадлежащий произвольному ее собственному числу $ lambda_{*} $, то предел последовательности из теоремы будет равен именно этому числу; если при этом $ |lambda_{*} | ne max_{1le j le n} | lambda_j | $, то мы выйдем за пределы смысла выражения «как правило». Понятно, что вероятность настолько плохого выбора нулевая, но и выбор $ Y_0 $ вблизи $ mathfrak X_{ast} $ также может существенно замедлить скорость сходимости. Поэтому если возникает ситуация медленной «стабилизации» значащих цифр в десятичном приближении собственного числа, попробуйте сменить начальный вектор.
2.
Нарушение условия
предположения
,
выдвинутого в начале пункта: максимальное по модулю собственное число неединственно.
П
Пример. Найти максимальное по модулю собственное число матрицы примера Леверье
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение. Для столбца $ Y_0=[1,0,0,0]^{^{top}} $ имеем
$$y_{1}^{[100]}/y_{1}^{[99]}=-17.8_{displaystyle 3113} ,$$
т.е. на $ 100 $-й итерации получаем лишь $ 3_{} $ истинные десятичные цифры в представлении собственного числа. При этом
компонентами векторов $ Y_{K} $ являются числа порядка $ 10^{123} $. Если мы
посмотрим на ответ примера Леверье, то увидим, что имеются два собственных числа матрицы, близких по модулю.
♦
К сожалению, вероятность того факта, что у случайно выбранной матрицы два ее собственных числа будут иметь одинаковый модуль становится ненулевой если эта матрица выбирается из множества вещественных матриц. Дело в том, что в этом случае ее характеристический полином будет иметь вещественные коэффициенты, а мнимые корни такого полинома всегда пáрные — для любого невещественного корня $ lambda_{ast}^{} $ полинома, комплексно сопряженное к нему число $ overline{lambda_{ast}} $ также будет корнем. При этом $ |lambda_{ast}|= |overline{lambda_{ast}} | $.
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
3 & 2 &7\
-2 & -8 & 2 \
5 & -3 & -2
end{array}
right)
$$
итерационная последовательность из теоремы ведет себя хаотически: при выборе $ Y_0=[1,0,0]^{top} $ получим
$$
left{frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}right}_{K=1}^{infty} = 3; 13.3333; 5.9250;
4.6455; 15.9273; 0.8546; 68.0186;
$$
$$
0.4543; 91.7873; dots
$$
Спектр матрицы: $ { 6.9363, -6.9682pm 3.0186 mathbf i} $, и максимальное по модулю собственное число неединственно.
♦
Существуют приемы, позволяющие модифицировать метод на случай когда два числа спектра матрицы близки по модулю к максимальному; они подробно обсуждаются в [3].
Предположение 2
. Пусть два максимальных по модулю собственных числа матрицы разнесены по величине, например
$$ |lambda_1| > | lambda_2 | > | lambda_ j | quad npu j in {2,dots, n } . $$
Обобщение степенного метода основывается на использовании последовательностей из каких-то двух компонент векторов $ Y_{K+1}=AY_K $, например, наряду с уже использованной выше последовательностью первых компонент
$$y_{1}^{[1]},y_{1}^{[2]},dots,y_{1}^{[K]},dots $$
возьмем еще и аналогичную для вторых:
$$y_{2}^{[1]},y_{2}^{[2]},dots,y_{2}^{[K]},dots $$
Т
Теорема 26 [Эйткен]. При практически любом выборе стартового вектора $ Y_0 ne mathbb O $ для последовательности
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{K}=Acdot Y_{K-1},dots ,
$$
имеет место равенство
$$
lambda_1 lambda_2 = lim_{Kto +infty} frac{left|begin{array}{ll} y_1^{[K+1]} & y_1^{[K+2]} \ y_2^{[K+1]} & y_2^{[K+2]} end{array} right|}
{left|begin{array}{ll} y_1^{[K]} & y_1^{[K+1]} \ y_2^{[K]} & y_2^{[K+1]} end{array} right|} , .
$$
Доказательство. Построим квадратное уравнение
$$ p_0x^2+p_1x+p_2 = 0 $$
имеющее корнями $ lambda_1 $ и $ lambda_2 $.
Если существует базис рпостранства $ mathbb C^n $
$$Y_0=alpha_1{mathfrak X}_1+alpha_2{mathfrak X}_2+dots+alpha_n{mathfrak X}_n .$$
Тогда последовательным домножением на матрицу $ A_{} $ получаем :
$$begin{array}{llll}
Y_K=& alpha_1 lambda_1^K{mathfrak X}_1 &+alpha_2 lambda_2^K{mathfrak X}_2+dots &+alpha_nlambda_n^K{mathfrak X}_n, \
Y_{K+1}=& alpha_1 lambda_1^{K+1}{mathfrak X}_1 &+alpha_2 lambda_2^{K+1}{mathfrak X}_2+dots &+alpha_nlambda_n^{K+1}{mathfrak X}_n,\
Y_{K+2}=& alpha_1 lambda_1^{K+2}{mathfrak X}_1 & +alpha_2 lambda_2^{K+2}{mathfrak X}_2+dots &+alpha_nlambda_n^{K+2}{mathfrak X}_n.
end{array}
$$
Отбрасываем из правых частей равенств слагаемые порядков возрастания ниже, чем $ lambda_2^K, lambda_2^{K+1}, lambda_2^{K+2} $ соответственно, домножаем получившиеся приближенные равенства
$$begin{array}{lll|l}
Y_K & approx alpha_1 lambda_1^K{mathfrak X}_1 &+alpha_2 lambda_2^K{mathfrak X}_2, & color{Red} times p_2 \
Y_{K+1}& approx alpha_1 lambda_1^{K+1}{mathfrak X}_1 &+alpha_2 lambda_2^{K+1}{mathfrak X}_2, & color{Red} times p_1\
Y_{K+2} & approx alpha_1 lambda_1^{K+2}{mathfrak X}_1 & +alpha_2 lambda_2^{K+2}{mathfrak X}_2, & color{Red} times p_0
end{array}
$$
и складываем:
$$ p_2 Y_K + p_1Y_{K+1} + p_0 Y_{K+2} approx mathbb O , . $$
В получившемся векторном равенстве выбираем первые две компоненты:
$$
left{
begin{array}{ll}
p_2 y_1^{[K]} + p_1 y_1^{[K+1]} + p_0 y_1^{[K+2]} approx 0 , , \
p_2 y_2^{[K]} + p_1 y_2^{[K+1]} + p_0 y_2^{[K+2]} approx 0 , ,
end{array}
right.
$$
которые и позволят определить приближенное значение набора $ p_0,p_1,p_2 $. С точностью до числового сомножителя, искомый полином можно представить в виде определителя
$$
p_0x^2+p_1x+p_2 approx
left|begin{array}{lll}
y_1^{[K]} & y_1^{[K+1]} & y_1^{[K+2]} \
y_2^{[K]} & y_2^{[K+1]} & y_2^{[K+2]} \
1 & x & x^2
end{array}
right| , .
$$
Формулы Виета завершат доказательство.
♦
=>
При выполнении условия
предположения 2
имеет место равенство
$$ lambda_2 =
lim_{Kto +infty} frac{left|begin{array}{ll} y_1^{[K+1]} & y_1^{[K+2]} \ y_2^{[K+1]} & y_2^{[K+2]} end{array} right| y_{1}^{[K+1]}}
{left|begin{array}{ll} y_1^{[K]} & y_1^{[K+1]} \ y_2^{[K]} & y_2^{[K+1]} end{array} right| y_{1}^{[K+2]} } , .
$$
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & 4
end{array}
right)
$$
найти первые два по порядку убывания модулей собственных числа.
Решение. Для $ Y_0= [1,0,0]^{top} $ имеем:
$$
Y_1=left( begin{array}{r} 2 \ 7 \ -1 end{array} right),
Y_2=left( begin{array}{r} 26 \ 32 \ -20 end{array} right), dots,
$$
$$
Y_{18}=left( begin{array}{r} {scriptstyle 164983395620948} \ {scriptstyle 156537857759336} \ -{scriptstyle 219402049179956} end{array} right),
Y_{19}=left( begin{array}{r} {scriptstyle 1018982413699860} \ {scriptstyle 966291195084776} \ -{scriptstyle 1355667307859444} end{array} right),
Y_{20}=left( begin{array}{r} {scriptstyle 6292505720513492} \ {scriptstyle 5964748557575016} \ -{scriptstyle 8374234035307188} end{array} right), .
$$
Таким образом,
$$
lambda_1 approx frac{y_1^{[20]}}{y_1^{[19]}}= frac{1573126430128373}{254745603424965} approx mathbf{6.17}_5 ,
$$
$$
lambda_2 approx
frac{left|begin{array}{ll} y_1^{[19]} & y_1^{[20]} \ y_2^{[19]} & y_2^{[20]} end{array} right| y_{1}^{[19]}}
{left|begin{array}{ll} y_1^{[18]} & y_1^{[19]} \ y_2^{[18]} & y_2^{[19]} end{array} right| y_{1}^{[20]} }=
frac{300892177677465751832368453246033765185}{67074186846991590001957412392957971737 }
approx mathbf{4.48}_5
$$
♦
Обобщение этого подхода для поиска следующих по убыванию модулей собственных чисел проводится по аналогии с деления-вычитания вычисления корня полинома. Кстати, теоретически можно довести этот метод и до построения характеристического (точнее, минимального аннулирующего) полинома матрицы: при любом $ K in {0,1,2,dots } $ определитель
$$
left|begin{array}{llll}
y_1^{[K]} & y_1^{[K+1]} & dots & y_1^{[K+n]} \
y_2^{[K]} & y_2^{[K+1]} & dots & y_2^{[K+n]} \
vdots & vdots & & vdots \
y_n^{[K]} & y_n^{[K+1]} & dots & y_n^{[K+n]} \
1 & lambda & dots & lambda^n
end{array}
right|=
det left[begin{array}{c|c|c|c|c}
Y_K&Y_{K+1}&dots&Y_{K+n-1}&Y_{K+n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]
$$
совпадает — с точностью до числового сомножителя — с $ det (A-lambda E) $. И мы вернулись к
☝
методу Крылова вычисления характеристического полинома!
Для случая симметричной матрицы альтернативное обобщение степенного метода для поиска ранжированных по убыванию модулей собственных чисел и соответствующих им собственных векторов разбирается
☞
ЗДЕСЬ.
Задачи
Источники
[1]. Островский А.М. Решение уравнений и систем уравнений. М. ИЛ, 1963, c. 137-142
[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94
[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960
[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
Спектр матрицы и собственные векторы матрицы
Собственные числа и собственные векторы матрицы.
Из курса линейной алгебры известно, что если А х = l х , то вектор х называется собственным вектором матрицы А , а число l – собственным числом, соответствующим данному собственному вектору. Совокупность всех собственных чисел матрицы называется спектром матрицы. Если в спектре матрицы одно и тоже собственное число встречается k раз, то говорят, что кратность этого собственного числа равна k .
Для нахождения собственных чисел матрицы А используется команда eigenvalues(A). Для нахождения собственных векторов матрицы А используется команда eigenvectors(A). В результате выполнения этой команды будут получены собственные числа, их кратность и соответствующие собственные векторы.
Чтобы понять, в каком виде получаются результаты выполнения команды eigenvectors, внимательно разберитесь со следующим примером: матрица имеет 3 собственных вектора: , отвечающий собственному числу кратности 1, , отвечающий собственному числу кратности 1, , отвечающий собственному числу кратности 1. Найдем их в Maple :
В строке вывода перечислены в квадратных скобках собственное число, его кратность и соответствующий собственный вектор в фигурных скобках , затем следующие наборы таких же данных.
Характеристический и минимальный многочлены матрицы.
Для вычисления характеристического многочлена матрицы A используется команда charpoly(A,lambda).
Минимальный многочлен (делитель) матрицы А можно найти с помощью команды minpoly(A,lambda).
Канонические и специальные виды матрицы.
Привести матрицу А к нормальной форме Жордана можно командой jordan(A).
К треугольному виду матрицу А можно привести тремя способами:
команда gausselim(A) приводит матрицу А к треугольному виду методом Гаусса;
команда ffgausselim(A) приводит матрицу А к треугольному виду методом Гаусса без деления. Эта команда предпочтительней для работы с символьными матрицами, так как не производит нормировку элементов и исключает возможные ошибки, связанные с делением на нуль;
команда gaussjord(A) приводит матрицу А к треугольному виду методом Гаусса-Жордана.
Характеристическую матрицу можно вычислить командой charmat(A,lambda).
Задание 3.
- Дана матрица . Найти ее собственные векторы и собственные числа.
,
Дана матрица . Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.
Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.
Самостоятельно проверьте, чем будет отличаться результат выполнения команды ffgausselim(A) от gausselim(A) на этом примере.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Характеристический полином, собственные числа, собственные векторы матрицы
В настоящем разделе $ n_<> $ означает порядок квадратной матрицы $ A_<> $.
Характеристический полином
определяется для произвольной квадратной матрицы $ A_<> $ как 1) $ det (A_<>-lambda E) $, где $ E_<> $ – единичная матрица одинакового с $ A_<> $ порядка.
Пример. Для $ n=2_<> $:
Теорема 1.
Пример. Характеристический полином матрицы Фробениуса
$$ mathfrak F= left( begin 0 & 1 & 0 & 0 & dots & 0 & 0 \ 0 & 0 & 1 & 0 & dots & 0 & 0 \ 0 & 0 & 0 & 1 & dots & 0 & 0 \ vdots& &&&ddots & & vdots \ 0 & 0 & 0 & 0 & dots & 0 & 1 \ a_n & a_ & a_ & & dots & a_2 & a_1 end right)_ $$ равен $ (-1)^n(lambda^n-a_1lambda^-dots-a_) $.
Характеристический полином линейного оператора
определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее ☞ ЗДЕСЬ.
Характеристический полином линейного однородного разностного уравнения
$ n_<> $-го порядка $$ x_=a_1 x_+ dots+ a_n x_K, quad a_n ne 0, $$ определяется как $$ lambda^n — a_1 lambda^ — dots — a_n . $$ Подробнее ☞ ЗДЕСЬ.
Свойства
Теорема 2. Характеристический полином матрицы не меняется
1. при ее транспонировании: $$ det (A-lambda E) = det (A^<top>-lambda E_<>) , ;$$ 2. при переходе к подобной матрице: если $ B=C^<-1>AC^<> $ при произвольной неособенной матрице $ C_<> $, то $$ det (A-lambda E) equiv det (B-lambda E_<>) , . $$
Теорема 3. Пусть матрица $ A_<> $ имеет порядок $ mtimes n_<> $, а $ B_<> $ — порядок $ ntimes m_<> $. Тогда эти матрицы допускают умножение в любом порядке, т.е. определены $ AB_<> $ и $ BA_<> $ и оба произведения будут квадратными матрицами — порядков $ m_<> $ и $ n_<> $ соответственно. Тогда характеристические полиномы этих произведений различаются лишь на степень $ lambda_<> $:
$$ lambda^n det (AB — lambda E_)equiv lambda^m det (BA — lambda E_) . $$
Если матрицы $ A_<> $ и $ B_<> $ — квадратные одинакового порядка, то характеристические полиномы матриц $ AB_<> $ и $ BA_<> $ тождественны.
Теорема 4. Если характеристический полином матрицы $ A_<> $ равен
$$ f(lambda)=(-1)^n lambda^n+a_1lambda^+dots+a_lambda+a_n $$ и $ a_ ne 0 $, то характеристический полином матрицы $ A^<-1>_<> $ равен $$ f^<ast>(lambda)=frac<(-lambda)^n> f(1/lambda) = frac<(-1)^n> left[ (-1)^n+a_1 lambda + dots+ a_lambda^+a_nlambda^ right] . $$
Теорема Гамильтона-Кэли
Теорема 5. Результатом подстановки в характеристический полином $ det (A_<>-lambda E) $ самой матрицы $ A_<> $ будет нулевая матрица:
$$ det (A-lambda E)= (-1)^n lambda^n +a_1 lambda^+dots+a_lambda+ a_n Rightarrow $$ $$ Rightarrow (-1)^n A^n +a_1 A^+dots+a_A+ a_n E = <mathbb O>_ . $$
матрица является корнем своего характеристического полинома.
Доказательство ☞ ЗДЕСЬ.
Пример. Для $ n_<>=2 $:
$$ left(begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right)^2 — (a_<11>+a_<22>)left(begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right) + (a_<11>a_<22>-a_<12>a_<21>) left(begin 1 & 0 \ 0 & 1 end right) = left(begin 0 & 0 \ 0 & 0 end right) . $$
Собственное число
определяется для квадратной матрицы $ A_<> $ как произвольный корень ее характеристического полинома $ det (A_<>-lambda E) $. Набор всех собственных чисел матрицы $ A_<> $ (с учетом их кратностей) называется спектром матрицы (таким образом спектр матрицы $ A_<> $ порядка $ n_<> $ всегда состоит из $ n_<> $ чисел, часть из которых могут быть одинаковыми). Максимальный из модулей собственных чисел матрицы $ A_<> $ называется ее спектральным радиусом, он иногда обозначается $ rho(A) $.
Пример. Найти спектр матрицы
$$ A= left(begin 0&1&2&3\ -1&0&4&7\ -2&-4&0&2\ -3&-7&-2&0 endright). $$ Решение. Характеристический полином $$ det (A-lambda E)=left|begin -lambda&1&2&3\ -1&-lambda&4&7\ -2&-4&-lambda&2\ -3&-7&-2&-lambda endright|=lambda^4+ 83lambda^2 $$ имеет корни $ lambda_1=0, lambda_2 = <mathbf i>sqrt<83>, lambda_3 = — <mathbf i>sqrt <83>$, причем $ lambda_ <1>$ — второй кратности.
Ответ. Спектр матрицы $ A_<> $: $ <0,0, <mathbf i>sqrt<83>,- <mathbf i>sqrt <83>> $. Спектральный радиус матрицы $ A_<> $: $ rho(A)= sqrt <83>$.
Теорема 6. Если $ <lambda_<1>,lambda_<2>,dots,lambda_ > $ — спектр матрицы $ A_<> $, то
$$ lambda_1+lambda_<2>+dots+lambda_n = operatorname(A)=a_<11>+a_<22>+dots+a_, $$ $$ lambda_1cdotlambda_<2>times dots times lambda_n = (-1)^ndet (A) . $$
Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета. ♦
Для того, чтобы матрица $ A_<> $ была неособенной необходимо и достаточно, чтобы среди ее собственных чисел не было нулевого.
Теорема 7. Пусть $ g(x)=b_<0>x^m+dots+b_m in <mathbb C>[x] $ — произвольный полином. Вычислим полином от матрицы $ A_<> $: $ g(A)=b_<0>A^m+dots+b_m E $. Тогда если $ <lambda_<1>,dots,lambda_ > $ — спектр матрицы $ A_<> $, то $ ),dots,g(lambda_n) > $ — спектр матрицы $ g(A_<>) $.
Результат теоремы обобщается и на более широкий класс функций $ g_<>(x) $ — фактически на любую функцию, которая может быть определена на спектре матрицы $ A_<> $. В частности, если $ det A_<> ne 0 $, то спектр матрицы $ A^<-1>_<> $ совпадает с $ <1/lambda_j>_^n $.
Имеет место следующее равенство, связывающее степени матрицы $ A_<> $ с суммами Ньютона ее характеристического полинома:
$$ operatorname(A^k)=lambda_1^k+dots+lambda_n^k . $$ Здесь $ operatorname_<> $ обозначает след матрицы (т.е. сумму ее диагональных элементов). Утверждение остается справедливым и для отрицательных показателей $ k_<> $ при условии, что $ det A_<> ne 0 $.
Имеет место следующее равенство:
$$ det g(A) = (-1)^ <mathcal R>(f,g_<>) , $$ где $ <mathcal R>(f,g_<>) $ означает результант полиномов $ f(x) =det (A-x_<> E) $ и $ g_<>(x) $.
Теорема 8. Собственные числа вещественной симметричной матрицы $ A_<> $ все вещественны.
Доказательство ☞ ЗДЕСЬ.
Теорема 9. Собственные числа вещественной кососимметричной матрицы $ A_<> $ все мнимы, за исключением, возможно, $ lambda_<> = 0 $.
Доказательство ☞ ЗДЕСЬ.
Теорема 10. Собственные числа вещественной ортогональной матрицы все равны $ 1_<> $ по абсолютной величине (модулю). Характеристический полином ортогональной матрицы является возвратным если $ +1 $ не является его корнем или является корнем четной кратности. Хотя бы одно собственное число ортогональной матрицы нечетного порядка равно $ +1 $ или $ (-1) $.
Доказательство ☞ ЗДЕСЬ.
Теорема 11. Спектр циклической матрицы
$$ left(begin a_1 & a_2 & a_3 & dots & a_n \ a_n & a_1 & a_2 & dots & a_ \ a_ & a_n & a_1 & dots & a_ \ vdots & & & & vdots \ a_2 & a_3 & a_4 & dots & a_1 end right) . $$ совпадает с набором чисел $$ ) > ,$$ при $$ f(x)=a_<1>+a_2x+a_3x^2+dots+a_nx^ $$ и $$ varepsilon_k=cos frac<2,pi k> + <mathbf i>sin frac<2,pi k> $$ — корне n-й степени из единицы.
Доказательство ☞ ЗДЕСЬ.
Локализация собственных чисел
Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть
$$A=left[a_ right]_^n quad , quad B=left[b_ right]_^n . $$ Обозначим $$M= max_> left <|a_|, |b_ | right> quad , quad delta = frac<1>sum_^n |a_ — b_ | . $$ Тогда любому собственному числу $ lambda_<ast>^<> $ матрицы $ A_<> $ можно поставить в соответствие такое собственное число $ mu_<ast>^<> $ матрицы $ B_<> $, что $$ |lambda_<ast>-mu_ <ast>| le (n+2) M sqrt[n] <delta> . $$
Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы ☞ ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы. Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.
Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.
Пример [Уилкинсон] [2]. Найти собственные числа матрицы
$$ A= left( begin 20 & 20 & & & & \ & 19 & 20 & & & \ & & 18 & 20 & & \ & & & ddots & ddots & \ & & & & 2 & 20 \ <colorvarepsilon > & & & & & 1 \ end right)_ <20times 20>$$ при $ <colorvarepsilon >=10^ <-10>$ (все неуказанные элементы матрицы считаются равными нулю).
Решение. Характеристический полином $$ det(A-lambda E) = prod_^ <20>(j-lambda) — 20^ <19> <colorvarepsilon > = $$ $$ =lambda^<20>-<scriptstyle 210>,lambda^<19>+<scriptstyle 20615>,lambda^<18>-<scriptstyle 1256850>, lambda^ <17>+<scriptstyle 53327946>, lambda^<16>-<scriptstyle 1672280820>, lambda^<15>+ <scriptstyle 40171771630>, lambda^<14>-<scriptstyle 756111184500>, lambda^<13>+ $$ $$ +<scriptstyle 11310276995381>, lambda^ <12>- <scriptstyle 135585182899530>, lambda^ <11>+<scriptstyle 1307535010540395>, lambda^<10>-<scriptstyle 10142299865511450>, lambda^9 + $$ $$ +<scriptstyle 63030812099294896>, lambda^8 — <scriptstyle 311333643161390640>, lambda^7+<scriptstyle 1206647803780373360>, lambda^6 -<scriptstyle 3599979517947607200>, lambda^5 +<scriptstyle 8037811822645051776>, lambda^4- $$ $$ -<scriptstyle 12870931245150988800>, lambda^3 +<scriptstyle 13803759753640704000>, lambda^2 -<scriptstyle 8752948036761600000>,lambda + <scriptstyle 2432377720176640000>$$ очень похож на полином из другого ☞ ПРИМЕРА Уилкинсона. Он имеет корни $$ lambda_1=0.995754, lambda_2=2.109241, lambda_3=2.574881, $$ $$ lambda_<4,5>=3.965331pm 1.087735, mathbf i, lambda_<6,7>=5.893977pm 1.948530 , mathbf i, $$ $$ lambda_<8,9>=8.118073 pm 2.529182 , mathbf i, lambda_<10,11>=10.5pm 2.733397 , mathbf i, $$ $$ lambda_<12,13>=12.881926pm 2.529182 , mathbf i, lambda_<14,15>=15.106022 pm 1.948530 , mathbf i, $$ $$ lambda_<16,17>=17.034669pm 1.087735 , mathbf i, $$ $$ lambda_<18>=18.425118, lambda_<19>=18.890758, lambda_<20>=20.004245 . $$ Итак, нановозмущение 2) в одном-единственном элементе матрицы приводит к существенному изменению спектра: из $ 20 $ вещественных собственных чисел «остаются в живых» только $ 6_<> $; кроме того, у образовавшихся мнимых корней оказываются достаточно большими мнимые части. В данном примере допустимые возмущения для $ <colorvarepsilon > $, т.е. такие, при которых сохранится свойство вещественности всех корней характеристического полинома, находятся в пределах 3) $$ -8.636174times 10^<-14> ♦
Теорема 13 [Гершгорин]. 4) Обозначим $ mathbb D_ $ круг на комплексной плоскости $ mathbb C_<> $ с центром в точке $ a_^<> $ и радиуса
$$ r_j=sum_<ell=1 atop ellne j>^n left|a_right| .$$ Тогда спектр матрицы $ A_<> $ лежит внутри объединения этих кругов: $$ <lambda_1,dots, lambda_n >subset bigcup_^n mathbb D_j . $$ Иными словами: любое собственное число матрицы должно удовлетворять хотя бы одному из неравенств $$ |z- a_ |
Если все главные миноры $ A_1,A_2,dots,A_ $ симметричной матрицы $ A_<> $ отличны от нуля, то число положительных собственных чисел матрицы $ A_<> $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:
$$ operatorname < det (A-lambda E) =0 | lambda>0 > = <mathcal P>(1,A_1,dots,A_n), $$ $$ operatorname < det (A-lambda E) =0 | lambda ненулевойстолбец $$ X_<ast>= left( begin x_<1>^ <ast>\ vdots \ x_^ <ast>end right) in mathbb^n $$ такой, что $$ AX_<ast>=lambda_ <ast>X_ <ast>quad iff quad (A -lambda_<ast>E) X_ <ast>= mathbb O_ . $$ По определению собственного числа, $ det (A^<> -lambda_<ast>E) = 0 $ и, следовательно, система однородных уравнений $ (A -lambda_<ast>E) X^<> = mathbb O $ всегда имеет нетривиальное решение; более того, этих решений бесконечно много. Таким образом, одному и тому же собственному числу матрицы принадлежит бесконечное множество собственных векторов. Эту бесконечность можно описать с помощью фундаментальной системы решений (ФСР).
Пример. Найти собственные векторы матрицы
Решение. Спектр матрицы найден выше. $$(A-0 cdot E)X=mathbb O quad Longrightarrow mbox< ФСР>= left< <mathfrak X>_1=left(begin 4 \ -2 \ 1 \ 0 endright), <mathfrak X>_2=left(begin 7 \ -3 \ 0 \ 1 end right) right>.$$ Любой вектор вида $ alpha_ <1><mathfrak X>_1 + alpha_2 <mathfrak X>_2 $ будет собственным, принадлежащим $ lambda_<>=0 $. $$ begin (A- mathbf i, sqrt <83>E)X=mathbb O \ \ Downarrow \ \ <mathfrak X>_3= left(begin 1- mathbf i , sqrt <83>\ 8-2, mathbf i , sqrt <83>\ 12 \ 17+mathbf i , sqrt <83>endright) end qquad begin (A+mathbf i sqrt <83>E)X=mathbb O \ \ Downarrow \ \ <mathfrak X>_4= left(begin 1+mathbf i , sqrt <83>\ 8+2mathbf i , sqrt <83>\ 12 \ 17- mathbf i ,sqrt <83>endright) end . $$ ♦
Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.
Теорема 15. Пусть $ lambda_<ast>^<> $ — собственное число матрицы $ A_<> $. Обозначим частное от деления характеристического полинома на линейный множитель $ lambda_<> — lambda_ <ast>$ через $ f_<ast>(lambda)^<> $:
$$ f_<ast>(lambda) equiv f(lambda) / (lambda-lambda_<ast>) . $$ Тогда любой ненулевой столбец матрицы $ f_<ast>(A)^<> $ является собственным вектором, принадлежащим $ lambda_<ast>^<> $.
Доказательство следует из равенства $$(A-lambda_ <ast>E)f_<ast>(A)=mathbb O_ . $$ На основании определения любой ненулевой столбец $ f_<ast>(A)^<> $ должен быть собственным вектором матрицы $ A_<> $. ♦
Пример. Найти собственные векторы матрицы
$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) . $$
Решение. $$ det (A-lambda E)=-lambda^3+ 7, lambda + 6 equiv -(lambda_<>-3) (lambda+2)(lambda+1) , .$$ Пренебрегая знаком – , имеем: $$ begin f_1(lambda)=lambda^2+3lambda+2 & u & f_1(A)= left( begin 40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20 end right) , \ f_2(lambda)=lambda^2-2lambda-3 & u & f_2(A)= left( begin -10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0 end right) , \ f_3(lambda)=lambda^2-lambda-6 & u & f_3(A)= left( begin -4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8 end right) . end $$
Если $ lambda_<ast>^<> $ является простым корнем характеристического полинома 5) , то ненулевые столбцы $ f_<ast>(A)^<> $ будут пропорциональными. Или, что то же, $ operatorname f_<ast>(A)^<> = 1 $.
Тогда очевидно, что и строки матрицы $ f_<ast>(A)^<> $ тоже должны быть пропорциональны!
Доказать, что любая ненулевая строка матрицы $ f_<ast>(A)^<> $ является собственным вектором матрицы $ A^<^<top>>_<> $, принадлежащим $ lambda_<ast>^<> $. Доказать, что собственный вектор матрицы $ A_<> $ ортогонален собственному вектору матрицы $ A^<top>_<> $, если эти векторы принадлежат различным собственным числам 6) .
На практике вычисление полинома $ f_<ast>(lambda)^<> $ может быть осуществлено с помощью схемы Хорнера.
Пример. Вычислить собственный вектор матрицы
$$ A=left( begin 23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87 end right) , $$ принадлежащий ее вещественному собственному числу.
Решение. Характеристический полином $$ f(lambda)= -lambda^3+184,lambda^2-14751,lambda+611404 $$ имеет единственное вещественное собственное число $ lambda_ <ast>approx 96.8817 $. Составляем схему Хорнера $$ begin & -1 & 184 & -14751 & 611404 \ hline 96.8817 & -1 & 87.1183 & -6310.8310 & -0.0352 end $$ За счет ошибок округления мы получили ненулевое значение для $ f(lambda_<ast>) $. В качестве частного от деления $ f(lambda) $ на $ lambda-lambda_ <ast>$ берем $$ f_<ast>(lambda)= -lambda^2 + 87.1183, lambda — 6310.8310 . $$ Подставляем в него матрицу $ A_<> $ и вычисляем первый столбец матрицы $$ -A^2+87.1183,A -6310, E = left( begin -1882.1101 & * & * \ -2723.2902 & * & * \ -708.6229 & * & * end right) .$$ Проверяем: $$ left( begin 23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87 end right) left( begin -1882.1101 \ -2723.2902 \ -708.6229 end right) — 96.8817 left( begin -1882.1101 \ -2723.2902 \ -708.6229 end right)= left( begin 0.0356 \ 0 \ -0.0002 end right) . $$ ♦
Можно развить последний метод далее: найти универсальную формулу для собственного вектора как функции ее собственного числа. Действительно, найдем частное от деления характеристического полинома $$ f(lambda) =a_0lambda^n+a_0lambda^+dots+ a_n, quad a_0=(-1)^n $$ на линейный полином $ lambda- lambda_ <ast>$, где $ lambda_ <ast>$ — произвольное число из $ mathbb C $. С помощью той же схемы Хорнера, получаем $$ q(lambda)=a_0lambda^+(a_0lambda_<ast>+a_1)lambda^+(a_0lambda_<ast>^2+a_1lambda_<ast>+a_2)lambda^+dots+ (a_0lambda_<ast>^+a_1lambda_<ast>^+dots+a_) , . $$ Если $ lambda_ <ast>$ является собственным числом матрицы $ A_<> $, то любой ненулевой столбец матрицы $$ q(A)= a_0A^+(a_0lambda_<ast>+a_1)A^+(a_0lambda_<ast>^2+a_1lambda_<ast>+a_2)A^+dots+ (a_0lambda_<ast>^+a_1lambda_<ast>^+dots+a_)E $$ будет собственным вектором, принадлежащим $ lambda_ <ast>$.
Пример. Найти представление всех собственных векторов матрицы
$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) $$ в виде функции ее собственных чисел.
Решение. Характеристический полином матрицы был вычислен выше: $ f(lambda)=-lambda^3+ 7, lambda + 6 $. Имеем, $$ q(lambda)=-lambda^2-lambda_<ast>lambda+(7-lambda_<ast>^2) $$ и $$ q(A)=-A^2-lambda_<ast>A+(7-lambda_<ast>^2)E= left(begin -lambda_<ast>^2-9lambda_<ast>-4 & -22lambda_<ast>-14 & 6lambda_<ast>+2 \ lambda_<ast>-3 & -lambda_<ast>^2+4lambda_<ast>-3 & -lambda_<ast>+3 \ -8lambda_<ast>-16 & -16lambda_<ast>-32 & -lambda_<ast>^2+5lambda_<ast>+14 end right) , . $$ Берем произвольный столбец этой матрицы, например, первый: $$ X_<ast>(lambda_<ast>)= left(begin -lambda_<ast>^2-9lambda_<ast>-4 \ lambda_<ast>-3 \ -8lambda_<ast>-16 end right) , . $$ Утверждается, что $ X_ <ast>(lambda_<ast>) $ — универсальное представление всех собственных векторов матрицы. Действительно, $$ X_<ast>(-1) = left(begin 4 \ -4 \ -8 end right), X_<ast>(-2) = left(begin 10 \ -5 \ 0 end right), X_<ast>(3) = left(begin -40 \ 0 \ -40 end right) , . $$ ♦
Теорема 16. Пусть $ g(x)=b_0x^m+dots+b_ in <mathbb C>[x] $ – произвольный полином. Если $ X_<ast>in mathbb C^ $ — собственный вектор матрицы $ A_<> $, соответствующий собственному числу $ lambda_<ast>^<> $, то он же будет собственным и для матрицы $ g(A)^<> $, принадлежащим собственному числу $ g(lambda_<ast>)^<> $.
Доказательство. Домножим равенство $ A<mathfrak X>_<ast>=lambda_<ast>^<><mathfrak X>_ <ast>$ слева на матрицу $ A_<> $: $$ A^2<mathfrak X>_<ast>=lambda_<ast>A<mathfrak X>_<ast>=lambda_<ast>^2<mathfrak X>_ <ast>.$$ По индукции доказывается и общее равенство: $$ A^k<mathfrak X>_<ast>=lambda_<ast>^k<mathfrak X>_ <ast>.$$ Домножим его на $ b_^<> $ и просуммируем по $ k_<> $ от $ 0_<> $ до $ m_<> $: $$ g(A)<mathfrak X>_<ast>=g(lambda_<ast>)<mathfrak X>_ <ast>,$$ что и доказывает утверждение теоремы. ♦
Если матрица $ A $ невырождена, то теорема остается справедливой и для произвольного полинома от $ A^ <-1>$. В частности, собственные векторы $ A^ <-1>$ совпадают с собственными векторами матрицы $ A $.
Теорема 17. Собственные векторы, принадлежащие различным собственным числам матрицы $ A_<> $, линейно независимы.
Теорема 18. Собственные векторы, принадлежащие различным собственным числам вещественной симметричной матрицы $ A_<> $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_ <1>$, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_ <2>$ и $ lambda_1 ne lambda_2 $, то
$$ langle mathfrak X_1, mathfrak X_2 rangle =0 , $$ где $ langle , rangle $ означает скалярное произведение, определяемое стандартным образом: $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.
Доказательство ☞ ЗДЕСЬ.
Теорема Перрона-Фробениуса
Теорема 19 [Перрон, Фробениус]. Для положительной матрицы $ A_<> $ существует положительное собственное число $ lambda_ <+>$ такое, что все остальные собственные числа этой матрицы меньше $ lambda_ <+>$ по абсолютной величине (модулю). Соответствующий этому собственному числу собственный вектор может быть выбран положительным:
$$ exists mathfrak X_ <+>> mathbb O: quad A mathfrak X_ <+>= lambda_ <+>mathfrak X_ <+> . $$
Число $ lambda_ <+>$ из теоремы называется собственным числом Перрона или собственным числом Перрона-Фробениуса матрицы $ A_<> $, а соответствующий ему произвольный положительный собственный вектор — собственным вектором Перрона-Фробениуса матрицы $ A_<> $.
Спектральный радиус положительной матрицы $ A_<> $ совпадает с ее собственным числом Перрона-Фробениуса:
Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы
$$ A= left(begin 2 & 7 & 18 & 28 \ 1 & 8 & 2 & 8 \ 3 & 1 & 4 & 1 \ 5 & 9 & 26 & 5 end right) , . $$
Решение. Характеристический полином матрицы $ A_<> $ $$ det(A-lambda E)=lambda^4-19, lambda^3-175, lambda^2-285, lambda+10390 $$ имеет корнями $$ lambda_ <1,2>approx -6.260463 pm 5.452465 mathbf i, lambda_3 approx 5.878976, lambda_4 approx 25.641950 . $$ Числом Перрона-Фробениуса является $ lambda_4 $, а соответствующий ему собственный вектор Перрона-Фробениуса можно взять равным $$ left( begin 1 \ 0.365240 \ 0.184802 \ 0.634244 end right) quad mbox < или >quad left( begin 2.737922 \ 1 \ 0.505974 \ 1.736510 end right) quad mbox < или >left( begin 5.411185 \ 1.976383 \ 1 \ 3.432010 end right) quad mbox < или >quad left( begin 1.576681 \ 0.575868 \ 0.291374 \ 1 end right) quad mbox < или >quad left( begin 0.798133 \ 0.291510 \ 0.147496\ 0.506210 end right) quad mbox < или >dots $$ (напоминаю: собственный вектор определяется с точностью до ненулевого сомножителя!). Последний вектор имеет длину равную $ 1_<> $. ♦
1. Собственное число Перрона-Фробениуса всегда простое для характеристического полинома матрицы $ A_<> $. Отсюда следует, что собственный вектор Перрона-Фробениуса определяется единственным образом — с точностью до домножения на положительный скаляр.
2. Любой собственный вектор положительной матрицы $ A_<> $, не соответствующий собственному числу Перрона-Фробениуса, не может состоять исключительно только из положительных элементов. Иными словами, хотя бы одна компонента такого вектора должна быть либо отрицательной либо мнимой.
3. Для собственного числа Перрона-Фробениуса справедливо неравенство $$ min_> sum_^n a_ le lambda_ <+>le max_> sum_^n a_ . $$
4. Собственное число Перрона-Фробениуса матрицы $ A_<> $ совпадает с собственным числом Перрона-Фробениуса матрицы $ A^ <top>$.
Какие из перечисленных свойств можно распространить на случай неотрицательных матриц ? Каждую такую матрицу можно рассматривать как предел последовательности (строго) положительных матриц. Воспользовавшись теоремой о непрерывной зависимости собственных чисел матрицы от ее элементов, можем сделать вывод, о том, что для неотрицательной матрицы $ A_<> $ всегда найдется вещественное неотрицательное собственное число, которое будет являться максимальным по модулю среди всех собственных чисел матрицы. Другое дело, что в данном случае — в отличие от случая положительных матриц — такое мажорирующее собственное число может оказаться не единственным.
Пример. Спектр неотрицательной матрицы
$$ A=left( begin 0 & 1 \ 1 & 0 end right) $$ состоит из чисел $ lambda_1=+1 $ и $ lambda_1=-1 $ одинакового модуля. ♦
Однако, по-прежнему, хотя бы одно неотрицательное вещественное число $ lambda_ <+>$ со свойством $ rho(A) = lambda_ <+>$ существовать будет; более того, ему будет соответствовать неотрицательный собственный вектор $ mathfrak X ge mathbb O $. Это число (вектор) по-прежнему называются числом (вектором) Перрона-Фробениуса 7) матрицы $ A_<> $.
Частным случаем неотрицательных матриц являются стохастические матрицы, т.е. неотрицательные матрицы, в которых сумма элементов каждой строки равна $ 1_<> $: $$ P=left[p_right]_^n, \ge 0 >_^n, sum_^n p_ = 1 npu quad j in <1,2,dots,n> . $$
Теорема 20. Собственное число Перрона-Фробениуса стохастической матрицы равно $ 1_<> $. Этому собственному числу соответствует собственный вектор $ X=[1,1,dots,1]^ <top>$.
Доказательство существования собственного числа равного $ 1_<> $ и соответствующего ему собственного вектора $ X=[1,1,dots,1]^ <top>$ следует из равенства $$ P left( begin 1 \ 1 \ vdots \ 1 end right) = left( begin 1 \ 1 \ vdots \ 1 endright) . $$ Далее, из теоремы Гершгорина следует, что любое собственное число $ lambda_<>in mathbb C $ стохастической матрицы должно удовлетворять неравенству $$|lambda — p_|le sum_ |p_|=1-p_ $$ хотя бы при одном $ j_<> $. Воспользовавшись следствием к неравенству треугольника получаем: $$|lambda| — |p_|le |lambda — p_| le 1-p_ Rightarrow |lambda| le 1 . $$ ♦
Методы вычисления характеристического полинома
Вычисление коэффициентов характеристического полинома матрицы $ A_<> $ непосредственным разложением определителя $ det (A-lambda_<> E) $ на $ n!_<> $ слагаемых — крайне неэффективно. Элементами этого разложения являются выражения, полиномиально зависящие от параметра $ lambda_<> $. На каждом этапе вычислений мы получаем проблему символьных вычислений: хранения таких полиномов и действий над ними.
Основной метод вычисления числовых определителей — метод Гаусса — также неэффективен в приложении к вычислению определителя, элементы которого зависят от параметра. Источником вычислительных проблем является неудобное расположение переменной $ lambda_<> $ — на главной диагонали матрицы. Первый же шаг метода Гаусса приводит к делению на элемент $ a_ <11>- lambda $, и, в дальнейшем, элементы преобразованной матрицы будут уже не полиномами, а рациональными функциями относительно $ lambda_<> $. Следующие шаги метода приводят к возрастанию степеней знаменателей. Необходимость в организации хранения рациональных функций и программировании действий с ними кажется тем более неоправданной, если вспомнить, что окончательный ответ — выражение для $ det (A-lambda_<> E) $ — должно быть полиномом по $ lambda_<> $; т.е. знаменатели дробей в конечном ответе сократятся.
А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.
Какой выход предлагается? — Предварительно преобразовать определитель $ det (A-lambda_<> E) $ к виду, когда переменная $ lambda_<> $ оказывается «выметенной» с диагонали на крайний ряд (в столбец или в строку). При этом допускается увеличение размеров (порядка) определителя. Такое представление дает возможность разложения определителя по этому исключительному ряду, и, тем самым, позволяет свести задачу к вычислению числовых определителей — а уж для этой задачи применение метода Гаусса вполне эффективно.
Метод Леверье
Метод основан на формуле (см. следствие к теореме $ 7 $ ☞ ЗДЕСЬ ): $$ operatorname (A^k)=lambda_1^k+dots+lambda_n^k=s_k , $$ т.е. след $ k_<> $-й степени матрицы $ A_<> $ равен $ k_<> $-й сумме Ньютона ее характеристического полинома $ f(lambda)=det (A-lambda E ) $. Вычисляем последовательные степени матрицы $ A_<> $: $$s_1=operatorname (A), s_2=operatorname (A^2), dots, s_n=operatorname (A^n) .$$ Неизвестные коэффициенты $ f(lambda)=(-1)^n(lambda^n+a_1lambda^+ dots+a_n) $ находим по рекурсивным формулам Ньютона: $$ a_1=-s_1, a_2=-(s_2+a_1s_1)/2, $$ $$ a_k=-(s_+a_1s_+a_2s_+dots+a_s_1)/k npu k le n. $$ Очевидно, что не имеет смысла вычислять все элементы матрицы $ A^ $ — достаточно обойтись лишь элементами ее главной диагонали.
Пример [Леверье]. Найти характеристический полином матрицы
$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$
Решение. $$ A^2=left(begin 30.91795128&-30.56848188&2.878480155&0.0031325713\ -4.705449283&164.6764010&-141.3504639&-0.4143169528\ 0.3341843103&-106.6094396&193.1869924& -6.756396001\ 0.0022236138&-1.904168948&-41.16923134& 309.9628536 end right), $$ $$ A^3=left(begin -179.0125092&431.2849919&-198.8601505& -0.9173897610\ 66.38829278&-2562.954533& 2771.458834& -15.49709921\ -23.08728044&2090.291485&-3124.010318& 156.9329019\ -0.649145142&-71.21907809&956.2502143& -5463.723497 end right), $$ $$ A^4=left(begin 1100.720103& ast& ast& ast \ ast& 42332.23816& ast& ast \ ast& ast& 52669.62534& ast \ ast& ast& ast& 96355.91518 end right) . $$ Вычисляем следы матриц: $$s_1=-47.888430, s_2=698.7441983, s_3=-11329.70086, s_4= 192458.4988 ,$$ и по формулам Ньютона получаем: $$a_1= 47.888430, a_2 = 797.278764_ <displaystyle 8>, a_3 = 5349.45551_<displaystyle 3>, a_4 = 12296.550_ <displaystyle 68> . $$ ♦
После нахождения коэффициентов характеристического полинома можно найти его корни каким-либо 
Степени матрицы $ A_<> $ уже нами посчитаны при вычислении коэффициентов характеристического полинома.
Пример. Для приведенного выше примера находим собственные числа:
$$ lambda_1=-17.86326, lambda_2=-17.15242, lambda_3=-7.57404, lambda_4= -5.29869 . $$ Коэффициенты $ f_1(lambda) $ можно определить по схеме Хорнера: $$ begin &1 & 47.888430 & 797.2787648 & 5349.455513 & 12296.55068 \ hline -17.86326 & 1 & underbrace<30.025170>_>& underbrace<260.9313465>_> &underbrace<688.371028>_>& approx 0 \ end $$ Собственным вектором, принадлежащим $ lambda_ <1>$, будет $$left[ -0.0256_<displaystyle 67>, 0.21938_<displaystyle 0>, -0.24187_<displaystyle 1>, 1.044526 right]^<^<top>> .$$ ♦
Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:
$$ f(lambda)=frac<1>left| begin s_1 &1 & & & &\ s_2&s_1& 2 & &mathbb O & \ s_3&s_2&s_1&3& & \ vdots& & & ddots &ddots & \ s_n&s_& s_ & dots &s_1&n \ lambda^n&lambda^&lambda^& dots &lambda&1 end right|_ <(n+1)times (n+1)> . $$
Биографические заметки о Леверье ☞ ЗДЕСЬ.
Метод Крылова
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_<1>^<[0]>,dots,y_^ <[0]>right]^<^<top>> in mathbb C^n $. Cоставим итерационную векторную последовательность $$ Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_=Acdot Y_ . $$
Теорема 22. Определитель
$$ det left[begin Y_0&Y_<1>&dots&Y_&Y_\ 1& lambda&dots&lambda^&lambda^n end right]_ <(n+1)times (n+1)>$$ совпадает — с точностью до постоянного множителя — с характеристическим полиномом матрицы $ A_<> $. Здесь $ |_<> $ означает конкатенацию.
Доказательство. Легко видеть, что $$ Y_K=A^KY_0 quad npu quad K in <1,dots,n> . $$ Если $$ f(lambda)=det(A-lambda E) =(-1)^n lambda^n+a_1 lambda^+a_2 lambda^+dots+a_n , $$ то по теореме Гамильтона-Кэли: $$ (-1)^n A^n+a_1A^+dots+a_nE=mathbb O_ . $$ Это равенство останется справедливым и после умножения его на произвольный вектор, в том числе на $ Y_ <0>$: $$ (-1)^n A^ncdot Y_0+a_1A^ cdot Y_0 +dots+a_ncdot Y_0=mathbb O_ iff $$ $$ iff quad (-1)^n Y_n+a_1Y_ +dots+a_nY_0=mathbb O . $$ Последнее равенство представляет линейную систему относительно неизвестных коэффициентов характеристического полинома. Можно решать ее по формулам Крамера, но мы пойдем другим путем. Дополним эту систему тождеством $ f(lambda)=(-1)^n lambda^n+a_1 lambda^+a_2 lambda^+dots+a_n $. Рассмотрим получившуюся систему как линейную однородную относительно столбца $ left[ a_n,a_,dots,a_1,1right]^ <top>$. Поскольку эта система имеет нетривиальное решение, то ее определитель должен равняться нулю: $$ 0=det left[begin Y_0&Y_<1>&dots&Y_&(-1)^nY_\ 1& lambda&dots&lambda^&(-1)^nlambda^n-f(lambda) end right]= $$ (представляем последний столбец в виде суммы двух столбцов и используем свойство 5 определителя) $$ =det left[begin Y_0&Y_<1>&dots&Y_&(-1)^nY_\ 1& lambda&dots&lambda^&(-1)^nlambda^n end right]-f(lambda) det left[begin Y_0&Y_<1>&dots&Y_ end right] . $$ Таким образом, $$ f(lambda)=(-1)^n frac<det left[begin Y_0&Y_<1>&dots&Y_&Y_\ 1& lambda&dots&lambda^&lambda^n end right]><det left[begin Y_0&Y_<1>&dots&Y_ end right]> , $$ если только знаменатель в этой дроби не обратится в нуль. ♦
Пример. Найти характеристический полином матрицы примера Леверье
$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$
Решение. Возьмем $ Y_0=left[ 1,0,0,0 right]^ <top>$. Имеем $$ begin Y_1=A Y_0= & Y_2=AY_1= & Y_3=AY_2= & Y_4=AY_3= \ left(begin -5.509882\ 0.287865 \ 0.049099 \ 0.006235 end right), & left(begin 30.917951\ -4.705449 \ 0.334184 \ 0.002223 end right), & left(begin -179.012509\ 66.388293 \ -23.087280\ -0.649145 end right), & left(begin 1100.720101\ -967.597333\ 576.522644\ -4.040153 end right) . end $$ $$ det left[begin Y_0&Y_<1>&Y_2& Y_<3>& Y_<4>\ 1& lambda&lambda^2 &lambda^<3>&lambda^4 end right]= left| begin 1 & -5.509882 & 30.917951 & -179.012509 & 1100.720101 \ 0 & 0.287865 & -4.705449 & 66.388293 & -967.597333\ 0 & 0.049099 & 0.334184 & -23.087280 & 576.522644\ 0 & 0.006235 & 0.002223 & -0.649145 & -4.040153 \ 1 & lambda & lambda^2 & lambda^3 & lambda^4 end right|= $$ $$ =0.348621 lambda^4+16.694915lambda^3+277.948166lambda^2+1864.932835lambda+4286.836454 = $$ $$ =0.348621 left(lambda^4+47.888430lambda^3+797.27876_<displaystyle 3>lambda^2+5349.4555_<displaystyle 0>lambda+12296.550_ <displaystyle 5>right) . $$ ♦
После нахождения характеристического полинома можно найти его корни каким-либо 10) методом. Пусть $ lambda_<ast>^<> $ — одно из собственных чисел, и оно — простое; тогда для нахождения соответствующего собственного вектора можно воспользоваться тем же приемом, что был задействован в предыдущем ПУНКТЕ. Вычислим 11) частное от деления $ f(lambda_<>) $ на $ lambda-lambda_ <ast>$ $$ f_<ast>(lambda)= f(lambda)/(lambda-lambda_<ast>)=(-1)^n(lambda^ +p_1lambda^+dots+p_lambda+p_) . $$ Тогда любой ненулевой столбец матрицы $ f_<ast>(A)^<> $ будет собственным вектором, принадлежащим $ lambda_<ast>^<> $. Но тогда и произвольная комбинация столбцов этой матрицы тоже будет собственным вектором (если только не обратится в нулевой вектор). В частности, это относится и к комбинации, записываемой в матричном виде $$ (-1)^n f_<ast>(A) Y_0 = A^Y_0 +p_1A^Y_0+dots+p_Y_0=Y_+p_1Y_+dots+p_Y_0 . $$ А комбинируемые векторы уже посчитаны.
Теперь обсудим исключительные случаи. При неудачном выборе $ Y_ <0>$ определитель $$ det left[begin Y_0&Y_<1>&dots&Y_ end right] $$ может обратиться в нуль. Эта неприятность обязательно произойдет если, например, наш выбор пал на вектор $ Y_0 $, совпадающий с собственным вектором матрицы $ A_<> $. Вероятность такого события — нулевая. В общем же случае, трудно ожидать, чтобы $ n_<> $ почти произвольных столбцов $ Y_0,Y_<1>,dots,Y_ $ оказались линейно зависимыми — если только сама матрица $ A_<> $ не обладает «скрытым дефектом» — типа рассмотренного в следующем примере.
Пример. Найти характеристический полином матрицы
Решение. При любом выборе $ Y_0 $ векторы $ $ оказываются линейно зависимыми: $$ Y_0= left(begin 1\ 0\ 0 end right), Y_1= left(begin 2\ 1\ 1 end right), Y_2= left(begin 6\ 5\ 5 end right),dots ; Y_0= left(begin 1\ 1\ 1 end right), Y_1= left(begin 4\ 4\ 4 end right),dots $$ Объяснение этого феномена состоит в том, что для матрицы $ A_<> $ ее аннулирующий полином имеет степень меньшую ее порядка: $$ A^2-5 A+4 E = mathbb O . $$ Домножение этого равенства на произвольный столбец $ Y_0 $ и доказывает линейную зависимость системы $ $. ♦
Такая ситуация возможна только в случае, когда характеристический полином матрицы $ A_<> $ имеет кратные корни (в рассмотренном выше примере $ lambda_<>=1 $ являлся двойным корнем $ det (A-lambda_<> E) $); она исключительно редко встречается на практике.
Поиск всех собственных чисел
Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.
QR-алгоритм
Этот алгоритм основан на QR-разложении матрицы $ A $.
Теорема 23. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^ <top>A P $ при произвольной ортогональной матрице $ P $.
Доказательство. $$ det (P^ <top>A P-lambda E)=det (P^ <top>A P- lambda P^ <top>E P)=det P^ <top>(A -lambda E ) P = det (A -lambda E ) P P^ <top>= det (A -lambda E ) , . $$ ♦
Пусть QR-разложение матрицы $ A $ имеет вид $$ A=Q_1R_1 , , $$ где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица $$ A_2=R_1Q_1 $$ имеет тот же спектр, что и матрица $ A $. Действительно, поскольку $$ A_2=Q_1^ <top>A Q_1 , $$ то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $ $$ A_2=Q_2R_2 $$ и переставим местами матрицы этого произведения: $$ A_3=R_2Q_2 , . $$ Матрица $$ A_3= Q_2^ <top>A_2 Q_2=Q_2^ <top>Q_1^ <top>A Q_1 Q_2 $$ продолжаем иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц $$ Q_>_^ <infty>$$ как правило, сходится к матрице $ A_ <infty>$, которая будет верхнетреугольной.
Теорема 24 [4]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_ <infty>$ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.
Пример. Найти все собственные числа матрицы $$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) , . $$
Решение. $$ A_1=Aapprox underbrace<left(begin 0.272165 & 0.759752 & 0.590511 \ 0.952579 & -0.299517 & -0.053683 \ -0.136083& -0.577119 & 0.805242 end right)>_ underbrace<left(begin 7.348469 & 3.946400 & 2.041241\ 0 & 2.534941 & -3.966781 \ 0 & 0 & 2.469409 end right)>_ $$ Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы: $$ quad Rightarrow quad A_2 = R_1Q_1approx left(begin 5.481481 & 3.222957 & 5.771191 \ 2.954542 & 1.530046 & -3.3303021 \ -0.336044 & -1.425143 & 1.988472 end right)approx $$ $$ approxunderbrace<left(begin -0.878992 & 0.022595 & 0.476300\ 0.473781 & -0.154267 & -0.867026 \ 0.053886 & -0.987771 & 0.146304 end right)>_ underbrace<left(begin -6.236096& -3.634658 & -3.387848\ 0 & 1.244502 & -1.319999\ 0 & 0 & 5.927198 end right)>_ $$ Продолжим процесс: $$ quad Rightarrow quad A_3 = R_2Q_2approx left(begin 7.020952& 3.766220 & -0.314568\ -0.660752 & 1.111870 & -1.272137\ 0.319398 & -5.854713 & 0.867177 end right) approx $$ $$ approx underbrace<left(begin -0.994581 & -0.065879 & 0.080426 \ 0.093601 & -0.230749 & 0.968501 \ -0.045246 & 0.970780 & 0.235665 end right)>_ underbrace<left(begin -7.059205 & -3.376839 & 0.154554 \ 0 & -6.188319 & 1.156106 \ 0 & 0 & -1.053002 end right)>_ $$ Замечаем тенденцию убывания элементов матриц $ $, стоящих под главной диагональю. $$ Rightarrow dots Rightarrow A_ <10>approx left(begin mathbf<6.>_ <246022>& 2.758769 & -2.160057\ -0.0467437 & mathbf<4.4>_ <09292>& -5.341014\ 0.000018 &-0.005924 & mathbf<-1.6>_ <55314>end right) approx $$ $$ underbrace<left(begin -0.999972 & -0.007483 & 0.000007 \ 0.007483 & -0.999971 & 0.001339 \ -0.000003 & 0.001339 & 0.999999 end right)>_> underbrace<left(begin -6.246197 & -2.725694 & 2.120031\ 0 & -4.429817 & 5.354807 \ 0 & 0 & -1.662479 end right)>_> , . $$ Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна. $$ Rightarrow dots Rightarrow A_ <20>approx left(begin mathbf<6.17>_ <5608>& 2.805821 & -2.020513 \ -0.001776 & mathbf<4.48>_ <4917>& -5.388407\ 0 & 0 & -mathbf <1.660525>end right) approx $$ Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел. $$ Rightarrow dots Rightarrow A_ <30>approx left(begin mathbf<6.172>_ <778>& 2.807524 & -2.015076\ -0.000073 & mathbf<4.487>_ <747>& -5.390442\ 0 & 0 & -mathbf <1.660525>end right) , . $$ ♦
К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю.
Как это обстоятельство сказывается на структуре матрицы $ A_ <infty>$ и дальнейшее развитие метода ☞ ЗДЕСЬ
Частичная проблема собственных чисел
Задача. Найти максимальное по модулю собственное число матрицы $ A_<> $.
Предположение . Будем считать сначала, что максимальное по модулю собственное число матрицы единственно.
Излагаемый ниже метод поиска этого собственного числа называется методом степенны́х итераций 12) .
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_<1>^<[0]>,dots,y_^ <[0]>right]^<^<top>> in mathbb C^n $. Cоставим такую же итерационную векторную последовательность, как и в методе Крылова $$ Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_=Acdot Y_,dots , $$ (только теперь, в отличие от метода Крылова, считаем ее неограниченно продолжающейся) и выделим последовательность первых элементов этих векторов: $$y_<1>^<[1]>,y_<1>^<[2]>,dots,y_<1>^<[K]>,dots $$
Теорема 25. Как правило, предел
$$ lim_frac^<[K+1]>>^<[K]>> $$ существует и он равен максимальному по модулю собственному числу матрицы $ A_<> $.
Доказательство. Перенумеруем собственные числа $ lambda_<1>,dots,lambda_n $ матрицы $ A_<> $ так, чтобы $ lambda_ <1>$ обозначило максимальное по модулю: $$|lambda_1|= max_> |lambda_j| , quad |lambda_1|>|lambda_j| quad npu quad jin <2,dots,n> . $$ Очевидно, $$ Y_=A^Kcdot Y_0 ; $$ отсюда следует, что любой элемент столбца $ Y_ $ может быть линейно выражен через $ lambda_<1>^K,dots,lambda_n^K $. В частности, это справедливо и для первого элемента: $$ y_<1>^<[K]>=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K . $$ В этом представлении $ _^n $ — будут константами из $ mathbb C_<> $ в случае если все собственные числа являются простыми, и полиномами из $ mathbb C[K] $ в случае, если имеются кратные собственные числа. Действительно, в первом случае существует базис пространства $ mathbb C^n $, состоящий из собственных векторов матрицы $ A_<> $: $$ A<mathfrak X>_j=lambda_j<mathfrak X>_j quad npu quad jin <1,dots,n>. $$ Вектор $ Y_0 $ можно разложить по этому базису: $$Y_0=alpha_1<mathfrak X>_1+dots+alpha_n<mathfrak X>_n .$$ Тогда последовательным домножением на матрицу $ A_<> $ получаем : $$begin Y_1=AY_0&=& alpha_1 lambda_1<mathfrak X>_1+dots+alpha_nlambda_n<mathfrak X>_n, \ dots & & dots \ Y_K=A^KY_0&=& alpha_1 lambda_1^K<mathfrak X>_1+dots+alpha_nlambda_n^K<mathfrak X>_n end $$ откуда и следует доказываемое равенство.
Во втором случае — когда имеются кратные собственные числа матрицы $ A_<> $ — придется применять «тяжелую артиллерию» в виде жордановой нормальной формы; см. теорему $ 5 $ ☞ ЗДЕСЬ. Для простоты рассуждений, будем в оставшейся части доказательства считать все собственные числа матрицы различными. Имеем тогда $$ lim_ frac^<[K+1]>>^<[K]>>= lim_ frac <lambda_1^left[C_1+ C_2(lambda_2/lambda_1)^+dots+ C_n(lambda_n/lambda_1)^ right]> <lambda_1^left[C_1+C_2(lambda_2/lambda_1)^+dots+ C_n(lambda_n/lambda_1)^ right]> =lambda_1 $$ поскольку $$ lim_ left| frac<lambda_j> <lambda_1>right|^K = 0 quad npu quad jin <2,dots,n> . $$ Исключительным случаем является ситуация $ C_1=0 $, в этом случае утверждение теоремы может оказаться несправедливым 13) . ♦
Как правило, вектор
$$ left[1, lim_frac^<[K]>>^<[K]>>,dots, lim_frac^<[K]>>^<[K]>>right]^<^<top>> $$ будет собственным, принадлежащим максимальному по модулю собственному числу матрицы $ A_<> $.
Пример. Для матрицы
$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & -4 end right) $$ найти максимальное по модулю собственное число и принадлежащий ему собственный вектор.
Решение. Возьмем в качестве стартового столбца $ Y_0=[1,0,0]^<^<top>> $. Имеем: $$ Y_1=AY_0=left( begin 2 \ 7 \ -1 end right), Y_2=AY_1=left( begin 26 \ 32 \ -12 end right), Y_3=AY_2=left( begin 160 \ 242 \ -42 end right),dots, $$ $$ Y_<19>=left( begin <scriptstyle 4259667747238636>\ <scriptstyle 6435097324667832>\ <scriptstyle -1571397155909260>end right), Y_<20>=AY_<19>=left( begin <scriptstyle 29396024624390028>\ <scriptstyle 44408774736946168>\ <scriptstyle -10844273772937260>end right) $$ Смотрим на отношения первых элементов векторов: $$ begin K & 1 & 2 & 3 & 4 & 5 & dots & 15 & dots & 19 \ hline y_<1>^<[K+1]>/y_<1>^ <[K]>& 2 & 13 & 6.153846 & 6.8 & 7.180147 & dots & 6.900726 & dots & mathbf<6.90101>_ <displaystyle 3>end $$ Далее, в соответствии со следствием, собственный вектор, принадлежащий найденному числу $$ approx left[1, frac^<[20]>>^<[20]>>,frac^<[20]>>^<[20]>>right]^<^<top>> approx left[1, 1.51070_<displaystyle 6>, -0.368902 right]^<^<top>> $$ ♦
Теперь обсудим исключительные случаи алгоритма.
1. Нарушение сходимости итерационного процесса за счет неудачного выбора стартового вектора. Если в качестве $ Y_ <0>$ оказался случайно взят собственный вектор $ mathfrak X_ <ast>$ матрицы $ A_<> $, принадлежащий произвольному ее собственному числу $ lambda_ <*>$, то предел последовательности из теоремы будет равен именно этому числу; если при этом $ |lambda_ <*>| ne max_ <1le j le n>| lambda_j | $, то мы выйдем за пределы смысла выражения «как правило». Понятно, что вероятность настолько плохого выбора нулевая, но и выбор $ Y_0 $ вблизи $ mathfrak X_ <ast>$ также может существенно замедлить скорость сходимости. Поэтому если возникает ситуация медленной «стабилизации» значащих цифр в десятичном приближении собственного числа, попробуйте сменить начальный вектор.
2. Нарушение условия предположения , выдвинутого в начале пункта: максимальное по модулю собственное число неединственно.
Пример. Найти максимальное по модулю собственное число матрицы примера Леверье
$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$
Решение. Для столбца $ Y_0=[1,0,0,0]^<^<top>> $ имеем $$y_<1>^<[100]>/y_<1>^<[99]>=-17.8_ <displaystyle 3113> ,$$ т.е. на $ 100 $-й итерации получаем лишь $ 3_<> $ истинные десятичные цифры в представлении собственного числа. При этом компонентами векторов $ Y_ $ являются числа порядка $ 10^ <123>$. Если мы посмотрим на ответ примера Леверье, то увидим, что имеются два собственных числа матрицы, близких по модулю. ♦
К сожалению, вероятность того факта, что у случайно выбранной матрицы два ее собственных числа будут иметь одинаковый модуль становится ненулевой если эта матрица выбирается из множества вещественных матриц. Дело в том, что в этом случае ее характеристический полином будет иметь вещественные коэффициенты, а мнимые корни такого полинома всегда пáрные — для любого невещественного корня $ lambda_<ast>^<> $ полинома, комплексно сопряженное к нему число $ overline<lambda_<ast>> $ также будет корнем. При этом $ |lambda_<ast>|= |overline<lambda_<ast>> | $.
Пример. Для матрицы
Предположение 2 . Пусть два максимальных по модулю собственных числа матрицы разнесены по величине, например $$ |lambda_1| > | lambda_2 | > | lambda_ j | quad npu j in <2,dots, n >. $$
Обобщение степенного метода основывается на использовании последовательностей из каких-то двух компонент векторов $ Y_=AY_K $, например, наряду с уже использованной выше последовательностью первых компонент $$y_<1>^<[1]>,y_<1>^<[2]>,dots,y_<1>^<[K]>,dots $$ возьмем еще и аналогичную для вторых: $$y_<2>^<[1]>,y_<2>^<[2]>,dots,y_<2>^<[K]>,dots $$
Теорема 26 [Эйткен]. При практически любом выборе стартового вектора $ Y_0 ne mathbb O $ для последовательности
Доказательство. Построим квадратное уравнение $$ p_0x^2+p_1x+p_2 = 0 $$ имеющее корнями $ lambda_1 $ и $ lambda_2 $. Если существует базис рпостранства $ mathbb C^n $ $$Y_0=alpha_1<mathfrak X>_1+alpha_2<mathfrak X>_2+dots+alpha_n<mathfrak X>_n .$$ Тогда последовательным домножением на матрицу $ A_<> $ получаем : $$begin Y_K=& alpha_1 lambda_1^K<mathfrak X>_1 &+alpha_2 lambda_2^K<mathfrak X>_2+dots &+alpha_nlambda_n^K<mathfrak X>_n, \ Y_=& alpha_1 lambda_1^<mathfrak X>_1 &+alpha_2 lambda_2^<mathfrak X>_2+dots &+alpha_nlambda_n^<mathfrak X>_n,\ Y_=& alpha_1 lambda_1^<mathfrak X>_1 & +alpha_2 lambda_2^<mathfrak X>_2+dots &+alpha_nlambda_n^<mathfrak X>_n. end $$ Отбрасываем из правых частей равенств слагаемые порядков возрастания ниже, чем $ lambda_2^K, lambda_2^, lambda_2^ $ соответственно, домножаем получившиеся приближенные равенства $$begin Y_K & approx alpha_1 lambda_1^K<mathfrak X>_1 &+alpha_2 lambda_2^K<mathfrak X>_2, & color times p_2 \ Y_& approx alpha_1 lambda_1^<mathfrak X>_1 &+alpha_2 lambda_2^<mathfrak X>_2, & color times p_1\ Y_ & approx alpha_1 lambda_1^<mathfrak X>_1 & +alpha_2 lambda_2^<mathfrak X>_2, & color times p_0 end $$ и складываем: $$ p_2 Y_K + p_1Y_ + p_0 Y_ approx mathbb O , . $$ В получившемся векторном равенстве выбираем первые две компоненты: $$ left< begin p_2 y_1^ <[K]>+ p_1 y_1^ <[K+1]>+ p_0 y_1^ <[K+2]>approx 0 , , \ p_2 y_2^ <[K]>+ p_1 y_2^ <[K+1]>+ p_0 y_2^ <[K+2]>approx 0 , , end right. $$ которые и позволят определить приближенное значение набора $ p_0,p_1,p_2 $. С точностью до числового сомножителя, искомый полином можно представить в виде определителя $$ p_0x^2+p_1x+p_2 approx left|begin y_1^ <[K]>& y_1^ <[K+1]>& y_1^ <[K+2]>\ y_2^ <[K]>& y_2^ <[K+1]>& y_2^ <[K+2]>\ 1 & x & x^2 end right| , . $$ Формулы Виета завершат доказательство. ♦
При выполнении условия предположения 2 имеет место равенство
Пример. Для матрицы
$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) $$ найти первые два по порядку убывания модулей собственных числа.
Задачи
Источники
[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94
[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960
[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
Спектральная кластеризация
Дата публикации Feb 21, 2019
Введение
В этом посте мы рассмотрим тонкости спектральной кластеризации для графиков и других данных. Кластеризация является одной из главных задач в машинном обучении без учителя. Цель состоит в том, чтобы назначить немаркированные данные группам, где, возможно, аналогичные точки данных будут назначены в одну группу.
Спектральная кластеризация — это метод с корнями в теории графов, где этот подход используется для идентификации сообществ узлов в графе на основе соединяющих их ребер. Этот метод является гибким и позволяет кластеризовать не графовые данные.
Спектральная кластеризация использует информацию из собственных значений (спектра) специальных матриц, построенных из графика или набора данных. Мы узнаем, как построить эти матрицы, интерпретировать их спектр и использовать собственные векторы для назначения наших данных кластерам.
Собственные векторы и собственные значения
Критическим для этой дискуссии является концепция собственных значений и собственные векторы. Для матрицы A, если существует вектор x, который не является всеми 0 и скалярным λ, таким, что Ax = λx, то x называется собственным вектором A с соответствующим собственным значением λ.
Мы можем думать о матрице A как о функции, которая отображает векторы на новые векторы. Большинство векторов окажутся где-то совершенно разными, когда к ним будет применен A, но собственные векторы меняются только по величине. Если вы проведете линию через начало координат и собственный вектор, то после отображения собственный вектор все равно попадет на линию. Величина, по которой вектор масштабируется вдоль линии, зависит от λ.
Мы можем легко найти собственные значения и собственные векторы матрицы, используя numpy в Python:
Собственные векторы являются важной частью линейной алгебры, потому что они помогают описать динамику систем, представленных матрицами. Существует множество приложений, в которых используются собственные векторы, и мы будем использовать их непосредственно здесь для выполнения спектральной кластеризации.
диаграммы
Графики являются естественным способом представления многих типов данных. Граф — это набор узлов с соответствующим набором ребер, которые соединяют узлы. Края могут быть направленными или ненаправленными и даже иметь веса, связанные с ними.
Сеть роутеров в интернете легко представить в виде графика. Маршрутизаторы — это узлы, а ребра — это соединения между парами маршрутизаторов. Некоторые маршрутизаторы могут разрешать трафик только в одном направлении, поэтому границы могут быть направлены в направлении направления трафика. Веса на краях могут представлять полосу пропускания, доступную вдоль этого края. При такой настройке мы могли бы затем запросить график, чтобы найти эффективные пути для передачи данных от одного маршрутизатора к другому по сети.
Давайте использовать следующий неориентированный граф в качестве рабочего примера:
Этот граф имеет 10 узлов и 12 ребер. Он также имеет два соединенных компонента <0,1,2,8,9>и <3,4,5,6,7>. Связанный компонент — это максимальный подграф узлов, у всех из которых есть пути к остальным узлам подграфа.
Связанные компоненты кажутся важными, если наша задача — назначить эти узлы сообществам или кластерам. Простая идея — сделать каждый связанный компонент отдельным кластером. Это кажется разумным для нашего примера графа, но возможно, что весь граф может быть связан, или что связанные компоненты очень велики. Могут также быть меньшие структуры в связанном компоненте, которые являются хорошими кандидатами для сообществ. Вскоре мы увидим важность идеи связанного компонента для спектральной кластеризации.
Матрица смежности
Мы можем представить наш примерный граф в виде матрицы смежности, где индексы строк и столбцов представляют узлы, а записи представляют отсутствие или наличие ребра между узлами. Матрица смежности для нашего примера графа выглядит следующим образом:
В матрице мы видим, что строка 0, столбец 1 имеет значение 1. Это означает, что существует ребро, соединяющее узел 0 с узлом 1. Если ребра были взвешены, веса ребер были бы в этой матрице вместо только 1 и 0. Так как наш график не направлен, записи для строки i, col j будут равны записи в строке j, col i. Последнее, что следует отметить, это то, что диагональ этой матрицы равна 0, поскольку ни один из наших узлов не имеет ребер.
Степень Матрица
Степень узла — это количество ребер, соединенных с ним. В ориентированном графе мы могли бы говорить о степени и степени, но в этом примере у нас просто есть степень, так как ребра идут в обе стороны. Глядя на наш график, мы видим, что узел 0 имеет степень 4, поскольку он имеет 4 ребра. Мы также можем получить степень, взяв сумму строки узла в матрице смежности.
Матрица степеней — это диагональная матрица, где значение на входе (i, i) является степенью узла i Давайте найдем матрицу степеней для нашего примера:
Сначала мы взяли сумму по оси 1 (строки) нашей матрицы смежности, а затем поместили эти значения в диагональную матрицу. Из матрицы степеней мы легко видим, что узлы 0 и 5 имеют 4 ребра, в то время как остальные узлы имеют только 2.
График лапласианский
Теперь мы собираемся вычислить граф Лапласа. Лапласиан — это просто еще одно матричное представление графа. У него есть несколько прекрасных свойств, которыми мы воспользуемся для спектральной кластеризации. Чтобы вычислить нормальный лапласиан (есть несколько вариантов), мы просто вычитаем матрицу смежности из нашей матрицы степеней:
Диагональ лапласиана — это степень наших узлов, а вне диагонали — вес отрицательного края. Это представление, которое мы ищем для выполнения спектральной кластеризации.
Собственные значения графа лапласиана
Как уже упоминалось, лапласиан обладает некоторыми прекрасными свойствами. Чтобы понять это, давайте рассмотрим собственные значения, связанные с лапласианом, когда я добавлю ребра в наш граф:
Мы видим, что когда граф полностью отключен, все десять наших собственных значений равны 0. Когда мы добавляем ребра, некоторые из наших собственных значений увеличиваются. Фактически, число собственных значений 0 соответствует числу связанных компонент в нашем графе!
Посмотрите внимательно, как добавлен этот последний край, соединяя два компонента в один. Когда это происходит, все собственные значения, кроме одного, были отменены:
Первое собственное значение равно 0, потому что у нас есть только один связный компонент (весь граф связен). Соответствующий собственный вектор всегда будет иметь постоянные значения (в этом примере все значения близки к 0,32).
Первое ненулевое собственное значение называется спектральной щелью. Спектральная щель дает нам некоторое представление о плотности графика. Если бы этот граф был плотно связан (все пары из 10 узлов имели ребро), то спектральный разрыв был бы 10.
Второе собственное значение называется значением Фидлера, а соответствующий вектор является вектором Фидлера. Значение Фидлера приблизительно соответствует минимальному срезу графа, необходимому для разделения графа на два связанных компонента. Напомним, что если бы в нашем графе уже было два связанных компонента, то значение Фидлера было бы равно 0. Каждое значение в векторе Фидлера дает нам информацию о том, какой стороне разреза принадлежит этот узел. Давайте раскрасим узлы в зависимости от того, положительна ли их запись в векторе Филдера:
Этот простой трюк разделил наш график на две группы! Почему это работает? Помните, что нулевые собственные значения представляют связанные компоненты. Собственные значения около нуля говорят нам, что существует почти разделение двух компонентов. Здесь у нас есть одно преимущество: если бы его не было, у нас было бы два отдельных компонента. Таким образом, второе собственное значение мало.
Подводя итог, что мы знаем до сих пор: первое собственное значение 0, потому что у нас есть один связанный компонент. Второе собственное значение около 0, потому что мы на расстоянии одного края от двух соединенных компонентов. Мы также видели, что вектор, связанный с этим значением, говорит нам, как разделить узлы на эти приблизительно связанные компоненты.
Возможно, вы заметили, что следующие два собственных значения также довольно малы. Это говорит нам о том, что мы «близки» к четырем отдельным подключенным компонентам. В общем, мы часто ищем первый большой разрыв между собственными значениями, чтобы найти число кластеров, выраженных в наших данных. Видите разрыв между собственными значениями четыре и пять?
Наличие четырех собственных значений перед разрывом указывает на то, что, вероятно, существует четыре кластера. Векторы, связанные с первыми тремя положительными собственными значениями, должны дать нам информацию о том, какие три разреза необходимо сделать на графике, чтобы назначить каждый узел одному из четырех приближенных компонентов. Давайте построим матрицу из этих трех векторов и выполним кластеризацию K-средних для определения назначений:
График был сегментирован на четыре квадранта, причем узлы 0 и 5 произвольно назначены одному из их связанных квадрантов. Это действительно круто, и это спектральная кластеризация!
Подводя итог, мы сначала взяли наш граф и построили матрицу смежности. Затем мы создали лапласиан графа, вычтя матрицу смежности из матрицы степеней. Собственные значения лапласиана указывали на наличие четырех кластеров. Векторы, связанные с этими собственными значениями, содержат информацию о том, как сегментировать узлы. Наконец, мы выполнили K-средства для этих векторов, чтобы получить метки для узлов. Далее мы увидим, как это сделать для произвольных данных.
Спектральная кластеризация произвольных данных
Посмотрите на данные ниже. Точки нарисованы из двух концентрических кругов с добавлением шума Нам бы хотелось, чтобы алгоритм позволял группировать эти точки в два круга, которые их генерировали.
Эти данные не в форме графика. Итак, во-первых, давайте просто попробуем алгоритм обрезки печенья, такой как K-Means. K-Means найдет два центроида и пометит точки, в зависимости от того, к какому центроиду они ближе всего. Вот результаты:
Очевидно, K-Means не собирался работать. Он действует на евклидовом расстоянии и предполагает, что скопления примерно сферические. Эти данные (и часто данные реального мира) нарушают эти предположения. Давайте попробуем решить эту проблему с помощью спектральной кластеризации.
График ближайших соседей
Есть несколько способов обработать наши данные как график. Самый простой способ — построить граф k-ближайших соседей. Граф k-ближайших соседей обрабатывает каждую точку данных как узел в графе. Затем ребро рисуется от каждого узла до его k ближайших соседей в исходном пространстве. Как правило, алгоритм не слишком чувствителен к выбору k. Меньшие числа, такие как 5 или 10, обычно работают довольно хорошо.
Посмотрите на изображение данных еще раз и представьте, что каждая точка связана со своими 5 ближайшими соседями. Любая точка во внешнем кольце должна быть в состоянии следовать по пути вдоль кольца, но во внутреннем круге не будет никаких путей. Довольно легко увидеть, что этот график будет иметь два связанных компонента: внешнее кольцо и внутренний круг.
Поскольку мы разделяем эти данные только на два компонента, мы должны использовать наш векторный метод Фидлера ранее. Вот код, который я использовал для спектральной кластеризации этих данных:
И вот результаты:
Другие подходы
Граф ближайших соседей — хороший подход, но он основан на том факте, что «близкие» точки должны принадлежать одному кластеру. В зависимости от ваших данных, это может быть не так. Более общий подход заключается в построении аффинной матрицы. Матрица сходства похожа на матрицу смежности, за исключением того, что значение для пары точек показывает, насколько эти точки похожи друг на друга. Если пары точек сильно различаются, то сродство должно быть 0. Если точки идентичны, то сродство может быть 1. Таким образом, сродство действует как вес для ребер нашего графа.
Как решить, что означает совпадение двух точек данных, является одним из наиболее важных вопросов в машинном обучении. Часто знание предметной области — лучший способ построить меру подобия. Если у вас есть доступ к экспертам по доменам, задайте им этот вопрос.
Есть также целые поля, посвященные изучению того, как строить метрики подобия непосредственно из данных. Например, если у вас есть некоторые помеченные данные, вы можете обучить классификатор, чтобы предсказать, похожи ли два входа или нет, основываясь на том, имеют ли они одинаковую метку. Затем этот классификатор можно использовать для присвоения сходства парам немаркированных точек.
Вывод
Мы рассмотрели теорию и применение спектральной кластеризации для графов и произвольных данных. Спектральная кластеризация — это гибкий подход для поиска кластеров, когда ваши данные не соответствуют требованиям других распространенных алгоритмов.
Сначала мы сформировали график между нашими точками данных. Края графика отражают сходство точек. Собственные значения графа лапласиана могут затем использоваться для поиска наилучшего числа кластеров, а собственные векторы могут использоваться для поиска фактических меток кластеров.
Я надеюсь, что вам понравился этот пост, и вы нашли спектральную кластеризацию полезной в вашей работе или исследовании.
http://vmath.ru/vf5/algebra2/charpoly
http://www.machinelearningmastery.ru/spectral-clustering-aba2640c0d5b/
From Wikipedia, the free encyclopedia
In mathematics, the spectrum of a matrix is the set of its eigenvalues.[1][2][3] More generally, if 


From this point of view, we can define the pseudo-determinant for a singular matrix to be the product of its nonzero eigenvalues (the density of multivariate normal distribution will need this quantity).
In many applications, such as PageRank, one is interested in the dominant eigenvalue, i.e. that which is largest in absolute value. In other applications, the smallest eigenvalue is important, but in general, the whole spectrum provides valuable information about a matrix.
Definition[edit]
Let V be a finite-dimensional vector space over some field K and suppose T : V → V is a linear map. The spectrum of T, denoted σT, is the multiset of roots of the characteristic polynomial of T. Thus the elements of the spectrum are precisely the eigenvalues of T, and the multiplicity of an eigenvalue λ in the spectrum equals the dimension of the generalized eigenspace of T for λ (also called the algebraic multiplicity of λ).
Now, fix a basis B of V over K and suppose M ∈ MatK (V) is a matrix. Define the linear map T : V → V pointwise by Tx = Mx, where on the right-hand side x is interpreted as a column vector and M acts on x by matrix multiplication. We now say that x ∈ V is an eigenvector of M if x is an eigenvector of T. Similarly, λ ∈ K is an eigenvalue of M if it is an eigenvalue of T, and with the same multiplicity, and the spectrum of M, written σM, is the multiset of all such eigenvalues.
[edit]
The eigendecomposition (or spectral decomposition) of a diagonalizable matrix is a decomposition of a diagonalizable matrix into a specific canonical form whereby the matrix is represented in terms of its eigenvalues and eigenvectors.
The spectral radius of a square matrix is the largest absolute value of its eigenvalues. In spectral theory, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements in the spectrum of that operator.
Notes[edit]
- ^ Golub & Van Loan (1996, p. 310)
- ^ Kreyszig (1972, p. 273)
- ^ Nering (1970, p. 270)
- ^ Golub & Van Loan (1996, p. 310)
- ^ Herstein (1964, pp. 271–272)
- ^ Nering (1970, pp. 115–116)
References[edit]
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins University Press, ISBN 0-8018-5414-8
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
Функции от матриц
Пусть — числовая квадратная матрица и
— скалярная функция переменной
. В этом разделе понятие функции распространяется на матричные значения аргумента. Если
— многочлен, то задача нахождения многочлена
, получающегося при подстановке матрицы
вместо переменной
, была решена ранее. Требуется определить, что следует понимать под выражением
для достаточно произвольной функции
. Разумеется, что определение функции от матрицы, когда функция является многочленом, должно совпадать с определением многочлена от матрицы.
Функции, определенные на спектре матрицы
Напомним, что спектром квадратной матрицы называется совокупность всех ее собственных значений (корней характеристического многочлена). Все собственные значения являются также корнями минимального многочлена (см. свойство 3 минимального многочлена):
(7.54)
где — корень кратности
,
— корень кратности
и т.д. Степень
минимального многочлена не превосходит порядка
матрицы
.
Говорят, что скалярная функция переменной
определена на спектре матрицы
, если для функции
определены значения
(7.55)
т.е. функция определена в окрестности каждой точки
вместе со своими производными до указанного порядка. Совокупность (7.55) значений функции и ее производных будем обозначать
.
Две функции и
называются равными на спектре матрицы
, если
(7.56)
Эти равенства будем записывать в форме .
Теорема 7.10 (основное свойство многочленов от матриц). Если и
— многочлены, то
(7.57)
т.е. многочлены, равные на спектре матрицы, имеют равные матричные значения, и наоборот, если равны матричные значения многочленов, то равны их значения на спектре матрицы. Другими словами, значения многочлена на спектре матрицы полностью определяют его значение
от матрицы
.
В самом деле, пусть , тогда разность
является аннулирующим многочленом:
. Разделим его на минимальный многочлен
(свойство 1 в разд.7.2.4). Из (7.54) следует, что число
является корнем многочлена
, причем его кратность больше или равна
. Тогда:
что равносильно (7.56). Следовательно, . Достаточность доказана. Для доказательства необходимости нужно все рассуждения провести в обратном порядке, либо вернуться ко второму способу нахождения многочлена от матрицы: в системе (7.46), которая позволяет найти коэффициенты искомого многочлена, левые части уравнений являются значениями многочлена
на спектре матрицы
.
Определение и свойства функций от матриц
Основное свойство (7.57), справедливое для многочленов, переносится на произвольные функции и фактически берется за основу определения функции от матрицы.
Пусть — произвольная функция, определенная на спектре матрицы
. Значение
функции
от матрицы
определяется равенством
(7.58)
где — любой многочлен, принимающий на спектре матрицы
те же значения, что
.
Поскольку функции от матриц определяются через многочлены, то на них переносятся свойства многочленов от матриц.
1. Функции от подобных матриц подобны.
2. Функция от блочно-диагональной матрицы является блочно- диагональной матрицей, т.е. если матрица имеет вид
, где
некоторые квадратные матрицы, то
3. Функция от жордановой клетки
имеет вид
(7.59)
Это верхняя треугольная матрица r-го порядка, на главной диагонали которой стоят значения функции в точке
, над диагональю — значения первой производной в этой же точке и т.д., т.е. коэффициенты формулы Тейлора для функции
.
Способы нахождения функций от матриц
Из определения функции от матрицы следует, что первый и второй способы нахождения многочлена от матрицы, пригодны и для любой функции, определенной на спектре матрицы. Поэтому они могут считаться первым и вторым способами нахождения функции от матрицы. Далее излагается третий (интерполяционный) способ решения этой же задачи.
Пример 7.21. Найти функцию от матрицы
.
Решение. Первый способ. 1. Жорданова форма и преобразующая матрица
были найдены в примере 7.15:
2. Жорданова форма состоит из одной жордановой клетки
2-го порядка, соответствующей собственному значению
. Найдем значение функции
и ее производной
. Запишем функцию от жордановой формы (7.59):
3. Найдем функцию от матрицы
Второй способ. 1. Минимальный многочлен матрицы А найден в примере 7.18: . Степень v минимального многочлена равна 2. Значит, многочлен (7.44) линейный:
.
2. Для двойного корня составляем уравнения (7.46):
3. Решая систему, получаем и
.
4. Находим функцию от матрицы
Полученные разными способами результаты, разумеется, совпадают.
Интерполяционный способ нахождения функции от матрицы
Рассмотрим сначала частный случай, когда все корни минимального многочлена простые: . В этом случае значения функции на спектре матрицы
— это совокупность значений функции
в точках
. Обозначим через
интерполяционный многочлен Лагранжа:
(7.60)
для которого . Тогда
Таким образом, для нахождения функции от матрицы
в случае простых корней минимального многочлена, нужно выполнить следующие действия.
1. Найти минимальный многочлен одним из способов, рассмотренных ранее. Убедиться в том, что все корни
минимального многочлена простые.
2. Вычислить значения функции на спектре матрицы
и составить по формуле (7.60) интерполяционный многочлен Лагранжа
.
3. Найти значение функции от матрицы .
Пример 7.22. Найти функцию от матрицы
.
Решение. Интерполяционный способ (случай простых корней). 1. Минимальный многочлен найден в примере 7.12: . Все его корни
простые.
2. Находим значения функции на спектре матрицы . Составляем по формуле (7.60) интерполяционный многочлен Лагранжа:
3. Находим функцию от матрицы
Рассмотрим общий случай, когда минимальный многочлен (7.54)
имеет кратные корни: — корень кратности от
,
— корень кратности
и т.д. Степень
минимального многочлена не превосходит порядка
матрицы
.
Многочлен степени меньшей, чем
, удовлетворяющий условиям:
называется интерполяционным многочленом Лагранжа-Сильвестра для функции , определенной на спектре матрицы
.
Многочлен Лагранжа-Сильвестра однозначно определяется значениями функции на спектре матрицы и находится по формуле:
(7.61)
где — многочлен, равный отношению минимального многочлена и соответствующего элементарного делителя:
, а выражение в квадратных скобках равно сумме первых от, членов разложения функции
по формуле Тейлора, то есть
Замечания 7.10.
1. Если минимальный многочлен имеет один корень (кратности ):
то многочлен Лагранжа-Сильвестра совпадает с многочленом Тейлора. Действительно, в этом случае
, поэтому формула (7.61) принимает вид
что совпадает с первыми членами ряда Тейлора.
2. Если все корни минимального многочлена простые: , тогда
поэтому формула (7.61) принимает вид (7.60), т.е. многочлен Лагранжа-Сильвестра совпадает с многочленом Лагранжа.
Для нахождения функции от матрицы
при наличии кратных корней минимального многочлена нужно выполнить следующие действия.
1. Найти минимальный многочлен матрицы одним из способов, рассмотренных ранее:
2. Для каждого корня кратности
найти многочлен
и вычислить коэффициенты
разложения функции
в точке
по формуле Тейлора:
3. Составить по формуле (7.61) интерполяционный многочлен Лагранжа-Сильвестра.
4. Найти значение функции от матрицы .
Пример 7.23. Найти функцию от матрицы
.
Решение. Интерполяционный способ (случай кратных корней). 1. Минимальный многочлен найден в примере7.15: . Корень
— двойной, а
— простой, т.е. количество различных корней
, кратности корней
.
2. Для двойного корня находим многочлен
и соответствующие коэффициенты
Для простого корня находим многочлен
и коэффициент
.
3. Составляем по формуле (7.61) интерполяционный многочлен Лагранжа–Сильвестра:
4. Находим функцию от матрицы
Проверим полученный результат, используя первый способ нахождения функции от матрицы.
1. В примере 7.15 были найдены жорданова форма матрицы и преобразующая матрица
2. Жорданова форма состоит из двух жордановых клеток 2-го и 1-го порядков
, соответствующих собственным значениям
и
. Найдем значения функции на спектре матрицы:
и
. Запишем функцию от жордановой формы
Найдем функцию от матрицы
Результаты, полученные разными способами, совпадают.
Свойства функций от матриц
Многие свойства функций скалярного аргумента распространяются на функции от матриц. Рассмотрим некоторые из них.
1. Если функция разлагается в степенной ряд
(7.62)
сходящийся в круге , то для любой матрицы
, собственные значения которой лежат внутри круга сходимости, справедливо разложение
(7.63)
Здесь предел последовательности матриц (частичных сумм ряда) понимается поэлементно, как совокупность пределов элементов матрицы. Напомним, что .
В самом деле, степенной ряд можно почленно дифференцировать любое число раз внутри круга сходимости. Поэтому функция определена на спектре любой матрицы, собственные значения которой лежат внутри круга сходимости.
Из свойства 1 следуют, например, разложения в ряд (7.62) при
справедливые для любой квадратной матрицы .
2. Если функция разлагается в степенной ряд, а собственные значения функциональной матрицы
при всех
лежат внутри круга сходимости этого ряда, то определена сложная функция
, производная которой находится по формуле:
В самом деле, подставим в ряд (7.62) вместо матрицу
Найдем производную этой матричной функции. Учитывая, что многочлены от одной и той же матрицы перестановочны, по правилу 3 дифференцирования произведения матриц получаем
то есть . Поэтому
.
Сравнивая полученный ряд с производной ряда (7.62) при подстановке вместо
матрицы
, приходим к доказываемому равенству.
Пример 7.24. Используя разложение в степенной ряд, найти матричную функцию
где
Решение. Запишем степенной ряд (7.63)
Учитывая разложение , получаем
Результат совпадает с полученным в примере 7.23.
Применение функций от матриц для решения систем дифференциальных уравнений
Рассмотрим систему линейных дифференциальных уравнений с постоянными коэффициентами
(7.64)
где — коэффициенты системы,
— заданные, a
— неизвестные функции аргумента
. При описании непрерывных динамических систем аргумент
обозначает время.
Систему (7.64) можно записать в матричном виде:
(7.65)
где — квадратная матрица n-го порядка,
— столбец заданных функций, a
— столбец неизвестных.
Решением системы (7.65) называют столбец дифференцируемых функций, при подстановке которых в (7.65) получаются верные равенства, тождественно выполняющиеся при
.
Поставим задачу нахождения решения системы (7.65), удовлетворяющего начальным условиям
(7.66)
где — заданный столбец.
Как известно, решение системы (7.65) с начальными условиями (7.66) имеет вид:
(7.67)
В самом деле, найдем производную функции (7.67). Применяя правило Лейбница
и свойство 2 функций от матриц, получаем
т.е. является решением системы (7.65). При
формула (7.67) дает
, где
— нулевая, а
— единичная матрицы. Равенство
следует, например, из разложения в ряд функции
. Следовательно, решение (7.67) удовлетворяет и начальным условиям (7.66).
Поэтому для нахождения решения нужно выполнить следующие действия.
1. Найти выражение для функции одним из способов, рассмотренных ранее.
2. Записать искомое решение по формуле (7.67).
Замечания 7.11.
1. Нахождение функции от функциональной матрицы
облегчается, если учитывать, что собственные значения
матрицы
пропорциональны собственным значениям
матрицы
. Действительно, характеристический многочлен матрицы
имеет вид
Поэтому, если число — корень характеристического многочлена матрицы
, то число
— корень многочлена
, причем той же кратности. Такая же связь между корнями минимальных многочленов
и
: если
— корень минимального многочлена
, то
— корень минимального многочлена
.
2. Решение линейного дифференциального уравнения с постоянными коэффициентами сводится к решению системы вида (7.64), получающейся после замены
.
3. Для нахождения функции можно использовать следующий способ. Найти
линейно независимых решений
однородной системы
и составить из этих столбцов фундаментальную матрицу
системы (7.65). В силу линейной независимости столбцов
определитель фундаментальной матрицы (определитель Вронского) отличен от нуля:
для
. Поэтому определена обратная матрица
. Функция
(называемая матрицей Коши, или переходной матрицей) может быть найдена по формуле
Пример 7.25. Найти решение системы дифференциальных уравнений, удовлетворяющее начальным условиям
, матричным способом:
Решение. 1. Составим матрицу коэффициентов системы:
и функцию
. Найдем выражение для функции
от матрицы
(т.е. функции
), используя второй способ нахождения функции от матрицы. Минимальный многочлен
матрицы
был найден в примере 7.18. Согласно пункту 1 замечаний 7.11, минимальный многочлен матрицы
имеет вид
. Степень
минимального многочлена равна 2. Значит, многочлен (7.44) линейный:
. Для двойного корня
составляем уравнения (7.46) (см. пример 7.21):
Решая систему, получаем и
. Находим функцию
от матрицы
По формуле (7.67) записываем искомое решение
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Одно
из важных приложений жордановой формы
– вычисление функции от матриц (от
линейных операторов). В п.11 определили



где

Как
определить функцию от матрицы?
Пусть




максимальный размер жордановой клетки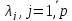
Определение
12.1
Пусть



если существуют значения:
которые называются значениями на
спектре матрицы.
Замечание
1.
Любой многочлен определен на спектре
матрицы.
Определение
12.2
Пусть

матрицы
Пусть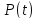
матрицы
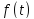
Положим по определению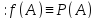

Существует
много многочленов, совпадающих с данной
функцией на спектре матрицы. Среди них
выделим так называемый интерполяционный
многочлен Лагранжа – Сильвестра.
Определение
12.3
Пусть

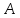
Многочлен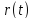
многочлена матрицы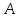
и совпадающий на спектре матрицы

называется интерполяционным многочленом
Лагранжа – Сильвестра.
Обозначение:
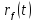
Замечание
2.
Можно показать, что для любой


интерполяционный многочлен
Рассмотрим
применение жордановой формы матрицы и
жорданова базиса к вычислению функции
от матрицы.
Пример
1.

минимальный (аннулирующий) многочлен
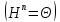

собственное значение,
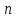
Пусть


т.е. существуют значения
Интерполяционный многочлен Лагранжа
– Сильвестра имеет вид:

(Степень
многочлена меньше степени минимального
многочлена и совпадает на спектре
матрицы.) Из определения 12.2 следует, что

Пример
2.

минимальный (аннулирующий) многочлен

где

Пусть


тогда
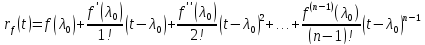

Отсюда
вытекает способ вычисления функций от
матриц.
Пусть




Тогда

где
13. Инвариантные подпространства минимальной размерности.
Теорема
13.1
У всякого линейного оператора в
комплексном пространстве существует
одномерное инвариантное подпространство.
∎
У


существует хотя бы один собственный
вектор

относительно
Теорема
13.2
У всякого л.о.


одномерное или двумерное инвариантное
подпространство.
∎

вещественное пространство;

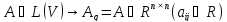

с вещественными коэффициентами. Пусть
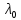

-
,
—
собственное значение— собственный вектор, отвечающий с.з.
,⟹
— одномерное подпространство, инвариантное
относительно.
-
—
тоже корень характеристического
уравнения. Рассмотрим
как комплексную матрицу. Если
— собственный вектор -столбец, отвечающий
с.з.,
то
Векторы


векторы, отвечающие различным собственным
значениям.
Пусть




В
векторной форме будем иметь. Пусть

Системе уравнений для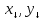
уравнений:



независимы). Следовательно,
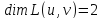
Вещественный
аналог жордановой формы.
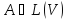
вещественном пространстве


многочлен с вещественными коэффициентами.
Если
то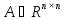
матрицу⟹
существуют жордановы клетки с
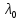


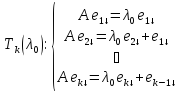
Обозначим
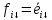


Если
⟹


векторы
— столбцы
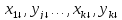
Таким
образом, любой комплексный корень (не
вещественный) порождает матрицу порядка


в
базисе подпространства, соответствующем
координатным столбцам

Теорема
13.3
Для любого


оператора имеет квазидиагональную
форму с вещественными клетками Жордана
и вещественными клетками вида (13.1) на
главной диагонали.
1. 21



 ,
,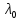 —
— — собственный вектор, отвечающий с.з.
— собственный вектор, отвечающий с.з. ,⟹
,⟹ — одномерное подпространство, инвариантное
— одномерное подпространство, инвариантное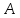 .
. —
— как комплексную матрицу. Если
как комплексную матрицу. Если — собственный вектор -столбец, отвечающий
— собственный вектор -столбец, отвечающий ,
,

