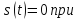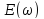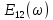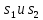Как найти спектральную плотность импульса - Исправление недочетов и поиск решений вместе с Examum.ru

Спектральные плотности некоторых сигналов

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Спектральная плотность прямоугольного импульса

Рассмотрим спектральную плотность прямоугольного импульса $s(t) = A п_{tau}(t)$ длительности tau и амплитуды . Функция $п_{tau}(t)$ описывает прямоугольный импульс длительности tau и единичной амплитуды:

(1)

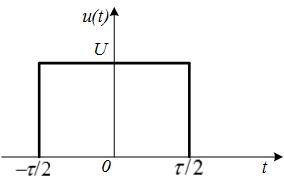
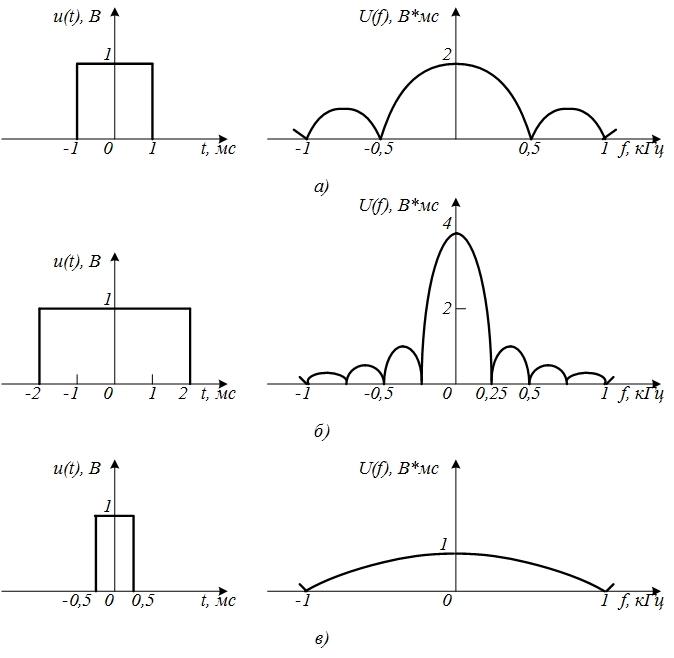
График прямоугольного импульса показан на рисунке 1а.

Рисунок 1. Спектральная плотность прямоугольного импульса
а — временно́й сигнал; б — спектральная плотность

Спектральная плотность прямоугольного импульса $A п_{tau}(t)$ равна:

(2)

где . График спектральной плотности прямоугольного импульса показан на рисунке 1б.
Приведем основные частотные свойства .

Спектральная плотность треугольного импульса

Рассмотрим треугольный импульс s(t) длительности tau и амплитуды :

(3)

График треугольного импульса показан на рисунке 2а.

Рисунок 2. Спектральная плотность треугольного импульса
а — временно́й сигнал; б — спектральная плотность

Для рассмотрения спектральной плотности треугольного импульса мы не будем вычислять интеграл Фурье непосредственно, потому что это потребует громоздких выкладок, а воспользуемся свойством преобразования Фурье свертки двух сигналов.

Можно заметить, что треугольный импульс длительности tau и амплитуды может быть представлен как результат свертки прямоугольного импульса $p(x) = sqrt{2A/tau} , п_{tau/2}(x)$ длительности tau/2 и амплитуды c самим собой, как это показано на рисунке 3.

Рисунок 3. Треугольный импульс как результат
свертки прямоугольных импульсов

Обратим внимание, что один из углов p(x) маркирован черным квадратиком для того, чтобы показать инверсию во времени сдвинутого сигнала p(t-x) , входящего в интеграл свертки.

Для различного сдвига мы будем иметь линейно нарастающую площадь (заштрихованная область) произведения сигнала p(x) и его сдвинутой инверсной во времени копии p(t-x) .

Таким образом, мы можем применить

свойство преобразования Фурье свертки сигналов

и записать спектральную плотность треугольного импульса как квадрат спектральной плотности прямоугольного импульса p(x) длительности tau/2 и амплитуды :

(4)

График спектральной плотности треугольного импульса показан на рисунке 2б.
Приведем основные частотные свойства .

Спектральная плотность гауссова импульса

Гауссов импульс s(t) задается выражением:

(5)

где — амплитуда, а sigma — положительный параметр, который задает ширину импульса.

График гауссова импульса при различном значении sigma и A = 1 показан на рисунке 4а.

Рисунок 4. Спектральная плотность гауссова импульса
а — временно́й сигнал; б — спектральная плотность

Рассмотрим спектральную плотность гауссова импульса:

(6)

Преобразуем показатель экспоненты (6) следующим образом:

(7)

Тогда (6) с учетом (7):

(8)

Из курса математического анализа [1, стр. 401] известно, что:

(9)

Введем в выражении (8) замену переменной $xi = frac{t}{sigma} + jfrac{omegasigma}{2}$ , тогда , пределы интегрирования остаются неизменными при положительном значении sigma . Тогда (8) можно представить как:

(10)

и с учетом (9) окончательно можно записать:

(11)

Можно заметить, что временно́й гауссов импульс s(t) имеет спектральную плотность , которая также описывается гауссовской функцией.

График спектральной плотности гауссова импульса для различного значения параметра sigma показан на рисунке 4б.
C увеличением sigma увеличивается ширина гауссова импульса во временно́й области, и сужение спектральной плотности. При этом, убывание импульса во времени и по частоте носит экспоненциальный характер.

Спектральная плотность экспоненциального импульса

Рассмотрим двусторонний экспоненциальный импульс s(t) , который задается выражением:

(12)

где — амплитуда, а sigma — положительный параметр, который определяет ширину импульса.
График двустороннего экспоненциального импульса при A = 1 и различном значении параметра sigma показан на рисунке 5а.

Рисунок 5. Спектральная плотность двустороннего экспоненциального импульса
а — временно́й сигнал; б — спектральная плотность

Как можно видеть из рисунка 5а, увеличение параметра sigma приводит к сужению импульса во временно́й области.

Рассмотрим спектральную плотность двустороннего экспоненциального импульса:

(13)

Разобьем ось времени на положительную и отрицательную полуоси, и учтем что для отрицательной полуоси времени. Тогда (13) можно записать:

(14)

Объединим показатели экспонент в обоих интегралах и получим:

(15)

Таким образом, спектральная плотность двустороннего экспоненциального импульса (12) представляет собой вещественную функцию частоты, обладающую следующими свойствами.

На рисунке 5б показан вид спектральной плотности при различном значении sigma . Можно видеть, что при увеличении параметра sigma , спектральная плотность сужается (импульс во временно́й области —расширяется).

Рисунок 6. Односторонний экспоненциальный импульс

Рассмотрим теперь односторонний экспоненциальный импульс, который получается из двустороннего при обнулении значения отрицательной полуоси времени:

(16)

График одностороннего экспоненциального импульса показан на рисунке 6 при A = 1 и различном sigma .

Спектральная плотность одностороннего экспоненциального импульса равна:

(17)

Приведем основные частотные свойства одностороннего экспоненциального импульса:

Поскольку спектральная плотность одностороннего экспоненциального импульса является комплексной функцией частоты omega , то можно представить в виде амплитудно- и фазочастотной характеристик:

(18)

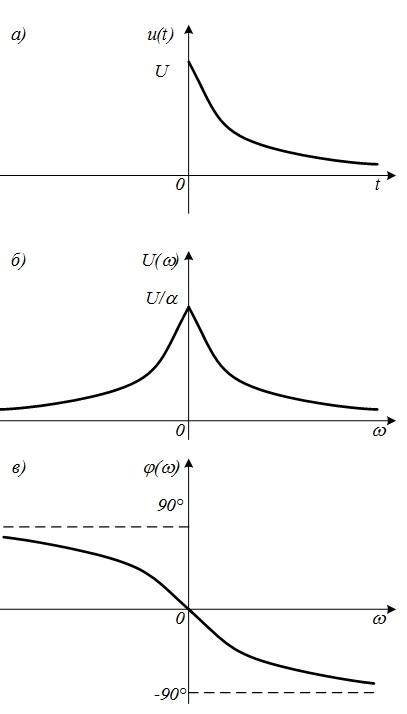
На рисунке 7 показаны АЧХ и ФЧХ одностороннего экспоненциального импульса для различных значения параметра sigma .

Рисунок 7. АЧХ и ФЧХ одностороннего экспоненциального импульса
а — АЧХ; б — ФЧХ

Спектральная плотность функции

Рассмотрим спектральную плотность сигнала вида , где alpha — параметр определяющий ширину главного лепестка функции , как это показано на рисунке 8а.

Рисунок 8. Спектральная плотность функции
а — временно́й сигнал; б — спектральная плотность

Для получения спектральной плотности сигнала воспользуемся

свойством двойственности преобразования Фурье,

рассмотренным в
в предыдущем параграфе.
Тогда из выражения (2) можно записать:

(19)

Произведем замену переменных omega и , а также обозначим $alpha = frac{tau}{2}$ , откуда :

(20)

Вынесем множитель 2alpha из под оператора преобразования Фурье, и окончательно спектральная плотность сигнала равна:

(21)

График спектральной плотности сигнала показан на рисунке 8б.

Важным частным случаем является , тогда $s(t) = frac{alpha}{pi} operatorname{sinc}(alpha t)$ будет иметь спектральную плотность $S(omega) = п_{2alpha}(omega)$ , что соответствует частотной характеристике идеального фильтра нижних частот. Временно́й сигнал $s(t) = frac{alpha}{pi} operatorname{sinc} (alpha t)$ определяет импульсную характеристику идеального фильтра нижних частот.

Выводы

В данном разделе мы рассмотрели спектральные плотности некоторых непериодических сигналов: прямоугольного, треугольного, гауссова импульса,
а также одностороннего и двустороннего экспоненциальных импульсов.

Были приведены аналитические выражения для спектральных плотностей каждого из сигналов, а также их частотные свойства.

Смотри также

Представление периодических сигналов рядом Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье

Спектральные плотности некоторых сигналов

Список литературы

[1]

Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.

[2]

Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

[4]

Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 12.05.2022 (19:42:52)

Страница создана Latex to HTML translator ver. 5.20.11.14

Источник

Спектральные плотности амплитуд и фаз непериодических сигналов

Величина
в (4.27) илиU(jf)
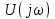
в (4.29), называетсякомплексной
спектральной плотностьюнепериодического сигналаu(t).Она
может быть записана в показательной и
алгебраической формах:

(4.31)

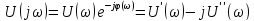
и содержит в себе
сведения о спектральной
плотности амплитуд

испектральной
плотности фаз
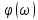
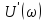
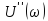
сигнала, где величиныиопределяются
формулами

Определим физический
смысл преобразования Фурье (4.28). Для
этого подставим в выражение (4.28) вместо
его
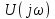
значения из (4.31):

Учитывая, что
– четная, а синус – нечетная функция
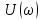
частоты, интеграл от второго слагаемого
равен нулю. Следовательно, интеграл
Фурье (4.28) имеет вид

Отсюда
следует важнейший вывод о том, что
непериодический
сигнал может быть представлен пределом
суммы (интегралом) бесконечно большого
числа гармонических колебаний с
бесконечно малыми амплитудами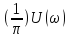и
начальными фазами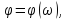причем
разность частот соседних гармоник
бесконечно мала:.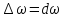
Это означает, что спектр непериодического
сигнала являетсясплошным
или непрерывным.

Определимспектральную плотностьпрямоугольного
импульса, изображенного на рис.
4.14. Для расчета его комплексной
спектральной плотности воспользуемся

Рис. 4.14. Прямоугольный
импульс

Уравнение
(4.34) удобнее преобразовать к виду

так как это выражение
содержит функцию
,
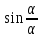
поведение которой хорошо известно: эта
затухающая функция максимальна и равна1,
когда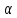=0;
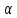
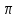
она принимает нулевые значения при=±k.

График комплексной
спектральной плотности прямоугольного
импульса изображен на рис. 4.15. В тех
областях частот, где функция
положительна,
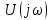
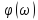
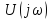
спектральная плотность фазравна нулю; там же, гдеотрицательна,
спектральная плотность фаз равна ±180°.
Поэтому на графиках можно изобразить
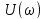
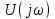
отдельно спектральную плотность амплитуд– модуль ||
и спектральную плотность фаз(рис.
4.16)

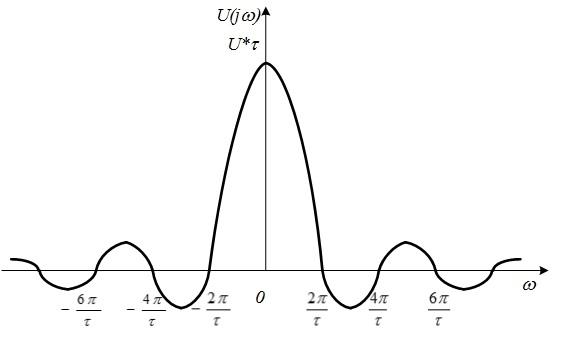
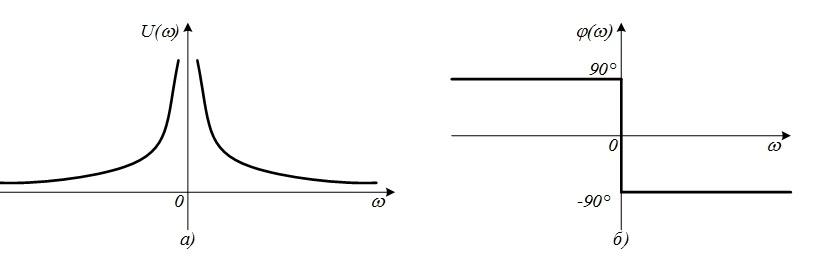
Рис. 4.15. Спектральная
плотность прямоугольного импульса

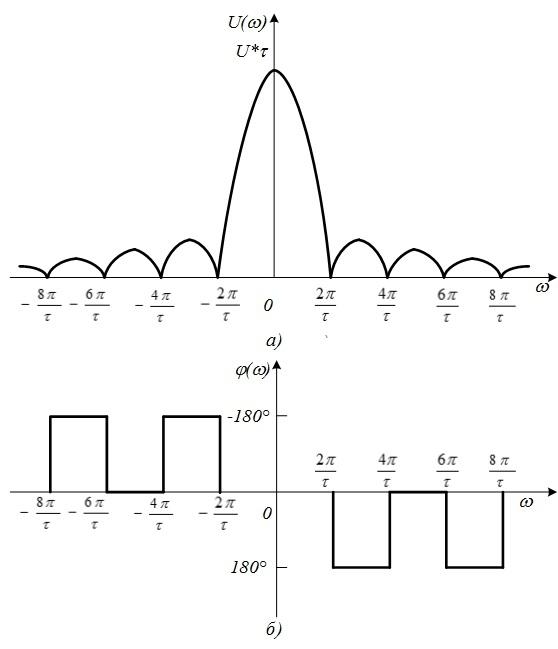
Рис.4.16.
Спектральные плотности (спектры) амплитуд
(а) и фаз (б)
прямоугольного импульса

Определимспектральную плотность амплитудпрямоугольного импульса,
изображенного на (рис.4.17),
если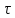= 1 мс,U
=10 В.

Комплексную
спектральную плотность прямоугольного
импульса (рис. 4.17) определим, используя
прямое преобразование Фурье (4.27):

Рис. 4.17. Прямоугольный
импульс

Полученное выражение

отличается
от комплексной спектральной плотности
(4.35) прямоугольного импульса,
изображенного на (рис. 4.14), множителем,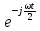
учитывающим запаздывание сигнала
(рис. 4.17) на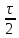и
влияющим только на спектральную
плотность фаз.

Спектральная
плотность амплитуд – это модуль
комплексной спектральной плотности,
поэтому

Обратим внимание
на то, что спектральная плотность
амплитуд
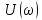
прямоугольных импульсов, изображенных
на рис. 4.14 и 4.17, рассчитывается по одной
и той, же формуле. Это означает, что
графики спектральной плотности амплитуд
импульсов также совпадают (рис. 4.16,а).

Построим график
Для этого прежде всего рассчитаем
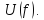
значение спектральной плотности
амплитуд на нулевой частоте, которое
равно площади прямоугольного импульса:

Рис.
4.18. Спектральная плотность амплитуд
прямоугольного импульса

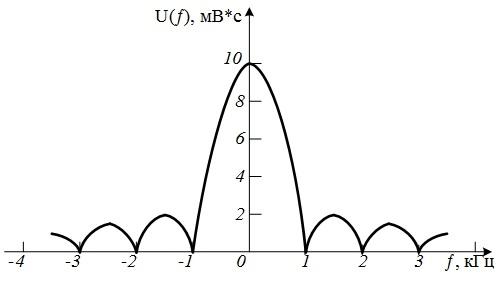
Частоты f,
на который
спектральная плотность обращается в
нуль, можно найти из соотношения

Эти частоты равны
,
т.е. 1;
2; 3 кГц и т.д. На частотах 1,5 и 2,5 кГц
лепестки функцииU(f)
принимают
максимальные значения, равные
соответственно 2 и 1,3 мВ-с. График
спектральной плотности амплитуд приведен
на рис. 4.18.

Найдемкомплексную спектральную плотностьтреугольного импульса, изображенного
на рис. 4.19, на частотеf
= 200 Гц,
еслиU
=10 В,=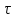
5 мс.

Сигнал u(t)можно записать следующим образом:

Комплексную
спектральную плотность импульса (рис.
4.19) рассчитываем, используя формулу
(4.27):

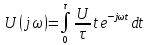
Берем интеграл по
частям и получаем

На частоте f
=200 Гц комплексная спектральная плотность

равна 8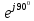, т.е. спектральная плотность амплитуд
равна8мВ·с, а спектральная плотность фаз равна
90°.

Рис.
4.19. Треугольный импульс

Из прямого
преобразования Фурье легко определить
спектры типовых, часто встречающихся
в технике импульсов. Рассмотрим
некоторые из них.

Импульс
включения.При анализе переходных процессов в
электрических цепях используется
импульс включения (единичная функция)
(рис. 4.20), который возникает при подключении
к цепи источника постоянного
напряжения:

Строго говоря, эта
функция не удовлетворяет условиям
интегрирования по Фурье, поэтому
воспользуемся следующим приемом:
умножим ее на «гасящий» множитель
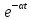
, а затем после интегрирования перейдем
к пределу при

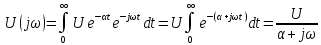
Совершая предельный
переход, получаем спектральную плотность
импульса включения:

Рис. 4.20. Импульс
включения

Рис. 4.21. Спектры
амплитуд (а) и фаз (б) импульса включения

Спектральная
плотность амплитуд при этом
,
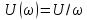
а спектральная плотность фаз=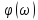
-90°. Графики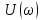ипоказаны на рис. 4.21.

-импульс.Этот импульс является математической
моделью очень узкого и большого по
амплитуде импульса (рис. 4.22,а):

удовлетворяющему
условию

,
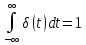
(4.36,б)

т.е. площадь его
равна единице.

Для
нахождения спектра
-импульса
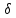
воспользуемся прямым преобразованием
Фурье

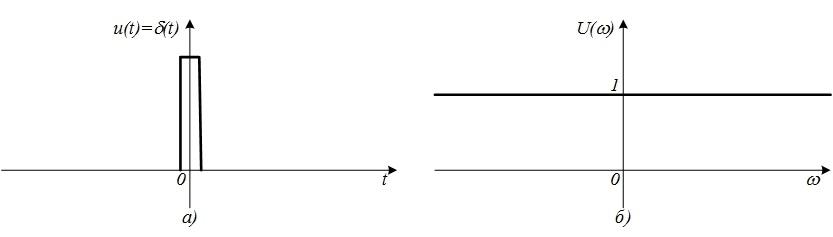
Рис. 4.22.
-импульс
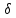
(a)
и его спектр (б)

Так как второе
слагаемое равно нулю (в силу нечетности
подынтегрального выражения), то

В силу свойства
(4.36, а) -импульса подынтегральное
выражение существует только при t
=0,
а это означает, что согласно (4.36, б)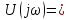1. График спектра -импульса приведен на
рис. 4.22,б.

Обратное
преобразование Фурье для -импульса
имеет вид

Так как спектр
—импульса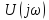= 1, то

Рис. 4.22. Постоянное
напряжение (а)и его спектр (б)

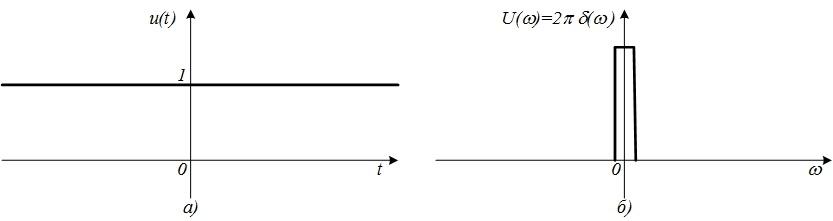
Постоянное
напряжение U
=1 В существует во все моменты времени,
а не только приt
≥0.

Учитывая
взаимозаменяемость параметров t
и,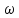
выражение (4.37, б) можно переписать в
виде

Сравнивая его с
выражением для спектра постоянного
напряжения

приходим к выводу,
что
=

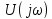
Таким образом,
спектр постоянного напряжения (рис.
4.23, б) равен нулю на всех частотах, кроме
=0,
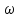
где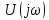обращается в бесконечность.

Экспоненциальный
импульс.Переходные процессы в цепях с одним
реактивным элементом описываются
экспоненциальной функцией (рис. 4.24,а)

Спектральная
плотность этого импульса

где спектр амплитуд

а спектр фаз

Графики
ипоказаны
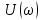
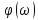
на рис. (4.24,бив).

Рис. 4.24. Экспоненциальный
импульс (а) и его спектры амплитуд (б) и
фаз (в).

Для вычисления
спектров при различных преобразованиях
сигналов можно воспользоваться теоремами
о спектрах. Остановимся на физической
интерпретации основных теорем
спектрального анализа.

Спектр
суммы сигналов(теорема линейности). Если сигналы,
спектры которых известны, суммируются,
то для вычисления результирующего
спектра можно воспользоваться теоремой
линейности:спектр
суммы сигналов равен сумме спектров
этих сигналов.

Итак,
если

то

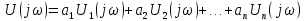
Сдвиг
сигнала во времени(теорема запаздывания). Часто при
обработке сигнала приходится осуществлять
его задержку на время: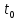

В этом случае
спектр задержанного сигнала умножается
на множитель
:

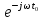
При
запаздывании сигнала на время
его
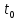
спектральная плотность амплитуд остается
неизменной, а спектральная плотность
фаз изменяет свой наклон на величину

Дифференцирование
и интегрирование сигнала.
Если сигнал
подвергается
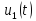
дифференцированию,

то его спектр
умножается на оператор
:

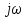
где
— значение сигналав
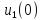
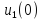
момент времениt
=0.

При интегрировании
сигнала

его спектр делится
на
(при условии=0):

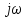
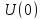
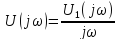
Изменение
масштаба сигнала(теорема подобия). Пусть сигнал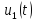имеет
спектр.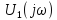
Изменение масштаба по шкале времени

приводит к изменению
масштаба спектра по шкале частот:

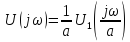
Сжатие
сигнала во времени приводит к расширению
его спектра и,
напротив,
растяжение сигнала
— к
сужению спектра. Другими
словами, чем
короче импульс, тем шире его спектр.

Построимграфики спектральных плотностей
амплитуд прямоугольных импульсов,
имеющих одинаковую амплитудуU,
но разные
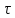
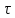
длительности т:а)= 2 мс,б)=
4 мс,в)
= 1 мс (рис. 4.25).

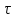
Ранее было
установлено, что спектральная плотность
амплитуд U(f) прямоугольного
импульса изменяется по закону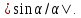ЗначениеU(f)
на
нулевой частоте равно площади импульсаU(0)
=U,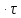
а нули
функцииU(f)
располагаются
на частотах, кратных величинам1/.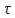

Рис. 4.25. Прямоугольный
импульс и его спектр при длительности
импульса 2 мс (а), 4 мс (б) и 1 мс (в)

Для импульса,
имеющего параметры U
= 1 В и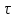= 2 мс, получаемU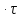(0)
=U=2 Вмс,
нули расположены на частотах 0,5; 1;
1,5 кГц и т.д. График спектральной плотности
амплитуд такого импульса изображен на
рис. 4.25,а.

Увеличение
длительности импульса в 2 раза (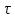= 4 мс) приводит, в соответствии с теоремой
подобия, к сужению спектра в 2 раза.
Это означает, что нули спектраU(f)
располагаются
на частотах, кратных 1/= 0,25 кГц, а значениеU(0)
=U
=4 В·мс.

График спектральной
плотности амплитуд импульса, имеющего
параметры U
= 1 В и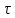= 4 мс, изображен на рис. 4.25, б.

Уменьшение
длительности импульса в 2 раза (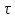=1
мс) по сравнению с исходным
приводит к расширению спектра, т.е.
нули располагаются на частотах 1; 2; 3 кГц
и т.д., а значение спектра на нулевой
частотеU(0) = 1 В⋅мс.
ГрафикU(f)
прямоугольного
импульса с параметрамиU
=1 В и
=1
мс изображен на рис.
4.25,в.

Смещение
спектра сигнала(теорема модуляции). Эта теорема
является двойственной (дуальной) по
отношению к теореме запаздывания. Если
спектр сигнала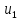(t)
сместить вниз или вверх по шкале частот
на величину
,т.е.,
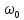
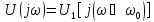
то
это соответствует умножению сигнала
на комплексную гармонику с частотой: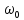

u(t)=

Другими
словами, при
умножении сигнала на гармоническое
колебание с частотой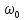спектр
сигнала смещается по шкале частот на
величину.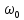

Найдем
спектр
радиоимпульса, изображенного на (рис.
4.26, б).

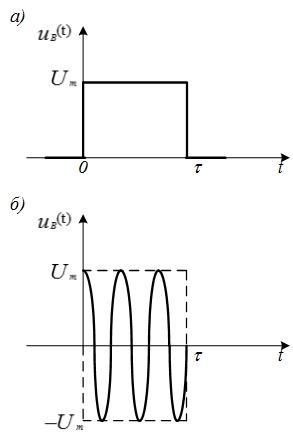
Радиоимпульс
можно получить как произведение
видеоимпульса прямоугольной формы
(рис. 4.26, а)
и
гармонического колебания
.

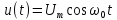
Воспользовавшись
формулой Эйлера

получаем

Обозначив
спектр видеоимпульса как

и,
применив теорему смещения, находим
спектр

радиоимпульса:

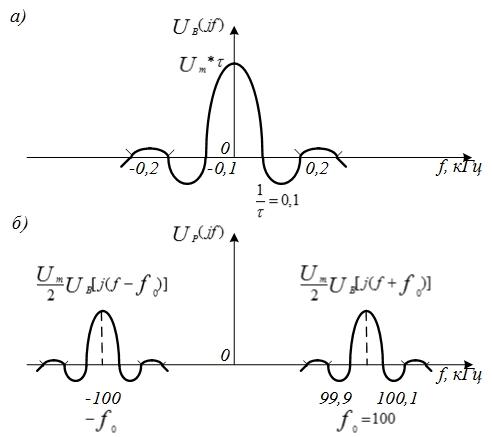
На
рис. 4.27, а
изображен
спектр видеоимпульса, имеющего
длительность
= 10 мс. На рис. 4.27,б
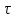
изображен
спектр радиоимпульса с частотой
гармонических колебаний
= 100 кГц.

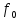
Рис
4.26. Видеоимпульс (а)
и
радиоимпульс (б)

Рис.
4.27. Спектры видеоимпульса (а) и радиоимпульса
(б)

Перемножение
двух сигналов
(теорема свертки спектров).Спектр
произведения сигналов соответствует
свертке их спектров. Так, если

то

Свертка
двух сигналов
(теорема о произведении спектров
сигналов). Спектр
свертки двух сигналов соответствует
произведению их спектров. Так,
если

(4.38)

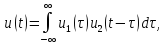
то

Между
спектрами непериодического и периодического
сигналов существует связь: графики
модуля спектральной плотности
непериодического сигнала и огибающей
дискретного спектра аналогичного
периодического сигнала совпадают
по форме и отличаются только масштабом.
Из
уравнения (4.22)

следует,
что если периодически повторять одиночным
импульс, то амплитуды
и
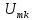
фазы
получающегося
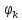
при этом дискретного спектра можно
определить, заменив в комплексной
спектральной плотности U(j)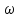
одиночного импульса текущую частоту
на значения частот гармоники
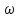
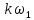
пронумеровав эту плотность относительно
величины полупериода. Таким образом,

Если
мы будем периодически с периодом Т
повторять прямоугольный импульс,
изображенный на рис. 4.14, то в соответствии
с последним выражением можно записать
для комплексного спектра
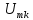
периодической последовательности
прямоугольных импульсов, вытекающее
непосредственно из спектральной
плотности (4.35) одиночного прямоугольного
импульса при замене частоты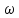на

Используя
понятие скважности
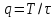
последовательности прямоугольных
импульсов и учитывая, что,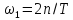
получаем комплексный спектр

Можно
обобщить о преобразовании Фурье сигнала
s(t)
и его изображения
:

;
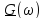
функции,
сопряженные по Фурье (4.27), (4.28)

функции,
свернутые по времени

энергия периодического
сигнала

Свойства
преобразования Фурье сведены в таблицу
4.2

Таблица
4.2

№

п/

Характер,
свойство

преобразования

Вид
колебания

Спектр

Примечания

Свойство
симметрии

Инверсия
аргумента

функции

Свойство

линейности

Изменение
масштаба

времени

Дифференцирование

по
времен

n-
кратное

дифференцирование

по
времени

n-
кратное

дифференцирование

по
частоте

Интегрирование

по
времени

Свойство
временного

сдвига
(теорема

запаздывания)

Свойство
частотного

сдвига

Умножение
на

гармоническую

функцию

Произведение

двух
функций

Свертка
функции

по
времени

Автокорреляционная

функция
(АКФ)

Взаимная

корреляционная

функция
АКФ

—

—
знак инверсии аргумента

—
знак комплексной

сопряженности

A,
B
– постоянные переменные

a
– постоянная

a>1
– сжатие сигнала

и
растяжение спектра

a<1
– растяжение

сигнала

и
сжатие спектра

—

Результат
справедлив,

если

– постоянная
величина

Перенос
спектра на частоту

—

АКФ
и спектр энергии

финитного
сигнала s

ВКФ
и спектр взаимной

энергии

финитных

сигналов

Основные
положения изложенных в п. 4.5 материалов:

Спектр
непериодического сигнала является
непрерывным; он состоит из бесконечно
большого числа частотных составляющих
с бесконечно близкими смежными частотами
и с бесконечно малыми амплитудами.
Чем
короче импульс любой формы, тем шире
его спектр.
Запаздывание
сигнала приводит лишь к изменению
наклона характеристики спектра фаз.
Для
смещения спектра по шкале частот
необходимо «заполнить» сигнал
гармоническим колебанием.
Операция
свертки сигналов ведет к перемножению
их спектров.
Дискретный
спектр «вписывается» в огибающую
непрерывного спектра.

Источник

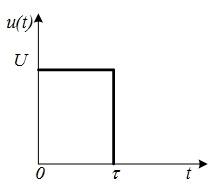
В качестве примера рассмотрим спектральную плотность импульса прямоугольной формы (рис 1.7 А).

В соответствии с определением спектральной плотности для импульса длительности t и амплитудой E будем иметь . Используя формулу Эйлера получим . Эта функция имеет вид показанный на рис. 1.7 Б.

Спектральная плотность обращается в нуль когда , т. е. , K=1, 2, 3 …, откуда , и точки пересечения графика спектральной плотности с осью w есть ….

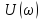
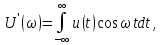
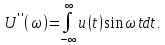
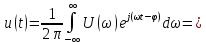
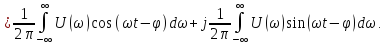
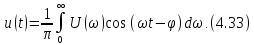
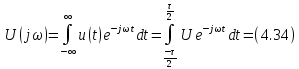
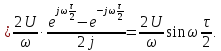
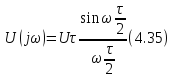
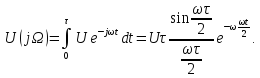
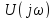
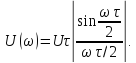
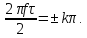
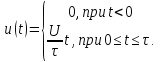
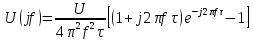
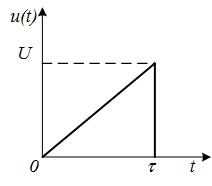
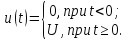
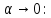
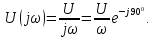
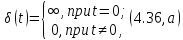
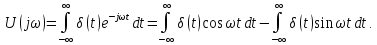
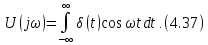
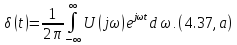
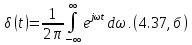
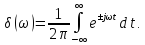
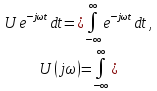
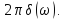
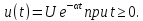
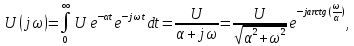
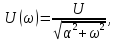
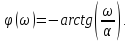
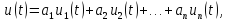
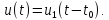
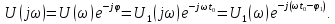
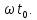
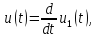
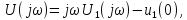
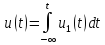
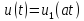
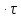
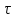
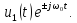
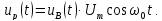
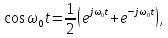
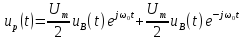
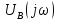
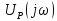
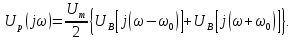
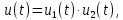
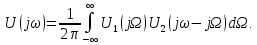
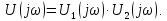
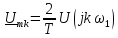
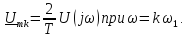
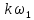
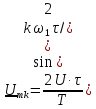
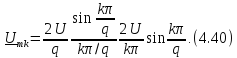
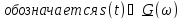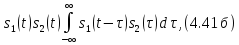
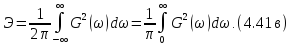
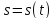
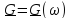
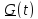
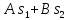
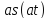
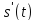
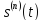
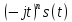
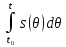
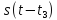
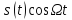
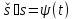
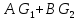
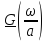
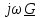
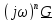
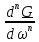
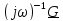
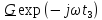
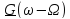
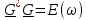
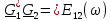
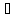Источник

Спектральные плотности некоторых сигналов

Спектральные плотности амплитуд и фаз непериодических сигналов