Как найти спираль архимеда - Исправление недочетов и поиск решений вместе с Examum.ru

Спираль Архимеда

Опубликовано 02.05.2021

Спираль Архимеда – это линия, которая напоминает спираль и выражается определенным уравнением. Открытие кривой приписывается Конону Самосскому, ученику Архимеда. В честь его учителя – спираль названа спиралью Архимеда. Давайте же разберемся с этой линией и попробуем ее самостоятельно построить.

Спираль Архимеда

Линия, которую называют спиралью Архимеда, строится в полярных координатах и определяется уравнением:

Здесь – это положительное число, – полярный радиус.

Другие названия: равносторонняя спираль, неоид.

Как построить спираль Архимеда

Чтобы построить спираль Архимеда, нужно присваивать некоторые произвольные значения и определять . Построим таблицу значений:


0	0
$frac{pi}{2}$	$frac{pi}{2}a$

$frac{3pi}{2}$	$frac{3pi}{2}a$

Данная таблица показывает, что при возрастании угла в арифметической прогрессии с разностью $frac{pi}{2}$ полярный радиус возрастает тоже в арифметической прогрессии с разностью $a frac{pi}{2}$ . Кроме того, заметим, что всякой точке этой линии с положительными координатами соответствует на этой линии точка , то есть спираль Архимеда симметрично расположена относительно прямой, проходящей через полюс перпендикулярно к полярной оси.

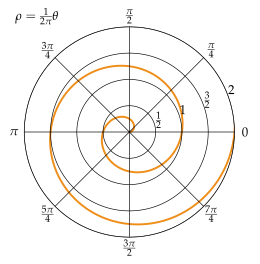
На рисунке изображена спираль Архимеда – сплошной линией изображена ветвь, соответствующая положительным значениям , а пунктирной – отрицательным.

Благодаря этой спирали можно рассчитать площадь круга, по записям Архимед умел это делать и знал, что “поверхность первого витка спирали равна одной трети поверхности круга, радиус которого равен длине, пройденной точкой на прямой, во время рисования первого витка”.

Спираль Архимеда – это траектория точки, равномерно движущейся по прямой линии плоскости, причем эта линия равномерно поворачивается вокруг одной из своих точек.

Спираль Архимеда активно используется в искусстве, посмотрите:

Видео – как нарисовать спираль Архимеда

( 4 оценки, среднее 5 из 5 )

Источник

From Wikipedia, the free encyclopedia

Three 360° loops of one arm of an Archimedean spiral

The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation

with real numbers a and b. Changing the parameter a moves the centerpoint of the spiral outward from the origin (positive a toward θ = 0 and negative a toward θ = π) essentially through a rotation of the spiral, while b controls the distance between loops.

From the above equation, it can thus be stated: position of particle from point of start is proportional to angle θ as time elapses.

Archimedes described such a spiral in his book On Spirals. Conon of Samos was a friend of his and Pappus states that this spiral was discovered by Conon.^[1]

Derivation of general equation of spiral[edit]

A physical approach is used below to understand the notion of Archimedean spirals.

Suppose a point object moves in the Cartesian system with a constant velocity v directed parallel to the x-axis, with respect to the xy-plane. Let at time t = 0, the object was at an arbitrary point (c, 0, 0). If the xy plane rotates with a constant angular velocity ω about the z-axis, then the velocity of the point with respect to z-axis may be written as:

The xy plane rotates to an angle ωt (anticlockwise) about the origin in time t. (c, 0) is the position of the object at t = 0. P is the position of the object at time t, at a distance of R = vt + c.

${displaystyle {begin{aligned}|v_{0}|&={sqrt {v^{2}+omega ^{2}(vt+c)^{2}}}\v_{x}&=vcos omega t-omega (vt+c)sin omega t\v_{y}&=vsin omega t+omega (vt+c)cos omega tend{aligned}}}$

Here vt + c is the modulus of the position vector of the particle at any time t, v_x is the velocity component along the x-axis and v_y is the component along the y-axis. The figure shown alongside explains this.

${displaystyle {begin{aligned}int v_{x},dt&=x\int v_{y},dt&=yend{aligned}}}$

The above equations can be integrated by applying integration by parts, leading to the following parametric equations:

${displaystyle {begin{aligned}x&=(vt+c)cos omega t\y&=(vt+c)sin omega tend{aligned}}}$

Squaring the two equations and then adding (and some small alterations) results in the Cartesian equation

${displaystyle {sqrt {x^{2}+y^{2}}}={frac {v}{omega }}cdot arctan {frac {y}{x}}+c}$

(using the fact that ωt = θ and θ = arctan y/x) or

${displaystyle tan left(left({sqrt {x^{2}+y^{2}}}-cright)cdot {frac {omega }{v}}right)={frac {y}{x}}}$

Its polar form is

${displaystyle r={frac {v}{omega }}cdot theta +c.}$

Arc length and curvature [edit]

Osculating circles of the Archimedean spiral, tangent to the spiral and having the same curvature at the tangent point. The spiral itself is not drawn, but can be seen as the points where the circles are especially close to each other.

Given the parametrization in cartesian coordinates

the arc length from $theta _{1}$ to $theta _{2}$ is

${displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+ln left(theta +{sqrt {1+theta ^{2}}}right)right]_{theta _{1}}^{theta _{2}}}$

or, equivalently:

${displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+operatorname {arsinh} theta right]_{theta _{1}}^{theta _{2}}.}$

The total length from to ${displaystyle theta _{2}=theta }$ is therefore

${displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+ln left(theta +{sqrt {1+theta ^{2}}}right)right].}$

The curvature is given by

${displaystyle kappa ={frac {theta ^{2}+2}{b(theta ^{2}+1)^{frac {3}{2}}}}}$

Characteristics[edit]

Archimedean spiral represented on a polar graph

The Archimedean spiral has the property that any ray from the origin intersects successive turnings of the spiral in points with a constant separation distance (equal to 2πb if θ is measured in radians), hence the name «arithmetic spiral». In contrast to this, in a logarithmic spiral these distances, as well as the distances of the intersection points measured from the origin, form a geometric progression.

The Archimedean spiral has two arms, one for θ > 0 and one for θ < 0. The two arms are smoothly connected at the origin. Only one arm is shown on the accompanying graph. Taking the mirror image of this arm across the y-axis will yield the other arm.

For large θ a point moves with well-approximated uniform acceleration along the Archimedean spiral while the spiral corresponds to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity^[2] (see contribution from Mikhail Gaichenkov).

As the Archimedean spiral grows, its evolute asymptotically approaches a circle with radius |v|/ω.

General Archimedean spiral[edit]

Sometimes the term Archimedean spiral is used for the more general group of spirals

${displaystyle r=a+bcdot theta ^{frac {1}{c}}.}$

The normal Archimedean spiral occurs when c = 1. Other spirals falling into this group include the hyperbolic spiral (c = −1), Fermat’s spiral (c = 2), and the lituus (c = −2).

Applications[edit]

One method of squaring the circle, due to Archimedes, makes use of an Archimedean spiral. Archimedes also showed how the spiral can be used to trisect an angle. Both approaches relax the traditional limitations on the use of straightedge and compass in ancient Greek geometric proofs.^[3]

Mechanism of a scroll compressor

The Archimedean spiral has a variety of real-world applications. Scroll compressors, used for compressing gases, have rotors that can be made from two interleaved Archimedean spirals, involutes of a circle of the same size that almost resemble Archimedean spirals,^[4] or hybrid curves.

Archimedean spirals can be found in spiral antenna, which can be operated over a wide range of frequencies.

The coils of watch balance springs and the grooves of very early gramophone records form Archimedean spirals, making the grooves evenly spaced (although variable track spacing was later introduced to maximize the amount of music that could be cut onto a record).^[5]

Asking for a patient to draw an Archimedean spiral is a way of quantifying human tremor; this information helps in diagnosing neurological diseases.

Archimedean spirals are also used in digital light processing (DLP) projection systems to minimize the «rainbow effect», making it look as if multiple colors are displayed at the same time, when in reality red, green, and blue are being cycled extremely quickly.^[6] Additionally, Archimedean spirals are used in food microbiology to quantify bacterial concentration through a spiral platter.^[7]

They are also used to model the pattern that occurs in a roll of paper or tape of constant thickness wrapped around a cylinder.^[8]^[9]

Many dynamic spirals (such as the Parker spiral of the solar wind, or the pattern made by a Catherine’s wheel) are Archimedean. For instance, the star LL Pegasi shows an approximate Archimedean spiral in the dust clouds surrounding it, thought to be ejected matter from the star that has been shepherded into a spiral by another companion star as part of a double star system.^[10]

References[edit]

^ Bulmer-Thomas, Ivor. «Conon of Samos». Dictionary of Scientific Biography. Vol. 3. p. 391.
^ Sloane, N. J. A. (ed.). «Sequence A091154». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Boyer, Carl B. (1968). A History of Mathematics. Princeton, New Jersey: Princeton University Press. pp. 140–142. ISBN 0-691-02391-3.
^ Sakata, Hirotsugu; Okuda, Masayuki. «Fluid compressing device having coaxial spiral members». Retrieved 2006-11-25.
^ Penndorf, Ron. «Early Development of the LP». Archived from the original on 5 November 2005. Retrieved 2005-11-25.. See the passage on Variable Groove.
^ Ballou, Glen (2008), Handbook for Sound Engineers, CRC Press, p. 1586, ISBN 9780240809694
^ Gilchrist, J. E.; Campbell, J. E.; Donnelly, C. B.; Peeler, J. T.; Delaney, J. M. (1973). «Spiral Plate Method for Bacterial Determination». Applied Microbiology. 25 (2): 244–52. doi:10.1128/AEM.25.2.244-252.1973. PMC 380780. PMID 4632851.
^ Peressini, Tony (3 February 2009). «Joan’s Paper Roll Problem» (PDF). Archived from the original (PDF) on 3 November 2013. Retrieved 2014-10-06.
^ Walser, H.; Hilton, P.; Pedersen, J. (2000). Symmetry. Mathematical Association of America. p. 27. ISBN 9780883855324. Retrieved 2014-10-06.
^ Kim, Hyosun; Trejo, Alfonso; Liu, Sheng-Yuan; Sahai, Raghvendra; Taam, Ronald E.; Morris, Mark R.; Hirano, Naomi; Hsieh, I-Ta (March 2017). «The large-scale nebular pattern of a superwind binary in an eccentric orbit». Nature Astronomy. 1 (3): 0060. arXiv:1704.00449. Bibcode:2017NatAs…1E..60K. doi:10.1038/s41550-017-0060. S2CID 119433782.

External links[edit]

Jonathan Matt making the Archimedean spiral interesting — Video : The surprising beauty of Mathematics — TedX Talks, Green Farms
Weisstein, Eric W. «Archimedes’ Spiral». MathWorld.
archimedean spiral at PlanetMath.
Page with Java application to interactively explore the Archimedean spiral and its related curves
Online exploration using JSXGraph (JavaScript)
Archimedean spiral at «mathcurve»

Источник

Спираль Архимеда

Первый ученый который открыл и изучил свойства этой линии, был великий математик и философ из древней Греции, Архимед. Его именем она и была названа.

Спираль Архимеда

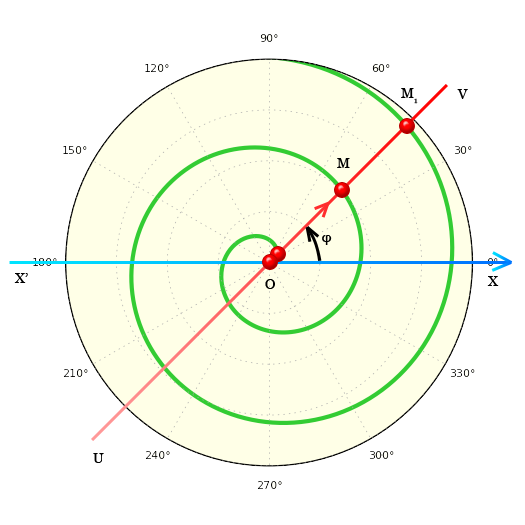
Построение спирали Архимеда

Некоторая прямая UV изначально совпадает с прямой XX`. Прямая UV равномерно вращается относительно точки O. По прямой UV равномерно перемещается точка M отдаляясь от точки O. В результате точка M, перемещаясь по вышеуказанным правилам, описывает линию — спираль Архимеда.

Шаг спирали Архимеда

При повороте прямой UV из любого положения на некоторый угол Δφ точка M смещается на расстояние Δρ. Смещение MM₁ происходит за один оборот прямой UV, и всегда равно одному и тому же числу. Это число называется шагом спирали Архимеда

[ a = MM_1 ]

Полярное уравнение спирали Архимеда

[ frac{ρ}{a} = frac{φ}{2π} ]

В этом уравнении можно перейти от шага спирали Архимеда a к параметру спирали Архимеда k

[ k = frac{a}{2π} ]

Тогда уравнение спирали примет вид

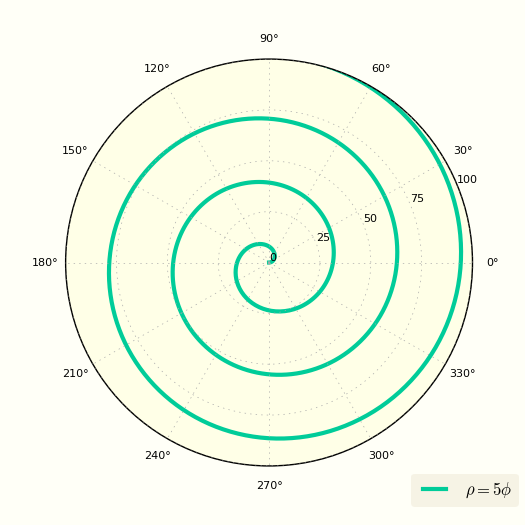
[ ρ = kφ ]

Построить спираль Архимеда

Спираль Архимеда	стр. 123

Источник

Наверх

Построение Спираль Архимеда начинается с представления что это такое?

Представляет собой плоскую кривую линию, движущаяся равномерно с постоянным углом по кривой траектории от центра до радиуса окружности.

Алгоритм построение Спираль Архимеда:

1.) Построение начинается с окружности необходимого диаметра.

2.) Делится окружность на 12 равных частей и нумеруется.

3.) Горизонтальная линия также делится на 12 равных отрезков.

4.) Чертятся вспомогательные окружности, таким образом, чтобы начало имело с номера на горизонтальной прямой и заканчивалось на отрезке окружности с той же цифрой.

5.) Полученные точки соединяются плавной линией (с помощью инструмента лекало).

Смотрите чертеж Спираль Архимеда. Диаметр окружности 12 см.

Также посмотрите видео:

Просмотрели 1 612

Источник

Содержание:

Пример с решением
Спираль Архимеда
Гиперболическая спираль
Вычисление площадей. Полярные координаты
Примеры с решением

До сих пор для определения положения точки на плоскости мы пользовались ее прямоугольными координатами. Теперь мы рассмотрим другую важную систему координат — полярную.

Эта система состоит из некоторой точки О (полюса) и проходящей через нее оси Ох (полярной оси). С помощью указанных Объектов можно определить положение любой точки М. Для этого соединим точку М с полюсом О и найдем угол 0, который луч ОМ образует с положительным направлением полярной оси Ох, и длину г этого луча **) ОМ (рис. 80).

Числа называются соответственно аргументом и радиусом-вектором точки М. Общее их название — полярные координаты этой точки.

Тот факт, что точка М имеет полярные координаты , обычно записывают в виде Эта запись мало удачна, так как неясно, что означает символ М (3, 2): точку, у которой абсцисса и ордината равны соответственно 3 и 2, или же точку, у которой эти числа являются радиусом-вектором и аргументом.

В дальнейших частях книги эта неясность будет устраняться сопровождающими пояснениями, а в данном параграфе мы введем обозначение М, хотя оно и не является общепринятым.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Полярная система координат имеет некоторые недостатки по сравнению с прямоугольной.

Прежде всего, аргументом полюса может считаться любое число. Так*), суть различные обозначения одной и той же точки — полюса. Далее, и у любой другой точки плоскости имеется бесконечное множество аргументов, потому что прибавление, к аргументу точки угла **) не меняет этой точки. Поэтому, представляют собой одну и ту же точку. Иногда рассматривают и отрицательные значения радиуса-вектора.

Например, под понимают точку (рис. 81),

которая получается в результате следующих построений: сначала поворачивают полярную ось на 60° (как всегда против часовой стрелки). После этого на оси (в ее новом положении!) откладывают в отрицательном направлении отрезок 2. Полученная точка и будет точкой . Нетрудно, однако, понять, что ту же точку М можно записать и так:

Иными словами, ту же точку можно задать, пользуясь положительным значением радиуса-вектора. Аналогичным образом, прибавив к аргументу 180°, мы всегда можем превратить отрицательный радиус-вектор в положительный. Имея это в виду, мы раз навсегда условимся считать радиус-вектор любой точки неотрицательным, п°2. Расстояние между двумя точками.

Возможно вам будут полезны данные страницы:

Пример с решением

Найти расстояние между точками и Решение:

По теореме косинусов из треугольника (рис. 82) находим (1)

Связь между полярными и прямоугольными координатами. Пусть на плоскости построены две системы координат: полярная и прямоугольная, причем полюс и полярная ось первой совпа-абсцисс второй. Возьмем на

плоскости любую точку М (рис. 83), и пусть ее полярные и прямоугольные координаты соответственно будут . Как видно из треугольника ОМА, справедливы формулы (2) выражающие прямоугольные координаты через полярные. Можно доказать, что формулы (2) верны не только для простейшего положения точки М, изображенного на рис. 83, но и при любом ее положении. Мы, однако, на этом не будем останавливаться.

Из формул (2) (или непосредственно из треугольника ОМА) следует, что (3) причем согласно сделанному выше замечанию перед радикалом мы всегда будем брать знак

Наконец, из (2) следует, что (4) Формула (4) не позволяет находить угол ибо по тангенсу угла нельзя однозначно определить угол. Но, зная мы знаем и четверть, в которой лежит угол что в соединении с формулой (4) уже позволяет найти в с точностью до 360°.

Спираль Архимеда

Мы знаем, что различные линии на плоскости определяются с помощью уравнений, которым должны удовлетворять прямоугольные координаты точек линии. Но совершенно то же будет справедливо, если говорить не о прямоугольных, а о полярных координатах точек. Прямую, эллипс, параболу, гиперболу удобнее изучать по их уравнениям в прямоугольных координатах. Однако для некоторых линий более удобным средством изучения служат их уравнения именно в полярных координатах. Такой линией является, например, спираль Архимеда.

Определение. Спиралью Архимеда называется линия, описываемая точкой, равномерно двигающейся по лучу, который сам равномерно вращается вокруг своего начала.

Мы будем предполагать, что в начальный момент точка М, описывающая спираль, находится в начале луча, упомянутого в определении.

Выведем уравнение спирали Архимеда. Для этого надо прежде всего выбрать определенную систему координат. Мы возьмем за полюс начало луча, по которому движется точка М, а за положительное направление полярной оси — начальное положение этого луча.

Обозначим соответственно через шит» скорость вращения луча и скорость ‘Движения точки М вдоль по лучу. Поскольку оба движения равномерны, [то есть угол, на который поворачивается луч за единицу времени, a — расстояние, которое за единицу времени точка М, описывающая спираль, проходит вдоль по лучу.

Положение точки М мы будем определять ее полярными координатами В начальный момент . В момент же (т. е. в момент, отделенный от начального промежутком времени*) в t единиц) Стало быть, для любого момента t

Обозначая (постоянное!) число через находим, что уравнение спирали Архимеда имеет вид Таким образом, при движении точки по спирали Архимеда ее радиус-вектор изменяется прямо пропорционально аргументу. Это позволяет построить спираль Архимеда. На рис. 84 отмечены точки А, В, С, D, Е, F, О, Н, I, К, L спирали, аргументы которых равны соответственно 45°, 90°, 135°, 495°. Ясно, что

Гиперболическая спираль

Определение. Гиперболическая спираль есть такая линия, что полярные координаты точки, движущейся по ней, изменяются обратно пропорционально друг другу. Иными словами, гиперболическая спираль есть линия, соответствующая уравнению Применяя построения, сходные с теми, какие мы употребляли для спирали Архимеда, нетрудно построить ряд точек гиперболической спирали. Она имеет вид, изображенный на рис. 85. Легко понять,

что с безграничным увеличением аргумента точки М радиус-вектор этой точки будет приближаться неограниченно к нулю. Это показывает, что гиперболическая спираль, совершая бесконечное множество оборотов вокруг полюса, неограниченно приближается к нему, хотя никогда его и не достигает. Указанное обстоятельство выражают, говоря, что полюс служит асимптотической точкой гиперболической спирали.

Чтобы установить еще одно свойство гиперболической спирали, введем также прямоугольную систему координат, начало которой совпадает с полюсом, а ось абсцисс с полярной осью. Как мы знаем, для любой точки будет

Значит, для точек, лежащих на спирали (5), окажется

В следующей главе будет доказано, что по мере приближения 0 к нулю отношение стремится к 1. Но если приближается

к нулю, то согласно (5) точка будет уходить по спирали в бесконечность (так как будет безгранично возрастать). Таким образом, из (6) следует, что ордината у точки М, уходящей в бесконечность по гиперболической спирали, стремится к числу . Стало быть, прямая служит асимптотой спирали (5).

Вычисление площадей. Полярные координаты

Пусть из центра круга радиуса под углом (радианов!) проведены два радиуса. Площадь полученного таким образом сектора (рис. 223), как известно *), равна Этот результат позволяет решить следующую задачу: найти площадь сектора (уже не кругового!), ограниченного лучами и кривой (рис. 224). Именно, вырежем из нашего

сектора элементарный сектор, образованный лучами, наклоненными к полярной оси под углами (рис. 224). Если этот элементарный сектор принять за круговой**) [вырезанный из круга радиуса то его площадь согласно (5) будет Отсюда При использовании формулы надо заменять функцией входящей в уравнение .

Примеры с решением

Пример 1:

Найти площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда (рис. 225). Решение:

Здесь Значит, Этому результату можно дать наглядную формулировку. Именно, точка А пересечения спирали с полярной осью имеет радиус-вектор Стало быть, круг радиуса ОА имеет площадь Из сопоставления этого равенства с (7) получается открытое еще Архимедом предложение: площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна у площади круга с радиусом, равным наибольшему из радиусов-векторов точек витка.

Пример 2:

Найти площадь F фигуры, ограниченной лемнискатой Решение:

Еще в первой главе было показано, что в полярных координатах наша лемниската имеет уравнение Лемниската симметрична относительно обеих осей, и та часть ее, которая расположена в первом координатном угле, лежит между лучами и Значит, площадь фигуры, ограниченной этой частью лемнискаты и осью (она заштрихована на рис. 226), равна