Вопросы
занятия:
·
разобрать, каким образом сравнивают выражения;
·
показать что такое двойное неравенство;
·
ввести понятия «строгое неравенство», «нестрогое неравенство».
Материал
урока
Прежде, чем приступить к рассмотрению новой темы,
вспомним, что:
Например, выражение 10(2 + 1,5) является числовым.
Выполнив действия этого числового выражения,
соблюдая правильный порядок действий, получим число 35, которое называют значением
данного числового выражения.
А теперь, чтобы разобраться, каким образом
сравнивают значения выражений, решим следующую задачу.
Результат сравнения можно записать в виде следующего
неравенства:
Таким образом, для любых двух числовых выражений
можно установить, равны их значения или не равны. Если они не равны, то можем
определить, какое из них больше и какое меньше.
Мы разобрались, как сравнить два числовых выражения.
А как же быть с выражениями, содержащими переменные.
Давайте сравним значения выражений:
Видим, что для разных значений переменных
результат сравнения выражений с переменными может оказаться различным.
Иногда перед нами может встать задача
установить, между какими числами заключено значение выражения.
Пример.
Пример.
Определение.
Решим упражнение.
Ещё одно упражнение.
Пример.
Как сравнить два выражения
Алгоритм решения задач по алгебре на тему «Как сравнить два выражения».
При сравнении чисел составляют их разность и выясняют, ка кое число получается в ответе – положительное, отрицательное или нуль.
Число а больше числа b, если разность чисел а – b положительное число: а > b, если а – b > 0.
Число а меньше числа b, если разность а – b отрицательное число: а < b, если а – b < 0.
Подробнее о сравнении чисел смотрите в конспекте «Числовые неравенства. Сравнение чисел».
АЛГОРИТМ
«Как сравнить два выражения»
- Составьте разность двух выражений и упростите (раскройте скобки, приведите подобные слагаемые).
- Определите знак полученной разности: если разность больше нуля, то первое выражение больше второго; если разность меньше нуля, то первое выражение меньше второго; если знак установить нельзя при всех значениях букв, входящих в разность, то нельзя утверждать, что одно из выражений больше другого при любых значениях букв.
ПРИМЕР 1. Даны выражения: 4b(b + 1) (I) и (2b + 7)(2b – 
1). Сравните значения выражений при b = –2; b = 10.
2). Можно ли утверждать, что при любом значении b значение первого выражения больше, чем значение второго?
Решение.
I. ⇒ 1). Если b = –2, то 4 • (–2)(–2 + 1) = –8 • (–1) = 8 (I)
2). (2 • (–2) + 7)(2 • (–2) – 
3). 8 – (–36) = 44; 44 > 0
II. ⇒ 1). Если b = 10, то 4 • 10 • (10 + 1) = 40 • 11 = 440 (I)
2). (2 • 10 + 7)(2 • 10 – 
3). 440 – 324 = 116; 116 > 0
В обоих случаях значение первого выражения больше значения второго.
III. Найдем разность первого и второго выражений (I) – (II):
4b(b + 1) – (2b + 7)(2b – 
Разность (I) и (II) выражений равна 6b + 56. Это выражение не при всех значениях b положительно. Например, при b = –10, –11, –12… значение выражения отрицательно. Поэтому нельзя утверждать, что мри всех значениях b значение (I) выражения больше значений (II) выражения.
ПРИМЕР 2. Верно ли неравенство (3х + 
Решение.
1). Преобразуем выражения, стоящие в левой и правой частях неравенства:
(3х +  2 > 3х(х + 16) (I) 2 > 3х(х + 16) (I)(3х)2 + 2 • 3х • 8 + 64 > 3х2 + 48х 9х2 + 48х + 64 > 3х2 + 48х (II)2). Составим разность:(3х +  2 – 3х(х + 16) = 9х2 +48х + 64 – (3х2 +48х) = 2 – 3х(х + 16) = 9х2 +48х + 64 – (3х2 +48х) == 9х2 +48х + 64 – 3х2 – 48х = 6х2 +64 (III) |
(a + b)2 = a2 + 2 ab + b2 если a – b > 0, то а > b |
3). 6х2 + 64 > 0 при всех значениях х, так как х2 ≥ 0 при любых значениях х; значит, неравенство (III) верно при любых значениях х, значит, и неравенство (I) верное.
Ответ: неравенство верно.
ПРИМЕР 3. Докажите, что а + 1/а ≥ 2, а > 0.
Доказательство.
| Составим разность и упростим:
что и требовалось доказать. |
если а – b ≥ 0, то а ≥ b a > 0 по условию (а — 1)2 > 0, при а = 1 получаем нуль |
ПРОВЕРЬ СЕБЯ
- Сравните числа х и у, если разность х – у равна: 1) –3; 2) 5; 3) 0.
Посмотреть ОТВЕТ
Ответ: 1) х < у; 2) х > у; 3) х = у.
- Что больше: a3 + b3 или ab(a + b), a > 0, b > 0, a ≠ b?
Посмотреть ОТВЕТ
Ответ: а3 + b3 > ab(a + b).
Вы смотрели алгоритм решения задач по алгебре на тему «Как сравнить два выражения».
Вернуться в раздел «АЛГЕБРА»
Как сравнить два выражения
Алгоритм решения задач по алгебре на тему «Как сравнить два выражения».
При сравнении чисел составляют их разность и выясняют, ка кое число получается в ответе – положительное, отрицательное или нуль.
Число а больше числа b, если разность чисел а – b положительное число: а > b, если а – b > 0.
Число а меньше числа b, если разность а – b отрицательное число: а < b, если а – b < 0.
Подробнее о сравнении чисел смотрите в конспекте «Числовые неравенства. Сравнение чисел».
АЛГОРИТМ
«Как сравнить два выражения»
- Составьте разность двух выражений и упростите (раскройте скобки, приведите подобные слагаемые).
- Определите знак полученной разности: если разность больше нуля, то первое выражение больше второго; если разность меньше нуля, то первое выражение меньше второго; если знак установить нельзя при всех значениях букв, входящих в разность, то нельзя утверждать, что одно из выражений больше другого при любых значениях букв.
ПРИМЕР 1. Даны выражения: 4b(b + 1) (I) и (2b + 7)(2b – 
1). Сравните значения выражений при b = –2; b = 10.
2). Можно ли утверждать, что при любом значении b значение первого выражения больше, чем значение второго?
Решение.
I. ⇒ 1). Если b = –2, то 4 • (–2)(–2 + 1) = –8 • (–1) = 8 (I)
2). (2 • (–2) + 7)(2 • (–2) – 
3). 8 – (–36) = 44; 44 > 0
II. ⇒ 1). Если b = 10, то 4 • 10 • (10 + 1) = 40 • 11 = 440 (I)
2). (2 • 10 + 7)(2 • 10 – 
3). 440 – 324 = 116; 116 > 0
В обоих случаях значение первого выражения больше значения второго.
III. Найдем разность первого и второго выражений (I) – (II):
4b(b + 1) – (2b + 7)(2b – 
Разность (I) и (II) выражений равна 6b + 56. Это выражение не при всех значениях b положительно. Например, при b = –10, –11, –12… значение выражения отрицательно. Поэтому нельзя утверждать, что мри всех значениях b значение (I) выражения больше значений (II) выражения.
ПРИМЕР 2. Верно ли неравенство (3х + 
Решение.
1). Преобразуем выражения, стоящие в левой и правой частях неравенства:
(3х +  2 > 3х(х + 16) (I) 2 > 3х(х + 16) (I)(3х)2 + 2 • 3х • 8 + 64 > 3х2 + 48х 9х2 + 48х + 64 > 3х2 + 48х (II)2). Составим разность:(3х +  2 – 3х(х + 16) = 9х2 +48х + 64 – (3х2 +48х) = 2 – 3х(х + 16) = 9х2 +48х + 64 – (3х2 +48х) == 9х2 +48х + 64 – 3х2 – 48х = 6х2 +64 (III) |
(a + b)2 = a2 + 2 ab + b2 если a – b > 0, то а > b |
3). 6х2 + 64 > 0 при всех значениях х, так как х2 ≥ 0 при любых значениях х; значит, неравенство (III) верно при любых значениях х, значит, и неравенство (I) верное.
Ответ: неравенство верно.
ПРИМЕР 3. Докажите, что а + 1/а ≥ 2, а > 0.
Доказательство.
| Составим разность и упростим:
что и требовалось доказать. |
если а – b ≥ 0, то а ≥ b a > 0 по условию (а — 1)2 > 0, при а = 1 получаем нуль |
ПРОВЕРЬ СЕБЯ
- Сравните числа х и у, если разность х – у равна: 1) –3; 2) 5; 3) 0.
- Что больше: a3 + b3 или ab(a + b), a > 0, b > 0, a ≠ b?
Вы смотрели алгоритм решения задач по алгебре на тему «Как сравнить два выражения».
Вернуться в раздел «АЛГЕБРА»
- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
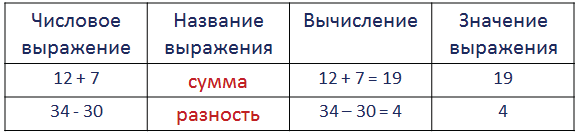
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
Чтение числовых выражений
12 + 9 — сумма
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
14 — 6 = 8
18 — 9 = 9
8 < 9, значит,
14 — 6 < 18 — 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
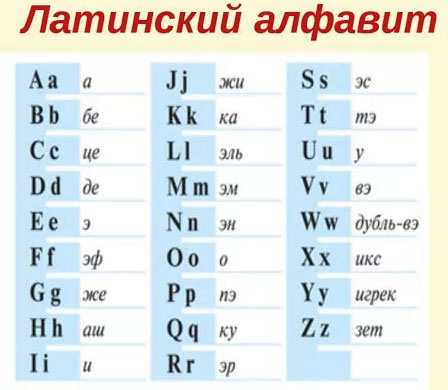
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
1 класс
Страница 18. Урок 11,
Петерсон, Учебник, часть 1
Страница 10. Урок 6,
Петерсон, Учебник, часть 2
Страница 43. Урок 22,
Петерсон, Учебник, часть 2
Страница 45. Урок 23,
Петерсон, Учебник, часть 2
Страница 51. Урок 26,
Петерсон, Учебник, часть 2
Страница 19. Урок 10,
Петерсон, Учебник, часть 3
Страница 22. Урок 12,
Петерсон, Учебник, часть 3
Страница 37. Урок 19,
Петерсон, Учебник, часть 3
Страница 44. Урок 23,
Петерсон, Учебник, часть 3
Страница 88. Урок 35,
Петерсон, Учебник, часть 3
2 класс
Страница 80,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 45. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 41. Урок 16,
Петерсон, Учебник, часть 2
Страница 65. Урок 26,
Петерсон, Учебник, часть 2
Страница 78. Урок 32,
Петерсон, Учебник, часть 2
Страница 12. Урок 4,
Петерсон, Учебник, часть 3
Страница 38. Урок 13,
Петерсон, Учебник, часть 3
3 класс
Страница 25,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 21. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89. Урок 33,
Петерсон, Учебник, часть 1
Страница 102. Урок 39,
Петерсон, Учебник, часть 1
Страница 70. Урок 29,
Петерсон, Учебник, часть 2
Страница 5. Урок 2,
Петерсон, Учебник, часть 3
4 класс
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 5. ПР. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14. Урок 5,
Петерсон, Учебник, часть 1
Страница 26. Урок 9,
Петерсон, Учебник, часть 1
5 класс
Задание 427,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 430,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 566,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1327,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1845,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 926,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 253,
Мерзляк, Полонский, Якир, Учебник
Номер 256,
Мерзляк, Полонский, Якир, Учебник
Номер 432,
Мерзляк, Полонский, Якир, Учебник
Номер 433,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 361,
Мерзляк, Полонский, Якир, Учебник
Номер 401,
Мерзляк, Полонский, Якир, Учебник
Номер 898,
Мерзляк, Полонский, Якир, Учебник
Номер 962,
Мерзляк, Полонский, Якир, Учебник
Номер 1037,
Мерзляк, Полонский, Якир, Учебник
Номер 1100,
Мерзляк, Полонский, Якир, Учебник
Номер 1106,
Мерзляк, Полонский, Якир, Учебник
Задание 569,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 704,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 989,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 259,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 316,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 481,
Мерзляк, Полонский, Якир, Учебник
Номер 906,
Мерзляк, Полонский, Якир, Учебник
Номер 1040,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 392,
Мерзляк, Полонский, Якир, Учебник
Сравнение значений выражений
План урока:
- Сравнение числовых выражений;
- Сравнения выражений с переменными;
- Двойные неравенства;
- Строгие и нестрогие неравенства.
Цели урока:
- Уметь сравнивать значения выражений;
- Знать, что такое строгое и нестрогое неравенства;
- Знать, как выглядит и читается двойное неравенство.
Разминка
- Что тяжелее, килограмм железа или килограмм пуха?
- Кто быстрее бегает, кролик или черепаха?
Представьте себе, что вы с другом на перемене решили сыграть в необычные крестики-нолики. Выигрывает тот человек, кто нарисует наибольшее количество крестиков или ноликов за определённое время. Вы нарисовали 105 крестиков за 5минут, а ваш друг нарисовал 184 нолика за то же время. Как узнать, кто быстрее рисовал значки на бумаге?
Можно подойти к этой задаче логически и сделать вывод, что ваш друг быстрее рисовал нолики, т. к. он нарисовал их больше, чем вы, за то же количество времени.
Можно подойти к этому вопросу математически, ведь если разделить количество знаков на время, за которое мы их нарисовали, то получится скорость рисования этих знаков, иначе — производительность нашей работы. Чтобы узнать, кто быстрее рисовал значки, нужно найти скорость их рисования. Вы рисовали их со скоростью 105 ÷ 5 знаков в минуту, а ваш друг — 184 ÷ 5 знаков в минуту. Мы получили два числовых выражения, их можно сравнить и установить, равны они или нет, и если они не равны, то установить, какое их них больше и какое меньше. Это работает для двух любых числовых выражений.
105 ÷ 5 < 184 ÷ 5
Рассмотрим, какие варианты записи результата сравнения выражений существуют.
Сравните значения выражений 3,67 — 2,71 и 3,01 + 2,33.
Решение
1. Найдём значение каждого выражения:
3,67 — 2,71 = 0,96
3,01 + 2,33 = 5,34
2. Сравним значения выражений: 0,96 < 5,34.
3. Поставим соответствующий знак неравенства в исходное выражение.
Ответ: 3,67 — 2,71 < 3,01 + 2,33.
Кроме числовых выражений есть выражения с переменными, в которых для разных значений переменных результат сравнения значения этих выражений может быть разным.
Сравните значения выражений 4h и 6 + h при h=0; 2; 4.
Решение
1. Если h = 0, то 4h = 0, а 6 + h = 6, т. е. при h = 0 верно неравенство 4h < 6 + h
(4h меньше, чем 6 + h).
2. Если h = 2, то 4h = 4 · 2 = 8, а 6 + h = 6 + 2 = 8, т. е. при h = 2 верно равенство 4h = 6 + h (4h равно 6 + h).
3. Если h = 4, то 4h = 4 · 4 = 16, а 6 + h = 6 + 4 = 10, т. е. при h = 4 верно неравенство 4h > 6 + h (4h больше, чем 6 + h).
1. Сравните значения выражений 5,72 ÷ 0,2 и 3,64 + 5.
2. Сравните значения выражений 3е + 4 и 5 — 2е при е = 0; 0,2; 1.
Рассмотрим ещё одну ситуацию: в размерной сетке женской одежды 42-му размеру одежды соответствует обхват талии от 62 до 66 см. Это значит, что если ваша талия равняется 62, 63, 64, 65, 66 см, то, скорее всего, вы носите 42-й размер одежды. Как мы можем записать это с помощью неравенства? Пусть обхват талии будет обозначаться буквой w. Получается
двойное неравенство
: 62 ≤ w ≤ 66, которое читают так: w больше или равно 62, но меньше или равно 66.
Запишите неравенством фразу: число m находится между числами 12 и 18.
Решение
Если число находится между числами 12 и 18, значит, оно больше 12 и меньше 18. Запишем эти утверждения с помощью неравенства:
m > 12 и m < 18.
Объединим эти два неравенства в одно:
12 < m < 18
Ответ: 12 < m < 18.
Неравенства, составленные с помощью знаков > и <, называют
строгими
, а неравенства, составленные с помощью знаков ≥ и ≤, называют
нестрогими
.
1. Запишите в виде двойного неравенства: число k больше или равно 3, но меньше 10.
2. Запишите в виде двойного неравенства: число x меньше y, и y меньше z.
Контрольные вопросы
1. Какие неравенства называются двойными? Как вы думаете, почему их так назвали?
2. Приведите пример двойного неравенства и прочитайте его.
3. Какие знаки используются для записи неравенств?
4. С помощью каких знаков записывают строгие неравенства?
5. С помощью каких знаков записывают нестрогие неравенства?
Ответы
Упражнение 1
1. 5,72 ÷ 0,2 > 3,64 + 5.
2. При e = 0: 3e + 4 < 5 — 2e;
При e = 0,2: 3e + 4 = 5 — 2e;
При e = 1: 3e + 4 > 5 — 2e.
Упражнение 2
1. 3 ≤ k < 10.
2. x > y > z.