Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Найдите среде данных дробей
24
27
,
1
10
,
6
60
,
8
9
,
40
45
равные между собой и запишите соответствующие равенства.
reshalka.com
Математика 6 класс Мерзляк. Номер №216
Решение
1
10
=
6
60
;
24
27
=
8
9
=
40
45
.
В данной публикации мы рассмотрим, какие дроби являются равными, а также как сравнить две дроби с одинаковыми числителями/знаменателями или с разными знаменателями.
- Равные дроби
-
Сравнение простых дробей
- С одинаковыми знаменателями
- С одинаковыми числителями
- С разными знаменателями
- Другие правила сравнения дробей
Равные дроби
Две дроби являются равными, если их числители и знаменатели соответственно равны (пропорционально равны).
Пример: дроби
4/5
и
8/10
равны, т.к. числитель и знаменатель первой дроби в два раза меньше числителя и знаменателя второй дроби.
Равные дроби соответствует:
- одной и той же точке на числовой оси;
- одной и той же десятичной дроби, которая вычисляется путем деления числителя на знаменатель. В нашем случае 4/5 = 8/10 = 0,8.
Сравнение простых дробей
С одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями, больше та, у которой числитель больше.
Пример:
5/7
>
3/7
, т.к. 5>3.
С одинаковыми числителями
Из двух дробей с одинаковыми числителями, больше та, у которой знаменатель меньше.
Пример:
6/4
>
6/11
, т.к. 4<11.
С разными знаменателями
Для того, чтобы иметь возможность сравнить дроби с разными знаменателями, для начала их нужно привести к общему знаменателю, после чего их уже можно сравнить по одинаковому знаменателю.
Пример: сравним дроби
3/8
и
2/16
.
В данном случае нам нужно представить первую дробь со знаменателем 16 путем умножения числителя и знаменателя на число 2.
Теперь у нас имеются две дроби с одинаковыми знаменателями, которые мы можем сравнить по соответствующему правилу, рассмотренному выше.
Другие правила сравнения дробей
1. Любая правильная дробь меньше 1.
2. Любая неправильная дробь больше 1.
Пример:
8/3
>1, т.к.
8/3
=2
2/3
>1.
3. Любая неправильная дробь всегда больше правильной, что следует из правил 1 и 2 выше.
Перейти к контенту
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Найдите среди данных дробей равные между собой.
Рубрика: ГДЗ

§ 8. Сокращение дробей ГДЗ по Математике 6 класс Мерзляк А.Г.
215. Найдите среди данных дробей равные между собой. Запишите соответствующие равенства.
Ответ

6 класс
- 2 класс
- 3 класс
- 4 класс
- Информатика
- Математика
- Алгебра
- Геометрия
Содержание:
- Равные дроби
- Принципы сравнения дробей
- Сравнение дробей с разными знаменателями
Равные дроби
Пример
Задание. Найти при каком значении $x$ и $y$ дроби $frac{x}{3}$ и $frac{4}{y}$ будут равны.
Решение. Заданные дроби равны, то есть $frac{x}{3}=frac{4}{y}$ , если равны их числители и знаменатели
соответственно. А тогда имеют место следующие равенства:
$x=4$ $3=y$ или $x=4$ $y=3$
Ответ. $x=4, y=3$
Две дроби считаются равным, если величины, выражаемые этими числами при одной и той же единице измерения, равны между собой.
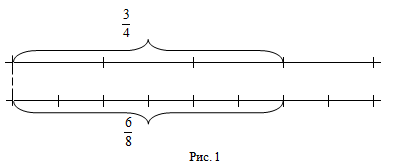
Например. Дроби $frac{3}{4}$ и
$frac{6}{8}$ равны, так как две длины, из которых одна составляет $frac{3}{4}$ м, а вторая — $frac{6}{8}$ м, равны (рис 1).
Принципы сравнения дробей
Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше.
Например. $frac{7}{18}>frac{5}{18}$ , так как $7>5$
Из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Например. $frac{7}{3}>frac{7}{6}$, так как $3<6$ .
Любая правильная дробь меньше 1.
Например. $frac{4}{5} < 1$
Неправильная дробь, числитель которой равен знаменателю, равна 1.
Например. $frac{3}{3}=1, frac{7}{7}=1$
Неправильная дробь, у которой числитель больше знаменателя, больше 1.
Например. $frac{7}{6}>1$
Любая правильная дробь меньше произвольной неправильной дроби.
Например. $frac{4}{5}<frac{5}{4}$
В общем случае дроби по величине сравниваются следующим образом. Умножают числитель первой дроби на
знаменатель второй, а знаменатель первой на числитель второй. И сравнивают полученные произведения. Если первое
из этих произведений больше/равно/меньше второго, то соответственно и первая дробь больше/равно/меньше второй.
Например. $frac{5}{6}>frac{7}{9}$ , так как $5 cdot 9>6 cdot 7 Leftrightarrow 45>42$
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю. Для этого
приводят либо к общему знаменателю, либо числитель и знаменатель первой дроби домножают на знаменатель второй и наоборот,
числитель и знаменатель второй дроби на знаменатель первой. И далее дроби сравнивать как дроби с одинаковым знаменателем
(описано выше).

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Сравнить дроби
$frac{3}{4}$ и $frac{5}{7}$
Решение. Приведем дроби к общему знаменателю, для этого
числитель и знаменатель
первой дроби домножим на 7 (знаменатель второй дроби); а числитель и знаменатель второй дроби — на 4, будем иметь:
$frac{3 cdot 7}{4 cdot 7}$ и $frac{5 cdot 4}{7 cdot 4}$
$frac{21}{28}$ и $frac{20}{28}$
Первая дробь больше: $frac{21}{28}>frac{20}{28} Leftrightarrow frac{3}{4}>frac{5}{7}$ , так как ее числитель $21 > 20$
Ответ. $frac{3}{4}>frac{5}{7}$
Читать следующую тему: основное свойство дроби.