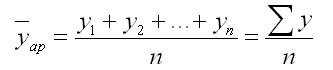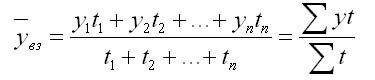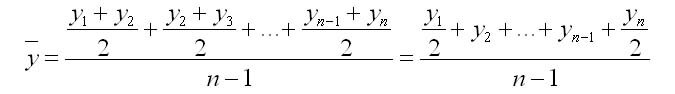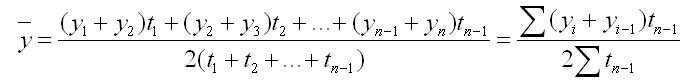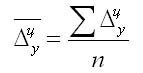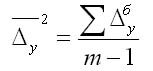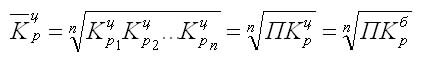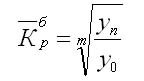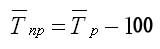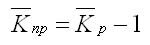Расчет средних показателей динамического ряда
Для
обобщающей характеристики динамики
исследуемого явления
определяют средние показатели: средние
уровни ряда и средние показатели
изменения уровней ряда.
Средний
уровень ряда
характеризует обобщённую величину
абсолютных
уровней. Он рассчитывается по средней
хронологической, т.е. по
средней исчисленной из значений,
изменяющихся во времени.
Методы
расчета среднего уровня интервального
и моментного рядов
динамики различны.
Для
интервальных рядов динамики из абсолютных
уровней средний за период времени
определяется по формуле средней
арифметической:
а)
при равных интервалах применяется
средняя
арифметическая простая:
,
где у1,…,уn– абсолютные уровни ряда;n– число уровней ряда.
б) при неравных
интервалах – средняя арифметическая
взвешенная:
,
где у1,…,уn– уровни ряда динамики, сохраняющиеся
без изменения в течение промежутка
времени,t;t1,…,
tn– веса, длительность интервалов времени
(дней, месяцев) между смежными датами.
Средний уровень
производства электроэнергии за 1989-1994
гг.:
.
Средний
уровень моментного ряда динамики с
равноотстоящими уровнями определяется
по формуле средней хронологической
моментного
ряда:
,
где у1,…,уn– уровни периода, за который делается
расчет;n– число
уровней;n–1 –
длительность периода времени.
Обобщающий
показатель скорости изменения уровней
во времени
— средний
абсолютный прирост (убыль),
представляющий собой обобщенную
характеристику
индивидуальных абсолютных приростов
ряда динамики.
По цепным данным об абсолютных приростах
за ряд лет можно
рассчитать средний годовой абсолютный
прирост как среднюю арифметическую
простую:
,
где n– число цепных абсолютных приростоввизучаемом
периоде.
Используя
данные табл.
5 о цепных абсолютных приростах
производства электроэнергии,
млрд кВт-ч:
(5
– 14 – 60 – 51 – 81) : 5 = ‑201 : 5 = ‑40,2
Средний
абсолютный прирост определим через
накопленный (базисный)
абсолютный прирост.
Для случая равных интервалов применим
следующую формулу:
,
где т
— число
уровней ряда динамики в изучаемом
периоде, включая базисный.
Для нашего примера,
млрд кВт-ч:
т.е. получен тот
же результат.
Сводной
обобщающей характеристикой интенсивности
изменения уровней
ряда динамики служит средний темп роста
(снижения), показывающий во сколько раз
в среднем за единицу времени изменяется
уровень
ряда динамики.
Средний
темп роста (снижения)
— обобщенная характеристика индивидуальных
темпов роста ряда динамики. В качестве
основы и критерия
правильности исчисления среднего темпа
(снижения) применяется
определяющий показатель — произведение
цепных темпов роста, равное
темпу роста за весь рассматриваемый
период. Следовательно, если значение
признака образуется как произведение
отдельных вариантов,
то нужно применять среднюю геометрическую.
Поскольку средний темп роста представляет
собой средний коэффициент роста,
выраженный
в процентах,
,
то для равностоящих рядов динамикирасчеты
по средней геометрической сводятся к
исчислению средних
коэффициентов роста из цепных коэффициентов
роста (по цепному способу):
,
где n– число цепных коэффициентов роста;‑
цепные коэффициенты роста;‑
базисный коэффициент роста за весь
период.
В
нашем примере среднегодовой темп
изменения производства электроэнергии
с 1990 по 1994г.:
;
Следовательно,
с 1990 по 1994г. производство электроэнергии
в России
снижалось в среднем на 4 % в год, т.е. (0,96
* 100) – 100.
Если
известны уровни динамического ряда, то
расчет среднего коэффициента
роста упрощается. Так как произведение
цепных коэффициентов
роста равно базисному, то в подкоренное
выражение подставляется
базисный коэффициент роста. Базисный
коэффициент, как известно,
получается непосредственно как частное
от деления уровня последнего
периода уп
на
уровень базисного периода у0.
Тогда
формула для расчета среднего коэффициента
роста для равностоящих
рядов динамики (по «базисному способу»)
выглядит следующим образом:
,
где т
— число
уровней ряда динамики в изучаемом
периоде, включая базисный.
Для
расчета средних коэффициентов роста
не нужно
знать годовые темпы. Для нашего примера:
Получен тот же
результат, расчеты упрощены.
Средние
темпы прироста (сокращения)
рассчитываются на основе
средних темпов роста, вычитанием из
последних 100%. Соответственно
при исчислении средних коэффициентов
прироста из значений
коэффициентов роста вычитается единица:
;
,
где
‑ средний темп прироста.
Если
уровни ряда динамики снижаются, то
средний темп роста будет
меньше 100 %, а средний темп прироста —
отрицательной величиной.
Отрицательный темп прироста
представляет собой средний
темп сокращения и характеризует среднюю
относительную скорость снижения
уровня.
При
анализе развития явлений, отражаемых
двумя динамическими рядами,
представляет интерес сравнение
интенсивностей изменения во
времени обоих явлений. Такое сопоставление
интенсивностей изменения
производится при сравнении динамических
рядов одинакового
содержания, но относящихся к разным
территориям (странам, республикам,
районам и т.п.), или к различным организациям
(министерствам,
предприятиям, учреждениям), или при
сравнении рядов разного
содержания, но характеризующих один и
тот же объект. Например,
сравнение рядов динамики, характеризующих
производство важнейших
видов продукции в Российской Федерации
и других странах.
Сравнение
интенсивности изменений уровней рядов
во времени возможно
с помощью коэффициентов
опережения (отставания),
представляющих
собой отношение базисных темпов роста
(или прироста) двух
рядов динамики за одинаковые отрезки
времени:


где
‑базисные
темпы роста и прироста первого и второго
рядов динамики (соответственно).
Коэффициенты
опережения (отставания) могут быть
исчислены на основе
сравнения средних темпов роста (или
прироста) двух динамических
рядов за одинаковый период времени:

где
‑средние
темпы роста первого и второго рядов
динамики
соответственно; n– число лет в периоде.
Коэффициент
опережения (отставания) показывает, во
сколько раз быстрее
растет (отстает) уровень одного ряда
динамики по сравнению с другим. При этом
сравнении темпы должны характеризовать
тенденцию
одного направления.
Статистика
населения
-
Понятие
статистики населения, ее объект
предмет изучения -
Население как
объект исследования
1. Статистика
населения —
отрасль статистической науки, изучающая
население и процессы, связанные с его
динамикой, с
количественной
стороны в конкретных условиях общественного
развития и
разрабатывающая
методы
статистического учета и
анализа
демографических
явлений и процессов.
Объект
изучения
—
население в целом, отдельные группы
населения (трудоспособные, инвалиды,
мужчины, женщины и др.), молодые
семьи, родившиеся (умершие) за определенный
промежуток времени.
Предмет
статистики населения —
население и закономерности его развития.
Основные
задачи статистики населения:
-
определение
численности населения; -
анализ размещения
населения по территории страны; -
характеристика
состава населения; -
изучение процессов
воспроизводства населения; -
определение
перспективной численности и состава
населения.
Единица
наблюдения — отдельный
человек как индивидуум, семья,
домохозяйство,
населенный пункт.
При
этом источниками информации являются:
текущий учет; единовременный
учет (микропереписи; выборочные переписи;
сплошные переписи).
2. Население
— совокупность
людей, проживающих в пределах
определенной
территории:
-
части страны;
-
всей страны;
-
группы стран;
-
всего земного
шара.
Также
это социальная
категория, т.е.
совокупность лиц, проживающих
на определенной территории, и одновременно
экономическая
категория, т.
е. совокупность участников процесса
производства
и потребителей его результатов.
Различаются
следующие группировки
населения:
-
п
о
полу; -
национальному
составу; -
возрасту;
-
уровню
образования; -
размещению;
-
доходу;
-
семейному положению.
Рис. Возрастно-половая
пирамида населения РФ на 01.01.1998
Соседние файлы в папке Статистика
- #
- #
- #
Крайне неудобно анализировать множество значений за ряд периодов, поэтому целесообразнее вычислять средний показатель роста (убыли) определенного параметра. Средний темп роста является показателем статистической динамики для анализа явлений и процессов (интенсивности изменения и скорости роста) в различных областях жизнедеятельности: финансовой сфере, сфере производства и торговли, статического анализа и пр.
Коэффициент, отражающий средний за ряд периодов рост показателя в процентном измерении.
Структура формулы:
- значение на начало измерения;
- значение в конце измерения;
- промежуточные показания, через равные интервальные моменты.
T‾=n−1TсрT1100%overline {T}=^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}100%
Tср=∑1nTkntext{Tср}=sum _1^n frac{T_k}{n}
где T1T_1 – начальное значение показателя,
TkT_k – значение показателя за период k(1…n)k (1…n),
nn – число периодов расчета,
Tсрtext{Tср} – среднее значение показателя.
Алгоритм расчета:
- Определение периода сравнения nn;
- Вычисление суммы параметров за период nn;
- Нахождение среднего параметра путем деления суммы (п.2) на число периодов nn;
- Вычисление среднего темпа роста как корень степени n−1n-1 от частного среднего и начального T$$ на 100%.100%.
Определить средний темп роста прибыли фирмы по следующим данным:
| Месяц | Сумма |
|---|---|
| Январь | 142000 руб. |
| Февраль | 146000 руб. |
| Март | 136000 руб. |
| Апрель | 151000 руб. |
| Май | 163000 руб. |
| Июнь | 113000 руб. |
| Июль | 122000 руб. |
| Август | 125000 руб. |
| Сентябрь | 132000 руб. |
| Октябрь | 156000 руб. |
| Ноябрь | 167000 руб. |
| Декабрь | 178000 руб. |
Решение
- Период n=12n = 12;
- Сумма прибыли за год:
142000+146000+136000+151000+163000+113000+122000+125000+132000+156000+167000+178000=1731000142000+146000+136000+151000+163000+113000+122000+125000+132000
+156000+167000+178000 = 1731000 руб.
- Средняя прибыль за год:
Tср=173100012=144250text{Tср}=173100012=144250руб.
- Средний темп роста:
T‾=14425014200011100%=1,00143⋅100%=100,143%overline{T}=sqrt[11]{frac{144250}{142000}}100%=1,00143cdot100%=100,143%
Ответ: Средний темп роста прибыли составил $100,143%$ в год.
Найти значение выручки в апреле, если известно, что в январе было заработано 6132 тыс. руб., в феврале – 5861 тыс. руб., в марте – 6318 тыс. руб. Показатель среднего темпа роста за 4 месяца — 113%.
Решение
- Средний темп роста
T‾=n−1TсрT1100%=113%overline {T}=^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}100%=113%
n−1TсрT1=1,13^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}=1,13
4−1Tср6132=1,13^{4-1} sqrt{frac{text{Tср}}{6132}}=1,13
Tср6132=1,133frac{text{Tср}}{6132}=1,13^3
Tср6132=1,4429frac{text{Tср}}{6132}=1,4429
Tср=8847,86text{Tср}=8847,86 тыс. руб.
- Средняя выручка (XX – выручка за апрель):
Tср=∑1nTkn=8847,86text{Tср}=sum _1^n frac{T_k}{n}=8847,86
∑1nTk4=8847,86frac{sum_{1}^{n}T_k}{4}=8847,86
6132+5861+6318+X4=8847,866132+5861+6318+X4=8847,86
6132+5861+6318+X=35391,446132+5861+6318+X=35391,44
X=35391,44−6132−5861−6318=17080,44X=35391,44-6132-5861-6318=17080,44 тыс. руб.
Ответ: Выручка в апреле 17080,4417080,44 тыс. руб.
Средний темп роста является многогранным показателем, позволяющим наглядно отразить результаты изменения тех или иных экономических данных. По результатам анализа компания может оценить динамику роста, выявить влияющие факторы и спрогнозировать будущие показатели с учетом сезонных изменений.
Тест по теме «Формула среднего темпа роста»
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.
Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.
Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:
Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.
Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.
Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.
Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.
Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.
Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».
Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Средняя хронологическая
Краткая теория
Средняя хронологическая — это средний
уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений
показателя в разные моменты или периоды времени. В зависимости от вида ряда
динамики применяются различные способы ее расчета, а именно расчет средней
хронологической интервального ряда и средней хронологической моментного ряда.
Ряды динамики состоят из числовых значений двух показателей:
моментов или периодов времени t, к которым относятся приводимые данные, и
соответствующих им статистических данных у, которые называются уровнями
динамического ряда. В зависимости от того, к моментам или периодам времени
привязываются статистические данные, различают два вида рядов динамики:
моментные и интервальные.
Когда уровни ряда динамики характеризуют размеры общественных
явлений за определенные интервалы (периоды) времени (за сутки, месяц, квартал,
год и т. п.), то такие ряды называются интервальными (или периодическими). В
отличие от моментного ряда динамики уровни интервального ряда динамики могут
быть суммированы. Например, сложив данные выпуска станков за четыре квартала,
можно получить показатель их выпуска за год.
Для интервальных рядов с равноотстоящими уровнями средняя
хронологическая имеет вид средней арифметической простой:
где
– уровни интервального ряда
— количество равных периодов времени
В интервальных рядах с неравноотстоящими
уровнями средняя хронологическая имеет вид средней
арифметической взвешенной:
где
– периоды времени, отделяющие один уровень
ряда от другого
Если уровни ряда динамики выражают состояние явления на
определенные моменты времени или даты, то такие ряды называют моментными рядами
динамики. Особенность моментного ряда динамики в том, что некоторые его уровни
содержат элементы повторного счета, т. е. каждый последующий уровень полностью
или частично включает в себя предыдущий уровень. Поэтому суммирование уровней
моментного динамического ряда не имеет смысла, но разность уровней имеет
определенное значение.
В моментном ряду динамики с равноотстоящими уровнями средняя хронологическая
имеет вид:
Средний уровень моментного ряда динамики с неравноотстоящими
уровнями характеризует средняя хронологическая взвешенная, которая исчисляется
по формуле:
где
и
– значение уровня моментного ряда динамики и
уровня, следующего за ним;
–
промежуток времени между датами.
Примеры решения задач
Задача 1
Остатки
готовой продукции на складе составили, тыс.руб.:
| Дата |
Остатки готовой продукции, тыс.руб. |
| 01.04.2011 | 506 |
| 01.05.2011 | 519 |
| 01.06.2011 | 587 |
| 01.07.2011 | 624 |
| 01.08.2011 | 624 |
| 01.09.2011 | 545 |
| 01.10.2011 | 580 |
| 01.11.2011 | 542 |
| 01.12.2011 | 576 |
| 01.01.2012 | 606 |
Требуется:
Определить средние остатки готовой
продукции на складе за II квартал, за III квартал, за IV квартал, за второе
полугодие 2011 года.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Средние
остатки продукции можно вычислить по формуле средней хронологической, так как
нам дан динамический моментный ряд с
равноотстоящими интервалами.
Средние
остатки за 2-й квартал:
Средние
остатки за 3-й квартал:
Средние
остатки за 4-й квартал:
Средние
остатки готовой продукции за второе полугодие:
Вывод
Таким
образом средние остатки готовой продукции за 2-й
квартал составили 557 тыс.р., за 3-й квартал 590,3 тыс.р., а за 4-й квартал 570,3 тыс.р.
Средние остатки готовой продукции за 2-е полугодие составили 580,3 тыс.р.
Задача 2
Известны
следующие данные об изменениях в списочном составе работников банка за январь,
человек.
| Число сотрудников | |
| Состояло по списку на 1 января | 205 |
| на 9 января | 200 |
| на 12 января | 198 |
| на 16 января | 201 |
| на 19 января | 197 |
| на 27 января | 199 |
| Состояло по списку на 1 февраля | 199 |
Определите
среднюю списочную численность работников банка в январе.
Решение
Данный
динамический ряд моментный, с неравноотстоящими датами.
Средняя
хронологическая взвешенная:
Вывод
Среднесписочная
численность работников банка в январе составила 200,2 чел.
Задача 3
Имеются
следующие данные о производстве молока в России за 1995-2000 годы (млн.т.)
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 39.2 | 35.8 | 34.1 | 33.3 | 32.3 | 32.3 |
Для
анализа ряда динамики определите средний уровень ряда динамики.
Решение
Так
как данный динамический ряд интервальный,
с равноотстоящими уровнями, то средний уровень исследуемого динамического
ряда найдем по формуле средней арифметической:
Вывод
Среднегодовое
производство молока в исследуемом периоде составило 34,5 млн. тонн.
Задача 4
Имеются
следующие данные о производстве продукции на заводе (млн. руб.)
| 2005 | 2008 | 2010 | 2011 | 2013 | 2014 |
| 45,4 | 48,3 | 41,5 | 39,6 | 42,5 | 46,8 |
Для
анализа ряда динамики определите средний уровень ряда динамики.
Решение
Так
как данный динамический ряд интервальный,
с неравноотстоящими уровнями, то средний уровень
исследуемого динамического ряда найдем по формуле средней арифметической
взвешенной:
Вывод
Среднегодовое производство продукции на предприятии в исследуемом
периоде составило 44,8 млн. рублей.
Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста
Средний уровень ряда в статистике
Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
где у — абсолютные уровни ряда;
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
где у1,…,уn — уровни ряда динамики;
t1,… tn — веса, длительность интервалов времени.
Средний уровень моментного ряда динамики рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:
где у1,…,уn — уровни периода, за который делается расчет;
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:
где у1,…,уn — уровни рядов динамики;
t — интервал времени между смежными уровнями
Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
где n — число степенных абсолютных приростов в исследуемом периоде.
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
Средний темп роста
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
где n — число цепных коэффициентов роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:
Средний темп прироста
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

 о
о