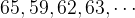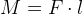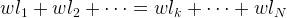Как оценить среднее значение и медиану любой гистограммы
17 авг. 2022 г.
читать 2 мин
Гистограмма — это диаграмма, которая помогает нам визуализировать распределение значений в наборе данных.
По оси X гистограммы отображаются интервалы значений данных, а по оси Y указано, сколько наблюдений в наборе данных приходится на каждый интервал.
Хотя гистограммы полезны для визуализации распределений, не всегда очевидно, что представляют собой средние и медианные значения, просто взглянув на гистограммы.
И хотя невозможно найти точное среднее и срединное значения распределения, просто взглянув на гистограмму, можно оценить оба значения. В этом руководстве объясняется, как это сделать.
Как оценить среднее значение гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку среднего значения любой гистограммы:
Наилучшая оценка среднего: Σm i n i / N
куда:
- m i : середина i -го бина
- n i : частота i -го бина
- N: общий размер выборки
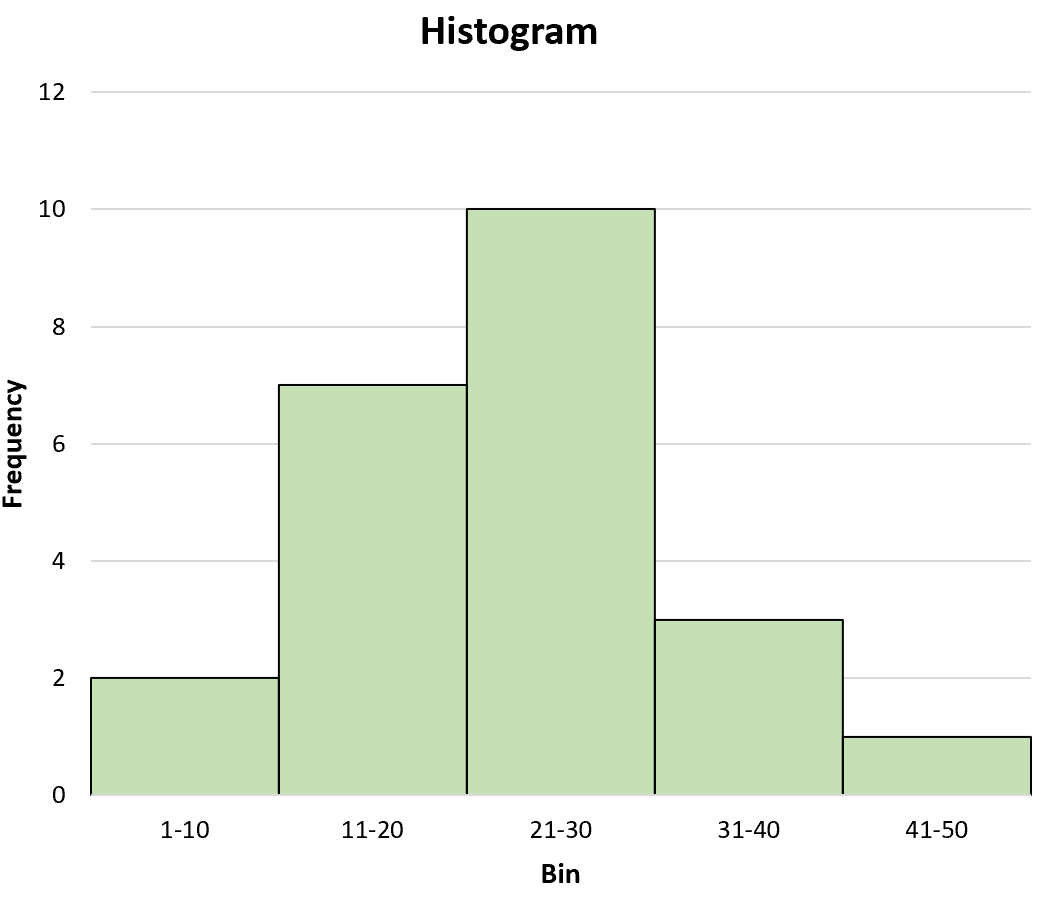
Например, рассмотрим следующую гистограмму:
Наилучшей оценкой среднего значения будет:
Среднее значение = (5,5*2 + 15,5*7 + 25,5*10 + 35,5*3 + 45,5*1) / 23 = 22,89 .
Глядя на гистограмму, это кажется разумной оценкой среднего значения.
Как оценить медиану гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку медианы любой гистограммы:
Наилучшая оценка медианы: L + ((n/2 – F)/f) * w
куда:
- L: Нижний предел средней группы
- n: общее количество наблюдений
- F: кумулятивная частота до средней группы
- f: частота срединной группы
- w: ширина срединной группы
Еще раз рассмотрим следующую гистограмму:
Наилучшей оценкой медианы будет:
Медиана = 21 + ((25/2 – 9)/10) * 9 = 24,15 .
Глядя на гистограмму, это также кажется разумной оценкой медианы.
Связанный: Как оценить стандартное отклонение любой гистограммы
Дополнительные ресурсы
Как найти среднее значение, медиану и моду в диаграммах «стебель-и-листья»
Как рассчитать среднее значение из таблиц частот
Когда использовать среднее значение против медианы
Среднее арифметическое: физический смысл и визуализация
Время на прочтение
4 мин
Количество просмотров 19K
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Два наблюдения:
- Среднее арифметическое находится посередине двух чисел (больше меньшего, но меньше большего).
- Среднее арифметическое не всегда входит в анализируемый набор чисел (не равно ни одному из двух чисел).
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
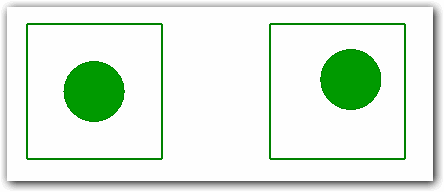
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
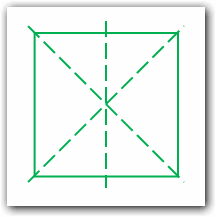
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
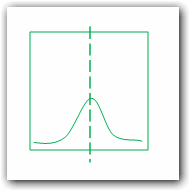
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
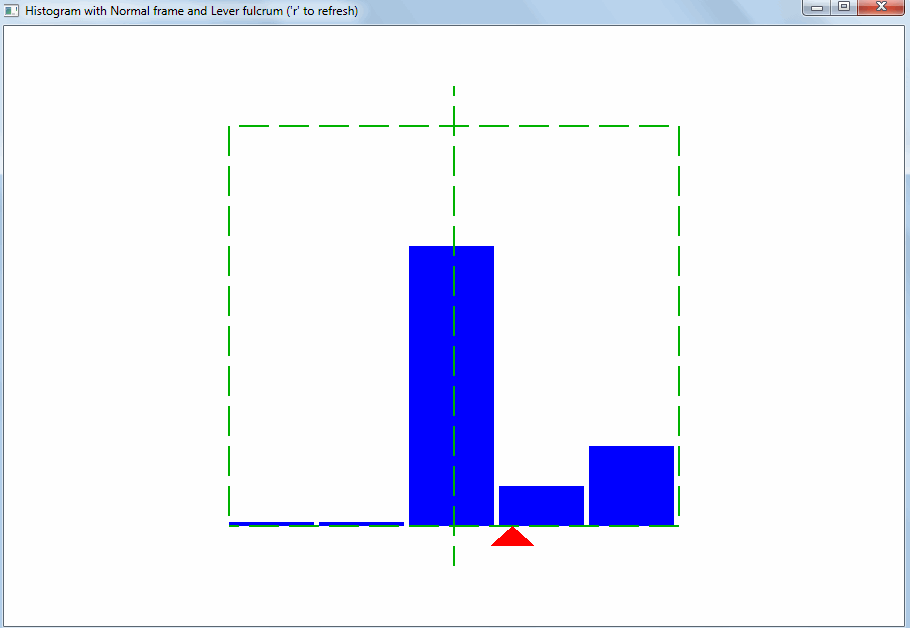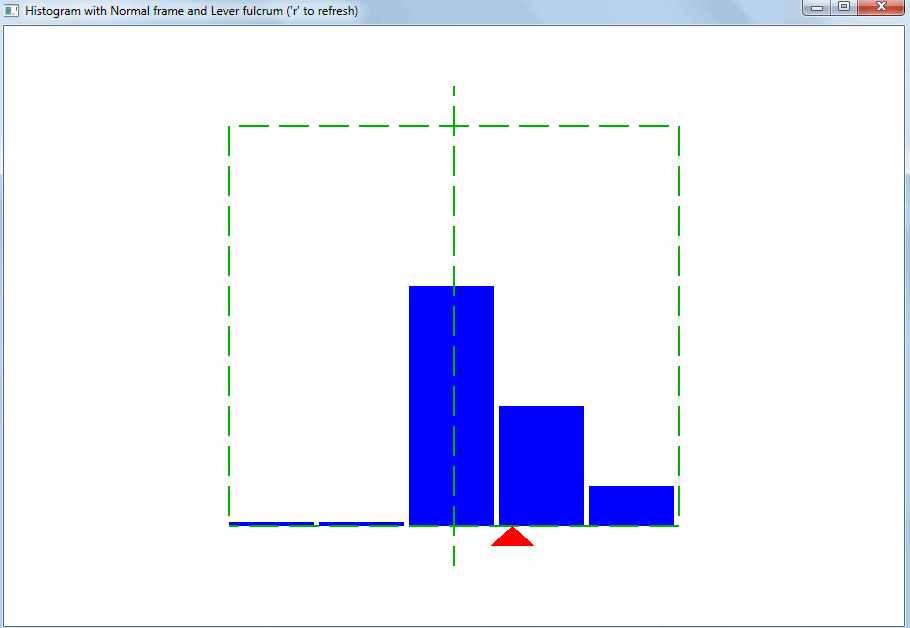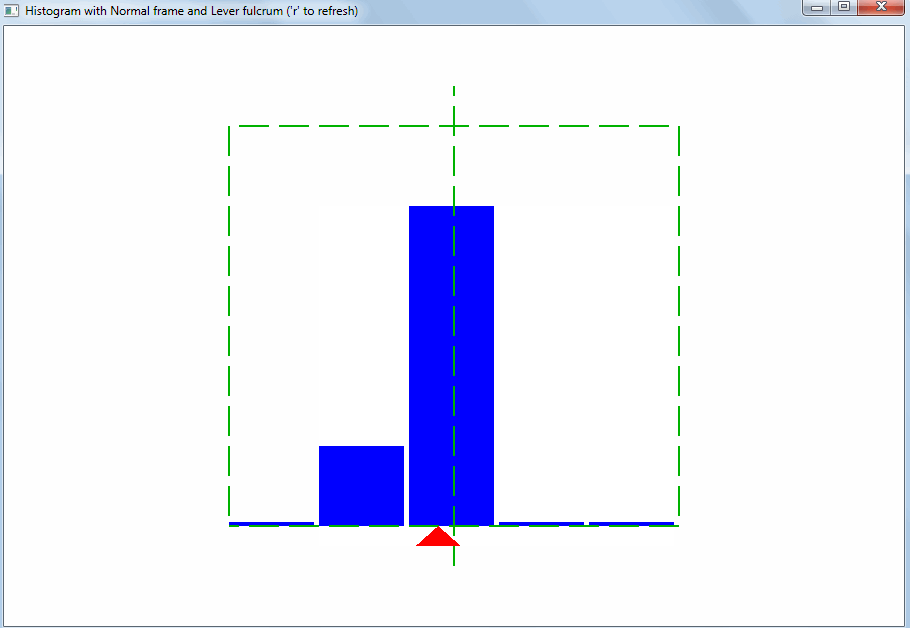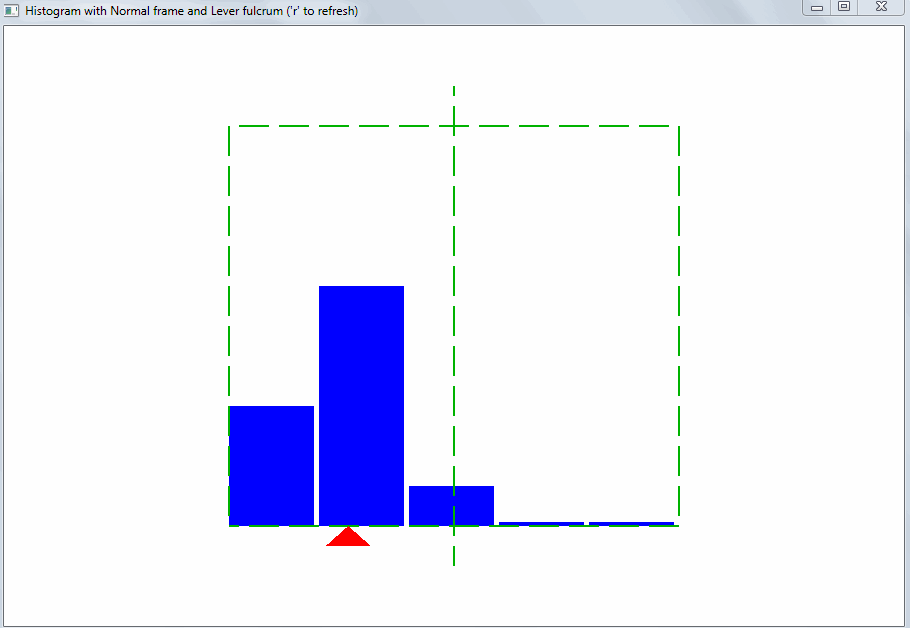
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
Выводы
- Среднее арифметическое – интегральная характеристика набора числовых данных (выборки). Применяется как описательная характеристика в совокупности с другими.
- Нормально, что среднее значение не входит в набор данных. Среднее арифметическое не может заменить полное описание полученной выборки.
- Интервал значений гистограммы должен быть подобран таким образом, чтобы ожидаемое среднее арифметическое было посередине. Тогда будет сразу видно отклонение параметров выборки от ожидаемых значений.
- Среднее арифметическое подвержено влиянию выбросов – значений, сильно отличающихся от остальных значений переменной величины.
Ссылки
- Wikipedia: Переменная величина, Моменты в статистике и механике, Момент силы, Математическое ожидание
- Рудольф Арнхейм. Искусство и визуальное восприятие: фрагменты
- Демонстрация гистограммы, ожидаемого среднего и среднего выборки: исходный код для PyOpenGL
Методику расчета
среднего значения и стандартного
отклонения рассмотрим на примере данных
табл. 3. Когда данных много и они обобщены
в таблице частот, среднее значение и
стандартное отклонение вычисляются по
следующему алгоритму:
1. Подготовьте
бланк для вычислений по форме таблицы
4.
Таблица 4
2. Запишите
в бланк границы классов, их середины и
частоты f.
3. Обозначьте
нулем ()
тот класс, которому соответствует
максимальная частотаfи запишите 0 в столбцеu.
Выпишите –1, –2, и
т.д. для классов, идущих к наименьшему
наблюдаемому значению, и +1, +2, и т.д. для
классов, идущих к наибольшему значению.
Соотношения между
величинами х
и u
описываются следующим уравнением:
,
где а
– середина класса, для которого ,
а h
– интервал класса.
4. Запишите
произведения uиfв столбецuf, а
произведенияuиuf– в столбецu2f.
Найдите суммы каждого из них и запишите
в соответствующих местах:
,
.
5. Вычислите
,
пользуясь следующим уравнением:
.
6. Вычислите s,
пользуясь следующим уравнением:
2.4. Чтение гистограмм
2.4.1 Типы гистограмм
Наиболее типичные
формы гистограмм приведены рис. 4 (а –
ж):
Рис. 4
а) Обычный тип
(симметричный или колоколообразный).
Среднее значение
гистограммы приходится на середину
размаха данных. Наивысшая частота
оказывается в середине и постепенно
снижается к обоим концам. Форма
симметрична.
Примечание.
Это именно та форма, которая встречается
чаще всего.
б) Гребенка
(мультимодальный тип). Классы через один
имеют более низкие частоты.
Примечание.
Такая форма встречается, когда число
единичных наблюдений, попадающих в
класс, колеблется от класса к классу
или когда действует определенное правило
округления данных.
в) Положительно
скошенное распределение
(отрицательно скошенное распределение).
Среднее значение гистограммы локализуется
слева (справа) от центра размаха. Частоты
довольно резко спадают при движении
влево (вправо) и, наоборот, медленно
вправо (влево). Форма асимметрична.
Примечание.
Такая форма встречается, когда нижняя
(верхняя) граница регулируется либо
теоретически, либо по значению допуска
или когда левое (правое) значение
недостижимо.
г) Распределение
с обрывом слева
(распределение с обрывом справа). Среднее
арифметическое гистограммы локализуется
далеко слева (справа) от центра размаха.
Частоты резко спадают при движении
влево (вправо) и, наоборот, медленно
вправо (влево). Форма асимметрична.
Примечание.
Это одна из тех форм, которые часто
встречаются 100 %-ном контроле изделий
из-за плохой воспроизводимости процесса,
а также когда проявляется резко выраженная
положительная (отрицательная) асимметрия.
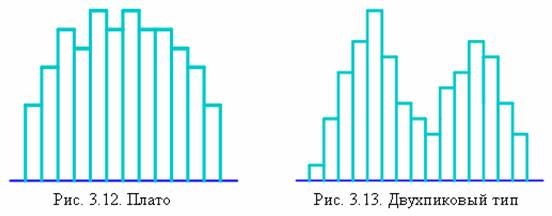
д) Плато
(равномерное и прямоугольное распределения).
Частоты в разных классах образуют плато,
поскольку все классы имеют более или
менее одинаковые ожидаемые частоты с
конечными классами.
Примечание.
Такая форма встречается в смеси нескольких
распределений, имеющих различные
средние.
е) Двухпиковый
тип (бимодальный
тип). В окрестностях центра диапазона
данных частота низкая, зато есть по пику
с каждой стороны.
Примечание.
Такая форма встречается, когда смешиваются
два распределения с далеко отстоящими
средними значениями.
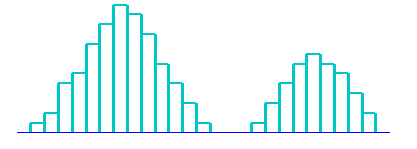
ж) Распределение
с изолированным пиком.
Наряду с распределением обычного типа
появляется маленький изолированный
пик.
Примечание.
Это форма, которая появляется при наличии
малых включений данных из другого
распределения, как, скажем, в случае
нарушения нормальности процесса,
появления погрешности измерения или
просто включения данных из другого
процесса.
В любом заданном множестве данных неизбежно будет рассеяние. Даже те несколько факторов, относительно которых мы предполагаем, что они постоянны, на самом деле не будут совершенно неизменными. Хотя сами значения все время меняются, они подчиняются некоторому правилу, а в таком случае говорят, что данные следуют определенному распределению. В контроле качества мы стремимся на основе собранных данных выявить факты, а затем, опираясь на эти факты, предпринять необходимые действия. Сбор данных — не самоцель, но средство отыскания тех фактов, которые стоят за данными. Пример — управление промышленным процессом с помощью контрольной карты средних — размахов, , Наша цель заключается не в определении характеристики выборки, взятой для нанесения на карту, а в том, чтобы выяснить, в каком состоянии находится сам процесс.
Вся совокупность рассматриваемых объектов называется генеральной совокупностью (популяцией). Один или несколько элементов, взятых из генеральной совокупности для получения информации о ней, называется выборкой. Так как выборка используется для оценивания характеристик всей генеральной совокупности, ее стоит выбирать таким образом, чтобы она отражала именно эти характеристики. Распространенный выборочный метод заключается в выборе любого члена генеральной совокупности с одинаковой вероятностью. Этот метод называют случайным выбором, а выборку, полученную случайным выбором, — случайной выборкой. При этом получаем данные, измеряя характеристики выборки. Пользуясь этими данными, мы делаем выводы относительно генеральной совокупности, а затем производим корректирующие действия. Правда, измеренные выборочные значения будут варьировать от выборки к выборке, затрудняя решение о необходимом действии. Статистический анализ должен подсказать нам, как интерпретировать такие данные.
Данные, полученные из выборки, служат основой для решений о генеральной совокупности. Чем больше объем выборки, тем больше информации об этой совокупности мы получим. Но рост объема выборки одновременно означает и рост количества данных, что затрудняет понимание совокупности по этим данным, даже если они табулированы. В таком случае нам нужен метод, благодаря которому мы могли бы понимать генеральную совокупность с первого взгляда. Нашим требованиям отвечает гистограмма.
Построим гистограмму для исследования распределения диаметров стальных осей, полученных на токарном станке. Измерено 90 осей, результаты представлены в табл. 3.4.
Этапы построения диаграммы.
Этап 1. Вычисление выборочного размаха (R). Получите наибольшее и наименьшее выборочные значения и вычислите R = (наибольшее наблюдаемое значение) — (наименьшее наблюдаемое значение).
В табл. 3.4 сначала надо вычислить наибольшее и наименьшее значения в каждой строке таблицы исходных данных, а затем взять самое большое из максимумов и самое маленькое из минимумов.
Таблица 3.4
Исходные данные диаметров осей
|
Номер выборки |
Результаты измерений |
|||||||||
|
1-10 |
2,510 |
2,517 |
2,522 |
2,510 |
2,511 |
2,519 |
2,532 |
2,543 |
2,525 |
2,522 |
|
11-20 |
2,527 |
2,536 |
2,506 |
2,541 |
2,512 |
2,515 |
2,521 |
2,536 |
2,529 |
2,524 |
|
21-30 |
2,529 |
2,523 |
2,523 |
2,523 |
2,519 |
2,528 |
2,543 |
2,538 |
2,518 |
2,534 |
|
31-40 |
2,520 |
2,514 |
2,512 |
2,534 |
2,526 |
2,530 |
2,532 |
2,526 |
2,523 |
2,520 |
|
41-50 |
2,535 |
2,523 |
2,526 |
2,525 |
2,532 |
2,522 |
2,502 |
2,530 |
2,522 |
2,514 |
|
51-60 |
2,533 |
2,510 |
2,542 |
2,524 |
2,530 |
2,521 |
2,522 |
2,535 |
2,540 |
2,528 |
|
61-70 |
2,525 |
2,515 |
2,520 |
2,519 |
2,526 |
2,527 |
2,522 |
2,542 |
2,540 |
2,528 |
|
71-80 |
2,531 |
2,545 |
2,524 |
2,522 |
2,520 |
2,519 |
2,519 |
2,529 |
2,522 |
2,513 |
|
81-90 |
2,518 |
2,527 |
2,511 |
2,519 |
2,531 |
2,527 |
2,529 |
2,528 |
2,519 |
2,521 |
Этап 2. Определение размеров классов. Размеры классов определяются так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов R делят на 1,2 или 5 (либо 10, 20, 50; 0,1, 0,2, 0,5 и т.д.), чтобы получилось от 5 до 20 интервалов равной ширины.
Этап 3. Подготовка бланка таблицы частот. Готовится бланк (табл. 3.5), куда можно занести класс, среднюю точку, отметки частот, частоты и т.д.
Этап 4. Определение границ класса. Определите границы интервалов так, чтобы они включали наименьшее и наибольшее значения и положите их в основу таблицы частот. Сначала определите нижнюю границу первого класса и прибавьте к ней ширину этого класса, чтобы получить границу между первым и вторым классами. Как только вы это сделаете, можно будет удостовериться, что первый класс включает наименьшее значение и что его граничное значение приходится на середину принятой единицы измерения (т.е. на число 5 в следующем десятичном разряде). Далее, продолжая прибавлять найденный интервал к предыдущему значению для получения второй границы, затем третьей и т.д., можно удостовериться, что последний класс включает максимальное значение.
Этап 5.
Вычисление середины класса. Средняя точка класса определяется полусуммой нижней и верхней границ класса.
Этап 6. Получение частот. Прочтите наблюденные значения одно за другим и запишите частоты, приходящиеся на каждый интервал, используя наклонные черточки, сгруппированные по пять.
Этап 7. Возьмите лист бумаги в клеточку, нанесите горизонтальную ось и выберите масштаб на этой оси. Не стоит ориентироваться при этом на интервалы классов, гораздо лучше основываться на единицах измерения данных, беря, например, 10 мм как 10 г. Так делается для удобства сравнений множества гистограмм, описывающих похожие факторы и характеристики, а также для сравнения гистограмм с допусками. На горизонтальной оси с обеих сторон (перед первым интервалом и после последнего) оставьте свободное место, приблизительно равное интервалу.
Этап 8. Разметьте левую вертикальную ось масштабом частот, а на правую (если понадобится) нанесите шкалу относительных частот. Высоту класса с максимальной частотой стоит выбирать так, чтобы она оказалась между 0,5 и 2,0 расстояниями от максимума до минимума на горизонтальной оси.
Таблица 3.5
Таблица частот
|
Порядковый номер |
Класс |
Середина класса |
Подсчет частот |
Частота f |
|
1 2 3 4 5 6 7 8 9 |
2,5005-2,5055 2,5055-2,5105 2,5105-2,5155 2,5155-2,5205 2,5205-2,5255 2,5255-2,5305 2,5305-2,5355 2,5305-2,5405 2,5405-2,5455 |
2,503 2,508 2,513 2,518 2,523 2,528 2,533 2,538 2,543 |
/ //// ///// //// ///// ///// //// ///// ///// ///// ///// //// ///// ///// ///// //// ///// ///// ///// ///// / |
1 4 9 14 22 19 10 5 6 |
|
Итого |
90 |
Этап 9. Нанесение на горизонтальную ось границы классов.
Этап 10. Пользуясь интервалом класса как основанием, постройте прямоугольник, высота которого соответствует частоте этого класса.
Этап 11. Нанесите на график линию, представляющую среднее арифметическое, а также линии, представляющие границы допуска, если они есть.
В завершение укажите происхождение ваших данных (период, в течение которого собирались данные и т.п.), число данных n, среднее арифметическое истандартное отклонение
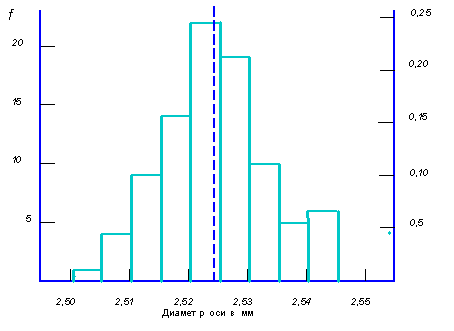
(рис. 3.7).
Рис. 3.7. Гистограмма распределения диаметров осей
Полезную информацию о характере популяции можно получить, взглянув на форму гистограммы. Формы, представленные на рис. 3.8–3.13, типичны. Воспользуемся ими как образцами при анализе процессов.
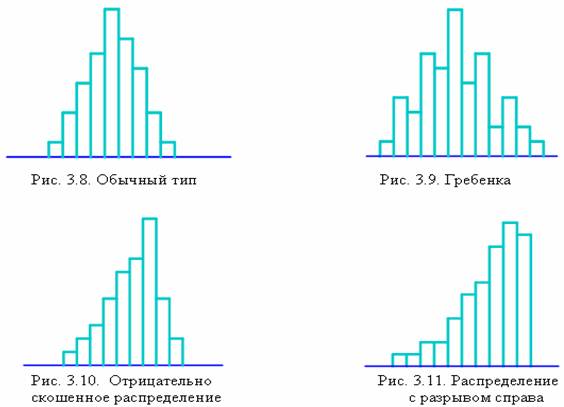
1) Обычный тип (симметричный или колоколообразный) (рис. 3.8). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична. Это именно та форма, которая встречается чаще всего.
2) Гребенка (мультимодальный тип) (рис. 3.9). Классы через один имеют более низкие частоты. Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило округления данных.
3) Положительно скошенное распределение (отрицательно скошенное распределение, рис. 3.10). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична. Такая форма встречается, когда нижняя (верхняя) граница регулируется либо теоретически, либо по значению допуска или когда левое (правое) значение недостижимо.
4) Распределение с обрывом слева (распределение с обрывом справа) (рис. 3.11). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо) и наоборот, медленно вправо (влево). Форма асимметрична. Это одна из тех форм, которые часто встречаются при 100-процентном просеивании изделий из-за плохой воспроизводимости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.
5) Плато (равномерное и прямоугольное распределения) (рис. 3.12). Частоты в
разных классах образуют плато, поскольку все классы имеют более или менее одинаковые ожидаемые частоты с конечными классами. Такая форма встречается в смеси нескольких распределений, имеющих различные средние.
6) Двухпиковый тип (бимодальный тип) (рис. 3.13). В окрестностях центра диапазона данных частота низкая, зато есть по пику с каждой стороны. Такая форма встречается, когда смешиваются два распределения с далеко отстоящими средними значениями.
7) Распределение с изолированным пиком. Наряду с распределением обычного типа, появляется маленький изолированный пик (рис. 3.14). Это форма, которая появляется при наличии малых включений данных из другого распределения, как, скажем, в случае нарушения нормальности процесса, появления ошибки измерения или просто включения данных из другого процесса.
Рис. 3.14. Распределение с изолированным пиком
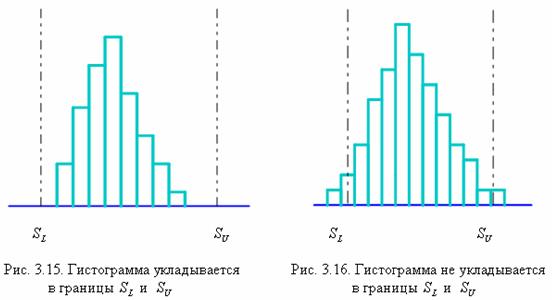
Если имеются верхнее и нижнее пороговые значения (границы и
) для показателя по техническим условиям, то можно нанести их на гистограмму, чтобы выполнить сравнение. Тогда вы увидите, хорошо ли располагается гистограмма внутри границ. Эту картину используют при оценивании популяций. Ниже (рис. 3.15 и рис. 3.16) представлены два возможных варианта.
Когда гистограмма укладывается внутри граници
, требуется только поддержание существующего состояния (рис. 3.14). Если гистограмма не укладывается внутри границ
и
, потребуются меры, направленные на снижение вариации и смещение среднего ближе к центру поля допуска.
Представленные в гистограммах характеристики качества промышленной продукции имеют случайную природу. Как для всякой случайной величины, мерой для представления центра данных служит среднее арифметическое, или математическое ожидание (ожидаемое значение). Когда у нас есть п отдельных значений ,…
среднее таких данных дается выражением
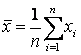
но для множества как целого среднее определяется выражением
,
где P(x)-вероятность случайной величины x.
Величина — среднее арифметическое полученных данных, она называется выборочным средним. Величина
— среднее арифметическое всего множества, которое мы рассматриваем, она называется генеральным средним.
Дисперсия и стандартное отклонение принадлежат к мерам, используемым для выражения степени концентрации данных относительно их центра. Когда у нас есть п отдельных значений ,…
, их дисперсия дается выражением
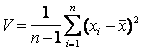
стандартное отклонение –
.
Дисперсия генеральной совокупности получается из формулы
,
а стандартное отклонение, которое представляет собой корень квадратный из дисперсии, обозначается через . Большая дисперсия означает большое рассеяние в данных. Величины V и
— значения, получаемые из имеющихся данных, они называются выборочной дисперсией и выборочным стандартным отклонением, соответственно. Величины
и
— значения, относящиеся к генеральной совокупности, их называют генеральной дисперсией и генеральным стандартным отклонением, соответственно. Вычисление указанных величин выполняют с помощью различных вычислительных средств.
Всякая гистограмма строится на основе некоторого числа данных. Но что произойдет с гистограммой, если мы станем наращивать число данных? Если интервал класса по мере роста числа данных будет все меньше и меньше, то сглаженная кривая распределения частот получится как предел распределения относительных частот. Она как раз и станет представлением для самой генеральной совокупности, поскольку получается из бесконечного числа данных.
Есть множество видов распределений, но самое типичное из них — нормальное распределение. Когда разброс характеристики качества обусловлен суммой большого числа независимых неограниченных ошибок, вызванных различными факторами, то распределение этой характеристики качества во многих случаях получается приблизительно нормальным. Нормальное распределение можно легко узнать по колоколообразной или вершиноподобной форме либо при более подробном описании: а) его наибольшая частота приходится на середину интервала и плавно спадает к его концам
(хвостам), б) оно симметрично. Математически эту кривую можно представить следующим образом:
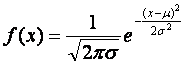
Нормальное распределение имеет два параметра и
. Эти параметры однозначно определяют нормальное распределение, которое поэтому обозначается просто как N(
). Сами параметры имеют следующий смысл:
— центр распределения (среднее арифметическое);
— разброс распределения (стандартное отклонение). Их можно представить графически (рис. 3.17).
Для подсчета вероятностей в нормальном распределении мы его стандартизуем и пользуемся таблицами нормального распределения. Стандартизация — это преобразование случайной величины х к u:
.
Тогда мы получаем стандартную меру u , распределенную как стандартное (нормированное) нормальное распределение . Указанное распределение представлено в справочниках.
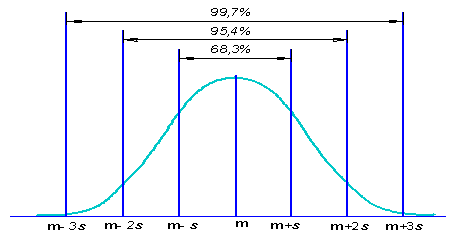
Определим вероятность того, что случайная величина х из распределения N() окажется в пределах
. На рис. 3.17 показаны вероятности для различных значений и. Теоретически нормальная переменная может принимать любое значение от —
до +
. Но из рисунка видно, что уже для и = 3 вероятность составит 99,7 %. Это означает, что на практике мы можем пренебречь шансами, что х окажется за пределами
. Этот факт представляет собой важное правило нормального распределения, называемое правилом трех сигм. Оно служит основанием для определения контрольных пределов в контрольных картах.
Рис. 3.17. Параметры m, и вероятности для нормального распределения
Предпримем исследование воспроизводимости процесса. Оно важно при оценке того, сможет ли процесс пересечь границы поля допуска или нет. Если допустить, что процесс имеет нормальное распределение, то можно сразу же определить процент дефектных изделий, оказавшихся за данными границами допуска при данных параметрах (m, ). Но более полезно оценить процесс с помощью Ср — индекса воспроизводимости процесса. При двусторонних границах допуска
и
,(3.1)
при односторонних границах допуска
.
Оценка процесса с помощью Ср: 1) 1,33 * Ср — вполне удовлетворительно;
2) 1,00 * Ср < 1,33 — адекватно; 3) Ср < 1,00 — неадекватно /5/.
Доступно с лицензией Geostatistical Analyst.
- Частотное распределение
- Суммарная статистика
- Примеры
Инструмент Гистограмма (Histogram) предоставляет одномерное (с одной переменной) описание данных. В диалоговом окне инструмента отображается частотное распределение интересующего набора данных и вычисляется суммарная статистика.
Частотное распределение
Частотное распределение представляет собой столбчатую диаграмму для отображения частотности попадания наблюдаемых значений в определенные интервалы или классы. Можно указать ряд классов с одинаковой шириной, которые будут использоваться в гистограмме. Относительная пропорция данных, которая распределяется по каждому классу, выражается высотой каждого столбца. Например, в гистограмме ниже показано частотное распределение (10 классов) для набора данных.
Суммарная статистика
Важные объекты распределения могут быть суммированы с помощью различных статистик, которые характеризуют их местоположение, распределение и форму.
Показатели расположения
Показатели расположения дают представление о том, где находятся центр и другие части распределения.
- Среднее значение — это среднее арифметическое данных. Среднее представляет собой один из показателей центра распределения.
- Значение медианы соответствует кумулятивной пропорции 0,5. Если данные организованы в порядке возрастания, 50 процентов значений будут находиться ниже медианы, а другие 50 процентов — выше медианы. Медиана предоставляет еще один показатель центра распределения.
- Первая и третья квартили соответствуют кумулятивной пропорции 0,25 и 0,75. Если данные организованы в порядке возрастания, 25 процентов значений будут находиться ниже первой квартили, а еще 25 процентов — выше третьей квартили. Первая и третья квартили являются особыми случаями квантилей. Квантили вычисляются следующим образом:
quantile = (i - 0.5) / Nгде i — упорядоченное i-тое значение данных.
Показатели разброса
Разброс точек вокруг среднего значения — еще одна характеристика отображаемого частотного распределения.
- Дисперсия данных представляет собой среднеквадратическое отклонение всех значений от среднего. Поскольку в нее включаются квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается суммированием квадратических отклонений от среднего и делением суммы на (N-1).
- Стандартное отклонение представляет собой квадратный корень из дисперсии и описывает разброс данных вокруг среднего. Чем меньше дисперсия и стандартное отклонение, тем гуще сконцентрирован кластер измерений вокруг среднего значения.
На диаграмме ниже показаны два распределения с различными стандартными отклонениями. Частотное распределение, представленное черной линией, более переменчиво (с широким разбросом), чем частотное распределение, представленное красной линией. Дисперсия и стандартное отклонение для черного частотного распределения больше, чем для красного.
Показатели формы
Частотное распределение также характеризуется формой.
Коэффициент асимметрии — это показатель симметрии распределения. Для симметричных распределений коэффициент асимметрии равен нулю. Если у распределения есть длинный правый хвост больших значений, то у него положительная асимметрия, а если длинный левый хвост малых значений — то отрицательная. Среднее значение для распределений с положительной асимметрией больше, чем медиана, а для распределений с отрицательной асимметрией — наоборот. На рисунке ниже показано распределение с положительной асимметрией.
Эксцесс основан на размере хвостов распределения и представляет собой показатель вероятности того, что распределение будет создавать выпадающие значения. Эксцесс нормального распределения равен трем. Распределения с относительно толстыми хвостами называются островершинными (лептокуртическими), и у них эксцесс больше трех. Распределения с относительно тонкими хвостами называются плосковершинными (платикуртическими), и у них эксцесс меньше трех. На следующей диаграмме нормальное распределение показано красным цветом, а островершинное (с толстыми хвостом) — черным.
Примеры
С помощью инструмента Гистограмма (Histogram) можно исследовать форму распределения путем прямого наблюдения. Просматривая статистику среднего значения и медианы, можно определить расположение центра распределения. На рисунке внизу обратите внимание на колоколообразное распределение, и так как значения среднего арифметического и медианы близки, это распределение близко к нормальному. Также можно выделить экстремальные значения в хвосте гистограммы и увидеть, как они расположены в пространстве на отображаемой карте.
Если асимметрия данных слишком большая, можно протестировать эффекты трансформации на данных. На этом рисунке показано распределение с асимметрией перед применением преобразования.
К асимметричным данным применяется логарифмическое преобразование, и в этом случае преобразование приближает распределение к нормальному.
Более подробно о преобразованиях, доступных в инструменте Гистограмма (Histogram), см. в разделе Преобразования по методу Box-Cox, арксинуса- и логарифмические.