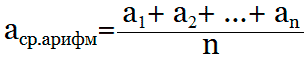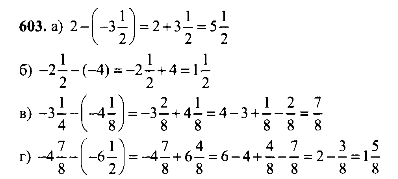Изображение рациональных чисел на координатной оси
Рациональные числа
Необходимо запомнить
ВАЖНО!
При обозначении единичного отрезка следует принимать во внимание знаменатель дроби, которую требуется изобразить на координатной оси. Единичный отрезок должен легко делиться на данный знаменатель, тогда отметить на оси рациональное число будет проще.
Среднее арифметическое
Значение выражения $frac{(a+b)}{2}$ – это не только координата середины отрезка, но и среднее арифметическое чисел $a$ и $b$. Можно находить среднее арифметическое и нескольких чисел, для этого их все нужно сложить, и сумму разделить на количество слагаемых.
Например, нужно найти среднее арифметическое чисел $frac{2}{7}$; $frac{4}{7}$ и $frac{6}{7}$.
Получаем: $(frac{2}{7}+frac{4}{7}+frac{6}{7})div3=frac{12}{7} div 3=frac{4}{7}$
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Работа на координатных осях, нахождение среднего арифметического
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Pril_2»
ЛИСТ САМООЦЕНКИ
ФИ________________________________________
|
Этап урока |
Диапазон баллов |
Самооценка |
|
Проверка д/з |
по 1 баллу за каждый правильный ответ (max – 5 баллов) |
|
|
Сообщение темы и целей урока (Задание 1) |
по 1 баллу за каждую разгаданную анаграмму (max – 3 балла) |
|
|
(Задание 2) |
1 балл – правильное решение спора |
|
|
Актуализация и пробное учебное действие. Фронтальный опрос (Задание 3) |
по 1 баллу за каждый правильный ответ (max – 6 баллов) |
|
|
Этап первичного закрепления с проговариванием во внешней речи |
№ 592 1 балл –правильный ответ |
|
|
№ 607 (а,б) по 1 баллу за каждый правильный ответ (max – 2 балла) |
||
|
Этап включения в систему знаний и повторения (Задание 4) |
1 балл –правильный ответ |
|
|
(Задание 5) |
1 балл –правильный ответ |
|
|
(Задание 6) |
1 балл –правильный ответ |
|
|
АБВГДейка 1 балл –правильный ответ |
||
|
Дополнительно (max – 3 балла) |
||
|
Всего (max – 25 баллов) |
||
|
ОЦЕНКА |
ЛИСТ САМООЦЕНКИ
ФИ________________________________________
|
Этап урока |
Диапазон баллов |
Самооценка |
|
Проверка д/з |
по 1 баллу за каждый правильный ответ (max – 5 баллов) |
|
|
Сообщение темы и целей урока (Задание 1) |
по 1 баллу за каждую разгаданную анаграмму (max – 3 балла) |
|
|
(Задание 2) |
1 балл – правильное решение спора |
|
|
Актуализация и пробное учебное действие. Фронтальный опрос (Задание 3) |
по 1 баллу за каждый правильный ответ (max – 6 баллов) |
|
|
Этап первичного закрепления с проговариванием во внешней речи |
№ 592 1 балл –правильный ответ |
|
|
№ 607 (а,б) по 1 баллу за каждый правильный ответ (max – 2 балла) |
||
|
Этап включения в систему знаний и повторения (Задание 4) |
1 балл –правильный ответ |
|
|
(Задание 5) |
1 балл –правильный ответ |
|
|
(Задание 6) |
1 балл –правильный ответ |
|
|
АБВГДейка 1 балл –правильный ответ |
||
|
Дополнительно (max – 3 балла) |
||
|
Всего (max – 25 баллов) |
||
|
ОЦЕНКА |
Просмотр содержимого документа
«Разработка урока»
урок № дата 31.01.2018г 6 класс
Тема: Изображение рациональных чисел на координатной оси.
Цели: сформировать систему новых понятий, расширить знания учеников за счет включения новых определений, терминов, описаний; научить учащихся отмечать рациональные числа на координатной оси, определять координаты точек и расстояние между ними, находить среднее арифметическое нескольких чисел; сформировать положительную мотивацию к учению посредствам применения мультимедийных технологий.
Задачи:
Обучающие:
-
повторить правила изображения чисел на координатной оси;
-
закрепить умения изображать числа на координатной оси, находить длину отрезка, находить среднее арифметическое чисел.
Развивающие:
-
развивать сообразительность, логическое мышление;
-
развивать навыки самоконтроля и самоанализа;
-
формировать навыки учебного сотрудничества в ходе индивидуальной работы;
-
развивать математическую речь учащихся.
Воспитательные:
-
воспитывать самостоятельность, ответственность, чувство коллективизма;
-
способствовать положительной мотивации учения;
-
воспитывать уважение к предмету, друг к другу.
Тип урока: открытия новых знаний.
Вид урока: мультимедиа-урок
Формы организации деятельности: фронтальная, групповая, индивидуальная.
Оборудование: Математика. 6 класс: учебник для общеобразовательных учреждений [С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин]. – М.: Просвещение.2016. – 256 с.; раздаточный материал: сигнальные карточки, оценочные листы, презентация PowerPoint (pril_1).
Результаты обучения: уметь изображать и определять точки на координатной прямой, уметь делать выводы, взаимопроверка знаний, значительная активизация деятельности учащихся, повышение интереса к знаниям; проводить рефлексию своей деятельности в конце урока.
Ход урока.
-
Организационный момент (1 мин). Учитель здоровается с учащимися, проверяет готовность к уроку. Учащиеся записывают дату в тетрадь. (Слайд 1).
-
Проверка домашнего задания (3 мин).
-
Мотивация (1 мин) (Слайд 2).
Продолжить урок я хочу с вопроса к вам. Как вы думаете, что самое ценное на Земле? (Варианты ответов учеников). Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный учёный Ал-Бируни: «Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит». Пусть эти слова станут девизом нашего урока.
-
Сообщение темы и целей урока (2 мин).
Задание 1.
Решение анаграмм (Слайд 3):
коодиртнаняа ьсо
еоньланоицар олсич
зоибраниеже
— Как они могут быть связаны?
— Каковы цели сегодняшнего урока?
Ученики формулируют тему и цели урока после решения анаграмм. Записывают тему урока в тетрадь. Изображение рациональных чисел на координатной оси. (Слайд 4).
-
Этап актуализации и пробного учебного действия (8 мин)
Задание 2.
Итак, ребята, мы с вами познакомившись с натуральными числами, первое, что научились – это их сравнивать. Узнав, что такое дроби, стали сразу их сравнивать. И теперь, выяснив о существовании рациональных чисел, перед нами встаёт вопрос об их сравнении.
Однажды числа стали спорить: Минус Один считает себя очень маленьким по сравнению с числом –20.
Минус Один: –20 –1, так как долг 20 тыс.руб. больше, чем долг 1тыс.руб. (Слайд 5)
Минус Двадцать: Правильно, –20 –1. Ведь, 200 мороза больше, чем 10 мороза! (Слайд 6)
Нолик: А я не согласен! Наоборот: –1 –20, потому что при температуре –10 больше тепла, чем при температуре–200. (Слайд 7)
Знак плюс: Я тоже считаю, что –1 –20. Ведь, легче отдать долг 1тыс.руб, чем 20 тыс.руб. Лучше иметь 1 литр перерасхода горючего, чем 20 литров. (Слайд 
К Нолику и Знаку Плюс присоединился Знак Равенства.
Знак Равенства: Чем выше находиться число на градуснике, тем теплее. Значит, чем выше число, тем оно больше. (Слайд 9)
Учитель: А вы, дети, как думаете, кто из них прав? (выслушав ответы учащихся, продолжает).
Правы были Нолик, Знак Плюс и Знак Равенства. [2]
Каждый выставляет в оценочный лист балл.
Задание 3. Фронтальный опрос.
(Слайды 10-13)
Учитель задает вопросы:
Из двух чисел меньшим является то, изображение которого на координатной прямой находиться… (ответ: левее, а большим — то, изображение которого находится правее).
Любое положительное число … (ответ: больше нуля),
а любое отрицательное число… (ответ: меньше нуля);
любое отрицательное число… положительного числа (ответ: меньше любого).
Каждый ученик выставляет в оценочный лист балл в соответствии с критериями.
-
Этап выявления места и причины затруднений (5 мин).
На координатной оси можно изобразить не только целые, но и рациональные числа. Например, числу 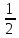
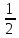
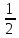
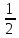
Рациональному числу 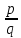
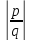
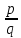
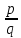
Пример1.
Изобразим на координатной оси число 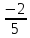
Так как 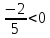
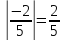
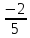
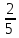
Стр. 115 в учебнике. Пример 2.
(Слайд 17).
Точки, изображающие рациональные числа на координатной оси, называют рациональными точками или точками с рациональными координатами. (Слайд18)
-
Физкультминутка (1,5 мин) (Слайд 19).
Нам пора передохнуть, потянуться и вздохнуть (глубокий вдох и выдох).
Для начала мы с тобой, крутим только головой.
Покрутили головой и усталость вся долой (вращение головой);
Прочь прогоним лень и скуку, разомнем сначала руки (выполняются волнообразные движения кистями рук).
Встали дружно. Наклонились
Раз – вперед, а два – назад.
Потянулись. Выпрямились.
Приседаем быстро, ловко
Здесь видна уже сноровка.
Чтобы мышцы развивать,
Надо много приседать.
Мы на месте снова ходим,
Но от парты не уходим (ходьба на месте).
По местам пора садиться (дети садятся за парты)
И опять начать учиться. [3]
-
Этап построение проекта выхода из создавшейся ситуации (4,5 мин).
Как же найти расстояние между рациональными точками a и b на координатной оси? (Слайд 20)
Если a и b – координаты двух точек и ab, то расстояние между точки равно b – a.
Как найти середину отрезка, соединяющего точки a и b? или
По какой формуле вычисляется середина отрезка AB, если точки имеют координаты A(a) и B(b)? (Ответ: 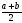
Число 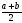
Например, среднее арифметическое чисел -3, 5, -7, 9 равно:
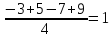
-
Этап первичного закрепления с проговариванием во внешней речи (9 мин)

№ 592
(Слайд 23)
Учащиеся решают задание в тетради и сравнивают с решением на доске.
№ 607 (а,б)
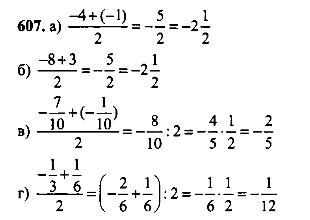
-
Этап включения в систему знаний и повторения (8 мин)
АВГДейка. Вставьте пропущенные буквы в следующие математические термины. (Слайды 29-30)
-
Домашнее задание (1мин)
Выучить правила п. 3.8.
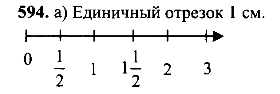
Выполнить № 594(а), 603 (а,б). (Слайд 31). Ученики слушают комментарии к выполнению домашнего задания.
Решения:
-
Этап рефлексии учебной деятельности на уроке (1 мин).
Метод «Цветовая рефлексия деятельности» (Слайд 32)
На столах у вас карточки трёх цветов.
Зеленая карточка.
Я плодотворно работал на уроке.
Мне было понятно всё на уроке.
Желтая карточка.
Я очень стремлюсь, но не всё получилось
Красная карточка.
Я не очень понимал, о чем идет речь.
Закончить урок я хочу такой фразой:
«И вечно вперед, как бы трудно не сталось!
Чтоб уйма заданий вам на радость досталась!
Чтоб гордость и счастье в сердцах бы зажглись,
когда «осенит вас решением» мысль!»
Перевод баллов в оценку:
1 – 1 балл
2 – 2-5 баллов
3 – 6-13 баллов
4 – 14-20 баллов
5 – 21-25 баллов.
3
Просмотр содержимого презентации
«Pril_1»
Третье февраля Классная работа
Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит Ал — Бируни
Задание 1
коодиртнаняа ьсо
еоньланоицар олсич
зоибраниеже
Изображение рациональных чисел на координатной оси

Задание 2
– 20 – 1,
так как долг 20 тыс.руб. больше, чем долг 1 тыс.руб.

– 20 – 1,
ведь,
20 0 мороза больше, чем 1 0 мороза!

– 1 – 20,
потому что при температуре – 1 0 больше тепла, чем при температуре –20 0

– 1 – 20
Ведь, легче отдать долг
1 тыс.руб, чем 20 тыс.руб.
Лучше иметь 1 литр перерасхода горючего, чем 20 литров.

– 1 – 20
Чем выше находиться число на градуснике, тем теплее. Значит, чем выше число, тем оно больше.
Фронтальный опрос :
Задание 3
- Как называется число, которое может быть представлено в виде дроби ,
где p – целое число, а q – целое число , (q0)
Рациональное число.
2 . Является ли :
а) натуральное число рациональным числом?
б) целое число рациональным число?
в) обыкновенная дробь рациональным числом?
Да.
Да.
Да.
3. Как называются числа, в состав которых входит целое число и правильная дробь?
Смешанные дроби.
4. Какие арифметические действия можно выполнять со смешанными дробями?
Сложение, вычитание, умножение и деление.
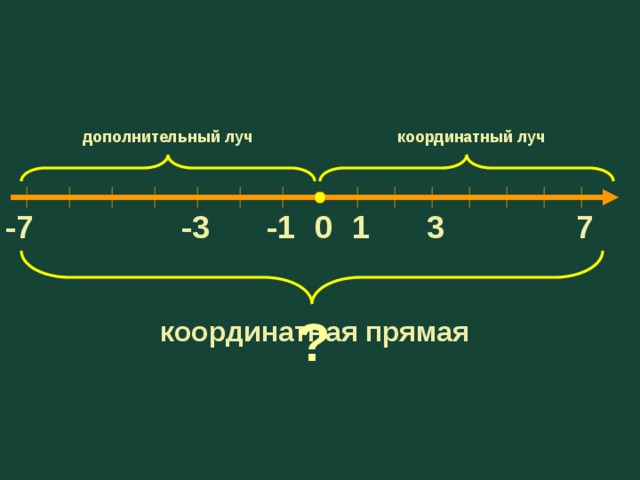
дополнительный луч
координатный луч
-7
-1
-3
7
3
1
0
?
координатная прямая
F
С
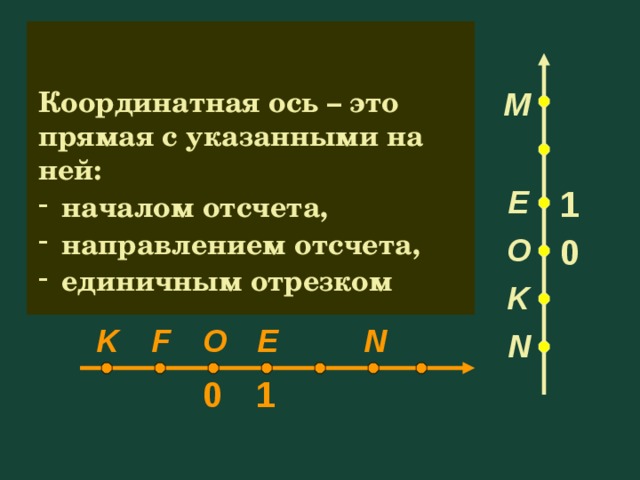
Координатная ось – это прямая с указанными на ней:
M
- началом отсчета,
- направлением отсчета,
- единичным отрезком
D
В
E
1
А
O
0
K
K
N
E
O
F
N
0
1
- Рациональному числу на координатной оси соответствует точка, находящаяся на расстоянии от точки 0 на положительной полуоси, если , и на отрицательной полуоси, если .
13
Составим алгоритм построения на координатной оси точки А( )
- провести координатную ось, выбрав на ней начало отсчета и «удобный» единичный отрезок;
- так как и , отложить на этой координатной оси влево от начала отсчета отрезок, равный двум единицам (на отрицательной полуоси);
- отложить влево от точки -2 отрезок, равный .
А
-2
1
0
-2
-1
- Точки, изображающие рациональные числа на координатной оси называются рациональными точками или точками с рациональными координатами
Физкультминутка
Расстояние между
рациональными точками с координатами
a и b
Если a и b – координаты двух точек и a b, то расстояние между точками равно
b – a.
Середина отрезка AB , если точки имеют координаты a и b, а точка С(с) – середина АВ
с=
Среднее арифметическое нескольких чисел
- Например:
- Пусть даны точки А и В . Найти длину отрезка АВ, середину отрезка АВ
№ 592,
№ 607 (а,б)
O
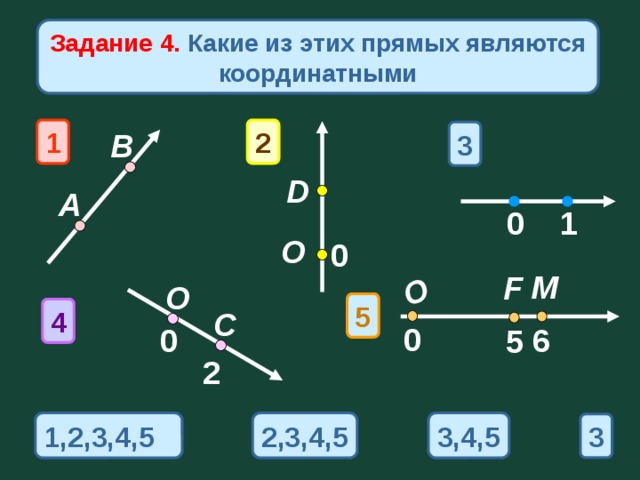
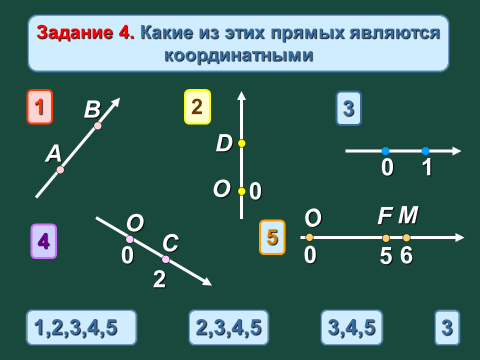
Задание 4. Какие из этих прямых являются координатными
1
2
3
В
D
А
1
0
O
0
M
F
O
5
4
C
0
6
0
5
2
1,2,3,4,5
3,4,5
2,3,4,5
3
молодцы!
ОШИБКА
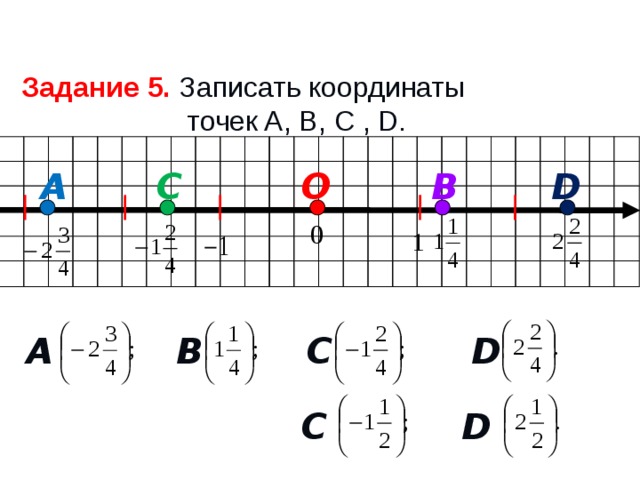
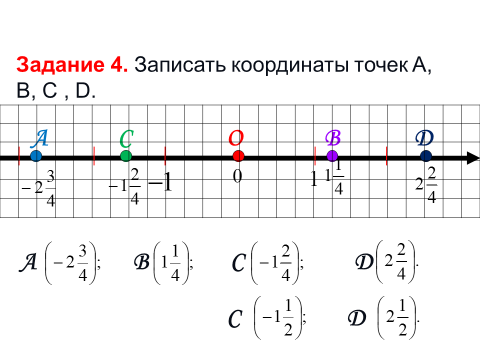
Задание 5. Записать координаты
точек A, B, C , D.
A
B
C
D
O
A
B
C
D
C
D
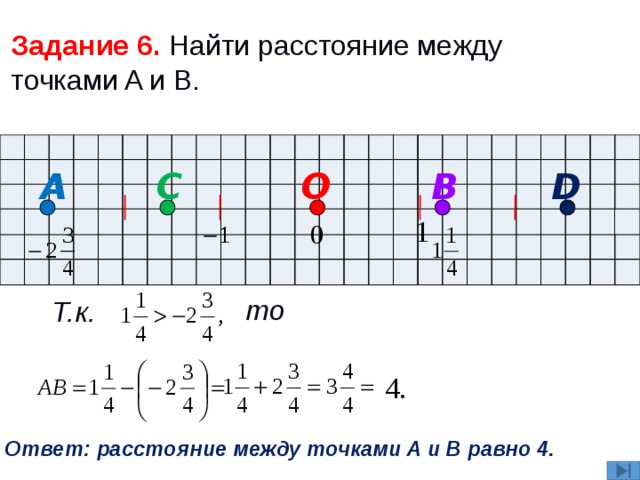
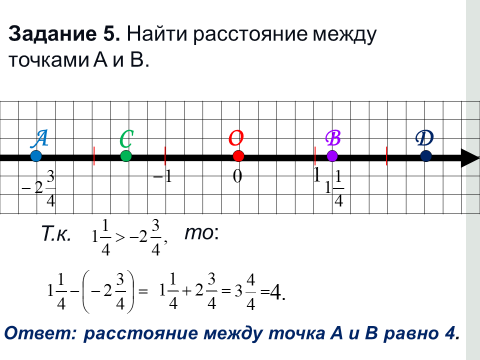
Задание 6. Найти расстояние между точками A и B.
B
D
C
O
A
то
Т.к.
Ответ: расстояние между точками A и B равно 4 .
АБВГДейка
_трицательное ч_сло
К__рдинатная пр_мая
Н_чало _тсчета
Изм_рение в_личин
Ед_ничный _трезок
П_л_жительное ч_сло
Ра__тояние
К__рдината точки
АБВГДейка
О трицательное ч и сло
К оо рдинатная пр я мая
Н а чало о тсчета
Изм е рение в е личин
Ед и ничный о трезок
П о л о жительное ч и сло
Ра сс тояние
К оо рдината точки
Домашнее задание
Выучить правила п. 3.8.
Выполнить № 594(а), 603 (а,б)
Я не очень понимал, о чем идет речь.
Я очень стремлюсь, но не всё получилось
Я плодотворно работал на уроке.
Мне было понятно всё на уроке
1 —
1
2 —
2-5
3 —
6-13
4 —
14-20
5 —
21-25
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
-
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
-
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.
-
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
-
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
-
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
-
Найдите объем и медиану числового ряда.
9; 7; 1; 1; 11; 5; 1.
-
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:
I II III IV V VI VII 37 34 35 32 36 33 38 Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
-
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
-
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.
-
Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
-
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
-
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.
Как найти среднее арифметическое
Это пригодится не только для решения школьных задачек, но и при различных подсчётах в обычной жизни.
Что такое среднее арифметическое
Среднее арифметическое — это сумма всех чисел в ряду, разделённая на количество слагаемых.
Как найти среднее арифметическое
Например, перед вами ряд чисел «1, 2, 3, 4, 5, 6». Как следует из определения, чтобы узнать среднее арифметическое, нужно сложить все данные вам числа, а потом разделить получившийся результат на количество этих чисел. В приведённом примере — на шесть. Вот как это выражается формулой:
Допустим, вам нужно определить среднее арифметическое для чисел 4, 5 и 6. Складываем 4 + 5 + 6 = 15. Теперь делим 15 на 3 и получаем 5. Это и будет среднее арифметическое.
Таким же образом оно подсчитывается для десятичных и обыкновенных дробей.
Пример расчёта среднего арифметического для обыкновенных дробей будет выглядеть так:
А это пример, как найти среднее арифметическое для десятичных дробей:
Как это пригодится в жизни
Среднее арифметическое помогает описать множество цифровых значений всего одним числом. Например, по выше представленной формуле можно подсчитать усреднённую цену на товар или среднюю зарплату сотрудников в одной организации, среднюю посещаемость заведения. Это полезно для ведения статистики и в случаях, когда нужно сжато изложить информацию.
Читайте также 🧐
- 7 причин полюбить математику
- 7 способов найти площадь прямоугольника
- 6 способов посчитать проценты от суммы с калькулятором и без
- Как освоить устный счёт школьникам и взрослым
- 10 увлекательных задач от советского математика